Correlation between Buoyancy Flux, Dissipation and Potential Vorticity in Rotating Stratified Turbulence
Abstract
1. Introduction
2. Equations and Numerical Settings
3. Scaling Properties of Rotating Stratified Turbulent Flows
4. The Dynamical Behavior of Potential Vorticity
4.1. Global Properties
4.2. Joint Probability Distribution Functions
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DNS | Direct Numerical Simulations |
| HIT | Homogeneous Isotropic Turbulence |
| KH | Kelvin-Helmoltz |
| MHD | Magnetohydrodynamic |
| Probability Distribution Functions | |
| QG | Quasi-Geostrophic |
| RST | Rotating Stratified Turbulence |
References
- Peltier, W.; Clark, T. Nonlinear mountain waves in two and three spatial dimensions. Q. J. R. Meteorol. Soc. 1983, 109, 527–548. [Google Scholar] [CrossRef]
- Vallis, G.; Maltrud, M. Generation of mean flows and jets on a beta-plane and over topography. J. Phys. Oceanogr. 1993, 23, 1346–1362. [Google Scholar] [CrossRef]
- Winters, K.; Armi, L. Topographic control of stratified flows: Upstream jets, blocking and isolating layers. J. Fluid Mech. 2014, 753, 80–103. [Google Scholar] [CrossRef]
- Rhines, P. Geostrophic Turbulence. Ann. Rev. Fluid Mech. 1979, 11, 401–441. [Google Scholar] [CrossRef]
- Kunze, E.; Llewellyn-Smith, S. The role of small-scale topography in turbulent mixing of the global ocean. Oceanography 2004, 17, 55–64. [Google Scholar] [CrossRef]
- Maffioli, A.; Davidson, P.; Dalziel, S.; Swaminathan, N. The evolution of a stratified turbulent cloud. J. Fluid Mech. 2014, 739, 229–253. [Google Scholar] [CrossRef]
- Afanasyev, Y.D.; Peltier, W. The Three-Dimensionalization of Stratified Flow over Two-Dimensional Topography. J. Atmos. Sci. 1998, 55, 19–39. [Google Scholar] [CrossRef]
- Geyer, W.; Lavery, A.; Scully, M.; Trowbridge, J. Mixing by shear instability at high Reynolds number. Geophys. Res. Lett. 2010, 37, L22607. [Google Scholar] [CrossRef]
- Fritts, D.; Wang, L.; Baumgarten, G.; Miller, A.; Geller, M.; Jones, G.; Limon, M.; Chapman, D.; Didier, J.; Kjellstrand, C.B.; et al. High-resolution observations and modeling of turbulence sources, structures, and intensities in the upper mesosphere. J. Atmos. Sol. Terr. Phys. 2017, 162, 57–78. [Google Scholar] [CrossRef]
- Mater, B.; Venayagamoorthy, S. The quest for an unambiguous parameterization of mixing efficiency in stably stratified geophysical flows. Geophys. Res. Lett. 2014, 41, 4646–4653. [Google Scholar] [CrossRef]
- Mellor, G.; Yamada, T. Development of a Turbulence Closure Model for Geophysical Fluid Problems. Rev. Geophys. Space Phys. 1982, 20, 851–875. [Google Scholar] [CrossRef]
- Lozovatsky, I.; Fernando, H. Mixing efficiency in natural flows. Philos. Trans. A 2013, 371, 20120213. [Google Scholar] [CrossRef]
- Brunner-Suzuki, A.M.; Sundermeyer, M.; Lelong, M.P. Upscale Energy Transfer by the Vortical Mode and Internal waves. J. Phys. Oceanogr. 2014, 44, 2446–2469. [Google Scholar] [CrossRef]
- Pouquet, A.; Marino, R. Geophysical turbulence and the duality of the energy flow across scales. Phys. Rev. Lett. 2013, 111, 234501. [Google Scholar] [CrossRef] [PubMed]
- Marino, R.; Pouquet, A.; Rosenberg, D. Resolving the paradox of oceanic large-scale balance and small-scale mixing. Phys. Rev. Lett. 2015, 114, 114504. [Google Scholar] [CrossRef] [PubMed]
- Klymak, J.M.; Pinkel, R.; Rainville, L. Direct Breaking of the Internal Tide near Topography: Kaena Ridge, Hawaii. J. Phys. Oceanogr. 2008, 38, 380–399. [Google Scholar] [CrossRef]
- Rosenberg, D.; Pouquet, A.; Marino, R.; Mininni, P. Evidence for Bolgiano-Obukhov scaling in rotating stratified turbulence using high-resolution direct numerical simulations. Phys. Fluids 2015, 27, 055105. [Google Scholar] [CrossRef]
- Pouquet, A.; Rosenberg, D.; Marino, R.; Herbert, C. Scaling laws for mixing and dissipation in unforced rotating stratified turbulence. J. Fluid Mech. 2018, 844, 519–545. [Google Scholar] [CrossRef]
- Pouquet, A.; Rosenberg, D.; Marino, R. Linking dissipation, anisotropy and intermittency in rotating stratified turbulence. Phys. Fluids 2019, 31, 105116. [Google Scholar] [CrossRef]
- Rosenberg, D.; Marino, R.; Herbert, C.; Pouquet, A. Variations of characteristic time-scales in rotating stratified turbulence using a large parametric numerical study. Eur. Phys. J. E 2016, 39, 8. [Google Scholar] [CrossRef] [PubMed]
- Craske, J.; Salizzoni, P.; van Reeuwijk, M. The turbulent Prandtl number in a pure plume is 3/5. J. Fluid Mech. 2017, 822, 774–790. [Google Scholar] [CrossRef]
- Rosenberg, D.; Mininni, P.D.; Reddy, R.; Pouquet, A. GPU Parallelization of a Hybrid Pseudospectral Geophysical Turbulence Framework Using CUDA. Atmosphere 2020, 11, 178. [Google Scholar] [CrossRef]
- Fontana, M.; Bruno, O.P.; Mininni, P.D.; Dmitruk, P. Fourier continuation method for incompressible fluids with boundaries. Comput. Phys. Commun. 2020, 256, 107482. [Google Scholar] [CrossRef]
- Dritschel, D.; McKiver, W. Effect of Prandtl’s ratio in geophysical turbulence. J. Fluid Mech. 2015, 777, 569–590. [Google Scholar] [CrossRef]
- Rorai, C.; Mininni, P.; Pouquet, A. Turbulence comes in bursts in stably stratified flows. Phys. Rev. E 2014, 89, 043002. [Google Scholar] [CrossRef]
- Feraco, F.; Marino, R.; Pumir, A.; Primavera, L.; Mininni, P.; Pouquet, A.; Rosenberg, D. Vertical drafts and mixing in stratified turbulence: Sharp transition with Froude number. Eur. Phys. Lett. 2018, 123, 44002. [Google Scholar] [CrossRef]
- Marino, R.; Feraco, F.; Primavera, L.; Pumir, A.; Pouquet, A.; Rosenberg, D. Turbulence generation by large-scale extreme drafts and the modulation of local energy dissipation in stratified flow. Phys. Rev. Lett. 2021. submitted. [Google Scholar]
- Ishihara, T.; Gotoh, T.; Kaneda, Y. Study of High Reynolds Number Isotropic Turbulence by Direct Numerical Simulation. Ann. Rev. Fluid Mech. 2009, 41, 165–180. [Google Scholar] [CrossRef]
- Van Haren, H.; Gostiaux, L. Where large deep-ocean waves break. Geophys. Res. Lett. 2015, 42, 2351–2357. [Google Scholar] [CrossRef]
- Lopez, D.H.; Rabbani, M.R.; Crosbie, E.; Raman, A.; Arellano, A.F.; Sorooshian, A. Frequency and Character of Extreme Aerosol Events in the Southwestern United States: A Case Study Analysis in Arizona. Atmosphere 2016, 7, 1. [Google Scholar] [CrossRef]
- Gotoh, T. Probability functions in steady-state Burgers turbulence. Phys. Fluids 1999, 11, 2143–2149. [Google Scholar] [CrossRef]
- Kim, E.J.; Anderson, J. Structure based statistical theory of intermittency. Phys. Plasmas 2008, 15, 114506. [Google Scholar] [CrossRef]
- Gurarie, V.; Migdal, A. Instantons in the Burgers equation. Phys. Rev. E 1996, 54, 4908–4914. [Google Scholar] [CrossRef]
- Falkovich, G.; Kolokolov, I.; Lebedev, V.; Migdal, A. Instantons and intermittency. Phys. Rev. E 1996, 54, 4896–4907. [Google Scholar] [CrossRef] [PubMed]
- Grafke, T.; Grauer, R.; Schafer, T. The instanton method and its numerical implementation in fluid mechanics. J. Phys. A 2015, 48, 332015. [Google Scholar] [CrossRef]
- Grigorio, L.S.; Bouchet, F.; Pereira, R.M.; Chevillard, L. Instantons in a Lagrangian model of turbulence. J. Phys. A 2017, 50, 055001. [Google Scholar] [CrossRef]
- Migdal, A. Clebsch Confinement and Instantons in Turbulence. Int. J. Mod. Phys. A 2020, 35, 2030018. [Google Scholar] [CrossRef]
- Bretherton, F.P. A note on Hamilton’s principle for perfect fluids. J. Fluid Mech. 1970, 44, 19–31. [Google Scholar] [CrossRef]
- Salmon, R. Hamiltonian fluid mechanics. Ann. Rev. Fluid Mech. 1988, 20, 225–256. [Google Scholar] [CrossRef]
- Herbert, C.; Pouquet, A.; Marino, R. Restricted Equilibrium and the Energy Cascade in Rotating and Stratified Flows. J. Fluid Mech. 2014, 758, 374–406. [Google Scholar] [CrossRef]
- Herbert, C.; Marino, R.; Pouquet, A.; Rosenberg, D. Waves and vortices in the inverse cascade regime of rotating stratified turbulence with or without rotation. J. Fluid Mech. 2016, 806, 165–204. [Google Scholar] [CrossRef][Green Version]
- Müller, P. Ertel’s potential vorticity theorem in physical oceanography. Rev. Geophys. 1995, 33, 67–97. [Google Scholar] [CrossRef]
- McIntyre, M.; Palmer, T. Breaking gravity waves in the stratosphere. Nature 1983, 305, 593–600. [Google Scholar] [CrossRef]
- Kurgansky, M.; Tatarskaya, M. The Potential Vorticity Concept in Meteorology: A Review. Izv. Atmos. Ocean. Phys. 1987, 23, 587–606. [Google Scholar]
- McIntyre, M.E. Isentropic Distributions of Potential Vorticity and their Relevance to Tropical Cyclone Dynamics. In Tropical Cyclone Disasters: Proceedings of ISCU/WMO International Symposium; Lighthill, J., Zheng, Z., Holland, G., Emanuel, K., Eds.; Beijing University Press: Beijing, China, 1993; pp. 143–156. [Google Scholar]
- Kolmogorov, A.N. Dissipation of energy in locally isotropic turbulence. Dokl. Akad. Nauk SSSR 1941, 32, 16–18, [English translation in Proc. Roy. Soc. Lond. A 1991, 434, 15–17]. [Google Scholar]
- Herring, J.R.; Kerr, R.; Rotunno, R. Ertel’s Potential Vorticity in Unstratified Turbulence. J. Atmos. Sci. 1994, 51, 35–47. [Google Scholar] [CrossRef]
- Wijesekera, H.W.; Dillon, T.M. Shannon entropy as an indicator for turbulent overturns in the oceanic thermocline. J. Geophys. Res. 1997, 102, 3279–3291. [Google Scholar] [CrossRef]
- Liu, H.L. On the large wind shear and fast meridional transport above the mesopause. Geophys. Res. Lett. 2007, 34, L08815. [Google Scholar] [CrossRef]
- Mare, F.D.; Sorriso-Valvo, L.; Retinò, A.; Malara, F.; Hasegawa, H. Evolution of Turbulence in the Kelvin-Helmholtz Instability in the Terrestrial Magnetopause. Atmosphere 2019, 10, 561. [Google Scholar] [CrossRef]
- Bartello, P. Geostrophic adjustment and inverse cascade in rotating stratified turbulence. J. Atmos. Sci. 1995, 52, 4410–4428. [Google Scholar] [CrossRef]
- Aluie, H.; Kurien, S. Joint downscale fluxes of energy and potential enstrophy in rotating stratified Boussinesq flows. Eur. Phys. Lett. 2011, 96, 44006. [Google Scholar] [CrossRef]
- Waite, M. Potential enstrophy in stratified turbulence. J. Fluid Mech. 2013, 722, R4. [Google Scholar] [CrossRef]
- Sujovolsky, N.; Mininni, P. From waves to convection and back again: The phase space of stably stratified turbulence. Phys. Rev. F 2020, 5, 064802. [Google Scholar] [CrossRef]
- Bos, W.J.; Shao, L.; Bertoglio, J. Spectral imbalance and the normalized dissipation rate of turbulence. Phys. Fluids 2007, 19. [Google Scholar] [CrossRef]
- Sreenivasan, K.R. On the scaling of the turbulence energy dissipation rate. Phys. Fluids 1984, 27, 1048–1049. [Google Scholar] [CrossRef]
- Sreenivasan, K.R. An update on the energy dissipation rate in isotropic turbulence. Phys. Fluids 1998, 10, 528–529. [Google Scholar] [CrossRef]
- Burattini, P.; Lavoie, P.; Antonia, R.A. On the normalized turbulent energy dissipation rate. Phys. Fluids 2005, 17, 098103. [Google Scholar] [CrossRef]
- Goto, S.; Vassilicos, J.C. The dissipation rate coefficient of turbulence is not universal and depends on the internal stagnation point structure. Phys. Fluids 2009, 21, 035104. [Google Scholar] [CrossRef]
- Abe, H.; Antonia, R.A. Scaling of normalized mean energy and scalar dissipation rates in a turbulent channel flow. Phys. Fluids 2011, 23, 055104. [Google Scholar] [CrossRef]
- Sujovolsky, N.; Mininni, P.; Pouquet, A. Generation of turbulence through frontogenesis in sheared stratified flows. Phys. Fluids 2018, 30, 086601. [Google Scholar] [CrossRef]
- Mihelich, M.; Faranda, D.; Paillard, D.; Dubrulle, B. Is turbulence a state of maximum entropy. Entropy 2017, 19, 154. [Google Scholar] [CrossRef]
- Davies, P. Experiments on Taylor columns and in rotating stratified fluids. J. Fluid Mech. 1972, 54, 691–717. [Google Scholar] [CrossRef]
- Hassanzadeh, P.; Marcus, P.; LeGal, P. The universal aspect ratio of vortices in rotating stratified flows: Theory and simulation. J. Fluid Mech. 2012, 706, 46–57. [Google Scholar] [CrossRef]
- Waite, M.; Bartello, P. The transition from geostrophic to stratified turbulence. J. Fluid Mech. 2006, 568, 89–108. [Google Scholar] [CrossRef]
- Shakespeare, C.; Taylor, J. A generalized mathematical model of geostrophic adjustment and frontogenesis: Uniform potential vorticity. J. Fluid Mech. 2013, 736, 366–413. [Google Scholar] [CrossRef]
- Gibbon, J.; Holm, D. The dynamics of the gradient of potential vorticity. J. Phys. A 2010, 43, 172001. [Google Scholar] [CrossRef]
- Pieri, A.; Godeferd, F.S.; Cambon, C.; Dubrulle, B.; Thalabard, S. Cross-Helicity in Rotating Homogeneous Shear-Stratified Turbulence. Phys. Rev. Lett. 2014, 112, 114501. [Google Scholar] [CrossRef]
- Pieri, A.B.; Godeferd, F.S.; Cambon, C.; Salhi, A. Non-geostrophic instabilities of an equilibrium baroclinic state. J. Fluid Mech. 2013, 734, 535–566. [Google Scholar] [CrossRef]
- Rorai, C.; Rosenberg, D.; Pouquet, A.; Mininni, P. Helicity dynamics in stratified turbulence in the absence of forcing. Phys. Rev. E 2013, 87, 063007. [Google Scholar] [CrossRef]
- Bewley, G.; Chang, K.; Bodenschatz, E. On integral length scales in anisotropic turbulence. Phys. Fluids 2012, 24, 061702. [Google Scholar] [CrossRef]
- Brethouwer, G. The effect of rotation on rapidly sheared homogeneous turbulence and passive scalar transport. Linear theory and direct numerical simulation. J. Fluid Mech. 2005, 542, 305–342. [Google Scholar] [CrossRef]
- Ozmidov, R. On the turbulent exchange in a stably stratified ocean. Izv. Acad. Sci. USSR Atmos. Ocean. Phys. 1965, 1, 853–860. [Google Scholar]
- Mininni, P.; Rosenberg, D.; Pouquet, A. Isotropization at small scale of rotating helically driven turbulence. J. Fluid Mech. 2012, 699, 263–279. [Google Scholar] [CrossRef]
- Forster, D.; Nelson, D.; Stephen, M. Long-time tails and the large-eddy behavior of a randomly stirred fluid. Phys. Rev. Lett. 1977, 36, 867–870. [Google Scholar] [CrossRef]
- Galperin, B.; Sukoriansky, S.; Anderson, P.S. On the critical Richardson number in stably stratified turbulence. Atmos. Sci. Lett. 2007, 8, 65–69. [Google Scholar] [CrossRef]
- Salehipour, H.; Peltier, W. Diapycnal diffusivity, turbulent Prandtl number and mixing efficiency in Boussinesq stratified turbulence. J. Fluid Mech. 2015, 775, 464–500. [Google Scholar] [CrossRef]
- Zilitinkevich, S.S.; Elperin, T.; Kleeorin, N.; Rogachevskii, I.; Esau, I.; Mauritsen, T.; Miles, M.W. Turbulence energetics in stably stratified geophysical flows: Strong and weak mixing regimes. Q. J. R. Meteorol. Soc. 2008, 134, 793–799. [Google Scholar] [CrossRef]
- Garnier, M.; Alemany, A.; Sulem, P.L.; Pouquet, A. Influence of an external magnetic field on large scale Reynolds number MHD turbulence. J. Mécanique 1981, 20, 233–251. [Google Scholar]
- Yousef, T.; Brandenburg, A.; Rüdiger, G. Turbulent magnetic Prandtl number and magnetic diffusivity quenching from simulations. Astron. Astrophys. 2003, 411, 321–327. [Google Scholar] [CrossRef]
- Clark di Leoni, P.; Mininni, P.D. Absorption of waves by large scale winds in stratified turbulence. Phys. Rev. E 2015, 91, 033015. [Google Scholar] [CrossRef] [PubMed]
- Lindborg, E. The effect of rotation on the mesoscale energy cascade in the free atmosphere. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef]
- Marino, R.; Rosenberg, D.; Herbert, C.; Pouquet, A. Interplay of waves and eddies in rotating stratified turbulence and the link with kinetic-potential energy partition. EuroPhys. Lett. 2015, 112, 49001. [Google Scholar] [CrossRef][Green Version]
- Meneguzzi, M.; Politano, H.; Pouquet, A.; Zolver, M. A sparse-mode spectral method for the simulations of turbulent flows. J. Comput. Phys. 1996, 123, 32–44. [Google Scholar] [CrossRef]
- Lanotte, A.S.; Benzi, R.; Malapaka, S.K.; Toschi, F.; Biferale, L. Turbulence on a Fractal Fourier Set. Phys. Rev. Lett. 2015, 115, 264502. [Google Scholar] [CrossRef] [PubMed]
- Ling, J.; Kurzawski, A.; Templeton, J. Reynolds averaged turbulence modelling using deep neural networks with embedded invariance. J. Fluid Mech. 2016, 807, 155–166. [Google Scholar] [CrossRef]
- Kutz, J. Deep learning in fluid dynamics. J. Fluid Mech. 2017, 814, 1–4. [Google Scholar] [CrossRef]


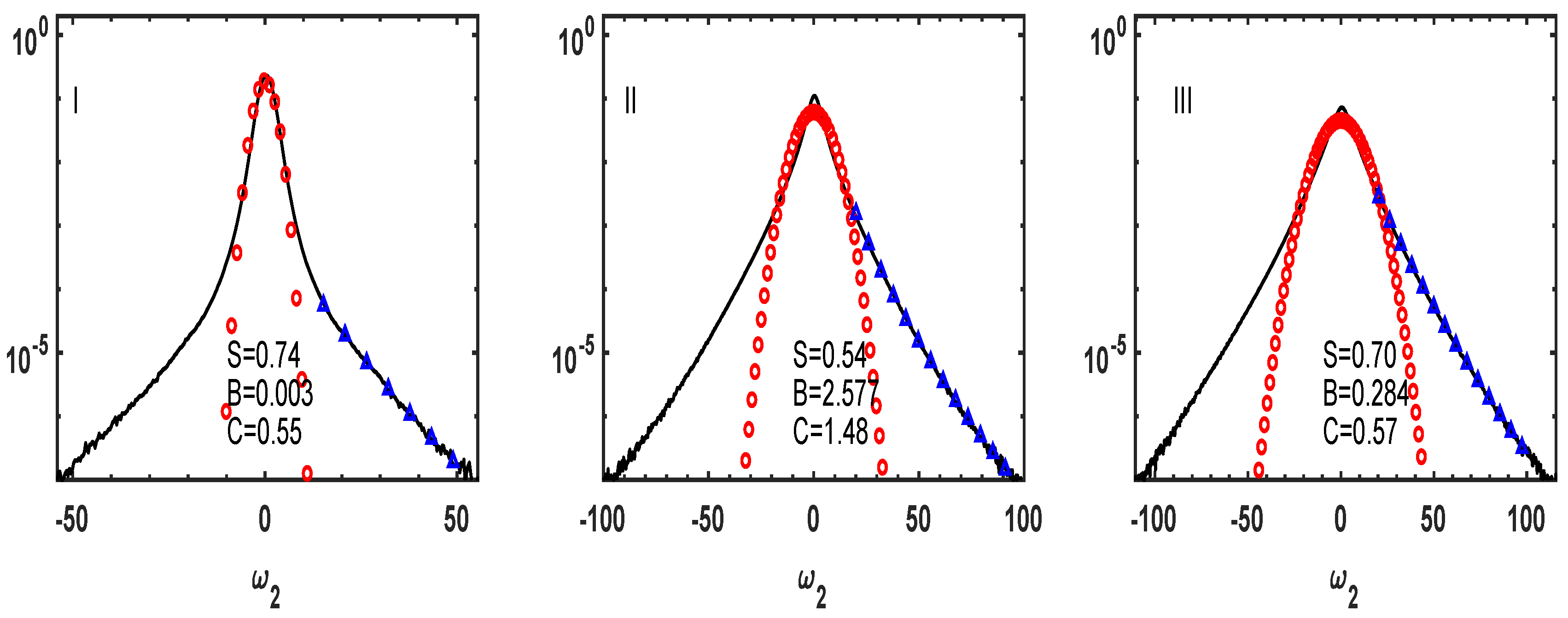



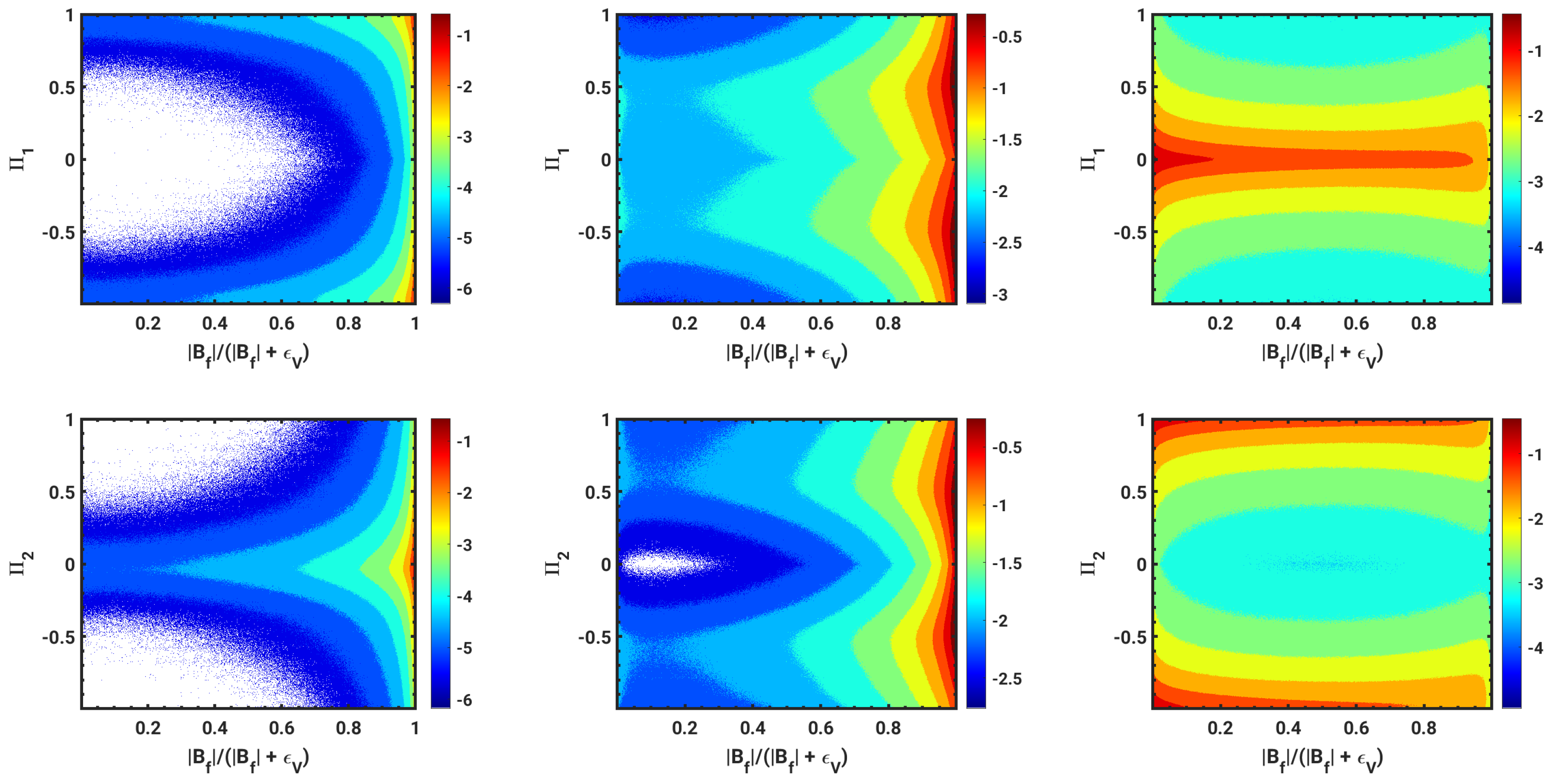
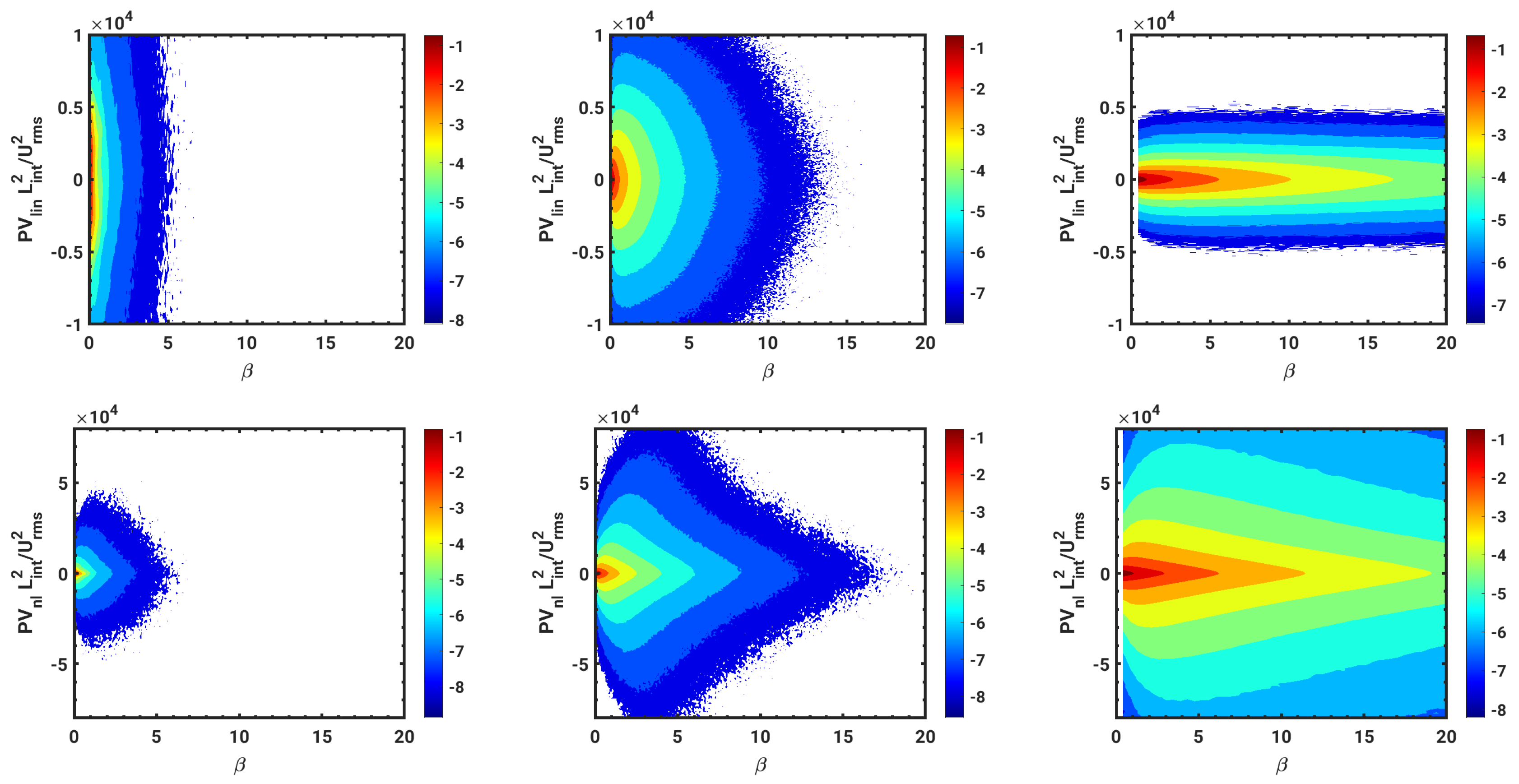
| Run ID | |||||
|---|---|---|---|---|---|
| rI (Run 5 in [18]) | 0.0073 | 0.225 | 30.7 | 13,945 | 0.75 |
| rII (Run 32 in [18]) | 0.073 | 3.04 | 41.7 | 12,211 | 65.2 |
| rIII (Run 58 in [18]) | 0.89 | 2.2 | 2.5 | 4708 | 3760 |
| r4k ( grid points) [17] | 0.024 | 0.1 | 5 | 54,000 | 32 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosenberg, D.; Pouquet, A.; Marino, R. Correlation between Buoyancy Flux, Dissipation and Potential Vorticity in Rotating Stratified Turbulence. Atmosphere 2021, 12, 157. https://doi.org/10.3390/atmos12020157
Rosenberg D, Pouquet A, Marino R. Correlation between Buoyancy Flux, Dissipation and Potential Vorticity in Rotating Stratified Turbulence. Atmosphere. 2021; 12(2):157. https://doi.org/10.3390/atmos12020157
Chicago/Turabian StyleRosenberg, Duane, Annick Pouquet, and Raffaele Marino. 2021. "Correlation between Buoyancy Flux, Dissipation and Potential Vorticity in Rotating Stratified Turbulence" Atmosphere 12, no. 2: 157. https://doi.org/10.3390/atmos12020157
APA StyleRosenberg, D., Pouquet, A., & Marino, R. (2021). Correlation between Buoyancy Flux, Dissipation and Potential Vorticity in Rotating Stratified Turbulence. Atmosphere, 12(2), 157. https://doi.org/10.3390/atmos12020157







