Long-Term Variations of Global Solar Radiation and Atmospheric Constituents at Sodankylä in the Arctic
Abstract
1. Introduction
2. Data and Methodology
2.1. Observations and Data Selection
2.2. Model Formulation, Development and Evaluation
3. Results
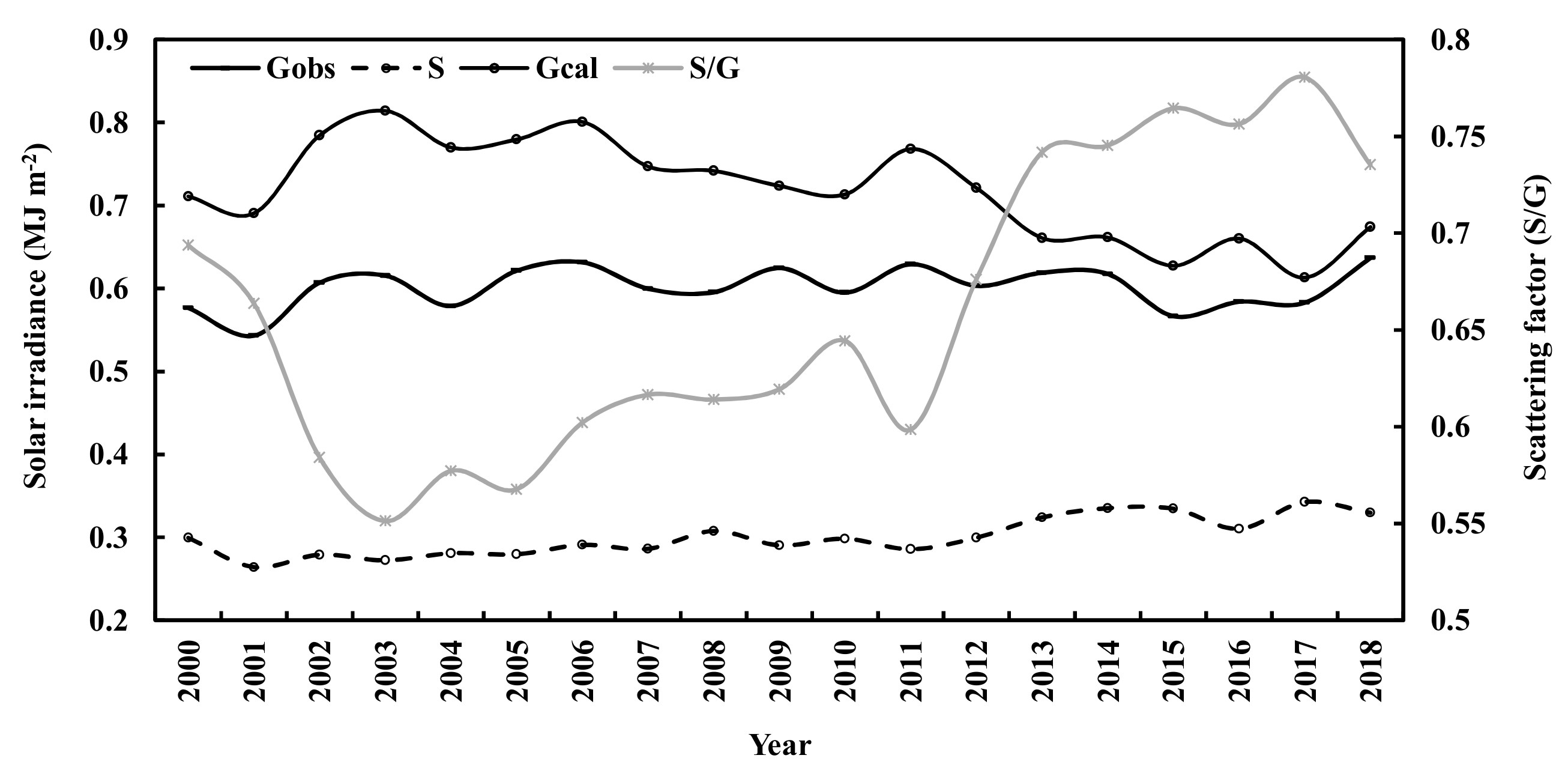
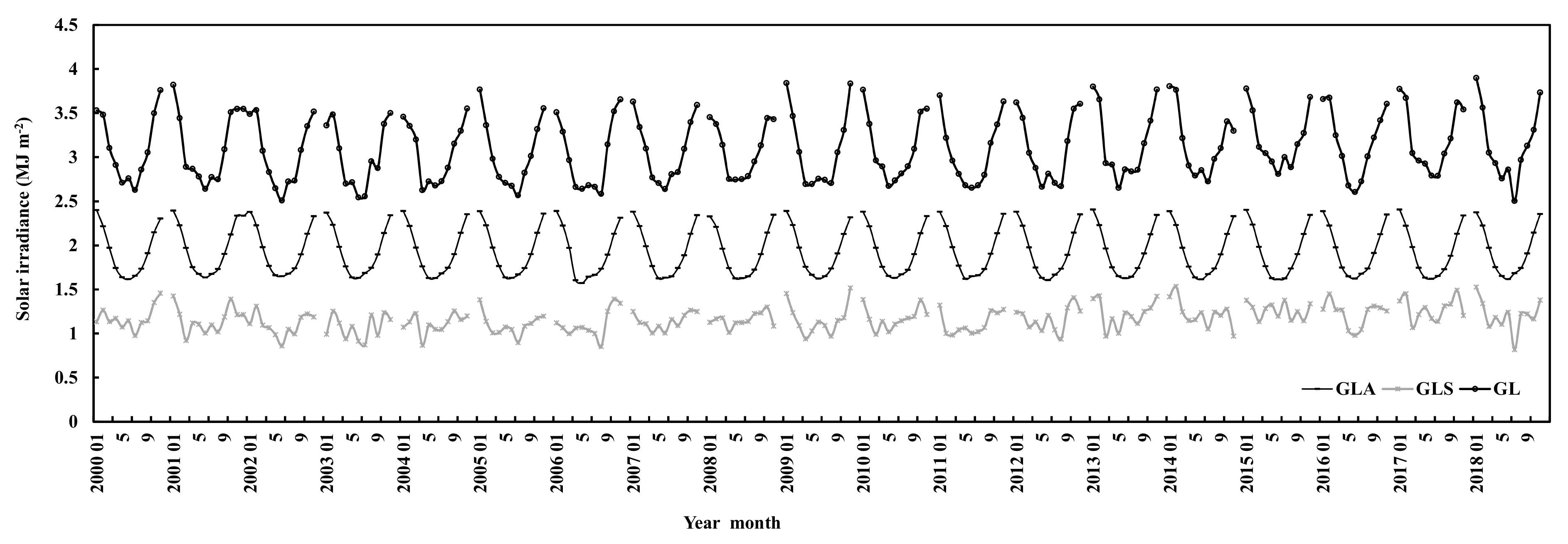
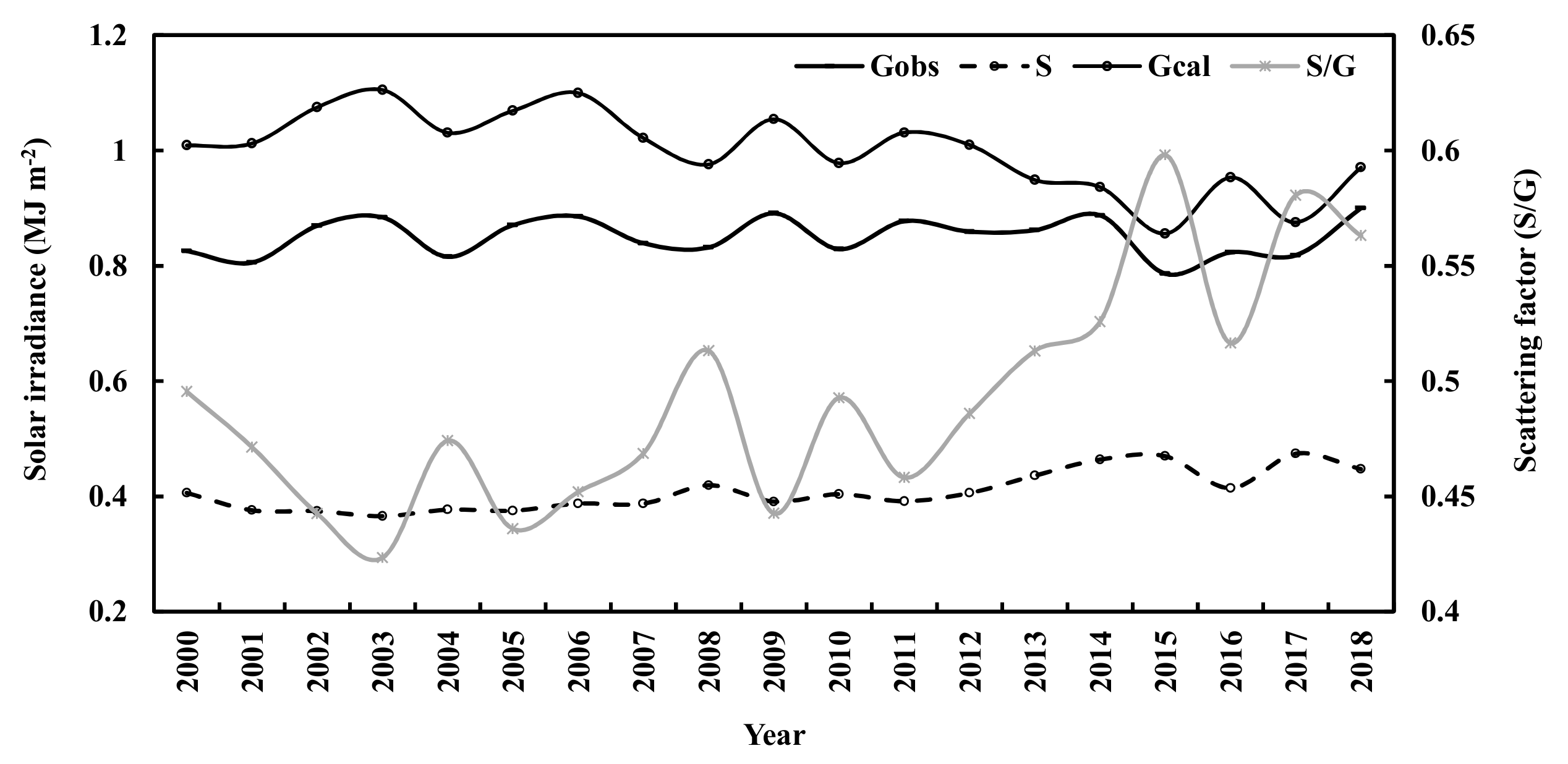
3.1. Global Solar Irradiance during 2000–2018
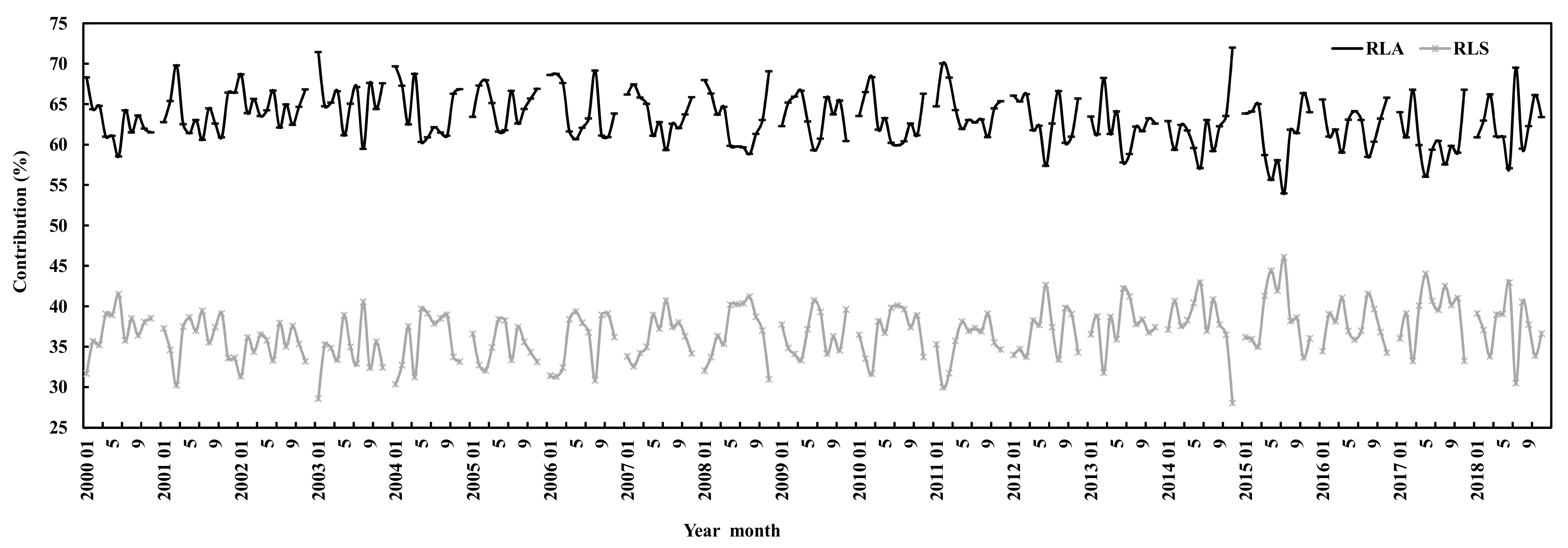
3.2. The Losses of Global Solar Irradiance in the Atmosphere during 2000–2018
3.3. Global Solar Irradiance and Its Loss in the Atmosphere from April to September during 2000–2018
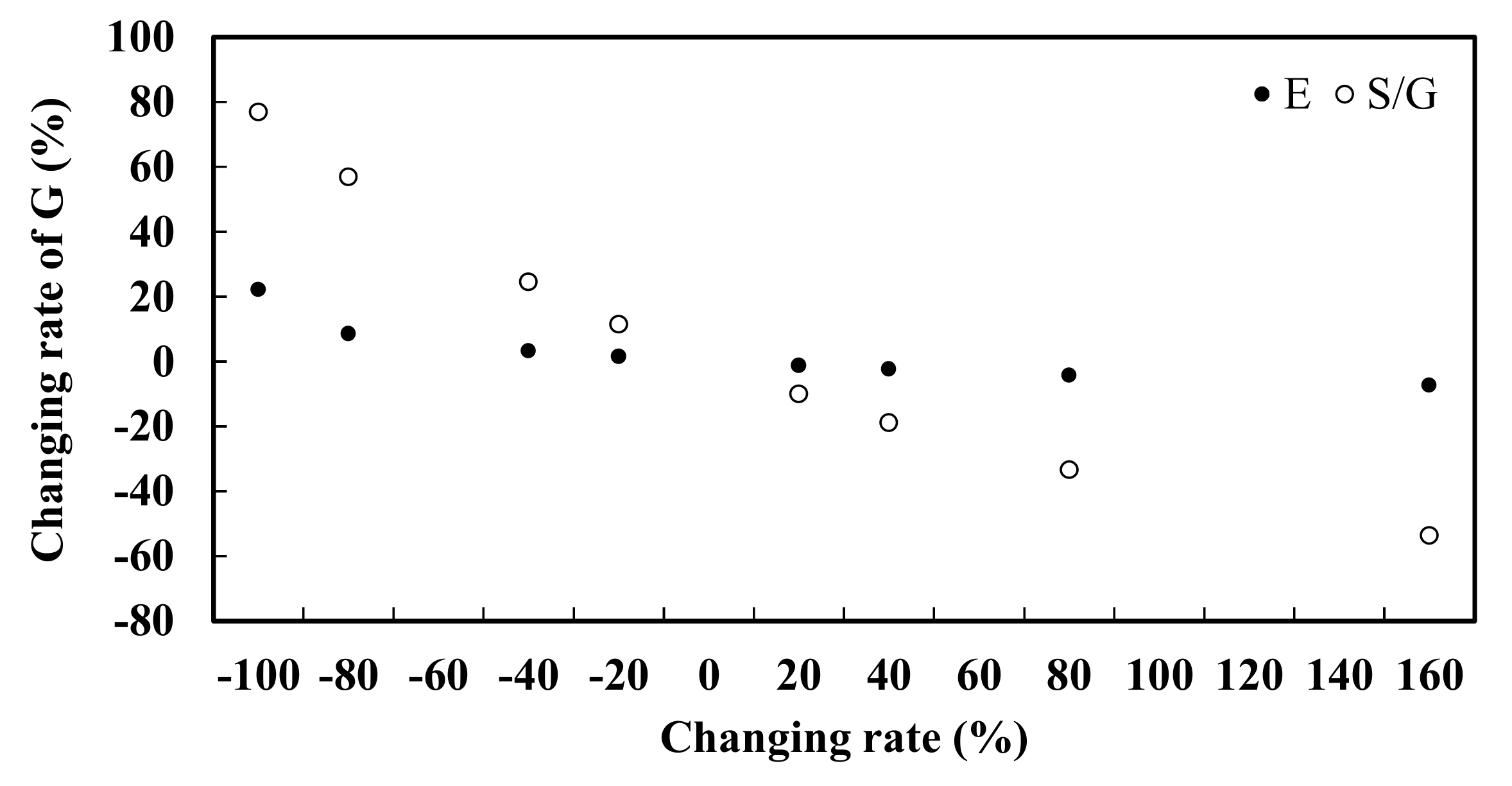
3.4. Sensitivity Analysis
3.5. Estimation and Comparison of Albedos at the TOA and the Surface
3.6. Further Evaluation of the Empirical Model
3.7. Estimation of Aerosol Optical Depth (AOD)
3.8. Estimation of Tropospheric NO2 Vertical Column Densities
- (1)
- (2)
- The absorption term: absorption and use of global solar radiation by GLPs, not including NO2. It is expressed as e−kWm ×cos(Z). The meaning of this term is discussed in detail in Reference [12].
- (3)
- The scattering term: scattering of global solar radiation by GLPs is described as e−S/G.
- (4)
- This empirical model is a further application of energy balance on a horizontal plane from for O3 and NO2 in UV and visible regions to for NO2 VCD in short wavelength region [12], or empirical model of global solar irradiance, Equation (1).
4. Discussion
4.1. Empirical Model and Estimation of Global Solar Irradiance
4.2. Contributions of Absorbing and Scattering
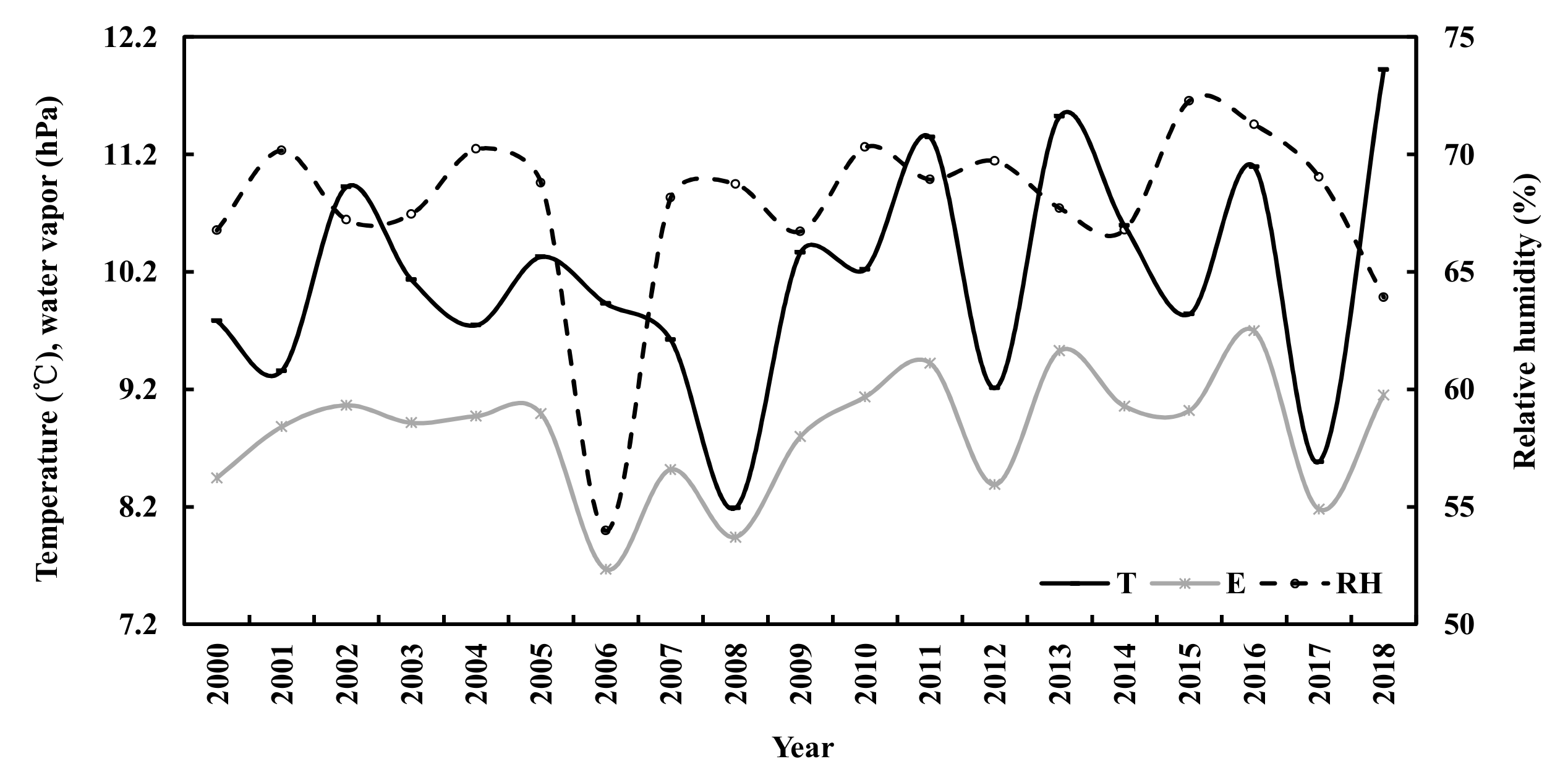
4.3. Long-Term Variations and Interactions in Global Solar Irradiance and Its Losses, Albedos at the TOA and the Surface, NO2, AOD and S/G
4.4. Comparisons of Global Solar Radiation and Its Related Parameters at Two Sites in the Northern Hemisphere
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cao, Y.F.; Liang, S.L. Recent advances in driving mechanisms of the Arctic amplification: A review. Chin. Sci. Bull. 2018, 63, 2757–2771. (In Chinese) [Google Scholar] [CrossRef]
- Cohen, J.; Screen, J.A.; Furtado, J.; Barlow, M.; Whittleston, D.; Coumou, D.; Francis, J.A.; Dethloff, K.; Entekhabi, D.; Overland, J.E.; et al. Recent Arctic amplification and extreme mid-latitude weather. Nat. Geosci. 2014, 7, 627–637. [Google Scholar] [CrossRef]
- Liu, S.Y.; Wang, B.Y.; Xie, Y.X.; Hu, S.H.; Wang, Z.Y.; Yue, L.Y. The Variation Characteristics of Temperature in Barrow Alaska during 1925–2018. Clim. Chang. Res. Lett. 2019, 8, 769–774. [Google Scholar] [CrossRef]
- Solanki, S.K. Solar variability and climate change: Is there a link. Astron. Geophys. 2002, 43, 5. [Google Scholar] [CrossRef]
- Elminir, H.K. Relative influence of weather conditions and air pollutants on solar radiation—Part 2: Modification of solar radiation over urban and rural sites. Meteorol. Atmos. Phys. 2007, 96, 257–264. [Google Scholar] [CrossRef]
- Lean, J.; Rind, D. Climate forcing by changing solar radiation. J. Clim. 1998, 11, 3069–3094. [Google Scholar] [CrossRef]
- Andreae, M.O.; Ramanathan, V. Climate’s Dark Forcings. Sciences 2013, 340, 280–281. [Google Scholar] [CrossRef] [PubMed]
- García, R.D.; Cuevas, E.; García, O.E.; Cachorro, V.E.; Pallé, P.; Bustos, J.J.; Romero-Campos, P.M.; de Frutos, A.M. Reconstruction of global solar radiation time series from 1933 to 2013 at the Izaña Atmospheric Observatory. Atmos. Meas. Tech. 2014, 7, 3139–3150. [Google Scholar] [CrossRef][Green Version]
- Rosenfeld, D.; Sherwood, S.; Wood, R.; Donner, L. Climate Effects of Aerosol-Cloud Interactions. Sciences 2014, 343, 379–380. [Google Scholar] [CrossRef] [PubMed]
- Williamson, C.E.; Zepp, R.G.; Lucas, R.M.; Madronich, S.; Austin, A.T.; Ballaré, C.L.; Norval, M.; Sulzberger, B.; Bais, A.F.; McKenzie, R.L.; et al. Solar ultraviolet radiation in a changing climate. Nat. Clim. Chang. 2014, 4, 434–441. [Google Scholar] [CrossRef]
- Calabrò, E.; Magazù, S. Correlation between Increases of the Annual Global Solar Radiation and the Ground Albedo Solar Radiation due to Desertification—A Possible Factor Contributing to Climatic Change. Climate 2016, 4, 64. [Google Scholar] [CrossRef]
- Bai, J.H.; Zong, X.M. Global solar radiation transfer and its loss in the atmosphere. Appl. Sci. 2021, 11, 2651. [Google Scholar] [CrossRef]
- Glover, J.; McCulloch, J.S.G. The empirical relation between solar radiation and hours of sunshine. Q. J. R. Meteorol. Soc. 1958, 84, 172–175. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, L.; Deng, S.; Xu, W.; Zhang, Y. A critical review of the models used to estimate solar radiation. Renew. Sustain. Energy Rev. 2017, 70, 314–329. [Google Scholar] [CrossRef]
- Gueymard, C.A. Critical analysis and performance assessment of clear sky solar irradiance models using theoretical and measured data. Sol. Energy 1993, 51, 121–138. [Google Scholar] [CrossRef]
- Gueymard, C.A. Clear-sky solar irradiance predictions for large-scale applications using 18 radiative models: Improved validation methodology and detailed performance analysis. Sol. Energy 2012, 86, 2145–2169. [Google Scholar] [CrossRef]
- Badescu, V.; Gueymard, C.A.; Cheval, S.; Oprea, C.; Baciu, M.; Dumitrescu, A.; Iacobescu, F.; Milos, I.; Rada, C. Accuracy analysis for fifty-four clear-sky solar radiation models using routine hourly global irradiance measurements in Romania. Renew. Energy 2013, 55, 85–103. [Google Scholar] [CrossRef]
- Bayrakc, H.C.; Demircan, C.; Keceba, A. The development of empirical models for estimating global solar radiation on horizontal surface: A case study. Renew. Sustain. Energy Rev. 2018, 81, 2771–2782. [Google Scholar] [CrossRef]
- Antonanzas-Torres, F.; Urraca, R.; Polo, J.; Perpinan-Lamigueiro, O.; Escobar, R. Clear sky solar irradiance models: A review of seventy models. Renew. Sustain. Energy Rev. 2019, 107, 374–387. [Google Scholar] [CrossRef]
- Zang, H.; Cheng, L.; Ding, T.; Cheung, K.W.; Wang, M.; Wei, Z.; Sun, G. Estimation and validation of daily global solar radiation by day of the year-based models for different climates in China. Renew. Energy 2019, 135, 984–1003. [Google Scholar] [CrossRef]
- Lakkala, K.; Kyro, E.; Turunen, T. Spectral UV Measurements at Sodankylä during 1990–2001. J. Geophys. Res. Atmos. 2003, 108, 4621. [Google Scholar] [CrossRef]
- Lakkala, K.; Jaros, A.; Aurela, M.; Tuovinen, J.-P.; Kivi, R.; Suokanerva, H.; Karhu, J.; Laurila, T. Radiation measurements at the Pallas-Sodankylä Global Atmosphere Watch station–diurnal and seasonal cycles of ultraviolet, global and photosynthetically—active radiation. Boreal Environ. Res. 2016, 21, 427–444, ISSN 1797-2469. [Google Scholar]
- Mäkelä, J.S.; Lakkala, K.; Koskela, T.; Karppinen, T.; Karhu, J.; Savastiouk, V.; Suokanerva, H.; Kaurola, J.; Arola, A.; Lindfors, A.; et al. Data flow of spectral UV measurements at Sodankylä and Jokioinen. Geosci. Instrum. Method. Data Syst. 2016, 5, 193–203. [Google Scholar] [CrossRef]
- Bilbao, J.; Mateos, D.; De Miguel, A. Analysis and cloudiness influence on UV total irradiation. J. Climatol. 2011, 31, 451–460. [Google Scholar]
- Kondratyev, K.Y.A. Solar Energy; Science Press: Beijing, China, 1962; pp. 123–132. [Google Scholar]
- Myers, D.R. Solar radiation modeling and measurements for renewable energy applications data and model quality. Energy 2005, 30, 1517–1531. [Google Scholar] [CrossRef]
- Post, E.; Alley, R.B.; Christensen, T.R.; Macias-Fauria, M.; Forbes, B.; Gooseff, M.N.; Iler, A.; Kerby, J.T.; Laidre, K.L.; Mann, M.E.; et al. The polar regions in a 2 °C warmer world. Sci. Adv. 2019, 5, eaaw9883. [Google Scholar] [CrossRef] [PubMed]
- Dickinson, R.E. Land surface processes and climate surface albedos and energy balance. Adv. Geophys. 1983, 25, 305–353. [Google Scholar]
- Li, Z.Q.; Garand, L. Estimation of Surface Albedo from Space: A Parameterization for Global Application. J. Geophys. Res. Atmos. 1994, 99, 8335–8350. [Google Scholar] [CrossRef]
- Psiloglou, B.E.; Kambezidis, H.D. Estimation of the ground albedo for the Athens area, Greece. J. Atmos. Sol. Terr. Phys. 2009, 71, 943–954. [Google Scholar] [CrossRef]
- Loeb, N.G.; Doelling, D.R.; Wang, H.; Su, W.; Nguyen, C.; Corbett, J.G.; Liang, L.; Mitrescu, C.; Rose, F.G.; Kato, S. Clouds and the Earth’s Radiant Energy System (CERES) Energy Balanced and Filled (EBAF) Top-of-Atmosphere (TOA) Edition 4.0 Data Product. J. Clim. 2018, 31, 895–918. [Google Scholar] [CrossRef]
- Kato, S.; Rose, F.G.; Rutan, D.A.; Thorsen, T.J.; Loeb, N.G.; Doelling, D.R.; Huang, X.; Smith, W.L.; Su, W.; Ham, S.H. Surface Irradiances of Edition 4.0 Clouds and the Earth’s Radiant Energy System (CERES) Energy Balanced and Filled (EBAF) Data Product. J. Clim. 2018, 31, 4501–4527. [Google Scholar] [CrossRef]
- Sun, Y.J.; Wang, Z.H.; Qin, Q.M.; Han, G.H.; Ren, H.Z.; Huang, J.F. Retrieval of surface albedo based on GF-4geostationary satellite image data. J. Remote Sens. 2018, 22, 220–233. [Google Scholar] [CrossRef]
- Guenther, A.B.; Zimmerman, P.R.; Harley, P.C.; Monson, R.K.; Fall, R. Isoprene and monoterpene emission rate variability: Model evaluations and sensitivity analyses. J. Geophys. Res. Atmos. 1993, 98, 12609–12617. [Google Scholar] [CrossRef]
- Bai, J.H.; Guenther, A.; Turnipseed, A.; Duhl, T.; Greenberg, J. Seasonal and interannual variations in whole-ecosystem BVOC emissions from a subtropical plantation in China. Atmos. Environ. 2017, 161, 176–190. [Google Scholar] [CrossRef]
- Bai, J.H. Photosynthetically active radiation loss in the atmosphere in North China. Atmos. Pollut. Res. 2013, 4, 411–419. [Google Scholar] [CrossRef]
- Shen, Z.B.; Wang, Y.Q.; Wang, W.H.; Wu, J.Z. The attenuation of solar radiation in the polluted urban atmosphere. Plateau Meteorol. 1982, 1, 74–83. [Google Scholar]
- Wild, M.; Gilgen, H.; Roesch, A.; Ohmura, A.; Long, C.; Dutton, E.; Forgan, B.; Kallis, A.; Russak, V.; Tsvetkov, A. From dimming to brightening: Decadal changes in solar radiation at the Earth’s surface. Science 2005, 308, 847–850. [Google Scholar] [CrossRef]
- Sweerts, B.; Pfenninger, S.; Yang, S.; Folini, D.; Van Der Zwaan, B.; Wild, M. Estimation of losses in solar energy production from air pollution in China since 1960 using surface radiation data. Nat. Energy 2019, 4, 657–663. [Google Scholar] [CrossRef]
- Zheng, Z.L.; Zhang, X.L. Long-term variation features of global solar radiation in Beijing. Acta Energ. Sol. Sin. 2013, 34, 1829–1834. (In Chinese) [Google Scholar]
- Qi, Y.; Fang, S.B.; Zhou, W.Z. Variation and spatial distribution of surface solar radiation in China over recent 50 years. Acta Ecol. Sin. 2014, 34, 7444–7453. (In Chinese) [Google Scholar]
- Wang, Y.; Wild, M. A new look at solar dimming and brightening in China. Geophys. Res. Lett. 2016, 43, 11777–11785. [Google Scholar] [CrossRef]
- Valero, F.P.J.; Pope, S.K.; Bush, B.C.; Nguyen, Q.; Marsden, D.; Cess, R.D.; Simpson-Leitner, A.S.; Bucholtz, A.; Udelhofen, P.M. Absorption of solar radiation by the clear and cloudy atmosphere during the Atmospheric Radiation Measurement Enhanced Shortwave Experiments (ARESE) I and II: Observations and models. J. Geophys. Res. Atmos. 2003, 108, 4016. [Google Scholar] [CrossRef]
- Psiloglou, B.; Kambezidis, H.; Kaskaoutis, D.; Karagiannis, D.; Polo, J. Comparison between MRM simulations, CAMS and PVGIS databases with measured solar radiation components at the Methoni station, Greece. Renew. Energy 2020, 146, 1372–1391. [Google Scholar] [CrossRef]
- Salomonson, V.V.; Barnes, W.L.; Maymon, P.W.; Montgomery, P.W.; Ostrow, H. MODIS: Advanced facility instrument for studies of the Earth as a system. IEEE Trans. Geosci. Remote Sens. 1989, 27, 145–153. [Google Scholar] [CrossRef]
- Hsu, N.C.; Tsay, S.C.; King, M.D.; Herman, J.R. Aerosol properties over bright-reflecting source regions. IEEE Trans. Geosci. Remote Sens. 2004, 42, 557–569. [Google Scholar] [CrossRef]
- Remer, L.A.; Kaufman, Y.J.; Tanré, D.; Mattoo, S.; Chu, D.A.; Martins, J.V.; Li, R.R.; Ichoku, C.; Levy, R.C.; Kleidman, R.G.; et al. The MODIS Aerosol Algorithm, Products, and Validation. J. Atmos. Sci. 2005, 62, 947–973. [Google Scholar] [CrossRef]
- Sayer, A.M.; Munchak, L.A.; Hsu, N.C.; Levy, R.C.; Bettenhausen, C.; Jeong, M.J. MODIS Collection 6 aerosol products: Comparison between Aqua’s e-Deep Blue, Dark Target, and “merged” data sets, and usage recommendations. J. Geophys. Res. Atmos. 2014, 119, 13965–13989. [Google Scholar] [CrossRef]
- Sogacheva, L.; de Leeuw, G.; Rodriguez, E.; Kolmonen, P.; Georgoulias, A.K.; Alexandri, G.; Kourtidis, K.; Proestakis, E.; Marinou, E.; Amiridis, V.; et al. Spatial and seasonal variations of aerosols over China from two decades of multi-satellite observations-Part 1: ATSR (1995–2011) and MODIS C6.1 (2000–2017). Atmos. Chem. Phys. 2018, 18, 11389–11407. [Google Scholar] [CrossRef]
- Kim, M.-H.; Omar, A.H.; Tackett, J.L.; Vaughan, M.A.; Winker, D.M.; Trepte, C.R.; Hu, Y.; Liu, Z.; Poole, L.R.; Pitts, M.C.; et al. The CALIPSO version 4 automated aerosol classification and lidar ratio selection algorithm. Atmos. Meas. Tech. 2018, 11, 6107–6135. [Google Scholar] [CrossRef] [PubMed]
- Kulmala, M.; Suni, T.; Lehtinen, K.E.J.; Maso, M.D.; Boy, M.; Reissell, A.; Rannik, Ü.; Aalto, P.; Keronen, P.; Hakola, H.; et al. A new feedback mechanism linking forests, aerosols, and climate. Atmos. Chem. Phys. Discuss. 2004, 4, 557–562. [Google Scholar] [CrossRef]
- Tarvainen, V.; Hakola, H.; Hell’en, H.; Back, J.; Hari, P.; Kulmala, M. Temperature and light dependence of VOC emissions of Scots pine. Atmos. Chem. Phys. Discuss. 2004, 4, 6691–6718. [Google Scholar]
- Claeys, M.; Graham, B.; Vas, G.; Wang, W.; Vermeylen, R.; Pashynska, V.; Cafmeyer, J.; Guyon, P.; Andreae, M.O.; Artaxo, P.; et al. Formation of Secondary Organic Aerosols Through Photooxidation of Isoprene. Science 2004, 303, 1173–1176. [Google Scholar] [CrossRef] [PubMed]
- Riccobono, F.; Schobesberger, S.; Scott, C.E.; Dommen, J.; Ortega, I.K.; Rondo, L.; Almeida, J.; Amorim, A.; Bianchi, F.; Breitenlechner, M.; et al. Oxidation Products of Biogenic Emissions Contribute to Nucleation of Atmospheric Particles. Science 2014, 344, 717–721. [Google Scholar] [CrossRef]
- Schneider, W.; Moortgat, G.K.; Tyndall, G.S.; Burrows, J.P. Absorption cross-sections of NO2 in the UV and visible region (200–700 nm) at 298 K. J. Photochem. Photobiol. A Chem. 1987, 40, 195–217. [Google Scholar] [CrossRef]
- IPCC (Intergovernmental Panel on Climate Change). Couplings between changes in the climate system and biogeochemistry. In Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: Cambridge, MA, USA, 2007; pp. 499–587. [Google Scholar]
- Potter, C.; Brooks-Genovese, V.; Klooster, S.; Torregrosa, A. Biomass burning emissions of reactive gases estimated from satellite data analysis and ecosystem modeling for the Brazilian Amazon region. J. Geophys. Res. Space Phys. 2002, 107, LBA-23-1–LBA-23-10. [Google Scholar] [CrossRef]
- Bray, C.D.; Battye, W.H.; Aneja, V.P.; Schlesinger, W.H. Global emissions of NH3, NOx, and N2O from biomass burning and the impact of climate change. J. Air Waste Manag. Assoc. 2021, 71, 102–114. [Google Scholar] [CrossRef]
- Bai, J.; de Leeuw, G.; De Smedt, I.; Theys, N.; Van Roozendael, M.; Sogacheva, L.; Chai, W. Variations and photochemical transformations of atmospheric constituents in North China. Atmos. Environ. 2018, 189, 213–226. [Google Scholar] [CrossRef]
- Bai, J.H. UV extinction in the atmosphere and its spatial variation in North China. Atmos. Environ. 2017, 154, 318–330. [Google Scholar] [CrossRef]
- Jokinen, T.; Berndt, T.; Makkonen, R.; Kerminen, V.-M.; Junninen, H.; Paasonen, P.; Stratmann, F.; Herrmann, H.; Guenther, A.B.; Worsnop, D.R.; et al. Production of extremely low volatile organic compounds from biogenic emissions: Measured yields and atmospheric implications. Proc. Natl. Acad. Sci. USA 2015, 112, 7123–7128. [Google Scholar] [CrossRef] [PubMed]
- Chu, B.; Kerminen, V.-M.; Bianchi, F.; Yan, C.; Petäjä, T.; Kulmala, M. Atmospheric new particle formation in China. Atmos. Chem. Phys. Discuss. 2019, 19, 115–138. [Google Scholar] [CrossRef]
- Arnold, S.; Law, K.; Brock, C.; Thomas, J.; Starkweather, S.; Von Salzen, K.; Stohl, A.; Sharma, S.; Lund, M.; Flanner, M.; et al. Arctic air pollution: Challenges and opportunities for the next decade. Elem. Sci. Anth. 2016, 4, 104. [Google Scholar] [CrossRef]
- Law, K.S.; Stohl, A.; Quinn, P.K.; Brock, C.A.; Burkhart, J.F.; Paris, J.-D.; Ancellet, G.; Singh, H.B.; Roiger, A.; Schlager, H.; et al. Arctic Air Pollution: New Insights from POLARCAT-IPY. Bull. Am. Meteorol. Soc. 2014, 95, 1873–1895. [Google Scholar] [CrossRef]
- Qiu, J.Y.; Huang, Q.; Tian, W.S.; Xie, F.; Liu, X.R.; Wang, F.Y. Numerical simulation study on the transport of pollution from China to the Arctic region. Plateau Meteorol. 2019, 38, 887–900. [Google Scholar]
- Bai, J.H. Study on surface O3 chemistry and photochemistry by UV energy conservation. Atmos. Pollut. Res. 2010, 1, 118–127. [Google Scholar] [CrossRef]
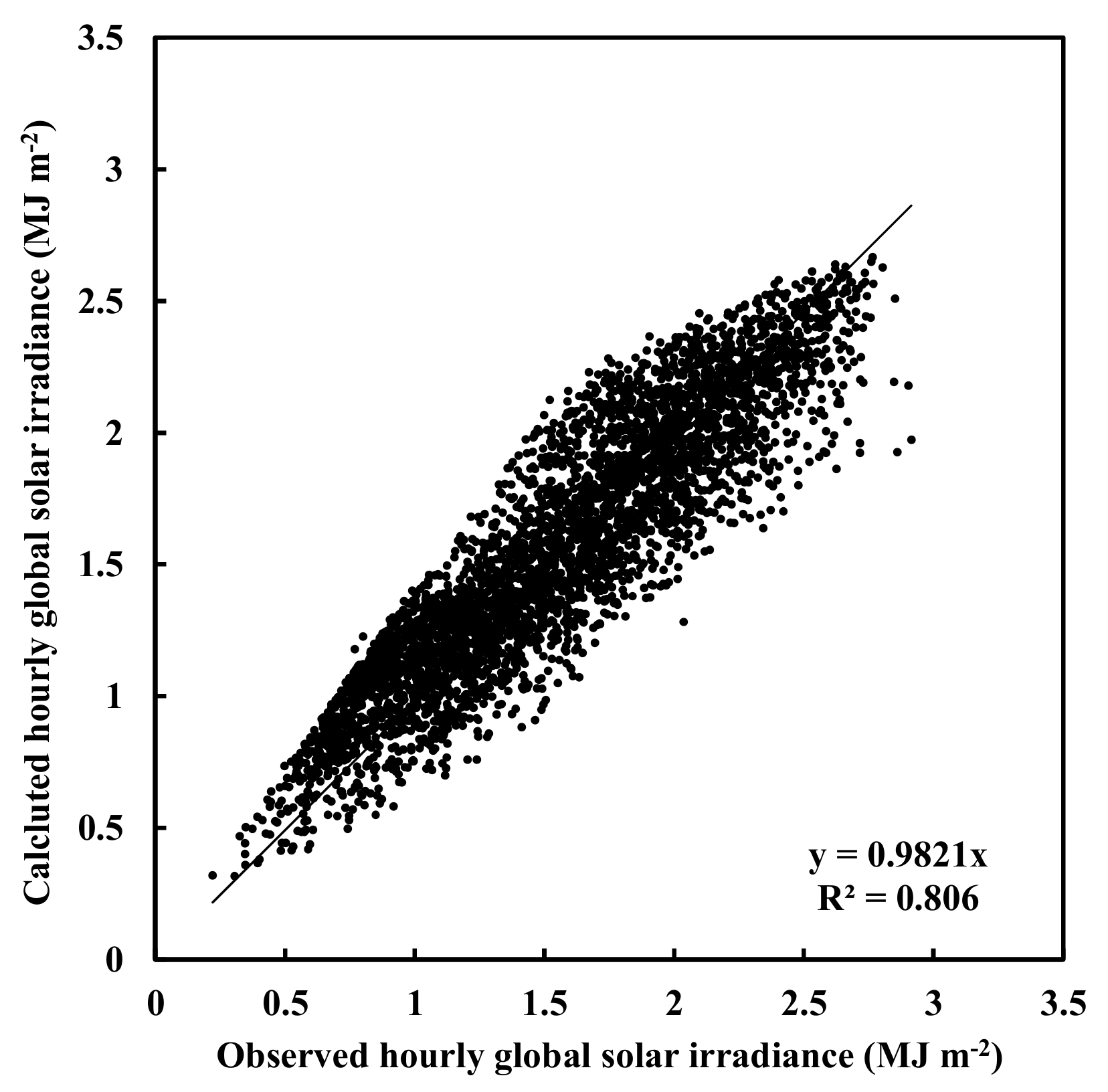
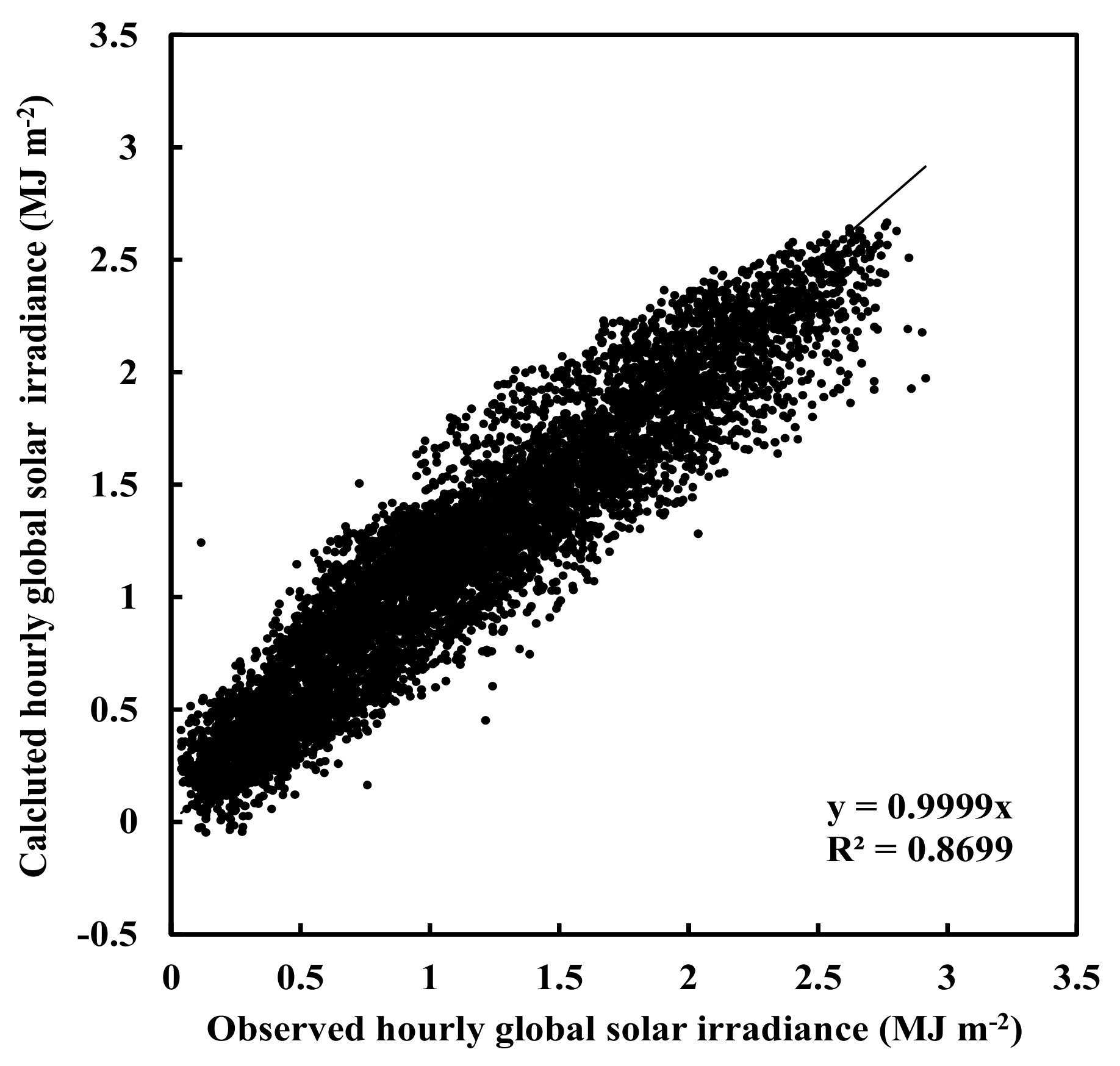





| A1 | A2 | A0 | R2 | δavg | δmax | NMSE | σcal | σobs | MAD | RMSE | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (MJ m−2) | (%) | (MJ m−2) | (%) | |||||||||
| 2.52 | 2.52 | −1.22 | 0.84 | 12.80 | 53.24 | 0.02 | 0.50 | 0.55 | 0.18 | 11.38 | 0.22 | 14.15 |
| E (%) | S/G (%) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| +20 | +40 | +80 | +160 | −20 | −40 | −80 | −100 | +20 | +40 | +80 | +160 | −20 | −40 | −80 | −100 |
| −1.25 | −2.37 | −4.30 | −7.41 | 1.44 | 3.17 | 8.52 | 22.08 | −10.03 | −18.82 | −33.37 | −53.69 | 11.45 | 24.57 | 56.93 | 76.86 |
| S/G Range | Ratio | δavg | δmax | RMSE | n | |
|---|---|---|---|---|---|---|
| (MJ m−2) | % | |||||
| ≤0.10 | 1.232 | 6.42 | 29.68 | 0.031 | 1.33 | 137 |
| ≤0.20 | 1.069 | 8.08 | 30.51 | 0.09 | 4.27 | 866 |
| ≤0.30 | 0.999 | 8.6 | 39.32 | 0.12 | 5.78 | 1322 |
| ≤0.40 | 1.094 | 9.17 | 49.22 | 0.143 | 7.03 | 1680 |
| ≤0.50 | 1.145 | 9.6 | 51.36 | 0.16 | 8.1 | 2035 |
| ≤0.60 | 1.178 | 10.19 | 52.11 | 0.175 | 9.18 | 2371 |
| ≤0.70 | 1.192 | 10.6 | 52.37 | 0.189 | 10.05 | 2662 |
| ≤0.80 | 1.216 | 11.17 | 52.96 | 0.198 | 11.17 | 3022 |
| δavg | δmax | NMSE | σcal | σobs | MAD | RMSE | ||
|---|---|---|---|---|---|---|---|---|
| (1015cm−2) | (%) | (1015cm−2) | (%) | |||||
| 13.45 | 33.23 | 0.02 | 0.10 | 0.12 | 0.00 | 0.12 | 0.09 | 15.29 |
| Site | Gcal | T | RH | E | S/G | GLA MJm−2 | GLS MJm−2 | GL | GLA Wm−2 | GLS Wm−2 | GL | RLA | RLS | alb | alb |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MJm−2 | °C | % | hPa | MJm−2 | Wm−2 | % | % | TOA | sur | ||||||
| Sod | 0.65 | 3.05 | 76 | 6.83 | 0.59 | 1.94 | 1.23 | 3.18 | 539.65 | 342.54 | 882.19 | 61.96 | 38.04 | 0.36 | 0.22 |
| QYZ | 1.42 | 22.71 | 75.76 | 22.38 | 0.83 | 1.68 | 0.27 | 1.95 | 466.37 | 75.35 | 541.71 | 89.31 | 13.69 | 0.29 | 0.22 |
| Ratio | 0.46 | 0.13 | 1 | 0.3 | 0.71 | 1.15 | 4.56 | 1.63 | 1.16 | 4.55 | 1.63 | 0.69 | 2.77 | 1.24 | 0.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, J.; Heikkilä, A.; Zong, X. Long-Term Variations of Global Solar Radiation and Atmospheric Constituents at Sodankylä in the Arctic. Atmosphere 2021, 12, 749. https://doi.org/10.3390/atmos12060749
Bai J, Heikkilä A, Zong X. Long-Term Variations of Global Solar Radiation and Atmospheric Constituents at Sodankylä in the Arctic. Atmosphere. 2021; 12(6):749. https://doi.org/10.3390/atmos12060749
Chicago/Turabian StyleBai, Jianhui, Anu Heikkilä, and Xuemei Zong. 2021. "Long-Term Variations of Global Solar Radiation and Atmospheric Constituents at Sodankylä in the Arctic" Atmosphere 12, no. 6: 749. https://doi.org/10.3390/atmos12060749
APA StyleBai, J., Heikkilä, A., & Zong, X. (2021). Long-Term Variations of Global Solar Radiation and Atmospheric Constituents at Sodankylä in the Arctic. Atmosphere, 12(6), 749. https://doi.org/10.3390/atmos12060749






