A Global Empirical Model of the Ion Temperature in the Ionosphere for the International Reference Ionosphere
Abstract
:1. Introduction
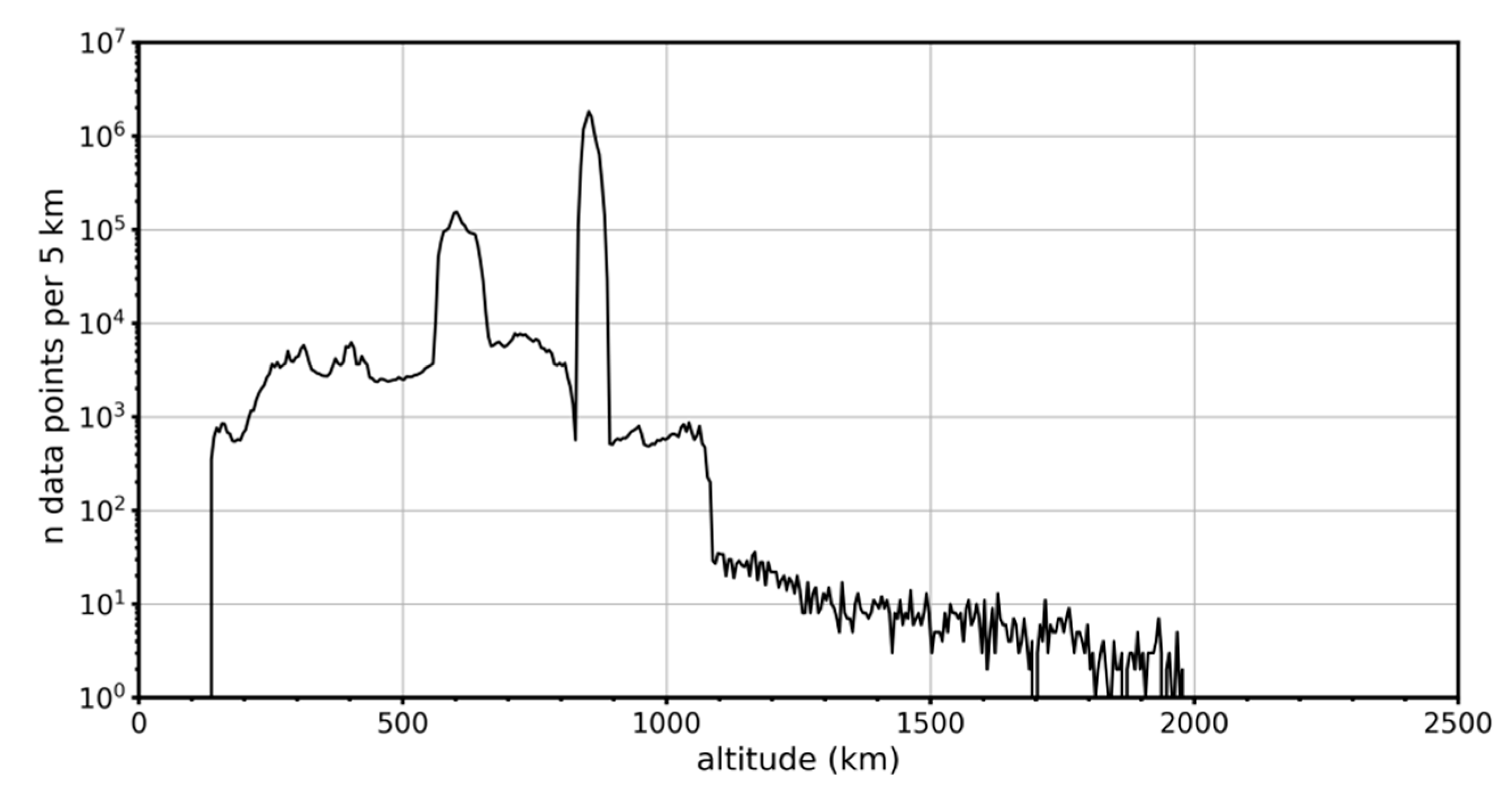
2. Data
2.1. Quality Data Assessment and Data Intercalibration
- –
- Four seasons (centered at March 21, June 21, September 23, and December 21 and extending ±30 days);
- –
- Six altitudes (centered at 350 km, 400 km, 450 km, 500 km, 550 km, 600 km and extending ±10% above and below of the given altitude);
- –
- Twenty-four magnetic local times (MLT) (centred at 0.5 h, 1 h, 1.5 h, …, 23.5 h and within ±0.5 h);
- –
- Twelve levels of solar activity (PF10.7 centred at 72.5, 87.5, ..., 237.5 and within ±7.5 s.f.u.).
3. Model
3.1. The Base Model
3.2. The Whole Model
4. Altitude Profiles
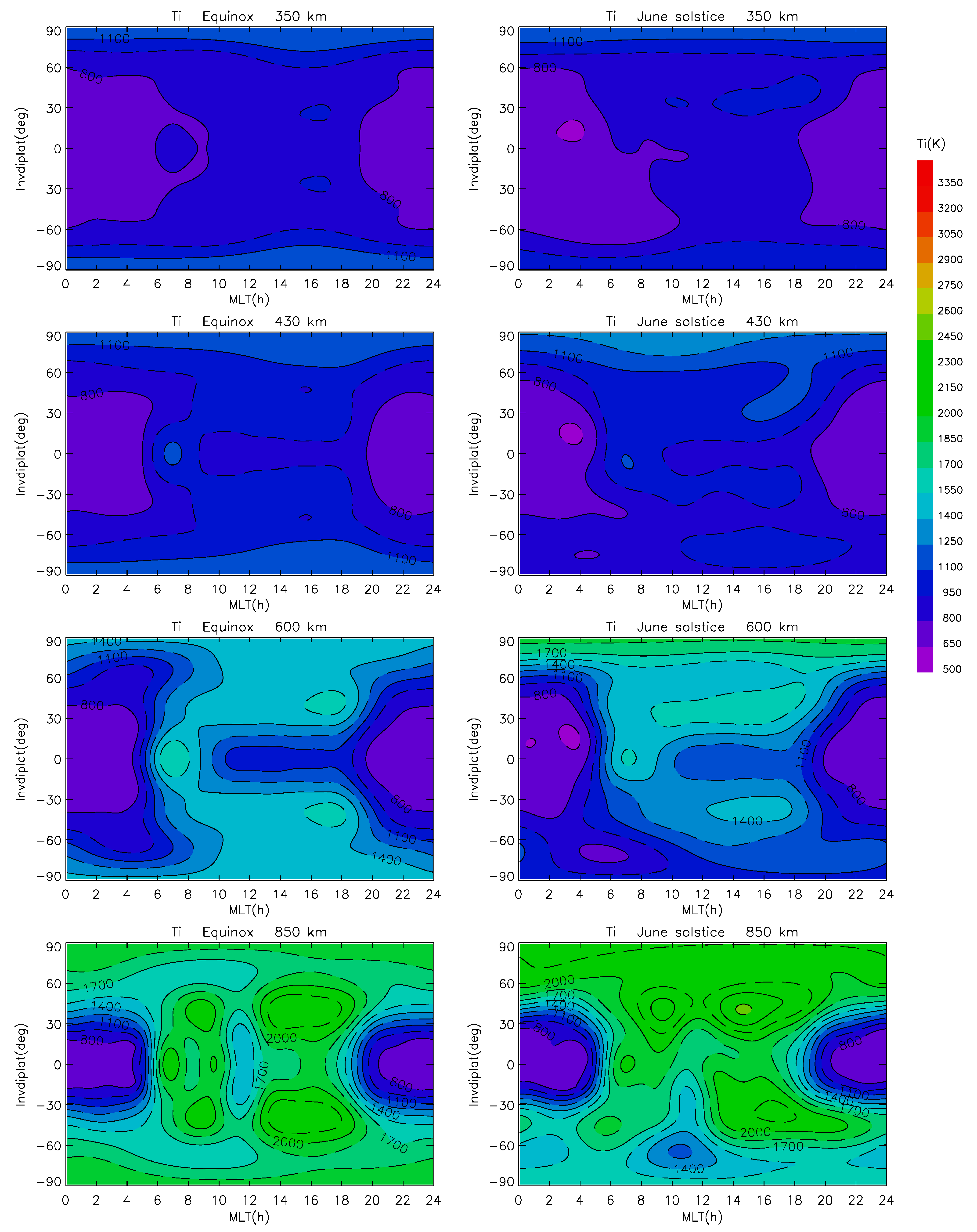
5. Model Results and Examples
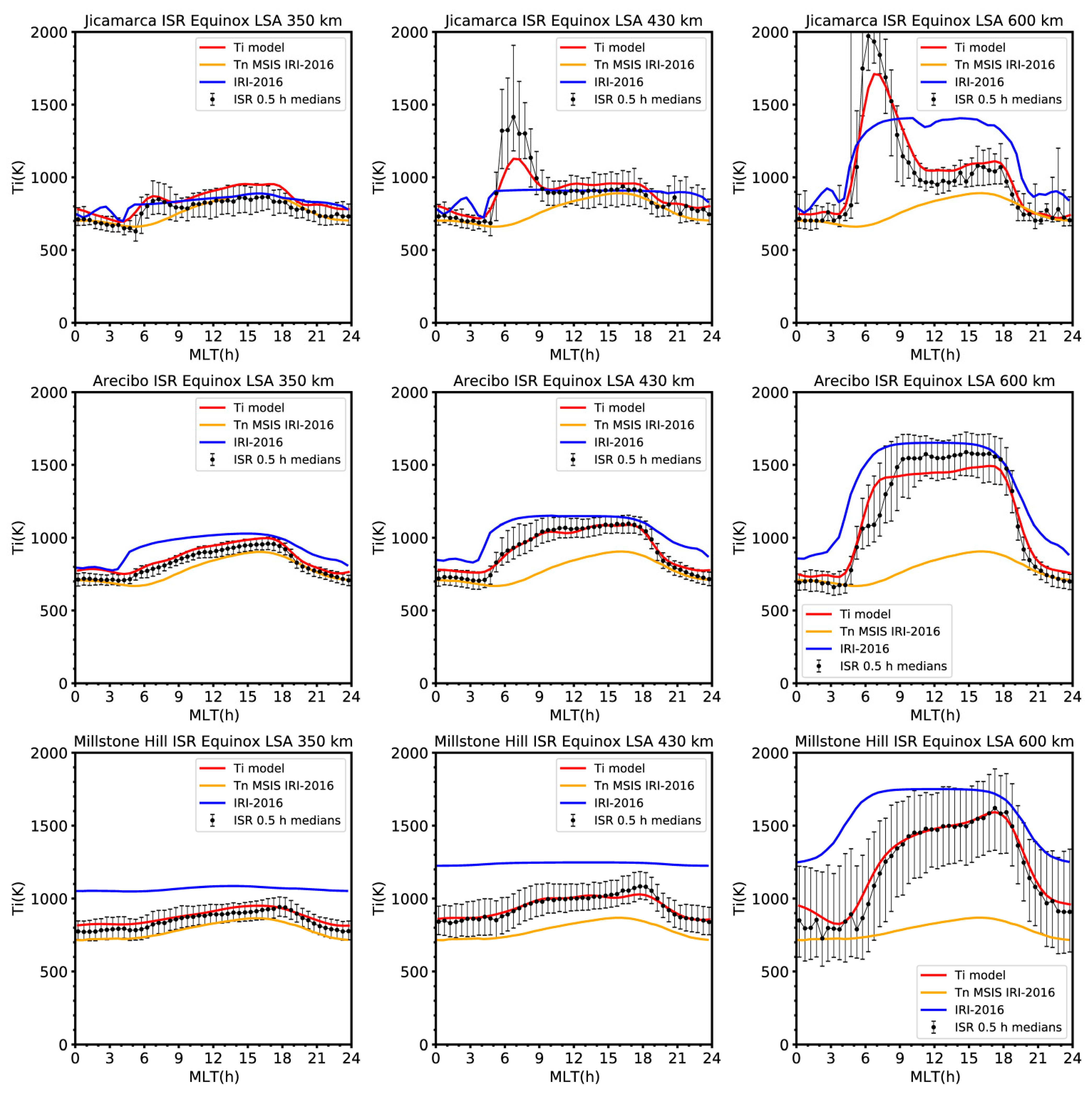
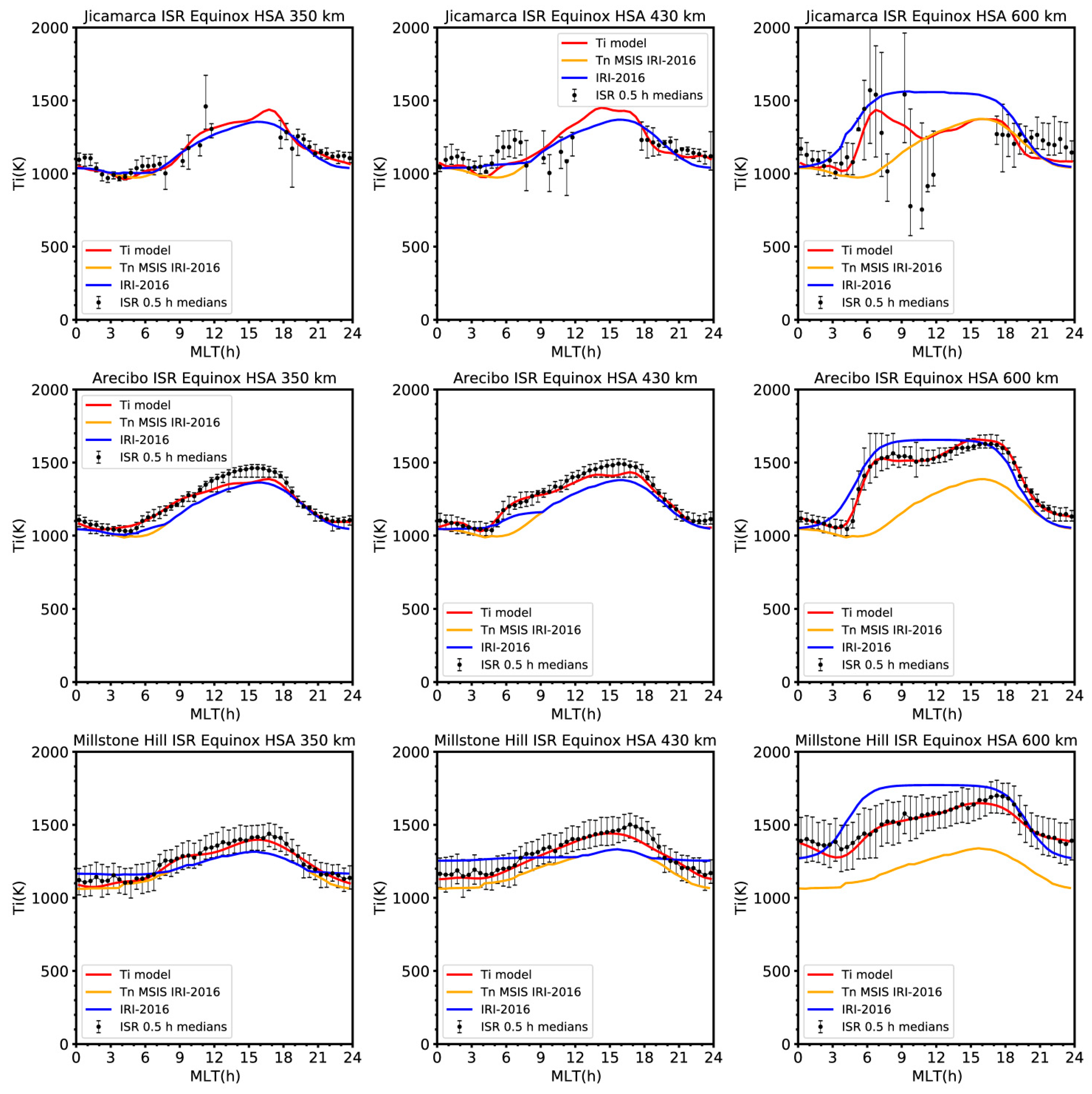
6. Comparisons with Data
6.1. Comparisons with Jicamarca, Arecibo and Millstone Hill ISR Data
6.2. Comparisons with Kharkiv ISR Ti Data
7. Discussion and Conclusions
- –
- Correction factors were determined for a large number satellite Ti measurements based on comparisons with ISR data.
- –
- A global ion temperature model was developed based on a database of these corrected satellite Ti measurements.
- –
- The model represents the climatology of the ion temperature at altitudes from 350 to 850 km using global sub-models at four fixed altitudes.
- –
- Below an altitude of 350 km, the model uses a connection to Tn and above 850 km a connection to Te.
- –
- The dependence on solar activity (PF10.7 as a proxy index) is expressed as an additive term that includes both linear and quadratic dependencies.
- –
- Comparison with ISR data (Jicamarca, Arecibo, Millstone Hill, and Kharkiv) shows that the model describes the diurnal variation quite well for both low and high solar activity at different altitudes and latitudes.
- –
- Different from the current IRI model the new model captures the morning peak and its dependence on solar activity and altitude, with the peak being most pronounced during periods of low solar activity and at ~600 km altitude.
- –
- A comparison of the IRI and our new model with the data used in the model developments highlights fundamental flaws of the current IRI Ti model, while the new model is fully consistent with this large data base and is therefore an appropriate alternative to the current model.
- –
- Future developments could include an extension to include third order dependencies such as magnetic activity or longitude and the use of data from more recent missions (COSMIC-2), and possibly fully integrate ISR data into the model including data from ISRs not yet included like EISCAT, Pokker Flat, etc.
- –
- The model is available as a subroutine in FORTRAN 77.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Banks, P.M.; Kockarts, G. Aeronomy; Academic Press: New York, NY, USA, 1973; p. 2. [Google Scholar]
- Truhlik, V.; Bilitza, D.; Triskova, L. A new global empirical model of the electron temperature with the inclusion of the solar activity variations for IRI. Earth Planets Space 2012, 64, 531–543. [Google Scholar] [CrossRef] [Green Version]
- Brace, L.H.; Theis, R.F. Global Empirical-Models of Ionospheric Electron-Temperature in the Upper F-Region and Plasmasphere Based on Insitu Measurements from the Atmosphere Explorer-C, Isis-1 and Isis-2 Satellites. J. Atmos. Terr. Phys. 1981, 43, 1317–1343. [Google Scholar] [CrossRef]
- Bilitza, D.; Brace, L.H.; Theis, R.F. Modelling of ionospheric temperature profiles. Adv. Space Res. 1985, 5, 53–58. [Google Scholar] [CrossRef]
- Bilitza, D.; Truhlik, V.; Richards, P.; Abe, T.; Triskova, L. Solar cycle variations of mid-latitude electron density and temperature: Satellite measurements and model calculations. Adv. Space Res. 2007, 39, 779–789. [Google Scholar] [CrossRef]
- Schunk, R.W.; Nagy, A.F. Electron Temperatures in F-Region of Ionosphere—Theory and Observations. Rev. Geophys. 1978, 16, 355–399. [Google Scholar] [CrossRef]
- Mott-Smith, H.M.; Langmuir, I. The theory of collectors in gaseous discharges. Phys. Rev. 1926, 28, 727. [Google Scholar] [CrossRef]
- Knudsen, W.C. Evaluation and Demonstration of Use of Retarding Potential Analyzers for Measuring Several Ionospheric Quantities. J. Geophys Res. 1966, 71, 4669–4678. [Google Scholar] [CrossRef]
- Knudsen, D.; Burchill, J.; Buchert, S.; Eriksson, A.; Gill, R.; Wahlund, J.E.; Åhlén, L.; Smith, M.; Moffat, B. Thermal ion imagers and Langmuir probes in the Swarm electric field instruments. J. Geophys. Res. Space Phys. 2017, 122, 2655–2673. [Google Scholar] [CrossRef]
- Bilitza, D. Electron and ion temperature data for ionospheric modelling. Adv. Space Res. 1991, 11, 139–148. [Google Scholar] [CrossRef]
- Schunk, R.W.; Nagy, A.F. Ionospheres of the Terrestrial Planets. Rev. Geophys. 1980, 18, 813–852. [Google Scholar] [CrossRef]
- Hsu, C.T.; Heelis, R.A. Measurement of Individual H+ and O+ Ion Temperatures in the Topside Ionosphere. J. Geophys. Res. Space Phys. 2018, 123, 1525–1533. [Google Scholar] [CrossRef]
- Bilitza, D.; Altadill, D.; Truhlik, V.; Shubin, V.; Galkin, I.; Reinisch, B.; Huang, X. International Reference Ionosphere 2016: From ionospheric climate to real-time weather predictions. Space Weather 2017, 15, 418–429. [Google Scholar] [CrossRef]
- Bilitza, D. International Reference Ionosphere 1990; Report 90-22; National Space Science Data Center: Greenbelt, MD, USA, 1990.
- Pignalberi, A.; Aksonova, K.D.; Zhang, S.-R.; Truhlik, V.; Gurram, P.; Pavlou, C. Climatological study of the ion temperature in the ionosphere as recorded by Millstone Hill incoherent scatter radar and comparison with the IRI model. Adv. Space Res. 2021, 68, 2186–2203. [Google Scholar] [CrossRef]
- Picone, J.M.; Hedin, A.E.; Drob, D.P.; Aikin, A.C. NRLMSISE-00 empirical model of the atmosphere: Statistical comparisons and scientific issues. J. Geophys. Res. Space Phys. 2002, 107, 1468–1483. [Google Scholar] [CrossRef]
- Heelis, R.; Hanson, W. Measurements of thermal ion drift velocity and temperature using planar sensors. Geophys. Monogr. Am. Geophys. Union 1998, 102, 61–72. [Google Scholar]
- Hanson, W.B.; Sanatani, S.; Zuccaro, D.; Flowerday, T.W. Plasma Measurements with Retarding Potential Analyzer on Ogo-6. J. Geophys. Res. 1970, 75, 5483–5501. [Google Scholar] [CrossRef]
- Spenner, K.; Dumbs, A. Retarding Potential Analyzer on Aeros-B. Z. Geophys. 1974, 40, 585–592. [Google Scholar]
- Hanson, W.B.; Zuccaro, D.R.; Lippincott, C.R.; Sanatani, S. Retarding-Potential Analyzer on Atmosphere Explorer. Radio Sci. 1973, 8, 333–339. [Google Scholar] [CrossRef]
- Hanson, W.; Heelis, R.; Power, R.; Lippincott, C.; Zuccaro, D.; Holt, B.; Harmon, L.; Sanatani, S. The retarding potential analyzer for Dynamics Explorer-B. Space Sci. Instrum. 1981, 5, 503–510. [Google Scholar]
- Broglio, L.; Ponzi, U.; Arduini, C. The San Marco 5 mission. Adv. Space Res. 1993, 13, 165–184. [Google Scholar] [CrossRef]
- Afonin, V.V.; Smirnova, N.F. Optimization of Complex Experiment on Measurement of the Cold Plasma Parameters; Space Research Institute: Moscow, Russia, 1990; pp. 1–21. [Google Scholar]
- Rich, F. Users Guide for the Topside Ionospheric Plasma Monitor (SSIES, SSIES-2 and SSIES-3) on Spacecraft of the Defense Meteorological Satellite Program., Volume 1: Technical Description; PHILLIPS LABORATORY, Hanscom Air Force Base: Bedford, MA, USA, 1994. [Google Scholar]
- Garg, S.; Anand, J.; Bahl, M.; Subrahmanyam, P.; Rajput, S.; Maini, H.; Chopra, P.; John, T.; Singhal, S.; Singh, V.; et al. RPA Aeronomy Experiment Onboard the Indian Satellite SROSS-C2—Some Important Aspects of the Payload and Satellite. Indian J. Radio Space Phys. 2003, 32, 5–15. [Google Scholar]
- Borgohain, A.; Bhuyan, P.K. Solar cycle variation of ion densities measured by SROSS C2 and FORMOSAT-1 over Indian low and equatorial latitudes. J. Geophys. Res. Space Phys. 2010, 115, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Su, S.-Y.; Yeh, H.C.; Heelis, R.A.; Wu, J.-M.; Yang, S.C.; Lee, L.-F.; Chen, H.L. The ROCSAT-1 IPEI preliminary results: Low-latitude ionospheric plasma and flow variations. Terr. Atmos. Ocean Sci. 1999, 10, 787–804. [Google Scholar] [CrossRef]
- Chao, C.K.; Su, S.Y.; Yeh, H.C. Ion temperature variation observed by ROCSAT-1 satellite in the afternoon sector and its comparison with IRI-2001 model. Adv. Space Res. 2006, 37, 879–884. [Google Scholar] [CrossRef]
- de La Beaujardière, O. C/NOFS: A mission to forecast scintillations. J. Atmos. Sol. Terr. Phys. 2004, 66, 1573–1591. [Google Scholar] [CrossRef]
- Heelis, R.A.; Stoneback, R.A.; Perdue, M.D.; Depew, M.D.; Morgan, W.A.; Mankey, M.W.; Lippincott, C.R.; Harmon, L.L.; Holt, B.J. Ion Velocity Measurements for the Ionospheric Connections Explorer. Space Sci. Rev. 2017, 212, 615–629. [Google Scholar] [CrossRef]
- Truhlik, V.; Bilitza, D.; Triskova, L. Latitudinal variation of the topside electron temperature at different levels of solar activity. Adv. Space Res. 2009, 44, 693–700. [Google Scholar] [CrossRef]
- Richards, P.G.; Fennelly, J.A.; Torr, D.G. Euvac—A Solar Euv Flux Model for Aeronomic Calculations. J. Geophys. Res. Space Phys. 1994, 99, 8981–8992. [Google Scholar] [CrossRef]
- Truhlik, V.; Triskova, L.; Smilauer, J.; Afonin, V.V. Global empirical model of electron temperature in the outer ionosphere for period of high solar activity based on data of three intercosmos satellites. Adv. Space Res. Ser. 2000, 25, 163–169. [Google Scholar] [CrossRef]
- Truhlik, V.; Triskova, L.; Saxonbergova-Jankovicova, D. Observations of the ion temperature in morning hours in the equatorial topside ionosphere from ICON and other satellites. In Proceedings of the AGU Fall Meeting, San Francisco, CA, USA, 1–17 December 2020; Available online: https://agu2020fallmeeting-agu.ipostersessions.com/Default.aspx?s=D7-4D-E6-A7-05-7A-3B-09-20-07-14-FC-3E-D4-09-D4 (accessed on 7 December 2020).
- Martinec, Z. Program to Calculate the Least-Squares Estimates of the Spherical Harmonic Expansion Coefficients of an Equally Angular-Gridded Scalar Field. Comput. Phys. Commun. 1991, 64, 140–148. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C: The Art of Scientific Computing, 2nd ed.; Cambridge University Press: New York, NY, USA, 1992. [Google Scholar]
- Oyama, K.I.; Watanabe, S.; Su, Y.; Takahashi, T.; Hirao, K. Season, local time, and longitude variations of electron temperature at the height of similar to 600 km in the low latitude region. Adv. Space Res. 1996, 18, 269–278. [Google Scholar] [CrossRef]
- Stolle, C.; Liu, H.; Truhlik, V.; Luhr, H.; Richards, P.G. Solar flux variation of the electron temperature morning overshoot in the equatorial F region. J. Geophys. Res. Space Phys. 2011, 116, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Coley, W.R.; Heelis, R.A.; Hairston, M.R.; Earle, G.D.; Perdue, M.D.; Power, R.A.; Harmon, L.L.; Holt, B.J.; Lippincott, C.R. Ion temperature and density relationships measured by CINDI from the C/NOFS spacecraft during solar minimum. J. Geophys. Res. Space Phys. 2010, 115, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Rana, G.; Bardhan, A.; Sharma, D.K.; Yadav, M.K.; Aggarwal, M.; Dudeja, J. Variations of ion density and temperature as measured by ROCSAT-1satellite over the Indian region and comparison with IRI-2016 model. Ann. Geophys. 2019, 62, 11. [Google Scholar] [CrossRef]
- Kotov, D.V.; Richards, P.G.; Bogomaz, O.V.; Chernogor, L.F.; Truhlik, V.; Emelyanov, L.Y.; Chepurnyy, Y.M.; Domnin, I.F. The importance of neutral hydrogen for the maintenance of the midlatitude winter nighttime ionosphere: Evidence from IS observations at Kharkiv, Ukraine, and field line interhemispheric plasma model simulations. J. Geophys. Res. Space Phys. 2016, 121, 7013–7025. [Google Scholar] [CrossRef] [Green Version]
- Kotov, D.V.; Richards, P.G.; Truhlik, V.; Bogomaz, O.V.; Shulha, M.O.; Maruyama, N.; Hairston, M.; Miyoshi, Y.; Kasahara, Y.; Kumamoto, A.; et al. Coincident Observations by the Kharkiv IS Radar and Ionosonde, DMSP and Arase (ERG) Satellites, and FLIP Model Simulations: Implications for the NRLMSISE-00 Hydrogen Density, Plasmasphere, and Ionosphere. Geophys. Res. Lett 2018, 45, 8062–8071. [Google Scholar] [CrossRef]
- Kotov, D.V.; Richards, P.G.; Truhlik, V.; Maruyama, N.; Fedrizzi, M.; Shulha, M.O.; Bogomaz, O.V.; Lichtenberger, J.; Hernandez-Pajares, M.; Chernogor, L.F.; et al. Weak Magnetic Storms Can Modulate Ionosphere-Plasmasphere Interaction Significantly: Mechanisms and Manifestations at Mid-Latitudes. J. Geophys. Res. Space Phys. 2019, 124, 9665–9675. [Google Scholar] [CrossRef]
- Kotov, D.V.; Truhlik, V.; Richards, P.G.; Stankov, S.; Bogomaz, O.V.; Chernogor, L.F.; Domnin, I.F. Night-time light ion transition height behaviour over the Kharkiv (50 degrees N, 36 degrees E) IS radar during the equinoxes of 2006–2010. J. Atmos. Sol. Terr. Phys. 2015, 132, 1–12. [Google Scholar] [CrossRef]
- Davidson, R.; Earle, G.; Klenzing, J.; Heelis, R. A numerical study of geometry dependent errors in velocity, temperature, and density measurements from single grid planar retarding potential analyzers. Phys. Plasmas 2010, 17, 082901. [Google Scholar] [CrossRef]
- Klenzing, J.; Earle, G.; Heelis, R.; Coley, W. A statistical analysis of systematic errors in temperature and ram velocity estimates from satellite-borne retarding potential analyzers. Phys. Plasmas 2009, 16, 052901. [Google Scholar] [CrossRef]





| No | Satellite (Experiment) | Time Period (Data Avail) | Altitude [km] | Latitude [deg] | SLT [h] | |
|---|---|---|---|---|---|---|
| 1 | OGO-6 (RPA) | 12. 1969–4. 1971 | 390–1090 | −82 .. +82 | 0–24 | 155 |
| 2 | AEROS A (RPA) | 1. 1973–8. 1973 | 200–870 | −83 .. +83 | 3, 15 fixed | 98 |
| 3 | AEROS B (RPA) | 7. 1974–9. 1975 | 140–880 | −83 .. +83 | 4, 16 fixed | 86 |
| 4 | AE-C (RPA) | 12. 1973–12. 1978 | 135–2010 | −68 .. +68 | 0–24 | 86 |
| 5 | AE-D (RPA) | 10. 1975–1. 1976 | 140–1980 | −89 .. +89 | 0–24 | 76 |
| 6 | AE-E (RPA) | 12. 1975–5. 1981 | 140–1580 | −20 .. +20 | 0–24 | 129 |
| 7 | DE-2 (RPA) | 8. 1981–2. 1983 | 200–1020 | −90 .. +90 | 0–24 | 180 |
| 8 | San Marco 5 (RPA) | 4. 1988–12. 1988 | 170–590 | −3 .. +3 | 0–24 | 151 |
| 9 | IK24 (RPA) | 10. 1989–2. 1993 | 500–2525 | −83 .. +84 | 0–24 | 195 |
| 10 | DMSP F11 (RPA) | 1. 1992–5. 2000 | 840–890 | −81 .. +87 | 6, 18 fixed | 119 |
| 11 | DMSP F12 (RPA) | 1. 1996–6. 2002 | 840–890 | −82 .. +89 | 9, 21 fixed | 132 |
| 12 | DMSP F13 (RPA) | 3. 1995–12. 2005 | 840–880 | −81 .. +82 | 6, 18 fixed | 131 |
| 13 | DMSP F14 (RPA) | 4. 1997–7. 2003 | 840–885 | −81 .. +82 | 9, 21 fixed | 121 |
| 14 | DMSP F15 (RPA) | 12. 1999–12. 2017 | 830–880 | −86 .. +86 | 9.5, 21.5 fixed | 116 |
| 15 | SROSS C2 (RPA) | 1. 1995–12. 2000 | 380–620 | −40 .. +45 | 0–24 | 110 |
| 16 | ROCSAT-1(RPA) | 3. 1999–6. 2004 | 560–665 | −35 .. +35 | 0–24 | 160 |
| 17 | C/NOFS (RPA) | 8. 2008–11. 2015 | 260–855 | −13 .. +13 | 0–24 | 106 |
| 18 | ICON IVM (RPA) | 10. 2019–6. 2020 | 575–610 | −27 .. 27 | 0–24 | 70 |
| ISR | Time Period (Data Availability) | Number of Ti Samples | Latitude (deg) | Longitude (deg) | Invdip (deg) |
|---|---|---|---|---|---|
| Jicamarca | 10. 1996–2. 2020 | 24,266 | −11.95 | −76.87 | 0.0 ± 0.6 |
| Arecibo | 4. 1982–3. 2015 | 68,088 | 18.35 | −66.75 | 28.2 ± 2.2 |
| Millstone Hill | 2. 1976–1. 2020 | 526,216 | 42.62 | 71.48 | 52.8 ± 2.1 |
| No | Satellite (Experiment) | Correction Formula |
|---|---|---|
| 1 | OGO-6 (RPA) | |
| 2 | AEROS A (RPA) | |
| 3 | AEROS B (RPA) | |
| 4 | AE-C (RPA) | |
| 5 | AE-D (RPA) | No coincidences-excluded |
| 6 | AE-E (RPA) | |
| 7 | DE-2 (RPA) | |
| 8 | San Marco 5 (RPA) | |
| 9 | IK24 (RPA) | Not enough coincidences-excluded |
| 10 | DMSP F11 (RPA) | |
| 11 | DMSP F12 (RPA) | |
| 12 | DMSP F13 (RPA) | |
| 13 | DMSP F14 (RPA) | |
| 14 | DMSP F15 (RPA) | |
| 15 | SROSS C2 (RPA) | |
| 16 | ROCSAT-1(RPA) | |
| 17 | C/NOFS (RPA) | |
| 18 | ICON IVM (RPA) |
| Month | Day Range | Year | |
|---|---|---|---|
| October | 28–30 | 2004 | 119 |
| September | 20–22 | 2006 | 75 |
| September | 24–27 | 2007 | 67 |
| September | 23–24 | 2008 | 68 |
| September–October | 29–01 | 2009 | 71 |
| September | 20–22 | 2010 | 82 |
| September | 25–27 | 2012 | 128 |
| March | 19–21 | 2013 | 111 |
| September | 24–26 | 2013 | 115 |
| March | 28–29 | 2018 | 69 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Truhlík, V.; Bilitza, D.; Kotov, D.; Shulha, M.; Třísková, L. A Global Empirical Model of the Ion Temperature in the Ionosphere for the International Reference Ionosphere. Atmosphere 2021, 12, 1081. https://doi.org/10.3390/atmos12081081
Truhlík V, Bilitza D, Kotov D, Shulha M, Třísková L. A Global Empirical Model of the Ion Temperature in the Ionosphere for the International Reference Ionosphere. Atmosphere. 2021; 12(8):1081. https://doi.org/10.3390/atmos12081081
Chicago/Turabian StyleTruhlík, Vladimír, Dieter Bilitza, Dmytro Kotov, Maryna Shulha, and Ludmila Třísková. 2021. "A Global Empirical Model of the Ion Temperature in the Ionosphere for the International Reference Ionosphere" Atmosphere 12, no. 8: 1081. https://doi.org/10.3390/atmos12081081
APA StyleTruhlík, V., Bilitza, D., Kotov, D., Shulha, M., & Třísková, L. (2021). A Global Empirical Model of the Ion Temperature in the Ionosphere for the International Reference Ionosphere. Atmosphere, 12(8), 1081. https://doi.org/10.3390/atmos12081081






