Aviation Turbulence Forecasting over the Portuguese Flight Information Regions: Algorithm and Objective Verification
Abstract
:1. Introduction
2. Materials and Methods
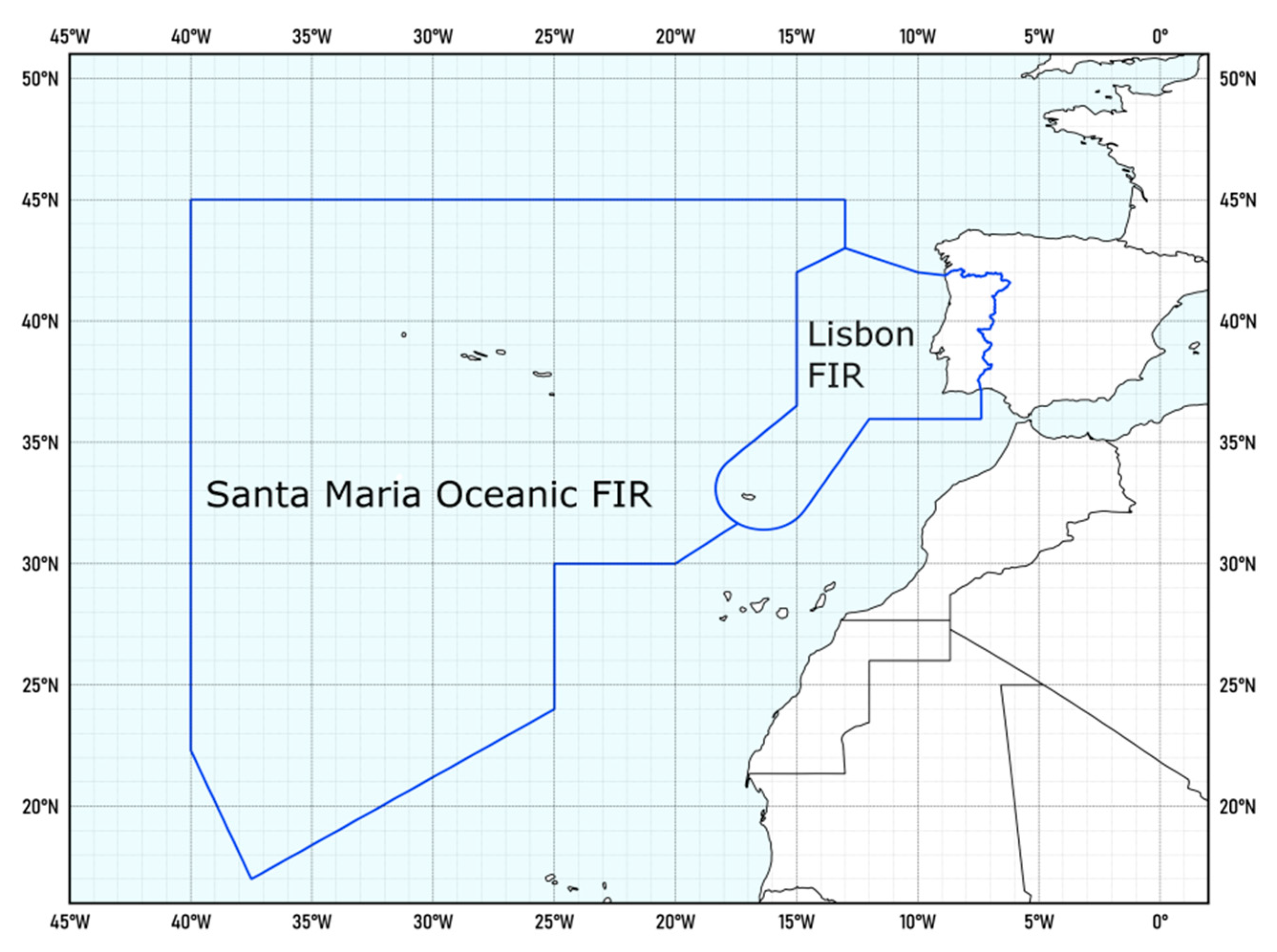
2.1. Turbulence Data
2.2. Forecast Data and Turbulence Indicators
2.3. Verification Methodology
3. Results and Discussion
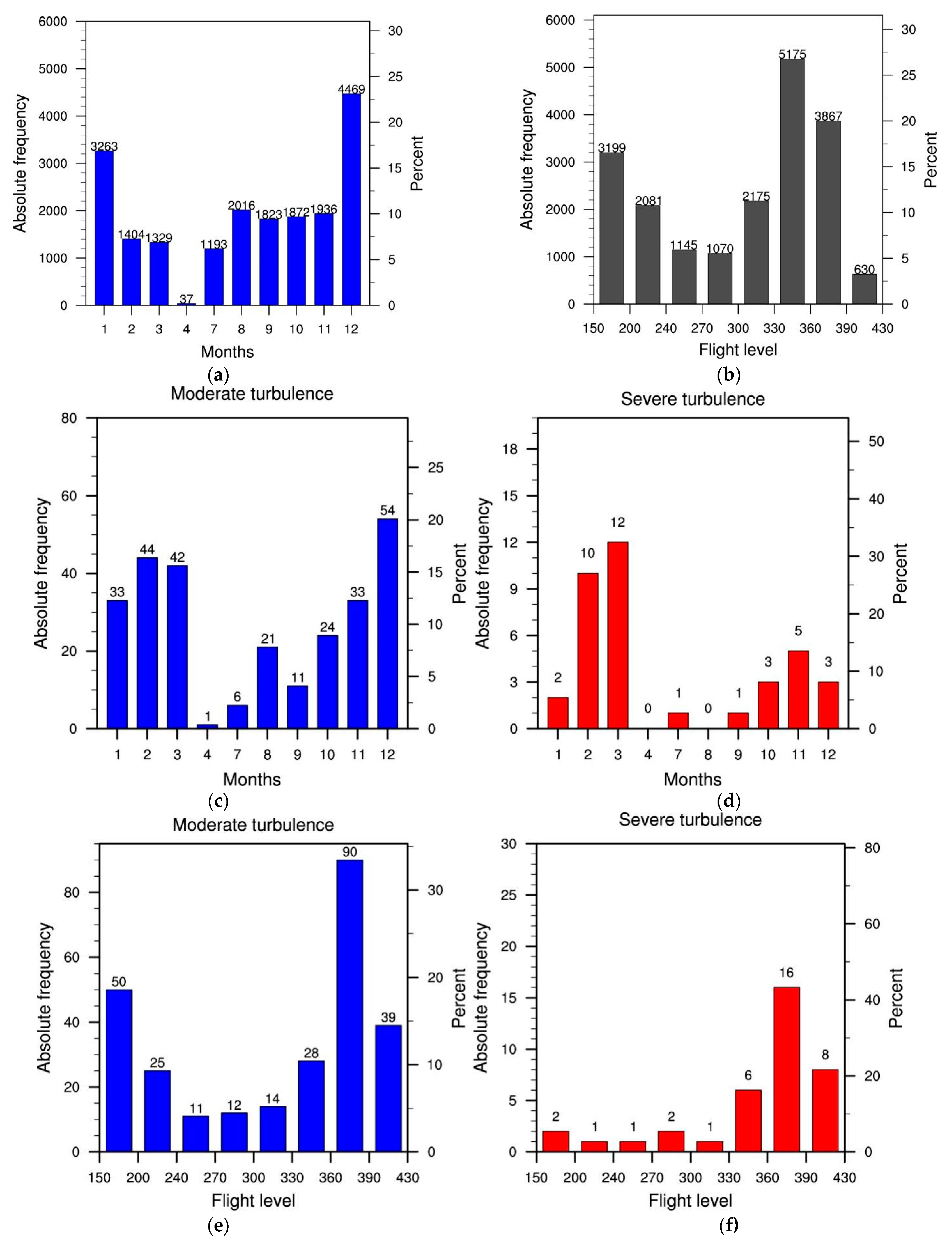
3.1. Characterization of Turbulence Observations
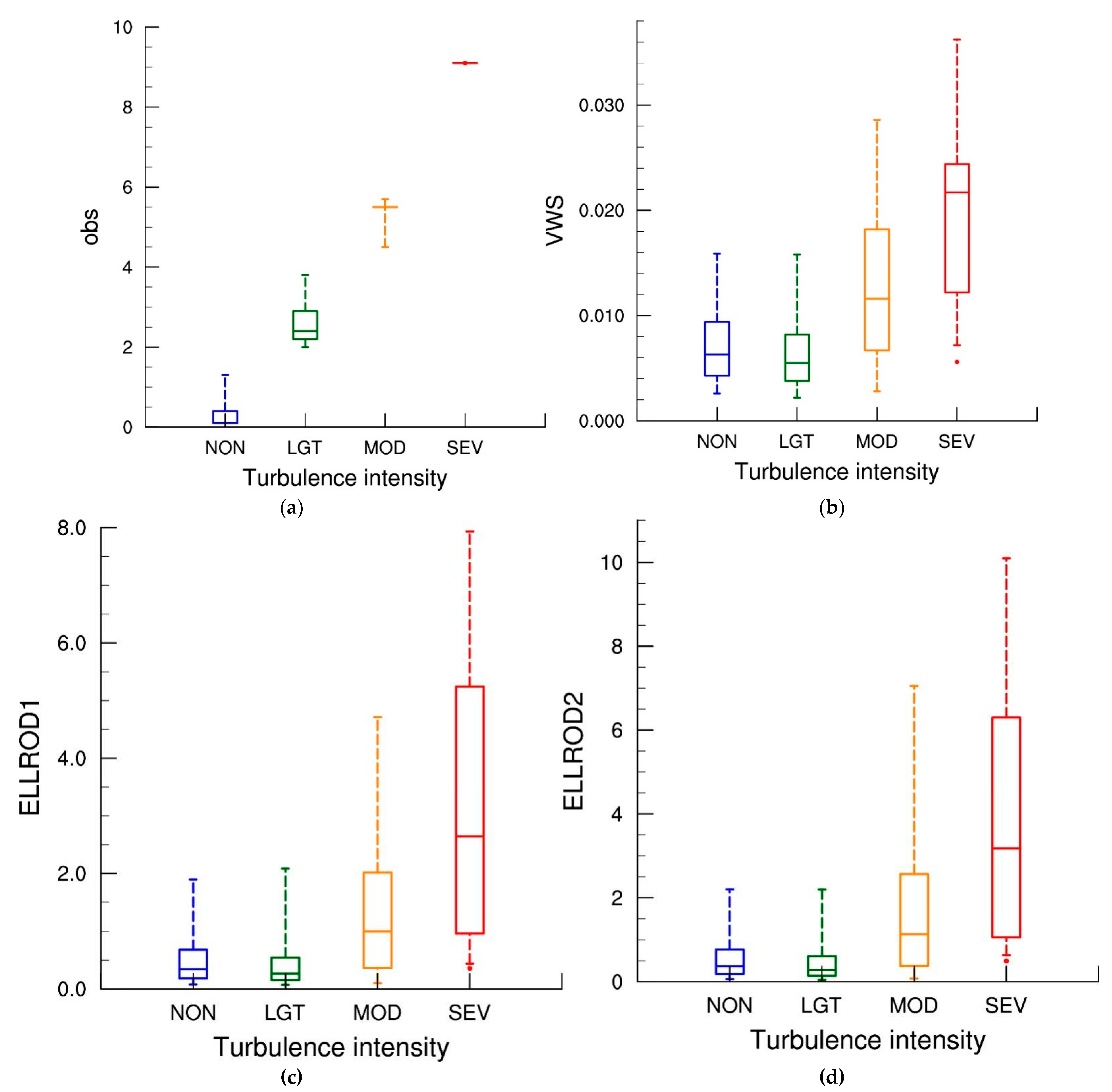
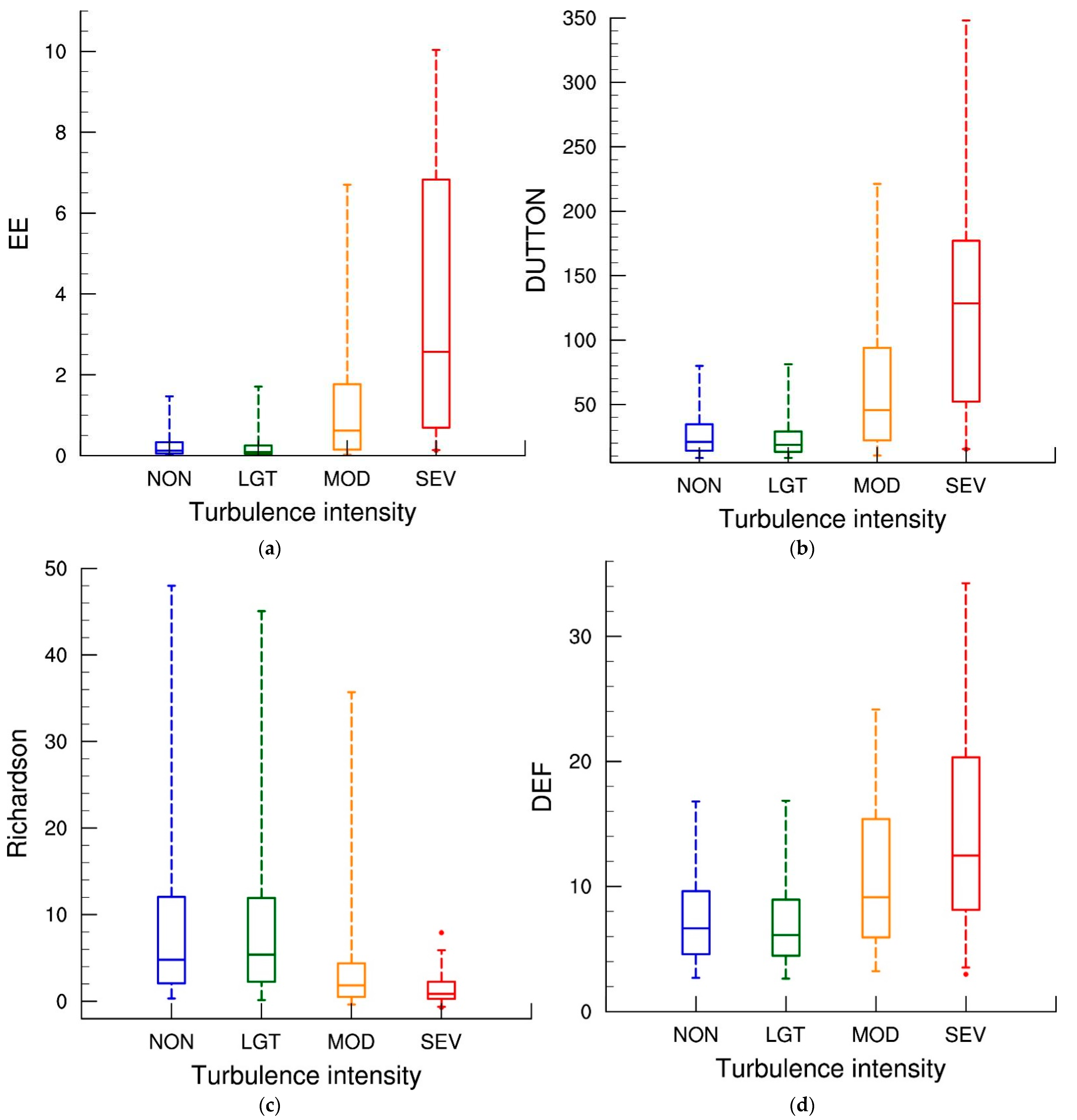
3.2. Distribution of Turbulence Indicators
3.3. Description and Evaluation of the Operational Turbulence Index
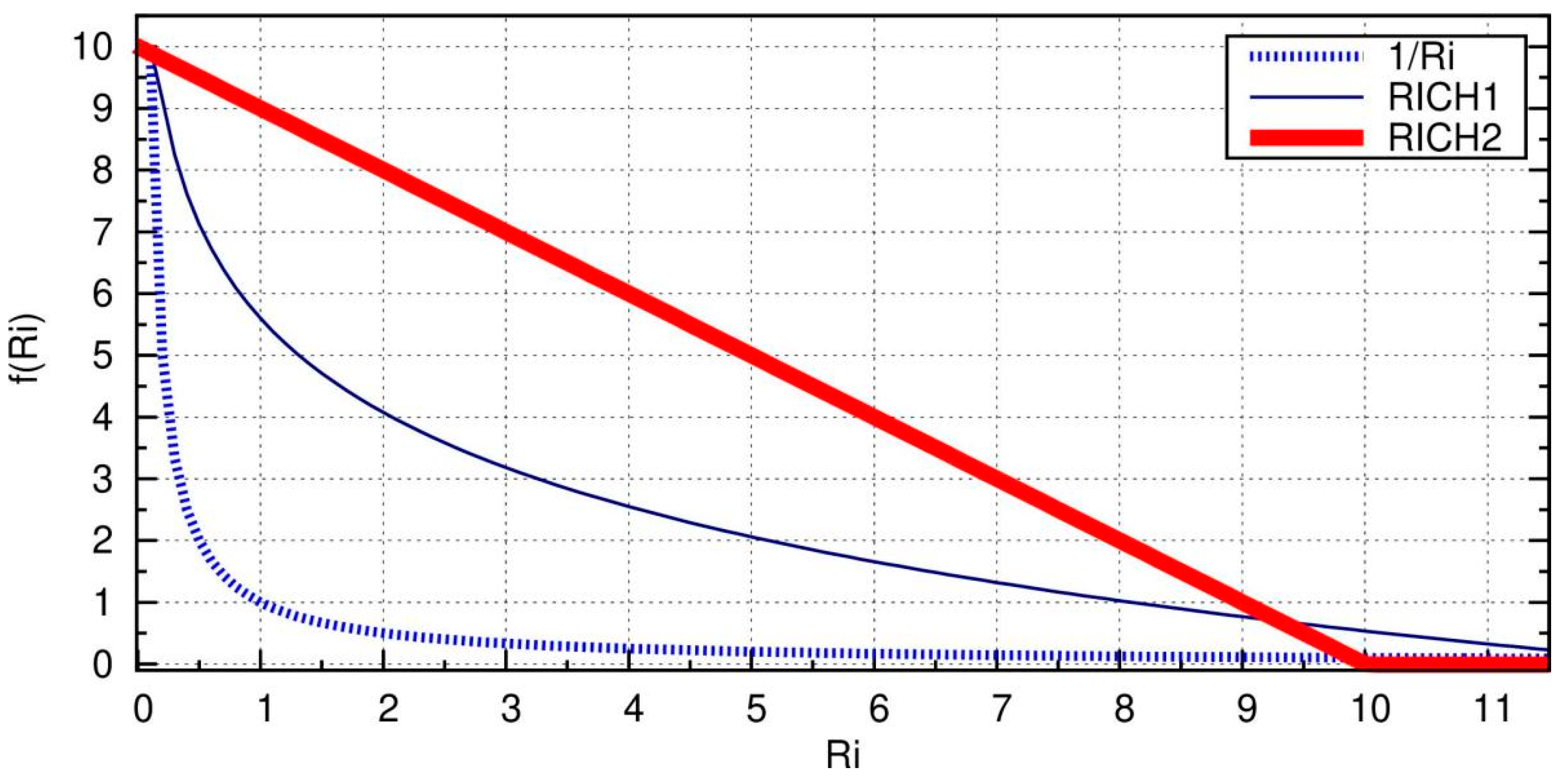
3.3.1. The Turbulence Predictors
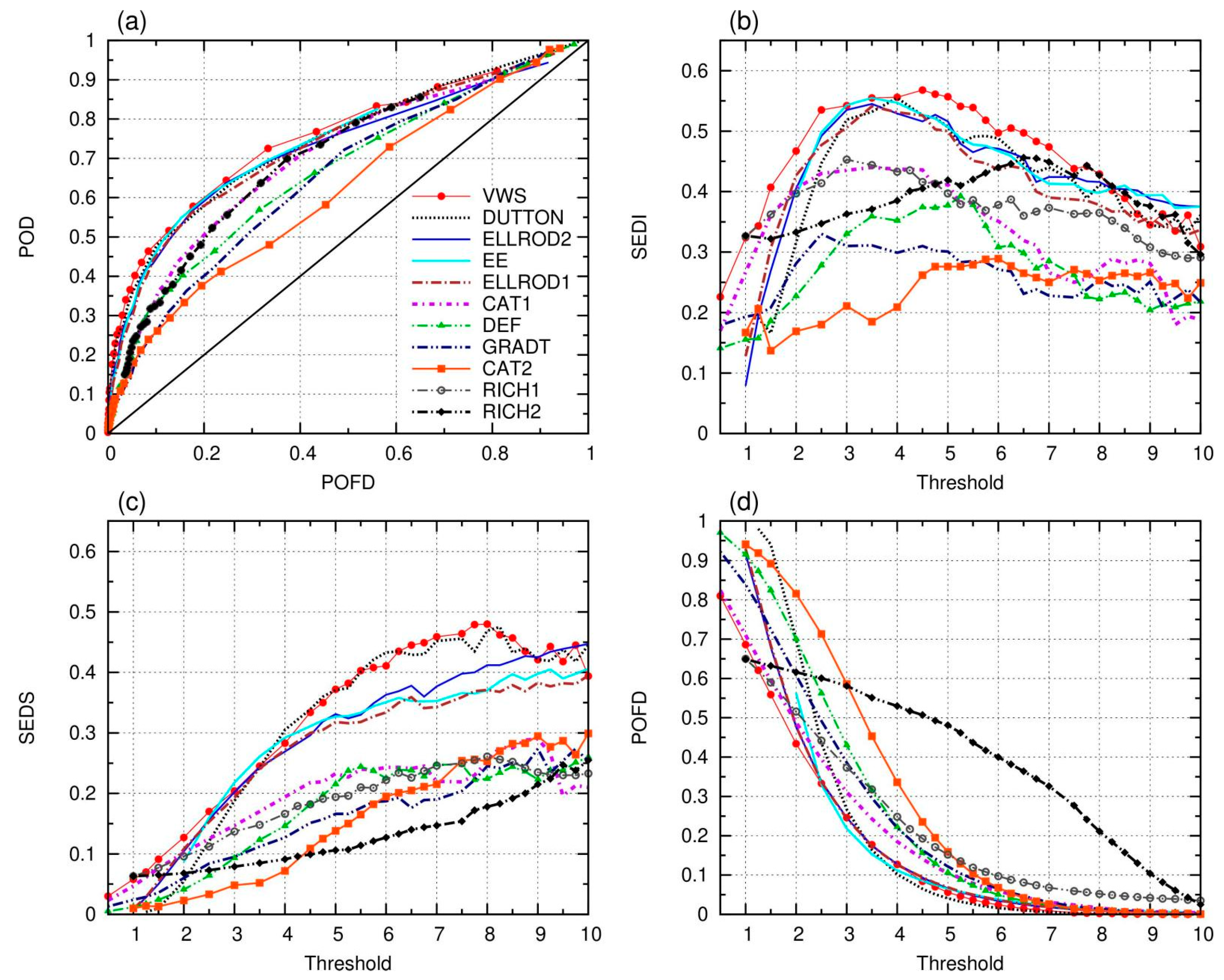
3.3.2. Evaluation of the Individual Turbulence Predictors
3.3.3. Combination of Turbulence Diagnostics
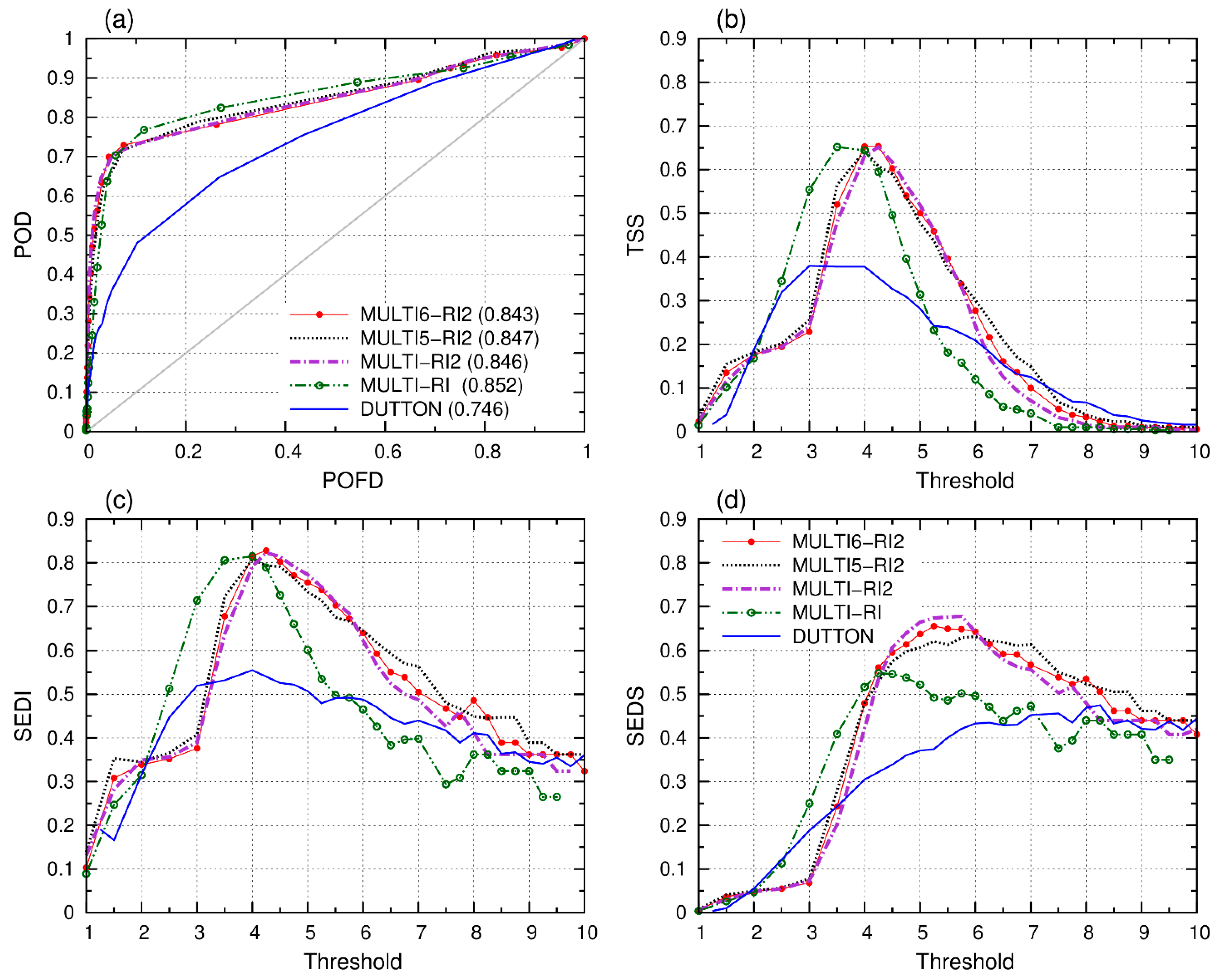
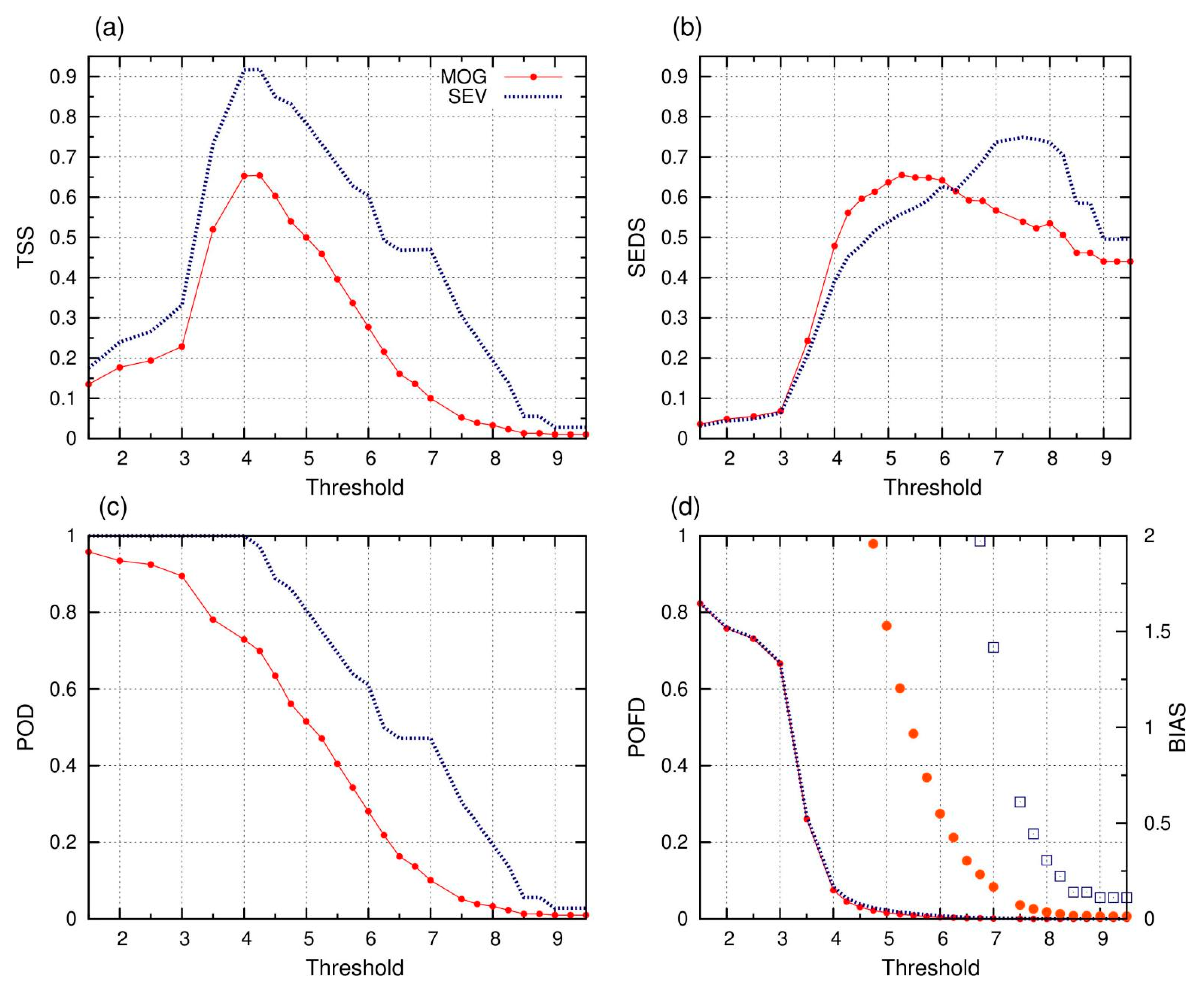
3.3.4. The Operational Turbulence Index and Its Forecasting Skill
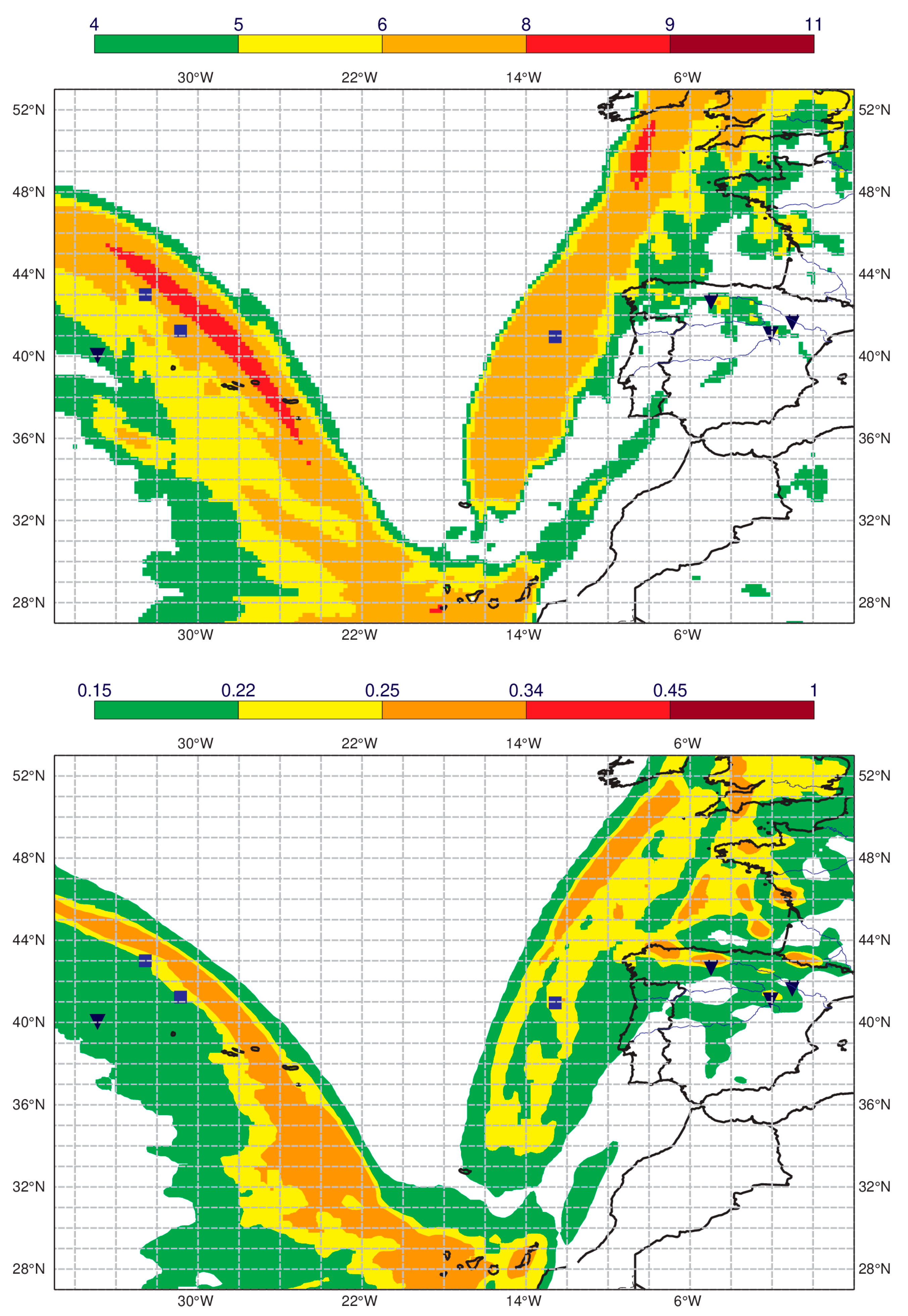
3.4. The Operational Turbulence Index
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Sharman, R.; Lane, T. Aviation Turbulence: Processes, Detection, Prediction; Springer International Publishing: Cham, Switzerland, 2016; pp. 42–273. [Google Scholar]
- Sharman, R.; Tebaldi, C.; Wiener, G.; Wolff, J. An Integrated Approach to Mid- and Upper-Level Turbulence Forecasting. Weather Forecast. 2006, 21, 268–287. [Google Scholar] [CrossRef]
- Mazon, J.; Rojas, J.I.; Lozano, M.; Pino, D.; Prats, X.; Miglietta, M.M. Influence of meteorological phenomena on worldwide aircraft accidents, 1967–2010. Met. Apps. 2018, 25, 236–245. [Google Scholar] [CrossRef]
- Gultepe, I.; Sharman, R.; Williams, P.D.; Zhou, B.; Ellrod, G.; Minnis, P.; Trier, S.; Griffin, S.; Yum, S.S.; Gharabaghi, B.; et al. A Review of High Impact Weather for Aviation Meteorology. Pure Appl. Geophys. 2019, 176, 1869–1921. [Google Scholar] [CrossRef]
- Kim, J.; Chun, H. A Numerical Study of Clear-Air Turbulence (CAT) Encounters over South Korea on 2 April 2007. J. Appl. Meteor. Climatol. 2010, 49, 2381–2403. [Google Scholar] [CrossRef]
- Lane, T.P.; Sharman, R.D.; Trier, S.B.; Fovell, R.G.; Williams, J.K. Recent Advances in the Understanding of Near-Cloud Turbulence. Bull. Am. Meteorol. Soc. 2012, 93, 499–515. [Google Scholar] [CrossRef] [Green Version]
- Sharman, R.D.; Trier, S.B.; Lane, T.P.; Doyle, J.D. Sources and dynamics of turbulence in the upper troposphere and lower stratosphere: A review. Geophys. Res. Lett. 2012, 39, L12803. [Google Scholar] [CrossRef] [Green Version]
- Lee, D.; Chun, H. A Numerical Study of Aviation Turbulence Encountered on 13 February 2013 over the Yellow Sea between China and the Korean Peninsula. J. Appl. Meteor. Climatol. 2018, 57, 1043–1060. [Google Scholar] [CrossRef]
- Maruhashi, J.; Serrão, P.; Belo-Pereira, M. Analysis of Mountain Wave Effects on a Hard Landing Incident in Pico Aerodrome Using the AROME Model and Airborne Observations. Atmosphere 2019, 10, 350. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Chun, H.; Sharman, R.D.; Keller, T.L. Evaluations of Upper-Level Turbulence Diagnostics Performance Using the Graphical Turbulence Guidance (GTG) System and Pilot Reports (PIREPs) over East Asia. J. Appl. Meteor. Climatol. 2011, 50, 1936–1951. [Google Scholar] [CrossRef]
- Ellrod, G.P.; Knapp, D.I. An Objective Clear-Air Turbulence Forecasting Technique: Verification and Operational Use. Weather Forecast. 1992, 7, 150–165. [Google Scholar] [CrossRef] [Green Version]
- Ellrod, G.P.; Knox, J.A. Improvements to an Operational Clear-Air Turbulence Diagnostic Index by Addition of a Divergence Trend Term. Weather Forecast. 2010, 25, 789–798. [Google Scholar] [CrossRef]
- Gill, P.G.; Buchanan, P. An ensemble based turbulence forecasting system. Met. Apps. 2014, 21, 12–19. [Google Scholar] [CrossRef]
- Kim, J.; Sharman, R.D.; Benjamin, S.G.; Brown, J.M.; Park, S.; Klemp, J.B. Improvement of Mountain-Wave Turbulence Forecasts in NOAA’s Rapid Refresh (RAP) Model with the Hybrid Vertical Coordinate System. Weather Forecast. 2019, 34, 773–780. [Google Scholar] [CrossRef]
- Kim, J.; Sharman, R.; Strahan, M.; Scheck, J.W.; Bartholomew, C.; Cheung, J.C.H.; Buchanan, P.; Gait, N. Improvements in Nonconvective Aviation Turbulence Prediction for the World Area Forecast System. Bull. Am. Meteorol. Soc. 2018, 99, 2295–2311. [Google Scholar] [CrossRef] [Green Version]
- ICAO. Meteorological Service for International Air Navigation: Annex 3 to the Convention on International Civil Aviation, 20th ed.; International Standards and Recommended Practices; International Civil Aviation Organization: Montreal, QC, Canada, 2018; p. 224, July 2018. [Google Scholar]
- Haiden, T.; Martin, J.; Frédéric, V.; Zied, B.-B.; Laura, F.; Fernando, P. Evaluation of ECMWF Forecasts, Including the 2021 Upgrade; Technical Memorandum; European Centre for Medium Range Weather Forecasts: Reading, UK, 2021; No. 884. [Google Scholar]
- Sherman, D.J. The Australian Implementation of AMDAR/ACARS and the Use of Derived Equivalent Gust Velocity as a Turbulence Indicator; Aeronautical Research Laboratories Structures Rep. 418: Melbourne, Australia, 1985; p. 28. [Google Scholar]
- Truscott, B.S. EUMETNET AMDAR AAA AMDAR Software Developments-Technical Specification; E_AMDAR/TSC/003; Met Office: Exeter, UK, 2000; p. 18. [Google Scholar]
- Kim, S.-H.; Chun, H.-Y. Aviation turbulence encounters detected from aircraft observations: Spatiotemporal characteristics and application to Korean Aviation Turbulence Guidance. Met. Apps. 2016, 23, 594–604. [Google Scholar] [CrossRef]
- Kim, S.-H.; Chun, H.-Y.; Kim, J.-H.; Sharman, R.D.; Strahan, M. Retrieval of eddy dissipation rate from derived equivalent vertical gust included in Aircraft Meteorological Data Relay (AMDAR). Atmos. Meas. Tech. 2020, 13, 1373–1385. [Google Scholar] [CrossRef] [Green Version]
- Gill, P.G. Objective verification of World Area Forecast Centre clear air turbulence forecasts. Met. Apps. 2014, 21, 3–11. [Google Scholar] [CrossRef]
- Storer, L.N.; Gill, P.G.; Williams, P.D. Multi-model ensemble predictions of aviation turbulence. Meteorol Appl. 2019, 26, 416–428. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Chun, H.; Chan, P.W. Comparison of Turbulence Indicators Obtained from In Situ Flight Data. J. Appl. Meteor. Climatol. 2017, 56, 1609–1623. [Google Scholar] [CrossRef]
- Malardel, S.; Wedi, N.; Deconinck, W.; Diamantakis, M.; Kühnlein, C.; Mozdzynski, G.; Hamrud, M.; Smolarkiewicz, P. A New Grid for the IFS. ECMWF Newsletter No. 146. 2016. Available online: https://www.ecmwf.int/en/elibrary/15041-newsletter-no-146-winter-2015-16 (accessed on 12 January 2022).
- Goecke, T.; Machulskaya, E. Aviation Turbulence Forecasting at DWD with ICON: Methodology, Case Studies, and Verification. Mon. Weather Rev. 2021, 149, 2115–2130. [Google Scholar] [CrossRef]
- Doswell, C.A., III; Davies-Jones, R.; Keller, D.L. On Summary Measures of Skill in Rare Event Forecasting Based on Contingency Tables. Weather Forecast. 1990, 5, 576–585. [Google Scholar] [CrossRef] [Green Version]
- McCann, D.W.; Knox, J.A.; Williams, P.D. An improvement in clear-air turbulence forecasting based on spontaneous imbalance theory: The ULTURB algorithm. Met. Apps. 2012, 19, 71–78. [Google Scholar] [CrossRef]
- Pearson, J.M.; Sharman, R.D. Prediction of Energy Dissipation Rates for Aviation Turbulence. Part II: Nowcasting Convective and Nonconvective Turbulence. J. Appl. Meteor. Climatol. 2017, 56, 339–351. [Google Scholar] [CrossRef] [Green Version]
- Ferro, C.A.T.; Stephenson, D.B. Extremal Dependence Index: Improved Verification Measures for Deterministic Forecasts of Rare Binary Events. Weather Forecast. 2011, 26, 699–713. [Google Scholar] [CrossRef] [Green Version]
- Mason, I. A model for assessment of weather forecasts. Aust. Meteor. Mag. 1982, 30, 291–303. [Google Scholar]
- Stephenson, D.B.; Casati, B.; Ferro, C.A.T.; Wilson, C.A. The extreme dependency score: A non-vanishing measure for forecasts of rare events. Met. Apps. 2008, 15, 41–50. [Google Scholar] [CrossRef]
- Hogan, R.J.; O’Connor, E.J.; Illingworth, A.J. Verification of cloud-fraction forecasts. Q.J.R. Meteorol. Soc. 2009, 135, 1494–1511. [Google Scholar] [CrossRef]
- Atlas, D.; Metcalf, J.I.; Richter, J.H.; Gossard, E.E. The Birth of “CAT” and Microscale Turbulence. J. Atmos. Sci. 1970, 27, 903–913. [Google Scholar] [CrossRef] [Green Version]
- Browning, K.A. Structure of the atmosphere in the vicinity of large-amplitude Kelvin-Helmholtz billows. Q.J.R. Meteorol. Soc. 1971, 97, 283–299. [Google Scholar] [CrossRef]
- Chapman, D.; Browning, K.A. Release of potential shearing instability in warm frontal zones. Q. J. R. Meteorol. Soc. 1999, 125, 2265–2289. [Google Scholar] [CrossRef]
- Thorpe, S.A. The axial coherence of Kelvin–Helmholtz billows. Q.J.R. Meteorol. Soc. 2002, 128, 1529–1542. [Google Scholar] [CrossRef]
- Medina, S.; Houze, R.A., Jr. Kelvin–Helmholtz waves in extratropical cyclones passing over mountain ranges. Q.J.R. Meteorol. Soc. 2016, 142, 1311–1319. [Google Scholar] [CrossRef] [Green Version]
- Storer, L.N.; Williams, P.D.; Gill, P.G. Aviation Turbulence: Dynamics, Forecasting, and Response to Climate Change. Pure Appl. Geophys. 2019, 176, 2081–2095. [Google Scholar] [CrossRef] [Green Version]
- Sharman, R.D.; Pearson, J.M. Prediction of Energy Dissipation Rates for Aviation Turbulence. Part I: Forecasting Nonconvective Turbulence. J. Appl. Meteor. Climatol. 2017, 56, 317–337. [Google Scholar] [CrossRef]
- Knox, J.A. Possible mechanisms of clear-air turbulence in strongly anticyclonic flows. Monthly Weather Review. 1997, 125, 1251–1259. [Google Scholar] [CrossRef]
- Overeem, A. Verification of Clear-Air Turbulence Forecasts; Technisch Rapport; KNMI: De Bilt, The Netherlands, 2002. [Google Scholar]


| Forecast | Observation | |
|---|---|---|
| Obs < oi (No) | Obs ≥ oi (Yes) | |
| Index < fi (No) | NN | NY |
| Index ≥ fi (Yes) | YN | YY |
| AMDAR DEVG (m s−1) | AIREP | ||||
|---|---|---|---|---|---|
| NON (0–2) | LGT (2–4.5) | MOD (4.5–7) | MOD-SEV (7–9) | MOD | SEV |
| 17,659 | 1377 | 76 | 8 | 185 | 37 |
| EE | log | 4.313 | 1 | 1 | 1.604 |
| ELLROD1 | log | 4.603 | 1 | 1 | 0.601 |
| ELLROD2 | log | 4.107 | 1 | 1 | 0.658 |
| VWS | SQRT | 7.239 | 100 | 0 | −3.995 |
| DUTTON | SQRT | 0.547 | 1 | 0 | −0.131 |
| CAT1 | log | 3.533 | 1 | 1 | 0.488 |
| DEF | SQRT | 2.14 | 1 | 0 | −2.773 |
| GRADT | SQRT | 4.697 | 100 | 0 | −2.549 |
| CAT2 | SQRT | 2.335 | 100 | 0 | −1.503 |
| Predictor | AUC | Combined Turbulence Index | |||
|---|---|---|---|---|---|
| MULTI | MULTI6 | MULTI5 | MULTI3 | ||
| EE | 0.744 | = AUC2 | = AUC2 | = AUC2 | = AUC2 |
| ELLROD1 | 0.735 | = AUC2 | = 0 | = AUC2 | = 0 |
| ELLROD2 | 0.730 | = AUC2 | = AUC2 | = AUC2 | = AUC2 |
| VWS | 0.756 | = AUC2 | = AUC2 | = AUC2 | = 0 |
| DUTTON | 0.746 | = AUC2 | = AUC2 | = AUC2 | = AUC2 |
| CAT1 | 0.703 | = AUC2 | = AUC2 | = 0 | = 0 |
| DEF | 0.669 | = AUC2 | = AUC2 | = 0 | = 0 |
| GRADT | 0.655 | = AUC2 | = 0 | = 0 | = 0 |
| CAT2 | 0.620 | = AUC2 | = 0 | = 0 | = 0 |
| Scores | Thresholds for MOD Turbulence | ||||
| 4 | 4.5 | 5 1 | 5.25 | 5.5 | |
| POD | 0.73 | 0.64 | 0.52 | 0.47 | 0.41 |
| POFD | 0.08 | 0.03 | 0.02 | 0.01 | 0.01 |
| BIAS | 5.42 | 2.58 | 1.53 | 1.20 | 0.97 |
| SEDI | 0.82 | 0.80 | 0.76 | 0.74 | 0.70 |
| SEDS | 0.48 | 0.60 | 0.64 | 0.66 | 0.65 |
| Scores | Thresholds for Severe Turbulence | ||||
| 4.25 | 7.0 | 7.5 | 7.75 | 8 | |
| POD | 0.97 | 0.47 | 0.31 | 0.25 | 0.19 |
| POFD | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 |
| BIAS | 30 | 1.42 | 0.61 | 0.44 | 0.31 |
| SEDI | 0.98 | 0.81 | 0.74 | 0.71 | 0.68 |
| SEDS | 0.45 | 0.74 | 0.75 | 0.74 | 0.74 |
| Forecast | Observation | |
|---|---|---|
| No | Yes | |
| < 5 (No) | 18,727 | 148 |
| ≥ 5 (Yes) | 310 | 158 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belo-Pereira, M. Aviation Turbulence Forecasting over the Portuguese Flight Information Regions: Algorithm and Objective Verification. Atmosphere 2022, 13, 422. https://doi.org/10.3390/atmos13030422
Belo-Pereira M. Aviation Turbulence Forecasting over the Portuguese Flight Information Regions: Algorithm and Objective Verification. Atmosphere. 2022; 13(3):422. https://doi.org/10.3390/atmos13030422
Chicago/Turabian StyleBelo-Pereira, Margarida. 2022. "Aviation Turbulence Forecasting over the Portuguese Flight Information Regions: Algorithm and Objective Verification" Atmosphere 13, no. 3: 422. https://doi.org/10.3390/atmos13030422
APA StyleBelo-Pereira, M. (2022). Aviation Turbulence Forecasting over the Portuguese Flight Information Regions: Algorithm and Objective Verification. Atmosphere, 13(3), 422. https://doi.org/10.3390/atmos13030422






