Predicting Daily PM2.5 Exposure with Spatially Invariant Accuracy Using Co-Existing Pollutant Concentrations as Predictors
Abstract
:1. Introduction
2. Methods
2.1. Study Area
2.2. Air Quality Measurements
2.3. Data
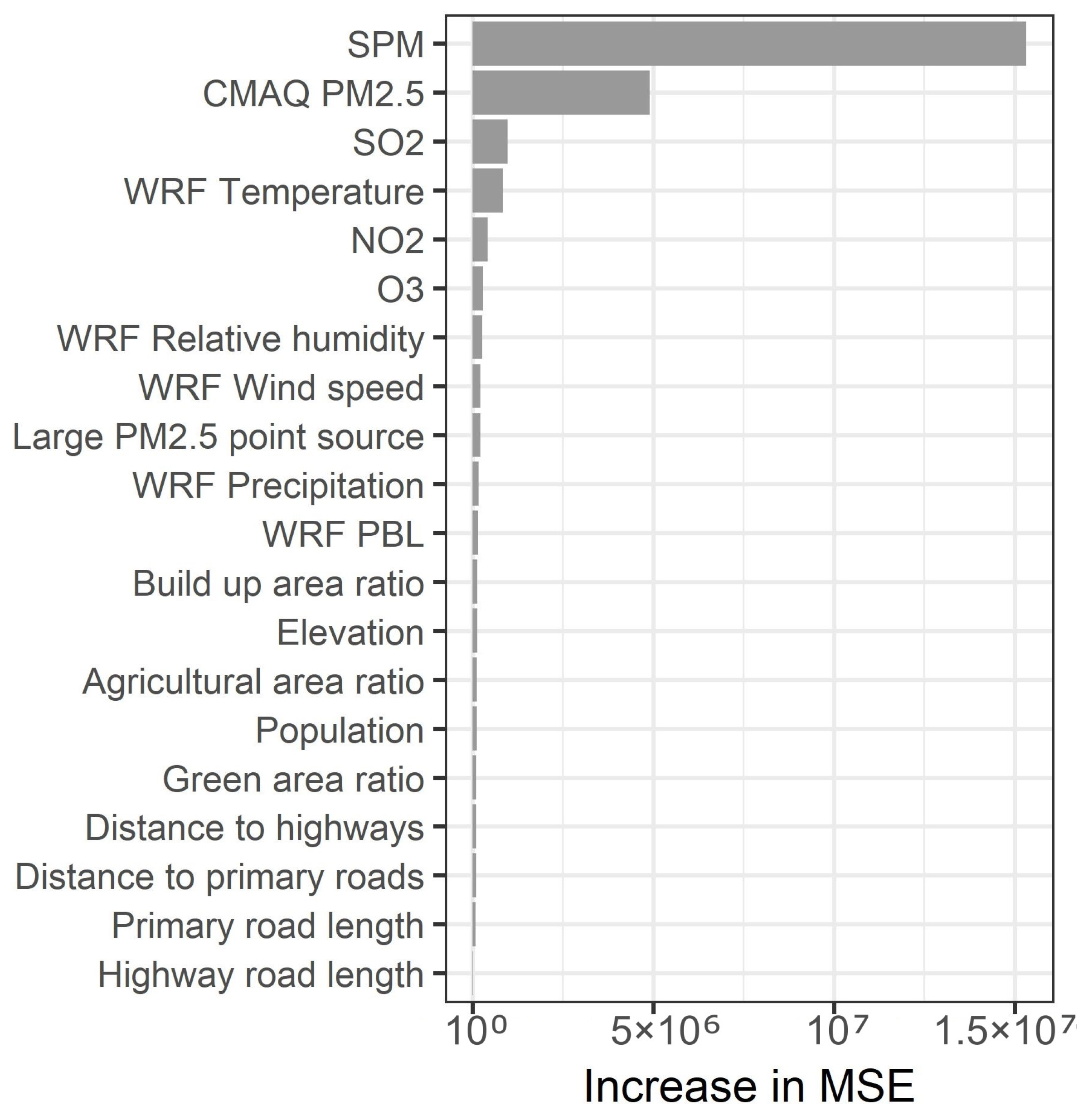
2.4. Random Forest
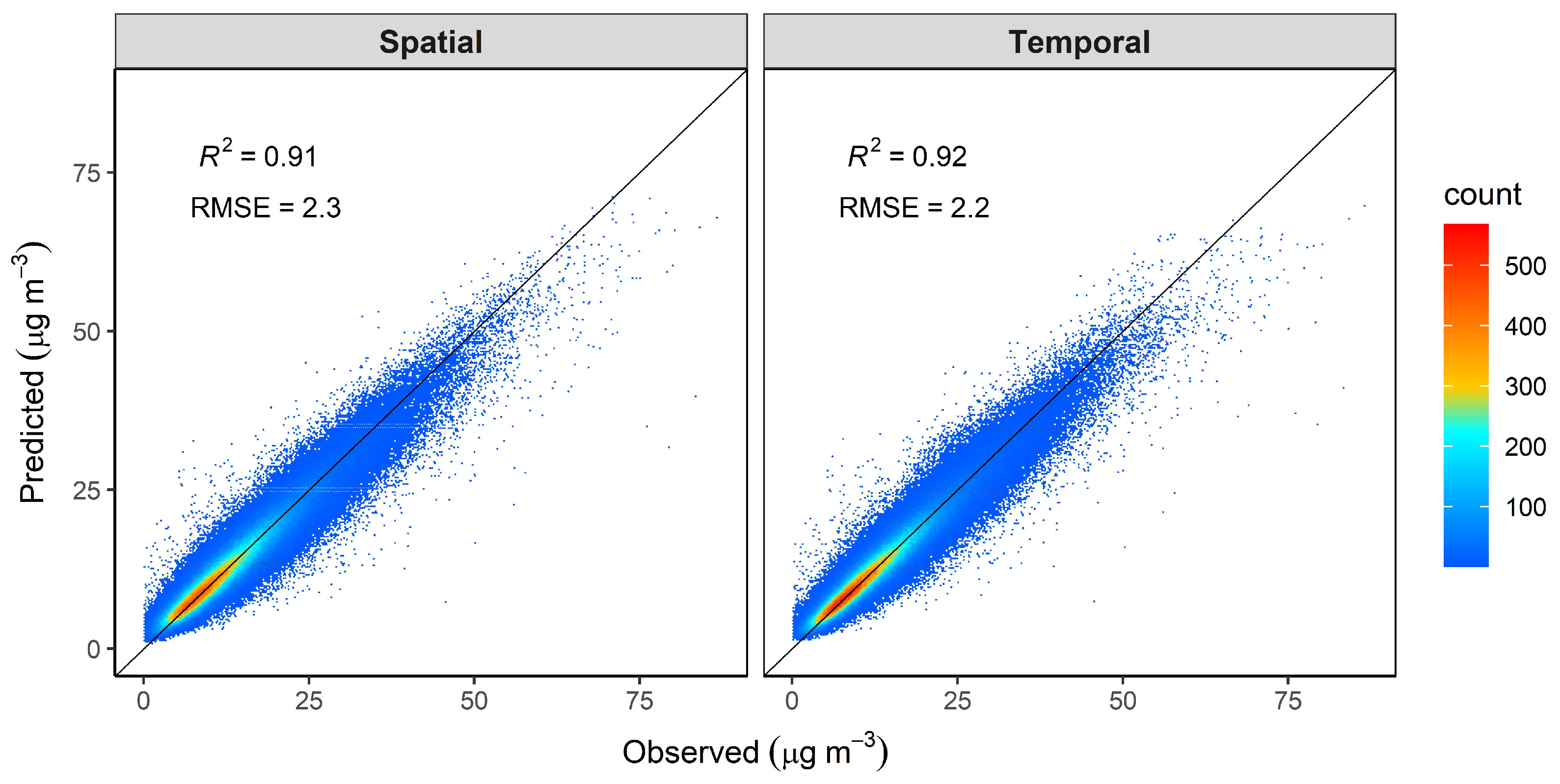
2.5. Validation
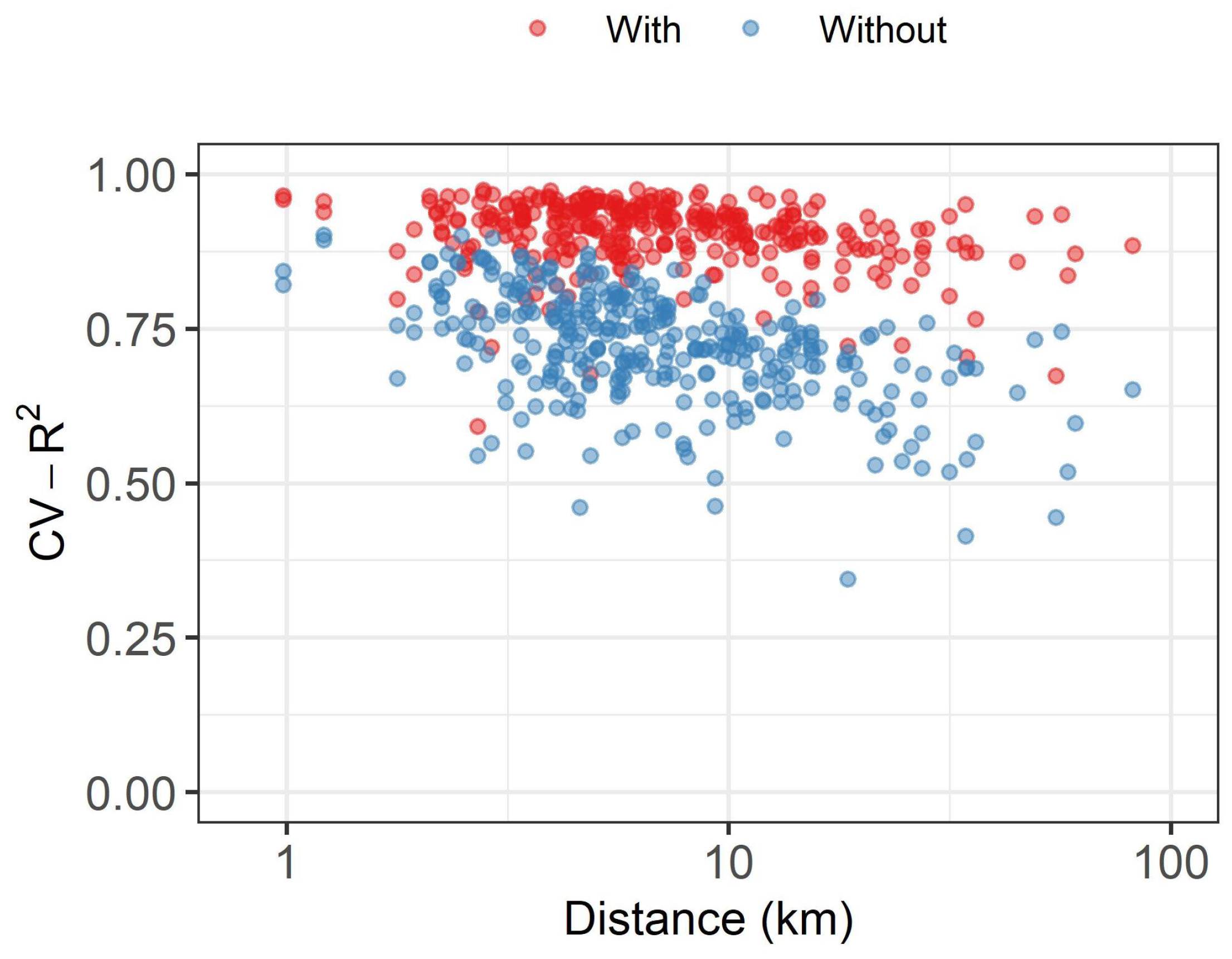
2.6. Spatial Dependency in the Model Performance
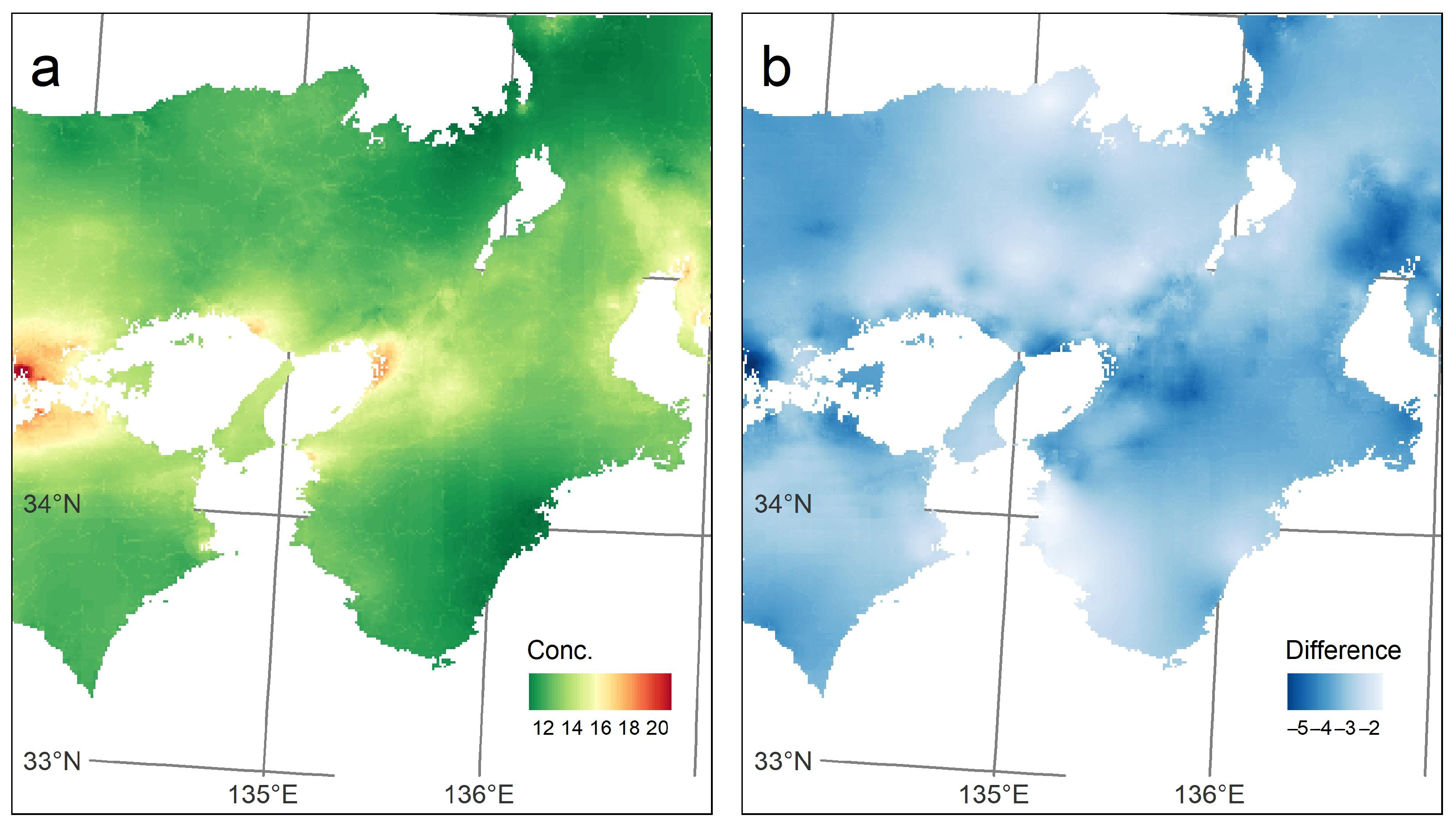
2.7. Estimation
2.8. Computation
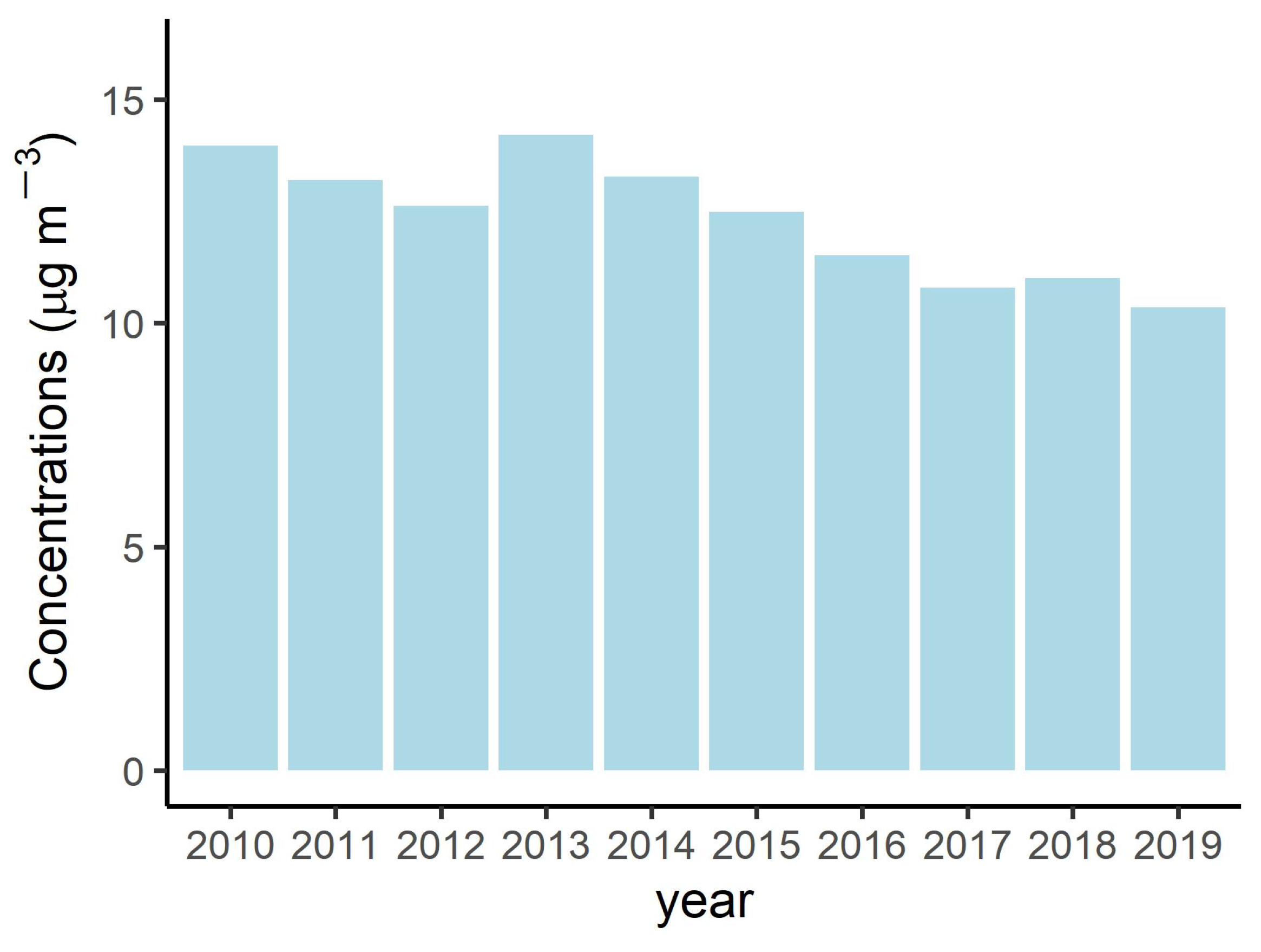
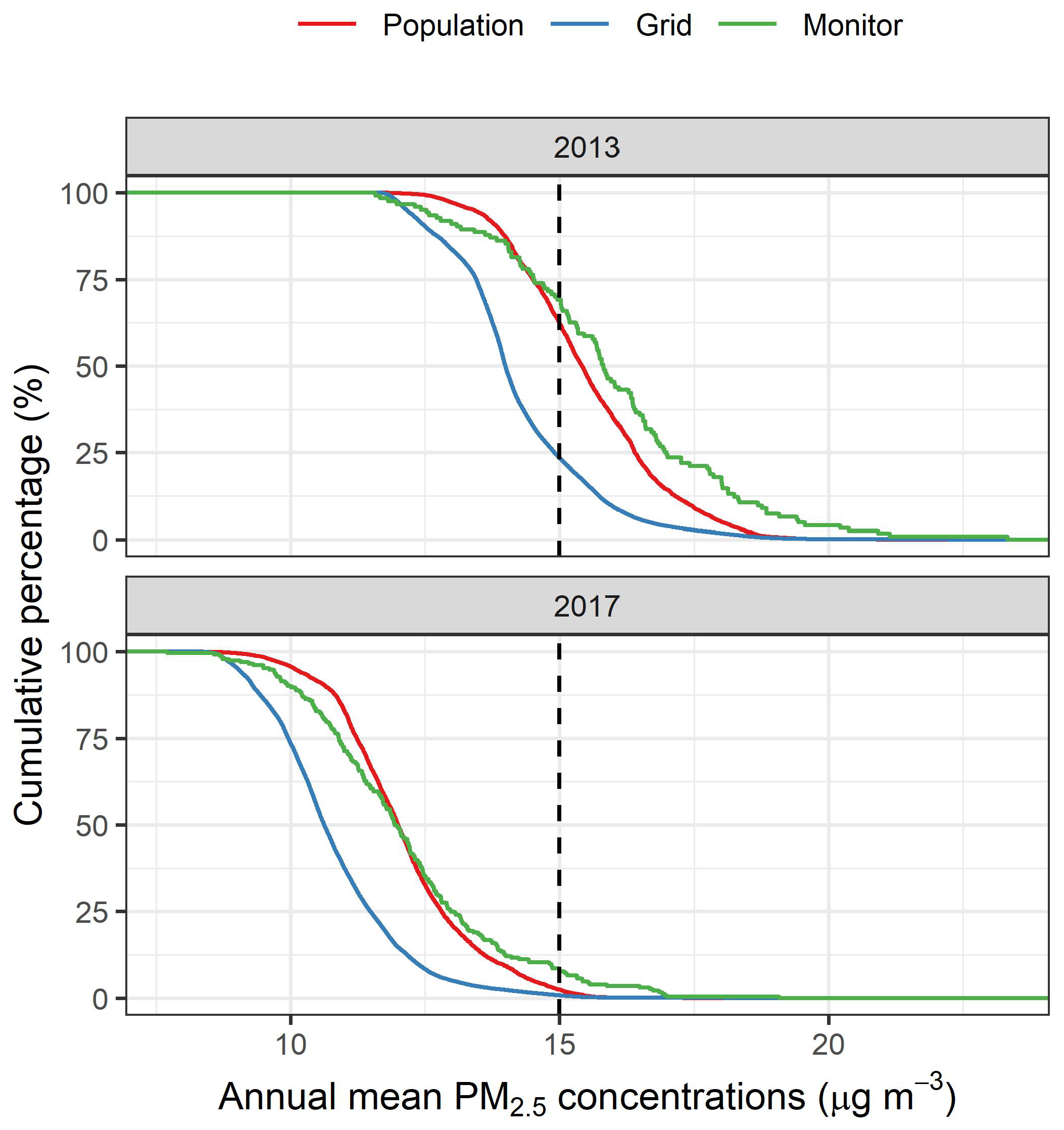
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rich, D.Q.; Demissie, K.; Lu, S.E.; Kamat, L.; Wartenberg, D.; Rhoads, G.G. Ambient air pollutant concentrations during pregnancy and the risk of fetal growth restriction. J. Epidemiol. Community Health 2009, 63, 488–496. [Google Scholar] [CrossRef] [PubMed]
- Faiz, A.S.; Rhoads, G.G.; Demissie, K.; Lin, Y.; Kruse, L.; Rich, D.Q. Does ambient air pollution trigger stillbirth? Epidemiology 2013, 24, 538–544. [Google Scholar] [CrossRef] [PubMed]
- Puett, R.C.; Hart, J.E.; Yanosky, J.D.; Spiegelman, D.; Wang, M.; Fisher, J.A.; Hong, B.; Laden, F. Particulate Matter Air Pollution Exposure, Distance to Road, and Incident Lung Cancer in the Nurses’ Health Study Cohort. Environ. Health Perspect. 2014, 122, 926–932. [Google Scholar] [CrossRef] [Green Version]
- Fleischer, N.L.; Merialdi, M.; van Donkelaar, A.; Vadillo-Ortega, F.; Martin, R.V.; Betran, A.P.; Souza, J.P. Outdoor Air Pollution, Preterm Birth, and Low Birth Weight: Analysis of the World Health Organization Global Survey on Maternal and Perinatal Health. Environ. Health Perspect. 2014, 122, 425–430. [Google Scholar] [CrossRef]
- Cohen, A.J.; Brauer, M.; Burnett, R.; Anderson, H.R.; Frostad, J.; Estep, K.; Balakrishnan, K.; Brunekreef, B.; Dandona, L.; Dandona, R.; et al. Estimates and 25-year trends of the global burden of disease attributable to ambient air pollution: An analysis of data from the Global Burden of Diseases Study 2015. Lancet 2017, 389, 1907–1918. [Google Scholar] [CrossRef] [Green Version]
- Hu, X.; Belle, J.H.; Meng, X.; Wildani, A.; Waller, L.A.; Strickland, M.J.; Liu, Y. Estimating PM2.5 Concentrations in the Conterminous United States Using the Random Forest Approach. Environ. Sci. Technol. 2017, 51, 6936–6944. [Google Scholar] [CrossRef]
- Stafoggia, M.; Bellander, T.; Bucci, S.; Davoli, M.; Hoogh, K.D.; Donato, F.D.; Gariazzo, C.; Lyapustin, A.; Michelozzi, P.; Renzi, M.; et al. Estimation of daily PM10 and PM2.5 concentrations in Italy, 2013–2015, using a spatiotemporal land-use random-forest model. Environ. Int. 2019, 124, 170–179. [Google Scholar] [CrossRef]
- Shtein, A.; Kloog, I.; Schwartz, J.; Silibello, C.; Michelozzi, P.; Gariazzo, C.; Viegi, G.; Forastiere, F.; Karnieli, A.; Just, A.C.; et al. Estimating Daily PM2.5 and PM10 over Italy Using an Ensemble Model. Environ. Sci. Technol. 2019, 54, 120–128. [Google Scholar] [CrossRef]
- Di, Q.; Amini, H.; Shi, L.; Kloog, I.; Silvern, R.; Kelly, J.; Sabath, M.B.; Choirat, C.; Koutrakis, P.; Lyapustin, A.; et al. An ensemble-based model of PM2.5 concentration across the contiguous United States with high spatiotemporal resolution. Environ. Int. 2019, 130, 104909. [Google Scholar] [CrossRef]
- Huang, C.; Hu, J.; Xue, T.; Xu, H.; Wang, M. High-Resolution Spatiotemporal Modeling for Ambient PM2.5 Exposure Assessment in China from 2013 to 2019. Environ. Sci. Technol. 2021, 55, 2152–2162. [Google Scholar] [CrossRef]
- Di, Q.; Kloog, I.; Koutrakis, P.; Lyapustin, A.; Wang, Y.; Schwartz, J. Assessing PM2.5 Exposures with High Spatiotemporal Resolution across the Continental United States. Environ. Sci. Technol. 2016, 50, 4712–4721. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Di, Q.; Amini, H.; Shi, L.; Kloog, I.; Silvern, R.F.; Kelly, J.T.; Sabath, M.B.; Choirat, C.; Koutrakis, P.; Lyapustin, A.; et al. Assessing NO2 Concentration and Model Uncertainty with High Spatiotemporal Resolution across the Contiguous United States Using Ensemble Model Averaging. Environ. Sci. Technol. 2019, 54, 1372–1384. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Wu, A.H.; Cheng, I.; Chen, J.C.; Wu, J. Spatiotemporal estimation of historical PM2.5 concentrations using PM10, meteorological variables, and spatial effect. Atmos. Environ. 2017, 166, 182–191. [Google Scholar] [CrossRef]
- Wang, X.; Sun, W. Meteorological parameters and gaseous pollutant concentrations as predictors of daily continuous PM2.5 concentrations using deep neural network in Beijing–Tianjin–Hebei, China. Atmos. Environ. 2019, 211, 128–137. [Google Scholar] [CrossRef]
- Araki, S.; Hasunuma, H.; Yamamoto, K.; Shima, M.; Michikawa, T.; Nitta, H.; Nakayama, S.F.; Yamazaki, S. Estimating monthly concentrations of ambient key air pollutants in Japan during 2010–2015 for a national-scale birth cohort. Environ. Pollut. 2021, 284, 117483. [Google Scholar] [CrossRef]
- Kawamoto, T.; Nitta, H.; Murata, K.; Toda, E.; Tsukamoto, N.; Hasegawa, M.; Yamagata, Z.; Kayama, F.; Kishi, R.; Ohya, Y.; et al. Rationale and study design of the Japan environment and children’s study (JECS). BMC Public Health 2014, 14, 25. [Google Scholar] [CrossRef] [Green Version]
- Katanoda, K.; Sobue, T.; Satoh, H.; Tajima, K.; Suzuki, T.; Nakatsuka, H.; Takezaki, T.; Nakayama, T.; Nitta, H.; Tanabe, K.; et al. An association between long-term exposure to ambient air pollution and mortality from lung cancer and respiratory diseases in Japan. J. Epidemiol. 2011, 21, 132–143. [Google Scholar] [CrossRef] [Green Version]
- Araki, S.; Shimadera, H.; Yamamoto, K.; Kondo, A. Effect of spatial outliers on the regression modelling of air pollutant concentrations: A case study in Japan. Atmos. Environ. 2017, 153, 83–93. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.D.; Zeng, Y.T.; Lung, S.C.C. A hybrid kriging/land-use regression model to assess PM2.5 spatial-temporal variability. Sci. Total Environ. 2018, 645, 1456–1464. [Google Scholar] [CrossRef]
- Chen, T.H.; Hsu, Y.C.; Zeng, Y.T.; Candice Lung, S.C.; Su, H.J.; Chao, H.J.; Wu, C.D. A hybrid kriging/land-use regression model with Asian culture-specific sources to assess NO2 spatial-temporal variations. Environ. Pollut. 2020, 259, 113875. [Google Scholar] [CrossRef]
- Byun, D.; Schere, K.L. Review of the Governing Equations, Computational Algorithms, and Other Components of the Models-3 Community Multiscale Air Quality (CMAQ) Modeling System. Appl. Mech. Rev. 2006, 59, 51–77. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B. A time-split nonhydrostatic atmospheric model for weather research and forecasting applications. J. Comput. Phys. 2008, 227, 3465–3485. [Google Scholar] [CrossRef]
- Thongthammachart, T.; Araki, S.; Shimadera, H.; Eto, S.; Matsuo, T.; Kondo, A. An integrated model combining random forests and WRF/CMAQ model for high accuracy spatiotemporal PM2.5 predictions in the Kansai region of Japan. Atmos. Environ. 2021, 262, 118620. [Google Scholar] [CrossRef]
- Araki, S.; Shima, M.; Yamamoto, K. Spatiotemporal land use random forest model for estimating metropolitan NO2 exposure in Japan. Sci. Total Environ. 2018, 634, 1269–1277. [Google Scholar] [CrossRef] [PubMed]
- Fukui, T.; Kokuryo, K.; Baba, T.; Kannari, A. Updating EAGrid2000-Japan emissions inventory based on the recent emission trends. J. Jpn. Soc. Atmos. Environ. 2014, 49, 117–125. [Google Scholar] [CrossRef]
- Vienneau, D.; de Hoogh, K.; Briggs, D. A GIS-based method for modelling air pollution exposures across Europe. Sci. Total Environ. 2009, 408, 255–266. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Brokamp, C.; Jandarov, R.; Rao, M.B.; LeMasters, G.; Ryan, P. Exposure assessment models for elemental components of particulate matter in an urban environment: A comparison of regression and random forest approaches. Atmos. Environ. 2017, 151, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Meng, X.; Hand, J.L.; Schichtel, B.A.; Liu, Y. Space-time trends of PM2.5 constituents in the conterminous United States estimated by a machine learning approach, 2005–2015. Environ. Int. 2018, 121, 1137–1147. [Google Scholar] [CrossRef]
- Ma, R.; Ban, J.; Wang, Q.; Zhang, Y.; Yang, Y.; He, M.Z.; Li, S.; Shi, W.; Li, T. Random forest model based fine scale spatiotemporal O3 trends in the Beijing-Tianjin-Hebei region in China, 2010 to 2017. Environ. Pollut. 2021, 276, 116635. [Google Scholar] [CrossRef]
- Wright, M.N.; Ziegler, A. ranger: A Fast Implementation of Random Forests for High Dimensional Data in C++ and R. J. Stat. Softw. 2017, 77, 1–17. [Google Scholar] [CrossRef] [Green Version]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Pebesma, E. Simple Features for R: Standardized Support for Spatial Vector Data. R J. 2018, 10, 439–446. [Google Scholar] [CrossRef] [Green Version]
- Pebesma, E. Stars: Spatiotemporal Arrays, Raster and Vector Data Cubes, R Package Version; 0.5-2; 2021. Available online: https://r-spatial.github.io/stars/ (accessed on 9 May 2022).
- Chen, G.; Li, S.; Knibbs, L.D.; Hamm, N.; Cao, W.; Li, T.; Guo, J.; Ren, H.; Abramson, M.J.; Guo, Y. A machine learning method to estimate PM2.5 concentrations across China with remote sensing, meteorological and land use information. Sci. Total Environ. 2018, 636, 52–60. [Google Scholar] [CrossRef] [PubMed]
- Jung, C.R.; Chen, W.T.; Nakayama, S.F. A national-scale 1-km resolution PM2.5 estimation model over japan using maiac aod and a two-stage random forest model. Remote Sens. 2021, 13, 3657. [Google Scholar] [CrossRef]
- Shimadera, H.; Kojima, T.; Kondo, A. Evaluation of Air Quality Model Performance for Simulating Long-Range Transport and Local Pollution of PM2.5 in Japan. Adv. Meteorol. 2016, 2016, 5694251. [Google Scholar] [CrossRef] [Green Version]
- Uno, I.; Wang, Z.; Yumimoto, K.; Itahashi, S.; Osada, K.; Irie, H.; Yamamoto, S.; Hayasaki, M.; Sugata, S. Is PM2.5 Trans-boundary Environmental Problem in Japan dramatically improving? J. Jpn. Soc. Atmos. Environ. 2017, 52, 177–184. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Araki, S.; Shimadera, H.; Hasunuma, H.; Yoda, Y.; Shima, M. Predicting Daily PM2.5 Exposure with Spatially Invariant Accuracy Using Co-Existing Pollutant Concentrations as Predictors. Atmosphere 2022, 13, 782. https://doi.org/10.3390/atmos13050782
Araki S, Shimadera H, Hasunuma H, Yoda Y, Shima M. Predicting Daily PM2.5 Exposure with Spatially Invariant Accuracy Using Co-Existing Pollutant Concentrations as Predictors. Atmosphere. 2022; 13(5):782. https://doi.org/10.3390/atmos13050782
Chicago/Turabian StyleAraki, Shin, Hikari Shimadera, Hideki Hasunuma, Yoshiko Yoda, and Masayuki Shima. 2022. "Predicting Daily PM2.5 Exposure with Spatially Invariant Accuracy Using Co-Existing Pollutant Concentrations as Predictors" Atmosphere 13, no. 5: 782. https://doi.org/10.3390/atmos13050782
APA StyleAraki, S., Shimadera, H., Hasunuma, H., Yoda, Y., & Shima, M. (2022). Predicting Daily PM2.5 Exposure with Spatially Invariant Accuracy Using Co-Existing Pollutant Concentrations as Predictors. Atmosphere, 13(5), 782. https://doi.org/10.3390/atmos13050782






