New Ways to Modelling and Predicting Ionosphere Variables
Abstract
:1. Introduction
1.1. About Linear and Complex Systems
1.2. About Complex Systems and Chaos
1.3. Solar–Terrestrial Physics/Space Weather and Chaos
1.4. The Advent of Machine Learning
1.5. The Machine-Learning “Black Box” Problem
2. The Need of a New Approach to Ionosphere Research
3. An Overview on Ionosphere Variability
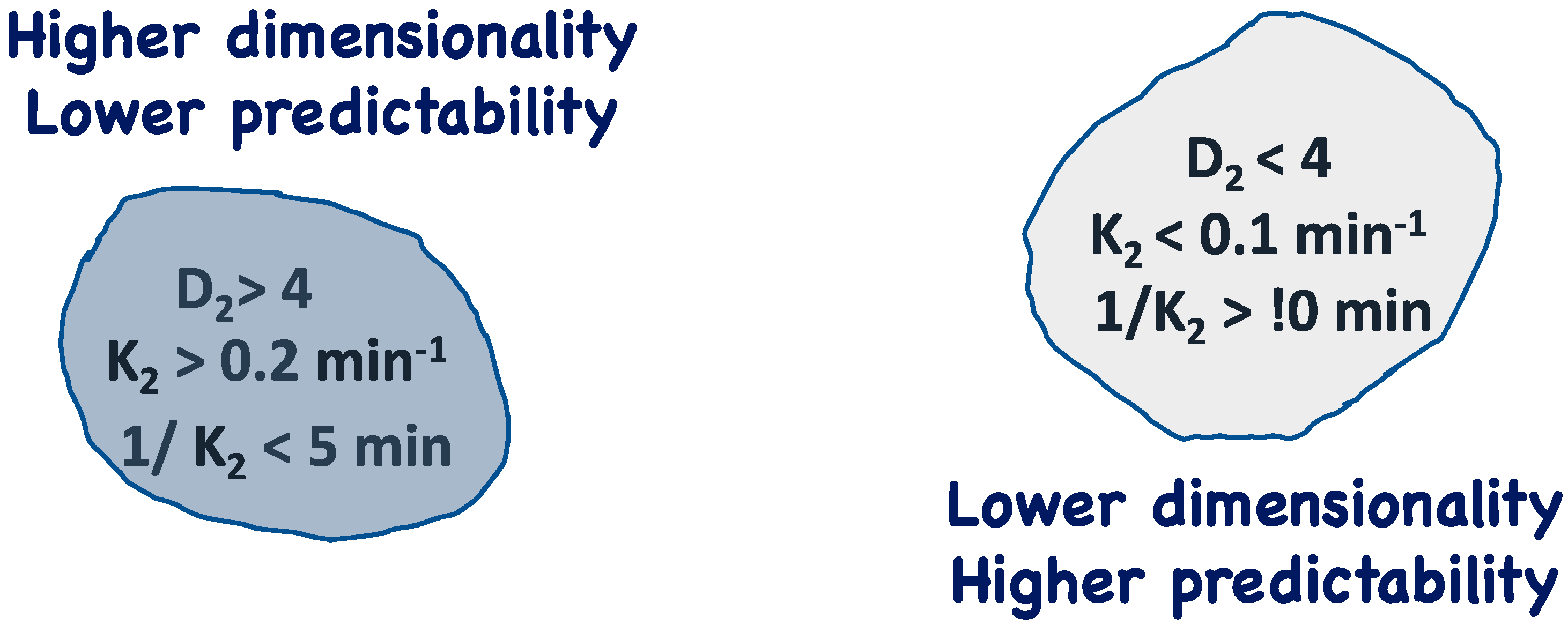
4. Chaos Theory and the Ionosphere
| Latitude | Solar Activity (F10.7) | Geomagnetic Activity | TEC Time Series Length | TEC Sampling Rate | D | Authors |
|---|---|---|---|---|---|---|
| Low | Low | Quiet | 4 days | 1 min | 2.23–2.74 | Unnikrishnan (2010) [37] |
| Low | Low | Disturbed | 4 days | 1 min | 3.37 | Unnikrishnan (2010) [37] |
| Low | Low | Monthly 5 quiet days | 1 year | 1 min | 3.5 | Ogunsua (2013) [38] |
| Low | Low | Monthly 5 disturbed days | 1 year | 1 min | 2.8 | Ogunsua (2013) [38] |
| Low | Low | Quiet | 4 months | 5 min | 4.61 * | Eapen et al. (2018) [39] |
| Low | Low | Disturbed | 4 months | 5 min | 3.74 * | Eapen et al. (2018) [39] |
| Middle | Low | Quiet | 4 months | 5 min | 4.63 * | Eapen et al. (2018) [39] |
| Middle | Low | Disturbed | 4 months | 5 min | 3.81 * | Eapen et al. (2018) [39] |
| Middle | Low | --- | 1 year | 1 min | 2.78 | Materassi et al. (2023) [12] |
| Middle | High | --- | 1 year | 1 min | 2.78 | Materassi et al. (2023) [12] |
| High | Low | Two intense storms in the period | 3 months (February–April) | 15 min | 5.63 | Kumar et al. (2004) [36] |
| High | Low | Quiet | 4 months | 5 min | 6.22 * | Eapen et al. (2018) [39] |
| High | Low | Disturbed | 4 months | 5 min | 3.77 * | Eapen et al. (2018) [39] |
Machine Learning and the Ionosphere
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baranger, M. Complexity, Chaos, and Entropy; New England Complex Systems Institute: Cambridge, MA, USA, 2000. [Google Scholar]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130. [Google Scholar] [CrossRef]
- Abarbanel, H.D.I.; Parlitz, U. Nonlinear Analysis of Time Series Data. In Handbook of Time Series Analysis—Recent Theoretical Developments and Applications; Schelter, B., Winterhalder, M., Timmer, J., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006; ISBN 9783527406234. [Google Scholar]
- Grassberger, P.; Procaccia, I. Characterization of Strange Attractors. Phys. Rev. Lett. 1983, 50, 346–349. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Estimation of the Kolmogorov entropy from a chaotic signal. Phys. Rev. A 1983, 28, 2591–2593. [Google Scholar] [CrossRef]
- Zeng, X. Chaos Theory and Its Application in the Atmosphere; Department of Atmospheric Sciences, Colorado State University: Fort Collins, CO, USA, 1992; Paper No. 504. [Google Scholar]
- Vassiliadis, D.V.; Sharma, A.S.; Eastman, T.E.; Papadopoulos, K. Low-dimensional chaos in magnetospheric activity from AE time series. Geophys. Res. Lett. 1990, 17, 1841–1844. [Google Scholar] [CrossRef]
- Consolini, G.; Alberti, T.; De Michelis, P. On the Forecast Horizon of Magnetospheric Dynamics: A Scale-to-Scale Approach. J. Geophys. Res. Space Phys. 2018, 123, 9065–9077. [Google Scholar] [CrossRef]
- Kurths, J.; Herzel, H. An attractor in a solar time series. Phys. D Nonlinear Phenom. 1987, 25, 165–172. [Google Scholar] [CrossRef]
- Romanelli, L.; Figliola, M.A.; Hirsch, F.A.; Radicella, S.M. Chaotic behaviour of solar radio flux. Sol. Phys. 1987, 110, 391–395. [Google Scholar] [CrossRef]
- Romanelli, L.; Figliola, M.A.; Hirsch, F.A. Deterministic chaos and natural phenomena. J. Stat. Phys. 1988, 53, 991–994. [Google Scholar] [CrossRef]
- Materassi, M.; Alberti, T.; Migoya-Orué, Y.; Radicella, S.M.; Consolini, G. Chaos and Predictability in Ionospheric Time Series. Entropy 2023, 25, 368. [Google Scholar] [CrossRef]
- Gimeno, L.; García, R.; Pacheco, J.; Hernández, E.; Ribera, P. Predictability of global surface temperature by means of nonlinear analysis. Earth Planet. Sci. Lett. 2001, 184, 561–565. [Google Scholar] [CrossRef]
- Baker, D.N. Solar-Terrestrial Data Science: Prior Experience and Future Prospects. Front. Astron. Space Sci. 2020, 7, 540133. [Google Scholar] [CrossRef]
- Ghosh, S.; Dasgupta, R. Machine Learning and Life Sciences. In Machine Learning in Biological Sciences; Springer: Singapore, 2022. [Google Scholar] [CrossRef]
- Genser, A. Machine Learning for Traffic Management In Urban Transportation Networks. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2022. [Google Scholar] [CrossRef]
- Musser, M.; Garriott, A. Machine Learning and Cybersecurity: Hype and Reality; Center for Security and Emerging Technology: Washington, DC, USA, 2021. [Google Scholar] [CrossRef]
- Batta, M. Machine Learning Algorithms—A Review. Int. J. Sci. Res. 2018, 18, 381–386. [Google Scholar]
- Brunette, E.S.; Flemmer, R.C.; Flemmer, C.L. A review of artificial intelligence. In Proceedings of the 4th International Conference on Autonomous Robots and Agents, Wellington, New Zealand, 10–12 February 2009; pp. 385–392. [Google Scholar]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 1–74. [Google Scholar] [CrossRef] [PubMed]
- Saha, N.; Swetapadma, A.; Mondal, M. A Brief Review on Artificial Neural Network: Network Structures and Applications. In Proceedings of the 9th International Conference on Advanced Computing and Communication Systems (ICACCS), Coimbatore, India, 17–18 March 2023; pp. 1974–1979. [Google Scholar]
- Camporeale, E.; Chu, X.; Agapitov, O.V.; Bortnik, J. On the generation of probabilistic forecasts from deterministic models. Space Weather 2019, 17, 455–475. [Google Scholar] [CrossRef]
- Li, S.; Sun, Y.; Chen, C. An interpretable machine learning procedure which unravels hidden interplanetary drivers of the low latitude dayside magnetopause. Space Weather 2023, 21, e2022SW003391. [Google Scholar] [CrossRef]
- Chapman, S. The absorption and dissociative or ionizing effect of monochromatic radiation in an atmosphere on a rotating earth. Proc. Phys. Soc. 1931, 43, 26. [Google Scholar] [CrossRef]
- Nishida, A. Early Japanese contributions to space weather research (1945–1960). Hist. Geo Space Sci. 2010, 1, 1–12. [Google Scholar] [CrossRef]
- Appleton, E.V. Two Anomalies in the Ionosphere. Nature 1946, 157, 691. [Google Scholar] [CrossRef]
- Balan, N.; Liu, L.; Le, H. A brief review of equatorial ionization anomaly and ionospheric irregularities. Earth Planet. Phys. 2018, 2, 257–275. [Google Scholar] [CrossRef]
- Rishbeth, H. How the thermospheric circulation affects the ionospheric F2-layer. J. Atmos. Sol. Terr. Phys. 1998, 60, 1385–1402. [Google Scholar] [CrossRef]
- Rishbeth, H.; Mendillo, M. Patterns of F2-layer variability. J. Atmos. Sol. Terr. Phys. 2001, 63, 1661–1680. [Google Scholar] [CrossRef]
- Yu, T.; Wan, W.; Liu, L.; Zhao, B. Global scale annual and semi-annual variations of daytime NmF2 in the high solar activity years. J. Atmos. Sol. Terr. Phys. 2004, 66, 1691–1701. [Google Scholar] [CrossRef]
- Chibbaro, S.; Rondoni, L.; Vulpiani, A. Reductionism, Emergence and Levels of Reality; Springer: Berlin/Heidelberg, Germany, 2014; ISBN 9783319063607. [Google Scholar]
- Mendillo, M. Day-to-day variability of the ionosphere. In The Dynamical Ionosphere; Elsevier: Amsterdam, The Netherlands, 2020; p. 442. [Google Scholar] [CrossRef]
- Liu, H.; Yamazaki, Y.; Lei, J. Space Physics and Aeronomy Collection Volume 4: Upper Atmosphere Dynamics and Energetics, Geophysical Monograph 261, 1st ed.; Wang, W., Zhang, Y., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2021. [Google Scholar] [CrossRef]
- Tsagouri, I.I.; Themens, D.D.R.; Belehaki, A.; Shim, J.-S.; Hoque, M.M.; Nykiel, G.; Borries, C.; Morozova, A.; Barata, T.; Miloch, W.J. Ionosphere Variability II: Advances in theory and modeling. Adv. Space Res. 2023, in press. [Google Scholar] [CrossRef]
- Mendez, A.L. How deterministic is the Earth ionosphere’s response to solar activity? Astrophys. Space Sci. 2022, 367, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Kumar, K.S.; Kumar, C.V.A.; George, B.; Renuka, G.; Venugopal, C. Analysis of the fluctuations of the total electron content (TEC) measured at Goose Bay using tools of nonlinear methods. J. Geophys. Res. Space Phys. 2004, 109, A02308. [Google Scholar] [CrossRef]
- Unnikrishnan, K. A comparative study on chaoticity of equatorial/low latitude ionosphere over Indian subcontinent during geomagnetically quiet and disturbed periods. Nonlinear Process. Geophys. 2010, 17, 765–776. [Google Scholar] [CrossRef]
- Ogunsua, B.O.; Laoye, J.A.; Fuwape, I.A.; Rabiu, A.B. The comparative study of chaoticity and dynamical complexity of the low-latitude ionosphere, over Nigeria, during quiet and disturbed days. Nonlinear Process. Geophys. 2014, 21, 127–142. [Google Scholar] [CrossRef]
- Eapen, S.; Asokan, K.; Kumar, K.S.; Ramamohan, T.R.; Kumar, A. Comparison of Variations of TEC at Disturbed and Quiet Time Using Nonlinear Dynamics Tools. J. Geophys. Res. Space Phys. 2018, 123, 7740–7754. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep Learning in Neural Networks: An Overview. Neural Netw. 2018, 61, 85–117. [Google Scholar] [CrossRef]
- Cander, L.R. Artificial neural network applications in ionospheric studies. Ann. Geophys. 1998, 41, 5–6. [Google Scholar] [CrossRef]
- Tulunay, E.; Senalp, E.T.; Radicella, S.M.; Tulunay, Y. Forecasting total electron content maps by neural network technique. Radio Sci. 2006, 41, 1–12. [Google Scholar] [CrossRef]
- Habarulema, J.B.; McKinnell, L.-A.; Cilliers, P.J. Prediction of global positioning system total electron content using Neural Networks over South Africa. J. Atmos. Solar-Terr. Phys. 2007, 69, 1842–1850. [Google Scholar] [CrossRef]
- Habarulema, J.B.; McKinnell, L.-A.; Cilliers, P.J.; Opperman, B.D. Application of neural networks to South African GPS TEC modelling. Adv. Space Res. 2009, 43, 1711–1720. [Google Scholar] [CrossRef]
- Habarulema, J.B.; McKinnell, L.-A.; Opperman, B.D.L. Regional GPS TEC modeling; Attempted spatial and temporal extrapolation of TEC using neural networks. J. Geophys. Res. Space Phys. 2011, 116, 1–14. [Google Scholar] [CrossRef]
- Huang, Z.; Yuan, H. Ionospheric single-station TEC short-term forecast using RBF neural network. Radio Sci. 2014, 49, 283–292. [Google Scholar] [CrossRef]
- Tebabal, A.; Radicella, S.; Nigussie, M.; Damtie, B.; Nava, B.; Yizengaw, E. Local TEC modelling and forecasting using neural networks. J. Atmos. Solar-Terr. Phys. 2018, 172, 143–151. [Google Scholar] [CrossRef]
- Tebabal, A.; Radicella, S.; Damtie, B.; Migoya-Orue’, Y.; Nigussie, M.; Nava, B. Feed forward neural network based ionospheric model for the East African region. J. Atmos. Solar-Terr. Phys. 2019, 191, 105052. [Google Scholar] [CrossRef]
- Li, X.; Zhou, C.; Tang, Q.; Zhao, J.; Zhang, F.; Xia, G.; Liu, Y. Forecasting Ionospheric foF2 Based on Deep Learning Method. Remote. Sens. 2021, 13, 3849. [Google Scholar] [CrossRef]
- Biswas, M.R.; Alzubaidi, M.S.; Shah, U.; Abd-Alrazaq, A.A.; Shah, Z. A Scoping Review to Find out Worldwide COVID-19 Vaccine Hesitancy and Its Underlying Determinants. Vaccines 2022, 9, 1243. [Google Scholar] [CrossRef]
- Taylor, S.J.; Letham, B. Forecasting at scale. Am. Stat. 2018, 72, 37–45. [Google Scholar] [CrossRef]
- Bi, C.; Ren, P.; Yin, T.; Xiang, Z.; Zhang, Y. Modeling and Forecasting Ionospheric foF2 Variation in the Low Latitude Region during Low and High Solar Activity Years. Remote. Sens. 2022, 14, 5418. [Google Scholar] [CrossRef]
- Reddybattula, K.D.; Jayaweera, D. Effective solar prosumer identification using net smart meter data. Int. J. Elect. Power Energy Syst. 2022, 118, 105823. [Google Scholar] [CrossRef]
- Smirnov, A.; Shprits, Y.; Prol, F.; Lühr, H.; Berrendorf, M.; Zhelavskaya, I.; Xiong, C. A novel neural network model of Earth’s topside ionosphere. Sci. Rep. 2023, 13, 1303. [Google Scholar] [CrossRef] [PubMed]
- Priyadarshi, S.; Syam, W.; Roqué, A.A.G.; Conesa, A.P.; Buscarlet, G.; Pérez, R.O.; Orso, M.D. Machine Learning-Based Ionospheric Modelling Performance During High Ionospheric Activity. In Proceedings of the International Technical Meeting, ION ITM 2023, Long Beach, CA, USA, 24–26 January 2023. [Google Scholar]
- Yu, S.; Ma, J. Experimental investigation on performance of hybrid PCM’s on addition of nano particles in thermal energy storage. Mater Today Proc. 2019, 17, 271–276. [Google Scholar]
- Duncan, D.; Räth, C. Optimizing the combination of data-driven and model-based elements in hybrid reservoir computing. Chaos 2023, 33, 103109. [Google Scholar] [CrossRef]




| System | Parameter | D2 | K2 | Authors |
|---|---|---|---|---|
| Sun | Radio pulsations | 3.2–3.8 | 0.04 | [9] Kurths Herzel (1987) |
| F10.7 | 3.3–4.5 | 0.02–0.04 | [10] Romanelli et al (1987) | |
| F10.7 | 3.5 | 0.07 | [11] Romanelli et al. (1988) | |
| Magnetosphere | AE | 3.3 | 0.08 | [11] Romanelli et al. (1988) |
| AE | 3.6 | 0.2 | [7] Vassiliadis et al. (1990) | |
| AE & SYM-H | 1–4 | 0.2–0.02 | [8] Consolini et al. (2018) | |
| Ionosphere | foF2 | 3.4 | 0.04 | [11] Romanelli et al. (1988) |
| TEC | 2.78 | 0.12–0.13 | [12] Materassi et al. (2023) | |
| Troposphere | Annual mean global surface temperature (1856–1998) | 1.99–3.25 * | 0.137 * | [13] Gimeno et al. (2001) |
| Latitude | Solar Activity (F10.7) | Geomagnetic Activity | foF2 Time Series Length | foF2 Sampling Rate | D | Authors |
|---|---|---|---|---|---|---|
| High | Low | --- | 2 years | 1 h | 3.4 | Romanelli et al., 1988 [11] |
| Middle high | Low | --- | 83 days | 1 h | 3.0 | Mendez, 2022 [35] |
| Middle high | Low | --- | 83 days | 1 h | 3.3 | Mendez, 2022 [35] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radicella, S.M. New Ways to Modelling and Predicting Ionosphere Variables. Atmosphere 2023, 14, 1788. https://doi.org/10.3390/atmos14121788
Radicella SM. New Ways to Modelling and Predicting Ionosphere Variables. Atmosphere. 2023; 14(12):1788. https://doi.org/10.3390/atmos14121788
Chicago/Turabian StyleRadicella, Sandro M. 2023. "New Ways to Modelling and Predicting Ionosphere Variables" Atmosphere 14, no. 12: 1788. https://doi.org/10.3390/atmos14121788
APA StyleRadicella, S. M. (2023). New Ways to Modelling and Predicting Ionosphere Variables. Atmosphere, 14(12), 1788. https://doi.org/10.3390/atmos14121788






