Rainfall Variability and Teleconnections with Large-Scale Atmospheric Circulation Patterns in West-Central Morocco

Abstract

Morocco is characterized by a semi-arid climate influenced by the Mediterranean, Atlantic, and Saharan environments, resulting in high variability in rainfall and hydrological conditions. Certain regions suffer from insufficient understanding concerning the spatiotemporal patterns of precipitation, along with facing recurrent periods of drought. This study aims to characterize the current trends and periodicities of precipitation in west-central Morocco at monthly and annual scales, using data from six rain gauges. The link between monthly precipitation and both the North Atlantic Oscillation (NAO) and the Western Mediterranean Oscillation (WeMO) indices was tested to identify potential teleconnections with large-scale variability modes. The results reveal interannual variability in precipitation and climate indices, while showing decreasing insignificant trends in annual precipitation. On a monthly scale, temporal precipitation patterns are similar to the annual scale. Furthermore, a remarkably robust and significant component with a periodicity of 6–8 years emerges consistently across all monitoring stations. Intriguingly, this band exhibits a more pronounced presence on the plains as opposed to the mountainous stations. Additionally, it is noteworthy that the NAO modulated winter precipitation, whereas the influence of the WeMO extends until March and April. This mode could be linked to the fluctuations of the WeMO from 1985 to 2005 and, subsequently, to NAO variations. Indeed, this is consistent with the strong significant correlations observed between rainfall and the NAO/WeMO. This study serves as a baseline for future research aiming to understand the influence of climate indices on rainfall in the North African region.

1. Introduction

A special report of The Intergovernmental Panel on Climate Change (IPCC) [1] predicts a global increase of 1.5 °C in temperature by 2050 at the current rate of greenhouse gas emissions. This warming is often accompanied by precipitation anomalies [2,3] and changes in atmospheric circulation. The link between these precipitation anomalies and global atmospheric circulations has long attracted the attention of researchers, and it is the subject of several studies and investigations in various regions of the world [4,5,6,7,8,9,10,11,12]. In the northern part of the Mediterranean, for example, the results of Tabari and Willems (2018) [13] show a large impact of the winter North Atlantic Oscillation (NAO) and the summer Western Mediterranean Oscillation (WeMO [14]) on the extreme variability of precipitation, with significant relationships of 70% and 45%, respectively.

Furthermore, in the Mediterranean region, the analysis of precipitation trends shows great variability and a significant decrease in precipitation since the 1970s [15,16,17,18]. This downward trend seems to be greater in winter [4]. Some works link the variability of Mediterranean precipitation with the NAO [19,20,21]. In this context, the arid and semi-arid zones of North Africa, particularly Morocco, are experiencing significant rainfall deficits manifested by periods of severe drought [2], threatening socioeconomic stability and natural resources. The work of Knippertzet al. (2003) [22] showed that precipitation in the northwest of the country shows a clear link with atmospheric pressure variations over the North Atlantic during boreal winter (DJF), with a relatively strong negative correlation with the NAO. Other works show that winter precipitation is negatively correlated with the NAO all over Morocco [23,24,25]. The negative phase normally leads to increased precipitation, and the positive phase is usually linked to precipitation deficits [26,27]. This is particularly important to understand in greater detail, given that central-western Morocco is an arid area at high risk of climate change consequences [28,29,30,31].

Admittedly, similar analyses have been conducted in the Mediterranean region or in a similar arid environment. However, we used wavelet analysis to better illustrate the variability of precipitation and to study the temporal and frequency characteristics of precipitation variations over time. Indeed, this study employs a wavelet transform to decompose a signal into different frequency components. By applying this technique to precipitation data, valuable information can be obtained regarding patterns of variation at different time scales. Additionally, this work explores the influence of well-known climate modes on the rainfall variability in the study area in order to best understand local climate drivers. The research also investigates how climate change influences rainfall patterns in the region and how changes in large-scale circulation patterns can exacerbate or mitigate local rainfall variability.

Herein, we investigate the occurrence of periodicities and trends in precipitation time series and climate indices, using the continuous wavelet transform (CWT) and Mann–Kendall trend test (MK) methods. In addition, we examine potential correlations between both the NAO and the WeMO indices and the rainfall series, to investigate the potential influence of these large-scale atmospheric circulations on the local precipitation.

2. Materials and Methods

2.1. Study Area and Data Description

Tensift, a region in west-central Morocco, comprises several watersheds with six rain gauges: Aghbalou, Marrakech, N’kouris, Sidi Rahal, Tahanaout, and Talmest. This rain-gauge network is managed by the Tensift Hydraulic Basin Agency, which ensures the monitoring of measurements and the categorization of data. These stations are located in the north of the High Atlas mountain range. This large sub-continental area is characterized by a well-developed hydrographic network and high slopes, as well as a poorly permeable substrate. The climate in this area is continental and arid, influenced by disturbing oceanic flows coming from the north and northwest. These morphological and climatic conditions favor significant rainfall that can reach 700 mm per year on the summits of the Atlas [32] (Figure 1).

The data used are based on long-term monthly precipitation statistics obtained from the Tensift Hydraulic Basin Agency over a common period of 36 years for six gauging stations between 1985 and 2021 (

Table 1. Precipitation Station Characteristics.

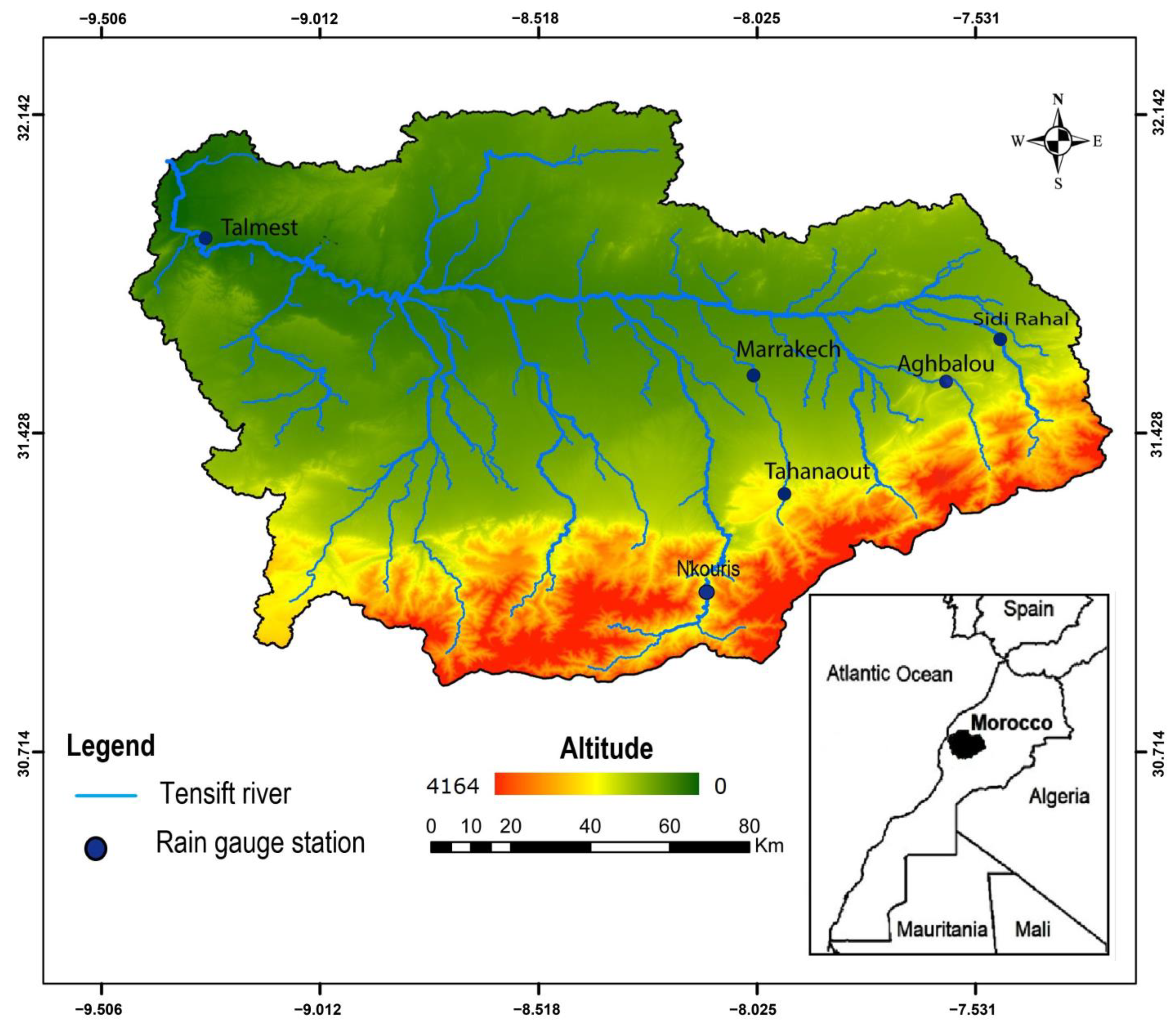
Station	Name	Latitude (°)	Longitude (°)	Elevation (m)	Period of Observation
S1	N’kouris	31.059	−8.141	1100	1985/86–2020/21
S2	Aghbalou	31.320	−7.751	1070	1985/86–2020/21
S3	Tahanaout	31.292	−7.963	925	1985/86–2020/21
S4	Sidi Rahal	31.639	−7.476	690	1985/86–2020/21
S5	Marrakech	31.613	−8.033	460	1985/86–2020/21
S6	Talmest	31.865	−9.271	53	1985/86–2020/21

). Moreover, we used the NAO index, which is based on the surface sea-level pressure difference between the Subtropical (Azores) High and the Subpolar Low (Iceland). The NAO index was obtained from the National Weather Service–Climate Prediction Center website at https://www.cpc.ncep.noaa.gov (accessed on 20 February 2023). Furthermore, the WeMO index is defined as the difference of normalized values of pressure at sea level between Padua (in the north of Italy) and the Cadiz-San Fernando (in the southwest of Spain). The WeMO was obtained from https://crudata.uea.ac.uk/cru/data/moi/ (accessed on 20 February 2023).

2.2. Data Quality Control

• Homogeneity

The precipitation data series, like any other meteorological parameter, are subject to potential errors. These could stem from issues with the measurement systems, changes in the measurement sites’ environment, or the influence of human behavior on the measured values [33]. The statistical analysis of nonhomogeneous data can lead to erroneous results, hence the particular importance of homogeneity analyses, especially considering the difficulty of finding homogeneous regions and chronological series with a common observation period [34].

The data were assessed for homogeneity using the nonparametric Levene test [35], which is tailored to exhibit reduced sensitivity towards deviations from the assumption of data normality. The P-values obtained from the test range from 0.23 to 0.98, indicating that the variances are homogeneous across the groups, since the P-values are not statistically significant.

• Autocorrelation

Autocorrelation plays a significant role in the realm of time series analysis, as it allows us to comprehend the interdependence between consecutive observations within the series. When the autocorrelation is strong in a time series, it greatly facilitates the prediction of future observations. Essentially, autocorrelation provides valuable insights into how each data point relates to its preceding data points, enabling us to make more accurate forecasts for the time series. This holds considerable importance numerous statistical tests that involve time series heavily rely on this assumption.

In the correlation plot below (Figure 2), the confidence band serves as a visual representation of the uncertainty associated with the mean estimate, providing a clear indication of the range within which the true value is likely to lie with 95% confidence. The graph indicates that the lags do not exert a significant effect, as they fall within the bounds, making it difficult to distinguish them from being zero. The autocorrelation function (ACF) examines whether the current value of the data consistently relies on its past values (lags). In this case, we notice a distinct spike at lag 0, which holds a particular implication. It implies that each monthly value is primarily independent of the previous ones when attempting to explain them solely through autocorrelation. In simpler terms, the lack of significant lags, except for the spike at lag 0, suggests that the monthly values do not rely heavily on their own past values to be explained. They exhibit a level of independence from one another, signifying that the autocorrelation property does not strongly influence their behavior.

2.3. Statistical Analyses

• Trend analysis

The nonparametric Mann–Kendall (MK) trend test [36,37,38,39] is a rank-based test of randomness against monotonic trends [40,41,42,43]. The MK test was utilized to identify a notable downward or upward trend in long-term time data. It relies on two hypotheses: one is null (H0) and the other is the alternative hypothesis (H1). The H0 hypothesis expresses the existence of a null trend, while the H1 elucidates a significant upward or downward trend in the rainfall data [42]. In this study, we applied the MK test to monthly, total, and seasonal rainfall data.

The Mann–Kendall test statistic S is calculated as:

$$S=\sum _{i=1}^{n-1}\sum _{j=i+1}^{n}sign(X_i-X_j)$$

(1)

where in the time series, X_i and X_j are the ordered data points at times i and j, and sign () is defined as:

$$Sign\left(X_j-X\right)=\left\{\begin{array}{c}+1, if \left(X_j-X_i\right)>0\\ 0, if \left(X_j-X_i\right)=0\\ -1, if \left(X_j-X_i\right)<0\end{array}\right.$$

(2)

S is asymptotically normally distributed with a mean of zero and variance given by Equation (3) [44].

$$Var\left(S\right)=\frac{\left[n\left(n-1\right)\left(2n+5\right)\right]-{\sum }_{i=1}^m{t}_i\left(t_i-1\right)\left(2t_i+5\right)}{18}$$

(3)

where n is the sample size, m is a correction term representing the number of groups with tied values, t_i is the number of ties in group i, and the summation is over all ties. The standardized normal test statistic, Z, is calculated as in Equation (4) using the values of S and Var (S) in Equations (1) and (3), respectively.

$$Z=\left\{\begin{array}{c}\frac{S-1}{\sqrt{Var\left(S\right)}} for S>0;\\ Z=0 for S=0;\\ \frac{S+1}{\sqrt{Var\left(S\right)}} for S>0;\end{array}\right.$$

(4)

A positive Z value indicates that there is an upward trend, whereas a negative value represents a downward trend in the time series. To determine the presence of statistically significant trends at level p, the absolute value of Z is compared with Z1 − p/2, and if Z > Z1 − p/2, then the trend is significant at level p. In this study, we have used a significance level of p = 0.05.

• Sen’s estimator

Sen’s slope is a nonparametric method developed by Sen (1968) [45] for estimating the slope of a trend in a sample of n pairs of data, computed based on the equation:

$$Q_i=\frac{X_j-X_i}{j-i} for i=1,\dots \dots .,n$$

(5)

where X_j and X_i are the data values at time j and i (j > i), respectively.

• Frequency analysis

The continuous wavelet transform (CWT) method is used to decompose a signal into a sum of waves of finite length, localized in time, to explore the frequency content of the precipitation series. This decomposition allows for analysis of the localized variations of power (variance) and visualization of the instationaries within the signal’s frequency content [46]. The frequency analysis shows the power (absolute value squared) of the wavelet transform for the monthly rainfall using the Morlet mother wavelet and the actual oscillations of the individual wavelets, rather than just their magnitude. The absolute value squared provides information on the relative power at a certain time and a certain scale.

The wavelet transform (WT) method enables the analysis of one-dimensional time series data by transforming it into a two-dimensional representation in the frequency–time domain [43]. This simultaneously preserves the temporal and spectral signatures of a series without assuming stationarity, which makes the WT a choice technique for hydroclimatic analyses because rarely are climatic and hydrologic time series stationary in nature [43].

In this study, we use the Morlet wavelet as the mother wavelet. This method has been widely used before for analyzing hydroclimatic time series [47]. The Morlet wavelet consists of a plane wave by a Gaussian time domain window and is given by the expression:

$${\mathsf{\varphi }}_0\left(\eta \right)={\pi }^{-1/4}{e}^{-i{\omega }_0\eta }{e}^{-{\eta }^2/2}$$

(6)

where ϕ₀ is a wavelet function that depends on a non−dimensional time parameter and ω₀ is dimensionless frequency j = √ − 1 [43].

In mathematical terms, a WT decomposes a signal s(t) from a mother function Ψ by dilation and translation to daughter wavelets [Ψ_b,a(t)] [48]:

$${\psi }_{b,a}\left(t\right)=\frac{1}{\sqrt{a}}\psi \left(\frac{t-b}{a}\right)$$

(7)

where a denotes the scale (dilation) parameter and b represents the translation of the scaled wavelet along the temporal axis. The factor (a)^−1/2 in Equation (7) is an energy normalization that keeps the daughter wavelets’ energy the same as the mother wavelet’s energy. The continuous wavelet transform (CWT) of a real signal s(t) with the analyzing wavelet Ψ(t) as a convolution integral is as follows:

$$\begin{array}{c}{W}_{\left(b,a\right)}=\frac{1}{{\left(a\right)}^{\frac{1}{2}}}\int \psi \mathrm{\ast }\left(\frac{t-b}{a}\right)\mathrm{s}\left(\mathrm{t}\right)\mathrm{d}\mathrm{t}\\ C_{\psi }={\int }_0^{+\propto }\frac{{\left|\widehat{\Psi }\right(\omega \left)\right|}^2}{\omega }d\omega <+\propto \end{array}$$

(8)

where W(b,a) are the wavelet coefficients, which measure the degree of similarity between the daughter wavelet and the original signal in each section. The variation of those coefficients describes the changing level of similarity between the original signal in time and frequency and the daughter wavelets. ψ ∗ is the complex conjugate of $\widehat{\Psi }$ and ψ is the Fourier transform of $\widehat{\Psi }$ (Equation (8)).

• Correlation between precipitation and climate oscillations

The analysis of the linear relationship between the climate indices, such as the NAO and the WeMO, and precipitation was performed by Pearson’s correlation coefficient on a monthly basis from September to August. The range of this coefficient is [−1, +1]. Negative values indicate a trend in which the increase in the values of one variable is associated with the decrease in the values of the other variable, whereas positive values indicate a tendency of one variable to decrease or increase together with another variable and vice versa.

3. Results and Discussion

3.1. Precipitation Variability in Tensift

The Mann–Kendall and Sen’s slope estimator tests were applied on monthly and annual time scales at each station. The analysis of monthly and annual sums of precipitation trends for the west-center of Morocco suggest that precipitation amounts vary unevenly across the study area (

Table 2. Summary of trend magnitudes detected for rainfall time series. (Mk corresponds to Z statistics of the Mann–Kendall test, and SS corresponds to Sens’s slope).

Station		September	October	November	December	January	February	March	April	May	June	July	August	Annual
N’kouris	Mk	1.23	0.62	0.91	−1.55	0.13	−0.77	−0.51	0.89	1.73	−0.32	1.06	0.63	−0.05
	SS	0.08	0.15	0.18	−0.5	0	−0.32	−0.13	0.04	0.09 *	0	0	0	−0.17
Aghbalou	Mk	1.33	−1.26	0.16	−1.10	−0.46	−1.73	0.57	0.91	0.17	−1.98	−0.23	1.22	−0.72
	SS	0.36	−0.66	0.08	−0.42	−0.33	−1.29 *	0.35	0.78	0.08	−0.24 *	0	0.10	−1.36
Tahnaout	Mk	0.95	−1.33	0.28	−0.51	0.10	−0.76	0.70	0.95	0.95	−1.71	0.49	1.62	0.04
	SS	0.13	−0.43	0.17	−0.26	0.01	−0.56	0.44	0.51	0.30	−0.18 *	0	0.09	0.09
Sidi Rahal	Mk	0.15	−1.18	0.24	−0.28	−0.08	−1.03	−0.55	0.47	0.19	−1.70	−0.63	0.81	−0.74
	SS	0	−0.37	0.09	−0.05	−0.03	−0.54	−0.17	0.2	0.02	−0.06 *	0	0.02	−1.03
Marrakech	Mk	0.33	−1.33	0.19	−0.80	−0.53	−0.45	−0.50	0.46	0.81	−0.61	1.36	1.71	−0.79
	SS	0	−0.2	0.09	−0.28	−0.13	−0.11	−0.18	0.03	0.02	0	0	0.00	−0.68
Talmest	Mk	0.06	−1.08	0.76	−1.51	−0.91	−0.57	−1.51	−0.34	0.58	−1.30	−0.48	0.57	−1.40
	SS	0	−0.17	0.41	−0.88	−0.45	−0.24	−0.51	−0.07	0	0	0	0	−3.02

Positive values = positive trend, (–) = negative trend, (*) = significant trend. Significance is at the 90% confidence level.

). The statistical significance trend (p-value < 0.1) of monthly precipitation was detected with the MK test, whereas the trend magnitude was evaluated with the Sen’s slope method. The MK test statistic Z indicates trends of both decreasing (Z < 0) and increasing (Z > 0) nature. In June, significant negative trends were observed in the Aghbalou, Sidi Rahal, and Tahnaout stations. Additionally, the Aghbalou station exhibited a significant negative trend in February. Conversely, the N’kouris station showed an increasing significant trend in May.The MK test did not detect any statistically significantly trends of monthly precipitation only in the Talmest station.

In fact, from the comparison of the results shown in Table 2, an increasing trend of monthly precipitations in almost all stations in September, November, May, and August is evident, while in December, February, and June a decreasing trend of precipitation is shown. Moreover, a mixed trend in October, January, March, April, and July is detected. The annual sum of precipitation and the winter months (DJF) showed a decreasing insignificant trend.

As the results indicate, the Sens’s slope estimator (SS) detected a greater lack of trends. All of the annual rainfall series were characterized by a negative trend ranging between −3.027 mm/y at Talmest station and −0.680 mm/y at Marrakech station. In particular, an upward trend was only recorded at the Tahanaout station, with 0.092 mm/y.

The results obtained for the Tensift basin are in line with Khomsi et al. 2013 [49], who detected a decreasing trend in rainfall at all stations except at Tahanaout station, where an increasing trend of 41.6 mm/decade was observed. The decreasing trends in rainfall as found in this research are consistent with previously published works in different geographical locations in Morocco that revealed a downward trend of about −19% of annual rainfall [50,51,52]. There has been a decreasing trend in rainfall since the 1970s, especially the winter and spring rainfalls [49,52,53], where the duration of the dry period increased with time during these two seasons. Indeed, the drought has become more pronounced after the 1970s from the south to the north of Morocco [28]. This tendency towards dry conditions confirms the warming observed on a global scale and can be related to atmospheric circulations and the decreasing frequency of disturbances from the north, which frequently affect this region in winter and spring [50,51].

3.2. Potential Relationship with Large-Scale Climate Variability Modes

Different studies have been carried out in order to determine the relationship between the large-scale patterns of atmospheric circulation and Moroccan precipitation variability [22,25,54,55,56]. Here, correlations of monthly precipitation for different stations are calculated with the NAO and the WeMo indices. The choice of monthly, rather than seasonal, correlation is based on the high intraseasonal variability (month-to-month) of these indices [22].

The correlation of the NAO variability and precipitation (Figure 3) shows a high significant negative value of correlation during December (−0.42 to −0.61) at all stations. The highest temporal variability occurs in Talmest, which is the closest station to the Atlantic Ocean in the study area. In order to achieve the predictability and estimation of NAO influence on the North Atlantic region, the study of its variability over the last decades in the context of past behavior is crucial [57]. Most NAO studies center around the boreal winter months, which experience the highest amplitudes of disturbances and the most dynamic atmospheric activity [58].

Our results show that precipitation is negatively correlated with the WeMO index in most of the stations, as shown in Figure 4. Significant negative correlation was found to be strong in November, between −0.39 and −0.56 at Tahnaout and Marrakech stations, respectively, and March, around −0.42 at Aghbalou station and −0.55 at Sidi Rahal station.

Highlighting the point that linear regression models can aid in exploring the in-fluence of global patterns on local effects, we can accurately evaluate the proportion of variability that is correlated with the relationships among the NAO, WeMO, and pre-cipitation in the respective time series. Indeed, several researchers [16,22,59,60] reported on the complexity of a possible link between natural climate variability modes and hydrological conditions [16,22].

Knippertz et al. (2003) [22] and Nouacer et al. (2016) [20] found that the variability of precipitation in Morocco is controlled by the variations of the NAO, particularly in winter months, when the correlation coefficients are generally stronger than during the summer months. Nouacer et al. (2016) [20] studied the mechanisms of winter precipitation variability in the European–Mediterranean region and found that NAO-related rainfall variability represents 20% to 50% of the seasonal variability of rainfall in Morocco. Meanwhile, Matthbout et al. (2019) [3] and Zamrane et al. (2016) [32] showed that the variability of precipitation can be controlled by the WeMO. Martin-Vide and Lopez-Bustins (2006) [61] found that the WeMO was significantly and statistically correlated with precipitation in areas that were weakly impacted by the North Atlantic Oscillation. Precisely, in the coastal areas of eastern Spain, some studies revealed that the WeMO exhibited the highest level of statistical significance in its correlation with annual, monthly, and daily precipitation [21,62].

Sebbar et al. (2012) [52] found that the spatial and temporal variability in precipitation in the central area of Morocco is related to three main components, namely altitude, seasonality, and latitude/longitude, complemented by the proximity of the ocean. In summary, this region is significantly influenced by two prominent atmospheric patterns: the NAO and WeMO. These patterns play a crucial role, especially during the winter months. Notably, the influence of the WeMO extends beyond winter, persisting until March and April.

In order to extract the common variability between precipitation and climate oscillations, we performed the continuous wavelet transform (CWT). The frequency analysis using CWT (Figure 5) highlights the concentration of power between the 0.25–0.5-year, 0.5−1-year, 1–2-year, 2–4-year, 4–8-year, and 8–16-year bands (dark pink/red areas). The black contour corresponds to the 5% significance level, which is equivalent to “the 95% confidence level”, and its envelope peaks above 95% confidence against a red-noise process [46]. To fill in the errors produced at the beginning and end of the wavelet power spectrum, zeros are added to the end of the time series prior to using the wavelet transform, and then eliminated afterwards. The region below the solid curve defines the cone of influence where the edge effects have become significant. Therefore, the cone of influence is the region where the wavelet power peaks are assumed to be reduced in magnitude because of the zero padding [46].

Several modes of variability are recorded in the study area (Figure 5). The 1-year band is identified with a strong power in all stations along the time series. The 1–2-year band appears in all stations except Talmest, with some discontinuities around 1995 and the 2000s.

These bands correspond to the hydrological cycle due to the seasonal change of precipitation every year. However, the 8-year band showed a low nonsignificant energy at Aghbalou, Tahanaout, and Talmest between 1985 and 2005, and a strong energy at Marrakech (1995–2015), N’kouris (1985–2000), and Sidi Rahal (1990–2005). Furthermore, this band also corresponds to the typical periodicity of the NAO as already confirmed by Massei et al. (2007) [63], who found that during the second half of the last century, the 8-year band presented a contribution to the total power of the NAO signal. The 8–16-year band is continuous and quite strong for the Marrakech and N’kouris watersheds. This is also consistent with changes identified by continuous wavelet analysis in the NAO index, where this band was observed around 1970 [59].

The comparison of rainfall series and climate indices (Figure 6 and Figure 7) shows that from the beginning of the study period to 1995, the WeMO was stronger and presented an inverse pattern with rainfall series; afterward, a stronger NAO pattern emerges, displaying an inverse template. Therefore, during the same period when the 8- and 16-year bands presented a strong energy, an inverse pattern is clearly identified between the two time series. This is also consistent with the previous results of correlation between the NAO and rainfall, where negative correlations are identified in winter months. Thus, when the NAO is in a negative phase, winter precipitation increases in Morocco [51,64,65]. According to Türkeş et al. (2003) [66], the NAO exerts control over the weather and climate patterns in the regions of the Atlantic and the Mediterranean basin, including Turkey. During the negative phase of NAO, precipitation tends to be wetter than the long-term average conditions. Conversely, positive NAO responses generally result in drier conditions throughout the year, except for in the summer.

Overall, the patterns of significant rainfall amounts are associated in Morocco with the negative phases of the two atmospheric oscillations (Figure 8).

Cross-wavelet analyses were also performed to detect the most significant periodicities and high common powers between the Tensift extended winter rainfall (November to April) and the NAO/WeMO indices. They allow us to study the changes in correlation for each scale between the two signals over time and to determine similar potential fluctuations and leading at specific time scales. The winter precipitation and NAO cross-wavelet transform is shown in Figure 9. Remarkably, a distinct and noteworthy significant band with a periodicity of 2 years prominently emerges on the cross-wavelet spectrum around 1995 in Aghbalou, Tahnaout, and Talmest. Similarly, around 2010, this significant 2-year pattern reappears in Aghbalou, Tahnaout, Sidi Rahal, and Marrakech. Additionally, a second remarkably robust and significant component with a periodicity of 6–8 years becomes evident between 1995 and 2000 across all monitoring stations. This particular band exhibits a stronger presence on the plains compared to the mountainous stations. Furthermore, the directional arrows in the analysis indicate a lead of the NAO over winter precipitation, with both exhibiting an antiphase relationship.

The 6–8-year band of precipitation could be associated with the interannual variability of the NAO.

Cross-wavelet analysis of the WeMO and winter precipitation also unveils the presence of a noteworthy 2-year band around 1995 at all stations and approximately 2015 at the Sidi Rahal station. Additionally, a robust 8-year band is prominently observed from the early part of the study period until the mid-2000s, gradually diminishing thereafter (see Figure 10). Importantly, this 8-year band demonstrates statistically significant strength across all stations. Moreover, the directional arrows in the analysis indicate a clear lead of the WeMO over winter precipitation, revealing an intriguing antiphase relationship between the two variables.

Through a comparison of the rainfall wavelet spectrum and cross-wavelet analysis results, the strong correlation found between the NAO and rainfall could be related to NAO fluctuations, as the 8-year peak specific to the NAO [63] was detected in rainfall for this period.

The wavelet transform analysis of several sub-basins in the Tensift precipitation time series shows somewhat similar behavior, as for the NAO. The annual cycle band exhibited high energy throughout the study series, which corresponds to the hydrological cycle. However, the 2-year mode appears with a high energy level from 1990. The 6–8-year band displays considerable strength throughout the entire duration of the study and demonstrates a more pronounced presence on the plains in contrast to the mountainous stations. Additionally, this band appears to be more closely associated with the NAO, suggesting a specific and significant connection between the two variables. The occurrence of the different energy bands of rainfall could be also related to fluctuations of the WeMO.

Previous works focused on the links between rainfall and climate fluctuations [19,67], especially the NAO, found that some modes could be linearly related to NAO fluctuations. The study carried out by Zamrane et al. (2021) [59] on the Tensift watershed showed that by using coherence, the total contribution of the NAO and WeMO climate indices on precipitation were 70% and 65%, respectively, and concluded that this basin seems to be more influenced by the NAO than the WeMO.

Seager et al. (2020) [68] studied the mechanisms of winter precipitation variability in the European–Mediterranean regions associated with the NAO and found that the NAO is the main mode of variability of the winter mean circulation in the Atlantic, European, and Mediterranean regions. In addition, the NAO-related precipitation variability accounts for 20–50% of seasonal precipitation variability in Morocco. Moreover, according to Djebbar et al. (2020) [69], the precipitation variability in the western part of North Africa is more susceptible to be affected by the NAO, associated with a strong significant negative value of correlation.

Based on the findings of the work of Türkeş et al. (2003) [66], it is evident that the NAO plays a significant role as one of the primary atmospheric drivers of spatial and temporal variations in precipitation patterns, not only in Turkey, but also in the Atlantic, Europe, and the Mediterranean basin.

Regarding the WeMO, the presence of a significant 8-year band observed in the cross-wavelet analysis between precipitation and the WeMO underscores the crucial role of the WeMO in modulating rainfall patterns in the northwest Mediterranean [3]. In the study conducted by Aksu et al. (2023) [34], it was discovered that the WeMO indices display the highest correlation with precipitation patterns. Furthermore, the WeMO has a significant impact on nearly all basin precipitations. Due to its predictive potential for the basin’s precipitation, the WeMO deserves particular attention and further investigations.

4. Conclusions

In this study, we employed a combined approach of the Mann–Kendall (MK) test and the wavelet analysis to identify trends and dominant periodic components of rainfall over the study area in central Morocco, along with their link to the NAO and WeMO oscillations.

Statistically significant negative trends (p < 0.1) in precipitation were observed in three stations during June and February. Conversely, one station exhibited an increasing trend in precipitation for May. However, the annual sum of precipitation and the winter months showed decreasing trends that were not statistically significant. The correlation coefficients obtained between precipitation and climate indices are stronger in winter, especially from December to February for the NAO and November to March for the WeMO.

The interannual spatial and temporal variabilities of rainfall data are structured in different bands (0.25–0.5, 0.5−1, 1–2, 2–4, 4–8, and 8–16 years) in the wavelet power spectrum. Each basin is characterized by several modes and specific variabilities of precipitation. The 1-year band is evidently the dominant mode observed of rainfall variability at all stations which corresponds to the hydrological cycle, whereas a second common mode of the 8-year band was identified in all stations with varying intensities. Cross-wavelet analyses were also performed to detect the most significant periodicities and high common powers between the Tensift winter rainfall and NAO/WeMO indices. A powerful, significant 6–8-year band was observed that showed relatively high consistency in rainfall response to the phase of the NAO and WeMO over time. This band can be associated with the specific interannual variability of the NAO and WeMO.

Indeed, the trend analyses showed some common frequency relationships with the continuous wavelet, and a decreasing trend was registered with high magnitude (−3.027 mm/y) in Talmest station associated with a discontinuity around 1990 and after 2000s. The findings are in good agreement with the results obtained in previous studies over central Morocco. The variations in rainfall can be reasonably attributed to major atmospheric patterns and the local climate, considering factors such as elevation, proximity to the sea, and other relevant local/regional parameters.

The implications of the study could be extended beyond Morocco and have relevance for other western Mediterranean countries that are facing similar large-scale atmospheric circulation patterns. They may gain valuable knowledge about their own regional climate processes and could develop more effective climate adaptation and mitigation strategies. Knowledge of teleconnections can aid in forecasting and preparing for extreme weather events, such as droughts or floods, which can be influenced by distant climate drivers. However, while this kind of study can offer valuable insights, it is essential to consider potential limitations that could affect the research and its findings. For example, the availability and quality of historical rainfall data over sparse gauge network regions might pose a limitation, making it challenging to draw robust conclusions. Indeed, climate studies often benefit from long-term data records to identify trends and patterns accurately. If such data arecking, it may hinder the ability to detect long-term changes in rainfall variability. In addition, the relationships between atmospheric circulation patterns and rainfall variability may not always be linear. Nonlinear interactions could make it harder to establish straightforward connections between the two. Also, the study focuses on large-scale atmospheric circulation patterns, potentially overlooking the role of local climate drivers that can also influence rainfall variability in the region. This may require advanced climatological analysis at the regional scale.

Overall, it is recommended to study the evolution of precipitation in Morocco, along with the different modes of variability and their relationships with the climate patterns at the global scale. Such analyses can enhance our comprehension of climate variability in North Africa. This is crucial due to the vulnerability of water resources to climate change and the significance of the socioeconomic activities that depend on these water resources.