Climatology of the Nonmigrating Tides Based on Long-Term SABER/TIMED Measurements and Their Impact on the Longitudinal Structures Observed in the Ionosphere
Abstract
:1. Introduction
2. Observations and Method for Data Analysis
2.1. SABER Temperature Data
2.1.1. Method for Extracting Waves from the SABER Temperatures
2.2. TEC Data and Methodology
2.3. FORMOSAT-3/COSMIC (F3/C) Electron Density Profiles Data and Methodology
3. Climatology (2002–2022), Seasonal and Interannual Variability of the SABER/TIMED Nonmigrating Tides in the Lower Thermosphere
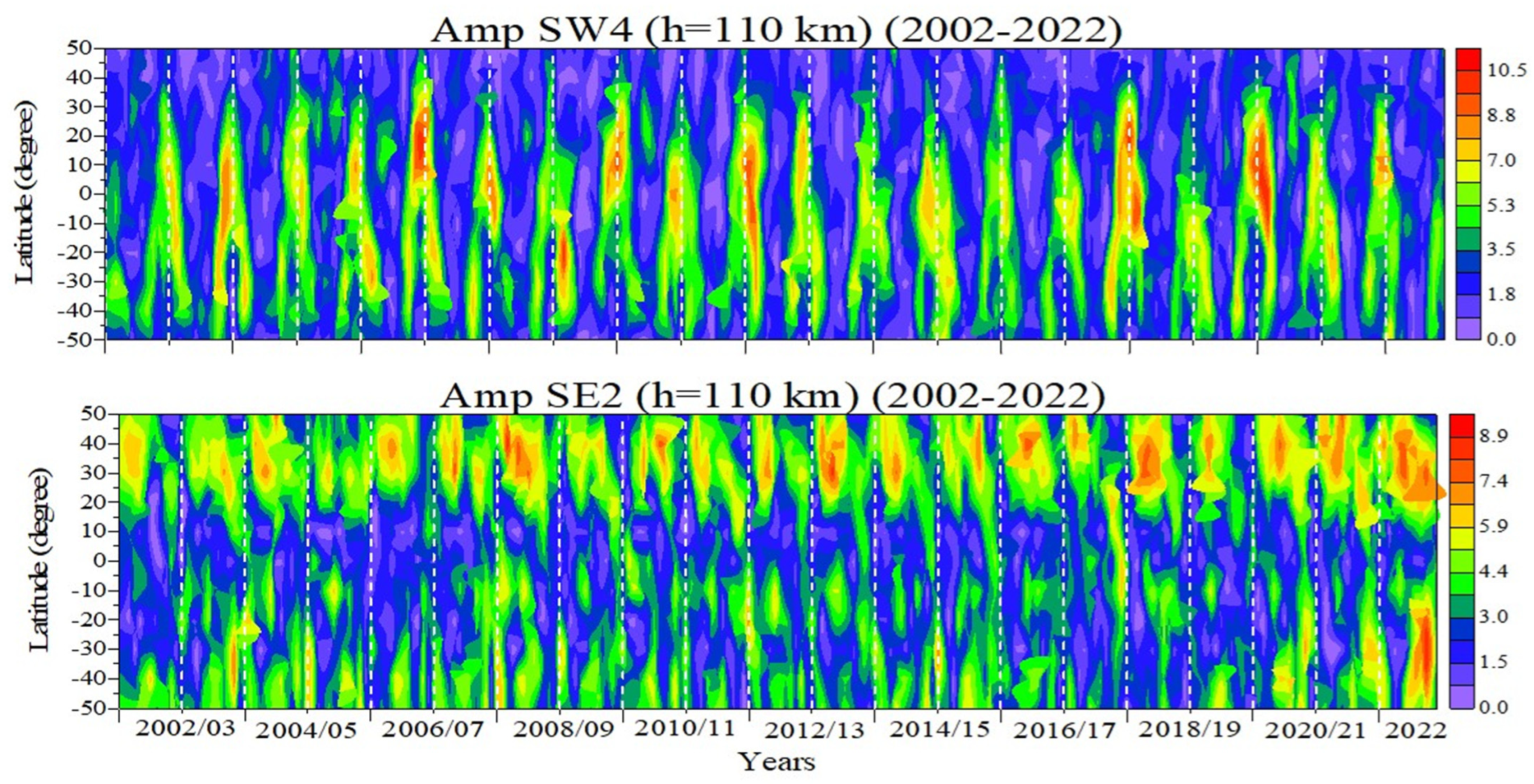
3.1. Climatology, Seasonal and Interannual Variability of the Nonmigrating Diurnal Tides
3.2. Climatology, Seasonal and Interannual Variability of the Nonmigrating Semidiurnal Tides
4. Climatology (2002–2022) of Longitudinal Structures in the Lower Thermosphere
4.1. SABER Temperature WN4 Structure
4.2. SABER Temperature WN3 Structure
4.3. SABER Temperature WN2 Structure
5. Climatology (2002–2022) of Longitudinal Structures in the Ionosphere
5.1. TEC WN4 Structure
5.2. TEC WN3 Structure
5.3. TEC WN2 Structure
6. Weddell Sea Anomaly
7. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chapman, S.; Lindzen, R.S. Atmospheric Tides: Thermal and Gravitational, 1st ed.; Springer: Dordrecht, The Netherlands, 1970; pp. 1–200. [Google Scholar] [CrossRef]
- Kato, S. Non-migrating tides. J. Atmos. Terr. Phys. 1989, 51, 673–682. [Google Scholar] [CrossRef]
- Hagan, M.E.; Roble, R.G. Modeling diurnal tidal variability with the National Center for Atmospheric Research thermosphere-ionosphere-mesosphere-electrodynamics general circulation model. J. Geophys. Res. Space Phys. 2001, 106, 24869–24882. [Google Scholar] [CrossRef]
- Angelats, I.; Coll, M.; Forbes, J.M. Nonlinear interactions in the upper atmosphere: The s = 1 and s = 3 nonmigrating semidiurnal tides. J. Geophys. Res. Space Phys. 2002, 107, 1157–1171. [Google Scholar] [CrossRef]
- Forbes, J.M.; Wu, D. Solar tides as revealed by measurements of mesosphere temperature by the MLS experiment on UARS. J. Atmos. Sci. 2006, 63, 1776–1797. [Google Scholar] [CrossRef]
- Pancheva, D.; Mukhtarov, P.; Andonov, B. Nonmigrating tidal activity related to the sudden stratospheric warming in the Arctic winter of 2003/2004. Ann. Geophys. 2009, 27, 975–987. [Google Scholar] [CrossRef]
- Hamilton, K. Latent heat release as a possible forcing mechanism for atmospheric tides. Mon. Weather Rev. 1981, 109, 3–17. [Google Scholar] [CrossRef]
- Hagan, M.E.; Forbes, J.M. Migrating and nonmigrating diurnal tides in the middle and upper atmosphere excited by tropical latent heat release. J. Geophys. Res. Atmos. 2002, 107, 4754–4768. [Google Scholar] [CrossRef]
- Oberheide, J.; Hagan, M.E.; Roble, R.G.; Offermann, D. Sources of nonmigrating tides in the tropical middle atmosphere. J. Geophys. Res. Atmos. 2002, 107, 4567–4580. [Google Scholar] [CrossRef]
- Zhang, X.; Forbes, J.M.; Hagan, M.E. Longitudinal variation of tides in the MLT region: 2. Relative effects of solar radiative and latent heating. J. Geophys. Res. Space Phys. 2010, 115, 1–19. [Google Scholar] [CrossRef]
- Miyoshi, Y.; Pancheva, D.; Mukhtarov, P.; Jin, H.; Fujiwara, H.; Shinagawa, H. Excitation mechanism of non-migrating tides. J. Atmos. Sol.-Terr. Phys. 2017, 156, 24–36. [Google Scholar] [CrossRef]
- Hagan, M.E.; Forbes, J.M. Migrating and nonmigrating semidiurnal tides in the upper atmosphere excited by tropospheric latent heat release. J. Geophys. Res. Space Phys. 2003, 108, 1062–1075. [Google Scholar] [CrossRef]
- Lieberman, R.S. Nonmigrating diurnal tides in the equatorial middle atmosphere. J. Atmos. Sci. 1991, 48, 1112–1123. [Google Scholar] [CrossRef]
- Talaat, E.R.; Lieberman, R.S. Nonmigrating diurnal tides in mesospheric and lower thermospheric winds and temperatures. J. Atmos. Sci. 1999, 56, 4073–4087. [Google Scholar] [CrossRef]
- Oberheide, J.; Gusev, O.A. Observations of migrating and nonmigrating diurnal tides in the equatorial lower thermosphere. Geophys. Res. Lett. 2002, 29, 2167–2170. [Google Scholar] [CrossRef]
- Forbes, J.M.; Zhang, X.; Talaat, E.R.; Ward, W. Nonmigrating diurnal tides in the thermosphere. J. Geophys. Res. Space Phys. 2003, 108, 1033–1042. [Google Scholar] [CrossRef]
- Forbes, J.M.; Russell, J.; Miyahara, S.; Zhang, X.; Palo, S.; Mlynczak, M.; Mertens, C.J.; Hagan, M.E. Troposphere–thermosphere tidal coupling as measured by the SABER instrument on TIMED during July–September 2002. J. Geophys. Res. Space Phys. 2006, 111, 1–15. [Google Scholar] [CrossRef]
- Huang, F.T.; Reber, C.A. Nonmigrating semidiurnal and diurnal tides at 95 km based on wind measurements from the High Resolution Doppler Imager on UARS. J. Geophys. Res. Atmos. 2004, 109, 1–13. [Google Scholar] [CrossRef]
- Lieberman, R.; Oberheide, J.; Hagan, M.; Remsberg, E.; Gordley, L. Variability of diurnal tides and planetary waves during November 1978–May 1979. J. Atmos. Sol.-Terr. Phys. 2004, 66, 517–528. [Google Scholar] [CrossRef]
- Mukhtarov, P.; Pancheva, D.; Andonov, B. Global structure and seasonal and interannual variability of the migrating diurnal tide seen in the SABER/TIMED temperatures between 20 and 120 km. J. Geophys. Res. Space Phys. 2009, 114, 1–17. [Google Scholar] [CrossRef]
- Pancheva, D.; Mukhtarov, P. Atmospheric tides and planetary waves: Recent progress based on SABER/TIMED temperature measurements (2002–2007). In Aeronomy of the Earth’s Atmosphere and Ionosphere, 1st ed.; IAGA Special Sopron Book Series; Abdu, M., Pancheva, D., Eds.; Springer: Dordrecht, The Netherlands, 2011; Volume 2, pp. 19–56. [Google Scholar] [CrossRef]
- Zhang, X.; Forbes, J.M.; Hagan, M.E.; Russell, J.M., III; Palo, S.E.; Mertens, C.J.; Mlynczak, M.G. Monthly tidal temperatures 20–120 km from TIMED/SABER. J. Geophys. Res. Space Phys. 2006, 111, 1–20. [Google Scholar] [CrossRef]
- Forbes, J.M.; Zhang, X.; Palo, S.; Russell, J.; Mertens, C.J.; Mlynczak, M. Tidal variability in the ionospheric dynamo region. J. Geophys. Res. Space Phys. 2008, 113, 1–17. [Google Scholar] [CrossRef]
- Oberheide, J.; Wu, Q.; Killeen, T.L.; Hagan, M.E.; Roble, R.G. Diurnal nonmigrating tides from TIMED Doppler Interferometer wind data: Monthly climatologies and seasonal variations. J. Geophys. Res. Space Phys. 2006, 111, 1–22. [Google Scholar] [CrossRef]
- Oberheide, J.; Wu, Q.; Killeen, T.L.; Hagan, M.E.; Roble, R.G. A climatology of nonmigrating semidiurnal tides from TIMED Doppler Interferometer (TIDI) wind data. J. Atmos. Sol.-Terr. Phys. 2007, 69, 2203–2218. [Google Scholar] [CrossRef]
- Pancheva, D.; Mukhtarov, P. Strong evidence for the tidal control on the longitudinal structure of the ionospheric F-region. Geophys. Res. Lett. 2010, 37, 1–5. [Google Scholar] [CrossRef]
- Pancheva, D.; Mukhtarov, P.; Andonov, B. Global structure, seasonal and interannual variability of the eastward propagating tides seen in the SABER/TIMED temperatures (2002–2007). Adv. Space Res. 2010, 46, 257–274. [Google Scholar] [CrossRef]
- Oberheide, J.; Forbes, J.M.; Zhang, X.; Bruinsma, S.L. Wave-driven variability in the ionosphere-thermosphere-mesosphere system from TIMED observations: What contributes to the “wave 4”? J. Geophys. Res. Space Phys. 2011, 116, 1–15. [Google Scholar] [CrossRef]
- Wan, W.; Xu, J. Recent investigation on the coupling between the ionosphere and upper atmosphere. Sci. China Earth Sci. 2014, 57, 1995–2012. [Google Scholar] [CrossRef]
- Li, X.; Wan, W.; Ren, Z.; Liu, L.; Ning, B. The variability of nonmigrating tides detected from TIMED/SABER observations. J. Geophys. Res. Space Phys. 2015, 120, 10793–10808. [Google Scholar] [CrossRef]
- Pancheva, D.; Mukhtarov, P.; Smith, A.K. Nonmigrating tidal variability in the SABER/TIMED mesospheric ozone. Geophys. Res. Lett. 2014, 41, 4059–4067. [Google Scholar] [CrossRef]
- Li, X.; Wan, W.; Ren, Z.; Yu, Y. The variability of SE2 tide extracted from TIMED/SABER observations. J. Geophys. Res. Space Phys. 2017, 122, 2136–2150. [Google Scholar] [CrossRef]
- Li, X.; Ren, Z.; Cao, J. The Spatiotemporal Variability of Non-Migrating Tides in the Zonal Wind Component Detected From TIMED/TIDI Observations. J. Geophys. Res. Space Phys. 2023, 128, e2022JA030879. [Google Scholar] [CrossRef]
- Sagawa, E.; Immel, T.J.; Frey, H.U.; Mende, S.B. Longitudinal structure of the equatorial anomaly in the nighttime ionosphere observed by IMAGE/FUV. J. Geophys. Res. Space Phys. 2005, 110, 1–10. [Google Scholar] [CrossRef]
- Immel, T.J.; Sagawa, E.; England, S.L.; Henderson, S.B.; Hagan, M.E.; Mende, S.B.; Frey, H.U.; Swenson, C.M.; Paxton, L.J. Control of equatorial ionospheric morphology by atmospheric tides. Geophys. Res. Lett. 2006, 33, 1–4. [Google Scholar] [CrossRef]
- Kil, H.; Oh, S.J.; Kelley, M.C.; Paxton, L.J.; England, S.L.; Talaat, E.; Min, K.W.; Su, S.Y. Longitudinal structure of the vertical E× B drift and ion density seen from ROCSAT-1. Geophys. Res. Lett. 2007, 34, 1–5. [Google Scholar] [CrossRef]
- Kil, H.; Talaat, E.R.; Oh, S.J.; Paxton, L.J.; England, S.L.; Su, S.Y. The wave structures of the plasma density and vertical E × B drift in low-latitude F region. J. Geophys. Res. Space Phys. 2008, 113, 1–12. [Google Scholar] [CrossRef]
- Richmond, A.D. The ionospheric wind dynamo: Effects of its coupling with different atmospheric regions. In The Upper Mesosphere and Lower Thermosphere: A Review of Experiments and Theory; As Part of the Geophysical Monograph Series; Johnson, R.M., Killeen, T.L., Eds.; American Geophysical Union (AGU): Washington, DC, USA, 1995; Volume 87, pp. 49–65. [Google Scholar] [CrossRef]
- Heelis, R.A. Electrodynamics in the low and middle latitude ionosphere: A tutorial. J. Atmos. Sol.-Terr. Phys. 2004, 66, 825–838. [Google Scholar] [CrossRef]
- England, S.L.; Immel, T.J.; Huba, J.D.; Hagan, M.E.; Maute, A.; DeMajistre, R. Modeling of multiple effects of atmospheric tides on the ionosphere: An examination of possible coupling mechanisms responsible for the longitudinal structure of the equatorial ionosphere. J. Geophys. Res. Space Phys. 2010, 115, 1–13. [Google Scholar] [CrossRef]
- England, S.L. Review of the effects of non-migrating atmospheric tides on Earth’s low-latitude ionosphere. Space Sci. Rev. 2012, 168, 211–236. [Google Scholar] [CrossRef]
- England, S.L.; Immel, T.J.; Sagawa, E.; Henderson, S.B.; Hagan, M.E.; Mende, S.B.; Frey, H.U.; Swenson, C.M.; Paxton, L.J. Effect of atmospheric tides on the morphology of the quiet-time post-sunset equatorial ionospheric anomaly. J. Geophys. Res. Space Phys. 2006, 111, 1–12. [Google Scholar] [CrossRef]
- Hartman, W.A.; Heelis, R.A. Longitudinal variations in the equatorial vertical drift in the topside ionosphere. J. Geophys. Res. Space Phys. 2007, 112, 1–6. [Google Scholar] [CrossRef]
- Ren, Z.; Wan, W.; Liu, L.; Zhao, B.; Wei, Y.; Yue, X.; Heelis, R.A. Longitudinal variations of electron temperature and total ion density in the sunset equatorial topside ionosphere. Geophys. Res. Lett. 2008, 35, 1–4. [Google Scholar] [CrossRef]
- England, S.L.; Maus, S.; Immel, T.J.; Mende, S.B. Longitudinal variation of the E-region electric fields caused by atmospheric tides. Geophys. Res. Lett. 2006, 33, 1–5. [Google Scholar] [CrossRef]
- Lühr, H.; Rother, M.; Häusler, K.; Alken, P.; Maus, S. Influence of nonmigrating tides on the longitudinal variations of the equatorial electrojet. J. Geophys. Res. Space Phys. 2008, 113, 1–8. [Google Scholar] [CrossRef]
- Häusler, K.; Lühr, H.; Rentz, S.; Köhler, W. A statistical analysis of longitudinal dependences of upper thermospheric zonal winds at dip equator latitudes derived from CHAMP. J. Atmos. Sol.-Terr. Phys. 2007, 69, 1419–1430. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, W.; Wang, H.; Dang, T.; Liu, J.; Wu, Q. The longitudinal variations of upper thermospheric zonal winds observed by the CHAMP satellite at low and midlatitudes. J. Geophys Res. Space Phys. 2018, 123, 9652–9668. [Google Scholar] [CrossRef]
- Lin, C.H.; Hsiao, C.C.; Liu, J.Y.; Liu, C.H. Longitudinal structure of the equatorial ionosphere: Time evolution of the four-peaked EIA structure. J. Geophys. Res. Space Phys. 2007, 112, 1–8. [Google Scholar] [CrossRef]
- Häusler, K.; Lühr, H. Nonmigrating tidal signals in the upper thermospheric zonal wind at equatorial latitudes as observed by CHAMP. Ann. Geophys. 2009, 27, 2643–2652. [Google Scholar] [CrossRef]
- Wan, W.; Liu, L.; Pi, X.; Zhang, M.L.; Ning, B.; Xiong, J.; Ding, F. Wavenumber-4 patterns of the total electron content over the low latitude ionosphere. Geophys. Res. Lett. 2008, 35, 1–5. [Google Scholar] [CrossRef]
- Fejer, B.G.; Jensen, J.W.; Su, S.Y. Quiet time equatorial F region vertical plasma drift model derived from ROCSAT-1 observations. J. Geophys. Res. Space Phys. 2008, 113, 1–10. [Google Scholar] [CrossRef]
- Bankov, L.; Heelis, R.; Parrot, M.; Berthelier, J.J.; Marinov, P.; Vassileva, A. WN4 effect on longitudinal distribution of different ion species in the topside ionosphere at low latitudes by means of DEMETER, DMSP-F13 and DMSP-F15 data. Ann. Geophys. 2009, 27, 2893–2902. [Google Scholar] [CrossRef]
- Liu, H.; Yamamoto, M.; Lühr, H. Wave-4 pattern of the equatorial mass density anomaly: A thermospheric signature of tropical deep convection. Geophys. Res. Lett. 2009, 36, 1–4. [Google Scholar] [CrossRef]
- Pancheva, D.; Mukhtarov, P. Global Response of the Ionosphere to Atmospheric Tides Forced from Below: Recent Progress Based on Satellite Measurements: Global Tidal Response of the Ionosphere. Space Sci. Rev. 2012, 168, 175–209. [Google Scholar] [CrossRef]
- Mukhtarov, P.; Pancheva, D. Global ionospheric response to nonmigrating DE3 and DE2 tides forced from below. J. Geophys. Res. Space Phys. 2011, 116, 1–16. [Google Scholar] [CrossRef]
- Pancheva, D.; Miyoshi, Y.; Mukhtarov, P.; Jin, H.; Shinagawa, H.; Fujiwara, H. Global response of the ionosphere to atmospheric tides forced from below: Comparison between COSMIC measurements and simulations by atmosphere ionosphere coupled model GAIA. J. Geophys. Res. Space Phys. 2012, 117, 1–19. [Google Scholar] [CrossRef]
- Miyoshi, Y.; Fujiwara, H. Day-to-day variations of migrating diurnal tide simulated by a GCM from the ground surface to the exobase. Geophys. Res. Lett. 2003, 30, 1789–1793. [Google Scholar] [CrossRef]
- Shinagawa, H. Ionosphere simulation. J. Natl. Inst. Comm. Technol. 2009, 56, 199–207. [Google Scholar]
- Jin, H.; Miyoshi, Y.; Fujiwara, H.; Shinagawa, H.; Terada, K.; Terada, N.; Ishii, M.; Otsuka, Y.; Saito, A. Vertical connection from the tropospheric activities to the ionospheric longitudinal structure simulated by a new Earth’s whole atmosphere-ionosphere coupled model. J. Geophys. Res. Space Phys. 2011, 116, 1–9. [Google Scholar] [CrossRef]
- Jin, H.; Miyoshi, Y.; Fujiwara, H.; Shinagawa, H. Electrodynamics of the formation of ionospheric wave number 4 longitudinal structure. J. Geophys. Res. Space Phys. 2008, 113, 1–7. [Google Scholar] [CrossRef]
- Ren, Z.; Wan, W.; Xiong, J.; Liu, L. Simulated wave number 4 structure in equatorial F-region vertical plasma drifts. J. Geophys. Res. Space Phys. 2010, 115, A05301. [Google Scholar] [CrossRef]
- England, S.L.; Zhang, X.; Immel, T.J.; Forbes, J.M.; DeMajistre, R. The effect of non-migrating tides on the morphology of the equatorial ionospheric anomaly: Seasonal variability. Earth Planets Space 2009, 61, 493–503. [Google Scholar] [CrossRef]
- Pedatella, N.M.; Forbes, J.M.; Oberheide, J. Intra-annual variability of the low-latitude ionosphere due to nonmigrating tides. Geophys. Res. Lett. 2008, 35, 1–4. [Google Scholar] [CrossRef]
- Mertens, C.J.; Mlynczak, M.; Lopez-Puertas, M.; Wintersteiner, P.P.; Picard, R.H.; Winick, J.R.; Gordley, L.L.; Russell III, J.M. Retrieval of mesospheric and lower thermospheric kinetic temperature from measurements of CO2 15μm earth limb emission under non-LTE conditions. Geophys. Res. Lett. 2001, 28, 1391–1394. [Google Scholar] [CrossRef]
- Mertens, C.J.; Schmidlin, F.J.; Goldberg, R.A.; Remsberg, E.E.; Pesnell, W.D.; Russell III, J.M.; Mlynczak, M.G.; Lopez-Puertas, M.; Wintersteiner, P.P.; Picard, R.H.; et al. SABER observations of mesospheric temperatures and comparisons with falling sphere measurements taken during the 2002 summer MaCWAVE campaign. Geophys. Res. Lett. 2004, 31, 1–5. [Google Scholar] [CrossRef]
- Christensen, A.B.; Bishop, R.L.; Budzien, S.A.; Hecht, J.H.; Mlynczak, M.G.; Russell III, J.M.; Stephan, A.W.; Walterscheid, R.W. Altitude profiles of lower thermospheric temperature from RAIDS/NIRS and TIMED/SABER remote sensing experiments. J. Geophys. Res. Space Phys. 2013, 118, 3740–3746. [Google Scholar] [CrossRef]
- Remsberg, E.E.; Marshall, B.T.; Garcia-Comas, M.; Krueger, D.; Lingenfelser, G.S.; Martin-Torres, J.; Mlynczak, M.G.; Russell III, J.M.; Smith, A.K.; Zhao, Y.; et al. Assessment of the quality of the Version 1.07 temperature-versus-pressure profiles of the middle atmosphere from TIMED/SABER. J. Geophys. Res. Atmos. 2008, 113, 1–27. [Google Scholar] [CrossRef]
- García-Comas, M.; López-Puertas, M.; Marshall, B.T.; Wintersteiner, P.P.; Funke, B.; Bermejo-Pantaleón, D.; Mertens, C.J.; Remsberg, E.E.; Gordley, L.L.; Mlynczak, M.G.; et al. Errors in Sounding of the Atmosphere using Broadband Emission Radiometry (SABER) kinetic temperature caused by non-local-thermodynamic-equilibrium model parameters. J. Geophys. Res. Atmos. 2008, 113, 1–16. [Google Scholar] [CrossRef]
- Dawkins, E.C.M.; Feofilov, A.; Rezac, L.; Kutepov, A.A.; Janches, D.; Höffner, J.; Chu, X.; Lu, X.; Mlynczak, M.G.; Russell, J., III. Validation of SABER v2.0 operational temperature data with ground-based lidars in the mesosphere-lower thermosphere region (75–105 km). J. Geophys. Res. Atmos. 2018, 123, 9916–9934. [Google Scholar] [CrossRef]
- Pancheva, D.; Mukhtarov, P. Climatology and interannual variability of the migrating quarterdiurnal tide (QW4) seen in the SABER/TIMED temperatures (2002–2022). J. Atmos. Sol.-Terr. Phys. 2023, 250, 106111. [Google Scholar] [CrossRef]
- Pancheva, D.; Mukhtarov, P.; Andonov, B. Global structure, seasonal and interannual variability of the migrating semidiurnal tide seen in the SABER/TIMED temperatures (2002–2007). Ann. Geophys. 2009, 27, 687–703. [Google Scholar] [CrossRef]
- Ho, C.M.; Mannucci, A.J.; Lindqwister, U.J.; Pi, X.; Tsurutani, B.T. Global ionosphere perturbations monitored by the orldwide GPS network. Geophys. Res. Lett. 1996, 23, 3219–3222. [Google Scholar] [CrossRef]
- Rawer, K. Meteorological and astronomical influences on radio wave propagation. In Proceedings of Papers Read at the NATO Advanced Study Institute; Corfu, 1961; Landmark, B., Ed.; Pergamon Press: Oxford, UK, 1963; Volume 3, pp. 221–250. [Google Scholar]
- Azpilicueta, F.; Brunini, C.; Radicella, S.M. Global ionospheric maps from GPS observations using modip latitude. Adv. Space Res. 2006, 38, 2324–2331. [Google Scholar] [CrossRef]
- Lei, J.; Syndergaard, S.; Burns, A.G.; Solomon, S.C.; Wang, W.; Zeng, Z.; Roble, R.G.; Wu, Q.; Kuo, Y.H.; Holt, J.M.; et al. Comparison of COSMIC ionospheric measurements with ground-based observations and model predictions: Preliminary results. J. Geophys. Res. Space Phys. 2007, 112, 1–10. [Google Scholar] [CrossRef]
- Cheng, C.Z.; Kuo, Y.H.; Anthes, R.A.; Wu, L. Satellite constellation monitors global and space weather. EOS Trans. 2006, 87, 166. [Google Scholar] [CrossRef]
- Tokioka, T.; Yagai, I. Atmospehric tides appearing in a global atmospheric general circulation model. J. Meteorol. Soc. Jpn. Ser. II 1987, 65, 423–438. [Google Scholar] [CrossRef]
- Niu, X.; Du, J.; Zhu, X. Statistics on Nonmigrating Diurnal Tides Generated by Tide-Planetary Wave Interaction and Their Relationship to Sudden Stratospheric Warming. Atmosphere 2018, 9, 416. [Google Scholar] [CrossRef]
- Forbes, J.M.; Zhang, X.; Marsh, D.R. Solar cycle dependence of middle atmosphere temperatures. J. Geophys. Res. Atmos. 2014, 119, 9615–9625. [Google Scholar] [CrossRef]
- Nath, O.; Sridharan, S. Long-term variabilities and tendencies in zonal mean TIMED–SABER ozone and temperature in the middle atmosphere at 10–158 N. J. Atmos. Sol.-Terr. Phys. 2014, 120, 1–8. [Google Scholar] [CrossRef]
- Holton, J.R.; Tan, H.C. The influence of the equatorial quasi-biennial oscillation on the global circulation at 50 mb. J. Atmos. Sci. 1980, 37, 2200–2208. [Google Scholar] [CrossRef]
- Hagan, M.E.; Maute, A.I.; Roble, R.G. Tropospheric tidal effects on the middle and upper atmosphere. J. Geophys. Res. Space Phys. 2009, 114, 1–6. [Google Scholar] [CrossRef]
- Truskowski, A.O.; Forbes, J.M.; Zhang, X.; Palo, S.E. New perspectives on thermosphere tides: 1. Lower thermosphere spectra and seasonal-latitudinal structures. Earth Planets Space 2014, 66, 136. [Google Scholar] [CrossRef]
- Moudden, Y.; Forbes, J.M. A decade-long climatology of terdiurnal tides using TIMED/SABER observations. J. Geophys. Res. Space Phys. 2013, 118, 4534–4550. [Google Scholar] [CrossRef]
- Oberheide, J.; Forbes, J.M. Thermospheric nitric oxide variability induced by nonmigrating tides. Geophys. Res. Lett. 2008, 35, 1–5. [Google Scholar] [CrossRef]
- Barth, C.A.; Mankoff, K.D.; Bailey, S.M.; Solomon, S.C. Global observations of nitric oxide in the thermosphere. J. Geophys. Res. Space Phys. 2003, 108, 1–11. [Google Scholar] [CrossRef]
- Li, D.; Gao, H.; Xu, J.; Zhu, Y.; Xu, Q.; Liu, Y.; Liu, H. Longitudinal structures of zonal wind in the thermosphere by the ICON/MIGHTI and the main wave sources. Earth Planets Space 2023, 75, 59. [Google Scholar] [CrossRef]
- Chang, L.C.; Lin, C.H.; Liu, J.Y.; Balan, N.; Yue, J.; Lin, J.T. Seasonal and local time variation of ionospheric migrating tides in 2007–2011 FORMOSAT-3/COSMIC and TIE-GCM total electron content. J. Geophys. Res. Space Phys. 2013, 118, 2545–2564. [Google Scholar] [CrossRef]
- Wang, S.; Huang, S.; Fang, H. Wave-3 and wave-4 patterns in the low- and mid-latitude ionospheric TEC. J. Atmos. Sol.-Terr. Phys. 2015, 132, 82–91. [Google Scholar] [CrossRef]
- Forbes, J.M.; Zhang, X.; Bruinsma, S.L. New perspectives on thermospheric tides: 2. penetration to the upper thermosphere. Earth Planets Space 2014, 66, 122. [Google Scholar] [CrossRef]
- Hagan, M.E.; Maute, A.; Roble, R.G.; Richmond, A.D.; Immel, T.J.; England, S.L. Connections between deep tropical clouds and the Earth’s ionosphere. Geophys. Res. Lett. 2007, 34, 1–4. [Google Scholar] [CrossRef]
- Fuller-Rowell, T.J. The ‘thermospheric spoon’: A mechanism for the semi-annual density variation. J. Geophys. Res. Space Phys. 1998, 103, 3951–3956. [Google Scholar] [CrossRef]
- Qian, L.; Burns, A.G.; Solomon, S.C.; Wang, W. Annual/semiannual variation of the ionosphere. Geophys. Res. Lett. 2013, 40, 1928–1933. [Google Scholar] [CrossRef]
- Jones, M., Jr.; Forbes, J.M.; Hagan, M.E.; Maute, A. Non-migrating tides in the ionosphere-thermosphere: In situ versus tropospheric sources. J. Geophys. Res. Space Phys. 2013, 118, 2438–2451. [Google Scholar] [CrossRef]
- Dudeney, J.R.; Piggott, W.R. Antarctic ionospheric research. In Upper Atmosphere Research in Antarctica; Lanzerotti, L.J., Park, C.G., Eds.; AGU: Washington, DC, USA, 1978; Volume 29, pp. 200–235. 029p. [Google Scholar]
- Bellchambers, W.H.; Piggott, W.R. Ionospheric measurements made at Halley Bay. Nature 1958, 182, 1596–1597. [Google Scholar] [CrossRef]
- Horvath, I.; Essex, E.A. The Weddell Sea Anomaly observed with the Topex satellite data. J. Atmos. Sol. Terr. Phys. 2003, 65, 693–706. [Google Scholar] [CrossRef]
- Lin, C.H.; Liu, C.H.; Liu, J.Y.; Chen, C.H.; Burns, A.G.; Wan, W. Midlatitude summer nighttime anomaly of the ionospheric electron density observed by FORMOSAT-3/COSMIC. J. Geophys. Res. 2010, 115, A03308. [Google Scholar] [CrossRef]
- He, M.; Liu, L.; Wan, W.; Ning, B.; Zhao, B.; Wen, J.; Yue, X.; Le, H. A study of the Weddell Sea Anomaly observed by FORMOSAT-3/COSMIC. J. Geophys. Res. Space Phys. 2009, 114, 1–10. [Google Scholar] [CrossRef]
- Chen, C.H.; Huba, J.D.; Saito, A.; Lin, C.H.; Liu, J.Y. Theoretical study of the ionospheric Weddell Sea Anomaly using SAMI2. J. Geophys. Res. Space Phys. 2011, 116, 1–10. [Google Scholar] [CrossRef]
- Mukhtarov, P.; Pancheva, D.; Andonov, B.; Pashova, L. Global TEC maps based on GNSS data: 1. Empirical background TEC model. J. Geophys. Res. Space Phys. 2013, 118, 4594–4608. [Google Scholar] [CrossRef]
- Chang, L.C.; Liu, H.; Miyoshi, Y.; Chen, C.-H.; Chang, F.-Y.; Lin, C.-H.; Liu, J.-Y.; Sun, Y.-Y. Structure and origins of the Weddell Sea Anomaly from tidal and planetary wave signatures in FORMOSAT-3/COSMIC observations and GAIA GCM simulations. J. Geophys. Res. Space Phys. 2015, 120, 1325–1340. [Google Scholar] [CrossRef]
- Oberheide, J.; Forbes, J.M.; Häusler, K.; Wu, Q.; Bruinsma, S.L. Tropospheric tides from 80 to 400 km: Propagation, interannual variability, and solar cycle effects. J. Geophys. Res. Atmos. 2009, 114, 1–18. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pancheva, D.; Mukhtarov, P.; Bojilova, R. Climatology of the Nonmigrating Tides Based on Long-Term SABER/TIMED Measurements and Their Impact on the Longitudinal Structures Observed in the Ionosphere. Atmosphere 2024, 15, 478. https://doi.org/10.3390/atmos15040478
Pancheva D, Mukhtarov P, Bojilova R. Climatology of the Nonmigrating Tides Based on Long-Term SABER/TIMED Measurements and Their Impact on the Longitudinal Structures Observed in the Ionosphere. Atmosphere. 2024; 15(4):478. https://doi.org/10.3390/atmos15040478
Chicago/Turabian StylePancheva, Dora, Plamen Mukhtarov, and Rumiana Bojilova. 2024. "Climatology of the Nonmigrating Tides Based on Long-Term SABER/TIMED Measurements and Their Impact on the Longitudinal Structures Observed in the Ionosphere" Atmosphere 15, no. 4: 478. https://doi.org/10.3390/atmos15040478
APA StylePancheva, D., Mukhtarov, P., & Bojilova, R. (2024). Climatology of the Nonmigrating Tides Based on Long-Term SABER/TIMED Measurements and Their Impact on the Longitudinal Structures Observed in the Ionosphere. Atmosphere, 15(4), 478. https://doi.org/10.3390/atmos15040478




