Seasonal Variations in Radon and Thoron Exhalation Rates from Solid Concrete Interior Walls Observed Using In Situ Measurements
Abstract
1. Introduction
2. Materials and Methods
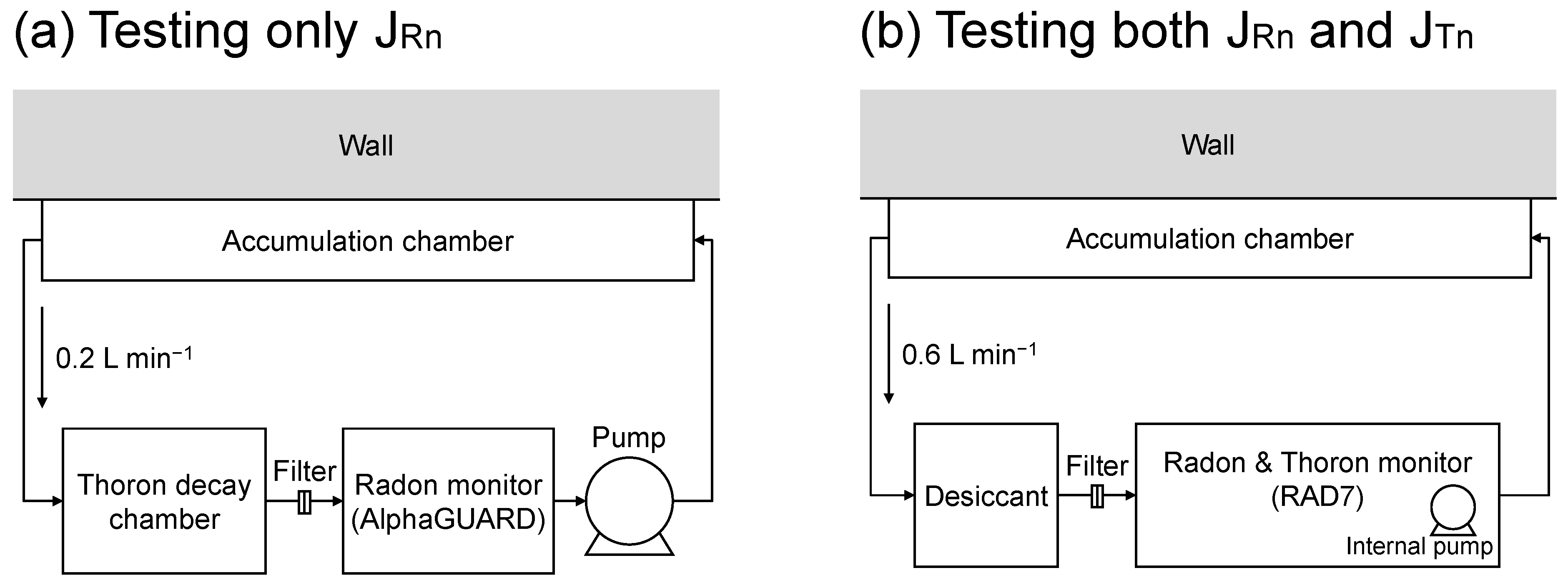
2.1. Testing Location and In Situ Measurement
2.2. Data Analysis
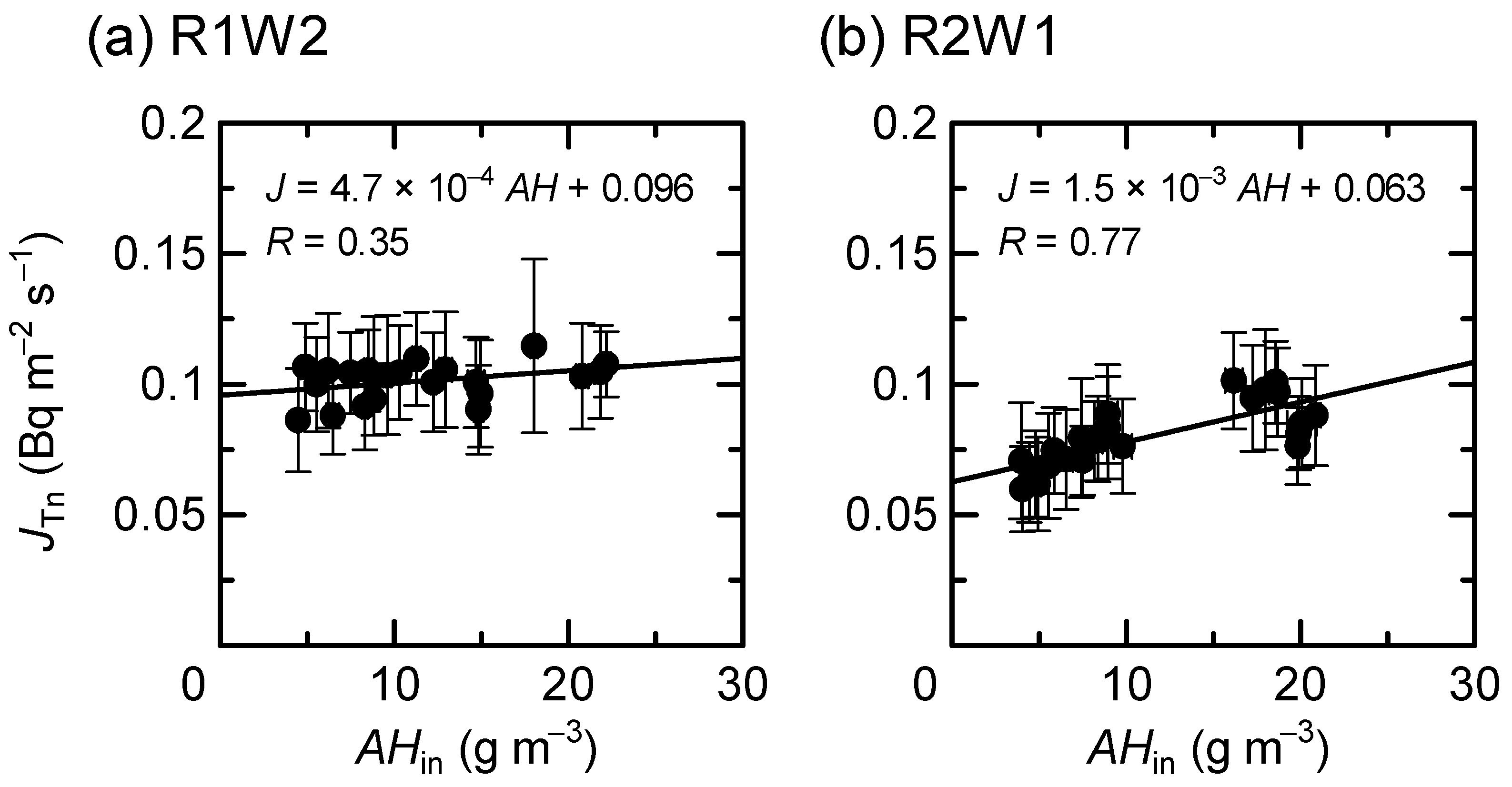
3. Results
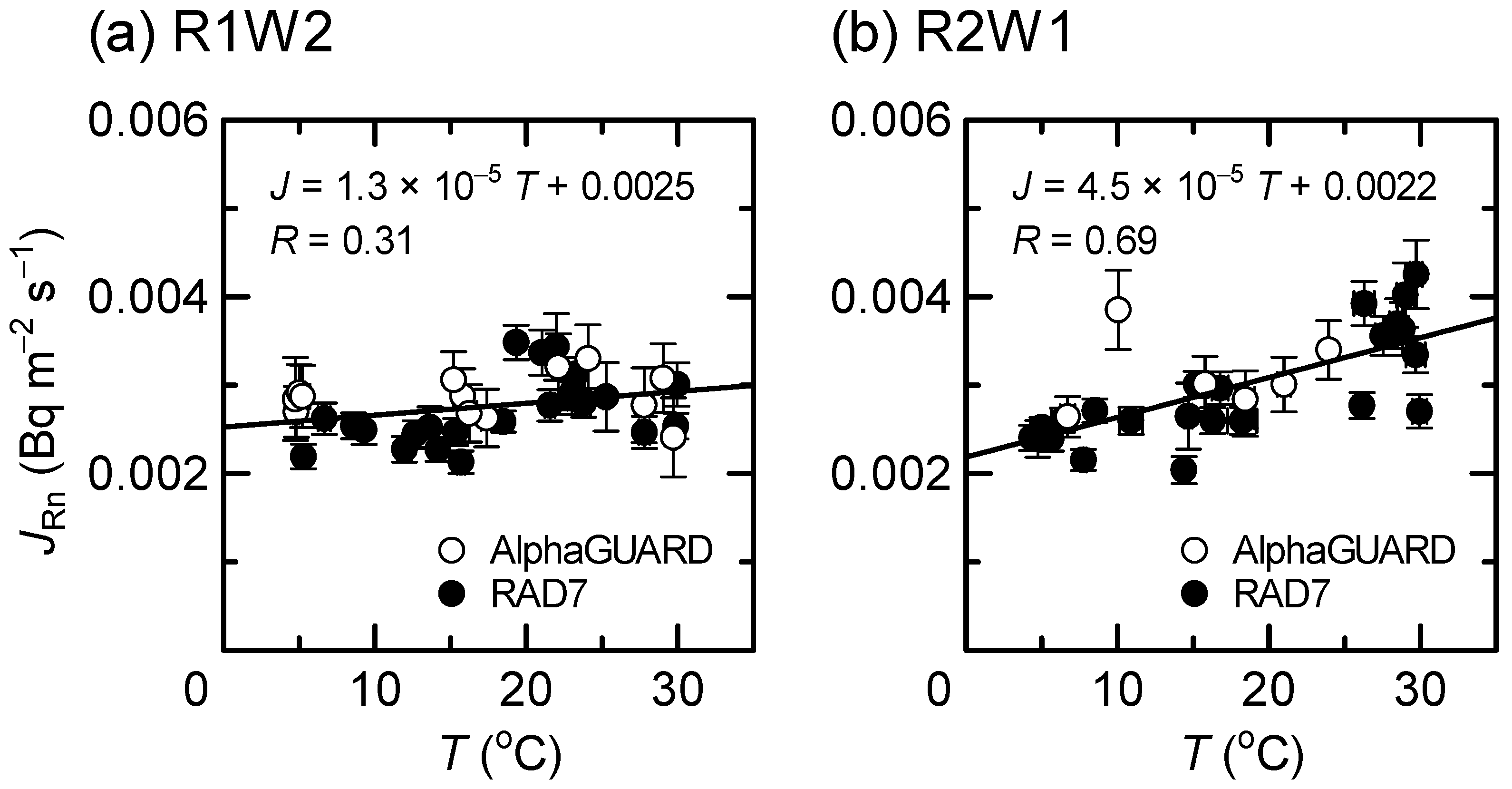
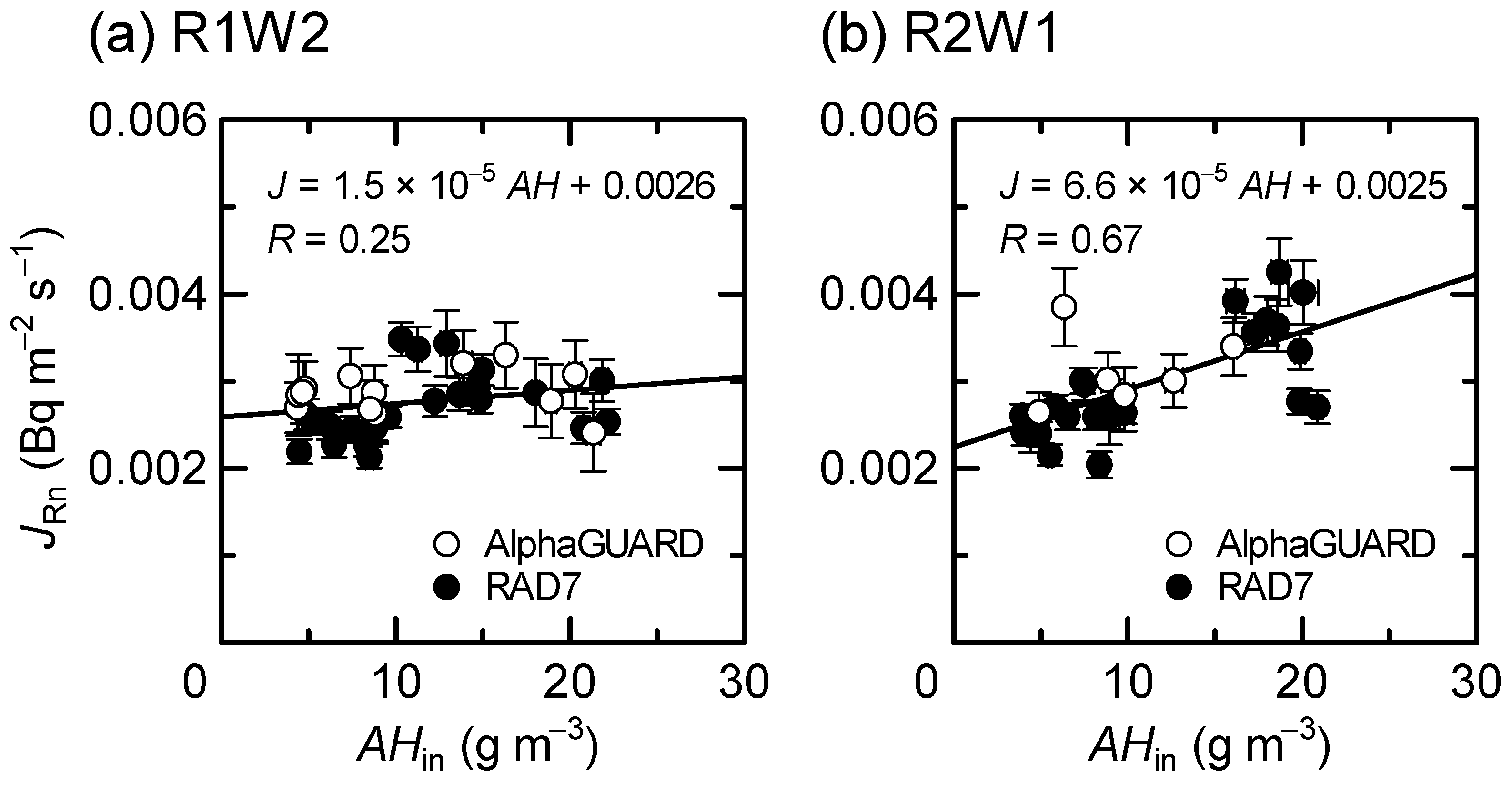
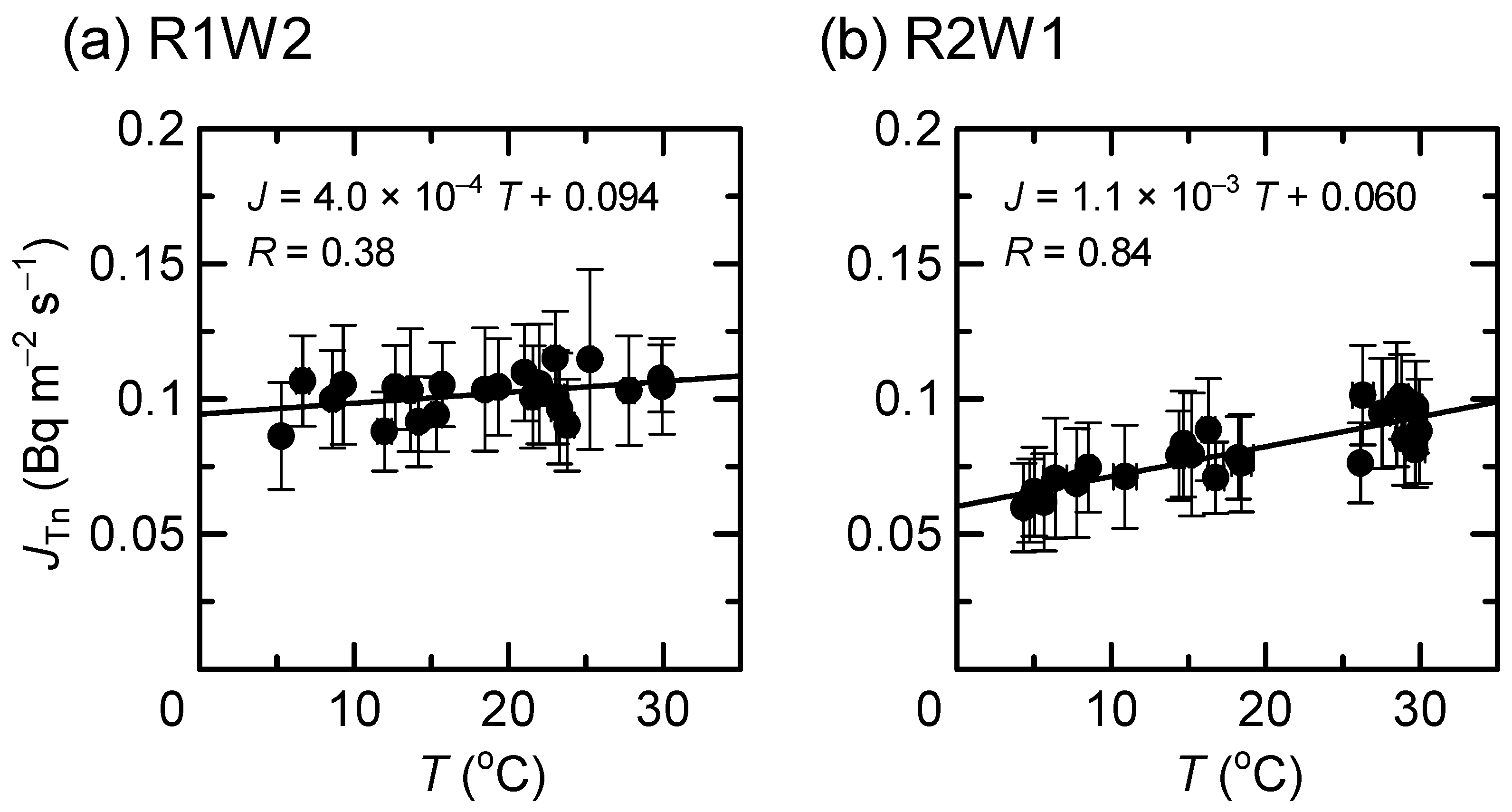
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tokonami, S. Characteristics of thoron (220Rn) and its progeny in the indoor environment. Int. J. Environ. Res. Public Health 2020, 17, 8769. [Google Scholar] [CrossRef] [PubMed]
- Font, L.; Baixeras, C. The RAGENA dynamic model of radon generation, entry and accumulation indoors. Sci. Total. Environ. 2003, 307, 55–69. [Google Scholar] [CrossRef] [PubMed]
- International Commission on Radiation Units and Measurements (ICRU). Measurement and Reporting of Radon Exposures; ICRU Report No.88; International Commission on Radiation Units and Measurements: Bethesda, MD, USA, 2012; Volume 12. [Google Scholar]
- Dvorzhak, A.; Mora, J.C.; Real, A.; Sainz, C.; Fuente, I. General model for estimation of indoor radon concentration dynamics. Environ. Sci. Pollut. Res. 2021, 28, 54085–54095. [Google Scholar] [CrossRef] [PubMed]
- Nazaroff, W.W. Radon transport from soil to air. Rev. Geophys. 1992, 30, 137–160. [Google Scholar] [CrossRef]
- Cinelli, G.; De Cort, M.; Tollefsen, T. (Eds.) European Atlas of Natural Radiation; Publication Office of the European Union: Luxembourg, 2019. [Google Scholar]
- United Nations Scientific Committee on the Effects of Atomic Radiation (UNSCEAR). Sources and Effects of Ionizing Radiation. UNSCEAR 2000 Report to the General Assembly, with Scientific Annexes; United Nations: New York, NY, USA, 2000.
- United Nations Scientific Committee on the Effects of Atomic Radiation (UNSCEAR). Sources and Effects of Ionizing Radiation. UNSCEAR 1993 Report to the General Assembly, with Scientific Annexes; United Nations: New York, NY, USA, 1993.
- United Nations Scientific Committee on the Effects of Atomic Radiation (UNSCEAR). Sources, Effects and Risks of Ionizing Radiation. UNSCEAR 1988 Report to the General Assembly, with Annexes; United Nations: New York, NY, USA, 1988.
- ISO 11665-9:2019; Measurement of Radioactivity in the Environment 1—Air: Radon-222—Part 9: Test Methods for Exhalation Rate of Building Materials. ISO: Geneva, Switzerland, 2019.
- Kanse, S.D.; Sahoo, B.K.; Gaware, J.J.; Sapra, B.K. A novel method based on 220Rn (thoron) exhalation rate of indoor surfaces for robust estimates of 220Rn concentration and equilibrium factor to compute inhalation dose. Chemosphere 2021, 267, 128908. [Google Scholar] [CrossRef] [PubMed]
- Nuccetelli, C.; Leonardi, F.; Trevisi, R. Building material radon emanation and exhalation rate: Need of a shared measurement protocol from the european database analysis. J. Environ. Radioact. 2020, 225, 106438. [Google Scholar] [CrossRef] [PubMed]
- Janik, M.; Omori, Y.; Yonehara, H. Influence of humidity on radon and thoron exhalation rates from building materials. Appl. Radiat. Isot. 2015, 95, 102–107. [Google Scholar] [CrossRef] [PubMed]
- Hassan, N.M.; Tokonami, S.; Fukushi, M. A simple technique for studying the dependence of radon and thoron exhalation rate from building materials on absolute humidity. J. Radioanal. Nucl. Chem. 2011, 287, 185–191. [Google Scholar] [CrossRef]
- De Jong, P.; Van Dijk, W.; De Rooij, M. Influence of the porosity on the 222Rn exhalation rate of concrete. Health Phys. 2011, 100, 127–137. [Google Scholar] [CrossRef] [PubMed]
- Stranden, E.; Kolstad, A.K.; Lind, B. The influence of moisture and temperature on radon exhalation. Radiat. Prot. Dosim. 1984, 7, 55–58. [Google Scholar] [CrossRef]
- Sahoo, B.K.; Sapra, B.K.; Gaware, J.J.; Kanse, S.D.; Mayya, Y.S. A model to predict radon exhalation from walls to indoor air based on the exhalation from building material sample. Sci. Total Environ. 2011, 409, 2635–2641. [Google Scholar] [CrossRef] [PubMed]
- Sakoda, A.; Ishimori, Y.; Jin, Q.; Iimoto, T. Improved data analysis techniques for calculating more accurate radon and thoron exhalation rates from building interior solid walls. Appl. Radiat. Isot. 2024, 207, 111180. [Google Scholar] [CrossRef] [PubMed]
- Joint Committee for Guides in Metrology (JCGM). Evaluation of Measurement Data—Supplement 1 to the Guide to the Expression of Uncertainty in Measurement Propagation of Distributions Using a Monte Carlo Method; JCGM: Geneva, Switzerland, 2008; Volume 101. [Google Scholar]
- Porstendörfer, J. Properties and behavior of radon and thoron and their decay products in the air. J. Aerosol Sci. 1994, 25, 219–263. [Google Scholar] [CrossRef]
- Sakoda, A.; Meisenberg, O.; Tschiersch, J. An approach to discriminatively determine thoron and radon emanation rates for a granular material with a scintillation cell. Radiat. Meas. 2016, 89, 8–13. [Google Scholar] [CrossRef]
- Ryu, D.-W.; Ko, J.-W.; Noguchi, T. Effects of simulated environmental conditions on the internal relative humidity and relative moisture content distribution of exposed concrete. Cem. Concr. Compos. 2011, 33, 142–153. [Google Scholar] [CrossRef]
- Garrabrants, A.C.; Kosson, D.S. Modeling moisture transport from a portland cement-based material during storage in reactive and inert atmospheres. Dry. Technol. 2003, 21, 775–805. [Google Scholar] [CrossRef]
- Akita, H.; Fujiwara, T.; Ozaka, Y. A practical procedure for the analysis of moisture transfer within concrete due to drying. Mag. Concr. Res. 1997, 49, 129–137. [Google Scholar] [CrossRef]
- Tan, Y.; Yuan, H.; Kearfott, K. A model comparison of diffusion-controlled radon exhalation from solid and cavity walls with application to high background radiation areas. Environ. Sci. Pollut. Res. 2020, 27, 43389–43395. [Google Scholar] [CrossRef] [PubMed]



| Wall | Monitor | n | T | RHin | AHin | RHsys | AHsys | JRn | JTn | α |
|---|---|---|---|---|---|---|---|---|---|---|
| (Testing Period) | (°C) | (%) | (g m−3) | (%) | (g m−3) | (Bq m−2 s−1) | (Bq m−2 s−1) | (s−1) | ||
| R1W2 (August 2021–December 2022) | AlphaGUARD | 13 | 16.7 ± 9.5 (4.7–29.7) | 66.9 ± 5.2 (56.9–74.6) | 11.0 ± 6.4 (4.3–21.4) | – | – | (2.9 ± 0.3) × 10−3 | – | (9.2 ± 1.1) × 10−5 |
| RAD7 | 23 | 18.3 ± 7.2 (5.3–29.9) | 67.7 ± 5.0 (60.6–77.2) | 11.6 ± 5.3 (4.5–22.2) | 1.9 ± 0.9 (0.1–3.9) | 0.5 ± 0.4 (0.1–1.7) | (2.7 ± 0.4) × 10−3 | 0.10 ± 0.01 | (7.9 ± 1.8) × 10−5 | |
| AlphaGUARD + RAD7 a | 36 | 17.7 ± 8.0 (4.7–29.9) | 67.4 ± 5.0 (56.9–77.2) | 11.4 ± 5.7 (4.3–22.2) | – | – | (2.8 ± 0.4) × 10−3 | – | (8.4 ± 1.7) × 10−5 | |
| R2W1 (April 2021–January 2023) | AlphaGUARD | 6 | 16.0 ± 6.6 (6.7–23.9) | 67.0 ± 4.1 (62.0–74.0) | 9.8 ± 4.1 (4.9–16.1) | – | – | (3.1 ± 0.4) × 10−3 | – | (8.7 ± 1.8) × 10−5 |
| RAD7 | 24 | 17.6 ± 9.5 (4.3–29.9) | 64.9 ± 6.4 (52.2–80.8) | 11.2 ± 6.3 (4.0–20.9) | 2.3 ± 1.6 (0.9–7.9) | 0.4 ± 0.4 (0.0–1.3) | (2.9 ± 0.6) × 10−3 | 0.080 ± 0.012 | (7.9 ± 2.3) × 10−5 | |
| AlphaGUARD + RAD7 a | 30 | 17.3 ± 8.9 (4.3–29.9) | 65.3 ± 6.0 (52.2–80.8) | 10.9 ± 5.9 (4.0–20.9) | – | – | (3.0 ± 0.6) × 10−3 | – | (8.0 ± 2.2) × 10−5 | |
| R1W2 + R2W1 a (April 2021–January 2023) | AlphaGUARD | 19 | 16.5 ± 8.5 (4.7–29.7) | 66.9 ± 4.8 (56.9–74.6) | 10.6 ± 5.7 (4.3–21.4) | – | – | (3.0 ± 0.3) × 10−3 | – | (9.0 ± 1.3) × 10−5 |
| RAD7 | 47 | 18.0 ± 8.4 (4.3–29.9) | 66.3 ± 5.9 (52.2–80.8) | 11.4 ± 5.8 (4.0–22.2) | 2.1 ± 1.3 (0.1–7.9) | 0.4 ± 0.4 (0.0–1.7) | (2.8 ± 0.5) × 10−3 | 0.089 ± 0.015 | (7.9 ± 2.1) × 10−5 | |
| AlphaGUARD + RAD7 a | 66 | 17.5 ± 8.4 (4.3–29.9) | 66.5 ± 5.5 (52.2–80.8) | 11.4 ± 5.8 (4.0–22.2) | – | – | (2.9 ± 0.5) × 10−3 | – | (8.2 ± 1.9) × 10−5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakoda, A.; Ishimori, Y.; Hasan, M.M.; Jin, Q.; Iimoto, T. Seasonal Variations in Radon and Thoron Exhalation Rates from Solid Concrete Interior Walls Observed Using In Situ Measurements. Atmosphere 2024, 15, 701. https://doi.org/10.3390/atmos15060701
Sakoda A, Ishimori Y, Hasan MM, Jin Q, Iimoto T. Seasonal Variations in Radon and Thoron Exhalation Rates from Solid Concrete Interior Walls Observed Using In Situ Measurements. Atmosphere. 2024; 15(6):701. https://doi.org/10.3390/atmos15060701
Chicago/Turabian StyleSakoda, Akihiro, Yuu Ishimori, Md. Mahamudul Hasan, Qianhao Jin, and Takeshi Iimoto. 2024. "Seasonal Variations in Radon and Thoron Exhalation Rates from Solid Concrete Interior Walls Observed Using In Situ Measurements" Atmosphere 15, no. 6: 701. https://doi.org/10.3390/atmos15060701
APA StyleSakoda, A., Ishimori, Y., Hasan, M. M., Jin, Q., & Iimoto, T. (2024). Seasonal Variations in Radon and Thoron Exhalation Rates from Solid Concrete Interior Walls Observed Using In Situ Measurements. Atmosphere, 15(6), 701. https://doi.org/10.3390/atmos15060701






