Southwest Pacific Tropical Cyclone Rapid Intensification Classification Utilizing Machine Learning

Abstract

This study evaluates the ability of three machine learning methods—decision tree classifier (DTC), random forest classifier (RFC), and XGBoost classifier (XGBC)—to classify and predict tropical cyclone (TC) rapid intensification (RI) and non-RI over the Southwest Pacific Ocean basin (SWPO) from 1982 to 2023. Among the 324 TCs within the domain, 81 were identified as RI TCs, exhibiting a 24-h intensity increase of at least 15 ms⁻¹ at least once in their lifetime. Environmental variables used for the input matrix are extracted from the nearest grid cell corresponding to each RI and non-RI event’s geographic location and time of occurrence. Additionally, the geographic location of each event and its initial intensity positions (24-h prior) are also included in the model. The XGBC, with 10-fold cross-validation, became the optimum classifier by achieving the highest classification accuracy, as well as the lowest probability of false detection and the highest AUC score on the unseen data. The model identified the longitude of RI and non-RI events, initial intensity latitude, extent of initial intensity, and relative humidity at 850 hPa as the most important variables in the classification decision. This study will advance storm preparedness strategies for the SWPO nations through correctly predicting RI-TCs and prioritizing early prediction of contributing environmental variables.

1. Introduction

The western region of the Southwest Pacific Ocean basin (130° E–180° and 5° S–40° S) encompasses the highly urbanized and economically developed northeastern and eastern coasts of mainland Australia, as well as numerous island nations of varying sizes, including Papua New Guinea, the Solomon Islands, Fiji, Vanuatu, Tonga, and New Caledonia. Tropical cyclones (TCs) are responsible for approximately 76% of all disasters in this region [1], often accompanied by extreme winds, severe storm surges, and prolonged, intense rainfall [2,3,4]. Among these hazards, wind speed is a critical factor in determining the extent of TC-related damage to both mainland areas and island nations. Over the past decade, the scientific community has made substantial advancements in forecasting tropical cyclone (TC) intensity [5,6,7,8]. In comparison, very little progress has been made in the forecasting of TC rapid intensification (RI). RI is typically defined as an increase in maximum sustained surface wind speed of at least 30 knots (15.4 ms⁻¹), corresponding to the 95th percentile, within a 24-h period [9]. RI can quickly transform a TC from a relatively predictable natural hazard to an unpredictable one with a reliable warning only hours in advance [10]. Statistical analysis has shown that 83% of all major TCs and all category 4 and 5 TCs undergo RI during their lifetime [9,11], highlighting their important role in TC climatology over a basin.

The National Hurricane Center (NHC) issues forecast guidance for RI events using the Statistical Hurricane Intensity Prediction Scheme (SHIPS) [12], and the logistic growth equation model [13,14]. SHIPS-based multiple studies of the North Atlantic showed the occurrence of RI depends on several environmental variables, such as a minimum sea surface temperature (SST) of 26 °C, large intensity change during the previous 12 h, weak vertical wind shear (VWS), higher mid-tropospheric (850 hPa) relative humidity (Rhum) [15], high ocean heat content, large upper-level divergence, high symmetric distribution of brightness temperature, and a large difference between TC maximum potential intensity and current TC intensity [6,9,16,17]. RI events in the South China Sea are strongly influenced by a combination of factors, including pronounced upper-tropospheric divergence, strong boundary layer convergence, weak deep-layer vertical wind shear (VWS), high translation speed, and elevated TC intensification potential [18]. RI climatology over the western North Pacific basin experiences a latitudinal shift due to El Nino Southern Oscillation (ENSO), which is associated with the changing gradient of upper ocean temperature, Rhum 850, and weak VWS [19]. Global warming is also considered one of the important contributors to the increasing frequency of RI events, as 51.3% of the variation in the proportion of RI experienced in a global warming-induced environment over the western North Pacific [20].

TC RI has been analyzed in previous studies using numerical data [21,22,23,24] and observational analysis [25,26,27]. TC RI trend analysis with observational data shows significant increases in TC RI rates over the Atlantic basin over the period 1982–2009 [28]. Statistical models for the classification investigation of RI have been finely developed by earlier studies [16,29,30]. A combination of SHIPS, logistic regression, and Bayesian statistical RI models used to forecast RI for the 12, 24, 36, and 48 h lead times shows that the models exhibit forecasting skills relative to climatological forecasts [16].

The accuracy of statistical models in RI classification and identifying contributing variables largely depends on multicollinearity. Machine learning is an emerging technique in the field of classifying RI and non-RI events (24 h intensity change is <15.4 ms⁻¹) and identifying important contributing variables in the classification decision [30,31,32]. The K-means clustering algorithm revealed RI events preferably associated with upper-tropospheric troughs of shorter zonal wavelengths that stay closer to the TC warm core than the non-RI episodes [29]. A support vector machine (SVM) efficiently classified RI and non-RI events by using base-state meteorological variables, including geopotential height, temperature, u and v wind components, vertical velocity, and Rhum 850 [33]. An RI event prediction performance comparison study between logistic regression, naive Bayes classifier, decision tree, and SVM for the North Atlantic using the SHIPS data revealed that the SVM with 10-fold cross validation (CV) outperformed by achieving high probability of detection (PoD) and the lowest false alarm [34]. A decision tree-based classification model to classify and predict RI events for the Pacific Ocean basin showcases that the model achieved misclassification errors of 13.5% and 21.85% for the rapidly weakening and rapidly intensifying events, accordingly [35]. Linear discriminant analysis, along with artificial neural networks, SVMs, and random forest, has been used to quantify RI predictability using proxy forecast model data [31] for the North Atlantic. A combination of principal component analysis with the K-means clustering algorithm quantified separability between RI and non-RI environments for the Atlantic Ocean TCs and showcased significant improvement, along with identifying mid- and upper-level Rhum in the classification decision [36]. An SVM classifier, along with a synthetic minority oversampling technique, classified RI and non-RI events for the Indian Ocean basin with a high PoD in a 24 h lead time [32]. A convolutional neural network (CNN) successfully classified RI events along with identifying potentially important features to RI, such as specific humidity, vorticity, and v wind component [37]. Another CNN classifier was used to predict RI events for both North Atlantic and eastern North Pacific TCs by using input variables at 12, 24, 36, 48, and 72 h lead times. The model was found to be more skillful in predicting RI events over 12 and 24 h lead times for the North Atlantic compared to operational guidance [38]. Applying the XGBoost classifier to the SHIPS database for RI classification and prediction yielded a PoD ranging from approximately 21% to 50%, while also maintaining a reduced false alarm rate [39]. An ensemble of 20 deep-learning models with different neural network designs and input combinations predicts intensity distribution of RI events at +24 h lead times with lower false alarm rates and high PoD for the western North Pacific [40]. Machine learning and deep learning models are significantly increasing the ability to discriminate between and forecast RI and non-RI events. However, compared to the North Atlantic and the eastern and western North Pacific basins, RI classification and prediction efforts are sparse over the SWPO.

The relatively isolated location of the SWPO mainland and island nations, and the high shoreline-to-land-area ratio [41], enhances the physical impact of major RI-TCs. The island nations are particularly at the forefront of the RI-TC impact due to limited accessibility, slow economic growth [42], fragile infrastructure [43], and dependence on subsistence farming [44,45,46]. RI in offshore regions is more threatening to coastal populations and the economic scenario. Compared to open oceans, offshore areas within 400 km of the coastline have experienced a significant increase in RI events, with counts tripling from 1980 to 2020 [27]. Approximately 50% of the TCs over the SWPO develop within 300 km of the coast [47], which enhances the risk of RI-TC-related disasters to the coastal communities.

Australia shows significant increase in RI trends from 1982 to 2017 [10]. Severe TC Kathy (1984) reached the RI stage (29 ms⁻¹ increase in 24 h) over the Gulf of Carpentaria offshore region near Vanderlin Island and caused approx. USD 12 million in damages [48]. TC Celeste (1995) rapidly intensified, with 22 ms⁻¹ intensity increases in 24 h near the Queensland coast. Severe TC Yasi (2011), which rapidly intensified into a category 2 within 24 h and gained 18 ms⁻¹ wind speed, made landfall near Mission Beach, Queensland, and caused USD 1412 million in damages. Severe TC Marcia (2015) intensified from category 1 to category 5 in 10 h, with a 36 ms⁻¹ wind speed increase, and made landfall over Yeppoon on the Queensland coast, causing approx. USD 587 million in damages. Severe TC Harold (2020) rapidly intensified from category 1 to category 4, with a 28 ms⁻¹ intensity increase within 24 h. It made landfall to the south of Fiji Island, impacted the Solomon and Vanuatu islands, and caused several lives to be lost along with USD 124 million in damages. Rapid urbanization in both the Australian mainland and SWPO Island nations increases risk from the adverse effects of rapidly intensifying TCs. For example, the small island nation of Fiji was affected by USD 0.9 billion in damage due to rapidly intensifying severe TC Winston (2011), primarily due to the very little time they had for disaster preparedness after being alerted about strong wind gusts. Insurance companies also bear a high amount of losses every year, primarily because communities have little time to prepare against RI-TCs. These challenges increase the need for correct classification of RI events well in advance and advanced prediction of RI-influencing environmental variables.

To overcome the limited data-driven RI classification in the SWPO basin, the goal of this research is to train tree-based machine learning classifiers to enhance the accurate differentiation between RI and non-RI events. The primary objective was to assess improvements in classifying and predicting RI events using a range of machine learning methods, including the decision tree classifier (DTC), random forest classifier (RFC), and XGBoost classifier (XGBC), while comparing model performance across various evaluation metrics. Additionally, the study aimed to identify and rank the key environmental variables that influence the classification decisions. By advancing RI classification, this study bridges the gap between data science and disaster resilience, enabling more accurate predictions of RI events and the prioritization of key variables for early forecasting. This empowers emergency managers to take proactive measures, enhancing preparedness and resilience in coastal communities.

Section 2 and Section 3 detailed the data and methods. Section 4 follows with the results and discussion of the machine learning classifiers’ performance. Section 5 will include a summary and conclusion.

2. Data

For optimum training of the classifiers, a thorough and robust database of RI is essential. TCs generated within 5° S–40° S and 130° E–180° are considered for this study. This study used six-hourly TC tracks data from the Southwest Pacific Enhanced Archive of Tropical Cyclones (SPEArTC) best track data. The SPEArTC dataset was built by [49] to enhance the spatio-temporal coverage of the International Best Tracks for Climate Stewardship (IBTrACS) database [50]. Only cyclones that have reached TC intensity (17 ms⁻¹) are considered. One individual TC season is comprised of storms formed over the SWPO region between November 1 and June 30 of the following year (e.g., season 1980 spans from November 1980 to June 1981) [51]. Based on the TC activity of the period, this study chose the active TC season between October and May of the following year.

This study follows the HURDAT database style [52] of determining RI and non-RI events for the SWPO basin. HURDAT is a database maintained by the NHC of all Atlantic basin TCs. The HURDAT database determines the RI and non-RI timesteps based on 24 h intensity changes of at least 15.4 ms⁻¹. Each TC’s temporal evolution included multiple timesteps, and each timestep was classified as an RI or non-RI timestep based on the previously mentioned definition. There were two important criteria for establishing these timesteps. First, the TC must have existed at 5 analysis periods (30 h) so that a 24 h intensity change could be measured. Second, the TC’s final timestep was no later than 24 h before landfall since RI is not predicted once TCs make landfall. The study includes non-RI events that occur immediately before and after RI events, ensuring a focused comparison within similar temporal and environmental contexts. This process legitimately focuses on the discriminative ability of the machine learning classifiers, i.e., how well the model distinguishes between RI and non-RI periods under similar contexts (Figure 1). These criteria resulted in 254 RI and 178 non-RI events from 1982 to 2023 (Figure 2). As RI events did not occur every year, the study has a few missing years.

Several geophysical variables are used in this study as the input to train the machine learning classifiers. Gridded multidimensional environmental variables are extracted from the nearest grid cell corresponding to each event’s geographic location and time of occurrence. This procedure ascertains a localized picture of the relationship. The input variables considered in this study are SST, Rhum 850 hPa, 850–200 hPa VWS or Ushear, 850–200 hPa horizontal wind shear or Vshear, the latitude and longitude of each RI and non-RI event, initial or 24 h prior intensity of each RI and non-RI events, and their associated latitude and longitude (

Table 1. The table includes the environmental variables used in machine learning classifiers for the input matrix. The spatial resolution and source information of each variable are mentioned.

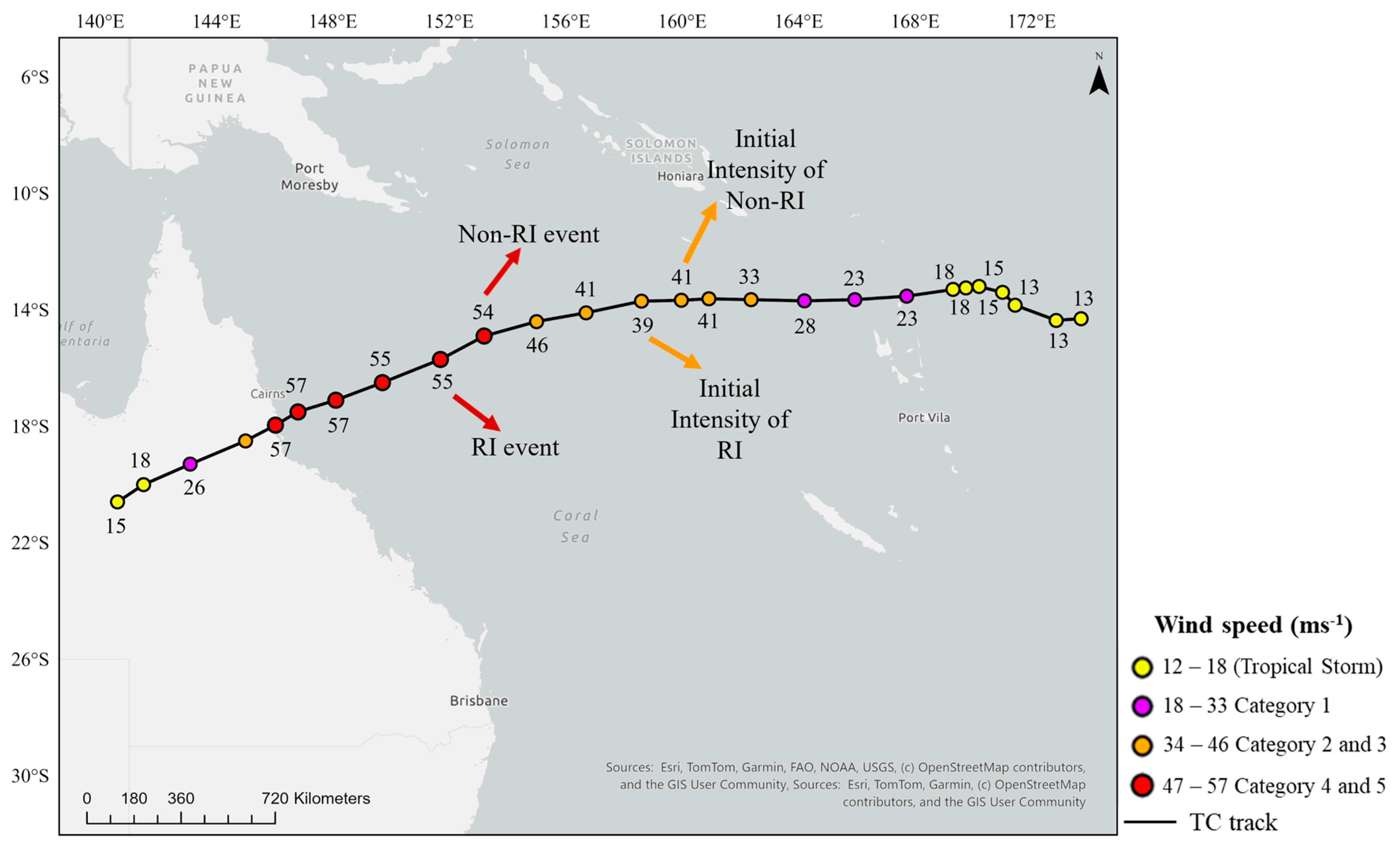
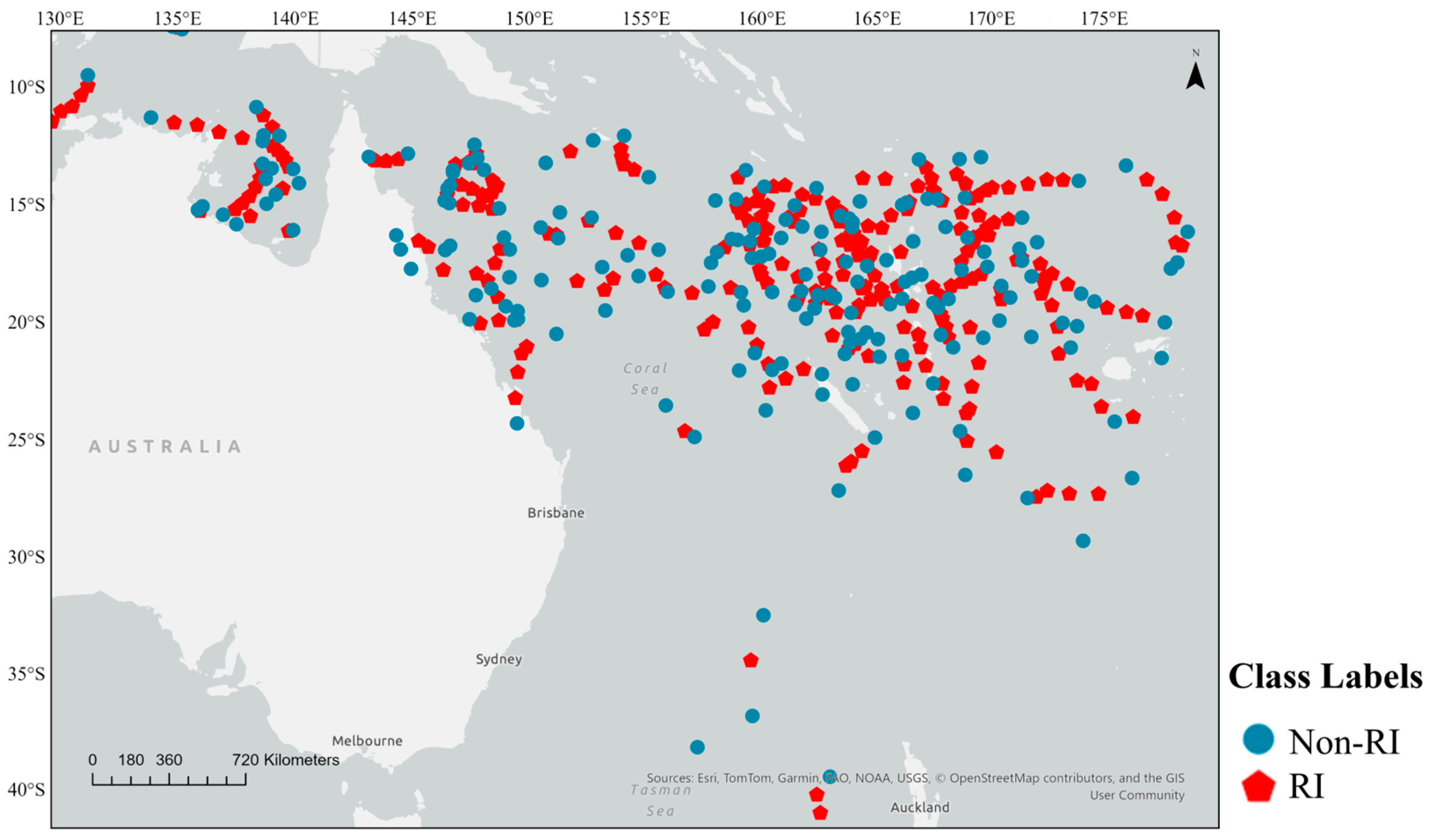
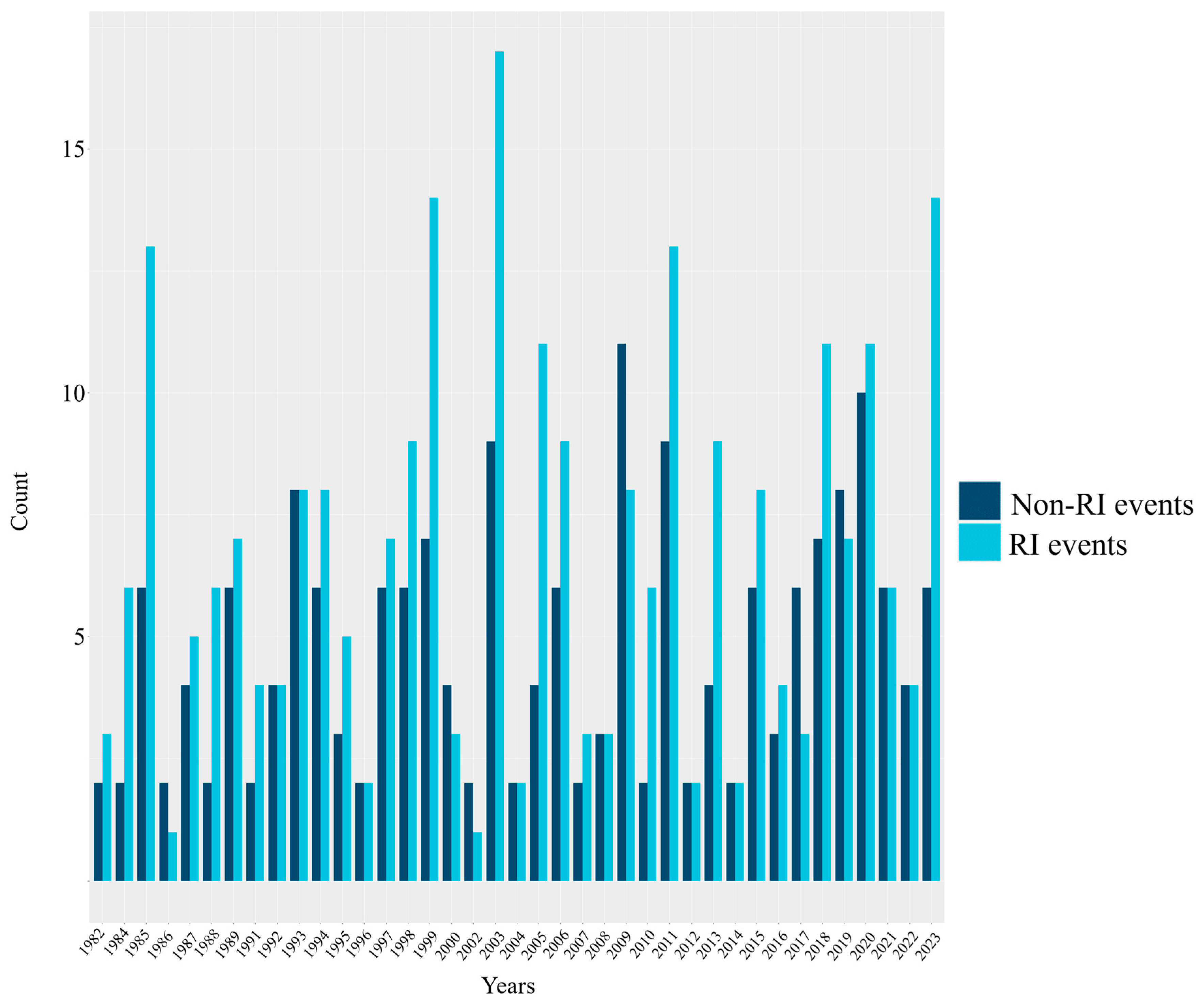
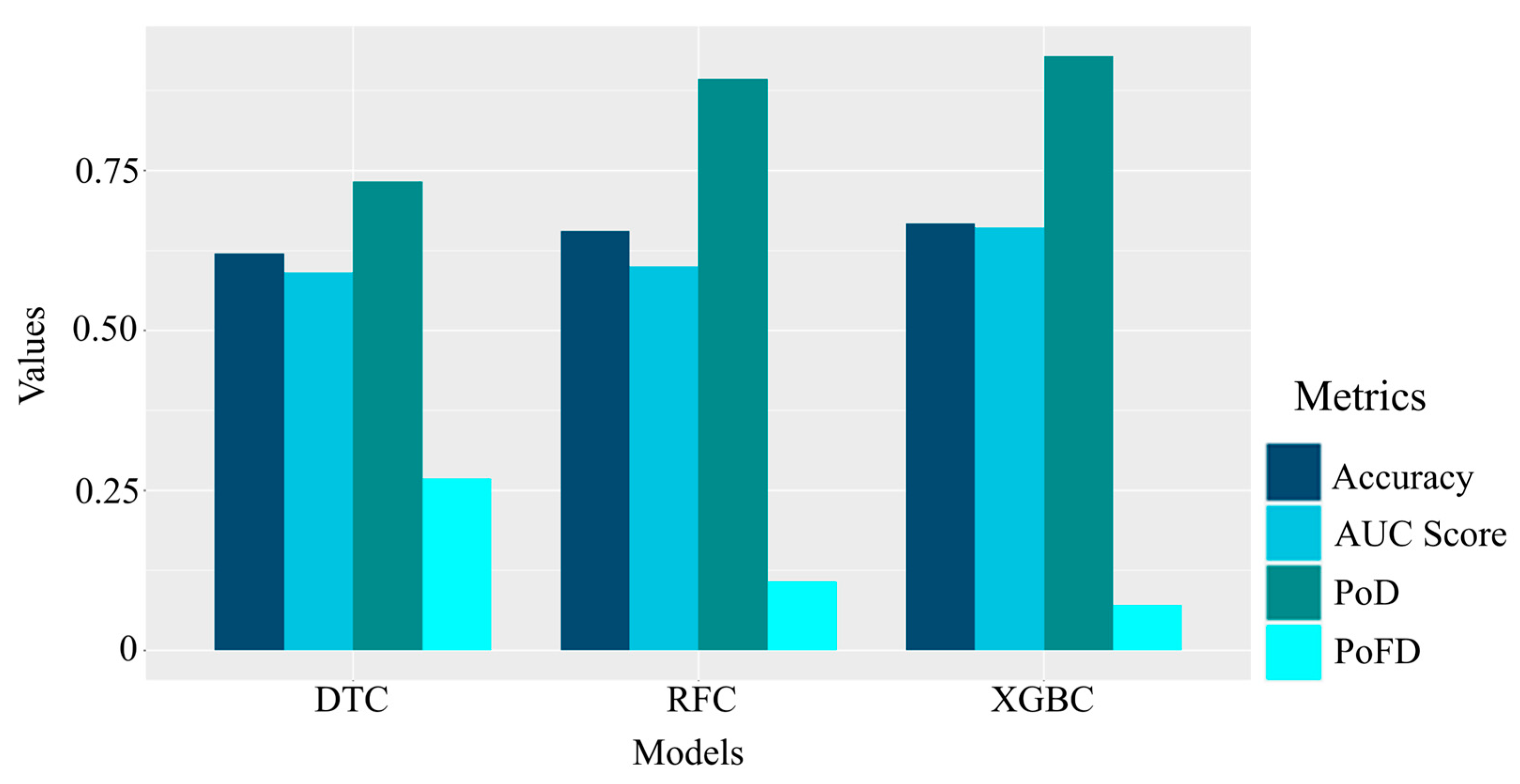
Variables	Spatial Resolution	Source
Longitude	Point	SPEArTC
Latitude	Point	SPEArTC
Initial intensity	Point	SPEArTC
Longitude_Initial intensity	Point	SPEArTC
Latitude_Initial intensity	Point	SPEArTC
SST	2.5° × 2.5°	NOAA ERSST
Rhum 850 hPa	2.5° × 2.5°	NCEP/DOE Reanalysis 2
Vshear	2.5° × 2.5°	NCEP/DOE Reanalysis 2
Ushear	2.5° × 2.5°	NCEP/DOE Reanalysis 2

).

The geophysical variables, excluding the SST, were collected from the National Centers for Environmental Prediction (NCEP)/Department of Energy (DOE) Reanalysis 2 model [53]. The SST data were taken from the NOAA Extended Reconstructed Sea Surface Temperature (ERSST) project [54]. The study used monthly data from the mentioned sources depending on the data point that was spatially and temporally closest to the RI and non-RI events.

3. Methods

A correlation matrix was used in this study to understand the magnitude and strength of multicollinearity between each contributing variable. The multicollinearity test was performed using the “Hmisc” package in R [55].

Tree-based classifiers are less affected by the multiciliary problem since they split the data based on feature importance rather than linear relationships. This study explores the utility of DTC, RFC, and XGBC implementation on the Jupyter Notebook framework (scikit learn 1.6.1). After compiling binary labels and their associated predictor variables, the dataset is split into two groups: training and testing. The purpose of the step is (1) to use the training data to generate the classifiers, and (2) to use the testing data to determine how well the prediction of the classifiers will generalize to previously unseen data [56].

3.1. Model Construction

DTC is used for pattern identification in the data, and the algorithm established correct decision rules by determining the relationship between the contributing and target variables [34,57]. The DTC structure contains a root node, multiple internal nodes, and a set of leaf nodes from top to bottom. The DTC constructs a tree on existing or training data using optimal partition attributes and makes predictions on unseen or testing data. This study generates a DTC model based on the Classification and Regression Tree (CART) algorithm [58]. The CART algorithm selects specific attributes at each node that best partition samples into classes following the information gain measurement. At any given node or branch, the CART algorithm selects the variable that shows the highest magnitude of discrimination between different classes. The CART algorithm with GINI coefficient was used to determine the optimal attributes for each split used to train the model. The CART algorithm was run on the training data with 10-fold CV, with at least two variables required to split an internal node, a maximum of five leaf nodes, and a maximum of five levels from the root node to the deepest leaf node. Each path of the DTC shows the influence of each variable that leads to the assignment of a target class label in the training data [59].

RFC is a non-parametric ensemble-based bagging algorithm popular for its higher accuracy and lower sensitivity to noise than any single classifier [60]. The RF classifier improves the accuracy and generalization capacity of a model via the integration of many weak classifiers [61,62]. The sampling method of bootstrap is employed to build the decision tree for each training subset, thus forming the forest. When the unknown data are predicted, randomly constructed N trees are used to jointly carry out the data classification, and the output of each tree is summarized to find the result with the most votes, which is identified as the result of the model [63]. Compared to the single tree models, RF reduced the inaccuracy by doing random sampling, reduced multicollinearity between variables, and brought a reduction in variance [60]. The RF model proved to be a good classifier of RI events [31,32,64]. The optimum performance of RFC depends on tuning its two major parameters: mtry (P), the number of input variables randomly selected for splitting at each tree node, and ntee (n), the total number of individual trees in the model. The study performed hyperparameter tuning using 10-fold CV, manually selecting 50, 100, and 200 n, and a fixed P from 1 to 9, using an interval of 1.

XGBC is a tree ensemble model consisting of a set of classification trees. By adding the prediction of multiple trees, the model overcomes the limitations of a single tree. Instead of stopping at one iteration improvement (K = 1), the process is repeated multiple times, with the learning of new error predictors for newly formed improved models until the accuracy or error is satisfactory [65]. It is a regularized gradient boosting method because it allows regularization or the constraining of variable weights. It helps reduce overfitting compared to any general gradient boosting method with no regularization, employing penalizing variable importance in high-dimensional scenarios, and thus performing the variable selection [65]. Penalty regularization decreases overfitting without generating a loss in predictive power, and as a result, fitted models generalize well to new or unseen data. XGBC is typically used in RI event discrimination to increase the prediction of unseen events [66,67,68]. The study performed hyperparameter tuning using 10-fold CV, a maximum of three, four, and five levels from the root node to the deepest leaf node, a learning rate of 0.1, and manually selecting 50, 100, and 200 n.

3.2. Feature Importance

The highly interpretable nature of the tree-based classifiers makes the model’s performance and prediction capability easily understandable. This study used the MINI Decrease GINI (MDG) index to rank the importance of each variable in the classification decision [69]. At each node within the binary tree, the optimal split can be achieved using the GINI impurity value, which measures how well a potential split separates the samples of the two classes in the particular node. This indicates the efficiency of the GINI index in explicit variable selection [70]. The MDG is the total decrease in node purity from the splitting of the variables, averaged over all the trees. The larger the MDG, the higher the rank of the variable in the classification decision [71] without requiring retention.

3.3. Evaluation Metrics

The ultimate standard of a machine learning classifier is its predictive capability using testing data (i.e., generalization error). The performance of each classifier is assessed using classification accuracy and a confusion matrix. To assess the class-specific performance, class-specific accuracy, PoD, and probability of false detection (PoFD) (type 2 error) are calculated from the confusion matrix [72,73] (

Table 2. The confusion matrix reports the number of false positives (FPs)—model indicates an RI event, when in the real world it was non-RI; false negatives (FNs)—model indicates a non-RI, when in the real world it was RI; true positives (TPs)—model correctly indicates an RI event; and true negatives (TNs)—model correctly indicates a non-RI event.

		Prediction
		Non-RI (0)	RI (1)
Actual	Non-RI (0)	True negative (TN)	False positive (FP)
	RI (1)	False negative (FN)	True positive (TP)

).

PoD refers to the model’s ability to correctly detect positive events or the model’s ability to correctly detect RI events when the storm is indeed going through RI. Since correctly detecting RI or positive events is more important for the advanced preparedness of the coastal communities, the study emphasizes using the sensitivity score [74]. PoFD showcases the model’s failure to predict positive events, even though it is positive.

$$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{b}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y} \mathrm{o}\mathrm{f} \mathrm{d}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}={\displaystyle \frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}}}$$

(1)

$$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{b}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y} \mathrm{o}\mathrm{f} \mathrm{f}\mathrm{a}\mathrm{l}\mathrm{s}\mathrm{e}\mathrm{d}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}={\displaystyle \frac{\mathrm{F}\mathrm{N}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}}}$$

(2)

The relationship between classification confidence/probability and correct labeling can be illustrated by using a receiver operating curve (ROC). The ROC curve helps to choose the optimum threshold to balance the true positive rate and the false positive rate [74]. The AUC reports the probability of false detection versus the probability of detection with a value approaching 1.0, indicating high sensitivity and specificity, and the model can differentiate between RI and non-RI events effectively [75].

4. Results and Discussion

4.1. Summary Statistics of Predictors and Target Variables

Figure 2 shows the geographic distribution of RI and non-RI events over the SWPO basin. Events are color-coded based on their RI or non-RI status, where red depicts the occurrence of an RI event and blue depicts the non-RI events. A cluster of RI events is observed over the western Coral Sea, the Gulf of Carpentaria, and the eastern region of the SWPO basin, with the highest concentration around Vanuatu, New Caledonia, and Fiji islands. Meanwhile, the lowest concentration of RI-TCs is observed near the eastern coast of mainland Australia and New Zealand, primarily due to mid-latitudinal impact, including below-average SST. The mean position of the 27 °C isothermal line between 10° S and 15° S makes the region conducive enough to produce strong TCs with the highest possibility of maximum RI events. The maximum RI-TC concentrated area over the eastern part of the basin experiences multiple major TCs, including Wilma (2011), Winston (2016), Keni (2018), and Yasa (2020).

The monthly frequency distribution of RI and non-RI events is plotted in Figure 3 for TC seasons from 1980 to 2023. The TC season over the SWPO is distinguished into two phases: the early TC season (November to January) and the late TC season (February to April), where the majority of the TCs occur during the late TC season. This study witnessed approximately 37% and 63% RI events generated during the early and late TC seasons, while approximately 35% and 65% non-RI events were generated during the early and late TC seasons. March is experiencing the highest occurrence of RI-TCs. The mean position of the monsoon trough and relative vorticity maxima over the western and eastern regions of the basin during March supports the highest occurrence of RI-TCs [76]. The ratio between RI and non-RI events shows approximately 61% and 39% of RI and non-RI events occurred during the early TC season, while approximately 58% and 42% of RI and non-RI events occurred during the late TC season. The late TC season shows lesser variability in producing RI and non-RI events compared to the early TC season, primarily due to the presence of favorable conditions such as above-average SST, Rhum 850, and weak VWS required to develop major TCs.

The interannual fluctuation of RI and non-RI events is shown in Figure 4. The ENSO is one of the influential teleconnections for the SWPO basin, contributing to interannual variation in the TC occurrence and intensity by modulating the SST and pressure gradient. Positive SST and Rhum 850 anomalies move towards the western side of the basin during La-Nina years, whereas the positive anomaly moves toward the eastern part of the basin and is centered around 180° during El-Nino years. The years 2003 and 2023 were El-Nino years with the presence of an above-average SST in the eastern equatorial Pacific, causing the higher occurrence of RI-TCs. Interestingly, 1985 and 1999 were La-Nina years, and the high occurrence of RI-TCs indicates the concentration of RI events towards the western edge of the basin. The years 2000 and 2017 show a higher occurrence of non-RI events compared to RI events due to the presence of La-Nina, which modulated below-average SSTs and low vorticity.

The Spearman’s rank correlation matrix was used to study the multicollinearity between input variables shown in

Table 3. The correlation matrix shows p-values between variables used for the input matrix in the machine learning classifier. Insignificant relationships (p-value ≥ 0.05) are shown in bold.

	Latitude	Longitude	SST	Rhum_850	Ushear	Vshear	Initial Intensity	Latitude Initial Intensity	Longitude Initial Intensity
Latitude	1	6 × 10−8	0	2 × 10−8	2 × 10−15	0	0.01	0	0.01
Longitude	6 × 10−8	1	0	1 × 10−5	4 × 10−3	0	0.16	0.09	0
SST	0 × 10−0	0	1	9 × 10−7	1 × 10−10	0.29	0.63	0	0.04
Rhum_850	2 × 10−8	0	9 × 10−7	1	7 × 10−2	0.11	0	0.9	0.13
Ushear	2 × 10−15	0	1 × 10−10	0.07	1	0.17	0.12	0.01	0.43
Vshear	6 × 10−3	0	3 × 10−1	0.11	0.17	1	0.83	0.5	0.03
Initial Intensity	1 × 10−2	0.16	6 × 10−1	0	0.12	0.83	1	0.11	0.79
Latitude Initial intensity	0 × 10−0	0.09	4 × 10−11	0.9	0.01	0.5	0.11	1	0.09
Longitude Initial intensity	9 × 10−3	0	4 × 10−2	0.13	0.43	0.03	0.79	0.09	1

. Insignificant correlations (p-value ≥ 0.05) are shown in bold. Rhum 850 shows that no significant correlation exists between Ushear and Vshear. Initial intensity has no significant correlation with SST and Rhum 850. The latitude of initial intensity shows no significant correlation with Vshear. SST has a significant correlation with Ushear, Vshear, and initial intensity through its thermodynamic structure, which possibly makes the relationship significant. The advantages of a tree-based machine learning algorithm are that the classification and prediction performance are not affected by the multicollinearity between the variables, which makes the model results non-biased.

4.2. Machine Learning Classifiers’ Outcome

The classifiers were generated with 80% training data (345 samples), and their performances have been evaluated with 20% (87 samples) testing data. To achieve the best performance in predicting unseen events, the study used hyperparameter tuning to train the models. The study primarily focuses on the best-performing model combination for each classifier.

4.2.1. Importance of Contributing Variables in Classification Decision

The most influential variables contributing to the classification decisions of the best-performing DTC, RFC, and XGBoost classifier (XGBC) are shown in Figure 5a–c, respectively. Initial intensity has been identified as the most important variable in classifying RI and non-RI events by both the DTC and RFC and was ranked the 3rd important variable by XGBC. Initial intensity indicates the stage of a TC at which the surrounding environment changes rapidly, causing an RI situation in a TC. Hence, the initiation phase of an RI storm holds an important place in discriminating between conducive and non-conducive environments.

The latitude of initial intensity was ranked the second most important variable by the RFC and XGBC, while it was ranked fifth by the DTC. SWPO basin TC intensity was significantly modulated by the ENSO phases due to shifts in the position of monsoon trough, SST, and vorticity gradient in different EL-Nino, La-Nina, and neutral phases [77]. TC genesis and intensification regions moved from the northeastern side of the basin near Fiji and the Tonga Islands during the later TC months of El-Nino seasons to the southwestern side of the basin, more towards the Coral Sea, during La-Nina seasons. This interannual latitudinal shift is influenced by the changing position of the Intertropical Convergence Zone (ITCZ) and South Pacific Convergence Zone (SPCZ).

Rhum 850 or mid-tropospheric humidity was ranked the second, third, and fourth most important variable in discriminating between RI and non-RI events by the DTC, RFC, and XGBC, respectively. The location of high Rhum 850 (70% or more) over the SWPO basin stretches between 10° S and 15° S from the Gulf of Carpentaria (130° E) in the west to the international date line or IDL (180°) [78]. The highest Rhum 850 region is concentrated around the New Caledonia islands, which also coincides with maximum RI-TC occurrence. The higher ranking of Rhum 850 implies the importance of a moist environment in TC maximum intensification at a rapid rate.

The latitudinal position of the RI and non-RI events was identified as an important determining factor in classification, as it was ranked fourth and fifth by the DTC, RFC, and XGBC, respectively. SWPO basin TC maximum intensification is primarily concentrated within a narrow band within 135° E 180° and 10° S–20° S because of the mean position of ITCZ, the monsoon trough, and SPCZ during the warm season. Both the ITCZ and the monsoon trough and SPCZ shift north and south as a response to ENSO. During El-Nino years, SPCZ moves northward, whereas during La-Nina years, SPCZ moves southward [79]. This interannual latitudinal shift of SPCZ shifts the favorable environmental parameters to RI-TC north and south, respectively, which leads to the identification of the latitude of RI and non-RI events as an important factor in classification decisions.

SST was identified as the fourth and sixth most important discriminating variable by RFC, DTC, and XGBC. An above-average SST belt (26–28 °C) is located over the 0–22° S stretching from the Gulf of Carpentaria in the west to the IDL in the east and coincides with higher tropical cyclone heat potential (TCHP). TCHP defines a measure of the integrated vertical temperature from the ocean surface to the depth of the 26 °C isotherm. The presence of high or deep TCHP reduces the TC-induced cold-water upwelling. The limiting opportunity of upwelling maintains warmer temperatures over the ocean surface and subsurface layer and supports further TC intensification in a shorter time frame [80]. TCHP is high within 10° S–15° S and around 160° E–180° within the domain and especially surrounds the Solomon, Vanuatu, northern Fiji, and Tonga islands [78], contributing to the maximum RI-C occurrence. The presence of TCHP over the region also makes SST an important contributing factor in the classification of RI and non-RI events.

Ushear or VWS is a key contributing environmental factor in RI and non-RI discrimination, making the variable rank sixth and eighth by the RFC, DTC, and XGBC classifiers. Weak Ushear (5–10%) necessary for TC intensification was identified within a 300 km radius for both RI and non-RI TCs over the SWPO basin at the genesis and mature times [78]. This is a possible reason for the comparatively lower rank in the classification decision.

The longitude of the RI and non-RI events is identified as the highest contributing variable in the classification decision by the XGBC. TC intensification over the SWPO basin was largely modulated by the ENSO, where the above-average SST, moist Rhum 850, weak VWS, high TCHP, and high vorticity zone located towards the eastern and central portion (180°) of the basin during El-Nino years shifts towards the gulf of Carpentaria and Coral Sea during La-Nina years. The interannual shift of the conducive zone also shifts the RI genesis and mature zones to the east and west in varying ENSO years, making longitude one of the most important variables in the classification decision.

4.2.2. Classification Accuracy

The prediction capabilities of the classifiers are evaluated using various metrics, as illustrated in Figure 6. This section evaluates and compares the classification and prediction performance of DTC, RFC, and XGBC. The classification accuracy scores of DTC, RFC, and XGBC on testing data are 0.62, 0.66, and 0.67, respectively. A confusion matrix is used to evaluate class-specific performance. The class-specific accuracy revealed that DTC, RFC, and XGBC were correctly classified as 73% and 39% (

Table 4. Confusion matrix for the testing dataset produced from the DTC with members trained using binary classes.

		Prediction
		Non-RI (0)	RI (1)
Actual	Non-RI (0)	13	18
	RI (1)	15	41

), 89% and 23% (

Table 5. Confusion matrix for the testing dataset produced from the RFC with members trained using binary classes.

		Prediction
		Non-RI (0)	RI (1)
Actual	Non-RI (0)	7	24
	RI (1)	6	50

), and 93% and 19% (

Table 6. Confusion matrix for the testing dataset produced from the XGBC with members trained using binary classes.

		Prediction
		Non-RI (0)	RI (1)
Actual	Non-RI (0)	6	25
	RI (1)	4	52

) RI and non-RI events, respectively. Correct and timely detection of RI events while reducing false detections is an important factor for coastal safety. Figure 6 compares the reliability of the models by comparing PoD, PoFD, and AUC scores. The class-specific accuracy for RI events also explains their model’s capability of PoD on unseen data. DTC struggled to correctly classify RI events, hence the PoFD score of DTC is comparatively high (27%). The PoFD score of both the RFC and XGBC is very low, at 11% and 7%, respectively. This result builds higher confidence in RFC and XGBC, as both produce very low false alarms, which is a crucial measurement, particularly for RI events. All the approaches struggled to classify non-RI events, possibly because of the lower number of events compared to the RI events.

The DTC, RFC, and XGBC achieved 0.59, 0.60, and 0.66 AUC scores, respectively. The ROC curves in Figure 7 display the sensitivity of the classifier by plotting the ratio of true positives to false positives. The purpose of the curve is to iteratively change the threshold value to check how it changes the sensitivity (true negative rate) of the model. The ROC curves in Figure 7a–c show that the DTC, RFC, and XGBC probabilities moderately separate the RI and non-RI events. The ensemble models perform better than single tree-based models. The results suggest that XGBC outperformed the DTC and RFC in terms of highest classification accuracy, PoD, and PoFD, and achieved the highest AUC score.

5. Summary and Conclusions

This study examined the utility of three machine learning models—DTC, RFC, and XGBC—for the problem of classifying RI and non-RI events using data from 1982 to 2023 for the SWPO basin. Compared to the northern hemisphere TC basins, the SWPO has been explored in a very limited way in terms of studying RI [78]. This present study provides a classification-based approach to identify favorable environments for RI-TCs at a localized spatial scale. The study adapted the definition of RI by the NHC to identify RI and non-RI TCs. A further three tree-based classifiers were trained using nine valuable environmental variables as an input matrix. Finally, evaluation metrics are used to measure the prediction capabilities of each classifier on unseen data. This study fills the gap of discriminating RI and non-RI events over the SWPO basin at a very local scale and provides a path to prioritize predicting the most influential variables in the classification decision.

The XGBC with 10-fold CV, 200 n, learning rate 0.1, and maximum four levels from the root node to the deepest leaf node was identified as the best-performing classifier compared to the DTC and RFC, as this model achieved highest accuracy, PoD, lowest PoFD, and highest AUC on the unseen data. One aim of the study was to lower PoFD, because incorrect classification of a strengthening RI event can be destructive to the coastal community. It particularly matters to the SWPO basin because many major TCs and RI events occur within 300 km of the coastal areas. The best-performing XGBC ranked RI and non-RI events’ longitudinal position, initial intensity latitudinal position, initial or 24 h prior intensity, Rhum 850, RI and non-RI events’ latitudinal position, and SST as the most influential variables in the classification decision.

The high importance of the longitudinal position of the RI and non-RI events provides future research motivation. Due to the consistent presence of high subsurface temperature and ocean–atmosphere teleconnections; SST, VWS, and high Rhum 850 play a significant role in modulating RI events near the SWPO island nations. Additionally, the different types of topography, the bathymetric characteristics of the ocean floor, and the environmental and social structures between mainland Australia and the SWPO island nations motivate the creation of two separate classification models for the mainland and islands [81]. Identifying the geographic location of incorrectly classified events from satellite or radar data will provide further information on the responsible atmospheric and oceanic variables. XGBC achieved comparatively lower accuracy for the non-RI events, primarily due to the lower number of events. Future investigations will be dedicated to improving model performance for both classes by applying alternative sampling strategies, such as SMOTE and ADASYN, more extensive hyperparameter optimization, simulating TC tracks, and integration with ensemble architectures to boost overall and class-wise accuracy.

The SWPO basin is enriched by the Great Barrier Reef, great biodiversity, indigenous and native communities, and the most urbanized and industrialized coastal cities in the southern hemisphere and offers ample opportunities for tourism and agriculture-based economies. Multiple small island nations, including the Solomon Islands, Fiji, Tonga, New Caledonia, and Vanuatu, in this domain are vulnerable due to a lack of infrastructure, weak governance, limited social security systems, high levels of relative poverty, remoteness, and a lack of financial and technical capacities [82]. The increasing frequency and intensity of RI events, particularly in the offshore areas of both the mainland and islands, pose significant risks in every aspect of this basin and amplify damage due to limited access to infrastructure and financial resources. In this context, advanced machine learning models that accurately classify and predict RI events while also identifying key environmental factors contributing to their onset can enhance early warning systems and help regions better prepare for RI TCs, ultimately reducing potential losses.