A New Approach to Estimating the Sensible Heat Flux in Bare Soils
Abstract
1. Introduction
2. Theory
Combining MOST and SR Theory
3. Data and Methods
3.1. Determining SR Parameters and and C Under Neutral Conditions
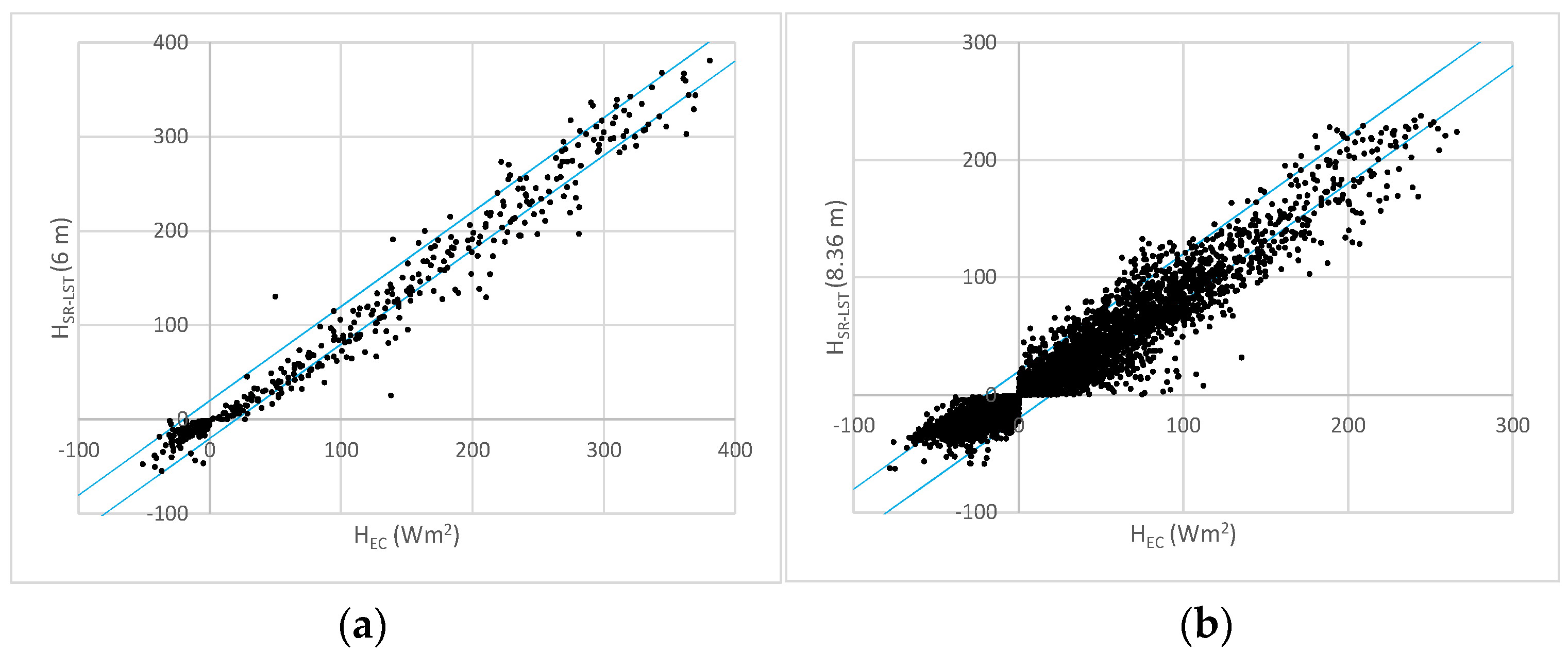
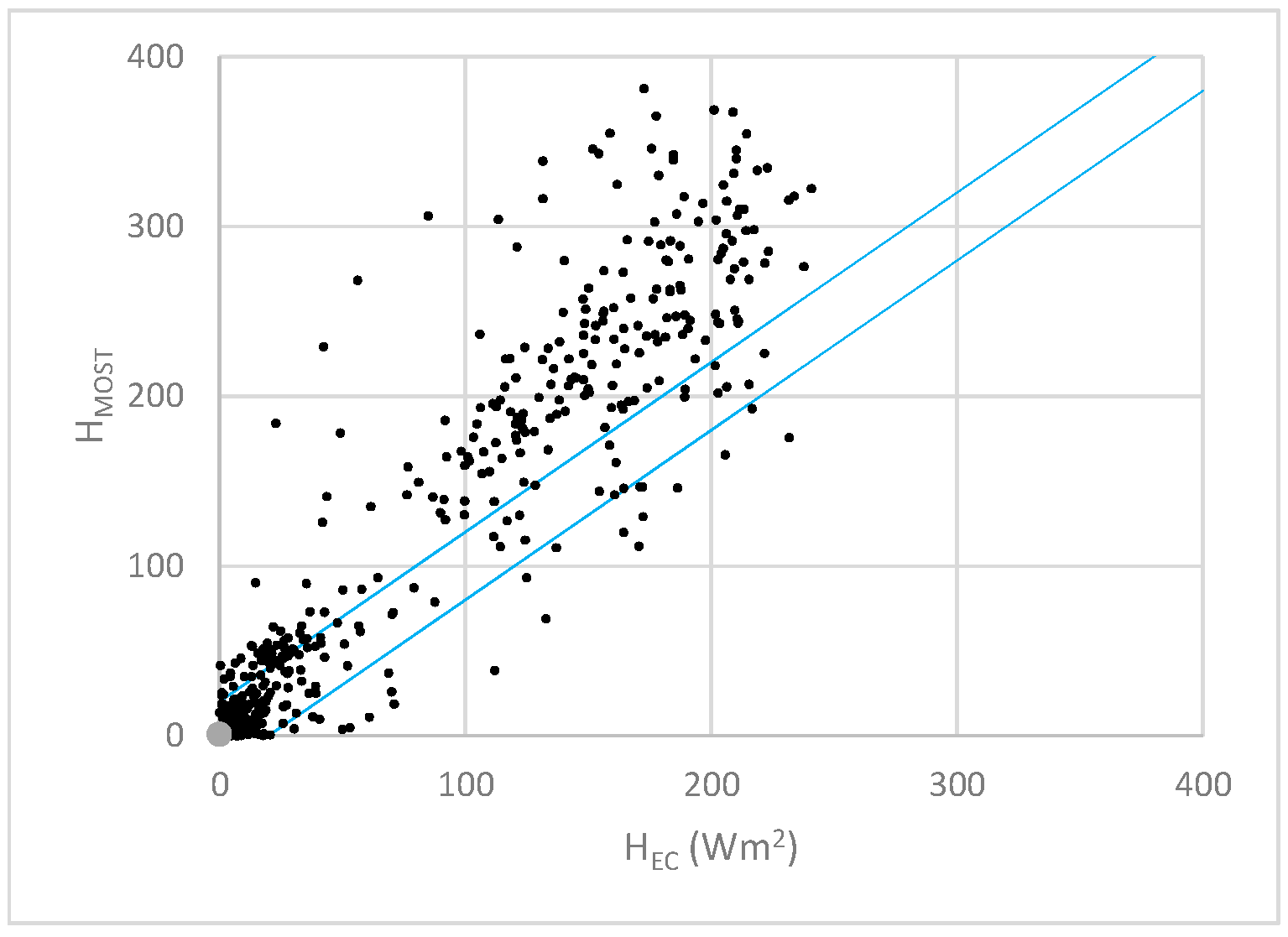
3.2. Estimating the Sensible Heat Flux. Comparison and Evaluation
4. Results and Discussion
4.1. Stable Cases
4.2. Unstable Cases
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schmid, P.; Niyogi, D. A method for estimating planetary boundary layer heights and its application over the ARM Southern Great Plains site. J. Atmos. Ocean. Technol. 2012, 29, 316–322. [Google Scholar] [CrossRef]
- Compton, J.C.; Delgado, R.; Berkoff, T.A.; Hoff, R.M. Determination of planetary boundary layer height on short spatial and temporal scales: A demonstration of the covariance wavelet transform in ground-based wind profiler and lidar measurements. J. Atmos. Ocean. Technol. 2013, 30, 1566–1575. [Google Scholar] [CrossRef]
- Brunet, Y. Turbulent flow in plant canopies: Historical perspective and overview. Bound-Layer Meteorol. 2020, 177, 315–364. [Google Scholar] [CrossRef]
- Kustas, W.P.; Blanford, J.H.; Stannard, D.I.; Daughtry, C.S.T.; Nichols, W.D.; Weltz, M.A. Local energy flux estimates for unstable conditions using variance data in semiarid rangelands. Water Resour. Res. 1994, 30, 1351–1361. [Google Scholar] [CrossRef]
- Drexler, J.Z.; Snyder, R.L.; Spano, D.; Paw, U.K.T. A review of models and micrometeorological methods used to estimate wetland evapotranspiration. Hydrol. Process. 2004, 18, 2071–2101. [Google Scholar] [CrossRef]
- Pozníková, G.; Fischer, M.; van Kesteren, B.; Orság, M.; Hlavinka, P.; Žalud, Z.; Trnka, M. Quantifying turbulent energy fluxes and evapotranspiration in agricultural field conditions: A comparison of micrometeorological methods. Agric. Water Manag. 2018, 209, 249–263. [Google Scholar] [CrossRef]
- Verhoef, A.; Mcnaughton, K.G.; Jacobs, A.F.G. A parameterization of momentum roughness length and displacement height for a wide range of canopy densities. Hydrol. Earth Syst. Sci. Discuss. 1997, 1, 81–91. [Google Scholar] [CrossRef]
- Timmermans, W.J.; Kustas, W.P.; Anderson, M.C.; French, A.N. An intercomparison of the Surface Energy Balance Algorithm for Land (SEBAL) and the Two-Source Energy Balance (TSEB) modeling schemes. Remote Sens. Environ. 2007, 108, 369–384. [Google Scholar] [CrossRef]
- Sun, S.K.; Li, C.; Wang, Y.B.; Zhao, X.N.; Wu, P.T. Evaluation of the mechanisms and performances of major satellite-based evapotranspiration models in Northwest China. Agric. For. Meteorol. 2020, 291, 108056. [Google Scholar] [CrossRef]
- Anderson, M.C.; Kustas, W.P.; Norman, J.M.; Diak, G.T.; Hain, C.R.; Gao, F.; Yang, Y.; Knipper, K.R.; Xue, J.; Yang, Y.; et al. A brief history of the thermal IR-based Two-Source Energy Balance (TSEB) model—Diagnosing evapotranspiration from plant to global scales. Agric. For. Meteorol. 2024, 350, 109951. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Sánchez, J.M.; López-Urrea, R.; Valentín, F.; Caselles, V.; Galve, J.M. Lysimeter assessment of the Simplified Two-Source Energy Balance model and eddy covariance system to estimate vineyard evapotranspiration. Agric. For. Meteorol. 2019, 274, 172–183. [Google Scholar] [CrossRef]
- Castellví, F.; González-Dugo, M.P. A one–source model to estimate sensible heat flux in agricultural landscapes. Agric. For. Meteorol. 2021, 310, 108628. [Google Scholar] [CrossRef]
- Paw, U.K.T.; Qiu, J.; Su, H.B.; Watanabe, T.; Brunet, Y. Surface renewal analysis: A new method to obtain scalar fluxes without velocity data. Agric. For. Meteorol. 1995, 74, 119–137. [Google Scholar] [CrossRef]
- Raupach, M.R.; Finnigan, J.J.; Brunet, Y. Coherent eddies in vegetation canopies: The mixing-layer analogy. Bound-Layer Meteorol. 1996, 78, 351–382. [Google Scholar] [CrossRef]
- Castellví, F. Combining surface renewal analysis and similarity theory: A new approach for estimating sensible heat flux. Water Resour. Res. 2004, 40, W05201. [Google Scholar] [CrossRef]
- Fisher, M.; Katul, G.G.; Noormets, A.; Poznikova, G.; Domec, J.C.; Orság, M.; Zalud, Z.; Trnka, M.; King, J.S. Merging flux-variance with surface renewal methods in the roughness sublayer and the atmospheric surface layer. Agric. For. Meteorol. 2023, 342, 109692. [Google Scholar] [CrossRef]
- Brutsaert, W.H. Evaporation into the Atmosphere. Environmental Fluid Mechanics, 1st ed.; Kluwer Academic Publishers: Dordrecht, Switzerland; Boston, MA, USA; London, UK, 1982; pp. 1–400. [Google Scholar]
- Dyer, A.J. A review of flux-profile relationships. Bound-Layer Meteorol. 1974, 7, 363–372. [Google Scholar] [CrossRef]
- Katul, G.G.; Hsieh, C.I.; Oren, R.; Ellsworth, D.; Philips, N. Latent and sensible heat flux predictions from a uniform pine forest using surface renewal and flux variance methods. Bound-Layer Meteorol. 1996, 80, 249–282. [Google Scholar] [CrossRef]
- Chen, W.; Novak, M.D.; Black, T.A.; Lee, X. Coherent eddies and temperature structure functions for three contrasting surfaces. Part I. Ramp model with finite micro-front time. Bound-Layer Meteorol. 1997, 84, 99–123. [Google Scholar] [CrossRef]
- Chen, W.; Novak, M.D.; Black, T.A.; Lee, X. Coherent eddies and temperature structure functions for three contrasting surfaces. Part II. Renewal model for sensible heat flux. Bound-Layer Meteorol. 1997, 84, 125–147. [Google Scholar] [CrossRef]
- Haymann, N.; Lukyanov, V.; Tanny, J. Effects of variable fetch and footprint on surface renewal measurements of sensible and latent heat fluxes in cotton. Agric. For. Meteorol. 2019, 268, 63–73. [Google Scholar] [CrossRef]
- Garai, A.; Kleissl, J. Air and surface temperature coupling in the convective atmospheric boundary layer. J. Atmos. Sci. 2011, 68, 2945–2954. [Google Scholar] [CrossRef]
- Castellví, F.; Gavilan, P.; Gonzalez-Dugo, M.P. Combining the bulk transfer formulation and surface renewal analysis for estimating the sensible heat flux without involving the parameter kB−1. Water Resour. Res. 2014, 50, 8179–8190. [Google Scholar] [CrossRef]
- Castellví, F.; Cammalleri, C.; Ciraolo, G.; Maltese, A.; Rossi, F. Daytime sensible heat flux estimation over heterogeneous surfaces using multitemporal land-surface temperature observations. Water Resour. Res. 2016, 52, 3457–3476. [Google Scholar] [CrossRef]
- Castellví, F.; Oliphant, A.J. Daytime sensible and latent heat flux estimates for a mountain meadow using in-situ slow-response measurements. Agric. For. Meteorol. 2017, 236, 135–144. [Google Scholar] [CrossRef]
- Grachev, A.; Fairall, C.; Bradley, E. Convective Profile Constants Revisited. Bound-Layer Meteorol. 2000, 94, 495–515. [Google Scholar] [CrossRef]
- Crago, R.D.; Qualls, R.J. Use of land surface temperature to estimate surface energy fluxes: Contributions of Wilfried Brutsaert and collaborators. Water Resour. Res. 2014, 50, 3396–3408. [Google Scholar] [CrossRef]
- Yang, K.; Koike, T.; Ishikawa, H.; Kim, J.; Li, X.; Liu, H.; Liu, S.; Ma, Y.; Wang, J. Turbulent Flux Transfer over Bare-Soil Surfaces: Characteristics and Parameterization. J. Appl. Meteorol. Climatol. 2008, 47, 276–290. [Google Scholar] [CrossRef]
- Tanaka, K.; Ishikawa, H.; Hayashi, T.; Tamagawa, I.; Ma, Y. Surface energy budget at Amdo on Tibetan Plateau using GAME/Tibet IOP98 data. J. Meteor. Soc. Jpn. 2001, 79, 505–517. [Google Scholar] [CrossRef]
- Yan, X.; Yang, H.; Liu, F. Modeling of surface flux in Tongyu using the Simple Biosphere Model (SiB2). J. For. Res. 2010, 21, 183–188. [Google Scholar] [CrossRef]
- Agam, N.; Berliner, P.R. Diurnal Water Content Changes in the Bare Soil of a Coastal Desert. J. Hydromet. 2004, 5, 922–933. [Google Scholar] [CrossRef]
- Mauder, M.; Liebethal, C.; Göckede, M.; Leps, J.P.; Beyrich, F.; Foken, T. Processing and quality control of flux data during LITFASS-2003. Bound-Layer Meteorol. 2006, 121, 67–88. [Google Scholar] [CrossRef]
- Frank, J.M.; Massman, W.J.; Ewers, B.E. Underestimates of sensible heat flux due to vertical velocity measurement errors in non-orthogonal sonic anemometers. Agric. For. Meteorol. 2013, 171, 72–81. [Google Scholar] [CrossRef]
- Mauder, M.; Oncley, S.P.; Vogt, R.; Weidinger, T.; Ribeiro, L.; Bernhofer, C.; Foken, T.; Kohsiek, W.; de Bruin, H.A.R.; Liu, H. The Energy Balance Experiment EBEX-2000. Part II: Intercomparison of eddy-covariance sensors and post-field data processing methods. Bound-Layer Meteorol. 2007, 123, 29–54. [Google Scholar] [CrossRef]
- Foken, T. Micrometeorology, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–306. [Google Scholar]
- Foken, T.; Oncley, S.P. Results of the workshop ‘Instrumental and methodical problems of land surface flux measurements’. Bull. Amer. Meteorol. Soc. 2005, 76, 1191–1193. [Google Scholar] [CrossRef]
- Castellví, F.; Snyder, R.L.; Baldocchi, D.D. Surface energy-balance closure over rangeland grass using the eddy covariance method and surface renewal analysis. Agric. For. Meteorol. 2008, 148, 1147–1160. [Google Scholar] [CrossRef]
- Horst, T.W.; Semmer, S.R.; Maclean, G. Correction of a Non-orthogonal, Three-Component Sonic Anemometer for Flow Distortion by Transducer Shadowing. Bound-Layer Meteorol. 2015, 155, 371–395. [Google Scholar] [CrossRef]
- Frank, J.M.; Massman, W.J.; Swiatek, E.; Zimmerman, H.A.; Ewers, B.E. All Sonic Anemometers Need to Correct for Transducer and Structural Shadowing in Their Velocity Measurements. J. Atmos. Ocean. Technol. 2016, 33, 149–167. [Google Scholar] [CrossRef]
- Frank, J.M.; Massman, W.J.; Stephen, C.W.; Nowicki, K.; Rafkin, S.C.R. Coordinate Rotation–Amplification in the Uncertainty and Bias in Non-orthogonal Sonic Anemometer Vertical Wind Speeds. Bound-Layer Meteorol. 2020, 175, 203–235. [Google Scholar] [CrossRef]
- Mauder, M.; Eggert, M.; Gutsmuths, C.; Oertel, S.; Wilhelm, P.; Voelksch, I.; Wanner, L.; Tambke, J.; Bogoev, I. Comparison of turbulence measurements by a CSAT3B sonic anemometer and a high-resolution bistatic Doppler lidar. Atmos. Meas. Tech. 2020, 13, 969–983. [Google Scholar] [CrossRef]
- Qi, Y.; Xiaodong, S.; Chen, G.; Gao, Z.; Bi, X.; Yu, L.; Mao, H. Re-estimation of the vertical sensible heat flux by determining the environmental temperature on a single-point tower measurement. Front. Earth Sci. 2024, 12, 1269252. [Google Scholar] [CrossRef]



| Site: 1 Project Lat, Lon, Alt (m) | Amdo GAME-Tibet 32.2, 91.6, 4700 | TY-Crop CEOP 44.4, 122.8, 184 | TY-Grass CEOP 44.4, 122.8, 184 | Wadi Mashash Nacional 31.13, 34.88, 400 |
|---|---|---|---|---|
| Campaign | May–September 1998 | October 2002–December 2004 | October 2002–December 2004 | January–August 2022 |
| Bare surface | Up to June 15 | November–March | November–March | Always |
| Landscape | Flat | Flat | Flat | Flat |
| Zom (mm) | 2.2 | 6.10 | 2.24 | 4.50 |
| Wind speed (m) | 1.9, 6.0, 14.1 | 2.36, 4.36, 8.36, 12.36, | 1.76, 4.36, 8.36, | 2 |
| 16.65 | 12.86, 17.46 | |||
| Air Temp. (m) | 1.55, 5.65, 13.75 | 1.95, 3.95, 7.95, | 1.35, 3.95, 7.95, | 2 |
| 11.95, 17.36 | 12.45, 17.05 | |||
| LST (m) | 4 | 3 | 2 | 2 |
| Emissivity | 0.97 | 0.96 | 0.96 | 0.95 |
| EC system (m) | 2.85 | 3.5 | 2 | 2 |
| Method: | HSR-LST | HMOST | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| H (m) | N: | a | b | R2 | RMSE | E (%) | a | b | R2 | RMSE | E (%) |
| Amdo | 177 | ||||||||||
| 1.95 | 0.78 | −3 | 0.58 | 8 | 63 | 1.08 | −3 | 0.53 | 11 | 81 | |
| 6 | 0.76 | −2 | 0.53 | 8 | 57 | 1.14 | −1 | 0.55 | 11 | 72 | |
| 14.1 | 0.70 | −1 | 0.53 | 8 | 56 | 1.11 | 1 | 0.53 | 10 | 65 | |
| TY-grass | 4401 | ||||||||||
| 1.76 | 0.49 | −8 | 0.42 | 10 | 61 | 0.60 | −11 | 0.40 | 12 | 70 | |
| 4.36 | 0.46 | −8 | 0.45 | 10 | 58 | 0.64 | −10 | 0.47 | 11 | 60 | |
| 8.36 | 0.46 | −7 | 0.51 | 10 | 58 | 0.68 | −7 | 0.54 | 9 | 50 | |
| 12.86 | 0.41 | −5 | 0.51 | 11 | 62 | 0.63 | −5 | 0.53 | 10 | 47 | |
| 17.46 | 0.40 | −5 | 0.54 | 11 | 63 | 0.62 | −4 | 0.54 | 10 | 48 | |
| TY-crop | 2985 | ||||||||||
| 2.36 | 0.84 | −8 | 0.63 | 11 | 59 | 1.05 | −11 | 0.62 | 16 | 81 | |
| 4.36 | 0.76 | −6 | 0.62 | 9 | 48 | 0.99 | −7 | 0.58 | 13 | 62 | |
| 8.36 | 0.63 | −4 | 0.62 | 9 | 47 | 0.86 | −3 | 0.52 | 11 | 47 | |
| 12.36 | 0.57 | −3 | 0.61 | 10 | 53 | 0.77 | −2 | 0.44 | 13 | 52 | |
| 17.05 | 0.51 | −2 | 0.62 | 12 | 58 | 0.69 | −1 | 0.40 | 10 | 39 | |
| Method: | HSR-LST | HMOST | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| H (m) | N: | a | b | R2 | RMSE | E (%) | a | b | R2 | RMSE | E (%) |
| Amdo | 312 | ||||||||||
| 1.95 | 1.04 | −15 | 0.96 | 23 | 15 | 1.26 | −12 | 0.93 | 53 | 33 | |
| 6 | 1.01 | −14 | 0.96 | 25 | 15 | 1.26 | −12 | 0.93 | 53 | 33 | |
| 14.1 | 0.97 | −11 | 0.95 | 28 | 17 | 1.25 | −10 | 0.93 | 51 | 32 | |
| TY-grass | 2744 | ||||||||||
| 1.76 | 0.93 | −2 | 0.83 | 23 | 38 | 1.18 | 3 | 0.85 | 31 | 50 | |
| 4.36 | 0.89 | 0 | 0.86 | 20 | 34 | 1.15 | 4 | 0.87 | 27 | 46 | |
| 8.36 | 0.88 | 0 | 0.87 | 20 | 34 | 1.15 | 3 | 0.88 | 26 | 44 | |
| 12.86 | 0.86 | 1 | 0.87 | 19 | 33 | 1.14 | 4 | 0.88 | 25 | 44 | |
| 17.46 | 0.85 | 1 | 0.87 | 20 | 34 | 1.13 | 3 | 0.88 | 24 | 42 | |
| TY-crop | 2386 | ||||||||||
| 2.36 | 1.27 | −13 | 0.89 | 33 | 40 | 1.51 | −10 | 0.87 | 56 | 68 | |
| 4.36 | 1.24 | −12 | 0.89 | 31 | 38 | 1.47 | −9 | 0.88 | 52 | 64 | |
| 8.36 | 1.20 | −7 | 0.88 | 30 | 37 | 1.44 | −5 | 0.88 | 52 | 64 | |
| 12.36 | 1.17 | −8 | 0.89 | 27 | 33 | 1.42 | −7 | 0.88 | 48 | 60 | |
| 17.05 | 1.12 | −6 | 0.89 | 25 | 32 | 1.38 | −5 | 0.89 | 45 | 58 | |
| Wadi M. | 1782 | ||||||||||
| 2 | 1.10 | −9 | 0.78 | 51 | 39 | 1.25 | −5 | 0.76 | 69 | 56 | |
| Morning | 470 | 1.04 | −10 | 0.66 | 50 | 44 | 1.21 | −8 | 0.63 | 69 | 64 |
| Noon | 768 | 1.17 | −19 | 0.70 | 64 | 34 | 1.26 | 26 | 0.45 | 133 | 70 |
| Afternoon | 464 | 1.11 | 1 | 0.89 | 33 | 40 | 1.37 | 6 | 0.86 | 62 | 78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castellví, F.; Agam, N. A New Approach to Estimating the Sensible Heat Flux in Bare Soils. Atmosphere 2025, 16, 458. https://doi.org/10.3390/atmos16040458
Castellví F, Agam N. A New Approach to Estimating the Sensible Heat Flux in Bare Soils. Atmosphere. 2025; 16(4):458. https://doi.org/10.3390/atmos16040458
Chicago/Turabian StyleCastellví, Francesc, and Nurit Agam. 2025. "A New Approach to Estimating the Sensible Heat Flux in Bare Soils" Atmosphere 16, no. 4: 458. https://doi.org/10.3390/atmos16040458
APA StyleCastellví, F., & Agam, N. (2025). A New Approach to Estimating the Sensible Heat Flux in Bare Soils. Atmosphere, 16(4), 458. https://doi.org/10.3390/atmos16040458







