Next Article in Journal
Optimization of Nitrogen Removal in Solid Carbon Source SND for Treatment of Low-Carbon Municipal Wastewater with RSM Method
Next Article in Special Issue
Spatial Variations in the Abundance and Chemical Speciation of Phosphorus across the River–Sea Interface in the Northern Beibu Gulf
Previous Article in Journal
Surface Water Dynamics in the North America Arctic Based on 2000–2016 Landsat Data
Previous Article in Special Issue
Phosphorus Fluxes from Three Coastal Watersheds under Varied Agriculture Intensities to the Northern Gulf of Mexico
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 10
Issue 7
10.3390/w10070826
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Influences of a Clay Lens on the Hyporheic Exchange in a Sand Dune

by
Chengpeng Lu
1,*,
Congcong Yao
1,
Xiaoru Su
1,
Yong Jiang
2,
Feifei Yuan
1 and
Maomei Wang
3
1
State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Hohai University, Nanjing 210098, Jiangsu, China
2
Water Resources Service Center of Jiangsu Province, Nanjing 210029, Jiangsu, China
3
Hydraulic Research Institute of Jiangsu Province, Nanjing 210017, Jiangsu, China
*
Author to whom correspondence should be addressed.
Water 2018, 10(7), 826; https://doi.org/10.3390/w10070826
Submission received: 4 April 2018 / Revised: 19 June 2018 / Accepted: 20 June 2018 / Published: 22 June 2018
(This article belongs to the Special Issue Recent Progress in River Biogeochemistry Research)
Browse Figures
Versions Notes

Abstract

:
A laboratory flume simulating a riverbed sand dune containing a low-permeability clay lens was constructed to investigate its influence on the quality and quantity of hyporheic exchange. By varying the depths and spatial locations of the clay lens, 24 scenarios and one blank control experiment were created. Dye tracers were applied to visualize patterns of hyporheic exchange and the extent of the hyporheic zone, while NaCl tracers were used to calculate hyporheic fluxes. The results revealed that the clay lens reduces hyporheic exchange and that the reduction depends on its spatial location. In general, the effect was stronger when the lens was in the center of the sand dune. The effect weakened when the lens was moved near the boundary of the sand dune. A change in horizontal location had a stronger influence on the extent of the hyporheic zone compared with a change in depth. The size of the hyporheic zone changed with the depth and position of the clay lens. There was a maximum of hyporheic extent with the lens at a depth of 0.1 m caused by changes of water flow paths.

1. Introduction

Hyporheic exchange is the exchange of water and matter in river sediments, including organic matter, oxygen, and anthropogenic contaminants [1,2]. Hyporheic flows are commonly distinguished from surface water and groundwater flows by their bidirectional nature [3]. They are driven by head variations, which induce the movement of pore water and lead to an exchange between the stream and the saturated streambed. The mixing area of stream and groundwater (i.e., the hyporheic zone) is regarded as a transient storage zone where mass can be temporarily stored and then released back into the stream [4]. The hyporheic zone is present at a wide range of spatial scales from bedform (dunes, steps, riffle) to catchment [5], providing a natural habitat for a large number of organisms, which has a significant effect on the nutrient cycle and contaminant transport in river systems [6,7,8]. Hence, the hyporheic zone is of immense importance for the river aquifer, and is referred to as the “liver” of the river [9]. Hyporheic exchange plays an important role in many environmental and biogeochemical issues, such as water quality [10,11,12] and the functioning of riverine ecosystems [7,13,14,15,16].
In this paper, we focus on the sand dune, which is a typical topography feature that drives hyporheic exchange. As the one of hydrodynamic forces, sand dunes influence hyporheic flow at a fine scale in stream sediment. Surface water enters the bed in the high pressure zone on the upstream and then reemerges in the low pressure zone on the downstream [3,17]. Elliott and Brooks [18] performed laboratory experiments and confirmed that pumping exchange was dominant in hyporheic exchange when sand dunes were constant or moved slowly, and when sand dunes moved rapidly, the turnover exchange became the major form. This work primarily explains the characteristics of hyporheic flow induced by sand dunes, and similar studies have been conducted to develop the flow mechanism [19,20,21]. Compared with other hydrostatic forces, the influence scale of sand dunes is smaller, usually ranging from several centimeters to tens of centimeters.
Heterogeneity is one of the main factors that strongly influences the interaction of local hyporheic exchange with larger-scale surface–groundwater interactions [10,22]. The flux of a heterogeneous streambed was found to be one order of magnitude higher than that of a homogeneous streambed [23]. Several studies have been conducted to examine the effect of heterogeneity on hyporheic exchange [5,24,25,26,27,28]. The spatial pattern of streambed permeability was well representative of heterogeneity. Salehin [2] constructed a two-dimensional heterogeneous streambed structure and found that water preferred to pass through the region with higher permeability. Meanwhile, the anisotropy of sediment restrained the vertical water flow to some extent. In the real world, fine particles are carried with water flow before being deposited, which changes the structure of the sediment. A clay lens is a low permeability medium that looks like a spindle and exists extensively in the streambed [8,29]. Due to the clay lens, the sediment hydraulic conductivity of the local area decreases sharply, which has an impact on water flow and hyporheic exchange [30,31,32]. Fox et al. [33] studied the hyporheic exchange flux and solute residence time under different hydraulic conditions. A two-dimensional (2-D) heterogeneous structure was generated using a Gaussian random field generator. The sediment was formed by several layers of different particle-size media (consisting mainly of three classes of hydraulic conductivity). They concluded that hyporheic exchange flux and solute residence time declined considerably when either losing or gaining fluxes.
However, there are few studies on the specific shape of clay lenses. An important objective for researching hyporheic exchange is identifying how a clay lens affects the process. Prior research was conducted by using a numerical model to simulate the flow field in a sand dune with a clay lens [34]. Thus, in order to quantity the influence of a low-permeability lens on the hyporheic exchange, especially the extent of the hyporheic zone, we constructed a two-dimensional sand channel model to perform laboratory physical experiments under a gaining condition. Twenty-five experimental schemes were designed by changing the spatial locations of the lens to investigate the hyporheic exchange flux, the depth of the hyporheic zone, and the area of hyporheic zone by injecting a tracer. We chose salt (NaCl) as the tracer to calculate the hyporheic exchange flux through the observed concentration attenuation. Moreover, we used a dye to visualize the hyporheic zone.

2. Materials and Methods

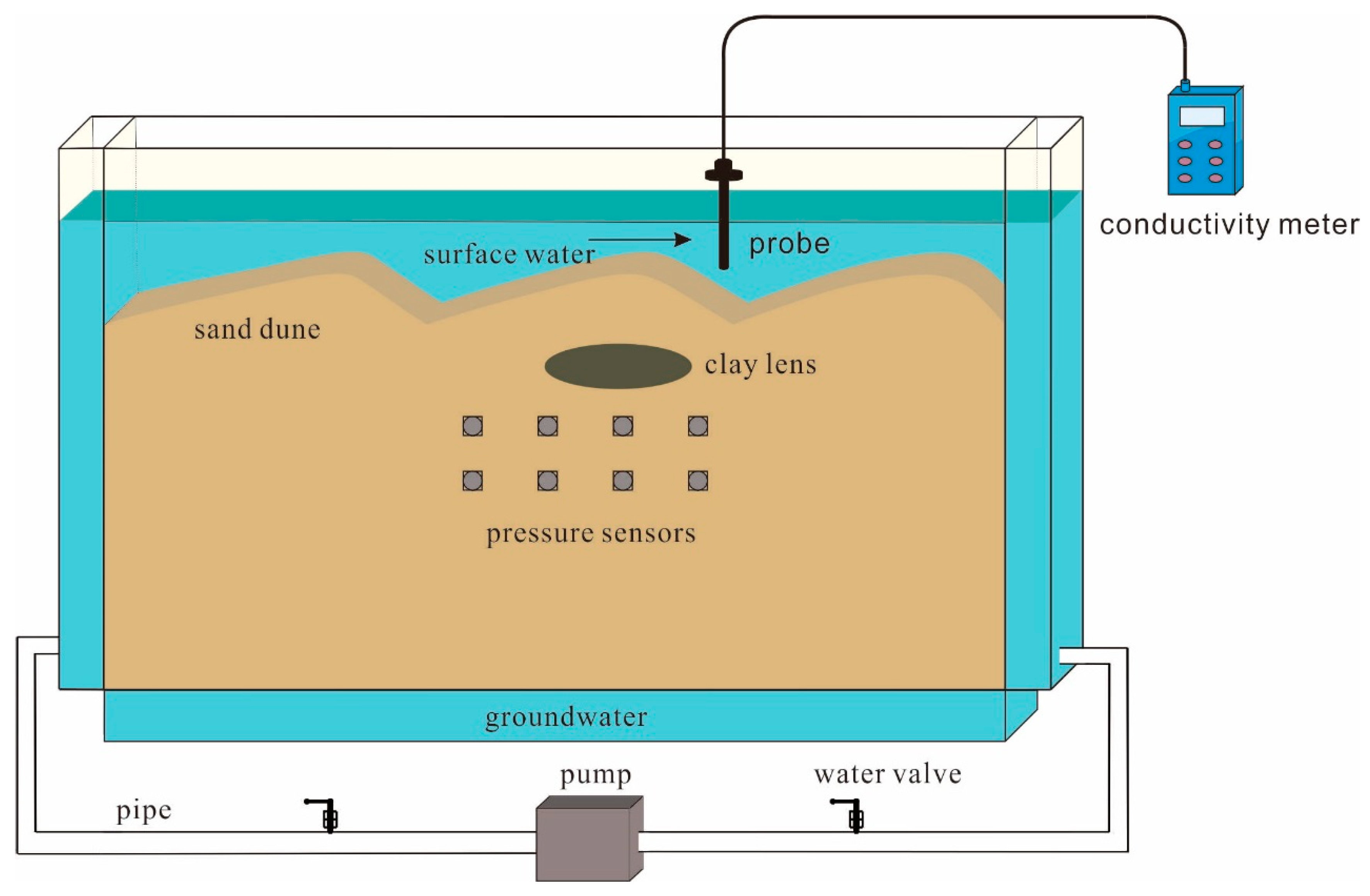
2.1. Experimental Setup

We constructed a similar sand channel model to the flume in Fox’s paper and conducted physical simulations (Figure 1) based on the experiments by Fox et al. [19,33], which used a laboratory flume system to simulate the change of the hyporheic zone under losing and gaining conditions. The model size was 2 m in length, 0.1 m in width, and 2 m in height, and this model consisted of a flume, a constant head device, a pump, and pipes. The flume was made of one main sand channel and three water tanks. The main channel filled with sand was the simulated streambed sediment. The depth of the streambed was 1.2 m. A triangular dune was pressed by a custom-made sand dune. Details about the size of the dune are described in Section 3.1. All components of the model flume were connected with pipes and a pump. A three-phase joint was set up at the upstream water tank for water supply and circulation. Similarly, another three-phase joint was set up at the downstream water tank for drainage and circulation. A groundwater tank was installed below the flume (Figure 1). The existence of the water tank influenced the water flow in the model to a certain degree and caused an upwelling flow. The head of the groundwater was equal to the upstream head so that the upwelling groundwater mixed with stream water in the hyporheic zone. In the preparing phase, valves were turned on so that the flume was connected with the water supply system in order to fill the whole flume with water. When the water level reached the specified height, the valves were turned off to cut off the connection before the experiments began. The bedform was pressed by a custom-made sand dune mold. We chose natural silica sand as the filling material of the sand channel and its mean grain size was 4 × 10−4 m. The porosity of the sand, measured by the water evaporation method, was 0.33, and the hydraulic conductivity of the sand was 0.12 m/s, as measured by the constant-head test [35,36]. The streambed was made of the same material, therefore the heterogeneity of the sediment and the anisotropy of hydraulic conductivity were not considered in this study. The priority was the change of the streambed’s inner characteristics that were influenced by the clay lens.

2.2. Clay Lens

Natural clay was used to manufacture the lens. The natural clay had good stability and was difficult to deform under the scoured condition. It could ensure that the conditions would not be changed and that the test would be carried out successfully and effectively. The lens was set up in the physical test using a random field generator, meaning that the lens was layered and had no obvious rule shape [2,33]. This experiment used a mold to make the specific size of the lens. The lens used in the test was an elliptic cylinder with same height, which was 0.1 m.

3. Methods of Test and Calculation

3.1. Scenario Design

We chose an industrial pigment as a tracer and injected it directly into the sediment bed to visualize the water flow. Traditional tracer tests in laboratory experiments often inject the dye into the surface water in order to observe the movement to determine water flow and the shape of the hyporheic zone [37]. However, this method is time-consuming in a small-scale laboratory physical test. Further, it can be difficult to see the specific flow patterns from the movement of the entire interface of the dyeing belt. Therefore, in our test, the tracer was injected on the inner surface of wall so that we could directly observe the variation of the dye. Before the test, we marked the positions of the injection points and the profile of the sand dune. The positions of the injection points had equal intervals. The injector was a special dropper, which was long enough to insert into the dune.
Besides the dye, we chose salt as a conservative tracer in this test to calculate the hyporheic flux. The solution, which was mixed with 30 g NaCl, was prepared and then added into the upstream water tank before testing. Packman [30] pointed out that the type of salt concentrations used here only produces negligible density gradients and thus will not induce buoyancy-driven flows. The process is regarded as an instantaneous point source delivery. The solute concentration was obtained based on the linear relationship between the salt concentration and electrical conductivity (EC). A conductivity meter (AZ8303, SENLOD) was used to monitor the EC values of the surface water flowing through the sand dune upstream slope. Eight pressure sensors (MEACON, MIK-P300) were installed on the back of the sand tank to measure the head in order to calculate the gaining flux (qG).
The lens was a symmetric figure, and we placed it horizontally to attach the two sides of the cylinder to the flume wall. Therefore, the height of the cylinder was equal to the width of the flume, which was 0.1 m. The bottom of the cylinder was regulated by changing the semimajor axis a and the semiminor axis b. The locations of the tracer and the clay lens were marked on the outer wall of the flume. The clay lens had different depths d and horizontal positions l at the different points. The interval between each two adjacent points was 0.025 m. The horizontal positions l were positive or negative depending on whether the lens was on the right or left of the sand dune top, respectively. The geometric center of the lens was regarded as the control center when changing the location of the lens. The geometry of the sand dune is shown in Figure 2.
Considering the scale of the lens and sand dune, we designed 24 scenarios based on different locations and one scenario as the reference, in which we did not put the lens in the sand dune. The experiment for each scenario was performed three times to prevent any discrepancies. Specific parameters are shown in Table 1.

3.2. Determining the Extent of the Hyporheic Zone

The basic principle for determining the extent of the hyporheic zone is that the water flow in the hyporheic zone is bidirectional, so that the water flows from the overlying water to the sand bed and returns back to the overlying water after a certain period of time [18]. Elliott and Brooks proposed an advective pumping model (AMP) based on the Darcy groundwater flow model, which has been validated experimentally to obtain an analytical description of the flow field [18,38]. This was seminal to many studies on the hyporheic zone performed using tracer experiments [2,39,40]. Based on the definition of the hyporheic flow, we found the points on the surface of the sand dune in terms of water inflow, water outflow, and the deepest streamline. Cardenas [1] pointed out that this streamline separated all of the streamtubes originating from and returning to the interface, from the deeper part of the porous media that is dominated by the mean flow from groundwater to surface water (i.e., upwelling flow). The area circled with the deepest streamline and the surface of the sand dune is the hyporheic zone.
Figure 3 shows the flow field diagram. The tracer test mentioned in Section 3.1 was modified in order to observe the water flow direction more clearly. Streamlines were determined by observing the movement of the tracer at each point.

3.3. Hyporheic Flux Calculation

The mass balance equations for a nonreactive tracer was adopted for hyporheic flux calculation [19,41]. Considering the interaction between surface water and groundwater, the equations are as follows when a net loss of water occurs:
W d C d t = A [ q H ( C S − C ) − q L C ]
W S d C d t = A [ − q H ( C S − C ) − q L C S + q L C ]
The equations for gaining flow conditions are similar to those for the losing conditions, which become:
W d C d t = A [ q H ( C S − C ) + q G C S − q G C ]
W S d C d t = A [ − q H ( C S − C ) − q G C S ]
where t is the time after the test starts, W is the total volume of the surface water (including water tanks, pump, and pipes), WS is the pore water volume, C(t) and CS(t) are the average tracer concentrations in the surface water and pore water, respectively, A is the streambed area, qH is the hyporheic flux, and qL and qG are the imposed losing and gaining flux per unit bed area, respectively. Because of the location of the circulatory system, the water in the tank beneath the flume flew vertically into the surface water so that gaining flow conditions were enforced in the sand bed (i.e., qL = 0). The mass balance equations then become:
{ W d C d t = A [ q H ( C S − C ) + q G C S − q G C ] C | t = 0 = C 0 C S | t = 0 = 0
The equation is simply given by dividing W on both sides of the equation:
d C d t = − ( q H + q G ) C D
where D = W/A represents the equivalent depth of the surface water. This equation is a first-order homogeneous linear differential equation and the solution is:
C = C 0 e − q H + q G D t
The qG is calculated by Darcy’s law:
q G = K i = K Δ h Δ L
where K is the hydraulic conductivity of sand in this test, i is the vertical hydraulic gradient, Δh is the head difference of two points in the vertical direction, and ΔL is the distance between these points.
According to the changes of measured concentrations over time, we fitted data based on the principle of least squares to calculate the characteristic parameter so that the hyporheic flux could be obtained.

4. Results and Discussion

4.1. Hyporheic Flux

Figure 4 shows the observed concentrations from nine scenarios. Concentrations at different times were calculated according to the relation between the concentration and EC, as well as the drawn time-concentration curves. Five scenarios (N1, N4, N9, N17, N23) that had the same x-location (l = 0 m) and five scenarios (N7, N8, N9, N10, N11) that had the same depth of clay lens (d = 0.1 m) were chosen as representatives. Among them, N9 was a duplication, i.e., the nine scenarios formed a vertical line (d = 0.1 m) and a horizontal line (l = 0 m) in the cross-section of the sand dune, and N9 was the intersection.
It was found that the concentrations basically followed an exponential type of decreasing trend. The measured points in the nine scenarios matched well with the fitting curve, and all of the coefficients of association were more than 0.99 except for the N4 scenario. It was also seen that the initial points fluctuated slightly. Variations between parallel tests, i.e., the length of the error bar in N1 and N4 were about 0.15 g/L, and the concentration in the whole test were more than 1.50 g/L. These two characteristics were slightly different than the other scenarios. Because of the clay lens, the flow field displayed apparent changes. This indicated that the flow field was sensitive when the lens was located in these zones. On the other hand, when the clay lens was far away from center of the sand dune, the flow field was smooth and the deviation from repeated measured data was relatively small. The “edge effect” (the mixing of solutions and surface water for several minutes) would affect the concentrations in the initial ~5 min. Hence, the initial concentrations were not used to fit the attenuation curves.
We performed several tests under different conditions, i.e., we changed the positions of the lens, and found that the deviation value of qG was negligible. The parameters of the fitting curves were plugged into Equation (7) to calculate the hyporheic flux when the clay lens was located in different positions. The results are summarized in Table 2 and Figure 5. The unit of exchange flux, including qH and qG, was cm/d, which is consistent with the units in the studies of Fox et al. [19,33].
The average hyporheic flux of the 25 experimental scenarios was 477 cm/d. The maximum hyporheic flux was 1227 cm/d, which appeared at l = 0 m and d = 0.1 m (N9) in the middle of the sand dune. The minimum hyporheic flux was 48 cm/d, which appeared at l = 0.025 m and d = 0.15 m (N24). In addition, flux at l = −0.025 m and d = 0.15 m (N22) and l = −0.05 m and d = 0.075 m (N2) were also very low; 81 cm/d and 99 cm/d, respectively. It was found that most hyporheic fluxes were below the flux of the blank control. Hyporheic flux in the sand dune was mainly influenced by surface water velocity, streambed topography, hydraulic conductivity of sediment, and so on [42]. The buried clay lens changed the spatial distribution of sediment hydraulic conductivity and led to the heterogeneity and anisotropy of local hydraulic parameters, which eventually suppressed hyporheic exchange. Meanwhile, there were still several fluxes (e.g., N6, N13, N16, and N17) close to the flux of the blank control. These results indicated that the suppression effect for hyporheic exchange was not strong compared to the other locations when the clay lens was in the middle or near the upstream surface of the sand dune. Specifically, when the clay lens was located at l = 0 m and d = 0.1 m, the hyporheic flux was even higher than the flux of the blank control. In addition, the hyporheic flux produced an abnormal and abrupt increase when the lens was near the upstream surface of the sand dune. From the above results, we concluded that the clay lens in the sand dune would restrain the hyporheic exchange overall. This effect would be weak or would even transform to enhance the hyporheic exchange in some specific zones (in this test, this was in the middle or near the upstream surface of the sand dune). When the clay lens moved out of this area (e.g., moved deeper or closer to the downstream surface of sand dune), the suppression effect was obviously enhanced. Considering the influence of depth (see three groups’ scenarios of l = −0.025 m, 0 m, and 0.025 m), it was found that the trend of the hyporheic fluxes increased first and then decreased as the depth of the lens increased. While considering horizontal locations (see three groups’ scenarios of d = 0.075 m, 0.1 m, and 0.125 m), the trend was similar to the depth, i.e., hyporheic fluxes increased first and then decreased as the lens moved from upstream to downstream. These trends also confirmed our opinion. Xiaoru Su [34] studied the impact of a low-permeability lens on dune-induced hyporheic exchange by using a VS2DH model and found that the clay lens in a streambed can hinder or enhance hyporheic exchange depending on its relative spatial location to dunes. This conclusion was consistent with our research.
Bardini [43] found that permeability heterogeneity produced more irregular flow cells within shallow sediments, which has a positive role in hyporheic flux. It partly explains why the hyporheic flux in N9 was significantly larger. Based on a laboratory physical model test, Fox et al. [19] found that on the upstream slope of a sand dune, the hyporheic exchange flux was greater and the extent of the hyporheic zone was wider. Because of that, when the clay lens was in the sand dune near the upstream slope, the hyporheic flow had the ability to go around the lens due to the change of the pressure field. However, when the lens was near the downstream slope, the extent of the hyporheic zone was smaller and the influence caused by the lens on the hyporheic exchange was more noticeable. Compared with the conditions in which the lens was near the upstream slope, the water flow could not overcome the obstruction from the lens, which showed a more significant inhibitory effect.

4.2. Change of Hyporheic Zone Flow Field: Three Different Kinds of Water Flow

The tracer experiments were used to determine the range of the hyporheic zone. We intended to show the range of the zone in a more intuitive way and explore the main factors influencing the range. In the dye test, we observed the movement of the tracer with time to draw the direction of the water flow and determine the extent of the hyporheic zone. Through several tests, we found that the hyporheic flow field would be basically stable after 30 min from the beginning of the test and that the EC declined steadily. Thus, each test was conducted by recording the observations during the first 30 min. Figure 6 shows the process of the tracer movement from t = 0 min to t = 30 min in the condition of l = 0 m and d = 0.1 m (N9).
The heterogeneity and anisotropy of streambed media mainly affected the flow path of water in the sand dunes and the residence time. This natural characteristic produced spatially variable interfacial fluxes and complex hyporheic exchange patterns [2]. From Figure 6, we can see that the tracer on different spatial positions mainly had three patterns of motion tendency movement. The first was that water flow moved along the direction perpendicular to the surface of the sand dune and eventually left the sand dune (see the red line in Figure 6). This type of tracer was distributed in the bottom of the upstream and downstream slopes. The second pattern of motion tendency movement was that water flow adhered to the surface of the clay lens from the upstream slope to the downstream slope (see the yellow line in Figure 6). This type was near the clay lens. The third was that the movement was curved irregularly and had horizontal flow trends, and the dying circle was obviously distorted so that a vortex appeared near the clay lens (see the blue line in Figure 6). This type was distributed in a small-scale area that was at the top of the upstream and downstream slopes. The water flow in the hyporheic zone was bidirectional in the flow direction, which was different from one-way recharge and discharge between the surface water and groundwater [44,45]. The vertical water flow was influenced by the pumping exchange. Jin [46] pointed out that shear flow induced by a triangle bed produced pressure change, which led to the movement of pore water and an exchange between the stream and the saturated bed. This exchange was called the pumping exchange. The horizontal water flow from the upstream slope to the downstream slope was mostly influenced by the surface water. The third flow, which did not have a specific flow direction, was influenced by both the pumping exchange and surface water.

4.3. Influence of the Spatial Distribution to the Extent of Hyporheic Zone

Gomez-Velez [47] pointed out that the extent of the hyporheic zone was modulated by the upwelling groundwater and the presence of a low-permeability layer, resulting in stagnation zones above and below the sediments. Our research focused on the clay lens, which was a typical low-permeability layer. The presence of the lenses increased the residence time and accumulation in the higher permeability zone.
We changed the depth d and horizontal location l to determine the spatial distribution of the clay lens. The method delimiting the extent of the hyporheic zone was mentioned above. For the photographs shown in Figure 6, we needed to obtain coordinate definitions in ArcGIS based on the actual size of the sand dune. According to the image resolution and the number of grids in the target area, the area of the hyporheic zone was calculated as the product of the resolution and numbers and compared in different spatial distributions.

4.3.1. Influence of the Depth on the Extent of the Hyporheic Zone

In order to investigate the influence of the depth of the clay lens on the extent of the hyporheic zone, we chose three columns of points (l = −0.025 m, 0 m, and 0.025 m) to test and then compared the data at each point. Figure 7 demonstrates the comparison of the hyporheic zone for which the clay lens was located at points with different depths in three columns. The arrow represents the direction of water flow in different locations, which was determined by the images of the hyporheic flow changing with time (Figure 6). The hyporheic zone was circled by asymptotes in the flow field and the sand dune boundaries. Therefore, asymptotes were the key to delimit the hyporheic zone. In the test, we determined the asymptotes through the hyporheic flow, which was represented by the movement of the tracer in each point. The yellow line in Figure 7 represents the asymptotes and the sand dune boundaries, and the circled area shows the hyporheic zone. It was found that when the clay lens was at different depths, there were obvious differences in the shape of the hyporheic zone. When the lens was in a shallow area (the depth was less than 0.075 m), it tended to insert into the hyporheic zone and cover a part of the hyporheic area. In particular, when d = 0.05 m and l = 0 m (N1), and d = 0.075 m and l = 0 m (N4), the lens was in the hyporheic zone. We could observe that the hyporheic water was hindered and driven to flow along the surface of the lens. With the lens moving to a deeper area, the shape of the hyporheic zone gradually became stable and was largely consistent with the shape found in the blank control. We believe that the influence for flow direction reduced and eventually disappeared as the depth of the lens increased. Comparing different scenarios, obvious changes of water flow appeared around the lens. For the points at the surface of the lens, water flow was attached to the outline of the lens. At the points near the lens, flow paths were distorted so that water flow would deviate from the lens. Wanger [48] pointed out that interstitial water preferentially flows in a complex network of areas of high hydraulic connectivity. It was changed or even cut off by a clay lens because the hydraulic conductivity of the clay lens was much lower than that of the sand dune. The clay lens would produce more resistance to water flow, which made it choose the “easiest” path. This was the reason why it appeared that the streamline was wrapping around the lens. For the points far from the lens, for which the distance between the lens and the hyporheic zone was about 0.025 m (i.e., the distance between two adjacent points), the influence from the clay lens was not obvious.
According to the area of the hyporheic zone, we drew the curves of the area so that they varied with depth and compared them with the hyporheic flux that varied with the depth location of the lens (Figure 8). Figure 8a shows that the area varied with depth. The solid line is the actual hyporheic zone area, and the imaginary line is the area removing the area of the clay lens when the lens was in the hyporheic zone. Figure 8b shows that the hyporheic flux varied with depth.
The largest and smallest areas of the hyporheic zone were 106.62 cm2, when the lens was located at l = −0.025 m and d= 0.075 m, and 40.42 cm2 when the lens was located at l = 0 m and d = 0.075 m, respectively. Significantly, there were two special scenarios (N1 and N4), in which the lens was in the hyporheic zone, which would increase the area greatly. Hester modeled the mixing of surface water and groundwater induced by riverbed dunes and found that introducing heterogeneity increased the mixing primarily by increasing the mixing-zone (i.e., hyporheic-zone) thickness [20]. In our test, each area of the hyporheic zone with the clay lens was higher than the area in the blank control. From Figure 7, it can be seen that the hyporheic exchange appeared near the top of the sand dune because of the upwelling water. Several studies have also claimed that, compared to neutral conditions, the hyporheic zone is restricted by the upwelling water [19,39]. The presence of the clay lens seemed to be a “barrier” that could block the upwelling water and decrease the influence on the hyporheic exchange. Focusing on the tendency of the three conditions (see Figure 8), the area of the hyporheic zone firstly increased and then dropped as the depth increased. This was similar to the change of the hyporheic flux that varied with depth (Figure 8b), which also increased in the beginning and then decreased. Apparently, each curve had a maximum. For the area of the hyporheic zone, the maximum appeared at d = 0.125 m in three horizontal locations. For the hyporheic flux, the situation was slightly different in that the maximum appeared between d = 0.1 m and d = 0.125 m.

4.3.2. Influence of the Horizontal Locations on the Extent of the Hyporheic Zone

Figure 9 shows the comparison of the hyporheic zone when the clay lens was located at different horizontal positions. The study of the influence of the horizontal positions was similar to the abovementioned methods. In this test, we chose d = 0.075 m, 0.1 m, and 0.125 m as three rows of data to compare the influence of the horizontal locations on the extent of the hyporheic zone. The hyporheic zone changed significantly with the lens moving to different horizontal positions. Observing the hyporheic zone, there were two scenarios in which the lens was in the hyporheic zone. This also occurred when the lens was located in the shallow zone (l = −0.05 m and d = 0.075 m, and l = 0 m and d = 0.075 m). The distinction was that the different horizontal positions influenced the lowest position and the depth of the hyporheic zone. Due to the shape of the lens, the lowest position of the hyporheic zone was the same as the lowest position of the lens. The lower boundaries of the zone and the lens overlapped. When the lens was at d = 0.1 m or 0.125 m, the lens was out of the hyporheic zone. In the conditions in which the lens was near the surface of the sand dune, it did not make contact with the hyporheic zone. Thus, the lens had little influence and the water flow was steady, with only some vortexes between the lens and the hyporheic zone. With the lens moving to the middle of the sand dune, the influence became apparent. Firstly, the lowest point of the hyporheic zone gradually approached the lens as if there was an “attraction” effect from the lens to the hyporheic zone. When the lens was near the middle of the sand dune, there was a small area in the hyporheic zone that was covered by the lens as if the lens was embedded into the zone. The overlapped zone was also observed in the results shown in Figure 7. The lens had obvious “transformation” effects on the lower boundary of the hyporheic zone. Compared with the variation of the depth, the x-locations of the lens had more influence on the “barrier effect” than the shape; in particular, the length of the hyporheic zone varied more obviously as the lens moved horizontally.
According to the area of the hyporheic zone, we drew a figure that area varied with the horizontal positions (Figure 10). Figure 10a shows that the area of the hyporheic zone varied with the horizontal positions. The solid lines are the actual area of the hyporheic zone. The imaginary lines are the area of the hyporheic zone, deducting the area of the clay lens when the lens was in the hyporheic zone. Figure 10b shows that the hyporheic flux varied with the horizontal positions.
From the data, the largest area was 106.62 cm2, which was seen when the lens was located at the shallow part of the sand dune (l = 0 m and d = 0.075 m). This is consistent with the depth mentioned above. The smallest area was 40.42 cm2, which was seen when the lens was shallow and near the upstream slope of the sand dune. Further, there were several points (e.g., l = −0.125 m and d = 0.125 m; l = 0.1 m and d = 0.125 m; and l = 0.05 m and d = 0.1 m) for which the area was close to the minima, which were 46.84 cm2, 48.27 cm2, and 47.72 cm2, respectively. Accordingly, the hyporheic fluxes were close to the value of the blank control. We found a similarity in situations in which the lens was in the deep area (bottom of the sand dune) and near the surface of the sand dune. We suspected that the lens in these areas was far from the hyporheic zone in the control. Thus, the areas of the hyporheic zone and the hyporheic flux were close to the corresponding values in the control. Compared with the depth, the variation of the area was more intuitive and fluctuation did not exist. When the clay lens was located at l = 0 m, the area of the hyporheic zone was largest at the current depth, and when the lens moved to both sides of the sand dune, the area of the hyporheic zone began to decrease gradually and linearly.

5. Conclusions

The objective of this paper was to identify the influence of a low-permeability clay lens on the hyporheic exchange and hyporheic zone induced by a sand dune. An indoor sand channel flume and tracer experiments were self-designed and constructed to investigate the influence. How the clay lens influenced the extent of the hyporheic zone and hyporheic flux in different spatial locations and depths were evaluated based on our experiments.
(i)
In the test, under the gaining streamflow condition, there was a ubiquitous inhibitory effect of the clay lens on the hyporheic flux in the sand dune, and this effect was related to the spatial positions of the lens. When the lens was in the middle region of the sand dune, the effect was weakest. It enhanced when the lens moved to the surface of the sand dune. Based on the scale itself, the effect had a range in the sand dune. When the lens was out of the range, the inhibitory effect was significantly reduced or disappeared altogether.
(ii)
Influenced by surface water flow and groundwater flow, there are three different kinds of hyporheic flow in sand dunes. When the surface water dominates, water flows horizontally. When the pumping exchange dominates, water flows perpendicularly to the surface of a sand dune. When the influences are combined, water flows irregularly and variably at any moment.
(iii)
Unlike the hyporheic flux, the area of the hyporheic zone is larger when there is a lens in the sand dune because the lens can reduce the restriction of the upwelling flow on the hyporheic zone. Different spatial positions of the clay lens will affect the extent of the hyporheic zone by changing the direction of the hyporheic flow. In addition, the lens is contained in the hyporheic zone when it is located near the top of the sand dune.
However, there are still some problems and flaws in our work. Due to the size of the sand dune and the clay lens, the data points, especially the depths, are relatively few. The tracer test using dye was good at reflecting the water flow in the sand dune, but the results were subjective. In the future, we will improve the test equipment and observation techniques and pay more attention to the shape and scale of the clay lens, i.e., the thickness, length, and quantity of the lens.

Author Contributions

All authors contributed extensively to the work presented in this paper. C.L. and X.S. conceived and designed the experiments; C.Y. and X.S. performed the experiments; C.Y. analyzed the data with the advice of Y.J., M.W., and F.Y. C.Y. and C.L. wrote the paper with contributions of the other authors. F.Y. polished this paper.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant Number 41572210), Fundamental Research Funds for the Central Universities of China (Grant Number 2018B10814 and 2016B40114), and Water Conservancy Science and Technology Project of Jiangsu (Grant Number 2017009), partially funded by the Jinan Water Conservancy Bureau (JNCZ(LXD)-GK-2017-0004).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Cardenas, M.B.; Wilson, J.L. Dunes, turbulent eddies, and interfacial exchange with permeable sediments. Water Resour. Res. 2007, 43, 199–212. [Google Scholar] [CrossRef]
  2. Salehin, M.; Packman, A.I.; Paradis, M. Hyporheic Exchange with Heterogeneous Streambeds: Laboratory Experiments and Modeling. Water Resour. Res. 2004, 40, 309–316. [Google Scholar] [CrossRef]
  3. Boano, F.; Harvey, J.W.; Marion, A.; Packman, A.I.; Revelli, R.; Ridolfi, L.; Wörman, A. Hyporheic flow and transport processes: Mechanisms, models, and biogeochemical implications. Rev. Geophys. 2015, 52, 603–679. [Google Scholar] [CrossRef]
  4. Bencala, K.E.; Walters, R.A. Simulation of solute transport in a mountain pool-and-riffle stream: A transient storage model. Water Resour. Res. 1983, 19, 718–724. [Google Scholar] [CrossRef]
  5. Tang, Q.; Kurtz, W.; Schilling, O.S.; Brunner, P.; Vereecken, H.; Franssen, H.J.H.; Tang, Q.; Kurtz, W.; Schilling, O.S.; Brunner, P. The influence of riverbed heterogeneity patterns on river-aquifer exchange fluxes under different connection regimes. J. Hydrol. 2017, 554, 383–396. [Google Scholar] [CrossRef]
  6. Boulton, A.J.; Datry, T.; Kasahara, T.; Mutz, M.; Stanford, J.A.; Silver, P.; Steinman, A.D.; Polls, I. Ecology and management of the hyporheic zone: Stream-groundwater interactions of running waters and their floodplains. J. N. Am. Benthol. Soc. 2010, 29, 26–40. [Google Scholar] [CrossRef]
  7. Findlay, S. Importance of surface-subsurface exchange in stream ecosystems: The hyporheic zone. Limnol. Oceanogr. 1995, 40, 159–164. [Google Scholar] [CrossRef] [Green Version]
  8. Huo, S.; Jin, M.; Liang, X. Impacts of low-permeability clay lens in vadose zone onto rainfall infiltration and groundwater recharge using numerical simulation of variably saturated flow. J. Jilin Univ. 2013, 43, 1579–1587. [Google Scholar]
  9. Fischer, H.; Kloep, F.; Wilzcek, S.; Pusch, M.T. A River’s Liver—Microbial Processes within the Hyporheic Zone of a Large Lowland River. Biogeochemistry 2005, 76, 349–371. [Google Scholar] [CrossRef]
  10. Angermann, L.; Krause, S.; Lewandowski, J. Application of heat pulse injections for investigating shallow hyporheic flow in a lowland river. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef] [Green Version]
  11. Fernald, A.G.; Landers, D.H.; Wigington, P.J. Water quality changes in hyporheic flow paths between a large gravel bed river and off-channel alcoves in Oregon, USA. River Res. Appl. 2006, 22, 1111–1124. [Google Scholar] [CrossRef]
  12. Gandy, C.J.; Smith, J.W.; Jarvis, A.P. Attenuation of mining-derived pollutants in the hyporheic zone: A review. Sci. Total Environ. 2007, 373, 435–446. [Google Scholar] [CrossRef] [PubMed]
  13. Baker, M.A.; Valett, H.M.; Dahm, C.N. Organic Carbon Supply and Metabolism in a Shallow Groundwater Ecosystem. Ecology 2000, 81, 3133–3148. [Google Scholar] [CrossRef]
  14. Battin, T.J.; Kaplan, L.A.; Denis, N.J.; Hansen, C.M. Contributions of microbial biofilms to ecosystem processes in stream mesocosms. Nature 2003, 426, 439–442. [Google Scholar] [CrossRef] [PubMed]
  15. Boulton, A.J.; Findlay, S.; Marmonier, P.; Stanley, E.H.; Valett, H.M. The Functional Significance of the Hyporheic Zone in Streams and Rivers. Annu. Rev. Ecol. Syst. 2003, 29, 59–81. [Google Scholar] [CrossRef]
  16. Brunke, M.; Gonser, T. The ecological significance of exchange processes between rivers and groundwater. Freshw. Biol. 1997, 37, 1–33. [Google Scholar] [CrossRef] [Green Version]
  17. Boano, F.; Revelli, R.; Ridolfi, L. Effect of streamflow stochasticity on bedform-driven hyporheic exchange. Adv. Water Resour. 2010, 33, 1367–1374. [Google Scholar] [CrossRef]
  18. Elliott, A.H.; Brooks, N.H. Transfer of nonsorbing solutes to a streambed with bed forms: Laboratory experiments, Allyn and Bacon. Water Resour. Res. 1997, 33, 137–151. [Google Scholar] [CrossRef]
  19. Fox, A.; Boano, F.; Arnon, S. Impact of losing and gaining streamflow conditions on hyporheic exchange fluxes induced by dune-shaped bed forms. Water Resour. Res. 2014, 50, 1895–1907. [Google Scholar] [CrossRef] [Green Version]
  20. Hester, E.T.; Young, K.I.; Widdowson, M.A. Mixing of surface and groundwater induced by riverbed dunes: Implications for hyporheic zone definitions and pollutant reactions. Water Resour. Res. 2013, 49, 5221–5237. [Google Scholar] [CrossRef] [Green Version]
  21. Marzadri, A.; Tonina, D.; Bellin, A.; Valli, A. Mixing interfaces, fluxes, residence times and redox conditions of the hyporheic zones induced by dune-like bedforms and ambient groundwater flow. Adv. Water Resour. 2015, 88, 139–151. [Google Scholar] [CrossRef]
  22. Schornberg, C.; Schmidt, C.; Kalbus, E.; Fleckenstein, J.H. Simulating the effects of geologic heterogeneity and transient boundary conditions on streambed temperatures—Implications for temperature-based water flux calculations. Adv. Water Resour. 2010, 33, 1309–1319. [Google Scholar] [CrossRef]
  23. Zhou, Y.; Ritzi, R.W., Jr.; Soltanian, M.R.; Dominic, D.F. The Influence of Streambed Heterogeneity on Hyporheic Flow in Gravelly Rivers. Ground Water 2014, 52, 206–216. [Google Scholar] [CrossRef] [PubMed]
  24. Ghysels, G.; Benoit, S.; Awol, H.; Jensen, E.P.; Tolche, A.D.; Anibas, C.; Huysmans, M. Characterization of meter-scale spatial variability of riverbed hydraulic conductivity in a lowland river (Aa River, Belgium). J. Hydrol. 2018, 559, 1013–1027. [Google Scholar] [CrossRef]
  25. Irvine, D.J.; Cranswick, R.H.; Simmons, C.T.; Shanafield, M.A.; Lautz, L.K. The effect of streambed heterogeneity on groundwater-surface water exchange fluxes inferred from temperature time series. Water Resour. Res. 2015, 51, 198–212. [Google Scholar] [CrossRef] [Green Version]
  26. Liu, S.; Chui, T. Impacts of Streambed Heterogeneity and Anisotropy on Residence Time of Hyporheic Zone. Ground Water 2018, 56, 425–436. [Google Scholar] [CrossRef] [PubMed]
  27. Sawyer, A.H.; Cardenas, M.B. Hyporheic flow and residence time distributions in heterogeneous cross-bedded sediment. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef] [Green Version]
  28. Tonina, D.; Barros, F.P.J.D.; Marzadri, A.; Bellin, A. Does streambed heterogeneity matter for hyporheic residence time distribution in sand-bedded streams? Adv. Water Resour. 2016, 96, 120–126. [Google Scholar] [CrossRef]
  29. Bosch, D.D.; Truman, C.C.; Davis, F.M. Vadose zone clay lens impacts on groundwater loading rates. In Proceedings of the International Symposium, Preferential Flow: Water Movement and Chemical Transport in the Environment, Honolulu, HI, USA, 3–5 January 2001. [Google Scholar]
  30. Packman, A.I.; Mackay, J.S. Interplay of stream-subsurface exchange, clay particle deposition, and streambed evolution. Water Resour. Res. 2003, 39, 122–137. [Google Scholar] [CrossRef]
  31. Reynolds, D.A.; Kueper, B.H. Multiphase flow and transport in fractured clay/sand sequences. J. Contam. Hydrol. 2001, 51, 41–62. [Google Scholar] [CrossRef]
  32. San, K.W.E.; Rowe, R.K. Effect of sand lenses on groundwater flow and contaminant migration. Int. J. Numer. Anal. Methods Geomech. 2010, 17, 217–241. [Google Scholar] [CrossRef]
  33. Fox, A.; Laube, G.; Schmidt, C.; Fleckenstein, J.H.; Arnon, S. The effect of losing and gaining flow conditions on hyporheic exchange in heterogeneous streambeds. Water Resour. Res. 2016, 52, 7460–7477. [Google Scholar] [CrossRef]
  34. Su, X.; Shu, L.; Lu, C. Impact of a low-permeability lens on dune-induced hyporheic exchange. Hydrol. Sci. J. 2018, 63, 818–835. [Google Scholar] [CrossRef]
  35. Cardenas, M.B.; Zlotnik, V.A. A Simple Constant-Head Injection Test for Streambed Hydraulic Conductivity Estimation. Ground Water 2003, 41, 867–871. [Google Scholar] [CrossRef] [PubMed]
  36. Landon, M.K.; Rus, D.L.; Harvey, F.E. Comparison of instream methods for measuring hydraulic conductivity in sandy streambeds. Ground Water 2001, 39, 870–885. [Google Scholar] [CrossRef] [PubMed]
  37. Ren, J.; Packman, A.I. Coupled stream-subsurface exchange of colloidal hematite and dissolved zinc, copper, and phosphate. Environ. Sci. Technol. 2005, 39, 6387–6394. [Google Scholar] [CrossRef] [PubMed]
  38. Elliott, A.H.; Brooks, N.H. Transfer of nonsorbing solutes to a streambed with bed forms: Theory. Water Resour. Res. 1997, 33, 123–136. [Google Scholar] [CrossRef] [Green Version]
  39. Cardenas, M.B.; Wilson, J.L. Exchange across a sediment–water interface with ambient groundwater discharge. J. Hydrol. 2007, 346, 69–80. [Google Scholar] [CrossRef]
  40. Zaramella, M.; Packman, A.I.; Marion, A. Application of the transient storage model to analyze advective hyporheic exchange with deep and shallow sediment beds. Water Resour. Res. 2003, 39, 3538–3540. [Google Scholar] [CrossRef]
  41. Boano, F.; Revelli, R.; Ridolfi, L.; Krause, S.; Hannah, D.M.; Fleckenstein, J.H. Quantifying the impact of groundwater discharge on the surface-subsurface exchange. Hydrol. Process. 2009, 23, 2108–2116. [Google Scholar] [CrossRef]
  42. Cranswick, R.H.; Cook, P.G.; Lamontagne, S. Hyporheic zone exchange fluxes and residence times inferred from riverbed temperature and radon data. J. Hydrol. 2014, 519, 1870–1881. [Google Scholar] [CrossRef]
  43. Bardini, L.; Boano, F.; Cardenas, M.B.; Sawyer, A.H.; Revelli, R.; Ridolfi, L. Small-scale permeability heterogeneity has negligible effects on nutrient cycling in streambeds. Geophys. Res. Lett. 2013, 40, 1118–1122. [Google Scholar] [CrossRef] [Green Version]
  44. Bhaskar, A.S.; Harvey, J.W.; Henry, E.J. Resolving hyporheic and groundwater components of streambed water flux using heat as a tracer. Water Resour. Res. 2012, 48, 1076. [Google Scholar] [CrossRef]
  45. Cardenas, M.B. Stream-aquifer interactions and hyporheic exchange in gaining and losing sinuous streams. Water Resour. Res. 2009, 45, 267–272. [Google Scholar] [CrossRef]
  46. Jin, G.Q.; Li, L. Advancement in the hyporheic exchange in rivers. Adv. Water Sci. 2008, 19, 285–293. [Google Scholar]
  47. Gomez-Velez, J.D.; Krause, S.; Wilson, J.L. Effect of low-permeability layers on spatial patterns of hyporheic exchange and groundwater upwelling. Water Resour. Res. 2014, 50, 5196–5215. [Google Scholar] [CrossRef] [Green Version]
  48. Wagner, F.H.; Bretschko, G. Interstitial flow through preferential flow paths in the hyporheic zone of the Oberer Seebach, Austria. Aquat. Sci. 2002, 64, 307–316. [Google Scholar] [CrossRef]
Water 10 00826 g001 550
Figure 1. The main view of the experimental setup.
Figure 1. The main view of the experimental setup.
Water 10 00826 g001
Water 10 00826 g002 550
Figure 2. The geometry of the sand dune. Black points and black crosses are the locations of the tracer injections. Black crosses are also the locations of the clay lens in different scenarios.
Figure 2. The geometry of the sand dune. Black points and black crosses are the locations of the tracer injections. Black crosses are also the locations of the clay lens in different scenarios.
Water 10 00826 g002
Water 10 00826 g003 550
Figure 3. Schematic illustration of the flow field diagram of the sand dune. The black arrows represent water flow and the red dashed lines are the margins of the hyporheic zone. The area enclosed by red dashed lines is the hyporheic zone.
Figure 3. Schematic illustration of the flow field diagram of the sand dune. The black arrows represent water flow and the red dashed lines are the margins of the hyporheic zone. The area enclosed by red dashed lines is the hyporheic zone.
Water 10 00826 g003
Water 10 00826 g004 550
Figure 4. The attenuations of concentrations in the surface water in nine scenarios. Black spots represent measured data. Red lines are fitting curves. Black vertical lines are error bars.
Figure 4. The attenuations of concentrations in the surface water in nine scenarios. Black spots represent measured data. Red lines are fitting curves. Black vertical lines are error bars.
Water 10 00826 g004
Water 10 00826 g005 550
Figure 5. Hyporheic flux qH when the clay lens was located in different positions. The dotted line is the qH in the blank control.
Figure 5. Hyporheic flux qH when the clay lens was located in different positions. The dotted line is the qH in the blank control.
Water 10 00826 g005
Water 10 00826 g006 550
Figure 6. Transport of the dye depicts the major flow path in the hyporheic zone. Three different types of water flow are displayed by yellow, blue, and red arrows, respectively. The location of the lens is l = 0 m and d = 0.1 m. The stream flow velocity is 0.12 m/s.
Figure 6. Transport of the dye depicts the major flow path in the hyporheic zone. Three different types of water flow are displayed by yellow, blue, and red arrows, respectively. The location of the lens is l = 0 m and d = 0.1 m. The stream flow velocity is 0.12 m/s.
Water 10 00826 g006
Water 10 00826 g007 550
Figure 7. The extent of the hyporheic zone and flow field in the sand dune under different depth conditions. The three columns indicate that the results were captured from l = −0.025 m, 0 m, and 0.025 m, respectively.
Figure 7. The extent of the hyporheic zone and flow field in the sand dune under different depth conditions. The three columns indicate that the results were captured from l = −0.025 m, 0 m, and 0.025 m, respectively.
Water 10 00826 g007
Water 10 00826 g008 550
Figure 8. The area of the hyporheic zone (a) and the hyporheic flux (b) varied with depth in conditions of l = −0.025 m, 0 m, and 0.025 m. The area and the hyporheic flux in the blank control were 34.62 cm2 and 822 cm/d, respectively.
Figure 8. The area of the hyporheic zone (a) and the hyporheic flux (b) varied with depth in conditions of l = −0.025 m, 0 m, and 0.025 m. The area and the hyporheic flux in the blank control were 34.62 cm2 and 822 cm/d, respectively.
Water 10 00826 g008
Water 10 00826 g009 550
Figure 9. The extent of the hyporheic zone and flow field in the sand dune when the lens was at different horizontal positions. The depth was 0.075 m, 0.1 m, and 0.125 m, respectively.
Figure 9. The extent of the hyporheic zone and flow field in the sand dune when the lens was at different horizontal positions. The depth was 0.075 m, 0.1 m, and 0.125 m, respectively.
Water 10 00826 g009
Water 10 00826 g010 550
Figure 10. The area of the hyporheic zone (a) and hyporheic flux (b) varied with the horizontal positions in conditions of d = 0.075 m, 0.1 m and 0.125 m. The area and the hyporheic flux in the blank control were 34.62 cm2 and 822 cm/d, respectively.
Figure 10. The area of the hyporheic zone (a) and hyporheic flux (b) varied with the horizontal positions in conditions of d = 0.075 m, 0.1 m and 0.125 m. The area and the hyporheic flux in the blank control were 34.62 cm2 and 822 cm/d, respectively.
Water 10 00826 g010
Table
Table 1. Summary of the number of test scenarios, x—location (l) and depth (d) of clay lens. N1–N25 are the test numbers. l = 0, l < 0 and l > 0 indicate the crest, upstream, and downstream of the sand dune, respectively. The velocity of the surface water was 0.12 m/s.
Table 1. Summary of the number of test scenarios, x—location (l) and depth (d) of clay lens. N1–N25 are the test numbers. l = 0, l < 0 and l > 0 indicate the crest, upstream, and downstream of the sand dune, respectively. The velocity of the surface water was 0.12 m/s.
L (m)
−0.125−0.1−0.075−0.05−0.02500.0250.050.0750.1
d (m)0.05 N1
0.075 N2N3N4N5
0.1 N6N7N8N9N10N11
0.125N12N13N14N15N16N17N18N19N20N21
0.15 N22N23N24
Blank Control (no clay lens)N25
Table
Table 2. Hyporheic flux qH (cm/d) according to the location and depth of the clay lens. The dimensions of the clay lens were 0.1 m in length and 0.05 m in height. qG was 450 cm/d.
Table 2. Hyporheic flux qH (cm/d) according to the location and depth of the clay lens. The dimensions of the clay lens were 0.1 m in length and 0.05 m in height. qG was 450 cm/d.
L (m)
−0.125−0.1−0.075−0.05−0.02500.0250.050.0750.01
d (m)0.05 550
0.075 99424477302
0.1 7813165921227470336
0.125625895441359760846302169255542
0.15 8165648
Blank Control (no clay lens)822

Share and Cite

MDPI and ACS Style

Lu, C.; Yao, C.; Su, X.; Jiang, Y.; Yuan, F.; Wang, M. The Influences of a Clay Lens on the Hyporheic Exchange in a Sand Dune. Water 2018, 10, 826. https://doi.org/10.3390/w10070826

AMA Style

Lu C, Yao C, Su X, Jiang Y, Yuan F, Wang M. The Influences of a Clay Lens on the Hyporheic Exchange in a Sand Dune. Water. 2018; 10(7):826. https://doi.org/10.3390/w10070826

Chicago/Turabian Style

Lu, Chengpeng, Congcong Yao, Xiaoru Su, Yong Jiang, Feifei Yuan, and Maomei Wang. 2018. "The Influences of a Clay Lens on the Hyporheic Exchange in a Sand Dune" Water 10, no. 7: 826. https://doi.org/10.3390/w10070826

APA Style

Lu, C., Yao, C., Su, X., Jiang, Y., Yuan, F., & Wang, M. (2018). The Influences of a Clay Lens on the Hyporheic Exchange in a Sand Dune. Water, 10(7), 826. https://doi.org/10.3390/w10070826

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop