Next Article in Journal
Factors That Limit the Adoption of Biofloc Technology in Aquaculture Production in Mexico
Previous Article in Journal
Prediction of Droughts in the Mongolian Plateau Based on the CMIP5 Model
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 12
Issue 10
10.3390/w12102770
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Susceptibility Prediction of Groundwater Hardness Using Ensemble Machine Learning Models

by
Amirhosein Mosavi
1,2,
Farzaneh Sajedi Hosseini
3,
Bahram Choubin
4,
Mahsa Abdolshahnejad
3,
Hamidreza Gharechaee
3,5,
Ahmadreza Lahijanzadeh
6 and
Adrienn A. Dineva
7,*
1
Environmental Quality, Atmospheric Science and Climate Change Research Group, Ton Duc Thang University, Ho Chi Minh City, Vietnam
2
Faculty of Environment and Labour Safety, Ton Duc Thang University, Ho Chi Minh City, Vietnam
3
Reclamation of Arid and Mountainous Regions Department, Faculty of Natural Resources, University of Tehran, Karaj 31585-77871, Iran
4
Soil Conservation and Watershed Management Research Department, West Azarbaijan Agricultural and Natural Resources Research and Education Center, AREEO, Urmia 57169-63963, Iran
5
Technical Expert at UNDP/DOE Conservation of Iranian Wetlands Project, Tehran 14639-14111, Iran
6
Deputy for Marine Environment and Wetlands, Iran Department of Environment, Tehran 73831-4155, Iran
7
Institute of Research and Development, Duy Tan University, Da Nang 550000, Vietnam
*
Author to whom correspondence should be addressed.
Water 2020, 12(10), 2770; https://doi.org/10.3390/w12102770
Submission received: 15 August 2020 / Revised: 27 September 2020 / Accepted: 30 September 2020 / Published: 5 October 2020
(This article belongs to the Section Hydrology)
Browse Figures
Versions Notes

Abstract

:
Groundwater resources, unlike surface water, are more vulnerable to disturbances and contaminations, as they take a very long time and significant cost to recover. So, predictive modeling and prevention strategies can empower policymakers for efficient groundwater governance through informed decisions and recommendations. Due to the importance of groundwater quality modeling, the hardness susceptibility mapping using machine learning (ML) models has not been explored. For the first time, the current research aimed to predict groundwater hardness susceptibility using the ML models. The performance of two ensemble models of boosted regression trees (BRT) and random forest (RF) is investigated through the arrangement of a comparative study with multivariate discriminant analysis (MDA). According to the hardness values in 135 groundwater quality monitoring wells, the hard and soft water are determined; then, 11 predictor variables including distance from the sea (DFS), land use, elevation, distance from the river (DFR), depth to groundwater (DTGW), pH, precipitation (PCP), evaporation (E), groundwater level (GWL), curvature, and lithology are used for predicting the groundwater hardness susceptibility map. Results indicated that the variables of DFR, DTGW, elevation, and DFS had a higher contribution to the modeling process. So, the high harness areas are mostly related to low elevations, low DTGW, and proximity to river and sea, which facilitate the percolation conditions for minerals containing calcium or magnesium into groundwater.

1. Introduction

Groundwater is the fundamental source of drinking water and agriculture irrigation for at least half of the world’s population [1]. From this perspective, the contribution of groundwater for implementing the United Nations’ Sustainable Development Goals (SDGs) is reported to be essential [2,3]. Furthermore, the International Groundwater Resources Assessment Centre (IGRAC) estimates that urbanization of more than 1.5 billion people solely depends on groundwater [1]. Therefore, constant quality assessment of groundwater, as one of the most valuable freshwater recourses, is reported to be of utmost importance for environmental monitoring, public health, and agriculture for sustainable development and circular economy [3]. Furthermore, in the arid and semi-arid areas of the earth, the dependency on the groundwater and its importance is magnified due to its relative stability in terms of quality and quantity [4]. Thus, ensuring the groundwater safety through the advancement of systematic quality control is considered crucial to the health of several ecosystems as well as human development [5]. Unlike surface water resources, groundwater is more vulnerable to disturbances and contaminations, as it takes a very long time and great cost to recover [6,7,8]. Therefore, predictive modeling and prevention strategies have gained popularity to empower policymakers for efficient groundwater governance through informed decisions and recommendations [9,10,11,12].
Among the prediction techniques for groundwater quality modeling, the susceptibility mapping methodologies have been well received within the hydrology research community as well as environmental management and policymakers [13,14,15,16,17,18]. The interactive and graphical nature of susceptibility models is highly efficient in communicating insight into the state of problems (Arabameri et al., 2019). Susceptibility models have recently been dramatically improved in terms of accuracy and performance due to the use of the integrated systems involving recent advancements in data-driven methodologies, remote sensing (RS) [19,20], and geographic information system (GIS) [21,22]. Among the data-driven methods, machine learning has recently shown promising results in the advancement of accurate models. The artificial neural networks (ANN) [23,24,25,26,27,28], support vector machines (SVM) [29,30,31,32], decision trees (DT) [33], adaptive network-based fuzzy inference system (ANFIS) [34,35,36], extreme learning machines (ELM) [37], multilayer perceptron (MLP) [38], K-nearest neighbors (KNN) [39], wavelet neural networks (WNN) [28], and supervised intelligence committee machine (SICK) [40] are among the notable machine learning methods used for advancing susceptibility mapping for groundwater quality.
Although machine learning models for groundwater quality susceptibility had been rapidly evolving at a fast pace, the performance of a wide range of machine learning methods is yet to be explored. Furthermore, various aspects of groundwater quality, e.g., nitrates; heavy metals; hardness; acidity; conductivity; turbidity; minerals; and a wide range of physical, chemical, and biological pollutants, are yet to be modeled using novel machine learning methods. The progress of research in this realm relies on experimenting with new machine learning methods and conducting comparative studies. The research gap in the applicability of ensemble machine learning methods in groundwater quality modeling has also been evident. Although ensemble models in the hydrological modeling often outperform regular machine learning models [41], their performance in groundwater quality modeling has not been explored. Ensemble learning algorithms parallelly employ learning machines to deliver higher performance than could be achieved from a single one [42,43].
Consequently, the contribution of this paper is to explore the performance of two ensemble models of boosted regression trees (BRT) and random forest (RF) for susceptibility mapping of groundwater quality. Through the arrangement of a comparative study with multivariate discriminant analysis (MDA), the performance of ensemble models is investigated. In this study, the groundwater hardness is modeled. The concentrations of calcium and magnesium, which are the two most prevalent divalent metal ions, are responsible for the formation of hard water [44,45,46]. Hardness is considered as one of the essential quality factors of water [47]. Hardness assessment is particularly important to avoid costly blockage and breakdowns in pipelines, channels, water distribution systems, boilers, cooling towers, appliances, and any civil structures that may handle water [48,49]. Despite the importance of hardness susceptibility mapping, there is a research gap in the advancement of novel models [50].
The rest of this paper is organized as follows. In Section 2, materials and methods are described. The results are presented in Section 3. Conclusion remarks are given in Section 4.

2. Materials and Methods

2.1. Study Area

The study area is situated in the east of Mazandaran province, Iran, with an area of about 3297 square kilometers which expands from longitudes 52°36′ to 53°23′ E and latitudes from 35°44′ to 36°46′ N (Figure 1). The Ghaemshahr-Joibar plain is surrounded from the north with the Caspian Sea, from the east with the Siahrood River, from the west with the Thalar River, and from the south with the Alborz mountains. This plain is located in the Talar and Siahrood River Basins which reaches in the north to the Caspian Sea. Because of the Caspian Sea adjacent to this plain, the climate is categorized as Caspian mild with a minimum temperature of 6 °C in winter and the average maximum temperature of 25 °C in summer times [51]. The rainfall is about 700 mm in the southern and 850 mm in the northern part of the plain, in which the wet period of the year occurs in November and December. There are agricultural and cultivation activities in this plain with the predominant cultivation of rice; vegetables, colza, broad bean, and clover are the other crops that are commonly cultivated in winter months of the year [52]. Groundwater is among the main sources of water supply; more than half of drinking water demand is provided by groundwater resources such as springs and wells. The use of groundwater in the agricultural sector is the highest with 87.8%, then it is followed by drinking needs (11.4%), and the lowest percentage is for the industrial sector with 0.9% [53].

2.2. Dataset

Datasets in this study are divided into dependent (output) and independent (inputs) data, respectively, including groundwater hardness values and geo-environmental factors:

2.2.1. Hardness Data

Hardness data from 135 groundwater monitoring wells (Figure 1) are received from the Iranian Water Resources Management Company (IWRMC) from 2001 to 2016. The average value of hardness data was calculated for each well, and the hard/soft water was determined using the World Health Organization (WHO) guideline considering a threshold equal to 500 mg/L [54].

2.2.2. Environmental Factors

There are some conditions and factors, especially environmental factors, which affect groundwater resources, and these factors have an essential role in sustainable groundwater management. Table 1 indicates the list of the considered factors in this study, in which each factor is described as follows:
Elevation: Elevation is a key environmental factor that influences the water surface and the groundwater flows [55]. In other words, there is an inverse relation between elevation and infiltration and recharge, so that the values of both of them will be lower at the higher altitudes [56]. Moreover, elevation changes with different climatic features will also affect soil and cover plant conditions [57,58]. The 30 × 30 m ASTER digital elevation model (DEM) was used as an elevation map. The highest and lowest values of this factor were, respectively, about 3877 and −61 m a.s.l. in the study area (Figure 2a).
Curvature: Curvature as one of the morphometric characteristics has a considerable effect on the divergence and convergence flowing pattern; so, what is remarkable in its role on the recharge potential of groundwater [59,60]? The DEM was used to derive the curvature map in ArcGIS software. The range of curvature in the study area was between −18 and 25.74 (Figure 2b).
Distance from sea (DFS): The Ghaemshahr-Joibar plain is near to the Caspian Sea; therefore, calculating DFS is an important parameter to detect the quality and hardness of groundwater. The DFS affects the hydraulic status among seawater and aquifer as well as makes changes in different elements of water balance. The map of the DFS was prepared by Euclidean Distance in ArcGIS (Figure 2c).
Distance from river (DFR): Siyahrood and Talar are the major rivers in the study area; hence, infiltration and charge from them are important. The map of DFR was calculated by the Euclidean Distance function in ArcGIS (Figure 2d).
Precipitation (PCP): By the infiltration of rain into the groundwater, the pressure of carbon dioxide due to oxidation of volatile organic matter was increased [61]. Besides increasing the pressure of CO2, the pressure of carbonic acid (HCO3−) and dissolution of the carbonate minerals were raised. Thus, the result of this process increased the Groundwater Hardness. Annual precipitation data of meteorological stations from 2001 to 2016 are obtained from the Iranian Meteorological Organization (IRIMO, http://www.irimo.ir/). The range of long-term mean precipitation value in the study area was recorded from 770 to 824 mm (Figure 2e).
Evaporation (E): Evaporation is a key reason for the discharge of groundwater in the arid region with low elevation and shallow depth of groundwater [62]. So, the evaporation process by influencing the groundwater level causes the initial quality water to change. The data of yearly evaporation (from 2001 to 2016) were obtained from the IRIMO. The range of long-term mean evaporation was from 360 mm to 1139 mm (Figure 2j).
Depth to groundwater (DTGW): DTQW (or unsaturated soil zone) has a significant effect on the hydrological process as infiltration capacity and runoff [63]. The DTGW data were collected from monitoring wells in the study area which were obtained from the Iranian Water Resource Management Company (IWRMC). In this study, the DTGW map was produced in ArcGIS, and according to Figure 2g, the highest value of that was 34.5m.
Groundwater level (GWL): GWL affects the quality of water, and by decreasing it, the quality also will be reduced [64]. Changes in GWL are directly affected by human activities and climate factors such as evaporation and precipitation. GWL data were obtained from all of the wells observed by the IWRMC. The range of this map was from −44.2 to 63.2 m (Figure 2h).
pH: Due to the influence of lithological and distance from sea parameters, pH causes a change in the quality and hardness of groundwater.
Landuse: Landuse is among the factors that have an impact on the surface, subsurface and groundwater flow, and evapotranspiration [65,66,67]. Overuse of land due to the increasing agricultural and urban land use with population growth will cause changes in groundwater quality and hardness. The land use map of the Ghaemshahr-Joibar plain includes six classes of agriculture, dry farming, forest, orchard, rangeland, and urban (Figure 2f).
Lithology: Due to different potential of permeability and stability of rocks and soil, hydrological parameters are influenced by lithological and geomorphological structures [42,68]. Moreover, the morphology of lithological composition and the dissolution of their minerals play an important role in increasing groundwater elements [69]. The weathering process of sedimentary rocks and clay minerals is an effective factor in groundwater quality and hardness. A 1:100,000-scale geological map was used to prepare the lithology map (Figure 2k).

2.3. Groundwater Hardness Susceptibility Modeling

2.3.1. Modeling Procedure

After preparing the input data, the multicollinearity analysis was performed to remove probably collinear variables from the modeling process. The Variance Inflation Factor (VIF) was used to investigate the rate of multicollinearity between ith independent variables and other independent variables. When the VIF is greater than 10, try to remove one or two factors often or combine some independent factors [70,71]. After ensuring the lack of multicollinearity between variables (see the results in Table 2), the k-fold cross-validation method was used to calibrate the models. In this method, basic data samples were divided into K same mutual subsets based on hierarchical sampling. K-1 subsamples were applied as training the model, and the remaining subsample was used for evaluation of the results [72]. Then, the validation process was repeated K times (equal to the number of subsets). Despite any intense rule for the value of K in this method, it is often reported as 10 [73].

2.3.2. Model Description

Machine learning models were applied to model hardness susceptibility of groundwater, which are described as follows:
Boosted Regression Trees (BRT): The BRT model was firstly introduced by Freund and Schapire [74] as a powerful algorithm for continuous and categorical variables. It is an ensemble technique that works based on both strengths of regression trees (models which use the recessive binary splits to answer their predictors) and boosting algorithms (a combination of different models to modify the forecast of performance). Some parameters which have the main roles on the BRT fitting include the rate of learning, rate of bagging, complexity of tree, minimum number of observations at the end nodes, and number of trees. In comparison to other predictive methods the BRT has some advantages such as (i) managing various kinds of predictor variables, (ii) improving the missing or lost data, (iii) no need to convert or delete outlier data, and (iv) fitting and controlling the complex nonlinear interaction between variables [75]. See Freund and Schapire [74], Schapire [76], and Elith et al. [75] for more details of the BRT model.
Random Forest (RF): Breiman [77] presented a developing method of new decision trees which combined several signal algorithms using the rules. RF as a non-parametric method consists of clusters of classification and regression trees. The description of the RF is based on a set of tree-structured classifiers is given as:
{ h ( X , Θ k ) , k = 1 , … }
where Θ k are independent identically distributed random vectors, and each tree casts a unit vote for the most popular class at input x. The number of trees and the number of predictor variables are the main parameters in the RF according to which the decision tree grows to the largest possible size without being pruned [78]. It should be noted that the general principles of group training are based on the assumption that the accuracy of them is higher than other training algorithms. To make a growth tree, the RF applies the best variables or dividing points in the variable subsets which are randomly selected, so it reduces the overall error of the model [77]. More details of the RF model are described in Breiman [77].
Multivariate discriminant analysis (MDA): The MDA is introduced by Hair et al. [79]. One of the purposes of MDA is related to forecasting the group membership based on the relation of a dependent variable and its observed features of predictor collection [80,81]. The main base of the MDA is a discriminant function that makes a linear compound for independent variables. It is necessary to note that the important assumptions of the MDA are: (i) the independent parameters are in careful multivariate normal distribution; (ii) the predictors should not be strongly correlated, and their average and variance have not been accounted for; also, (iii) two predictors should have a stable correlation between groups [81]. The equation of linear discriminant is presented as follows [70]:
Y = W1X1 + W2X2 + WnXn
in which Y is a discriminant score, Wi (i = 1,2,3,…,n) are discriminant weights, and Xi (i = 1,2,3,…,n) are independent variables.
More details of the MDA model are presented in Hair et al. [79].

2.3.3. Performance Evaluation

To evaluate the performance of predictive models, some metrics such as the area under curve (AUC) of the receiver operating characteristics (ROC), Accuracy, and True Skill Statistic (TSS) were used. The receiver operating characteristic was used to detect the quality rate of a produced map in addition to the quality value of the forecasting model [60,67]. According to Negnevitsky [82], this metric is defined as the potential of a predictive system to accurately forecast whether a specific event had happened. Basic components of the ROC curve were used to plot the test values as false positive rate (FPR) against the training values as true positive rate (TPR). The range of AUC changed from 0 to 1, and values more than 0.8 indicate very good performance. The Accuracy shows what fraction of the predicted data is correct, and it varies between 0 and 1 [83]. The TSS was calculated from the difference between the TPR and FPR values. The value of TSS varied between 1 and −1; + 1 shows the perfect agreement, and zero and smaller amounts reveal that the performance is not normal [84]. The AUC, Accuracy, and TSS can be achieved as follows [84,85,86]:
AUC = Σ TP + Σ TN/P + N
T P R = T P T P + F N × N
F P R = F P F P + T N × N
A c c u r a c y = T P + T N T P + T N + F P + F N
TSS = TPR − FPR
In which TP (true positive) and TN (true negative) are defined as the number of occurrences and non-occurrences, respectively, that are acceptably classified, while FP (false positive) and FN (false negative) are described as the amount of data which are incorrectly classified.

3. Results

3.1. Modeling Results

After ensuring the lack of the multicollinearity problems (Table 2) among the variables, the modeling process was conducted using the k-fold cross-validation methodology. The performance of the predictive models is presented in Table 3. As can be seen, the area under curve (AUC) values for all the models was more than 80% (Table 3, Figure 3). Accuracy values for the MDA and RF models were about 83% and were higher than the BRT model (Accuracy = 78%). Additionally, True Skill Statistic (TSS) values were equal to 0.73, 0.71, and 0.59, respectively, for RF, BRT, and MDA models (Table 3).

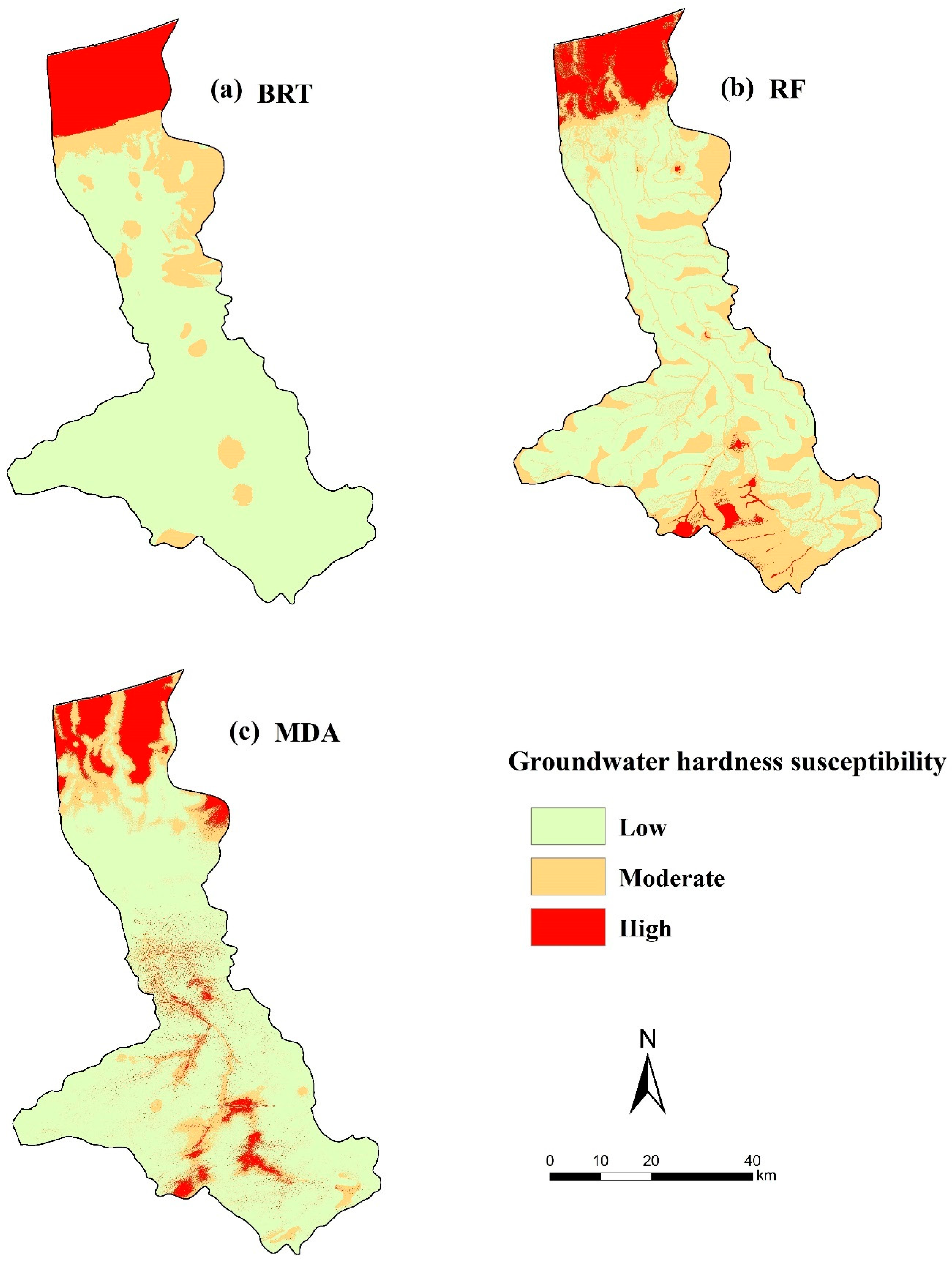
3.2. Spatial Prediction of Groundwater Hardness Susceptibility

Using all the pixel values for the whole region, the groundwater hardness susceptibility maps were predicted and classified into three classes of low, moderate, and high based on the natural breaks’ classification methodology. Figure 4 indicates the predicted maps in which low classes had a higher area, respectively—2474.14, 1924.30, and 2403.51 km2 for BRT, RF, and MDA models. Additionally, moderate class locations were covered by about 443.34, 1022.22, and 518.07 km2 for the BRT, RF, and MDA models, respectively. The high hardness susceptibility class was equal to 379.21, 350.17, and 375.11 km2, respectively, for BRT, RF, and MDA models, which are mostly located in the south of the Ghaemshahr-Joibar plain (Figure 4, Table 4).

3.3. Variable Importance Analysis

The importance of the variables was calculated using the decrease in AUC (DAUC) after removing each variable from the modeling process (Figure 5). Higher DAUC for a variable indicates the higher importance of that variable. As can be seen, variables of DFR, elevation, DTGW, and land use were identified as the most important inputs by the BRT model (respectively, with DAUC about 36%, 10%, 5%, and 4 %). Given the RF model, the variables of DFR, DTGW, elevation, and DFS (with the DAUC values of 62%, 34%, 12%, and 8%) had a higher contribution in the modeling process. Additionally, like the RF model, results of the MDA model demonstrated that the variables of DFR, DTGW, elevation, and DFS were the most important variables which had the DAUC values of 71%, 38%, 14%, and 9% (Figure 5).

4. Discussion

The current research considered two ensemble machine learning models namely boosted regression trees (BRT) and random forest (RF) for susceptibility mapping of groundwater hardness, for the first time. Results of the ensemble models were compared with the model of multivariate discriminant analysis (MDA). According to the modeling results, the RF, BRT, and MDA models, respectively, indicated better performance. The RF model may use some data more than once in a training dataset, whereas some inefficient data will never be used. Therefore, it has more stability and a higher performance to predict in comparison to other methods [77].
To the authors’ knowledge, although there is no previous study which used these models in this field, it should be noted that the good performance of the RF model has been demonstrated in other environmental fields such as groundwater nitrate prediction [39], earth fissure hazard prediction [87], and flash-flood hazard assessment [73]. Like our results, a study by Choubin et al. [88] demonstrated that the RF model had a superior performance than the MDA model for the prediction of air particulate matter (PM) hazard.
However, the Ensemble models such as BRT and RF have some advantages rather than other individual models. They can manage different types of predictor variables (e.g., both continuous and classification variables), improve the missing or lost data, have no need to convert or delete outlier data, have a lack of pre-analysis to select variables among a large number of predictors, increase the diversity of classification trees through the random selection of predictive variables over the different trees, and fit and control the complex nonlinear interaction between variables, and fitting the multiple trees in these models overcomes the biggest drawback (i.e., poor predictive performance) of single models [75,89,90,91].
Spatial prediction of groundwater hardness susceptibility indicated that the high harness areas mostly have low elevations, low depth to groundwater (DTGW), are located near to Caspian Sea, have the Qm (swamp and marsh) lithology unit, and correspond with the agricultural areas. However, the percolation conditions for minerals containing calcium or magnesium into groundwater in these areas are higher and easier due to the low unsaturated zone (i.e., low DTGW), proximity to seawater, low elevations with more drainage and more water accumulation, and irrigated water.
Although the considered period in this study was relatively short (17 years), the groundwater quality and hardness may be affected by climate change and land use change for a longer period. Therefore, in future studies, it is recommended to consider these issues for providing susceptibility maps.

5. Conclusions

The main objective of this study was to model the hardness of groundwater using machine learning models and geo-environmental factors. The predicted hardness susceptibility maps indicated that the areas located in the south of the region have high hardness susceptibility. Some of the possible reasons might include the following: (i) the low depth to groundwater, (ii) proximity to seawater, (iii) low elevations with more drainage and more water accumulation, and (iv) irrigated water, all of which facilitate the percolation conditions for minerals containing calcium or magnesium into groundwater. However, the actual relationships between the geo-environmental factors and groundwater hardness need further in-depth research. Although results from this study were promising, the use of more related and available parameters as input such as soil information may affect and improve the results of the hardness modeling in other regions. Results from this study can help policymakers to understand the groundwater quality, concerning the water hardness and managing the freshwater for sustainable development.

Author Contributions

Conceptualization, A.M.; data curation, F.S.H. and B.C.; formal analysis, A.M., F.S.H., M.A., H.G., B.C., A.L., and A.A.D.; investigation, A.M., F.S.H., M.A., H.G., B.C., A.L., and A.A.D.; methodology, A.M., F.S.H., M.A., H.G., B.C., A.L., and A.A.D.; project administration, A.M.; resources, A.M., F.S.H., M.A., H.G., B.C., A.L., and A.A.D.; software, A.M., F.S.H., M.A., H.G., B.C., A.L., and A.A.D.; supervision, B.C., and A.M.; validation, A.M., F.S.H., M.A., H.G., B.C., A.L., and A.A.D.; visualization, B.C.; writing—original draft, A.M., F.S.H., M.A., H.G., B.C., A.L., and A.A.D.; writing—review and editing, A.M., F.S.H., M.A., H.G., B.C., A.L., and A.A.D. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Conti, K.I.; Velis, M.; Antoniou, A.; Nijsten, G. Groundwater in the Context of the Sustainable Development Goals: Fundamental Policy Considerations. Br. GSDR 2016, 5, 111–133. [Google Scholar]
  2. Ahmed, I.; Tariq, N.; Al Muhery, A. Hydrochemical characterization of groundwater to align with sustainable development goals in the Emirate of Dubai, UAE. Environ. Earth Sci. 2019, 78, 44. [Google Scholar] [CrossRef]
  3. Mukherjee, A.; Duttagupta, S.; Chattopadhyay, S.; Bhanja, S.N.; Bhattacharya, A.; Chakraborty, S.; Sarkar, S.; Ghosh, T.; Bhattacharya, J.; Sahu, S. Impact of sanitation and socio-economy on groundwater fecal pollution and human health towards achieving sustainable development goals across India from ground-observations and satellite-derived nightlight. Sci. Rep. 2019, 9, 15193. [Google Scholar] [CrossRef] [Green Version]
  4. Kut, K.M.K.; Sarswat, A.; Bundschuh, J.; Mohan, D. Water as key to the sustainable development goals of South Sudan—A water quality assessment of Eastern Equatoria State. Groundw. Sustain. Dev. 2019, 8, 255–270. [Google Scholar] [CrossRef]
  5. Foster, S. Is UN Sustainable Development Goal 15 relevant to governing the intimate land-use/groundwater linkage? Hydrogeol. J. 2018, 26, 979–982. [Google Scholar] [CrossRef]
  6. Misi, A.; Gumindoga, W.; Hoko, Z. An assessment of groundwater potential and vulnerability in the Upper Manyame Sub-Catchment of Zimbabwe. Phys. Chem. Earth 2018, 105, 72–83. [Google Scholar] [CrossRef]
  7. Pacheco, F.A.L.; Martins, L.M.O.; Quininha, M.; Oliveira, A.S.; Sanches Fernandes, L.F. Modification to the DRASTIC framework to assess groundwater contaminant risk in rural mountainous catchments. J. Hydrol. 2018, 566, 175–191. [Google Scholar] [CrossRef]
  8. Rizeei, H.M.; Azeez, O.S.; Pradhan, B.; Khamees, H.H. Assessment of groundwater nitrate contamination hazard in a semi-arid region by using integrated parametric IPNOA and data-driven logistic regression models. Environ. Monit. Assess. 2018, 190, 633. [Google Scholar] [CrossRef] [PubMed]
  9. Ameli, A.A.; Creed, I.F. Groundwaters at Risk: Wetland Loss Changes Sources, Lengthens Pathways, and Decelerates Rejuvenation of Groundwater Resources. J. Am. Water Resour. Assoc. 2019, 55, 294–306. [Google Scholar] [CrossRef]
  10. Garcia, V.; Cooter, E.; Crooks, J.; Hinckley, B.; Murphy, M.; Xing, X. Examining the impacts of increased corn production on groundwater quality using a coupled modeling system. Sci. Total Environ. 2017, 586, 16–24. [Google Scholar] [CrossRef]
  11. Hossain, M.; Patra, P.K. Contamination zoning and health risk assessment of trace elements in groundwater through geostatistical modelling. Ecotoxicol. Environ. Saf. 2020, 189, 110038. [Google Scholar] [CrossRef] [PubMed]
  12. Wilson, S.R.; Close, M.E.; Abraham, P.; Sarris, T.S.; Banasiak, L.; Stenger, R.; Hadfield, J. Achieving unbiased predictions of national-scale groundwater redox conditions via data oversampling and statistical learning. Sci. Total Environ. 2020, 705, 135877. [Google Scholar] [CrossRef] [PubMed]
  13. Duarte, L.; Marques, J.E.; Teodoro, A.C. An open source GIS-based application for the assessment of groundwater vulnerability to pollution. Environment 2019, 6, 86. [Google Scholar] [CrossRef] [Green Version]
  14. Neshat, A.; Pradhan, B. Evaluation of groundwater vulnerability to pollution using DRASTIC framework and GIS. Arab. J. Geosci. 2017, 10, 501. [Google Scholar] [CrossRef]
  15. Shrestha, A.; Luo, W. Assessment of groundwater nitrate pollution potential in Central Valley aquifer using Geodetector-Based Frequency Ratio (GFR) and optimized-DRASTIC methods. ISPRS Int. J. Geo-Inf. 2018, 7, 211. [Google Scholar] [CrossRef] [Green Version]
  16. Singha, S.S.; Pasupuleti, S.; Singha, S.; Singh, R.; Venkatesh, A.S. A GIS-based modified DRASTIC approach for geospatial modeling of groundwater vulnerability and pollution risk mapping in Korba district, Central India. Environ. Earth Sci. 2019, 78, 628. [Google Scholar] [CrossRef]
  17. Zamanirad, M.; Sarraf, A.; Sedghi, H.; Saremi, A.; Rezaee, P. Modeling the Influence of Groundwater Exploitation on Land Subsidence Susceptibility Using Machine Learning Algorithms. Nat. Resour. Res. 2020, 29, 1127–1141. [Google Scholar] [CrossRef]
  18. Zhang, Y.; Weissmann, G.S.; Fogg, G.E.; Lu, B.; Sun, H.; Zheng, C. Assessment of groundwater susceptibility to non-point source contaminants using three-dimensional transient indexes. Int. J. Environ. Res. Public Health 2018, 15, 1177. [Google Scholar] [CrossRef] [Green Version]
  19. He, S.; Wu, J. Relationships of groundwater quality and associated health risks with land use/land cover patterns: A case study in a loess area, Northwest China. Hum. Ecol. Risk Assess. 2019, 25, 354–373. [Google Scholar] [CrossRef]
  20. He, S.; Li, P.; Wu, J.; Elumalai, V.; Adimalla, N. Groundwater quality under land use/land cover changes: A temporal study from 2005 to 2015 in Xi’an, Northwest China. Hum. Ecol. Risk Assess. 2019. [Google Scholar] [CrossRef]
  21. Darwishe, H.; El Khattabi, J.; Chaaban, F.; Louche, B.; Masson, E.; Carlier, E. Prediction and control of nitrate concentrations in groundwater by implementing a model based on GIS and artificial neural networks (ANN). Environ. Earth Sci. 2017, 76, 649. [Google Scholar] [CrossRef]
  22. El Hamidi, M.J.; Larabi, A.; Faouzi, M.; Souissi, M. Spatial distribution of regionalized variables on reservoirs and groundwater resources based on geostatistical analysis using GIS: Case of Rmel-Oulad Ogbane aquifers (Larache, NW Morocco). Arab. J. Geosci. 2018, 11, 104. [Google Scholar] [CrossRef]
  23. Azimi, S.; Azhdary Moghaddam, M.; Hashemi Monfared, S.A. Prediction of annual drinking water quality reduction based on Groundwater Resource Index using the artificial neural network and fuzzy clustering. J. Contam. Hydrol. 2019, 220, 6–17. [Google Scholar] [CrossRef]
  24. Güner, E.D.; Kuvvetli, Y. Analysis of groundwater quality for drinking purposes using combined artificial neural networks and fuzzy logic approaches. Desalin. Water Treat. 2020, 174, 143–151. [Google Scholar] [CrossRef]
  25. Heidarzadeh, N. A practical low-cost model for prediction of the groundwater quality using artificial neural networks Nima Heidarzadeh. J. Water Supply Res. Technol.—AQUA 2017, 66, 86–95. [Google Scholar] [CrossRef]
  26. Qaderi, F.; Babanezhad, E. Prediction of the groundwater remediation costs for drinking use based on quality of water resource, using artificial neural network. J. Clean. Prod. 2017, 161, 840–849. [Google Scholar] [CrossRef]
  27. Sunayana; Kalawapudi, K.; Dube, O.; Sharma, R. Use of neural networks and spatial interpolation to predict groundwater quality. Environ. Dev. Sustain. 2020, 22, 2801–2816. [Google Scholar] [CrossRef]
  28. Yang, Q.; Zhang, J.; Hou, Z.; Lei, X.; Tai, W.; Chen, W.; Chen, T. Shallow groundwater quality assessment: Use of the improved Nemerow pollution index, wavelet transform and neural networks. J. Hydroinform. 2017, 19, 784–794. [Google Scholar] [CrossRef]
  29. Isazadeh, M.; Biazar, S.M.; Ashrafzadeh, A. Support vector machines and feed-forward neural networks for spatial modeling of groundwater qualitative parameters. Environ. Earth Sci. 2017, 76, 610. [Google Scholar] [CrossRef]
  30. Fabbrocino, S.; Rainieri, C.; Paduano, P.; Ricciardi, A. Cluster analysis for groundwater classification in multi-aquifer systems based on a novel correlation index. J. Geochem. Explor. 2019, 204, 90–111. [Google Scholar] [CrossRef]
  31. Nadiri, A.A.; Norouzi, H.; Khatibi, R.; Gharekhani, M. Groundwater DRASTIC vulnerability mapping by unsupervised and supervised techniques using a modelling strategy in two levels. J. Hydrol. 2019, 574, 744–759. [Google Scholar] [CrossRef]
  32. Messier, K.P.; Wheeler, D.C.; Flory, A.R.; Jones, R.R.; Patel, D.; Nolan, B.T.; Ward, M.H. Modeling groundwater nitrate exposure in private wells of North Carolina for the Agricultural Health Study. Sci. Total Environ. 2019, 655, 512–519. [Google Scholar] [CrossRef] [PubMed]
  33. Avand, M.; Janizadeh, S.; Tien Bui, D.; Pham, V.H.; Ngo, P.T.T.; Nhu, V.H. A tree-based intelligence ensemble approach for spatial prediction of potential groundwater. Int. J. Digit. Earth 2020. [Google Scholar] [CrossRef]
  34. Kisi, O.; Azad, A.; Kashi, H.; Saeedian, A.; Hashemi, S.A.A.; Ghorbani, S. Modeling Groundwater Quality Parameters Using Hybrid Neuro-Fuzzy Methods. Water Resour. Manag. 2019, 33, 847–861. [Google Scholar] [CrossRef]
  35. Maroufpoor, S.; Fakheri-Fard, A.; Shiri, J. Study of the spatial distribution of groundwater quality using soft computing and geostatistical models. ISH J. Hydraul. Eng. 2019, 25, 232–238. [Google Scholar] [CrossRef]
  36. Aryafar, A.; Khosravi, V.; Zarepourfard, H.; Rooki, R. Evolving genetic programming and other AI-based models for estimating groundwater quality parameters of the Khezri plain, Eastern Iran. Environ. Earth Sci. 2019, 78, 69. [Google Scholar] [CrossRef]
  37. Liu, D.; Liu, C.; Fu, Q.; Li, T.; Imran, K.M.; Cui, S.; Abrar, F.M. ELM evaluation model of regional groundwater quality based on the crow search algorithm. Ecol. Indic. 2017, 81, 302–314. [Google Scholar] [CrossRef]
  38. Jafari, R.; Hassani, A.H.; Torabian, A.; Ghorbani, M.A.; Mirbagheri, S.A. Prediction of groundwater quality parameter in the Tabriz plain, Iran using soft computing methods. J. Water Supply Res. Technol.—AQUA 2019, 68, 573–584. [Google Scholar] [CrossRef]
  39. Rahmati, O.; Choubin, B.; Fathabadi, A.; Coulon, F.; Soltani, E.; Shahabi, H.; Mollaefar, E.; Tiefenbacher, J.; Cipullo, S.; Ahmad, B.; et al. Predicting uncertainty of machine learning models for modelling nitrate pollution of groundwater using quantile regression and UNEEC methods. Sci. Total Environ. 2019, 688, 855–866. [Google Scholar] [CrossRef]
  40. Nadiri, A.A.; Gharekhani, M.; Khatibi, R.; Sadeghfam, S.; Moghaddam, A.A. Groundwater vulnerability indices conditioned by Supervised Intelligence Committee Machine (SICM). Sci. Total Environ. 2017, 574, 691–706. [Google Scholar] [CrossRef]
  41. Mosavi, A.; Ozturk, P.; Chau, K.W. Flood prediction using machine learning models: Literature review. Water 2018, 10, 1536. [Google Scholar] [CrossRef] [Green Version]
  42. Sajedi-Hosseini, F.; Malekian, A.; Choubin, B.; Rahmati, O.; Cipullo, S.; Coulon, F.; Pradhan, B. A novel machine learning-based approach for the risk assessment of nitrate groundwater contamination. Sci. Total Environ. 2018, 644, 954–962. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  43. Papacharalampous, G.; Koutsoyiannis, D.; Montanari, A. Quantification of predictive uncertainty in hydrological modelling by harnessing the wisdom of the crowd: Methodology development and investigation using toy models. Adv. Water Resour. 2020, 136, 103471. [Google Scholar] [CrossRef] [Green Version]
  44. Adimalla, N.; Taloor, A.K. Hydrogeochemical investigation of groundwater quality in the hard rock terrain of South India using Geographic Information System (GIS) and groundwater quality index (GWQI) techniques. Groundw. Sustain. Dev. 2020, 10, 100288. [Google Scholar] [CrossRef]
  45. Ismail, E.; El-Rawy, M. Assessment of groundwater quality in west sohag, egypt. Desalin. Water Treat. 2018, 123, 101–108. [Google Scholar] [CrossRef]
  46. Nematollahi, M.J.; Clark, M.J.R.; Ebrahimi, P.; Ebrahimi, M. Preliminary assessment of groundwater hydrogeochemistry within Gilan, a northern province of Iran. Environ. Monit. Assess. 2018, 190, 242. [Google Scholar] [CrossRef]
  47. Amarasooriya, A.A.G.D.; Kawakami, T. Removal of fluoride, hardness and alkalinity from groundwater by electrolysis. Groundw. Sustain. Dev. 2019, 9, 100231. [Google Scholar] [CrossRef]
  48. Haddad, M.; Barbeau, B. Hybrid hollow fiber nanofiltration–calcite contactor: A novel point-of-entry treatment for removal of dissolved Mn, Fe, NOM and hardness from domestic groundwater supplies. Membranes 2019, 9, 90. [Google Scholar] [CrossRef] [Green Version]
  49. Liu, W.; Singh, R.P.; Jothivel, S.; Fu, D. Evaluation of groundwater hardness removal using activated clinoptilolite. Environ. Sci. Pollut. Res. 2019, 27, 17541–17549. [Google Scholar] [CrossRef]
  50. Balkaya, N.; Kurtulus Ozcan, H.; Nuri Ucan, O. Determination of relationship between hardness and groundwater quality parameters by neural networks. Desalin. Water Treat. 2009, 11, 258–263. [Google Scholar] [CrossRef] [Green Version]
  51. Vaghefi, S.A.; Keykhai, M.; Jahanbakhshi, F.; Sheikholeslami, J.; Ahmadi, A.; Yang, H.; Abbaspour, K.C. The future of extreme climate in Iran. Sci. Rep. 2019, 9, 1464. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  52. Gholami, V.; Yousefi, Z.; Rostami, H.Z. Modeling of ground water salinity on the Caspian Southern Coasts. Water Resour. Manag. 2010, 24, 1415–1424. [Google Scholar] [CrossRef]
  53. Moghimi, H. The Study of Processes Affecting Groundwater Hydrochemistry by Multivariate Statistical Analysis (Case Study: Coastal Aquifer of Ghaemshahr, NE-Iran). Open J. Geol. 2017, 7, 830–846. [Google Scholar] [CrossRef] [Green Version]
  54. WHO. World Health Organization Guidelines for Drinking-Water Quality, 4th ed.; WHO: Geneva, Switzerland, 2011. [Google Scholar]
  55. Saraf, A.K.; Choudhury, P.R. Integrated remote sensing and gis for groundwater exploration and identification of artificial recharge sites. Int. J. Remote Sens. 1998, 19, 1825–1841. [Google Scholar] [CrossRef]
  56. Manap, M.A.; Sulaiman, W.N.A.; Ramli, M.F.; Pradhan, B.; Surip, N. A knowledge-driven GIS modeling technique for groundwater potential mapping at the Upper Langat Basin, Malaysia. Arab. J. Geosci. 2013, 6, 1621–1637. [Google Scholar] [CrossRef]
  57. Aniya, M. Landslide-Susceptibility Mapping in the Amahata River Basin, Japan. Ann. Assoc. Am. Geogr. 1985, 75, 102–114. [Google Scholar] [CrossRef]
  58. Hong, H.; Pourghasemi, H.R.; Pourtaghi, Z.S. Landslide susceptibility assessment in Lianhua County (China): A comparison between a random forest data mining technique and bivariate and multivariate statistical models. Geomorphology 2016, 259, 105–118. [Google Scholar] [CrossRef]
  59. Oh, H.J.; Kim, Y.S.; Choi, J.K.; Park, E.; Lee, S. GIS mapping of regional probabilistic groundwater potential in the area of Pohang City, Korea. J. Hydrol. 2011, 399, 158–172. [Google Scholar] [CrossRef]
  60. Naghibi, S.A.; Ahmadi, K.; Daneshi, A. Application of Support Vector Machine, Random Forest, and Genetic Algorithm Optimized Random Forest Models in Groundwater Potential Mapping. Water Resour. Manag. 2017, 31, 2761–2775. [Google Scholar] [CrossRef]
  61. Hanson, P.J.; Edwards, N.T.; Garten, C.T.; Andrews, J.A. Separating root and soil microbial contributions to soil respiration: A review of methods and observations. Biogeochemistry 2000, 48, 115–146. [Google Scholar] [CrossRef]
  62. Yang, Q.; Wang, L.; Ma, H.; Yu, K.; Martín, J.D. Hydrochemical characterization and pollution sources identification of groundwater in Salawusu aquifer system of Ordos Basin, China. Environ. Pollut. 2016, 216, 340–349. [Google Scholar] [CrossRef] [PubMed]
  63. Fernández, D.S.; Lutz, M.A. Urban flood hazard zoning in Tucumán Province, Argentina, using GIS and multicriteria decision analysis. Eng. Geol. 2010, 111, 90–98. [Google Scholar] [CrossRef]
  64. Allen, D.M.; Suchy, M. Geochemical evolution of groundwater on Saturna Island, British Columbia. Can. J. Earth Sci. 2001, 38, 1059–1080. [Google Scholar] [CrossRef]
  65. Shankar, M.N.R.; Mohan, G. Assessment of the groundwater potential and quality in Bhatsa and Kalu river basins of Thane district, western Deccan Volcanic Province of India. Environ. Geol. 2006, 49, 990–998. [Google Scholar] [CrossRef]
  66. Palamuleni, L.G.; Ndomba, P.M.; Annegarn, H.J. Evaluating land cover change and its impact on hydrological regime in Upper Shire river catchment, Malawi. Reg. Environ. Chang. 2011, 11, 845–855. [Google Scholar] [CrossRef]
  67. Arabameri, A.; Rezaei, K.; Cerda, A.; Lombardo, L.; Rodrigo-Comino, J. GIS-based groundwater potential mapping in Shahroud plain, Iran. A comparison among statistical (bivariate and multivariate), data mining and MCDM approaches. Sci. Total Environ. 2019, 658, 160–177. [Google Scholar] [CrossRef] [PubMed]
  68. Ozdemir, A. Using a binary logistic regression method and GIS for evaluating and mapping the groundwater spring potential in the Sultan Mountains (Aksehir, Turkey). J. Hydrol. 2011, 405, 123–136. [Google Scholar] [CrossRef]
  69. Yuce, G.; Ugurluoglu, D.; Dilaver, A.T.; Eser, T.; Sayin, M.; Donmez, M.; Ozcelik, S.; Aydin, F. The effects of lithology on water pollution: Natural radioactivity and trace elements in water resources of Eskisehir Region (Turkey). Water Air. Soil Pollut. 2009, 202, 69–89. [Google Scholar] [CrossRef]
  70. Hair, J.; Black, W.; Babin, B.; Anderson, R. Multivariate Data Analysis: A Global Perspective; Elsevier: New York, NY, USA, 2010; Volume 7, pp. 88–122. [Google Scholar]
  71. Rafiei Sardooi, E.; Azareh, A.; Choubin, B.; Barkhori, S.; Singh, V.P.; Shamshirband, S. Applying the remotely sensed data to identify homogeneous regions of watersheds using a pixel-based classification approach. Appl. Geogr. 2019, 111, 102071. [Google Scholar] [CrossRef]
  72. Wang, G.; Jia, R.; Liu, J.; Zhang, H. A hybrid wind power forecasting approach based on Bayesian model averaging and ensemble learning. Renew. Energy 2020, 145, 2426–2434. [Google Scholar] [CrossRef]
  73. Hosseini, F.S.; Choubin, B.; Mosavi, A.; Nabipour, N.; Shamshirband, S.; Darabi, H.; Haghighi, A.T. Flash-flood hazard assessment using ensembles and Bayesian-based machine learning models: Application of the simulated annealing feature selection method. Sci. Total Environ. 2020, 711, 135161. [Google Scholar] [CrossRef] [PubMed]
  74. Freund, Y.; Schapire, R.E. Experiments with a New Boosting Algorithm. In Proceedings of the 13th International Conference on Machine Learning, Bari, Italy, 3–6 July 1996. [Google Scholar]
  75. Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef] [PubMed]
  76. Schapire, R.E. The Boosting Approach to Machine Learning: An Overview. In Nonlinear Estimation and Classification; Springer: New York, NY, USA, 2003; pp. 149–171. [Google Scholar]
  77. Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
  78. Aertsen, W.; Kint, V.; Van Orshoven, J.; Muys, B. Evaluation of Modelling Techniques for Forest Site Productivity Prediction in Contrasting Ecoregions Using Stochastic Multicriteria Acceptability Analysis (SMAA). Environ. Model. Softw. 2011, 26, 929–937. [Google Scholar] [CrossRef] [Green Version]
  79. Hair, J.F.; Black, W.C.; Babin, B.J.; Anderson, R.E. Multivariate Data Analysis; Pearson Education, Inc.: Jersey City, NJ, USA, 1998. [Google Scholar]
  80. Shin, P.K.S.; Fong, K.Y.S. Multiple discriminant analysis of marine sediment data. Mar. Pollut. Bull. 1999, 39, 285–294. [Google Scholar] [CrossRef]
  81. Hepelwa, A.S. Environmental and Socioeconomic Factors Influencing Crop Cultivation. An Application of Multivariate Discriminant Analysis (MDA) model in Sigi catchment, Tanzania; Springer: Heidelberg, Germany, 2010. [Google Scholar]
  82. Negnevitsky, M. Artificial Intelligence—A Guide to Intelligent Systems. J. Chir. 2002, 110, 439–444. [Google Scholar]
  83. Efron, B.; Tibshirani, R. Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy. Stat. Sci. 1986, 1, 54–75. [Google Scholar] [CrossRef]
  84. Allouche, O.; Tsoar, A.; Kadmon, R. Assessing the accuracy of species distribution models: Prevalence, kappa and the true skill statistic (TSS). J. Appl. Ecol. 2006, 43, 1223–1232. [Google Scholar] [CrossRef]
  85. Guzzetti, F.; Reichenbach, P.; Ardizzone, F.; Cardinali, M.; Galli, M. Estimating the quality of landslide susceptibility models. Geomorphology 2006, 81, 166–184. [Google Scholar] [CrossRef]
  86. Miraki, S.; Zanganeh, S.H.; Chapi, K.; Singh, V.P.; Shirzadi, A.; Shahabi, H.; Pham, B.T. Mapping Groundwater Potential Using a Novel Hybrid Intelligence Approach. Water Resour. Manag. 2019, 33, 281–302. [Google Scholar] [CrossRef]
  87. Choubin, B.; Mosavi, A.; Alamdarloo, E.H.; Hosseini, F.S.; Shamshirband, S.; Dashtekian, K.; Ghamisi, P. Earth fissure hazard prediction using machine learning models. Environ. Res. 2019, 179, 108700. [Google Scholar] [CrossRef] [PubMed]
  88. Choubin, B.; Abdolshahnejad, M.; Moradi, E.; Querol, X.; Mosavi, A.; Shamshirband, S.; Ghamisi, P. Spatial hazard assessment of the PM10 using machine learning models in Barcelona, Spain. Sci. Total Environ. 2020, 701, 134474. [Google Scholar] [CrossRef] [PubMed]
  89. Knoll, L.; Breuer, L.; Bach, M. Large scale prediction of groundwater nitrate concentrations from spatial data using machine learning. Sci. Total Environ. 2019, 668, 1317–1327. [Google Scholar] [CrossRef] [PubMed]
  90. Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
  91. Aertsen, W.; Kint, V.; van Orshoven, J.; Özkan, K.; Muys, B. Comparison and ranking of different modelling techniques for prediction of site index in Mediterranean mountain forests. Ecol. Modell. 2010, 221, 1119–1130. [Google Scholar] [CrossRef]
Water 12 02770 g001 550
Figure 1. Location of the Ghaemshahr-Joibar plain in Mazandaran province, Iran.
Figure 1. Location of the Ghaemshahr-Joibar plain in Mazandaran province, Iran.
Water 12 02770 g001
Water 12 02770 g002 550
Figure 2. Environmental factors used for hardness susceptibility modeling: (a) elevation, (b) curvature, (c) distance from sea (DFS), (d) distance from river (DFR), (e) precipitation (PCP), (f) evaporation (E), (g) depth to groundwater (DTGW), (h) groundwater level (GWL), (i) pH, (j) landuse, and (k) lithology.
Figure 2. Environmental factors used for hardness susceptibility modeling: (a) elevation, (b) curvature, (c) distance from sea (DFS), (d) distance from river (DFR), (e) precipitation (PCP), (f) evaporation (E), (g) depth to groundwater (DTGW), (h) groundwater level (GWL), (i) pH, (j) landuse, and (k) lithology.
Water 12 02770 g002
Water 12 02770 g003 550
Figure 3. The area under curve (AUC) values for the models.
Figure 3. The area under curve (AUC) values for the models.
Water 12 02770 g003
Water 12 02770 g004 550
Figure 4. Groundwater hardness susceptibility maps: predicted by the BRT (a), RF (b), and MDA (c) models.
Figure 4. Groundwater hardness susceptibility maps: predicted by the BRT (a), RF (b), and MDA (c) models.
Water 12 02770 g004
Water 12 02770 g005 550
Figure 5. Importance of the input variables.
Figure 5. Importance of the input variables.
Water 12 02770 g005
Table
Table 1. List of the considered environmental factors for susceptibility prediction of groundwater hardness.
Table 1. List of the considered environmental factors for susceptibility prediction of groundwater hardness.
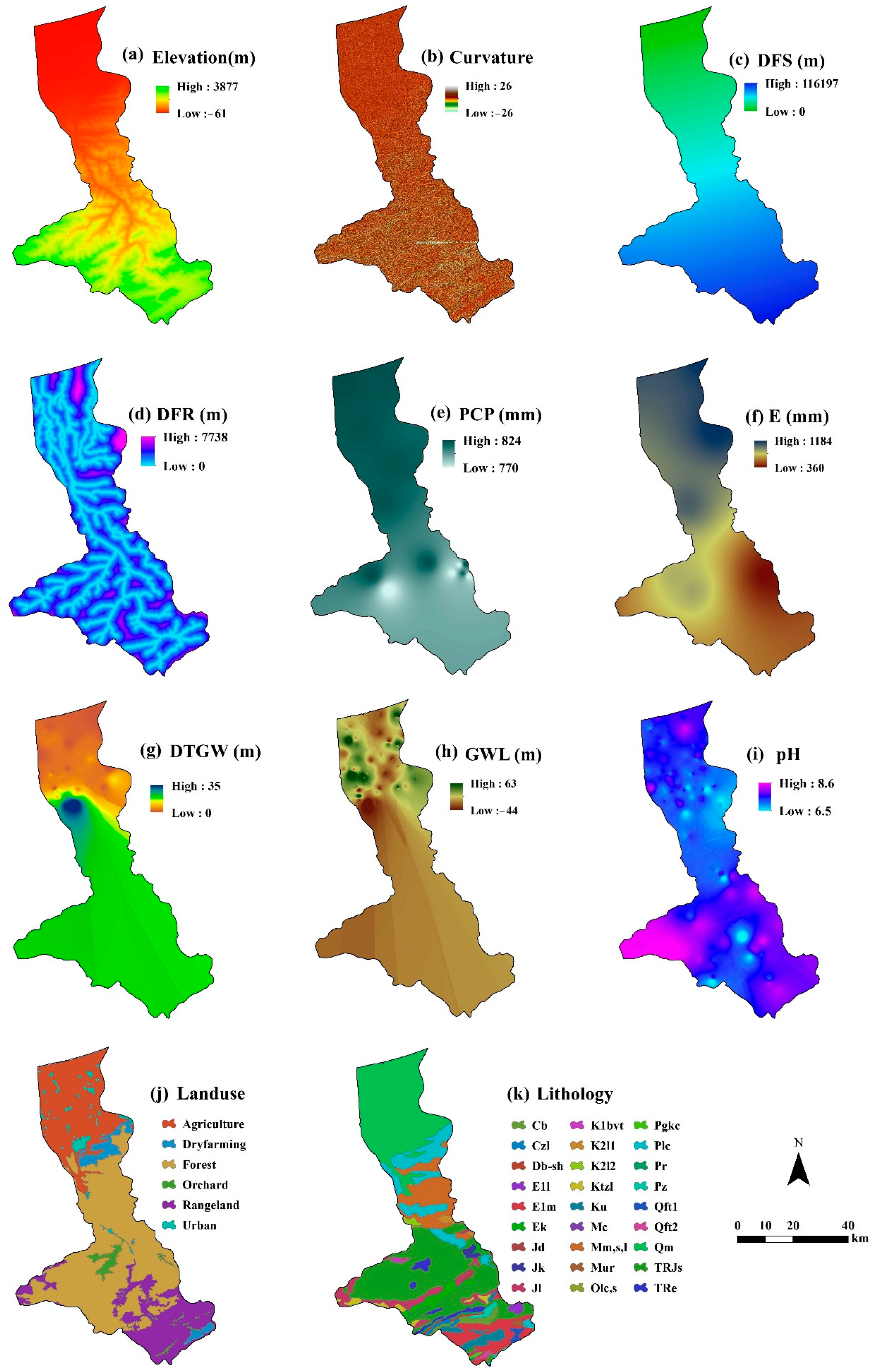
FactorRange/Class
Elevation−61 to 3877 m
Curvature−26 to 26
Distance From Sea (DFS)0 to 116197 m
Distance From River (DFR)0 to 7738 m
Precipitation (PCP)770 to 824 mm
Evaporation (E)360 to 1184 mm
Depth to Groundwater (DTGW)0 to 35 m
Groundwater Level (GWL)−44 to 63 m
pH6.5 to 8.6
LanduseAgriculture, Dry farming, Forest, Orchard, Rangeland, Urban
LithologyCb, Czl, Db-sh, E1l, E1m, Ek, Jd, Jk, Jl, K1bvt, K2l1, K2l2, Ktzl, Ku, Mc, Mm,s,l, Mur, Olc,s, Pgkc, Plc, Pr, Pz, Qft1, Qft2, Qm, TRJs, TRe
Note: Cb: alternation of dolomite, limestone and variegated shale; Czl: undifferentiated unit, composed of dark red micaceous siltstone and sandstone; Db-sh: undifferentiated limestone, shale and marl; E1l: nummulitic limestone; E1m: marl, gypsiferous marl and limestone; Ek: well-bedded green tuff and tuffaceous shale; Jd: well-to-thin-bedded, greenish-grey argillaceous limestone with intercalations of calcareous shale; Jk: conglomerate, sandstone and shale with plantremains and coal seams; Jl: light grey, thin-bedded to massive limestone; K1bvt: basaltic volcanic tuff; K2l1: hyporite bearing limestone; K2l2: thick-bedded to massive limestone; Ktzl: thick-bedded to massive, white to pinkish orbitolina bearing limestone; Ku: upper cretaceous, undifferentiated rocks; Mc: red conglomerate and sandstone; Mm,s,l: marl, calcareous sandstone, sandy limestone and minor conglomerate; Mur: red marl, gypsiferous marl, sandstone and conglomerate; Olc,s: conglomerate and sandstone; Pgkc: light-red coarse grained, polygenic conglomerate with sandstone intercalations; Plc: polymictic conglomerate and sandstone; Pr: dark grey medium-bedded to massive limestone; Pz: undifferentiated lower Paleozoic rocks, Qft1/Qft2: high/low level piedmont fan and valley terrace deposits; Qm: swamp and marsh; TRJs: dark grey shale and sandstone; Tre: thick bedded grey o’olitic limestone; thin-platy, yellow to pinkish shaly limestone with worm tracks and well to thick-bedded dolomite and dolomitic limestone.
Table
Table 2. Multicollinearity analysis using variance inflation factor (VIF).
Table 2. Multicollinearity analysis using variance inflation factor (VIF).
VariableVIFVariableVIF
Distance From Sea (DFS)9.09Landuse1.64
Elevation5.76Distance from river (DFR)1.29
Depth to Groundwater (DTGW)4.37PH1.86
Precipitation (PCP)2.82Evaporation (E)1.32
Groundwater Level (GWL)2.08Curvature1.01
Lithology2.14−−
Table
Table 3. Performance of the modeling results.
Table 3. Performance of the modeling results.
ModelBRTRFMDA
AUC0.920.900.81
Accuracy0.780.830.83
TSS0.710.730.59
Table
Table 4. Susceptibility classes area (km2) in each model.
Table 4. Susceptibility classes area (km2) in each model.
ClassBRTRFMDA
Low2474.141924.302403.51
Moderate443.341022.22518.07
High379.21350.17375.11

Share and Cite

MDPI and ACS Style

Mosavi, A.; Hosseini, F.S.; Choubin, B.; Abdolshahnejad, M.; Gharechaee, H.; Lahijanzadeh, A.; Dineva, A.A. Susceptibility Prediction of Groundwater Hardness Using Ensemble Machine Learning Models. Water 2020, 12, 2770. https://doi.org/10.3390/w12102770

AMA Style

Mosavi A, Hosseini FS, Choubin B, Abdolshahnejad M, Gharechaee H, Lahijanzadeh A, Dineva AA. Susceptibility Prediction of Groundwater Hardness Using Ensemble Machine Learning Models. Water. 2020; 12(10):2770. https://doi.org/10.3390/w12102770

Chicago/Turabian Style

Mosavi, Amirhosein, Farzaneh Sajedi Hosseini, Bahram Choubin, Mahsa Abdolshahnejad, Hamidreza Gharechaee, Ahmadreza Lahijanzadeh, and Adrienn A. Dineva. 2020. "Susceptibility Prediction of Groundwater Hardness Using Ensemble Machine Learning Models" Water 12, no. 10: 2770. https://doi.org/10.3390/w12102770

APA Style

Mosavi, A., Hosseini, F. S., Choubin, B., Abdolshahnejad, M., Gharechaee, H., Lahijanzadeh, A., & Dineva, A. A. (2020). Susceptibility Prediction of Groundwater Hardness Using Ensemble Machine Learning Models. Water, 12(10), 2770. https://doi.org/10.3390/w12102770

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop