Variability of the Initial Abstraction Ratio in an Urban and an Agroforested Catchment
Abstract
:1. Introduction
2. Materials and Methods
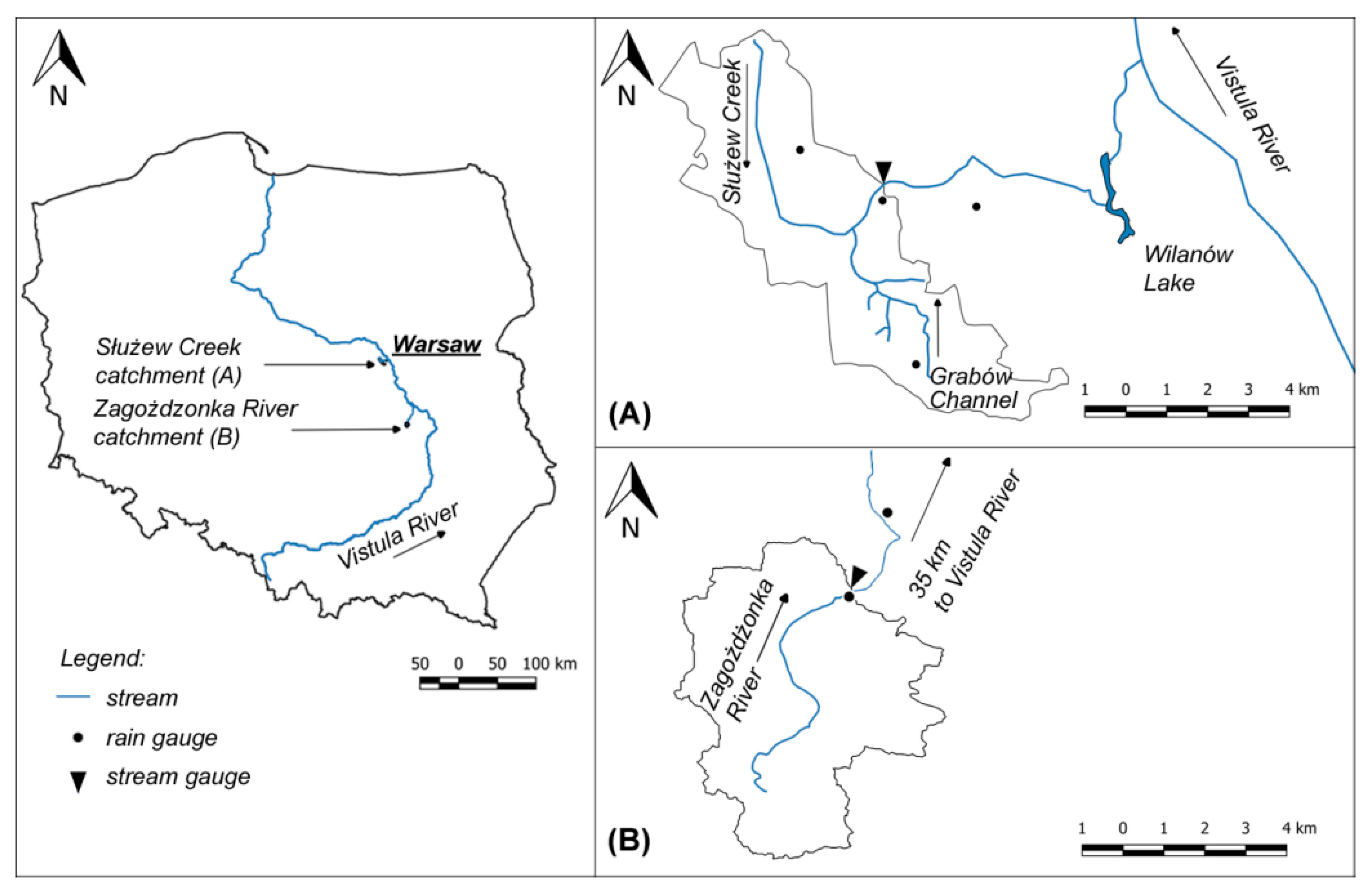
2.1. Characteristics of the Study Catchments
2.2. Recorded Data
2.3. Selection of Storm Rainfall-Runoff Events
2.4. Estimation of the Initial Abstraction Ratio from Recorded Data
2.5. Variability of the Initial Abstraction Ratio
3. Results and Discussion
3.1. Initial Abstraction Ratio Variation
3.2. Initial Abstraction Ratio Dependency on the Land Use Type
3.3. Initial Abstraction Ratio Dependence on the Vegetation State
3.4. Initial Abstraction Ratio Variation with Rainfall Depth
3.5. Initial Abstraction Ratio May Change Locally
4. Conclusions
- Estimated values of the initial abstraction ratio varied between storm events and were most often lower than the original value of 0.20 originally suggested. For the urbanized catchment, this ratio ranged from 0.002 to 0.188, with the average value of 0.025, while for the agroforested catchment, the average ratio equaled 0.047, ranging from 0.001 to 0.512;
- The initial abstraction ratio varies over seasons, especially in the case of non-urbanized catchments with a high percentage of area covered with vegetation. Its higher value is expected during the vegetation period due to the occurrence of plants’ interception. In urbanized catchments, a variation of the ratio over seasons is expected to be small;
- For large rainfall events, the initial abstraction ratio approaches a constant value after the rainfall depth exceeds a certain threshold value. This threshold is catchment dependent and in the case of the urbanized catchment it was p > 30 mm (λ → 0.0089) and in the case of the agroforested catchment it was p > 20 mm (λ → 0.0109);
- When using the SCS-CN method, special care should be taken to determine the initial abstraction ratio, as the suggested value of 0.20 may be too high. This may result in underestimation of the runoff depth that may have serious consequences in terms of the underestimation of flood risk.
Author Contributions
Funding
Conflicts of Interest
References
- Rabori, A.M.; Ghazavi, R. Urban Flood Estimation and Evaluation of the Performance of an Urban Drainage System in a Semi-Arid Urban Area Using SWMM. Water Environ. Res. 2018, 90, 2075–2082. [Google Scholar] [CrossRef] [PubMed]
- Banasik, K.; Gorski, D.; Popek, Z.; Hejduk, L. Estimating the annual sediment yield of a small agricultural catchment in central Poland. In Erosion and Sediment Yields in the Changing Environment; Collins, A.V.G., Horowitz, A.X.L., Stone, M., Walling, D., Eds.; IAHS Publ.: Wallingford, UK, 2012; Volume 256, pp. 267–275. [Google Scholar]
- Krajewski, A.; Sikorska-Senoner, A.E.; Ranzi, R.; Banasik, K. Long-Term Changes of Hydrological Variables in a Small Lowland Watershed in Central Poland. Water 2019, 11, 564. [Google Scholar] [CrossRef] [Green Version]
- Banasik, K.; Hejduk, L. Long-term changes in runoff from a small agricultural catchment. Soil Water Res. 2012, 7, 64–72. [Google Scholar] [CrossRef] [Green Version]
- National Engineering Handbook (NEH). National Engineering Handbook, Part 630 Hydrology; USDA: Washington, DC, USA, 2004.
- Sikorska, A.E.; Scheidegger, A.; Banasik, K.; Rieckermann, J. Bayesian uncertainty assessment of flood predictions in ungauged urban basins for conceptual rainfall-runoff models. Hydrol. Earth Syst. Sci. 2012, 16, 1221–1236. [Google Scholar] [CrossRef] [Green Version]
- Hawkins, R.H. Asymptotic Determination of Runoff Curve Numbers from Data. J. Irrig. Drain. Eng. 1993, 119, 334–345. [Google Scholar] [CrossRef]
- Shi, Z.-H.; Chen, L.-D.; Fang, N.-F.; Qin, D.-F.; Cai, C.-F. Research on the SCS-CN initial abstraction ratio using rainfall-runoff event analysis in the Three Gorges Area, China. Catena 2009, 77, 1–7. [Google Scholar] [CrossRef]
- Santikari, V.P.; Murdoch, L.C. Including effects of watershed heterogeneity in the curve number method using variable initial abstraction. Hydrol. Earth Syst. Sci. 2018, 22, 4725–4743. [Google Scholar] [CrossRef] [Green Version]
- Banasik, K.; Hejduk, L.; Woodward, D.; Banasik, J. Flood peak discharge vs various CN and rain duration in a small catchment. Rocz. Ochr. Srodowiska 2016, 18, 201–212. [Google Scholar]
- Li, C.; Liu, M.; Hu, Y.; Shi, T.; Zong, M.; Walter, M.T. Assessing the Impact of Urbanization on Direct Runoff Using Improved Composite CN Method in a Large Urban Area. Int. J. Environ. Res. Public Health 2018, 15, 775. [Google Scholar] [CrossRef] [Green Version]
- Singh, P.; Bhunya, P.; Mishra, S.; Chaube, U. A sediment graph model based on SCS-CN method. J. Hydrol. 2008, 349, 244–255. [Google Scholar] [CrossRef] [Green Version]
- Gupta, S.K.; Tyagi, J.; Singh, P.; Sharma, G.; Jethoo, A. Soil Moisture Accounting (SMA) based sediment graph models for small watersheds. J. Hydrol. 2019, 574, 1129–1151. [Google Scholar] [CrossRef]
- Banasik, K.; Krajewski, A.; Sikorska, A.; Hejduk, L. Curve Number Estimation for a Small Urban Catchment from Recorded Rainfall-Runoff Events. Arch. Environ. Prot. 2014, 40, 75–86. [Google Scholar] [CrossRef]
- Kowalik, T.; Walega, A. Estimation of CN Parameter for Small Agricultural Watersheds Using Asymptotic Functions. Water 2015, 7, 939–955. [Google Scholar] [CrossRef] [Green Version]
- Cogliandro, V.; Krajewski, A.; Rutkowska, A.; Porto, P.; Banasik, K. Effect of forest fire on lag time of direct runoff of rainfall in a small catchment in Calabria. Sylwan 2017, 161, 677–684. [Google Scholar]
- Azizian, A.; Shokoohi, A. Development of a new method for estimating SCS curve number using TOPMODEL concept of wetness index (case study: Kasilian and Jong watersheds, Iran). Acta Geophys. 2019, 67, 1163–1177. [Google Scholar] [CrossRef]
- Woodward, D.E.; Hawkins, R.H.; Jiang, R.; Hjelmfelt, J.A.T.; Van Mullem, J.A.; Quan, Q.D. Runoff Curve Number Method: Examination of the Initial Abstraction Ratio. World Water Environ. Resour. Congr. 2003. [Google Scholar] [CrossRef] [Green Version]
- Fu, S.; Zhang, G.; Wang, N.; Luo, L. Initial Abstraction Ratio in the SCS-CN Method in the Loess Plateau of China. Trans. ASABE 2011, 54, 163–169. [Google Scholar] [CrossRef]
- Junior, L.C.G.D.V.; Rodrigues, D.B.B.; De Oliveira, P.T.S. Initial abstraction ratio and Curve Number estimation using rainfall and runoff data from a tropical watershed. RBRH 2019, 24, 24. [Google Scholar]
- Lim, K.J.; Engel, B.A.; Muthukrishnan, S.; Harbor, J.; Harbor, J. Effects of Initial Abstraction and Urbanization on Estimated Runoff Using CN Technology. JAWRA J. Am. Water Resour. Assoc. 2006, 42, 629–643. [Google Scholar] [CrossRef]
- Lal, M.; Mishra, S.; Kumar, M. Reverification of antecedent moisture condition dependent runoff curve number formulae using experimental data of Indian watersheds. Catena 2019, 173, 48–58. [Google Scholar] [CrossRef]
- Durán-Barroso, P.; González, J.; Valdés, J.B. Sources of uncertainty in the NRCS CN model: Recognition and solutions. Hydrol. Process. 2017, 31, 3898–3906. [Google Scholar] [CrossRef]
- Dey, P.; Mishra, A. Separating the impacts of climate change and human activities on streamflow: A review of methodologies and critical assumptions. J. Hydrol. 2017, 548, 278–290. [Google Scholar] [CrossRef]
- Zhai, R.; Tao, F. Contributions of climate change and human activities to runoff change in seven typical catchments across China. Sci. Total. Environ. 2017, 605, 219–229. [Google Scholar] [CrossRef]
- Zhou, Y.; Lai, C.; Wang, Z.; Chen, X.; Zeng, Z.; Chen, J.; Bai, X. Quantitative Evaluation of the Impact of Climate Change and Human Activity on Runoff Change in the Dongjiang River Basin, China. Water 2018, 10, 571. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Chen, Y.; Li, B. Quantifying the effects of climate variability and human activities on runoff for Kaidu River Basin in arid region of northwest China. Theor. Appl. Climatol. 2013, 111, 537–545. [Google Scholar] [CrossRef]
- Lv, X.; Zuo, Z.; Xiao, P.; Ni, Y.; Sun, J. Effects of Climate Change and Human Activity on Runoff in a Typical Loess Gullied-Hilly Region Watershed. Pol. J. Environ. Stud. 2018, 27, 779–785. [Google Scholar] [CrossRef]
- Tan, X.; Gan, T.Y. Contribution of human and climate change impacts to changes in streamflow of Canada. Sci. Rep. 2015, 5, 17767. [Google Scholar] [CrossRef] [PubMed]
- Ranzi, R.; Caronna, P.; Tomirotti, M. Impact of Climatic and Land Use Changes on River Flows in the Southern Alps. In Sustainable Water Resources Planning and Management Under Climate Change; Kolokytha, E., Oishi, S., Teegavarapu, R., Eds.; Springer: Singapore, 2017; pp. 61–83. [Google Scholar]
- Hejduk, L.; Hejduk, A.; Banasik, K. Determination of Curve Number for snowmelt-runoff floods in a small catchment. In Proceedings of the International Association of Hydrological Sciences; IAHS Publ.: Prague, Czech Republic, 2015; Volume 370, pp. 167–170. [Google Scholar]
- Banasik, K.; Hejduk, L.; Barszcz, M. Flood flow consequences of land use changes in a small urban catchment of Warsaw. In 11th International Conference on Urban Drainage; IAHR/IWA: Edinburgh, UK, 2008; pp. 1–10. [Google Scholar]
- Sikorska, A.; Banasik, K. Parameter identification of a conceptual rainfall-runoff model for a small urban catchment. Ann. Warsaw Univ. of Life Sci. SGGW Land Reclam. 2010, 42, 279–293. [Google Scholar] [CrossRef]
- Sikorska, A.E.; Scheidegger, A.; Banasik, K.; Rieckermann, J. Considering rating curve uncertainty in water level predictions. Hydrol. Earth Syst. Sci. 2013, 17, 4415–4427. [Google Scholar] [CrossRef] [Green Version]
- Krajewski, A.; Sikorska, A.E.; Banasik, K. Modeling Suspended Sediment Concentration in the Stormwater Outflow from a Small Detention Pond. J. Environ. Eng. 2017, 143, 05017005. [Google Scholar] [CrossRef]
- Krajewski, A.; Banasik, K.; Sikorska, A. Stormflow and suspended sediment routing through a small detention pond with uncertain discharge rating curves. Hydrol. Res. 2019, 50, 1177–1188. [Google Scholar] [CrossRef]
- Krajewski, A.; Wasilewicz, M.; Banasik, K.; Sikorska, A.E. Operation of detention pond in urban area-example of Wyscigi Pond in Warsaw. In Environmental Engineering V; Pawlowska, M., Pawlowski, L., Eds.; CRC Press: London, UK, 2017; pp. 211–215. [Google Scholar]
- Krajewski, A.; Gladecki, J.; Banasik, K. Transport of suspended sediment during flood events in a small urban catchment. Acta Sci. Pol. Form. Circumiectus 2018, 17, 119–127. [Google Scholar] [CrossRef]
- Majewski, G.; Przewoźniczuk, W.; Kleniewska, M. Precipitation at the meteorological station in Ursynów WULS – SGGW in 1960–2009. Sci. Rev. Eng. Env. Sci. 2010, 19, 3–22. [Google Scholar]
- Majewski, G.; Odorowska, M.; Rozbicka, K. An analysis of the thermal conditions at Ursynów-SGGW station in Warsaw for the years 1970-2009. Water-Environ.-Rural Areas 2012, 2, 171–184. [Google Scholar]
- Department of Water Engineering and Applied Geology (DoWEaAG), Warsaw University of Life Sciences, Warsaw, Poland. Investigations Realised within the Statutory Activity of the DoWEaAG, Funded by the Ministry of Science and Higher Education, in Years 2010–2017, Internal Report; Department of Water Engineering and Applied Geology (DoWEaAG), Warsaw University of Life Sciences: Warsaw, Poland, 2017. [Google Scholar]
- Copernicus Land Monitoring Service, CORINE Land Cover 2018. Available online: https://www.copernicus.eu/en/services/land URL (accessed on 1 June 2019).
- Soil-Agricultural map, 1:500,000, Masovian Spatial Information System. Available online: https://msip.wrotamazowsza.pl/msip/Full.aspx (accessed on 1 June 2019).
- Kurowska-Łazarz, R.; Szulc, W.; Woźniak, B.; Piotrowska, M.; Drożdżyńska, J. Vademecum. Meteorological MEASUREMENTS and Observations; IMGW-PIB: Warsaw, Poland, 2015; pp. 9–23. [Google Scholar]
- Szumiejko, F.; Wdowikowski, M.; Hański, A.; Kańska, A.; Mielke, M.; Aneszko, J.; Jankowska, I.; Wydrych, M. Vademecum. Hydrological Measurements and Observations; IMGW-PIB: Warsaw, Poland, 2015; pp. 13–31. [Google Scholar]
- World Meteorological Organisation. Guide to Hydrological Practice, Hydrology—From Measurement to Hydrological Information, 6th ed.; World Meteorological Organisation: Geneva, Switzerland, 2008; pp. I.9-12–I.9-14. [Google Scholar]
- Kaznowska, E.; Bansik, K.; Hejduk, A.; Krajewski, A.; Wasilewicz, M.; Hejduk, L.; Gładecki, J. Hydrological characteristics since the mid–twentieth century of a small catchment in southern mazovian region, Poland. In Contemporary Problems of Polish Climate; Chojnacka-Ożga, L., Lorenc, H., Eds.; IMGW-PIB Press: Warszawa, Poland, 2019; pp. 135–146. [Google Scholar]
- Wanielista, M.; Kersten, R.; Eaglin, R. Hydrology, Water Quantity and Quality Control; John Wiley&Sons, Inc.: Wiley: New York, NY, USA, 1997; pp. 189–193. [Google Scholar]
- Ling, L.; Yusop, Z.; Yap, W.-S.; Tan, W.L.; Chow, M.F.; Ling, J.L. A Calibrated, Watershed-Specific SCS-CN Method: Application to Wangjiaqiao Watershed in the Three Gorges Area, China. Water 2020, 12, 60. [Google Scholar] [CrossRef] [Green Version]
- Walega, A.; Michalec, B.; Cupak, A.; Grzebinoga, M. Comparison of SCS-CN determination methodologies in a heterogeneous catchment. J. Mt. Sci. 2015, 12, 1084–1094. [Google Scholar] [CrossRef]
- Soulis, K.X.; Valiantzas, J.D. SCS-CN parameter determination using rainfall-runoff data in heterogeneous watersheds—the two-CN system approach. Hydrol. Earth Syst. Sci. 2012, 16, 1001–1015. [Google Scholar] [CrossRef] [Green Version]
- Soulis, K.; Valiantzas, J. Identification of the SCS-CN Parameter Spatial Distribution Using Rainfall-Runoff Data in Heterogeneous Watersheds. Water Resour. Manag. 2013, 27, 1737–1749. [Google Scholar] [CrossRef]
- Systat Software Inc. TableCurve 2D v5.01 for Windows; Systat Software Inc.: Chicago, IL, USA, 2002. [Google Scholar]
- Sikorska, A.; Seibert, J. Value of different precipitation data for flood prediction in an alpine catchment: A Bayesian approach. J. Hydrol. 2018, 556, 961–971. [Google Scholar] [CrossRef]
- Hawkins, R.H.; Hjelmfelt, A.T.; Zevenbergen, A.W. Runoff Probability, Storm Depth, and Curve Numbers. J. Irrig. Drain. Eng. 1985, 111, 330–340. [Google Scholar] [CrossRef]






| Category | Unit | Służew Creek (Years) [Source] | Zagożdżonka River (Years) [Source] |
|---|---|---|---|
| Catchment type | - | lowland, urbanized | lowland, agroforested |
| Area up to gauging station | km2 | 28.7 [41] | 23.4 [41] |
| Average channel slope | ‰ | 1.1 [41] | 3.0 [41] |
| Impervious surfaces | % | 25.3 [42] | 0.56 [42] |
| Average precipitation | mm | 541.9 (1960−2009) [39] | 612.0 (1963−2015) [3] |
| Average temperature | °C | 8.6 (1970–2009) [40] | 8.1 (1951–2015) [3] |
| Average discharge per sq. km | dm3∙s−1∙km−2 | 6.34 (2010–2017) [41] | 3.89 (2010–2017) [41] |
| Category | Land Cover (%) and Soil Structure (%) in | |
|---|---|---|
| Służew Creek | Zagożdżonka River | |
| Land cover type [42] | ||
| Residential areas | 28.9 | 3.6 |
| Airport | 19.3 | - |
| Arable lands | 12.9 | 43.4 |
| Forests | 12.5 | 45.1 |
| Industrial areas | 9.4 | - |
| Recreation areas | 7.9 | - |
| Roads and associated lands | 7.1 | - |
| Meadows | 2.0 | 7.8 |
| Soil type [43] | ||
| Loamy sand | 50.5 | - |
| Light loamy sand | 40.2 | - |
| Organic soil | 9.3 | - |
| Silt loam | - | 67.8 |
| Silt | - | 27.3 |
| Sand | - | 4.9 |
| Antecedent Moisture Condition | Total Number of Events with 5 Days of Rainfall for | |
|---|---|---|
| Dormant Period | Vegetation Period | |
| AMC I | (12 events) < 13 mm | (73 events) < 35 mm |
| AMC II | 13 mm ≤ (3 events) ≤ 28 mm | 35 mm ≤ (4 events) ≤ 53 mm |
| AMC III | (1 event) >28 mm | (2 events) > 53 mm |
| Category | Abbr. | Unit | Służew Creek | Zagożdżonka River | ||
|---|---|---|---|---|---|---|
| Range | Average | Range | Average | |||
| No. of events | n | - | - | 53 | - | 42 |
| Rainfall depth | P | mm | 4.3–75.8 | 22.8 | 5.8–145.1 | 25.8 |
| Direct runoff | H | mm | 0.2–16.3 | 3.0 | 0.2–21.8 | 2.9 |
| Runoff coefficient | c = H/P | - | 0.053–0.295 | 0.125 | 0.018–0.577 | 0.106 |
| Initial abstraction | Ia | mm | 0.1–4.8 | 2.2 | 0.4–12.5 | 3.7 |
| Maximum potential catchment retention | S | mm | 23.4–683.3 | 151.3 | 9.1–1342 | 280.4 |
| Initial abstraction ratio | λ = Ia/S | - | 0.002–0.188 | 0.026 | 0.001–0.512 | 0.047 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krajewski, A.; Sikorska-Senoner, A.E.; Hejduk, A.; Hejduk, L. Variability of the Initial Abstraction Ratio in an Urban and an Agroforested Catchment. Water 2020, 12, 415. https://doi.org/10.3390/w12020415
Krajewski A, Sikorska-Senoner AE, Hejduk A, Hejduk L. Variability of the Initial Abstraction Ratio in an Urban and an Agroforested Catchment. Water. 2020; 12(2):415. https://doi.org/10.3390/w12020415
Chicago/Turabian StyleKrajewski, Adam, Anna E. Sikorska-Senoner, Agnieszka Hejduk, and Leszek Hejduk. 2020. "Variability of the Initial Abstraction Ratio in an Urban and an Agroforested Catchment" Water 12, no. 2: 415. https://doi.org/10.3390/w12020415
APA StyleKrajewski, A., Sikorska-Senoner, A. E., Hejduk, A., & Hejduk, L. (2020). Variability of the Initial Abstraction Ratio in an Urban and an Agroforested Catchment. Water, 12(2), 415. https://doi.org/10.3390/w12020415






