Socio-Hydrological Modelling: The Influence of Reservoir Management and Societal Responses on Flood Impacts

Abstract

Over the last few years, several socio-hydrological studies have investigated the risk dynamics generated by the complex interactions between floods and societies, with a focus on either changing reservoir operation rules or raising levees. In this study, we propose a new socio-hydrological model of human–flood interactions that represents both changes in the reservoir management strategies and updating of the levee system. Our model is applied to simulate three prototypes of floodplain management strategies to cope with flood risk: green systems, in which societies resettle outside the flood-prone area; technological systems, in which societies implement structural measures, such as levees; and green-to-techno systems, in which societies shift from green to technological approaches. Floodplain dynamics are explored simulating possible future scenarios in the city of Brisbane, Australia. Results show that flood risk is strongly influenced by changes in flood and drought memory of reservoir operators, while risk-awareness levels shape the urbanisation of floodplains. Furthermore, scenarios of more frequent and higher magnitude events prove to enhance social flood memory in green systems, while technological systems experience much higher losses. Interestingly, green-to-techno systems may also evolve toward green floodplain management systems in response to large losses and technical/economical unfeasibility of larger structural measures.

1. Introduction

Between 1998 and 2017, around 91% of all the recorded natural hazards (more than 7000 events) were climate-related and 43% consisted of floods [1]. Floods and droughts are among the natural hazards that continue to affect the largest number of people: around 2.0 billion and 1.5 billion, respectively, over the past 20 years. Moreover, projections on climate change and global warming suggest that hydrometeorological events are likely to change in frequency and intensity in the near future [2]. Because future extreme flow conditions will continue to negatively affect the socio-economic sphere, it is necessary to better estimate their impact on people and assets and how improving water management strategies for mitigating risks.

Dams and reservoirs are examples of water management measures implemented also for reducing water-related disasters, providing drought alleviation together with flood mitigation. As a consequence, these infrastructures deliberately change streamflow hydrology and significantly affect hydrological regimes [3].

One significant example is the case of the 2011 flood of Brisbane (Australia) occurring after the so-called “Millennium Drought”, a decade-long drought that triggered changes in the management of Queensland’s main dam, Wivenhoe Dam [4]. Built in 1984 in response to severe floods occurred in 1974, Dam’s primary purpose of flood mitigation was changed during the Drought, and operation rules were instead aimed at alleviating drought conditions. Moreover, after the construction of Wivenhoe Dam, the city of Brisbane was perceived to be flood-proofed, encouraging further urbanisation of flood-prone areas [5,6,7]. Population growth and urbanisation combined with high levels of water stored within the reservoir made the 2011 Brisbane flood a cataclysmic event.

Concerning flood risk, since ancient times societies have made numerous efforts to lessen flood impacts, including the introduction of structural measures, such as building levees or dams (e.g., Koutsoyiannis et al. [8]) to protect human settlements and keep floodwaters away [9]. The presence of hydraulic structure can indeed create a false perception of risk that may decrease flood awareness and consequently increase urbanisation in the floodplains. However, when a catastrophic flood event occurs, flood damages due to levee overtopping can be drastically higher due to the increased exposure and vulnerability. The dynamic is known as levee effect [10]. A similar effect known as safe development paradox may emerge when the presence of the levee system reduces the individual measures leading to more severe consequences in case of extreme events [11]. On the contrary, adaptation effect can be observed following a flooding event as learning factors, such as reallocation, can help reducing the negative impact of an extreme event occurring shortly after a similar one [12,13].

Sivapalan et al. [14] claimed the emergence of a new methodology in flood risk assessment, to include the human factor in floodplain dynamics studies. Socio-hydrological researches provided useful insights into the bi-directional relationships between water and societies, focusing on either the two-way links between flood events and societal mitigation strategies, i.e., rising levees [9,15,16,17,18,19], or the reciprocal effects between hydrological extremes and water management policies implemented to control the hydrological variability [20]. In particular, through a socio-hydrological approach, Viglione et al. [9] and Di Baldassarre et al. [15,16] studied the interplay and co-evolution between floods and societies, identifying the risk perception as a key factor in shaping human responses. By exploring the interplay between hydrological extremes and human behaviours, Di Baldassarre et al. [20] found that reservoir management policies are also influenced by reservoir operators’ memory of the last experienced disaster. Indeed, the impacts of a flood event occurring soon after a dry period can even be exacerbated.

Yet, the mutual relations between changing reservoirs management strategies and societal responses to flood risk remain largely unexplored. Within the socio-hydrological context, no models able to clarify the interactions between the water management reality and the social sphere can be found.

The current work aims to understand the influence of reservoir management and societal responses on flood impacts. For this reason, we proposed a new socio-hydrological model that for the first time links a reservoir management model with a human–flood model of flood mitigation.

We considered three prototypes of floodplain management strategies: (i) green systems, in which societies cope with flood risk by resettling outside the flood-prone area; (ii) technological systems, in which societies cope with flood risk via structural measures, such as levees; and (iii) green-to-techno systems, which shift from green to technological approaches.

To gain insights into the interactions between water management strategies, societal responses, and the occurrence of floods, the following research questions were addressed in this paper:

• How do changes in water management policies influence flood risk and societal flood mitigation strategies?
• How do different possible future flow scenarios influence flood impacts?

A synthetic analysis to answer the first research question was initially carried out. The main objective was to assess how reservoir management policies may alter the occurrence and magnitude of extreme flood events and highlight how societal flood mitigation strategies can be affected by changes in the operating rules of reservoirs. Then, by addressing the second research question, we used the model to explore floodplain dynamics in response to future scenarios in the city of Brisbane, Australia. In particular, the reservoir management model was applied to Wivenhoe Dam, Queensland’s main dam.

2. Socio-Hydrological Model

The socio-hydrological model developed in this study couples the reservoir management module proposed by Di Baldassarre et al. [20] with the downstream flood module developed by Di Baldassarre et al. [16] to capture the influence of reservoir management policies on flood management. Indeed, reservoir operations are affected by the flood-to-drought regimes alternation. As a consequence, management of such hydrological variability influences water releases from the reservoir, which in turn can affect downstream flood propagation.

A loop diagram showing the relation and dynamics between the state variables of the socio-hydrological model is reported in Figure 1, which also shows an adapted version of the loop diagram reported in Di Baldassarre et al. [16] concerning the flood module. The loop diagram allows for a conceptual overview of the cascading effects and impacts of reservoir management and societal responses caused by floods. Thin arrows indicate gradual coevolution of variables over time, while thick arrows describe abrupt changes when flooding occurs. The reservoir management and flood modules were linked via the relationship between the outflow (Q_out) and the downstream flooding (F), describing that increasing water releases from the reservoir trigger increased risk of downstream flooding. In particular, water releases depend on the reservoir storage (S) and are influenced by the operators’ memory of flood (M_f) and drought (M_d) events.

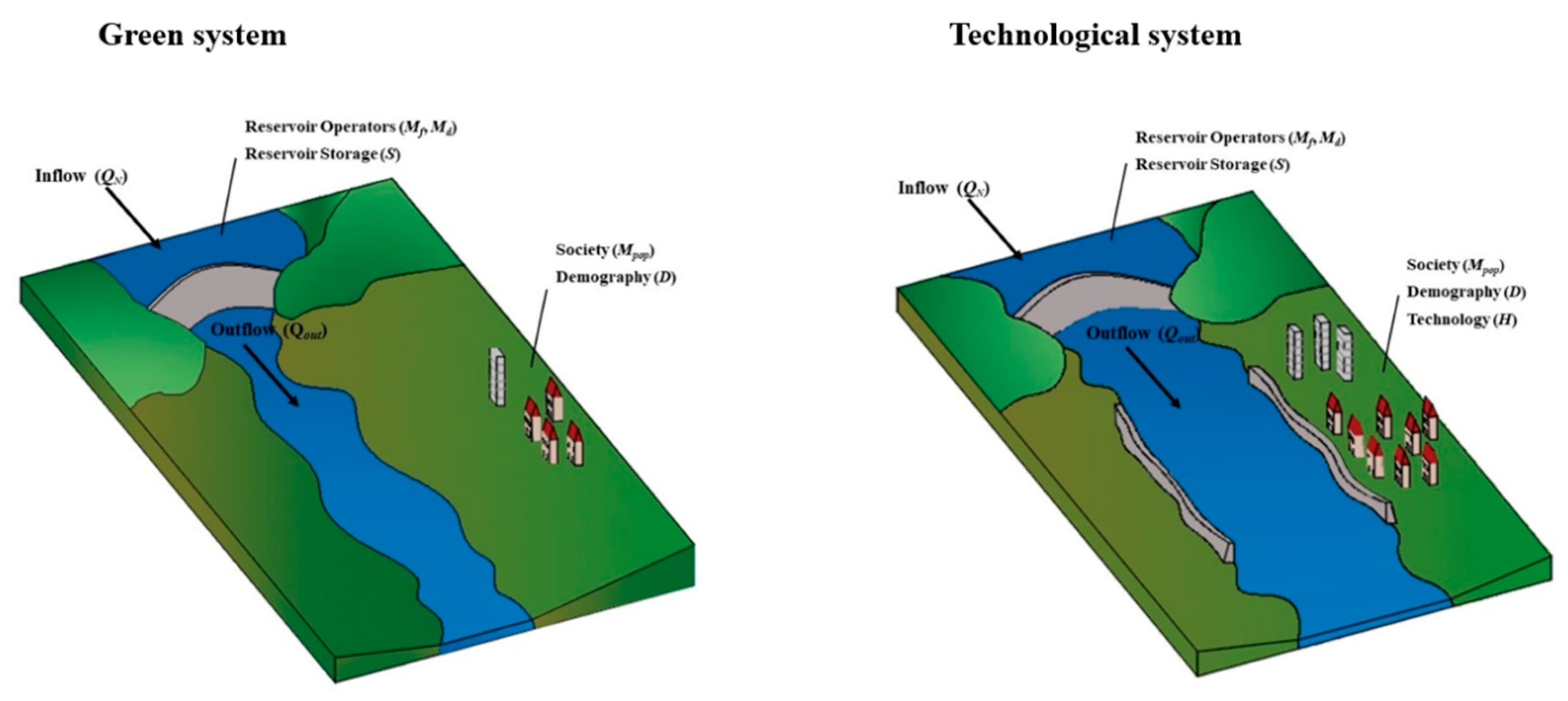
2.1. Hypothetical Systems

Feedback mechanisms and coevolution of water and societies reveal the complex nature of the socio-hydrological system. According to Blair and Buytaert [21], complexity is rooted in the human–water interactions, which involve non-linear dynamics, processes occurring at different spatio-temporal scales, feedbacks, and a certain level of uncertainty.

Within the socio-hydrological framework, the modelling technique adopted to study complex systems is system dynamics, which uses differential equations able to capture interactions among components [16]. In such a framework, the study of the two-way relations between floods and societies pointed out two main governing dynamics between agents (e.g., the adaptation and levee effects), which are affected by the flood-coping strategy adopted by the society. In particular, Di Baldassarre et al. [15] identified two main prototypes of floodplain management strategies to cope with flood risk, that is to say green and technological systems.

Green systems refer to societies characterised by a “living with floods” culture, which implement solely non-structural flood-risk reduction measures aimed at lowering the exposure of people and assets. Among flood risk mitigation practices, non-structural approaches include land-use controls and zoning regulations, regional and integrated territorial planning, as well as relocation away from at-risk areas [2,22]. Examples of green systems can be found in Bangladesh, where, despite the growing population, the proportion of people living in floodplain areas was almost constant over a period of 300 years [23], suggesting that Bangladesh community used to resettle away from watercourses after experiencing flood events.

Technological systems refer to societies characterised by a “fight with floods” culture, relying on structural measures, such as levees, dykes, retention ponds, diversion canals, reservoirs, and dams to reduce the probability of further flooding. For instance, The Netherlands has a long history of levee heightening, being one of the nations in the world with the highest flood protection level [24].

In real-world, floodplain management may also include a combination of structural and non-structural measures. We referred to this intermediate case as a system state, which may evolve toward either a green or a technological strategy according to changing societal inclination. We called this green-to-techno system, describing societies that, starting from a green approach, had shifted to a technological strategy at a certain point in time. Nevertheless, they may still decide to plan a different strategy according to cost-benefit analyses and socio-political actions.

In this work, we account for the management of a reservoir and the implementation of different societal systems (green, technological, green-to-techno) settled downstream (Figure 2). The presence of the reservoir implies the system to be technological if it is designed for flood mitigation purposes. However, we can still define the system as green if we only refer to the management of the downstream floodplain areas or if the reservoir is designed for irrigation, water supply, or hydroelectric purposes. In all of the cases, the hydrological regime and streamflow hydrology can be significantly affected by these infrastructures [3]. For this reason, we proposed a new socio-hydrological model aimed at analysing the influence of reservoir management policies on flood risk and societal flood mitigation strategies. Finally, it is worth mentioning that this is a simplified model, in which the dynamic system is described in a lumped way.

2.2. Reservoir Management Module

The reservoir management module simulates the mutual effects of hydrological extremes and water management policies. In this study, we made use of the models proposed by Di Baldassarre et al. [20] and Ridolfi et al. [25].

In this model, the reservoir storage S is a function of the natural river inflows Q_N and the human-modified outflow Q_out:

$$\frac{dS}{dt}=Q_N-Q_{out}$$

(1)

The human-modified outflow is expressed according to Ridolfi et al. [25]:

$$Q_{out}=k·A·\sqrt{2·g·h}$$

(2)

where h is the water level within the reservoir and k is the storage coefficient. The size of the outflow drain at the bottom A is expressed as a function of the maximum hydraulic head (h_max) and the bankfull discharge of the channel (Q_BF) so that the maximum designed outflow is linked to the maximum capacity of the river downstream [25]:

$$A=\frac{Q_{BF}}{\sqrt{2·g·h_{max}}}$$

(3)

Moreover, we considered the actual area A as including a coefficient of discharge to account for the effects of the contraction of the jet after leaving the bottom drain.

The relationship between reservoir storage (S) and water levels (h) is expressed with a modified formulation of traditional depth-volume power functions [25]:

$$S=\frac{1}{3}·shap{e}^2·h^3$$

(4)

where the shape factor is a parameter characterizing the shape of that particular reservoir.

The storage coefficient k is of crucial importance in our model as it defines the human-modified outflow as a function of flood and drought memories of the reservoir management system. In fact, according to Di Baldassarre et al. [20], the coefficient k is expressed by a weighted average between two different values, $k_f$ and $k_d$, that represent storage coefficients for copying with floods and droughts, respectively:

$$k=\frac{M_f· k_{f }+M_d·k_d}{ M_f+M_d}$$

(5)

Weights in Equation (5) are representative of the flood (M_f) and drought memory (M_d) of the reservoir management system. The laws expressing their exponential decay over time with a decay rate μ are [25]:

$$\frac{d{M}_f}{dt}=M_f+\mu \left(\frac{S^{\beta }}{S_{Max}^{\beta }}-M_f\right)$$

(6)

$$\frac{d{M}_d}{dt}=M_d+\mu \left[{\left(1-\frac{S}{S_{Max}}\right)}^{\beta }-M_d\right]$$

(7)

The parameter β in Equations (6) and (7) is called bias and describes how reservoir management policies are influenced by the difference between flood and drought memories of water managers, i.e., how much reservoir operators are biased by the precedent event [20]. In particular, a value of β = 0 implies the absence of bias between flood and drought memories, thus representing a rational decision-making system in which management operations are implemented trying to find a balance between flood and drought events. In this case, flood and drought memories change at the same rate and tend to the value of 1 over time, while k becomes a constant [20]. Increasing β implies a more dynamic variation of flood and drought memories. The higher β is, the higher the level of bias inducing faster changes of operation rules in order to adjust for one extreme rather than the other. For β = 10 management operations are implemented irrationally, continuously switching towards coping with flood or drought events.

Finally, in order to account for high-flow conditions that occur when the water level within the reservoir is above a certain threshold (h_spill), the outflow release is modelled as the flow through a spillway (Q_spill) according to Equation (8):

$$Q_{spill}=L·\sqrt{2g}·{\left(\left|h-h_{spill}\right|\right)}^{\frac{3}{2}} if h>h_{spill}$$

(8)

where L is the length of the spillway crest.

Spillway releases are necessary to avoid failures of the dam occurring if the water level is above the maximum permissible water level within the reservoir (h_max). In this case, the flow over the crest of the reservoir (Q_fail) can be modelled by Equation (9):

$$Q_{fail}=L·\sqrt{2g}·{\left(\left|h-h_{max}\right|\right)}^{\frac{3}{2}} if h>h_{max}$$

(9)

The length L of the spillway crest in Equations (8) and (9) was considered as including a coefficient of discharge to account for the contraction of the jet downstream of the gate.

Table 1. Time-varying variables of the reservoir management module and initial conditions used in the sensitivity analysis and the Brisbane case study.

			Initial Conditions
	Units	Description	Sensitivity Analysis	Brisbane Case Study
S	(m3)	Storage	0.5·Smax	0
Qout	(m3 s−1)	Human-modified outflow	1	0
Mf	(-)	Flood memory	0.1	0.01
Md	(-)	Drought memory	0.1	0
Shape	(-)	Shape factor	3000	135

and

Table 2. Time-invariant parameters of the reservoir management module and values used in the sensitivity analysis and the Brisbane case study.

			Values
	Units	Description	Sensitivity Analysis	Brisbane Case Study
Smax	(m3)	Maximum reservoir storage	2.8 × 1010	3 × 109
hmax	(m)	Reservoir maximum water level	21	80
hspill	(m)	Spillway crest	19	57
L	(m)	Spillway length	100	60
kf	(-)	Storage coefficient to cope with flood	1	1
kd	(-)	Storage coefficient to cope with drought	0	0
μ	(year−1)	Memory decay rate	0.01 0.15 0.20	0.06
β	(-)	Bias parameter	0 1 10	3

summarise the meaning, units, initial conditions, and values of the model variables and parameters.

2.3. Flooding Module

This module aims at simulating the co-evolution of flood events and societies, describing human feedbacks under the effect of flood risk. First of all, it is crucial to properly convert the output of the reservoir management module as input in the flooding module. In this respect, the daily time series of human-modified outflow from the reservoir was first converted into a water level time series using a power-law rating curve and then resampled into an annual maximum water level (y_max) time series. Finally, the high-water level (W) that exceeds bankfull capacity of the river channel (h_BF) was expressed as the difference between y_max and h_BF.

The model proposed by Di Baldassarre et al. [16], and implemented in this work, captures the main feedback mechanisms between flood events and societies, conceptualizing these dynamics through a Hydrology equation (Equation (10)).

$$F=1-\exp \left(-\frac{W+{\xi }_H{H}_{-}}{{\alpha }_H}\right) if W+{\xi }_H{H}_{-}>H_{-}$$

(10)

that simulates the impact of the human system on the flood system, and a set of differential equations (Equation (11)).

$$\{\begin{array}{cc}\frac{dD}{dt}={\rho }_D\left(1-D\left(1-{\alpha }_D{M}_{pop}\right)\right)-\Delta \left(\Psi \left(t\right)\right)·F{D}_{-}& \mathit{Demography}\mathrm{equation}\\ \frac{dH}{dt}=\Delta \left(\Psi \left(t\right)\right)R-{\kappa }_{T}H & \mathit{Technology}\mathrm{equation}\\ \frac{d{M}_{pop}}{dt}=\Delta \left(\Psi \left(t\right)\right)·F{D}_{-}-{\mu }_S{M}_{pop} & \mathit{Society}\mathrm{equation}\end{array}$$

(11)

that model the two-way feedbacks between the flood system and the human system, that is to say the gradual coevolution over time of population density (D, Demography), levees height (H, Technology), and collective memory of floods (M_pop, Society).

When the annual maximum water levels exceed the bankfull capacity of the channel, flooding occurs, and floodplain population density abruptly decreases due to flood losses (Demography equation). Moreover, the population accumulates flood memory (Society equation) and heightens levees to prevent the risk of further flooding (Technology equation), which then in turn reduce the frequency of flooding and thus reduces memory of flooding (i.e., the aforementioned levee effect). These dynamics are modelled as instantaneous via a non-periodic Dirac comb $\Delta \left(\Psi \left(t\right)\right)$, which is always zero except when $\Psi \left(t\right)$ = 0, in which case it is infinite with integral equal to 1. Variables with the “minus” subscript refer to the time immediately before the flooding.

In the case of technological systems, the amount by which the levee system is raised (R) is assumed to be proportional to the difference between the actual high-water level, that has led to flooding, and the flood protection level:

$$R={\epsilon }_T\left(W+{\xi }_H{H}_{-}-H_{-}\right)$$

(12)

Table 3. Time-varying variables of the flooding module and initial conditions used in the sensitivity analysis and the Brisbane case study.

			Initial Conditions
	Units	Description	Sensitivity Analysis	Brisbane Case Study
F	(-)	Relative flood damage	0	0
D	(-)	Population density	0.1	0.2
H	(m)	Flood protection level	0	0
Mpop	(-)	Societal memory of floods	0	0.2

and

Table 4. Time-invariant parameters of the flooding module, values, and references used in the sensitivity analysis and the Brisbane case study.

			Values
	Units	Description	Sensitivity Analysis	Brisbane Case Study
αH	(m)	Parameter related to relationship between flood water levels to relative damage	10 (Penning-Orwsell et al. [26])
ξH	(-)	Proportion of flood level enhancement due to presence of levees	0.2 (Heine & Pinter [27])
ρD	(year−1)	Maximum relative growth rate	0.03 (Me-Bar & Valdez Jr [28])	0.02 (Brisbane City Council [29])
αD	(-)	Ratio awareness	5 (Scolobig et al. [30])
εT	(-)	Safety factor for levee heightening	1.1 (Da Deppo et al. [31])
κT	(year−1)	Protection level decay rate	2 × 10 −5 (Di Baldassarre et al. [15,32])
μS	(year−1)	Memory loss rate	0.06 (Di Baldassarre et al. [15,32])	0.12 (Di Baldassarre et al. [16])

illustrate the meaning, units, initial conditions, values, and references of the variables and parameters of the model used in this study.

2.4. Assumptions

In this study, we considered three prototypes of floodplain management systems, i.e., green, green-to-techno, and technological systems. The main features of these systems were described in Section 2.1, highlighting different flood-risk reduction measures, which qualify a system as green or technological, or even green-to-techno if implements a combination of those strategies. However, it is worth noting that in this model, we only considered levees building as a structural measure implemented by the technological system, and communities’ resettlement outside the flood-prone area as a non-structural measure adopted by the green system. The combination of relocating and levees building allows us to qualify a system as green-to-techno.

The proposed model made use of a parameter (δ_D), called green-to-techno shift threshold, to identify green, green-to-techno, and technological systems. In detail, δ_D is related to the population density (D) size of the human settlement. If D exceeds δ_D the floodplain is significantly populated, and the human settlement needs to be protected by levees. Hence, levees are built only if D > δ_D. Also, both D and δ_D range from 0 to 1, which means that if δ_D = 1 then D never exceeds δ_D and the community never builds structural defences. For this reason, a green system is identified by a high value of δ_D, while a technological system by a low value of the parameter. An intermediate value of δ_D identifies a green-to-techno system.

Green, green-to-techno, and technological systems are characterized by variations of population density D, which increases or decreases according to the societal memory of floods (see Equations (11)). Hence, according to the lumped nature of the proposed model, it does not account for urban development plans, neither include where urbanisation occurs or its configuration in space.

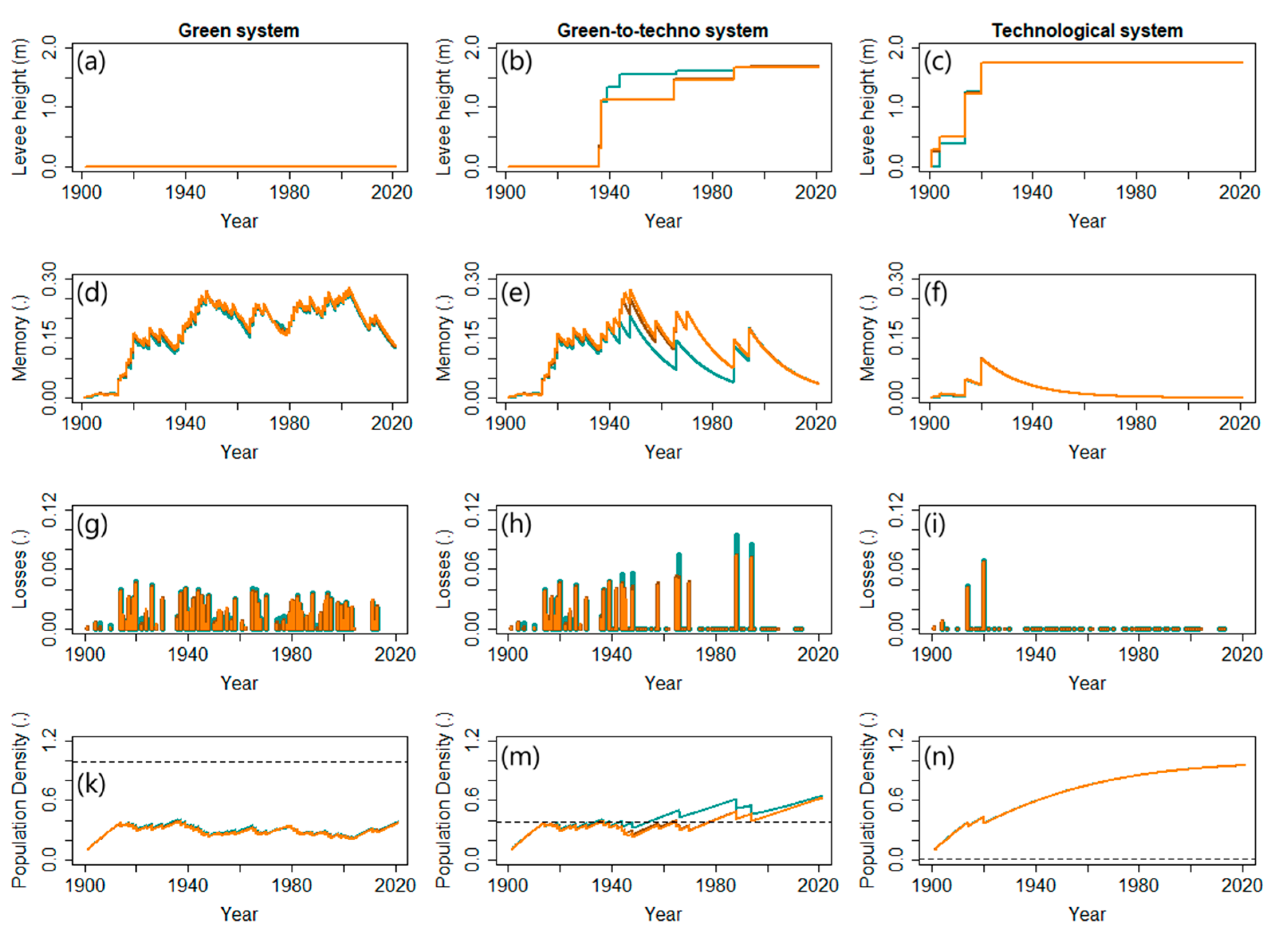
3. Sensitivity Analysis

3.1. Experimental Setup

A sensitivity analysis was carried out for exploring the impact of different reservoir management policies on the performances of the proposed socio-hydrological model. Two model parameters affect changes in reservoir management policies: (i) the level of bias between floods and droughts, quantified by the β parameter, and (ii) the memory decay rate, quantified by the μ parameter. In detail, three values of β were considered: β = 0 (rational management of the reservoir), β = 1 (more dynamic management of the reservoir); and β = 10 (completely irrational management of the reservoir). Similarly, three values of μ were considered: μ = 0.1 year⁻¹, μ = 0.15 year⁻¹, and μ = 0.20 year⁻¹.

Furthermore, we investigated how changes in water management strategies can alter the floodplain management of (i) green systems, identified by δ_D = 0.99; (ii) green-to-techno systems, identified by δ_D = 0.38; and (iii) technological systems, identified by δ_D = 0.01.

To assess whether flood-coping strategies of communities living downstream are influenced by changing reservoir management strategies, we independently analysed the effects of the parameters β and μ in combination with different values of the δ_D parameter.

The sensitivity analysis was performed simulating the management of a fictional reservoir and assuming a community that starts settling and developing in a flood-prone area below the reservoir (as represented in Figure 2). The time series of natural river inflow (Q_N) of the Rhine River between 1901 and 2017 were used as input to the reservoir model. In order to link this module with the flooding module, it was necessary to transform the human-modified outflow (Q_out) from the reservoir into flood peaks (W). To this end, a rating curve corresponding to a Manning equation for a wide rectangular river section, with width of 250 m, average depth of 11 m, longitudinal slope of 0.02%, and Manning coefficient of 0.04 s·m^−1/3, was used:

$$Q_{out}=\frac{1}{n}·B·y^{\frac{5}{3}}·s^{0.5}$$

(13)

3.2. Results

First, the results obtained changing only the bias parameter β (with μ = 0.1 year⁻¹) are described. From Figure 3 it can be observed that in the case of the rational decision-making system (β = 0), the storage coefficient is constant over time and equal to 0.5. This is due to the flood and drought memories varying at the same rate with a constant value equal to 1 (see Figure S1 in the supplementary materials). In this case, the willingness to best control the hydrological variability results in management strategies allowing the reservoir storage to fluctuate between the minimum value, to better cope with floods, and the maximum permissible value, to deal with droughts (Figure 3b). Therefore, water releases from the reservoir are more controlled and, as a consequence, the maximum water levels y_max are always below the bankfull capacity of the channel h_BF (Figure 4a).

The higher is the level of bias the more reservoir storage fluctuates in smaller ranges (Figure 3d,f), meaning that a certain amount of water is always kept within the reservoir. It follows that water releases are less controlled and high-flow conditions are more frequent, as well as higher in terms of magnitude, compared to the case of lower values of β (Figure 4b,c). This is especially due to lower levels of risk-awareness of both flood and drought events (see Figure S1) that results in higher values of the storage coefficient, which more rapidly changes between the extremes k_f and k_d (Figure 3c,e). In conclusion, lower values of β lead to a small number of flood events downstream. In particular, water releases never exceed the bankfull depth for β = 0, while the irrational management (β = 10) leads to more frequent flooding. Hence, high water levels (W) are recorded only in the case of β = 1 (3 flood events) and β = 10 (63 flood events) (Figure S2).

Figure 5 shows how different reservoir management strategies (model parameter β) influence different prototypes of floodplain management (green, green-to-techno, and technological systems) identified with different values of the δ_D parameter (δ_D = 0.99, δ_D = 0.38 and δ_D = 0.01). Results are expressed in terms of implementation of flood protection structures (i.e., levees heightening), collective memory, flood losses, and floodplain population density. Regarding the green system (δ_D = 0.99), levees are never built for both β = 1 and β = 10 (Figure 5a). It is interesting to observe the different evolution of collective memory and population density (Figure 5d,k), as for β = 1 the low flood frequency leads to a rapid loss of memory and, at the same time, to a significant urbanisation of the floodplain, while the high flood frequency that occurs for β = 10 enhances social flood memory and keeps the population density almost constant, at the cost of more flood losses (Figure 5k).

Regarding the green-to-techno system (δ_D = 0.38), the shift from non-structural measures to structural ones is particularly clear in the case of β = 10. Indeed, the frequent occurrence of flooding between 1904 and 1930 contributes to a high level of flood-risk awareness (Figure 5e) and leads the societal system to be initially a green type. However, the lack of extreme flood events between 1930 and 1936 leads the society to lose flood memory and to more intensively urbanise the floodplain (Figure 5m). As a consequence, when the following flooding occurs, the population density has reached such an extent (D > δ_D) that it needs to be protected by levees and the shift to technological approaches occurs. Indeed, the levee system is built in response to the 1936 flood (Figure 5b). Moreover, for β = 10, the levee effect can be repeatedly observed: the presence of levees leads to a misleading sense of security as flood peaks are limited by such structures and no flood losses are recorded (Figure 5h). The rapid decrease of flood memory levels encourages intensive urbanisation of floodplain areas, at the cost of catastrophic consequences when exceptional flood events exceeding the flood protection level occur.

The technological system (δ_D = 0.01) is not significantly affected by changes in reservoir management as levees are built when the first flood occurs for both β = 1 and β = 10 (Figure 5c). The dynamics of flood memory, flood losses, and population density are similar (Figure 5f,i,n).

Concerning the sensitivity of the reservoir model to the memory decay rate μ (with β = 10), the results showed that the model is slightly sensitive to this model parameter. Indeed, the storage coefficient and reservoir storage do not significantly change by changing μ (see Figure S3). Similar results are achieved with high-water levels W (Figure 6).

As depicted in Figure 7, flood-coping strategies of green, green-to-techno, and technological systems are not significantly influenced by changing reservoir operators’ memory decay rate. In particular, the green system (δ_D = 0.99) never shifts to a technological system due to the recurrence of flooding that contributes to high flood memory levels and low population density values (Figure 7d,k). Because no flood protection structures are built (Figure 7a), the community experiences frequent and high flood losses (Figure 7g) and never urbanises the floodplain to such an extent that requires the heightening of levees (Figure 7k).

The main effect of changing values of μ on floodplain dynamics of green-to-techno (δ_D = 0.38) and technological (δ_D = 0.01) systems is the levee height (Figure 7b,c) because of high-water levels of different magnitude. As a result, flood memory, flood losses and population density dynamics in green-to-techno (Figure 7e,h,m) and technological systems (Figure 7f,i,n) are not significantly affected by changing the μ parameter.

In conclusion, the results of the sensitivity analysis showed that reservoir management is significantly influenced by the level of bias between drought and flood memories, while is less sensitive to the memory loss rate. This has important consequences on the downstream flood propagation and to the implementation of different flood-coping management strategies.

4. Model Application

4.1. Case Study

To show an application of the proposed cascade model to a real case study, we implemented the socio-hydrological model to the Brisbane River region, Australia. In particular, we simulated operations of Wivenhoe Dam, Queensland’s main dam, to analyse the implications of future hydrological regime scenarios on the Dam management and, consequently, the effects on Brisbane community’s flood mitigation strategies. In this case, as Wivenhoe Dam was designed to provide flood mitigation, the system can be considered technological. However, if we refer to the management of the downstream floodplain areas, we can still define the system as a green type. It is worth mentioning that this model does not attempt to accurately reproduce Dam operations, neither it accounts for evaporation processes, water supply mechanisms or releases from Somerset Dam into Wivenhoe Dam.

Brisbane is the capital city and the most populated urban area of the state of Queensland in Australia (Figure 8). The estimated population of 2.4 million inhabitants grows at 2.1% a year [29]. Established on a floodplain, Brisbane has experienced serious flood events since 1900 [33]. The largest and most impacting flood occurred in January 1974, after which the decision of protecting the city with a structural defence was made. Flood regimes of eastern Australia were investigated by several studies (e.g., Ref. [34,35]), which highlighted the influence of multidecadal climate phenomena on flood risk. Flood risk downstream from the Dam may result from the combination of different rainfall patterns and variation in the amount of water stored in the Dam [33].

On the one hand, the construction of Wivenhoe Dam triggered the belief that Brisbane was flood-proof, leading to rapid urbanisation of flood-prone areas [5,6,7]. On the other hand, the occurrence of the Millennium Drought prioritized droughts management and led to changes in reservoir operation rules.

Located about 80 km upstream from Brisbane, Wivenhoe Dam is the South East Queensland’s largest water storage. It was completed in 1984 and it now provides both water supply and flood mitigation. The Dam also houses a hydro-electric power station and serves as a recreation destination.

The Water Supply Compartment of Wivenhoe Dam can store around 1.2 km³ of drinking water when the Dam is operated at its full supply level. Under these circumstances, it is designed to hold an additional 2 km³ in the Flood Storage Compartment. The full supply level is currently 67 m and the maximum flood storage level is 80 m, above which the Dam is overtopped. Five radial gates, each with a length of 12 m, and an auxiliary spillway are used to release water during flood events. Gate operations start when the Lake level reaches 57 m and the spillways are fully opened before it reaches 76.78 m [36].

Flow data used in this study were gathered from the Water Data Online website of the Australian Government Bureau of Meteorology (http://www.bom.gov.au/waterdata). Three gauging stations were selected for implementing the aforementioned model according to data availability and location with respect to Wivenhoe Dam (see Figure 8): (i) “Brisbane River at Gregors Creek” (station no. 143009A) was considered as inflow data into the Dam; (ii) “Brisbane River at Savages Crossing” station (station no. 143001C) was selected for both measuring the agreement between model outputs and observed data for the period 2010–2014 and for a qualitative comparison of the outputs for the period of simulation 1984–2014 (hereafter referred to as “reference period”); (iii) “Brisbane River at Wivenhoe Tailwater” (station no. 143035A), located immediately downstream from the Dam, was used after the calibration process to further evaluate the fitting between model outputs and recorded River discharge from May 1986 to June 2010.

4.2. Model Calibration and Setup

Calibration of the reservoir management module was performed to estimate the optimal values of the bias parameter (β) and memory decay rate (μ) that allowed us to schematize the management of the Wivenhoe Dam during the reference period and to apply the model to future scenarios. No calibration was performed for the flooding module.

Model calibration was performed using observed daily maxima of river flow from the station “Brisbane River at Gregors Creek” upstream the Wivenhoe Dam. In particular, flow data between 2010 and 2014, during which high-flow conditions were recorded, were used for training purposes, while the 1984–2014 inflow time series was used as testing dataset.

A random search approach was used as model calibration method to estimate two objective functions for a range of the parameters β and μ between 0 and 10 and 0.06 and 0.20 year⁻¹, respectively, and assess their optimal values. The two objective functions are the root mean square error (RMSE):

$$RMSE=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^n{\left(Q_{sim,i}-Q_{N,i}\right)}^2}{n}}$$

(14)

and the Bias coefficient:

$$Bias=\frac{{{\displaystyle \sum }}_{i=1}^n{Q}_{sim,i}}{{{\displaystyle \sum }}_{i=1}^n{Q}_{N,i}}$$

(15)

where n is the number of observations, Q_sim is the simulated flow value, Q_N is the observed flow value, and i represents the time step. A perfect fit to the observed data is described by a value of RMSE and Bias coefficient equal to 0 and 1, respectively. The result of the calibration procedure reported optimal values of β = 3 and μ = 0.06 year⁻¹, corresponding to a value of RMSE and Bias coefficient of 6.8 and 0.91, respectively.

The model was then evaluated considering inflow data for the reference period 1984–2014. A comparison between simulated results and observed data of River discharges recorded at Savages Crossing is shown in Figure 9. Overall, a good match of the peak flow values was achieved. However, it is important to note that flood levels in the Lower Brisbane River result from the concurrent effects of Dam releases and downstream tributary inflows. Consequently, water levels recorded at Savages Crossing station, which is located around 19 km downstream from the Dam, are affected by these downstream flows. For these reasons, data from the “Brisbane River at Wivenhoe Tailwater” station, located immediately downstream from the Dam, were used to qualitatively compare the fitting between model outputs and recorded River discharge and which are available from May 1986 to June 2010. Also, in this case, similar flow peak values between observed data and the calibrated model were obtained (Figure S4).

Following the calibration of the reservoir management module, it was necessary to link this module with the flooding one transforming the human-modified outflow (Q_out) from the reservoir into flood peaks (W) as previously described.

A power-law rating curve with parameter values obtained from the flow and water levels values recorded at the Savages Crossing station during the reference period 1984–2014 was used. In particular, the stage-discharge relation was developed based on values of Q > 500 m³/s (see Figure S5 in the supplementary materials).

$$Q_{out}=9.93\times y^{2.14}$$

(16)

Since flood peaks are expressed as the water levels exceeding the bankfull capacity of the river channel (h_BF), it was necessary to define h_BF. Kemp et al. [37] reported that with the current hydrological conditions of the Brisbane River the bankfull depth is 18 m, which corresponds to bankfull flows of 5500 m³/s.

4.3. Future Flow Scenarios

We simulated Dam operations under four different future hydrological regime scenarios over 124 years. It is worth noting that scenarios were generated based on the available historical flow data, and not on realistic future rainfall projections or climate scenarios.

Each scenario of high-water levels W that may threaten the society results from the regulation of water releases from Wivenhoe Dam operated with values of bias (β) and memory decay rate (μ) derived from the calibration process. This means that, by managing Wivenhoe Dam in the same manner as it was operated in the 31-year reference period 1984–2014, the aim of simulating different future flow scenarios was the evaluation of societal responses to flooding with respect to changes in (i) the magnitude of floods and (ii) duration of droughts. Hence, four scenarios of hydrological extremes were developed, as reported in

Table 5. Summary of future hydrological scenarios considered in this study.

		FLOODS Magnitude
		“As today”	Exacerbated
DROUGHTS Duration	“As today”	BASELINE SCENARIO	BIGGER FLOODS SCENARIO
	Reduced	SHORTER DROUGHTS SCENARIO	BIGGER FLOODS & SHORTER DROUGHTS SCENARIO

:

• Scenario 1—Baseline: Hydrological extremes “as today”. Floods and droughts occur with the same magnitude and frequency as in the reference period. This scenario was generated by repeating the original inflow data every 31 years.
• Scenario 2—Bigger Floods: Drought events “as today”, whereas flood peaks are exacerbated. A threshold to consider a flood event was set to 2000 m³/s. Inflow data exceeding the threshold in each time slice were multiplied by a factor equal to 1.2. This scenario can be representative of extreme rainfall events that become more extreme.
• Scenario 3—Shorter Droughts: Floods “as today”, whereas droughts duration is shorter. It was generated by adding artificial flood levels interrupting the Millennium Drought. This scenario can be representative of extreme rainfall events that become more frequent, or in other words, a scenario characterised by decreasing drought duration.
• Scenario 4—Bigger Floods & Shorter Droughts: Flood events increase in magnitude and droughts duration is shorter. This scenario is the combination of scenarios 1 and 2, in which all the inflow data above 2000 m³/s were amplified by a factor of 1.2. It can be considered as a scenario in which extreme rainfall events become more extreme in magnitude and frequency.

Figure 10 shows the synthetic future hydrological extremes scenarios used as input in the reservoir management module of our socio-hydrological model. These scenarios were developed by generating synthetic flow time series starting from the recorded data during the reference period and extending up to 124 years. This means that the first 31 years of inflow data are the same in all the scenarios.

4.4. Results

The high-water levels scenarios (W) resulting from the reservoir management module of Wivenhoe Dam under four different future flow conditions but the same level of bias (β) and memory decay rate (μ), are shown in Figure 11. In the baseline scenario (scenario 1), four flood events occur downstream Wivenhoe Dam, which correspond to recurring 2011 flood events each repeated every 31 years in the future. Regarding scenario 2, it should be noted that an increase in flow peaks magnitude upstream is reflected in a more frequent downstream flooding occurrence (six events). Similar results were obtained in scenario 4, where more frequent and extreme flood events lead to greater and more frequent downstream flooding (seven events). With regards to the shorter drought scenario (scenario 3), one can note that flooding occurrence is the same as in the baseline scenario (scenario 1). This means that, if the Dam is operated with that level of bias, an increased frequency of flooding upstream (reduced duration of drought) does not lead to increased downstream flooding. Indeed, not only the number of flood events is the same, but also their magnitude is similar.

We propose here a comparison between the baseline scenario (scenario 1) and the bigger floods and shorter droughts scenarios (scenario 4). Hence, the societal responses to flood risk for scenarios 1 and 4, considering the green, green-to-techno, and technological floodplain management systems, are analysed in the following. The dynamic evolution of these systems in terms of levees heightening, flood memory, flood losses, and population density is depicted in Figure 12. The lighter colour indicates scenario 1 while darker colour indicates scenario 4.

In general, higher flood risk contributes to the adaptation effect in green systems. From the comparison of scenarios 1 and 4 it emerges that the more extreme flood events are experienced, the more collective flood memory is refreshed and persists through time. In particular, increasing magnitude and frequency of floods (scenario 4) enhances social memory (Figure 12d), thus encouraging a significant reduction in the floodplain population density (Figure 12k) and reducing flood losses (Figure 12g).

Conversely, the Brisbane community starts building flood protection structures (Figure 12c) at the cost of more damage (Figure 12i) if a technological flood-coping strategy is assumed (scenario 4). The levee effect can be observed between the fourth and the last event (see Figure 12i). In this case, inundations and losses during flood events of minor magnitude are prevented by the presence of levees, leading to a rapid loss of memory (Figure 12f). Encouraged by the misleading sense of security given by these structures, the community urbanises the floodplain unaware of the risks (Figure 12n, scenario 4). However, when exceptional flooding occurs, as it happens during the fourth and the last events, levees are overtopped and the community experiences significant flood losses (Figure 12i).

The behaviours of green, green-to-techno, and technological systems in scenario 1 are similar to each other. This is mainly due to the result of inundations occurring once every 31 years and no minor flooding is experienced in between, which instead can encourage adaptation behaviours and contribute to the flood-risk awareness of the community.

Interestingly, the adaptation effect can also be observed in the green-to-techno system in scenario 4, starting from the fifth event. Analysing Figure 12b,e,h,m, one can observe that the shift from non-structural measures to structural ones occurs in response to the second event for both scenario 1 and 4. However, the fact that flood events become more frequent and intense leads to the decision not to continue heightening the levees. For this reason, the following events contribute to refresh collective memory and encourage society to adapt by reducing the population density in the floodplain area. Hence, the green-to-techno system experiences decreasing flood losses for increasing flood events.

5. Discussion and Conclusions

Sensitivity analysis was performed to assess the effects of different reservoir management strategies on flood risk and floodplain management systems. By analysing the sensitivity of the proposed socio-hydrological model against the level of bias between flood and drought memories β and the memory decay rate μ, results showed that the model is highly sensitive to the β parameter, while it is not significantly influenced by the μ parameter. Changes in the bias level (i.e., variations of the β parameter) strongly affect the dynamic variations of reservoir flow releases. In particular, increasing decisional bias levels induce fast changes in both flood and drought memories, leading to more difficult management of hydrological variability, while rational management of the reservoir (β = 0) allows for water releases to be more controlled. These mechanisms considerably influence the downstream flood propagation and have potential consequences on the implementation of different flood-risk mitigation strategies. To this end, we analysed how societal flood-coping strategies are affected by changes in water management policies. The simulations conducted in this paper demonstrated that societies are less prone to flood events in the case of decreasing β. This process has a twofold effect. Whilst flood risk decreases because of more controlled water releases from the reservoir, the human-induced lack of extreme flood events controls the development of human settlements, enabling intense urbanisation of flood-prone areas and reducing the incentive for green behaviours.

Model application to the Brisbane River region was implemented to analyse the influence of different flow scenarios on reservoir management strategies, as well as to assess societal responses to increased downstream flooding. By simulating the management of Wivenhoe Dam, model results suggested that reservoir management policies can mitigate the risk of downstream flooding in the case of scenarios of more frequent upstream flood events. Conversely, downstream flooding increases in the case of scenarios of more frequent and higher magnitude upstream flood events, in which case the impacts differ depending on whether the floodplain management system is a green or a technological type. Flood losses decrease in green systems, while they increase in technological systems as a consequence of different levels of flood memory. This process proves that the societal memory of people living in flood-prone areas is shaped by the occurrence and frequency of hydrological extremes and, in turn, it shapes flood risk. This is consistent with what was previously found in several studies [9,15,16,17]. Moreover, results from scenarios of increased flood frequency and magnitude proved that green-to-techno systems can plan a different flood-risk reduction strategy and evolve toward a green approach. A fully reversible shift back to green floodplain management would, instead, be possible only if a river floodplains restoration project is set up and economically sustained and the technological component removed.

This study represents the first and initial attempt to investigate the influence of reservoir management policies and societal flood-risk mitigation strategies on the impacts of flooding. In particular, we took account for flood-risk reduction measures of green and technological systems and also highlighted the behaviour of green-to-techno systems, as the shift from green to technological approaches is a common urbanisation process. The sensitivity analysis aimed at addressing the first fundamental research question, that is to say to study the influence of changing reservoir management policies on flood risk and societal mitigation strategies. Findings from this analysis proved that the bias level between flood and drought memories significantly influences reservoir operations and the downstream flood risk. Moreover, dynamics of flood-coping strategies of communities settled downstream of reservoirs are also strongly influenced by variations of the bias level. The Brisbane case study addressed the second research question by comparing results from four different hydrological extremes scenarios. In particular, model results showed that the downstream flood risk significantly increases in the case of more frequent and intense upstream flood events. This scenario has the potential to magnify the levee effect in technological systems and to enhance flood risk awareness in green systems and, interestingly, also in green-to-techno systems, in which adaptation behaviours were observed.

This study has sought to provide better insights into the coupled human–flood system by conducting a first evaluation of the interactions between hydrological extremes, reservoir management policies, and societal flood-coping strategies. In our opinion, the proposed model is able to reproduce the dynamics observed within the human–flood interactions, despite some assumptions. In particular, our modelling framework took account only for some of the possible riverine management strategies, i.e., levees heightening and relocation. However, there are other structural and non-structural mitigation practices, such as channelization, dykes, wetland restoration, etc., that should be considered in future studies. Moreover, according to the lumped nature of the model, variations in space of the urbanisation process are not described. Finally, it should be noted that this work focussed solely on the influence of reservoir operators’ memory on societies. However, two-way relations might also exist. The model also neglected aspects related to the simulation of reservoir operations, such as evaporation processes and the water supply–demand cycle, which instead can affect reservoir storage capacity and population dynamics [38]. Future works should also consider these aspects and look for feedback mechanisms between societies and reservoir operators.

This work can help decision-makers involved in the development of policies and measures for the mitigation of hydrological extremes, such as reservoir and floodplain management, as it gives insights about the potential effects of reservoir management policies on both flood and drought risks, under various flood-coping strategies.