A Survey of Pressure Control Approaches in Water Supply Systems
Abstract
:1. Introduction
Existing Reviews and This Review
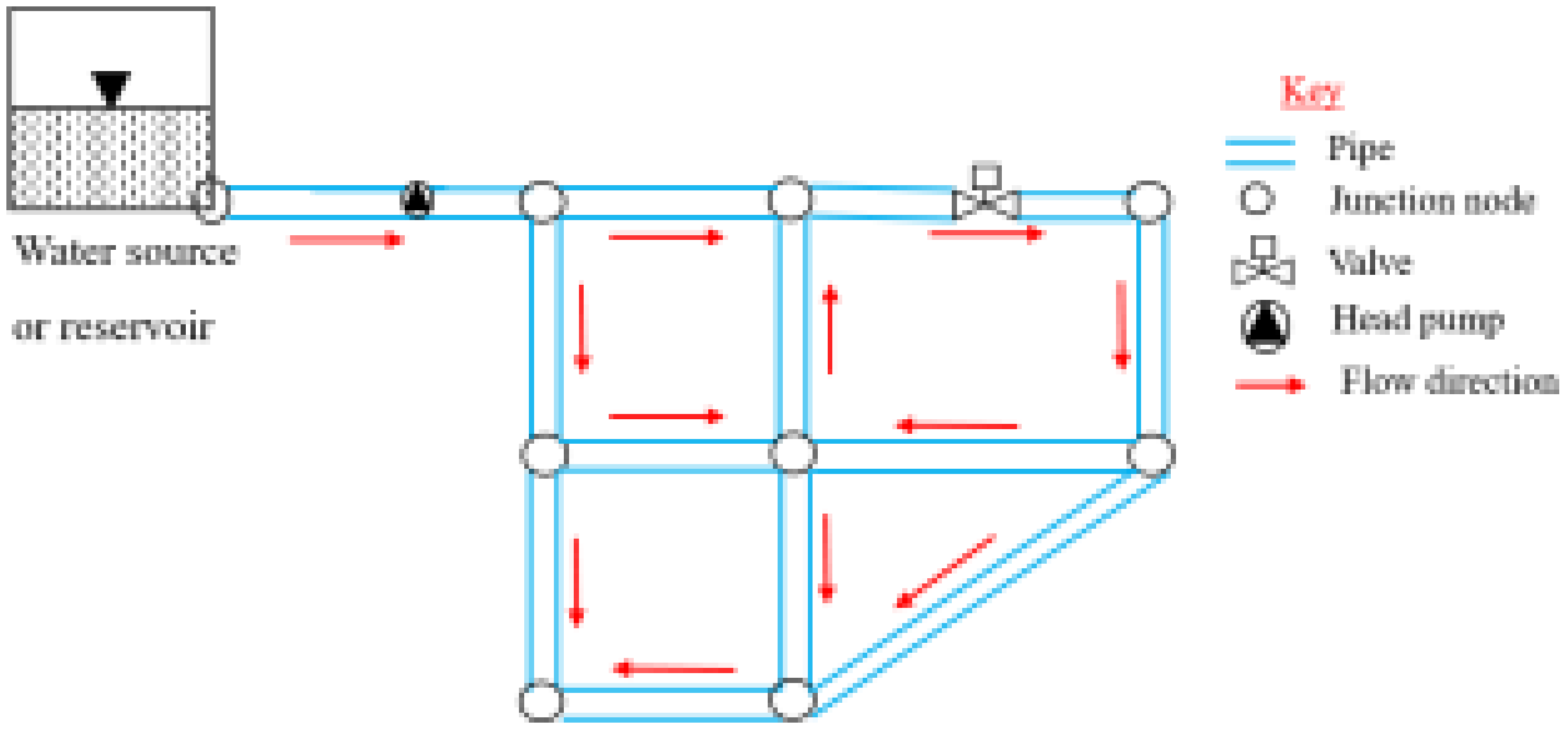
2. Water Distribution and Its Basic Equations
3. Pressure Control
3.1. Pressure Control Devices
3.2. Placement of Pressure Control Devices
3.2.1. Enumerative Method
3.2.2. Pressure Reference Method
3.2.3. Calculus-Based/Optimization Methods
3.3. Pressure Control Techniques
- Fixed outlet pressure control
- Time-modulated pressure control
- Flow-modulated pressure control
- Closed-loop pressure control
- Optimal pressure control
| Algorithm 1: Expert System Control Rule |
 |
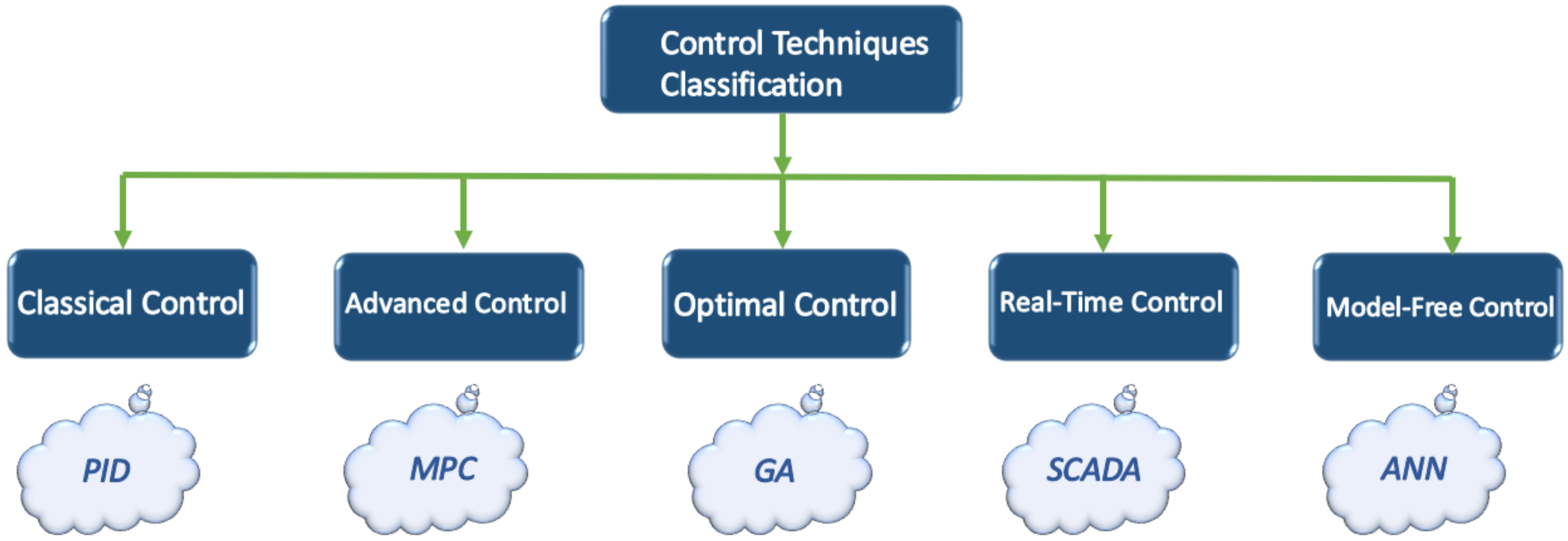
3.3.1. Classical Control Strategy
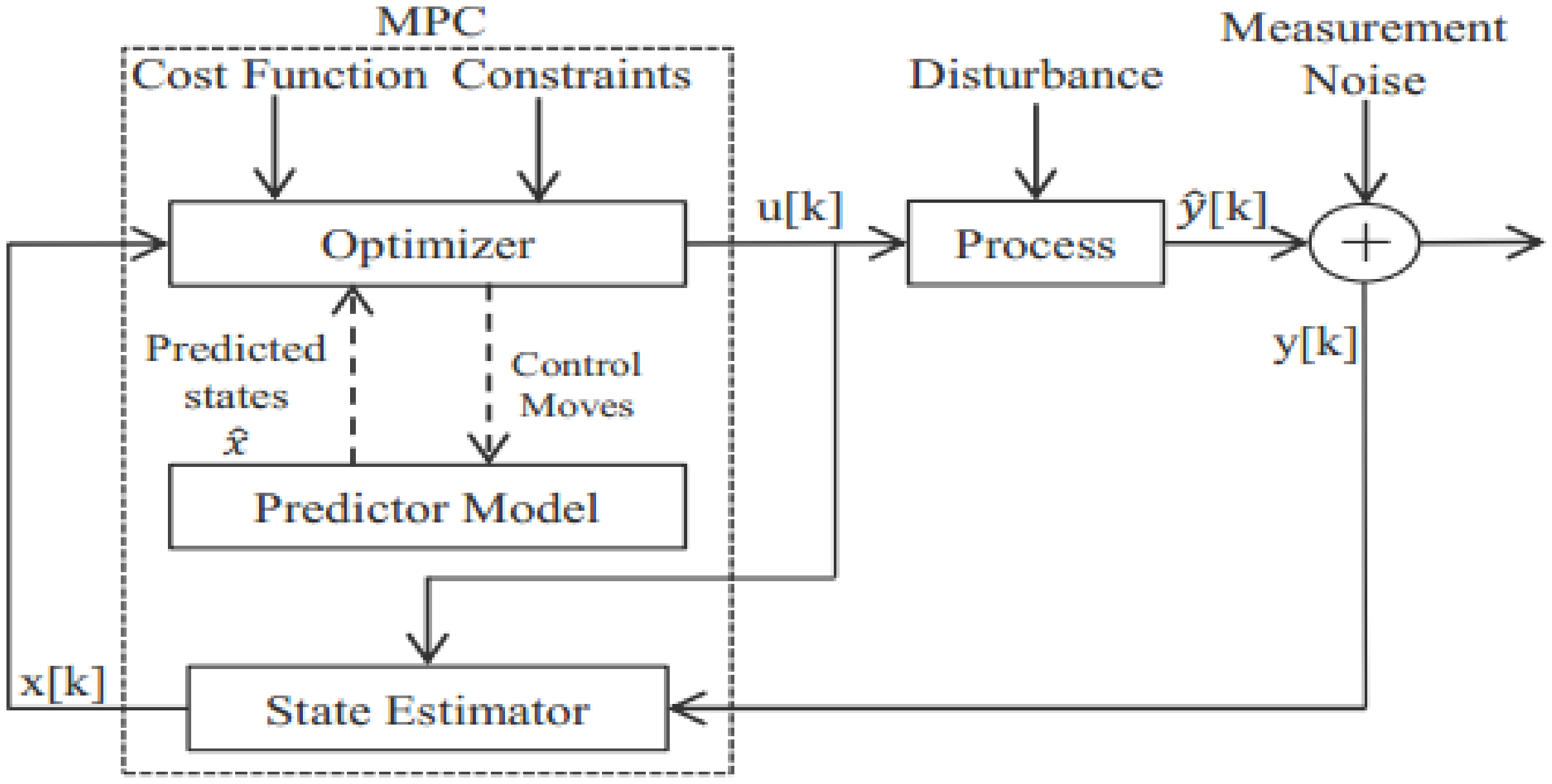
3.3.2. Advanced Control Strategies
3.3.3. Optimal Control
3.3.4. Real-Time Control
3.3.5. Model-Free Control
3.3.6. Summary and Comparison of Research Outputs
4. Discussion and Suggestion for Future Works
- Incorporating the demand uncertainties into the control problem to evaluate its robustness
- Deployment of the emulators in pressure controlDespite the existence of the literature [22,75,76] in this aspect, it can be noted that the niche is yet to be harmonized. This stems from [22] developing the emulator for the optimization procedure, whereas [75,76] developed the emulator for the hydraulic model. It is worth noting that all these works deployed back-propagation neural nets to develop the emulators. The strength of this method lies in the computations required to evaluate the model once it istrained. However, thousands of measurements have to be available for training of the model to increase its accuracy. The advances in the machine learning field offer some opportunities for improvement of MLPs in terms of their training and accuracy. The learning rate of these techniques could be investigated as related to WDN applications. Deep neural networks (DNNs) are paradigms that could be deployed and their suitability investigated in WDNs applications.
- Reinforcement learning (RL)-based controllersOwing to the advance mentioned in Item 2, RL-based controllers could be explored for pressure control in WDNs. The strength of this scheme could be based on the fact that prior knowledge of the system is not required to develop the controller. The RL-based controller learns from its experience as it interacts with the environment. This could be beneficial as the accuracy of the controller would not be lost as a result of estimating the parameters of the model.
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Bello, O.; Abu-Mahfouz, A.M.; Hamam, Y.; Page, P.R.; Adedeji, K.B.; Piller, O. Solving management problems in water distribution networks: A survey of approaches and mathematical models. Water 2019, 11, 562. [Google Scholar] [CrossRef] [Green Version]
- Adedoja, O.S.; Hamam, Y.; Khalaf, B.; Sadiku, R. Towards development of an optimization model to identify contamination source in a water distribution network. Water 2018, 10, 579. [Google Scholar] [CrossRef] [Green Version]
- Page, P.R.; Abu-Mahfouz, A.M.; Mothetha, M.L. Pressure Management of Water Distribution Systems via the Remote Real-Time Control of Variable Speed Pumps. J. Water Resour. Plan. Manag. 2017, 143, 04017045. [Google Scholar] [CrossRef] [Green Version]
- Page, P.R.; Abu-Mahfouz, A.M.; Yoyo, S. Real-time Adjustment of Pressure to Demand in Water Distribution Systems: Parameter-less P-controller Algorithm. Procedia Eng. 2016, 154, 391–397. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S.M. Monitoring and Control of Water Distribution Networks. Ph.D. Thesis, Indian Institute of Technology Madras, Chennai, India, 2008. [Google Scholar]
- Dai, P.D. Efficient Optimization of Pressure Regulation in Water Distribution Systems Using a New-Relaxed Pressure Reducing Valve Model. Vietnam J. Sci. Technol. 2018, 56, 503–514. [Google Scholar]
- Adedeji, K.B.; Hamam, Y.; Abe, B.T.; Abu-Mahfouz, A.M. Pressure management strategies for water loss reduction in large-scale water piping networks: A review. In Advances in Hydroinformatics; Springer: Singapore, 2018; pp. 465–480. [Google Scholar]
- Puust, R.; Kapelan, Z.; Savic, D.; Koppel, T. A review of methods for leakage management in pipe networks. Urban Water J. 2010, 7, 25–45. [Google Scholar] [CrossRef]
- De Corte, A.; Sörensen, K. Optimization of gravity-fed water distribution network design: A critical review. Eur. J. Oper. Res. 2013, 228, 1–10. [Google Scholar] [CrossRef]
- Xu, M.; Yang, J.; Hughes, D.M.; Lechevallier, M.W. Survey of pressure management in water distribution systems. J. Am. Water Work. Assoc. 2014, 106, E518–E524. [Google Scholar] [CrossRef]
- Kanakoudis, V.; Tsitsifli, S. Potable water security assessment—A review on monitoring, modeling and optimization techniques, applied to water distribution networks. Desalin. Water Treat 2017, 99, 18–26. [Google Scholar] [CrossRef]
- Creaco, E.; Campisano, A.; Fontana, N.; Marini, G.; Page, P.; Walski, T. Real time control of water distribution networks: A state-of-the-art review. Water Res. 2019, 161, 517–530. [Google Scholar] [CrossRef]
- Keedwell, E.; Khu, S.T. A novel evolutionary meta-heuristic for the multi-objective optimization of real-world water distribution networks. Eng. Optim. 2006, 38, 319–333. [Google Scholar] [CrossRef]
- Sankar, G.S.; Narasimhan, S.; Narasimhan, S. Online model predictive control of municipal water distribution networks. In Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2012; Volume 31, pp. 1622–1626. [Google Scholar]
- Wang, Y.; Cembrano, G.; Puig, V.; Urrea, M.; Romera, J.; Saporta, D.; Valero, J.G.; Quevedo, J. Optimal Management of Barcelona Water Distribution Network Using Non-Linear Model Predictive Control. Ifac-Papersonline 2017, 50, 5380–5385. [Google Scholar] [CrossRef]
- Hamam, Y.; Brameller, A. Hybrid method for the solution of piping networks. Proc. Inst. Electr. Eng. 1971, 118, 1607–1612. [Google Scholar] [CrossRef]
- Rossman, L.A. EPANET 2 Users Manual; United States Environmental Protection Agency: Washington, DC, USA, 2000. [Google Scholar]
- Todini, E. Towards realistic extended period simulations (EPS) in looped pipe network. In Proceedings of the Water Distribution Systems Analysis Symposium 2006, Cincinnati, OH, USA, 27–30 August 2006; pp. 1–16. [Google Scholar]
- Hindi, K.; Hamam, Y. Pressure control for leakage minimization in water supply networks Part 1: Single period models. Int. J. Syst. Sci. 1991, 22, 1573–1585. [Google Scholar] [CrossRef]
- Hindi, K.; Hamam, Y. Pressure control for leakage minimization in water supply networks: Part 2. Multi-period models. Int. J. Syst. Sci. 1991, 22, 1587–1598. [Google Scholar] [CrossRef]
- Gupta, A.; Bokde, N.; Marathe, D.; Kulat, K. Leakage Reduction in Water Distribution Systems with Efficient Placement and Control of Pressure Reducing Valves Using Soft Computing Techniques. Eng. Technol. Appl. Sci. Res. 2016, 7, 1528–1534. [Google Scholar]
- Hamam, Y.; Hindi, K. Optimised on-line leakage minimization in water piping networks using neural nets. In Proceedings of the IFIP Working Conference, Dagschul, Germany, 28 September–1 October 1992; Volume 28, pp. 57–64. [Google Scholar]
- Dai, P.D.; Li, P. Optimal Localization of Pressure Reducing Valves in Water Distribution Systems by a Reformulation Approach. Water Resour. Manag. 2014, 28, 3057–3074. [Google Scholar] [CrossRef]
- Lima, G.M.; Junior, E.L.; Brentan, B.M. Selection and location of Pumps as Turbines substituting pressure reducing valves. Renew. Energy 2017, 109, 392–405. [Google Scholar] [CrossRef]
- Lima, G.M.; Brentan, B.M.; Luvizotto, E., Jr. Optimal design of water supply networks using an energy recovery approach. Renew. Energy 2018, 117, 404–413. [Google Scholar] [CrossRef]
- Shao, Y.; Yu, Y.; Yu, T.; Chu, S.; Liu, X. Leakage Control and Energy Consumption Optimization in the Water Distribution Network Based on Joint Scheduling of Pumps and Valves. Energies 2019, 12, 2969. [Google Scholar] [CrossRef] [Green Version]
- Alberizzi, J.C.; Renzi, M.; Righetti, M.; Pisaturo, G.R.; Rossi, M. Speed and Pressure Controls of Pumps-as-Turbines Installed in Branch of Water-Distribution Network Subjected to Highly Variable Flow Rates. Energies 2019, 12, 4738. [Google Scholar] [CrossRef] [Green Version]
- Marchiori, I.N.; Lima, G.M.; Brentan, B.M.; Junior, E.L. Effectiveness of methods for selecting pumps as turbines to operate in water distribution networks. Water Supply 2019, 19, 417–423. [Google Scholar] [CrossRef]
- García, I.F.; Novara, D.; Mc Nabola, A. A Model for Selecting the Most Cost-Effective Pressure Control Device for More Sustainable Water Supply Networks. Water 2019, 11, 1297. [Google Scholar] [CrossRef] [Green Version]
- Eck, B.J.; Mevissen, M. Valve Placement in Water Networks: Mixed-Integer Non-Linear Optimization With Quadratic Pipe Friction; Report No RC25307 (IRE1209-014); IBM Research: Armonk, NY, USA, 2012. [Google Scholar]
- Jowitt, P.W.; Xu, C. Optimal valve control in water-distribution networks. J. Water Resour. Plan. Manag. 1990, 116, 455–472. [Google Scholar] [CrossRef]
- Liberatore, S.; Sechi, G.M. Location and Calibration of Valves in Water Distribution Networks Using a Scatter-Search Meta-heuristic Approach. Water Resour. Manag. 2009, 23, 1479–1495. [Google Scholar] [CrossRef]
- Gupta, A.; Bokde, N.; Kulat, K.; Yaseen, Z.M. Nodal Matrix Analysis for Optimal Pressure-Reducing Valve Localization in a Water Distribution System. Energies 2020, 13, 1878. [Google Scholar] [CrossRef] [Green Version]
- Hindi, K.; Hamam, Y. Locating pressure control elements for leakage minimization in water supply networks: An optimization model. Eng. Optim. 1991, 17, 281–291. [Google Scholar] [CrossRef]
- Nicolini, M.; Zovatto, L. Optimal location and control of pressure reducing valves in water networks. J. Water Resour. Plan. Manag. 2009, 135, 178–187. [Google Scholar] [CrossRef]
- Nicolini, M. Optimal pressure management in water networks: increased efficiency and reduced energy costs. In Proceedings of the Defense Science Research Conference and Expo (DSR), Singapore, 3–5 August 2011; pp. 1–4. [Google Scholar]
- Hindi, K.; Hamam, Y. Locating pressure control elements for leakage minimization in water supply networks by genetic algorithms. In Artificial Neural Nets and Genetic Algorithms; Springer: Vienna, Austria, 1993; pp. 583–587. [Google Scholar]
- Coelho, B.; Andrade-Campos, A. Energy recovery in water networks: Numerical decision support tool for optimal site and selection of micro turbines. J. Water Resour. Plan. Manag. 2018, 144, 04018004. [Google Scholar] [CrossRef]
- Shamir, U.; Salomons, E. Optimal real-time operation of urban water distribution systems using reduced models. J. Water Resour. Plan. Manag. 2008, 134, 181–185. [Google Scholar] [CrossRef] [Green Version]
- Laucelli, D.; Berardi, L.; Ugarelli, R.; Simone, A.; Giustolisi, O. Supporting Real-Time Pressure Control in Oppegård Municipality with WDNetXL. Procedia Eng. 2016, 154, 71–79. [Google Scholar] [CrossRef] [Green Version]
- Coulbeck, B.; Ulanicki, B.; Rance, J.P.; Deviatkov, V.V.; Kosov, S.; Glukhovsky, I. Pressure control of a Moscow water supply system using expert system technology. Trans. Inst. Measur. Control 1996, 18, 193–201. [Google Scholar] [CrossRef]
- Yang, Z.; Wu, L.; Dong, X. Control System Design for Contant-pressure Water Supply. In Proceedings of the 2010 Second International Conference on Multimedia and Information Technology (MMIT), Kaifeng, China, 24–25 April 2010; Volume 2, pp. 55–57. [Google Scholar]
- Lei, Z.; Jing, Z. Implement of increment-model PID control of PLC in constant-pressure water system. In Proceedings of the 2007 8th International Conference on Electronic Measurement and Instruments, Xi’an, China, 16–18 August 2007; pp. 4–336. [Google Scholar]
- Wang, D.L.; Wang, A.M. The Pressure Control on Non-negative Pressure Water Supply Based on the Fuzzy PID Control. In Proceedings of the 2009 International Joint Conference on Artificial Intelligence, Hainan Island, China, 25–26 April 2009; pp. 140–143. [Google Scholar]
- Peng, X.; Xiao, L.; Mo, Z.; Liu, G. The variable frequency and speed regulation constant pressure water supply system based on PLC and fuzzy control. In Proceedings of the 2009 International Conference on Measuring Technology and Mechatronics Automation, Zhangjiajie, China, 11–12 April 2009; Volume 1, pp. 910–913. [Google Scholar]
- Prescott, S.L.; Ulanicki, B. Improved control of pressure reducing valves in water distribution networks. J. Hydraul. Eng. 2008, 134, 56–65. [Google Scholar] [CrossRef]
- Bezerra, S.; da Silva, S.; Gomes, H. Operational optimization of water supply networks using a fuzzy system. Water 2012, 38, 565–572. [Google Scholar] [CrossRef] [Green Version]
- Kallesoe, C.S.; Jensen, T.N.; Wisniewski, R. Adaptive reference control for pressure management in water networks. In Proceedings of the 2015 European Control Conference (ECC), Linz, Austria, 15–17 July 2015; pp. 3268–3273. [Google Scholar]
- Bello, O.; Hamam, Y.; Djouani, K. Coagulation process control in water treatment plants using multiple model predictive control. Alex. Eng. J. 2014, 53, 939–948. [Google Scholar] [CrossRef] [Green Version]
- Zeilinger, M.N.; Raimondo, D.M.; Domahidi, A.; Morari, M.; Jones, C.N. On real-time robust model predictive control. Automatica 2014, 50, 683–694. [Google Scholar] [CrossRef] [Green Version]
- Bangura, M.; Mahony, R. Real-time model predictive control for quadrotors. IFAC Proc. Vol. 2014, 47, 11773–11780. [Google Scholar] [CrossRef]
- Sankar, G.S.; Mohan Kumar, S.; Narasimhan, S.; Narasimhan, S.; Murty Bhallamudi, S. Optimal control of water distribution networks with storage facilities. J. Process. Control. 2015, 32, 127–137. [Google Scholar] [CrossRef]
- Robles, D.; Puig, V.; Ocampo-Martinez, C.; Garza-Castañón, L.E. Reliable fault-tolerant model predictive control of drinking water transport networks. Control. Eng. Pract. 2016, 55, 197–211. [Google Scholar] [CrossRef] [Green Version]
- Jose, N.; Sumam, K. Optimal Water Distribution Network Design Accounting for Valve Closure. Procedia Technol. 2016, 24, 332–338. [Google Scholar] [CrossRef] [Green Version]
- Nicolini, M.; Giacomello, C.; Deb, K. Calibration and optimal leakage management for a real water distribution network. J. Water Resour. Plan. Manag. 2010, 137, 134–142. [Google Scholar] [CrossRef]
- Pecci, F.; Abraham, E.; Stoianov, I. Mathematical Programming Methods for Pressure Management in Water Distribution Systems. Procedia Eng. 2015, 119, 937–946. [Google Scholar] [CrossRef] [Green Version]
- Oikonomou, K.; Parvania, M.; Khatami, R. Optimal demand response scheduling for water distribution systems. IEEE Trans. Ind. Inform. 2018, 14, 5112–5122. [Google Scholar] [CrossRef]
- Vasudevan, D. Water Distribution Networks: Leakage Management Using Nonlinear Optimization of Pressure. Master’s Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2018. [Google Scholar]
- Wright, R.; Abraham, E.; Parpas, P.; Stoianov, I. Optimized control of pressure reducing valves in water distribution networks with dynamic topology. Procedia Eng. 2015, 119, 1003–1011. [Google Scholar] [CrossRef] [Green Version]
- Corcoran, L.; McNabola, A.; Coughlan, P. Optimization of water distribution networks for combined hydropower energy recovery and leakage reduction. J. Water Resour. Plan. Manag. 2016, 142, 04015045. [Google Scholar] [CrossRef]
- Araujo, L.S.; Ramos, H.; Coelho, S.T. Pressure Control for Leakage Minimisation in Water Distribution Systems Management. Water Resour. Manag. 2006, 20, 133–149. [Google Scholar] [CrossRef]
- El-Ghandour, H.A.; Elansary, A.S. Optimal selection of pressure relief valve parameters for surge pressure control in water distribution systems. Urban Water J. 2019, 16, 269–276. [Google Scholar] [CrossRef]
- Van Dijk, M.; van Vuuren, S.J.; Van Zyl, J.E. Optimising water distribution systems using a weighted penalty in a genetic algorithm. Water 2008, 34, 537–548. [Google Scholar] [CrossRef] [Green Version]
- Bonthuys, G.J.; van Dijk, M.; Cavazzini, G. Energy Recovery and Leakage-Reduction Optimization of Water Distribution Systems Using Hydro Turbines. J. Water Resour. Plan. Manag. 2020, 146, 04020026. [Google Scholar] [CrossRef]
- Cimorelli, L.; D’Aniello, A.; Cozzolino, L.; Pianese, D. A Derivative Free Non-Linear Programming Method for the Optimal Setting of PATs to Be Used in a Hybrid Genetic Algorithm: A Preliminary Work. Proceedings 2018, 2, 684. [Google Scholar] [CrossRef] [Green Version]
- Saldarriaga, J.; Salcedo, C.A. Determination of optimal location and settings of pressure reducing valves in water distribution networks for minimizing water losses. Procedia Eng. 2015, 119, 973–983. [Google Scholar] [CrossRef] [Green Version]
- De Paola, F.; Giugni, M.; Portolano, D. Pressure management through optimal location and setting of valves in water distribution networks using a music-inspired approach. Water Resour. Manag. 2017, 31, 1517–1533. [Google Scholar] [CrossRef] [Green Version]
- Fanni, A.; Liberatore, S.; Sechi, G.; Soro, M.; Zuddas, P. Optimization of water distribution systems by a tabu search metaheuristic. In Computing Tools for Modeling, Optimization and Simulation; Springer: Boston, MA, USA, 2000; pp. 279–298. [Google Scholar]
- Creaco, E.; Franchini, M. A new algorithm for real-time pressure control in water distribution networks. Water Sci. Technol. Water Supply 2013, 13, 875–882. [Google Scholar] [CrossRef]
- Page, P.R.; Abu-Mahfouz, A.M.; Yoyo, S. Parameter-Less Remote Real-Time Control for the Adjustment of Pressure in Water Distribution Systems. J. Water Resour. Plan. Manag. 2017, 143, 04017050. [Google Scholar] [CrossRef] [Green Version]
- Fontana, N.; Giugni, M.; Glielmo, L.; Marini, G.; Verrilli, F. A lab prototype of pressure control in water distribution networks. Ifac-Papersonline 2017, 50, 15373–15378. [Google Scholar] [CrossRef]
- Cheng, W.; Yu, T.; Xu, G. Real-Time Model of a Large-scale Water Distribution System. Procedia Eng. 2014, 89, 457–466. [Google Scholar] [CrossRef] [Green Version]
- Kang, D. Real-time optimal control of water distribution systems. Procedia Eng. 2014, 70, 917–923. [Google Scholar] [CrossRef] [Green Version]
- Sira-Ramírez, H.; Luviano-Juárez, A.; Ramírez-Neria, M.; Zurita-Bustamante, E.W. Active Disturbance Rejection Control of Dynamic Systems: A Flatness Based Approach; Butterworth-Heinemann: Oxford, UK, 2018. [Google Scholar]
- Rao, Z.; Alvarruiz, F. Use of an artificial neural network to capture the domain knowledge of a conventional hydraulic simulation model. J. Hydroinform. 2007, 9, 15–24. [Google Scholar] [CrossRef] [Green Version]
- Rao, Z.; Salomons, E. Development of a real-time, near-optimal control process for water-distribution networks. J. Hydroinform. 2007, 9, 25–37. [Google Scholar] [CrossRef] [Green Version]
- Anele, A.O.; Hamam, Y.; Abu-Mahfouz, A.M.; Todini, E. Overview, comparative assessment and recommendations of forecasting models for short-term water demand prediction. Water 2017, 9, 887. [Google Scholar] [CrossRef] [Green Version]
- Anele, A.O.; Todini, E.; Hamam, Y.; Abu-Mahfouz, A.M. Predictive uncertainty estimation in water demand forecasting using the model conditional processor. Water 2018, 10, 475. [Google Scholar] [CrossRef] [Green Version]

| Themes | References | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | This review | |
| Effects of excessive pressure | ✔ | ✔ | |||||
| Model formulation discussion | ✔ | ✔ | ✔ | ||||
| Principles of pressure control | ✔ | ✔ | |||||
| Placement of PCDs | ✔ | ||||||
| Classification of pressure control techniques | ✔ | ✔ | |||||
| Pressure control valves (PCV) | ✔ | ✔ | |||||
| Focused, real-time control | ✔ | ✔ | |||||
| Recommendation on future works | ✔ | ✔ | ✔ | ✔ | ✔ | ||
| Element | Use |
|---|---|
| Pressure reducing valves (PRV) | Regulation of pressure when and if it exceeds the set out values |
| Pressure sustaining valves (PSV) | Sustain a certain specified pressure value |
| Pressure control valves (PCV) | Control the pressure in the identified pressure management area |
| Pressure breaker valve (PBV) | Force and maintain specified pressure loss across the valve |
| Pumps as turbines (PATs) | Regulation of pressure when and if it exceeds the set out values and the recovery of energy. |
| Method | Pros | Cons |
|---|---|---|
| Enumerative method [31] | Easier to apply | Optimal placement and numbers of PRVs cannot be guaranteed |
| Pressure reference method [21,32,33] | Less computational burden | Optimal placement of PRVs cannot be guaranteed |
| Calculus-based/optimization methods [6,24,30,34,35,36,37,38] | Optimal placement, numbers of PRVs can be guaranteed | Computationally demanding |
| Technique | Operation Strategy | Remarks | Limitation | Application | Classification |
|---|---|---|---|---|---|
| Classical Control [4,43,44,45,46] | Based on one-at-a-time parameter control (On-Off) or PID controllers | Cost-effective and easy implementation, however not suitable for large-scale WDN | One parameter control at a time | Suitable for small-scale systems | Physical model-driven |
| Advanced Control [14,32,40,48,50,51] | A model is required to mimic the behavior of the system. Based on prior knowledge of the requirements in the system, these controllers adjust the controlled variable to reduce the error between the reference and required quantities. | Their implementation is cumbersome, and the accuracy of the model will determine the accuracy of the results. | Difficulty in their implementation | Suitable for large-scale networks | Physical model-driven |
| Optimal Control [19,36,58,59,60,61,67] | Based on the principles of calculus, the best operating parameters are selected. These parameters may be selected under various constraints or no constraints at all. | The computational requirements of this class of methods have proven to be very cumbersome. Therefore, this method may not be ideal for real-time applications. | Computational resources limit the number of control variables in time constraint applications | For large-scale networks | Physical model-driven |
| Real-Time Control [4,72,73] | Based on the measurements obtained in real time, through the SCADA or other application, a control law is applied, and necessary adjustment instructions are produced | A sizable capital investment is required to get these systems running | Control laws that may be applied are limited by the available processing power | Can be used in any systems where real-time infrastructure is available | Physical model-driven |
| Model-Free Control [22,75,76] | Based on the utilization of emulators to mimic the model of the chosen control law | Requires a large training dataset to realize an accurate emulator | Challenges in adapting the said emulator as the topology of the network changes | Suitable to a network with minimal changes in the topological design | Data-driven |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mosetlhe, T.C.; Hamam, Y.; Du, S.; Monacelli, E. A Survey of Pressure Control Approaches in Water Supply Systems. Water 2020, 12, 1732. https://doi.org/10.3390/w12061732
Mosetlhe TC, Hamam Y, Du S, Monacelli E. A Survey of Pressure Control Approaches in Water Supply Systems. Water. 2020; 12(6):1732. https://doi.org/10.3390/w12061732
Chicago/Turabian StyleMosetlhe, Thapelo C., Yskandar Hamam, Shengzhi Du, and Eric Monacelli. 2020. "A Survey of Pressure Control Approaches in Water Supply Systems" Water 12, no. 6: 1732. https://doi.org/10.3390/w12061732
APA StyleMosetlhe, T. C., Hamam, Y., Du, S., & Monacelli, E. (2020). A Survey of Pressure Control Approaches in Water Supply Systems. Water, 12(6), 1732. https://doi.org/10.3390/w12061732






