Modelling of Surface Runoff on the Yamal Peninsula, Russia, Using ERA5 Reanalysis
Abstract
:1. Introduction
2. Materials and Methods
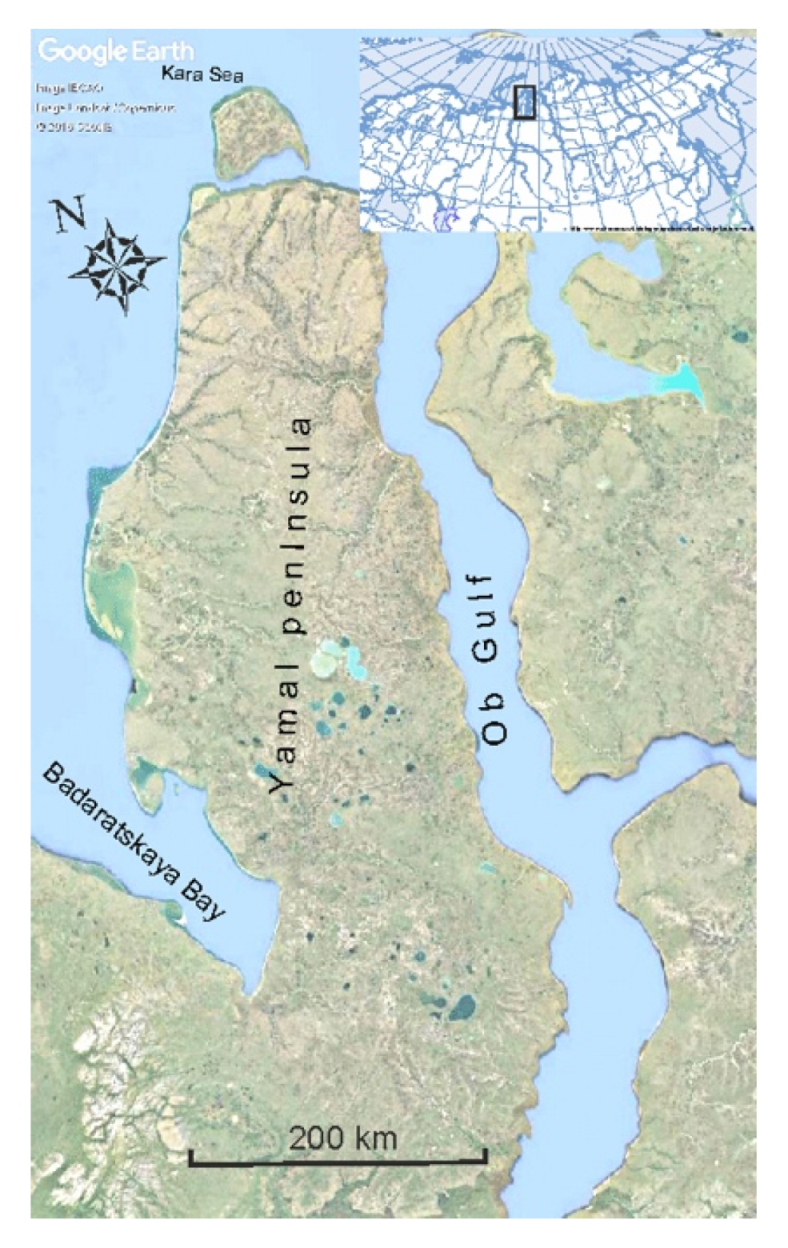
2.1. Climatic and Hydrological Characteristics of Yamal
2.1.1. Climatic Characteristics
2.1.2. Hydrological Characteristic
2.2. Data
2.2.1. Station Data and ERA5 Reanalysis
2.2.2. Hydrological Model Description
The Period of Snow Thaw
The Period of Summer Rains
2.2.3. The Model Calibration
3. Results
3.1. Evaluation of ERA5 Reanalysis Quality
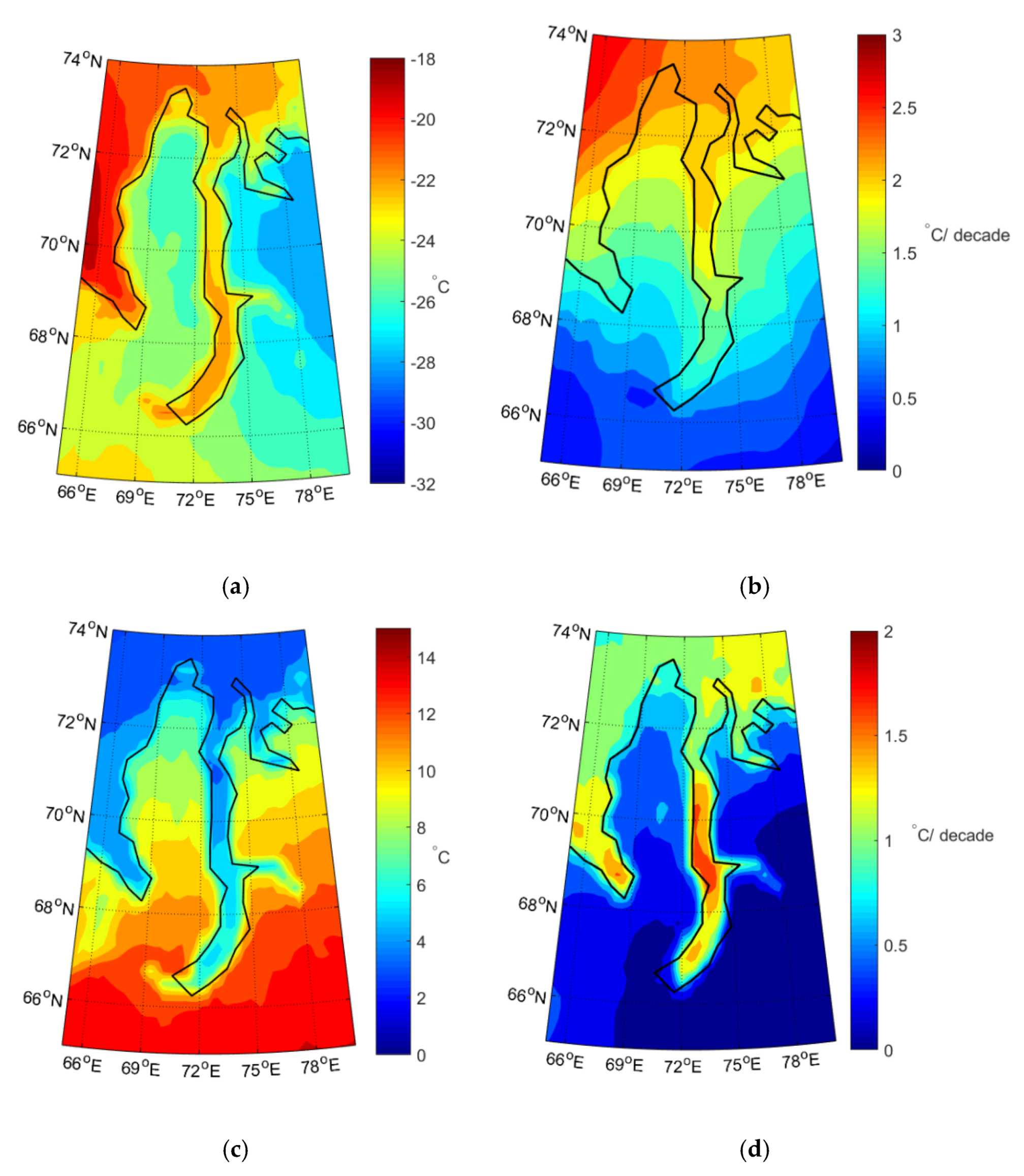
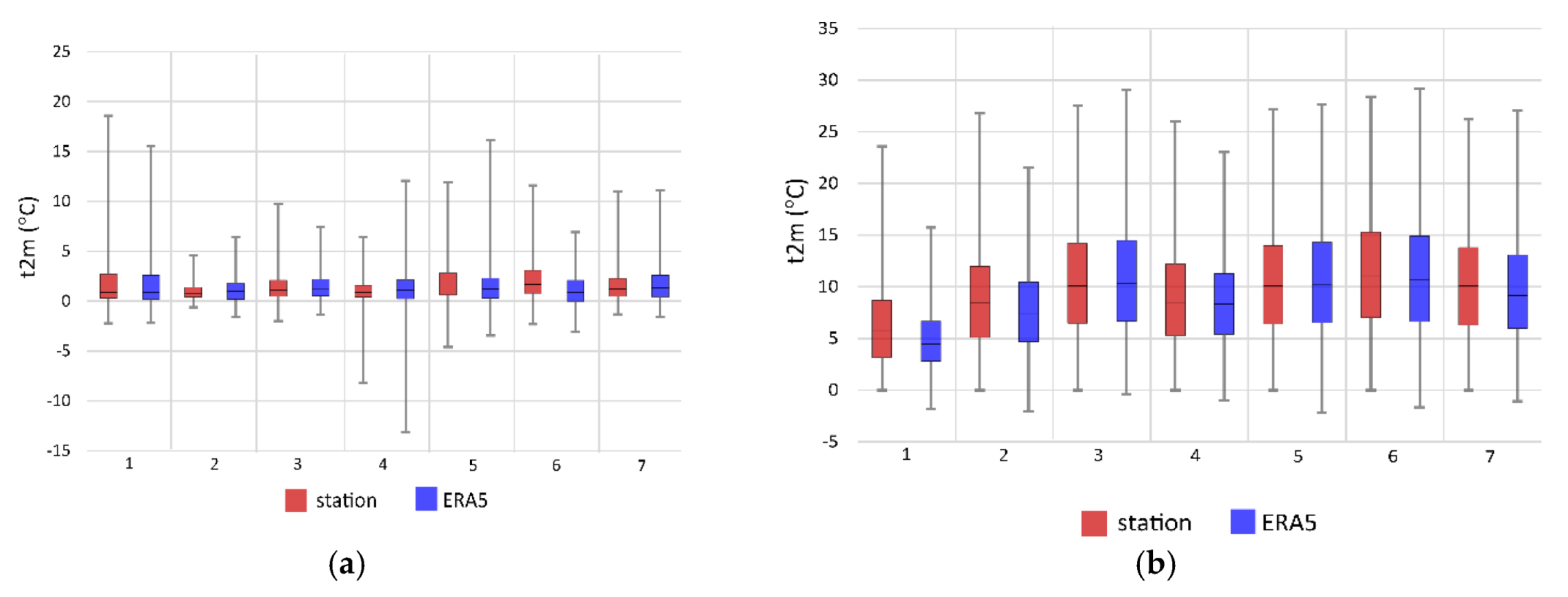
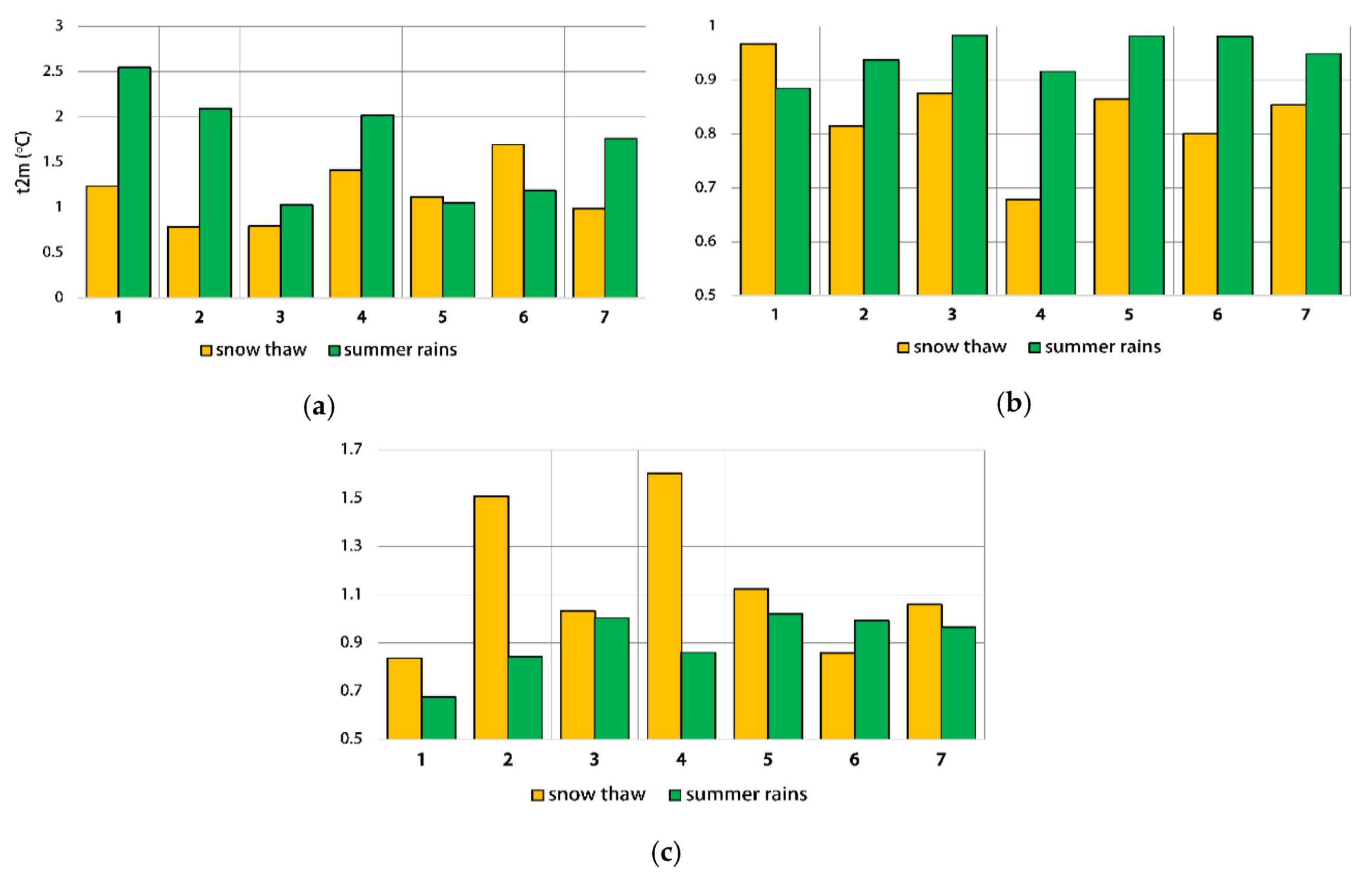
3.1.1. Surface Air Temperature
3.1.2. Precipitation
3.1.3. Snow Cover
3.2. Model Sensitivity Analysis
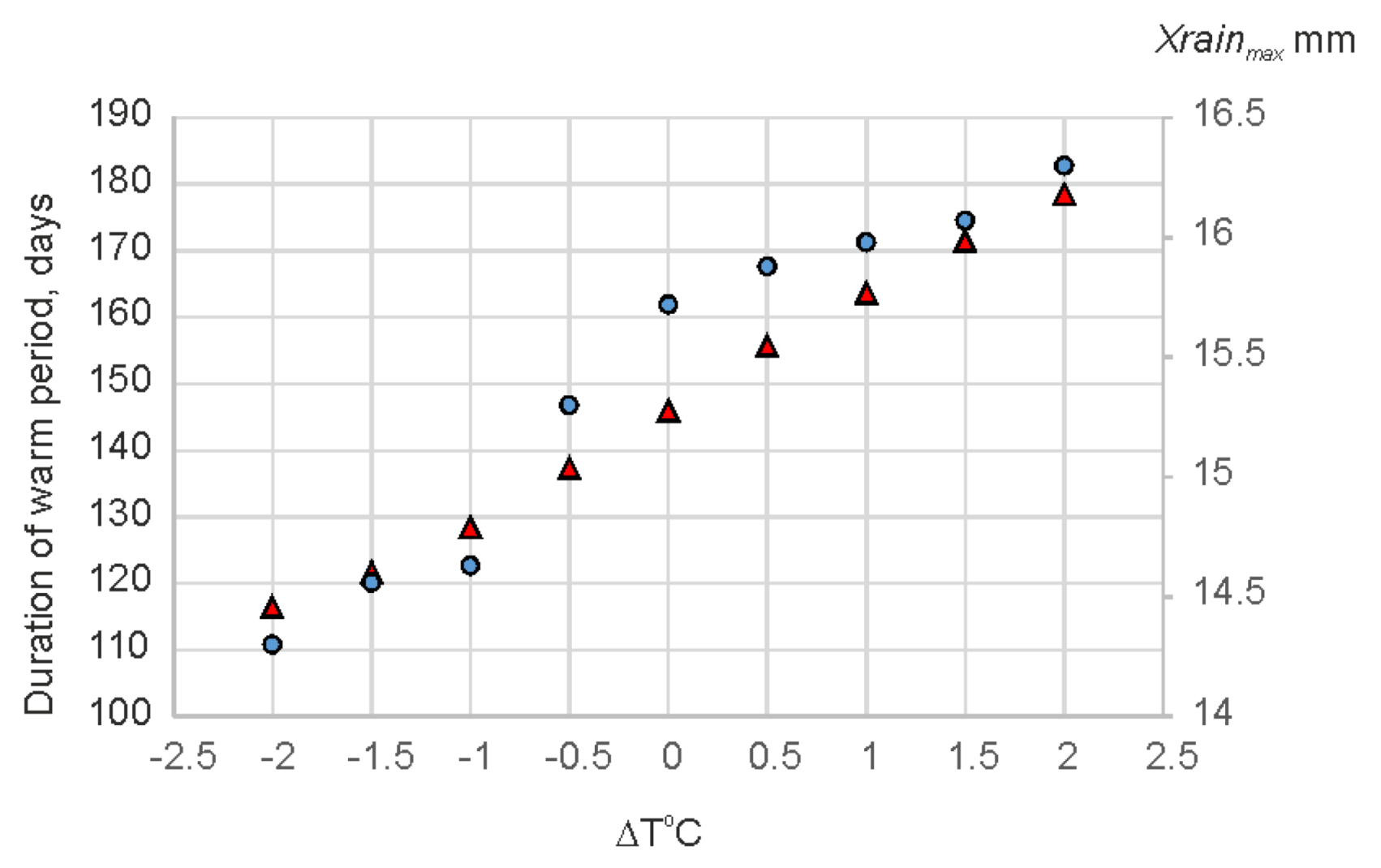
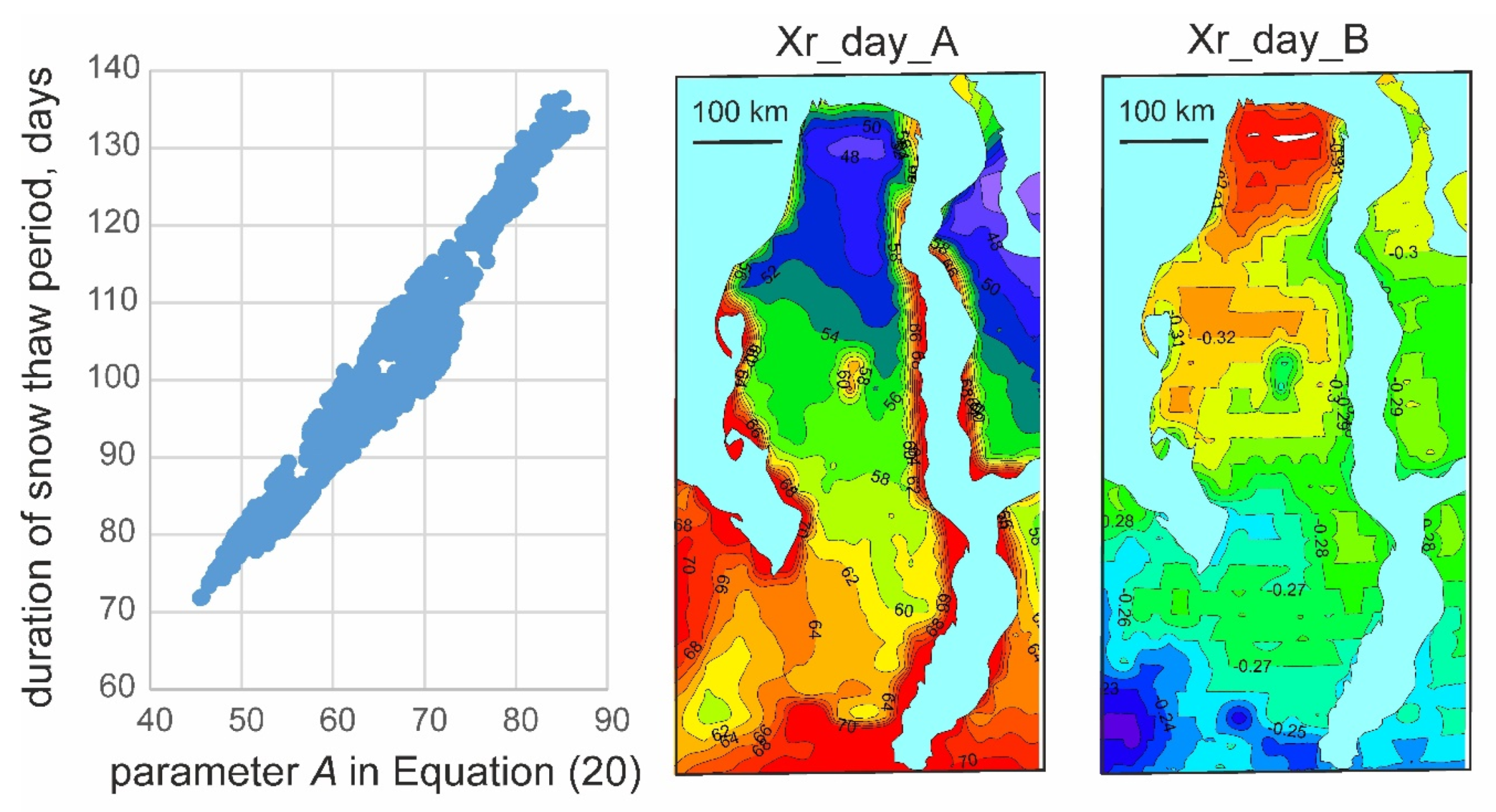
3.2.1. Snow Thaw Period
The Input Characteristics Variability
The Model Coefficients Variability
3.2.2. The Period of Summer Rains
3.3. Spatial Distribution of the Hydrological Characteristics on the Yamal Peninsula
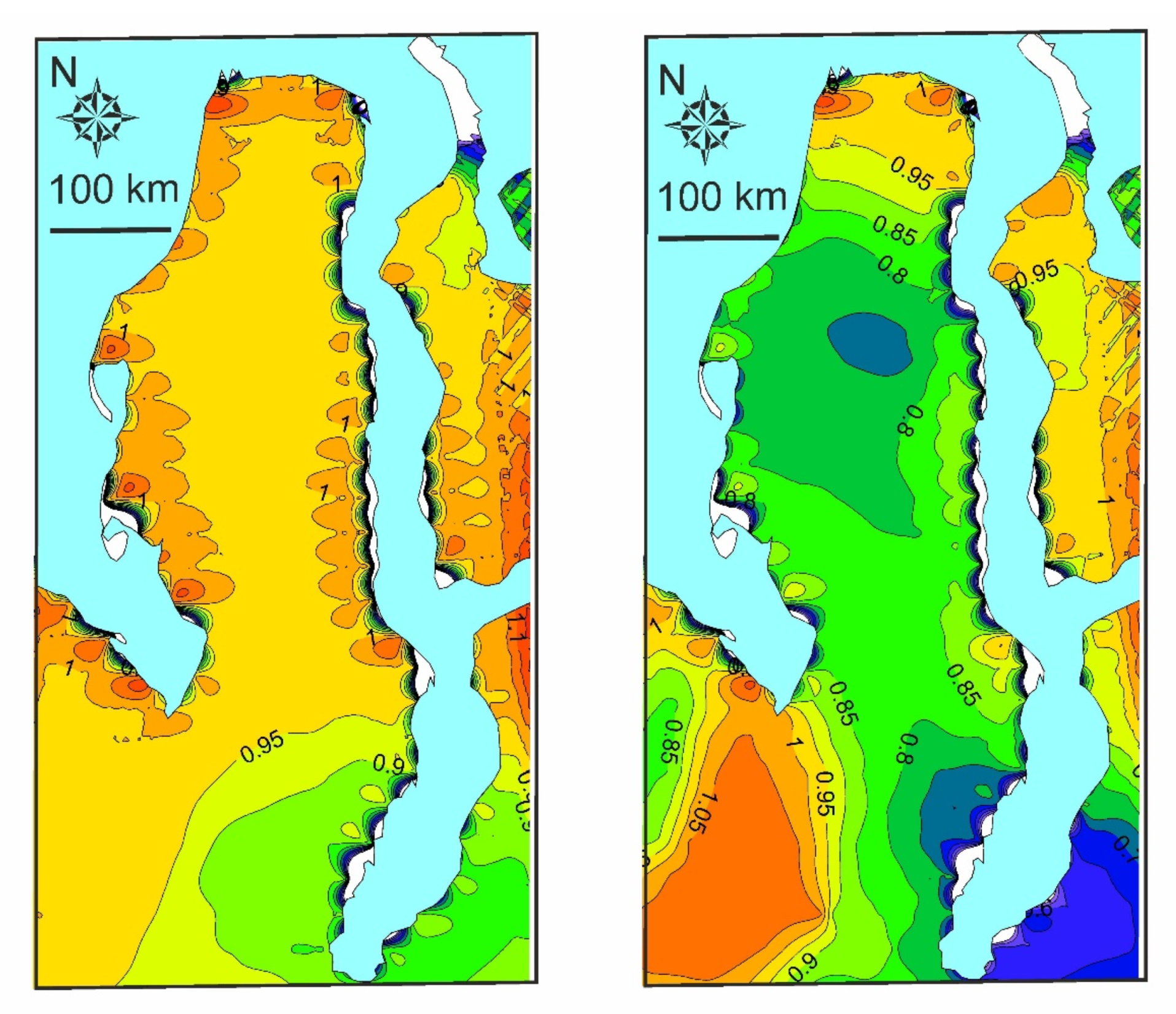
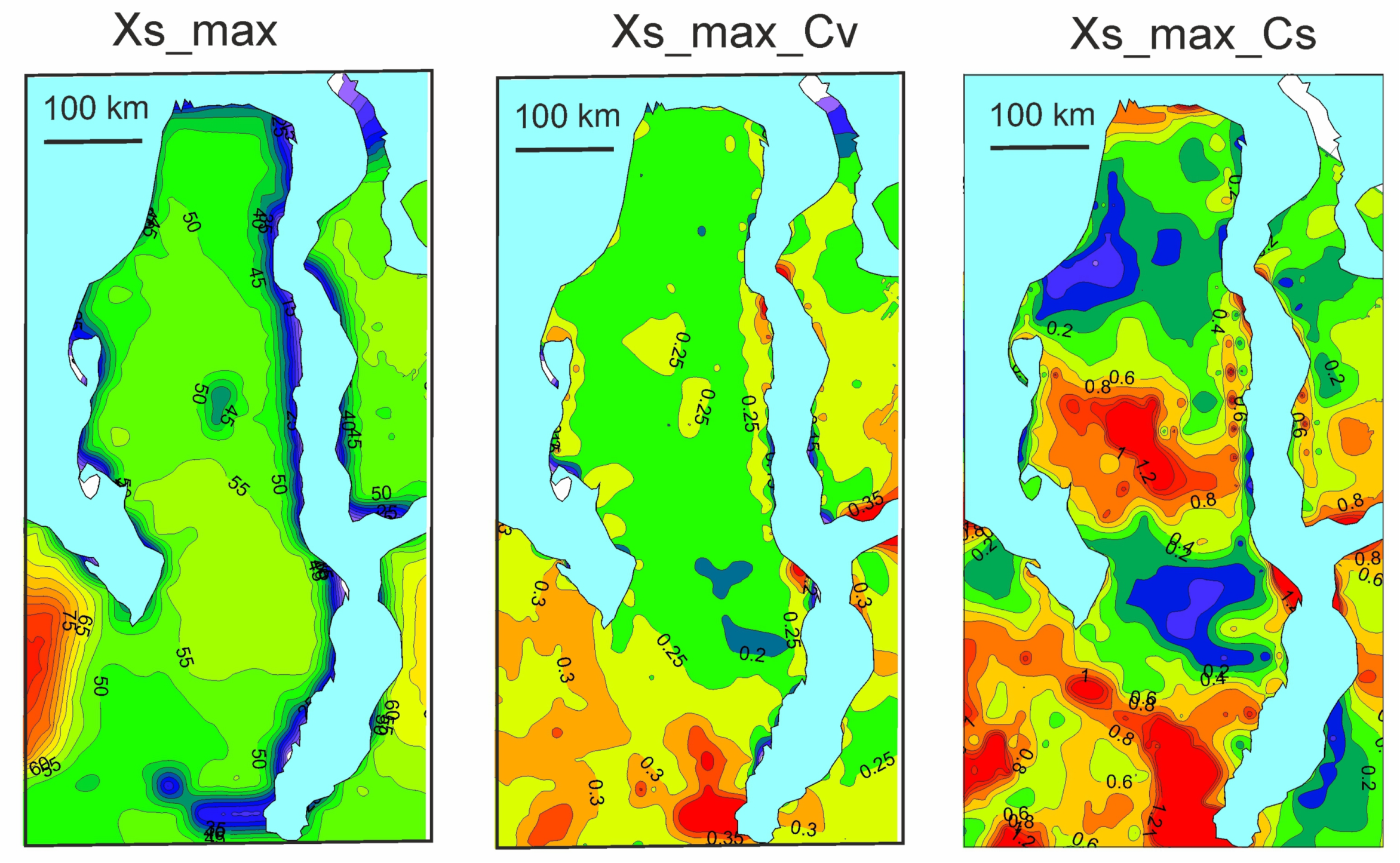
3.3.1. Mean Maximum Depth of Snow Cover and Surface Runoff Depth during the Snow Thaw Period
3.3.2. Daily Surface Runoff Depth During the Snow Thaw Period
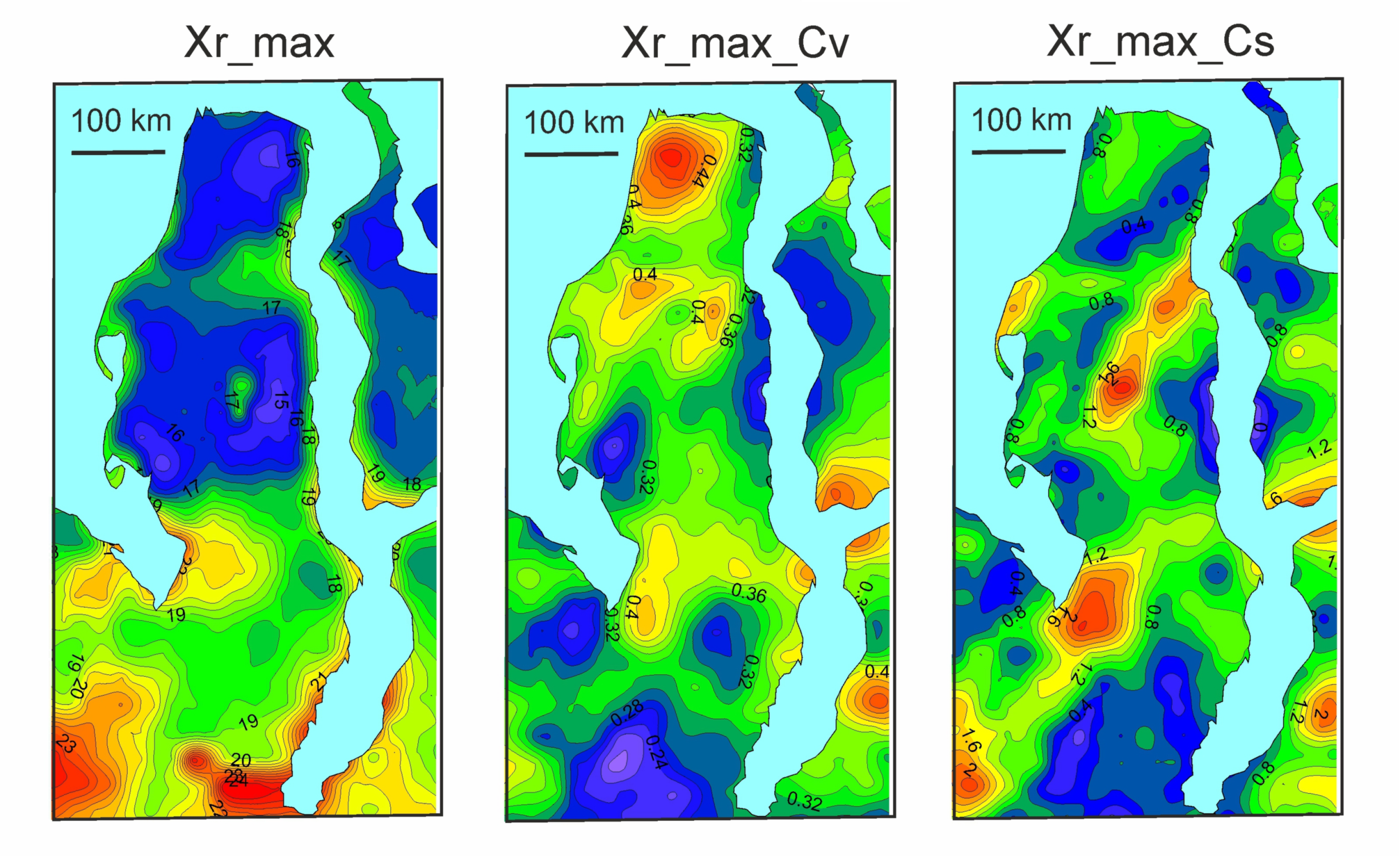
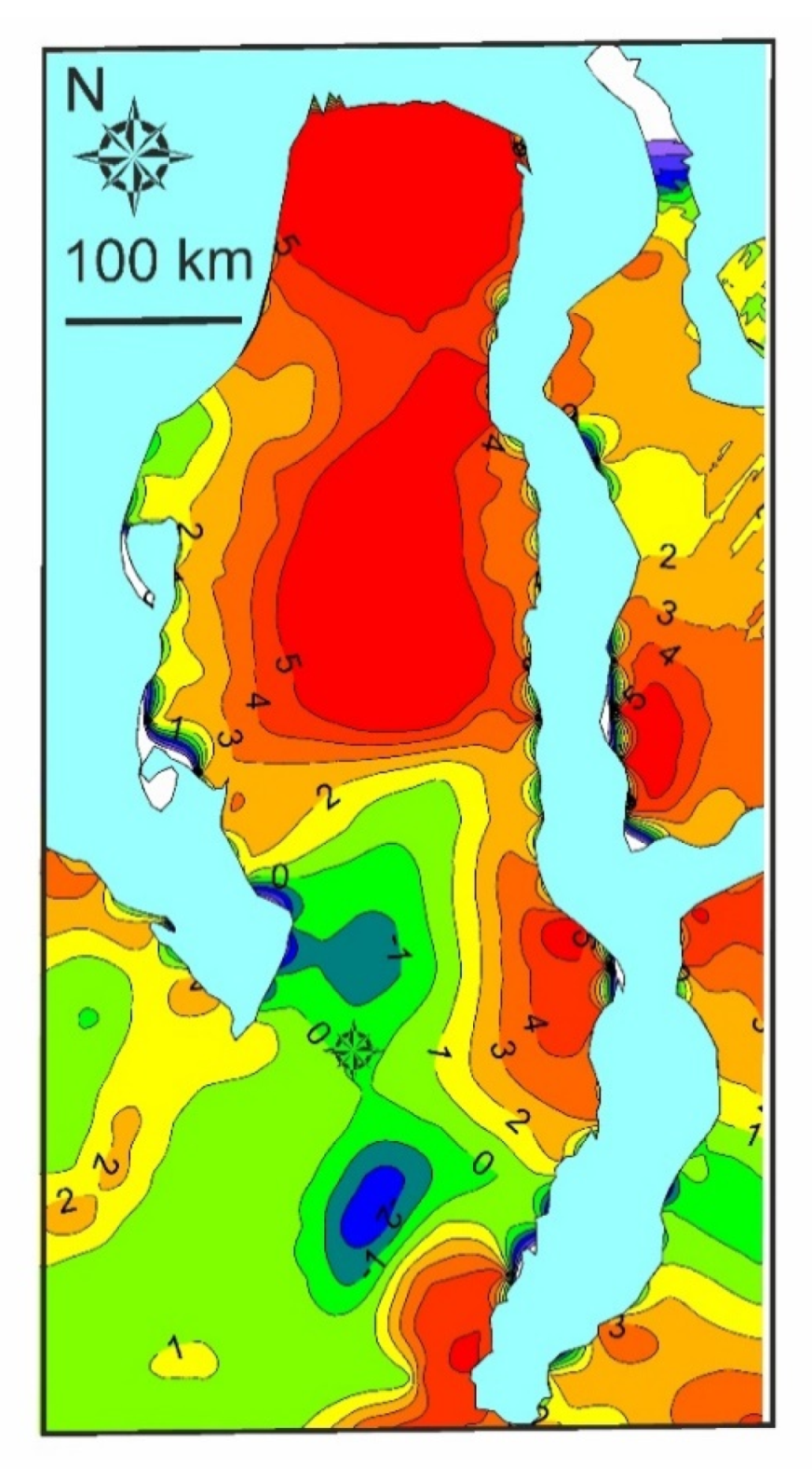
3.3.3. Mean Surface Runoff Depth of the Summer Rain Period
4. Discussion
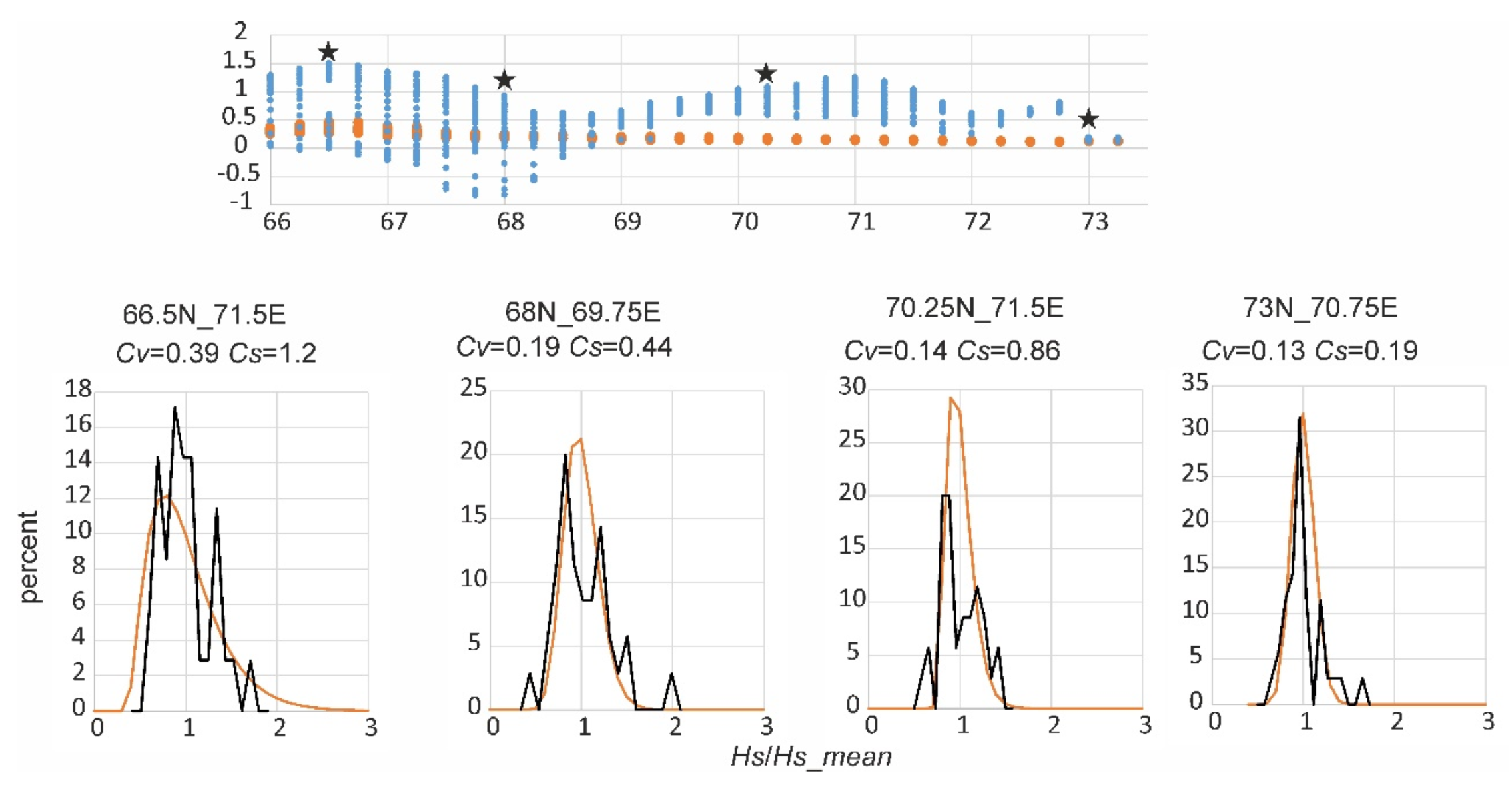
4.1. Statistical Characteristics of the Sequences with the Trends
4.2. Types of Probability Density Functions Used for Different Characteristics of Surface Runoff
4.3. Effects of Errors in ERA5 Data on the Results of Runoff Calculations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A


References
- Dobrinski, L.N. (Ed.) Nature of Yamal (Priroda Yamala); Nauka: Ekaterinburg, Russia, 1995; p. 435. (In Russian) [Google Scholar]
- Litvinenko, V. The Role of Hydrocarbons in the Global Energy Agenda: The Focus on Liquefied Natural Gas. Resources 2020, 9, 59. [Google Scholar] [CrossRef]
- Paltsev, S. Scenarios for Russia’s natural gas exports to 2050. Energy Econ. 2014, 42, 262–270. [Google Scholar] [CrossRef]
- Henderson, J.; Yermakov, V. Russian LNG: Becoming a Global Force. Working Paper; Oxford Institute for Energy Studies: Oxford, UK, 2019; p. 37. [Google Scholar]
- IGU. Global Gas Report 2019; International Gas Union: Barcelona, Spain, 2020. Available online: https://media-publications.bcg.com/SNAM-2019-GGR.pdf (accessed on 6 June 2020).
- IGU. World LNG Report 2020; International Gas Union: Barcelona, Spain, 2020. Available online: https://www.igu.org/sites/default/files/node-document-field_file/2020%20World%20LNG%20Report.pdf (accessed on 6 June 2020).
- Novikov, S.M. Hydrology of the Wetlands of the Permafrost Zone of Western Siberia (Gidrologiya Zabolochennykh Territoriy Zony Mnogoletney Merzloty Zapadnoy Sibiri); VVM Publicaiton House: St. Petersburg, Russia, 2009; p. 536. (In Russian) [Google Scholar]
- Bobrovitskaya, N.N.; Baranov, A.V.; Vasilenko, N.N.; Zubkova, K.M. Hydrological Conditions. In Erosion Processes at the Central Yamal (Erozionnyye Protsessy Tsentral’Nogo Yamala); Sidorchuk, A., Baranov, A., Eds.; RNII KPN: St. Petersburg, Russia, 1999; pp. 90–105. (In Russian) [Google Scholar]
- Sidorchuk, A. Gully erosion in the cold environment: Risks and hazards. Adv. Environ. Res. 2015, 44, 139–192. [Google Scholar]
- Sidorchuk, A. The potential of gully erosion on the Yamal peninsula, West Siberia. Sustainability 2020, 12, 260. [Google Scholar] [CrossRef] [Green Version]
- Patton, P.C.; Schumm, S.A. Gully erosion, northwestern Colorado: A threshold phenomenon. Geology 1975, 3, 83–90. [Google Scholar] [CrossRef]
- Vandaele, K.; Poesen, J.; Govers, G.; van Wesemael, B. Geomorphic threshold conditions for ephemeral gully incision. Geomorphology 1996, 16, 161–173. [Google Scholar] [CrossRef]
- Garrett, K.K.; Wohl, E.E. Climate-invariant area–slope relations in channel heads initiated by surface runoff. Earth Surf. Process. Landforms 2017, 42, 1745–1751. [Google Scholar] [CrossRef]
- Sidorchuk, A. Dynamic and static models of gully erosion. Catena 1999, 37, 401–414. [Google Scholar] [CrossRef]
- Sagintayev, Z.; Sultan, M.; Khan, S.D.; Khan, S.A.; Mahmood, K.; Yan, E.; Milewski, A.; Marsala, P. A remote sensing contribution to hydrologic modelling in arid and inaccessible watersheds, Pishin Lora basin, Pakistan. Hydrol. Process. 2012, 26, 85–99. [Google Scholar] [CrossRef]
- Cole, S.J.; Moore, R.J. Distributed hydrological modelling using weather radar in gauged and ungauged basins. Adv. Water Resour. 2009, 32, 1107–1120. [Google Scholar] [CrossRef] [Green Version]
- Lindsay, R.; Wensnahan, M.; Schweiger, A.; Zhang, J. Evaluation of seven different atmospheric reanalysis products in the Arctic. J. Clim. 2014, 27, 2588–2606. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Liu, Y.; Wang, S.; Yang, X.; Wang, L.; Baig, M.H.A.; Chi, W.; Wang, Z. Evaluation of spatial and temporal performances of ERA-Interim precipitation and temperature in mainland China. J. Clim. 2018, 31, 4347–4365. [Google Scholar] [CrossRef]
- Lader, R.; Bhatt, U.S.; Walsh, J.E.; Rupp, T.S.; Bieniek, P.A. Two-meter temperature and precipitation from atmospheric reanalysis evaluated for Alaska. J. Appl. Meteorol. Climatol. 2016, 55, 901–922. [Google Scholar] [CrossRef]
- Timmermans, B.; Wehner, M.; Cooley, D.; O’Brien, T.; Krishnan, H. An evaluation of the consistency of extremes in gridded precipitation data sets. Clim. Dyn. 2019, 52, 6651–6670. [Google Scholar] [CrossRef] [Green Version]
- Albergel, C.; Munier, S.; Bocher, A.; Bonan, B.; Zheng, Y.; Draper, C.; Leroux, D.J.; Calvet, J.-C. LDAS-Monde Sequential Assimilation of Satellite Derived Observations Applied to the Contiguous US: An ERA5 Driven Reanalysis of the Land Surface Variables. Remote Sens. 2018, 10, 1627. [Google Scholar] [CrossRef] [Green Version]
- Gampe, D.; Ludwig, R. Evaluation of gridded precipitation data products for hydrological applications in complex topography. Hydrology 2017, 4, 53. [Google Scholar] [CrossRef] [Green Version]
- Essou, G.R.; Brissette, F.; Lucas-Picher, P. The use of reanalyses and gridded observations as weather input data for a hydrological model: Comparison of performances of simulated river flows based on the density of weather stations. J. Hydrometeorol. 2017, 18, 497–513. [Google Scholar] [CrossRef]
- Raimonet, M.; Oudin, L.; Thieu, V.; Silvestre, M.; Vautard, R.; Rabouille, C.; Le Moigne, P. Evaluation of gridded meteorological datasets for hydrological modelling. J. Hydrometeorol. 2017, 18, 3027–3041. [Google Scholar] [CrossRef]
- Beck, H.E.; Vergopolan, N.; Pan, M.; Levizzani, V.; Van Dijk, A.I.; Weedon, G.P.; Brocca, L.; Pappenberger, F.; Huffman, G.J.; Wood, E.F. Global-Scale Evaluation of 22 Precipitation Datasets Using Gauge Observations and Hydrological Modelling. In Satellite Precipitation Measurement; Springer: Cham, Switzerland, 2020; pp. 625–653. [Google Scholar]
- Mahto, S.S.; Mishra, V. Does ERA-5 outperform other reanalysis products for hydrologic applications in India? J. Geophys. Res. Atmos. 2019, 124, 9423–9441. [Google Scholar] [CrossRef]
- Nkiaka, E.; Nawaz, N.R.; Lovett, J.C. Evaluating global reanalysis datasets as input for hydrological modelling in the Sudano-Sahel region. Hydrology 2017, 4, 13. [Google Scholar] [CrossRef] [Green Version]
- Fuka, D.R.; Walter, M.T.; MacAlister, C.; Degaetano, A.T.; Steenhuis, T.S.; Easton, Z.M. Using the Climate Forecast System Reanalysis as weather input data for watershed models. Hydrol. Process. 2014, 28, 5613–5623. [Google Scholar] [CrossRef]
- Essou, G.R.; Sabarly, F.; Lucas-Picher, P.; Brissette, F.; Poulin, A. Can precipitation and temperature from meteorological reanalyses be used for hydrological modelling? J. Hydrometeorol. 2016, 17, 1929–1950. [Google Scholar] [CrossRef]
- Ayzel, G.; Varentsova, N.; Erina, O.; Sokolov, D.; Kurochkina, L.; Moreydo, V. OpenForecast: The First Open-Source Operational Runoff Forecasting System in Russia. Water 2019, 11, 1546. [Google Scholar] [CrossRef] [Green Version]
- Lauri, H.; Räsänen, T.A.; Kummu, M. Using reanalysis and remotely sensed temperature and precipitation data for hydrological modelling in monsoon climate: Mekong River case study. J. Hydrometeorol. 2014, 15, 1532–1545. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Masih, I.; Mohamed, Y.A.; Van der Zaag, P. Validating Rainfall-Runoff Modelling Using Satellite-Based and Reanalysis Precipitation Products in the Sre Pok Catchment, the Mekong River Basin. Geosciences 2018, 8, 164. [Google Scholar] [CrossRef] [Green Version]
- Krogh, S.A.; Pomeroy, J.W.; McPhee, J. Physically based mountain hydrological modelling using reanalysis data in Patagonia. J. Hydrometeorol. 2015, 16, 172–193. [Google Scholar] [CrossRef] [Green Version]
- Jing, W.; Song, J.; Zhao, X. Validation of ECMWF Multi-Layer Reanalysis Soil Moisture Based on the OzNet Hydrology Network. Water 2018, 10, 1123. [Google Scholar] [CrossRef] [Green Version]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Vikhamar-Schuler, D.; Hanssen-Bauer, I.; Førland, E.J. Long-Term Climate Trends of the Yamalo-Nenets AO, Russia; Norwegian Meteorological Institute: Oslo, Norway, 2010; pp. 1–51. [Google Scholar]
- Bulygina, O.N.; Veselov, V.M.; Razuvaev, V.N.; Aleksandrova, T.M. Description of the Dataset of Observational Data on Major Meteorological Parameters from Russian Weather Stations. Database State Registration Certificate No. 1 49 2014. Available online: http://meteo.ru/data (accessed on 12 June 2020). (In Russian).
- Vasiliev, A.A.; Gravis, A.G.; Gubarkov, A.A.; Drozdov, D.S.; Korostelev, Y.V.; Malkova, G.V.; Oblogov, G.E.; Ponomareva, O.E.; Sadurtdinov, M.R.; Streletskaya, I.D.; et al. Permafrost degradation: Results of the long-term geocryological monitoring in the western sector of Russian Arctic. Kriosf. Zemli 2020, 24, 15–30. (In Russian) [Google Scholar] [CrossRef]
- Borodulin, V.V.; Gryazeva, L.I. The results of hydrological studies of the Yamal rivers. Meteorol. Hydrol. 1993, 3, 86–94. (In Russian) [Google Scholar]
- Sidorchuk, A. Gully Thermoerosion on the Yamal Peninsula. In Geomorphic Hazards; Slaymaker, O., Ed.; Wiley: Chichester, UK, 1996; pp. 141–153. [Google Scholar]
- Hersbach, H.; Dee, D. ERA5 reanalysis is in production. ECMWF Newsl. 2016, 147, 7. [Google Scholar]
- Rango, A.; Martinec, J. Revisiting the Degree-day Method for Snowmelt Computations. J. Am. Water Resour. Assoc. 2007, 31, 657–669. [Google Scholar] [CrossRef]
- Pistocchi, A.; Bagli, S.; Callegari, M.; Notarnicola, C.; Mazzoli, P. On the Direct Calculation of Snow Water Balances Using Snow Cover Information. Water 2017, 9, 848. [Google Scholar] [CrossRef] [Green Version]
- Komarov, V.D.; Makarova, T.T.; Sinegub, E.S. Calculation of the hydrograph of floods of small lowland rivers based on thaw intensity data. Proc. Hydrometeorol. Cent. USSR 1969, 37, 3–30. (In Russian) [Google Scholar]
- Vinogradov, Y.B. Mathematical Modelling of Flow Formation Processes (Matematicheskoye Modelirovaniye Protsessov Formirovaniya Stoka); Gidrometeoizdat: Leningrad, Russia, 1988; p. 312. (In Russian) [Google Scholar]
- Vinogradov, Y.B.; Vinogradova, T.A.; Zhuravlev, S.A.; Zhuravleva, A.D. Mathematical modelling of hydrographs from the unstudied river basins on the Yamal peninsula. Bull. St. Petersburg State Univ. 2014, 7, 71–81. (In Russian) [Google Scholar]
- Gelfan, A.N. Model of Formation of River Flow during Snowmelt and Rain. In Erosion Processes at the Central Yamal (Erozionnyye Protsessy Tsentral’Nogo Yamala); Sidorchuk, A., Baranov, A., Eds.; RNII KPN: St. Petersburg, Russia, 1999; pp. 205–225. (In Russian) [Google Scholar]
- Popov, Y.G. Analysis of River Flow Formation (Analiz Formirovaniya Stoka Ravninnykh Rek); Gidrometeoizdat: Leningrad, Russia, 1956; p. 131. (In Russian) [Google Scholar]
- Bosilovich, M.L.G.; Chen, J.; Robertson, F.R.; Adler, R.F. Evaluation of global precipitation in reanalyses. J. Appl. Meteorol. Climatol. 2008, 47, 2279–2299. [Google Scholar] [CrossRef]
- Donat, M.G.; Sillmann, J.; Wild, S.; Alexander, L.V.; Lippmann, T.; Zwiers, F.W. Consistency of temperature and precipitation extremes across various global gridded in situ and reanalysis datasets. J. Clim. 2014, 27, 5019–5035. [Google Scholar] [CrossRef]
- Recalculation of Coordinates. Available online: https://geobridge.ru/proj#null (accessed on 12 May 2020).
- Sood, A.; Smakhtin, V. Global hydrological models: A review. Hydrol. Sci. J. 2015, 60, 549–565. [Google Scholar] [CrossRef]
- Her, Y.; Yoo, S.; Cho, J.; Hwang, S.; Jeong, J.; Seong, C. Uncertainty in hydrological analysis of climate change: Multi-parameter vs. multi-GCM ensemble predictions. Sci. Rep. 2019, 9, 4974. [Google Scholar] [CrossRef] [Green Version]
- Gleick, P.H. Water in Crisis: A Guide to the World’s Fresh Water Resources; Oxford University Press: Oxford, UK, 1993; p. 473. [Google Scholar]
- Hurlimann, A.; Wilson, E. Sustainable Urban Water Management under a Changing Climate: The Role of Spatial Planning. Water 2018, 10, 546. [Google Scholar] [CrossRef] [Green Version]
- Versini, P.-A.; Pouget, L.; Mcennis, S.; Custodio, E.; Escaler, I. Climate change impact on water resources availability—Case study of the Llobregat River basin (Spain). Hydrol. Sci. J. 2016, 61, 2496–2508. [Google Scholar] [CrossRef]
- Bodian, A.; Diop, L.; Panthou, G.; Dacosta, H.; Deme, A.; Dezetter, A.; Ndiaye, P.M.; Diouf, I.; Vischel, T. Recent Trend in Hydroclimatic Conditions in the Senegal River Basin. Water 2020, 12, 436. [Google Scholar] [CrossRef] [Green Version]
- Deng, W.; Song, J.; Bai, H.; He, Y.; Yu, M.; Wang, H.; Cheng, D. Analyzing the Impacts of Climate Variability and Land Surface Changes on the Annual Water–Energy Balance in the Weihe River Basin of China. Water 2018, 10, 1792. [Google Scholar] [CrossRef] [Green Version]
- Krogh, S.A.; Pomeroy, J.W. Impact of future climate and vegetation on the hydrology of an Arctic headwater basin at the tundra–taiga transition. J. Hydrometeorol. 2019, 20, 197–215. [Google Scholar] [CrossRef]
- Sidorchuk, A.Y.; Matveeva, T.A. Periglacial gully erosion on the east European plain and its recent analog at the Yamal peninsula. Geogr. Environ. Sustain. 2020, 13, 183–194. [Google Scholar] [CrossRef] [Green Version]
- Thompson, S.A. Hydrology for Water Management, 1st ed.; Balkema Publication: Rotterdam, The Netherlands, 1999; p. 380. [Google Scholar]
- Meylan, P.; Favre, A.-C.; Musy, A. Predictive Hydrology: A Frequency Analysis Approach; Taylor & Francis Inc.: Abingdon, UK, 2012; p. 212. [Google Scholar]




















| Model Characteristics, Varied in Sensitivity Analysis | Min | Max | Step | |
|---|---|---|---|---|
| Input values | Snow depth at the beginning of snow thaw, mm | 10 | 350 | 10 |
| Variation of air temperature from reanalysis data, °C | −2 | +2 | 0.5 | |
| Model coefficients | melt coefficient ksm mm/°C | 2.5 × 10−5 | 2.35 × 10−4 | 1 × 10−5 |
| Coefficient of water freezing kf mm/(°C)0.5 | 1.85 × 10−6 | 3.7 × 10−5 | 1.85 × 10−6 | |
| Coefficient of water content in snow kwc | 0.0163 | 0.326 | 0.0163 | |
| Standard deviation in Equation (18) | 0.1 | 0.9 | 0.1 | |
| Meteorological Characteristic, Daily Mean | Error in ERA5 | Hydrological Model Sensitivity | |||||
|---|---|---|---|---|---|---|---|
| Xd_max, | A | B | |||||
| Aer (mm) | Rer, % | Aer, Days | Rer (%) | Aer (mm) | Rer (%) | ||
| Air temperature during snow thaw period, °C | 0.8/−0.6 | −2/+7 | −4/+14 | 1/−2 | 4/−11 | −0.005/0.008 | −9/14 |
| Air temperature during the summer, °C | 1.3/−0.9 | +0.3/−9 | +2/−6 | 11/−9 | 13/−11 | 0/−0.003 | 0/−0.8 |
| Maximum depth of snow pack (water equivalent), mm | 30/−60 | +4.4/8.8 | +10/−20 | 2/−5 | 9/−26 | 0.013/−0.035 | 13/−36 |
| Rainfall during the summer, mm | 2.6/−1.6 | 0.12/−0.1 | 0.6/−0.4 | <±1 | 0.7/−0.5 | 0.002/−0.001 | 0.6/−0.4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matveeva, T.; Sidorchuk, A. Modelling of Surface Runoff on the Yamal Peninsula, Russia, Using ERA5 Reanalysis. Water 2020, 12, 2099. https://doi.org/10.3390/w12082099
Matveeva T, Sidorchuk A. Modelling of Surface Runoff on the Yamal Peninsula, Russia, Using ERA5 Reanalysis. Water. 2020; 12(8):2099. https://doi.org/10.3390/w12082099
Chicago/Turabian StyleMatveeva, Tatiana, and Aleksey Sidorchuk. 2020. "Modelling of Surface Runoff on the Yamal Peninsula, Russia, Using ERA5 Reanalysis" Water 12, no. 8: 2099. https://doi.org/10.3390/w12082099
APA StyleMatveeva, T., & Sidorchuk, A. (2020). Modelling of Surface Runoff on the Yamal Peninsula, Russia, Using ERA5 Reanalysis. Water, 12(8), 2099. https://doi.org/10.3390/w12082099






