Sensitivity and Interdependency Analysis of the HBV Conceptual Model Parameters in a Semi-Arid Mountainous Watershed
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Observed Data
2.3. MODIS Snow Cover Area (SCA)
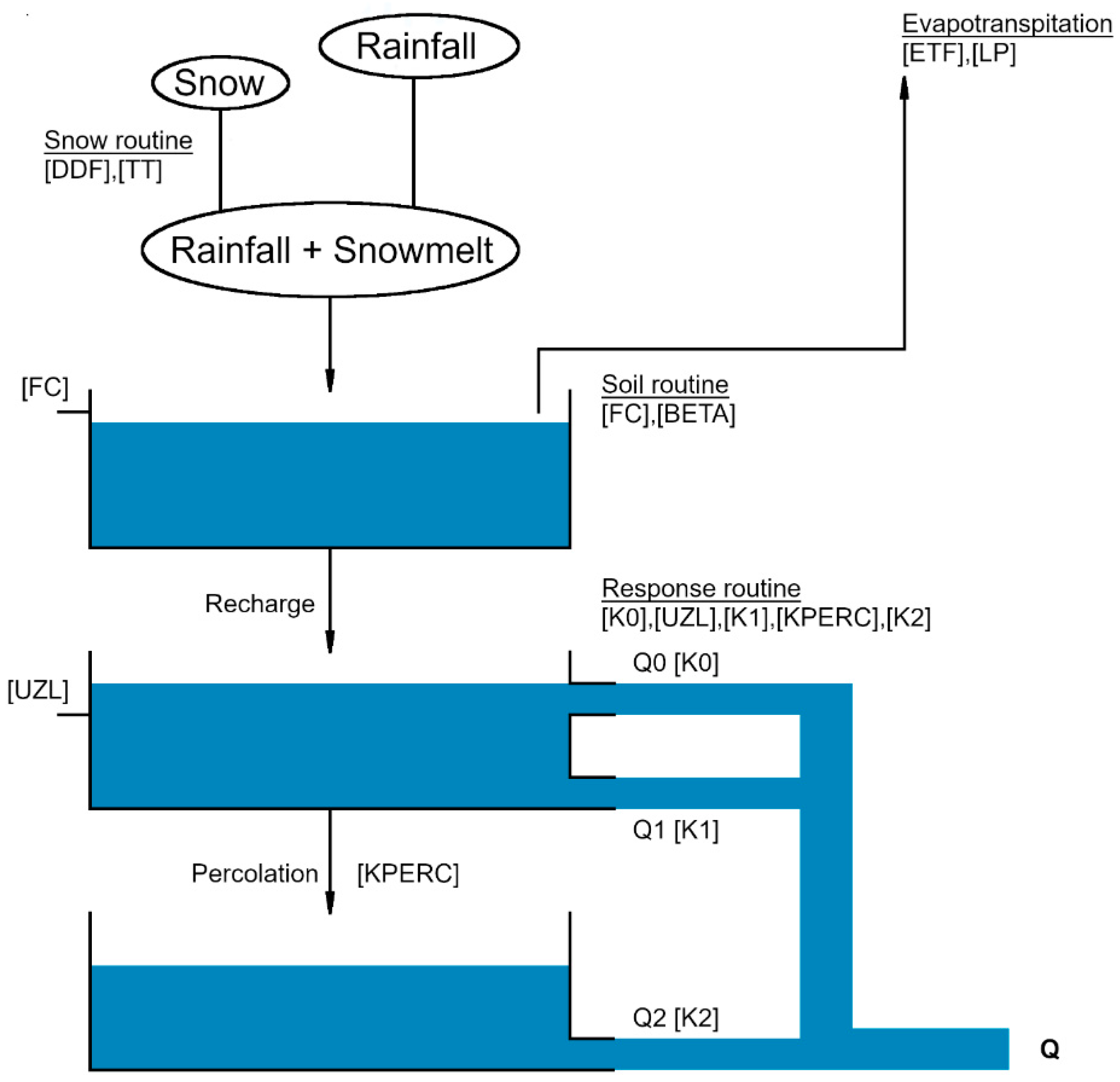
2.4. HBV Model
2.5. Methodology
3. Results and Discussion
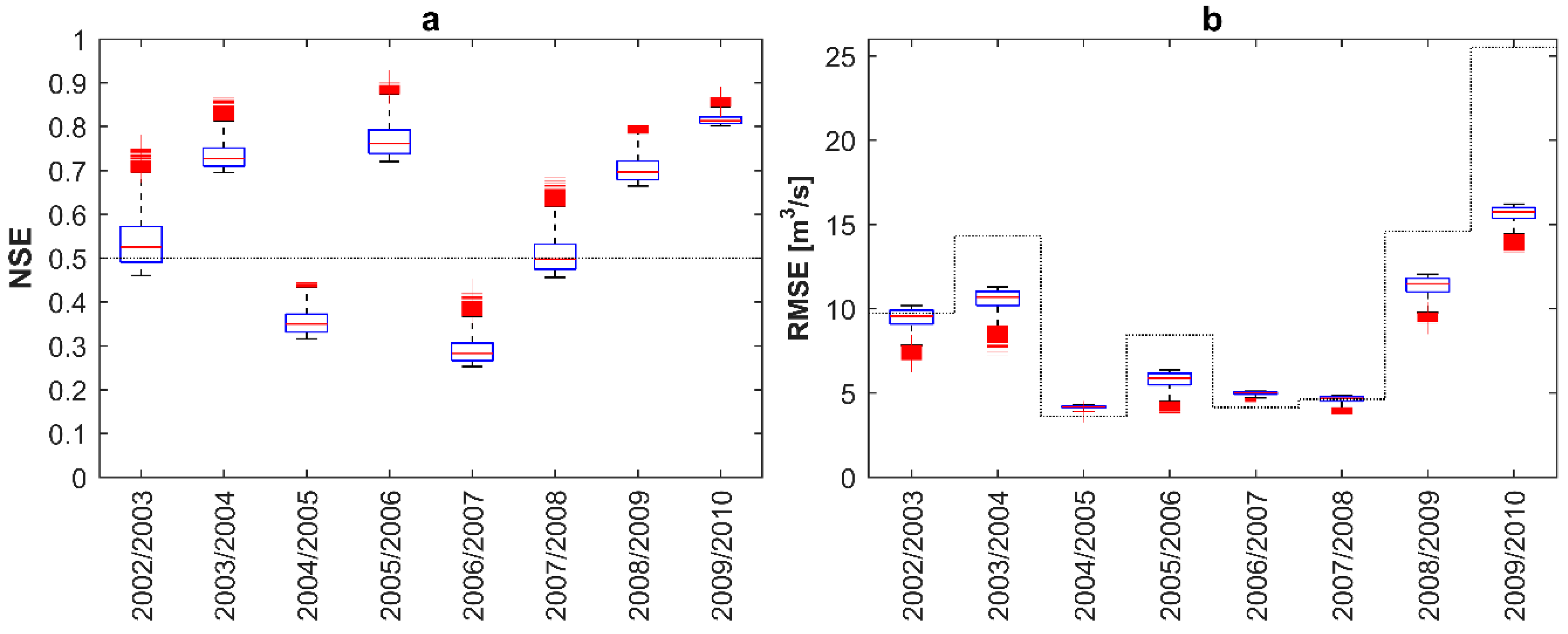
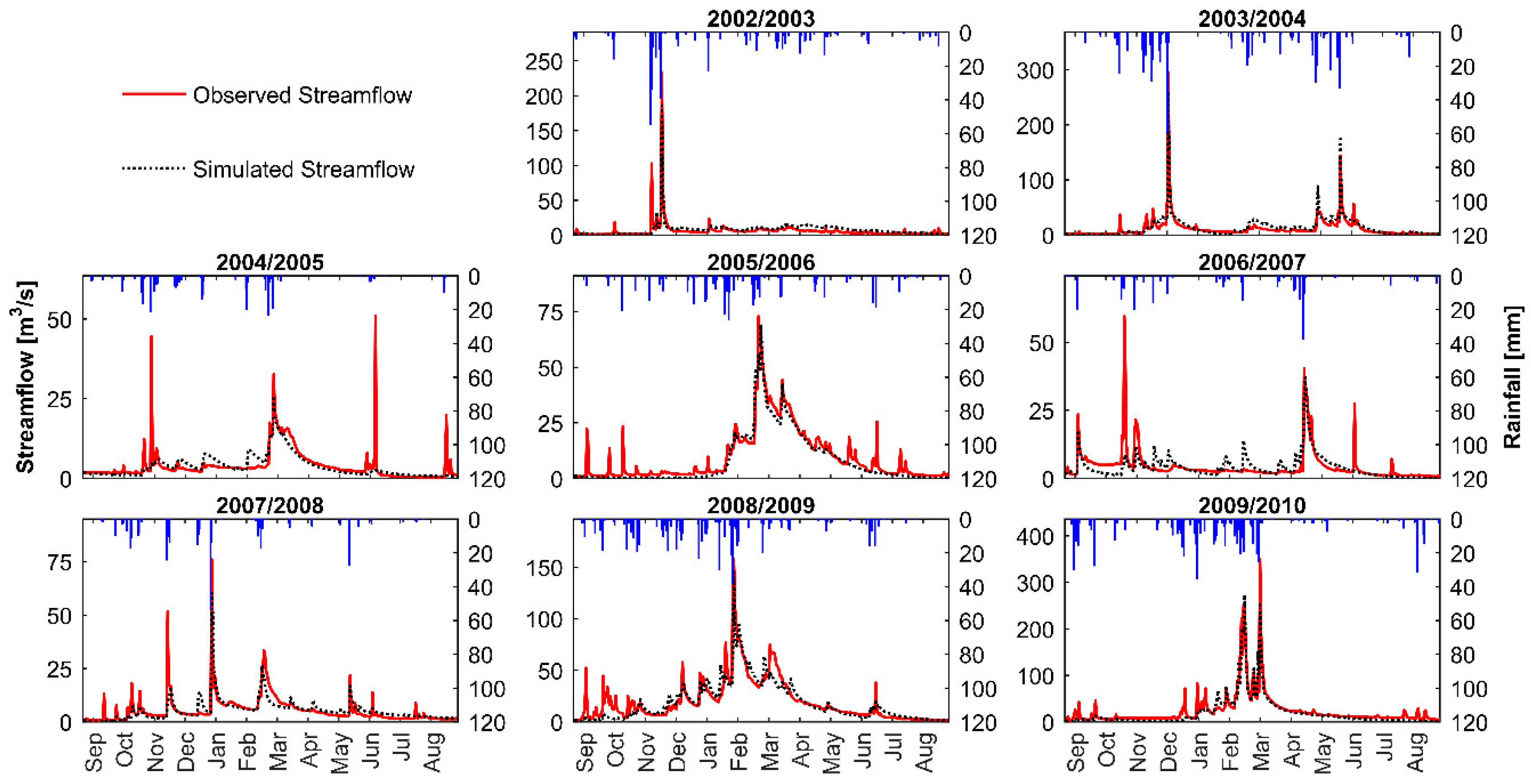
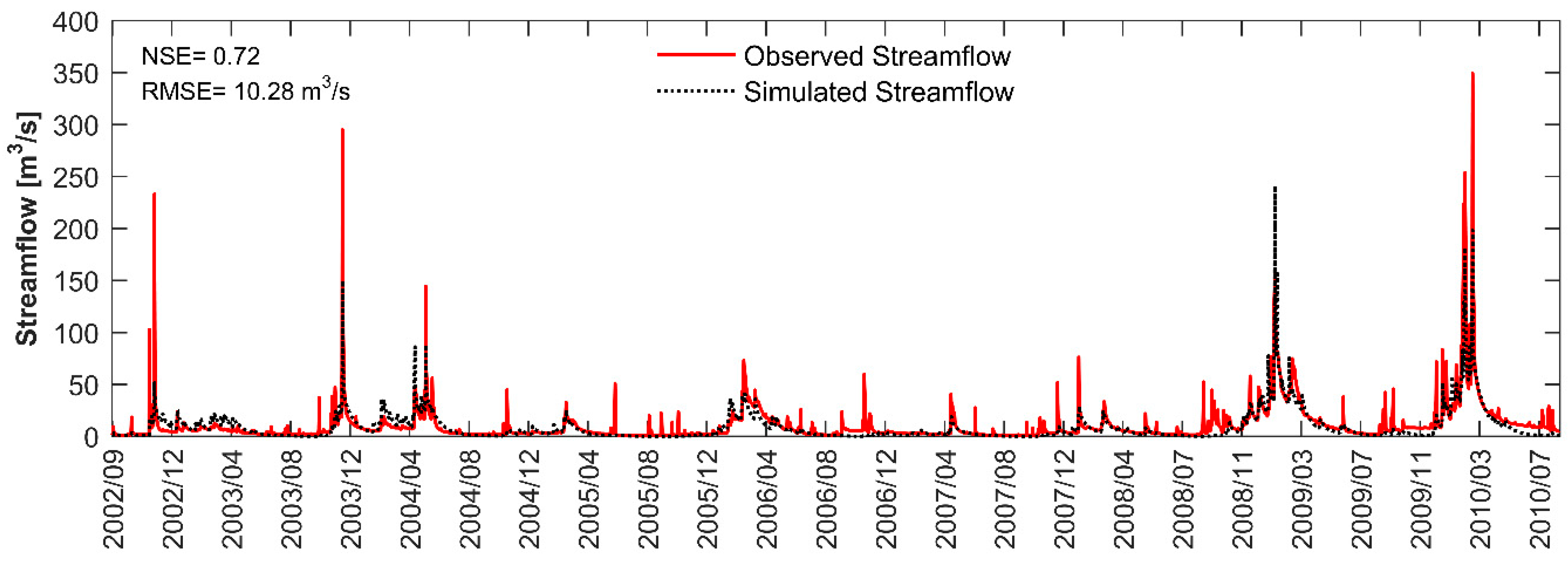
3.1. Model Calibration and Validation
3.2. Sensitivity Analysis
3.3. Parameters Interdependency
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bergström, S.; Lindström, G. Interpretation of runoff processes in hydrological modelling-experience from the HBV approach. Hydrol. Process. 2015, 29, 3535–3545. [Google Scholar] [CrossRef]
- Rango, A.; Martinec, J. Application of a Snowmelt-Runoff Model Using Landsat Data. Nord. Hydrol. 1979, 10, 225–238. [Google Scholar] [CrossRef]
- Vandewiele, G.L.; Xu, C.Y. Ni-Lar-Win Methodology and comparative study of monthly water balance models in Belgium, China and Burma. J. Hydrol. 1992, 134, 315–347. [Google Scholar] [CrossRef]
- Zhao, R.J. The Xinanjiang model applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar]
- Todini, E. The ARNO rainfall-runoff model. J. Hydrol. 1996, 175, 339–382. [Google Scholar] [CrossRef]
- Arnold, J.G.; Fohrer, N. SWAT2000: Current capabilities and research opportunities in applied watershed modelling. Hydrol. Process. 2005, 19, 563–572. [Google Scholar] [CrossRef]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A simple hydrologically based model of land surface water and energy fluxes for general circulation model. J. Geophys. Res. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
- Bergström, S.; Forsman, A. Development of a Conceptual Deterministic Rainfall-Runoff Model. Nord. Hydrol. 1973, 4, 147–170. [Google Scholar] [CrossRef]
- Orth, R.; Staudinger, M.; Seneviratne, S.I.; Seibert, J.; Zappa, M. Does model performance improve with complexity? A case study with three hydrological models. J. Hydrol. 2015, 523, 147–159. [Google Scholar] [CrossRef]
- Beven, K. Changing ideas in hydrology—The case of physically based models. J. Hydrol. 1989, 105, 157–172. [Google Scholar] [CrossRef]
- Bergström, S. Experience from Applications of the HBV Hydrological Model from the Perspective of Prediction in Ungauged Basins; MOPEX Experiments; IAHS Publ.: Wallingford, UK, 2006; Volume 307. [Google Scholar]
- Abulohom, M.S.; Shah, S.M.S.; Ghumman, A.R. Development of a Rainfall-Runoff Model, its Calibration and Validation. Water Resour. Manag. 2001, 15, 149–163. [Google Scholar] [CrossRef]
- WMO. Intercomparison of Conceptual Models Used in Operational Hydrological Forecasting; WMO: Geneva, Switzerland, 1975. [Google Scholar]
- WMO. Intercomparison of Models of Snowmelt Runoff; WMO: Geneva, Switzerland, 1986. [Google Scholar]
- Abdulla, F.; Al-Badranih, L. Application of a rainfall-runoff model to three catchments in Iraq. Hydrol. Sci. J. 2010, 45, 13–25. [Google Scholar] [CrossRef]
- Beven, K.; Freer, J. Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology. J. Hydrol. 2001, 249, 11–29. [Google Scholar] [CrossRef]
- Braun, J.N.; Renner, C.B. Application of a conceptual runoff model in different physiographic regions of Switzerland. Hydrol. Sci. J. 1992, 37, 217–231. [Google Scholar] [CrossRef]
- Seibert, J. HBV Light Version 2 User’s Manual; Stockholm University, Department of Physical Geography and Quaternary Geology: Stockholm, Sweden, 2005. [Google Scholar]
- Stahl, K.; Moore, R.D.; Shea, J.M.; Hutchinson, D.; Cannon, A.J. Coupled modelling of glacier and streamflow response to future climate scenarios. Water Resour. Res. 2008, 44, 1–13. [Google Scholar] [CrossRef]
- Krysanova, V.; Bronstert, A.; Müller-wohlfeil, D.-I. Modelling river discharge for large drainage basins: From lumped to distributed approach. Hydrol. Sci. J. 1999, 44, 313–331. [Google Scholar] [CrossRef]
- Lindström, G.; Johansson, B.; Persson, M.; Gardelin, M.; Bergström, S. Development and test of the distributed HBV-96 hydrological model. J. Hydrol. 1997, 201, 272–288. [Google Scholar] [CrossRef]
- Rientjes, T.H.M.; Muthuwatta, L.P.; Bos, M.G.; Booij, M.J.; Bhatti, H.A. Multi-variable calibration of a semi-distributed hydrological model using streamflow data and satellite-based evapotranspiration. J. Hydrol. 2013, 505, 276–290. [Google Scholar] [CrossRef]
- Thapa, B.R.; Ishidaira, H.; Pandey, V.P.; Shakya, N.M. A multi-model approach for analyzing water balance dynamics in Kathmandu Valley, Nepal. J. Hydrol. Reg. Stud. 2017, 9, 149–162. [Google Scholar] [CrossRef]
- Vehviläinen, B.; Lohvansuu, J. The effects of climate change on discharges and snow cover in Finland. Hydrol. Sci. J. 1991, 36, 109–121. [Google Scholar] [CrossRef]
- Saelthun, N.R.; Aittoniemi, P.; Bergström, S. Climate Change Impacts on Runoff and Hydropower in the Nordic Countries Final Report from the Project “Climate Change and Energy Production”; Nordic Council of Ministers: Kobenhavn, Denmark, 1998. [Google Scholar]
- Bergström, S.; Carlsson, B.; Gardelin, M.; Lindström, G.; Petterson, A.; Rummukainen, M. Climate change impacts on runoff in Sweden—Assessments by global climate models, dynamical downscalling and hydrological modelling. Clim. Res. 2001, 16, 101–112. [Google Scholar] [CrossRef]
- Chen, H.; Xiang, T.; Zhou, X. Impacts of climate change on the Qingjiang Watershed ’ s runoff change trend in China. Stoch. Environ. Res. Risk Assess. 2012, 26, 847–858. [Google Scholar] [CrossRef]
- Brandt, M.; Bergström, S.; Gardelin, M. Modelling the effects of clearcutting on runoff—Examples from central Sweden. Ambio 1988, 17, 307–313. [Google Scholar]
- Teutschbein, C.; Grabs, T.; Laudon, H.; Karlsen, R.H.; Bishop, K. Simulating streamflow in ungauged basins under a changing climate: The importance of landscape characteristics. J. Hydrol. 2018, 561, 160–178. [Google Scholar] [CrossRef]
- Parra, V.; Arumí, J.L.; Muñoz, E. Identifying a Suitable Model for Low-Flow Simulation in Watersheds of South-Central Chile: A Study Based on a Sensitivity Analysis. Water 2019, 11, 1506. [Google Scholar] [CrossRef]
- Johansson, B. Runoff calculations in ungauged catchments—An evaluation of the Pulse model. Vatten 1992, 48, 111–116. [Google Scholar]
- Arheimer, B. Evaluation of water quantity and quality modelling in ungauged European basins. In Predictions in Ungauged Basins: Promise and Progress; IAHS Publ. No. 303: Foz do Iguaçu, Brazil, 2006; pp. 99–107. [Google Scholar]
- Samuel, J.; Coulibaly, P.; Metcalfe, R.A. Identification of rainfall-runoff model for improved baseflow estimation in ungauged basins. Hydrol. Process. 2012, 26, 356–366. [Google Scholar] [CrossRef]
- Seibert, J.; Beven, K.J. Gauging the ungauged basin: How many discharge measurements are needed? Hydrol. Earth Syst. Sci. 2009, 13, 883–892. [Google Scholar] [CrossRef]
- Parra, V.; Fuentes-Aguilera, P.; Muñoz, E. Identifying advantages and drawbacks of two hydrological models based on a sensitivity analysis: A study in two Chilean watersheds. Hydrol. Sci. J. 2018, 63, 1831–1843. [Google Scholar] [CrossRef]
- Dakhlaoui, H.; Ruelland, D.; Tramblay, Y.; Bargaoui, Z. Evaluating the robustness of conceptual rainfall-runoff models under climate variability in northern Tunisia. J. Hydrol. 2017, 550, 201–217. [Google Scholar] [CrossRef]
- Poméon, T.; Jackisch, D.; Diekkrüger, B. Evaluating the performance of remotely sensed and reanalysed precipitation data over West Africa using HBV light. J. Hydrol. 2017, 547, 222–235. [Google Scholar] [CrossRef]
- Bergström, S. The HBV Model—Its Structure and Applications; Swedish Meteorological and Hydrological Institute: Norrköping, Sweden, 1992. [Google Scholar]
- Uhlenbrook, S.; Seibert, J.; Leibundgut, C.; Rodhe, A. Prediction uncertainty of conceptual rainfall- runoff models caused by problems in identifying model parameters and structure. Hydrol. Sci. J. 1999, 44, 779–797. [Google Scholar] [CrossRef]
- Seibert, J. Estimation of parameter uncertainty in the HBV model. Nord. Hydrol. 1997, 28, 247–262. [Google Scholar] [CrossRef]
- Keith, B.; Andrew, B. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar]
- Sorooshian, S.; Gupta, V.K. Automatic calibration of conceptual rainfall-runoff models: The question of parameter observability and uniqueness. Water Resour. Res. 1983, 19, 260–268. [Google Scholar] [CrossRef]
- Gan, T.Y.; Biftu, G.F. Automatic calibration of conceptual rainfall-runoff models: Optimization algorithms, catchment conditions and model structure. Water Resour. Res. 1996, 32, 3513–3524. [Google Scholar] [CrossRef]
- Hamby, D.M. A review of techniques for parameter sensitivity analysis of environmental models. Environ. Monit. Assess. 1994, 32, 135–154. [Google Scholar] [CrossRef]
- McCuen, R.H. The role of sensitivity analysis in hydrologic modeling. J. Hydrol. 1973, 18, 37–53. [Google Scholar] [CrossRef]
- Abebe, N.A.; Ogden, F.L.; Pradhan, N.R. Sensitivity and uncertainty analysis of the conceptual HBV rainfall-runoff model: Implications for parameter estimation. J. Hydrol. 2010, 389, 301–310. [Google Scholar] [CrossRef]
- Zelelew, M.B.; Alfredsen, K. Sensitivity-guided evaluation of the HBV hydrological model parameterization. J. Hydroinform. 2013, 15, 967–990. [Google Scholar] [CrossRef]
- Herman, J.D.; Reed, P.M.; Wagener, T. Time-varying sensitivity analysis clarifies the effects of watershed model formulation on model behavior. Water Resour. Res. 2013, 49, 1400–1414. [Google Scholar] [CrossRef]
- El Azhari, M.; Loudyi, D. Analysis of the Water-Energy nexus in central Oum Er-Rbia sub-basin—Morocco. Int. J. River Basin Manag. 2019, 17, 13–24. [Google Scholar] [CrossRef]
- Ouatiki, H.; Boudhar, A.; Tramblay, Y.; Jarlan, L.; Benabdelouhab, T.; Hanich, L.; El Meslouhi, M.; Chehbouni, A. Evaluation of TRMM 3B42 V7 Rainfall Product over the Oum Er Rbia Watershed in Morocco. Climate 2017, 5, 1. [Google Scholar] [CrossRef]
- Lebrini, Y.; Boudhar, A.; Hadria, R.; Lionboui, H.; Elmansouri, L.; Arrach, R.; Ceccato, P.; Benabdelouahab, T. Identifying Agricultural Systems Using SVM Classification Approach Based on Phenological Metrics in a Semi-arid Region of Morocco. Earth Syst. Environ. 2019, 3, 277–288. [Google Scholar] [CrossRef]
- Htitiou, A.; Boudhar, A.; Lebrini, Y.; Hadria, R.; Lionboui, H.; Elmansouri, L.; Tychon, B.; Benabdelouahab, T. The Performance of Random Forest Classification Based on Phenological Metrics Derived from Sentinel-2 and Landsat 8 to Map Crop Cover in an Irrigated Semi-arid Region. Remote Sens. Earth Syst. Sci. 2019, 2, 208–224. [Google Scholar] [CrossRef]
- Ouatiki, H.; Boudhar, A.; Ouhinou, A.; Arioua, A.; Hssaisoune, M.; Bouamri, H.; Benabdelouahab, T. Trend analysis of rainfall and drought over the Oum Er-Rbia River Basin in Morocco during 1970–2010. Arab. J. Geosci. 2019, 12, 128. [Google Scholar] [CrossRef]
- Boudhar, A.; Ouatiki, H.; Bouamri, H.; Lebrini, Y.; Karaoui, I.; Hssaisoune, M.; Arioua, A.; Benabdelouahab, T. Hydrological Response to Snow Cover Changes Using Remote Sensing over the Oum Er Rbia Upstream Basin, Morocco. In Mapping and Spatial Analysis of Socio-Economic and Environmental Indicators for Sustainable Development; Rebai, N., Mastere, M., Eds.; Springe Cham: Cham, Switzerland, 2020; pp. 95–102. [Google Scholar]
- Boudhar, A.; Hanich, L.; Boulet, G.; Duchemin, B.; Berjamy, B.; Chehbouni, A. Evaluation of the Snowmelt Runoff model in the Moroccan High Atlas Mountains using two snow-cover estimates. Hydrol. Sci. J. 2009, 54, 1094–1113. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An Approach toward a Rational. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A. MODIS/Terra Snow Cover Daily L3 Global 500m SIN Grid, Version 6. [h17v5]; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2016. [Google Scholar]
- Marchane, A.; Jarlan, L.; Hanich, L.; Boudhar, A.; Gascoin, S.; Tavernier, A.; Filali, N.; Page, M.L.; Hagolle, O.; Berjamy, B. Assessment of daily MODIS snow cover products to monitor snow cover dynamics over the Moroccan Atlas mountain range. Remote Sens. Environ. 2015, 160, 72–86. [Google Scholar] [CrossRef]
- Lee, S.; Klein, A.G.; Over, T.M. A comparison of MODIS and NOHRSC snow-cover products for simulating streamflow using the Snowmelt Runoff Model. Hydrol. Process. 2005, 19, 2951–2972. [Google Scholar] [CrossRef]
- Li, X.; Williams, M.W. Snowmelt runoff modelling in an arid mountain watershed, Tarim Basin, China. Hydrol. Process. 2008, 22, 3931–3940. [Google Scholar] [CrossRef]
- Sorman, A.A.; Sensoy, A.; Tekeli, A.E.; Sorman, A.Ü.; Akyurek, Z. Modelling and forecasting snowmelt runoff process using the HBV model in the eastern part of Turkey. Hydrol. Process. 2009, 23, 1031–1040. [Google Scholar] [CrossRef]
- Boudhar, A.; Boulet, G.; Hanich, L.; Sicart, J.E.; Chehbouni, A. Energy fluxes and melt rate of a seasonal snow cover in the Moroccan High Atlas. Hydrol. Sci. J. 2016, 61, 931–943. [Google Scholar] [CrossRef]
- Baba, M.W.; Gascoin, S.; Jarlan, L.; Simonneaux, V.; Hanich, L. Variations of the snow water equivalent in the ourika catchment (Morocco) over 2000–2018 using downscaled MERRA-2 data. Water 2018, 10, 1120. [Google Scholar] [CrossRef]
- Li, C.Z.; Wang, H.; Liu, J.; Yan, D.H.; Yu, F.L.; Zhang, L. Effect of calibration data series length on performance and optimal parameters of hydrological model. Water Sci. Eng. 2010, 3, 378–393. [Google Scholar]
- Xia, Y.; Yang, Z.-L.; Jackson, C.; Stoffa, P.L.; Sen, M.K. Impacts of data length on optimal parameter and uncertainty estimation of a land surface model. J. Geophys. Res. 2004, 109, 1–13. [Google Scholar] [CrossRef]
- Sorooshian, S. Evaluation of Maximum Likelihood Parameter Estimation Techniques for and Length on Model Credibility. Water Resour. Res. 1983, 19, 251–259. [Google Scholar] [CrossRef]
- Anctil, F.; Perrin, C.; Andréassian, V. Impact of the length of observed records on the performance of ANN and of conceptual parsimonious rainfall-runoff forecasting models. Environ. Model. Softw. 2004, 19, 357–368. [Google Scholar] [CrossRef]
- Viviroli, D.; Zappa, M.; Schwanbeck, J.; Gurtz, J.; Weingartner, R. Continuous simulation for flood estimation in ungauged mesoscale catchments of Switzerland—Part I: Modelling framework and calibration results. J. Hydrol. 2009, 377, 191–207. [Google Scholar] [CrossRef]
- Jain, S.K. Calibration of conceptual models for rainfall-runoff simulation. Hydrol. Sci. J. 1993, 38, 431–441. [Google Scholar] [CrossRef]
- Gan, T.Y.; Dlamini, E.M.; Biftu, G.F. Effects of model complexity and structure, data quality, and objective functions on hydrologic modeling. J. Hydrol. 1997, 192, 81–103. [Google Scholar] [CrossRef]
- Tripp, D.R.; Niemann, J.D. Evaluating the parameter identifiability and structural validity of a probability-distributed model for soil moisture. J. Hydrol. 2008, 353, 93–108. [Google Scholar] [CrossRef]
- Osuch, M.; Romanowicz, R.J.; Booij, M.J. The influence of parametric uncertainty on the relationships between HBV model parameters and climatic characteristics. Hydrol. Sci. J. 2015, 60, 1299–1316. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J., Jr. Evaluating the use of “Goodness of Fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 2013, 2, 37–41. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Am. Soc. Agric. Biol. Eng. 2007, 50, 885–900. [Google Scholar]
- Ritter, A.; Muñoz-carpena, R. Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]
- Biondi, D.; Freni, G.; Iacobellis, V.; Mascaro, G.; Montanari, A. Validation of hydrological models: Conceptual basis, methodological approaches and a proposal for a code of practice. Phys. Chem. Earth 2012, 42, 70–76. [Google Scholar] [CrossRef]
- Pushpalatha, R.; Perrin, C.; Le, N.; Andréassian, V. A review of efficiency criteria suitable for evaluating low-flow simulations. J. Hydrol. 2012, 420, 171–182. [Google Scholar] [CrossRef]
- Willmott, C.J.; Ackleson, S.G.; Davis, R.E.; Feddema, J.J.; Klink, K.M.; Legates, D.R.; O’Donnell, J.; Rowe, C.M. Statistics for the evaluation and comparison of models. J. Geophys. Res. 1985, 90, 8995–9005. [Google Scholar] [CrossRef]
- Garrick, M.; Cunnane, C.; Nash, J.E. A criterion of efficiency for rainfall-runoff models. J. Hydrol. 1978, 36, 375–381. [Google Scholar] [CrossRef]
- Singh, J.; Knapp, H.V.; Demissie, M. Hydrologic Modeling of the Iroquois River Watershed Using HSPF and SWAT. J. Am. Water Resour. Assoc. 2005, 41, 343–360. [Google Scholar] [CrossRef]
- Beven, K. A manifesto for the equifinality thesis. J. Hydrol. 2006, 320, 18–36. [Google Scholar] [CrossRef]
- Klemeš, V. Operational testing of hydrological simulation models. Hydrol. Sci. J. 1986, 31, 13–24. [Google Scholar] [CrossRef]
- Xu, H.; Xu, C.; Chen, H.; Zhang, Z.; Li, L. Assessing the influence of rain gauge density and distribution on hydrological model performance in a humid region of China Hongliang. J. Hydrol. 2013, 505, 1–12. [Google Scholar] [CrossRef]
- Dong, X.; Dohmen-Janssen, C.M.; Booij, M.J. Appropriate spatial sampling of rainfall for flow simulation. Hydrol. Sci. J. 2005, 50, 279–297. [Google Scholar] [CrossRef]
- Merz, R.; Parajka, J.; Blöschl, G. Time stability of catchment model parameters: Implications for climate impact analyses. Water Resour. Res. 2011, 47, 1–17. [Google Scholar] [CrossRef]
- Coron, L.; Andréassian, V.; Perrin, C.; Lerat, J.; Vaze, J.; Bourqui, M.; Hendrickx, F. Crash testing hydrological models in contrasted climate conditions: An experiment on 216 Australian catchments. Water Resour. Res. 2012, 48, 1–17. [Google Scholar] [CrossRef]
- Uhlenbrook, S.; Holocher, J.; Leibundgut, C.; Seibert, J. Using a conceptual rainfall-runoff model on different scales by comparing a headwater with larger basins. In Hydrology, Water Resources and Ecology in Headwaters; IAHS Publ. No. 248: Meran, Italy, 1998; pp. 297–305. [Google Scholar]
- Ouyang, S.; Puhlmann, H.; Wang, S.; von Wilpert, K.; Sun, O.J. Parameter uncertainty and identifiability of a conceptual semi-distributed model to simulate hydrological processes in a small headwater catchment in Northwest China. Ecol. Process. 2014, 3, 1–14. [Google Scholar] [CrossRef][Green Version]
- Seibert, J. Regionalisation of parameters for a conceptual rainfall-runoff model. Agric. For. Meteorol. 1999, 98, 279–293. [Google Scholar] [CrossRef]

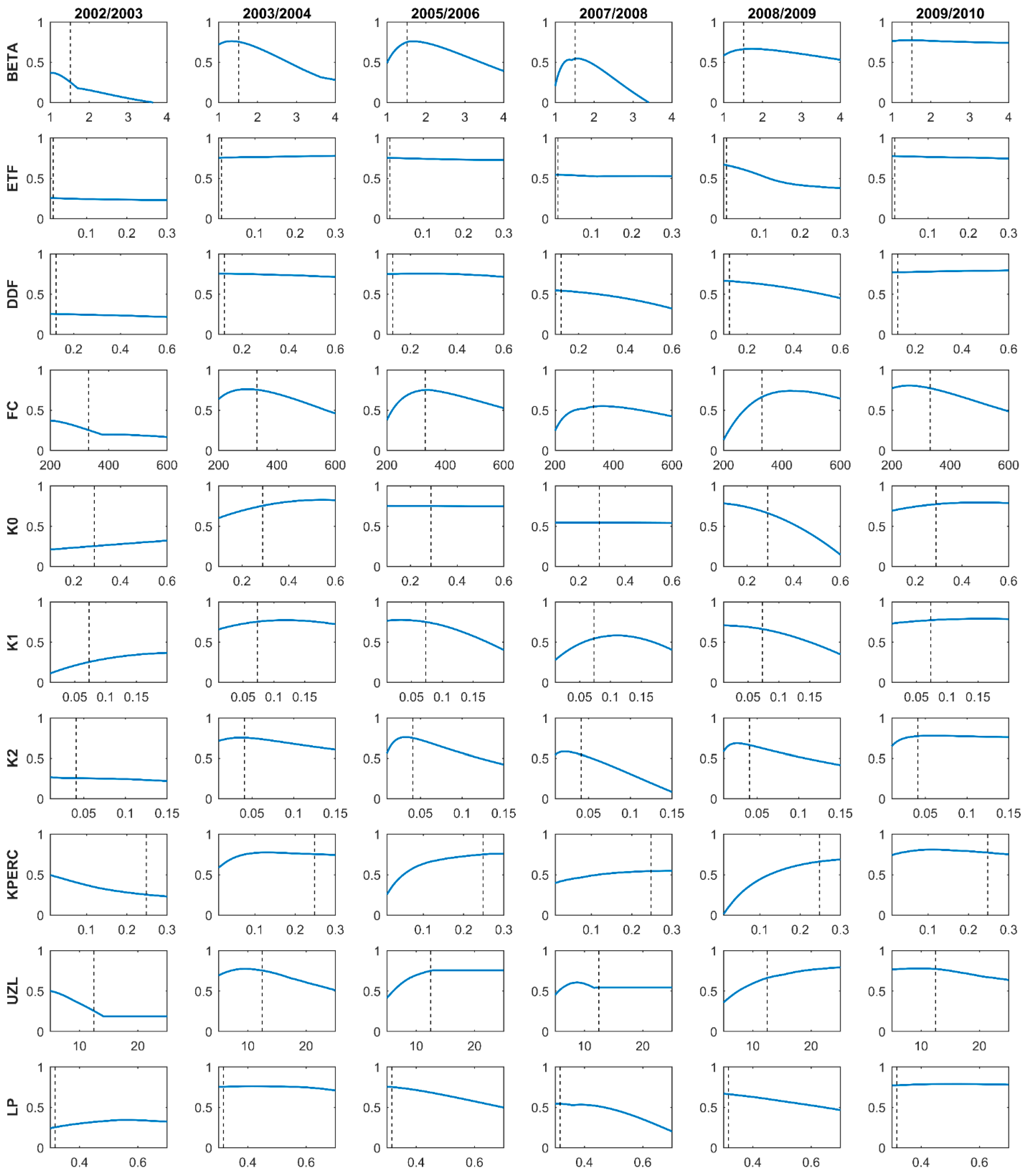
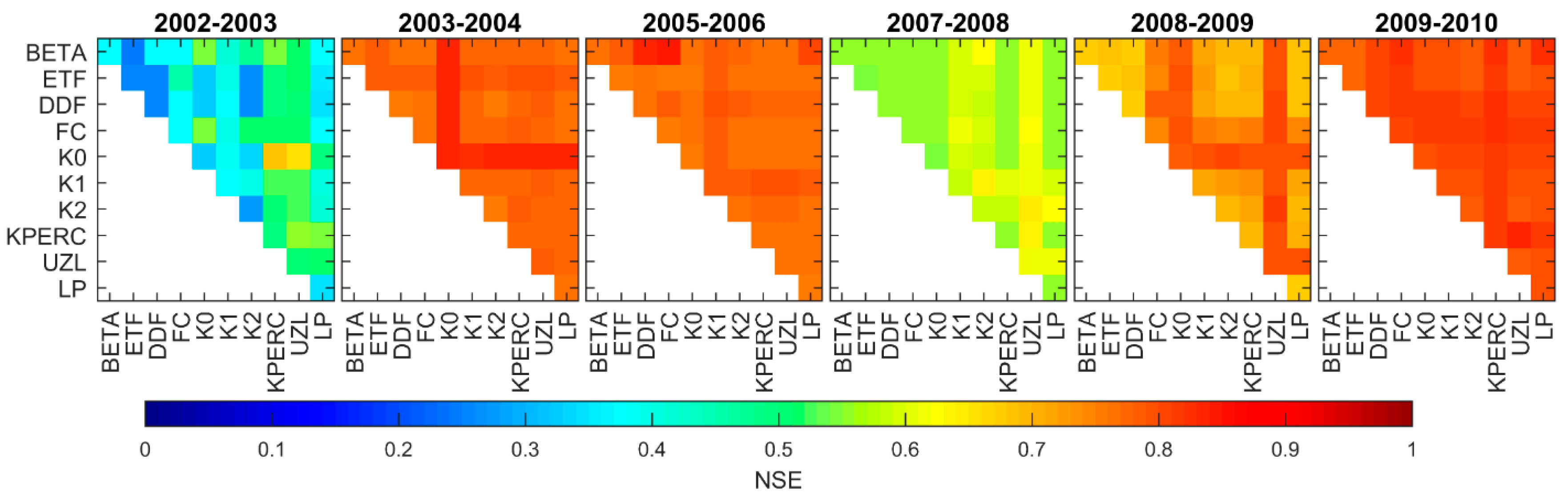
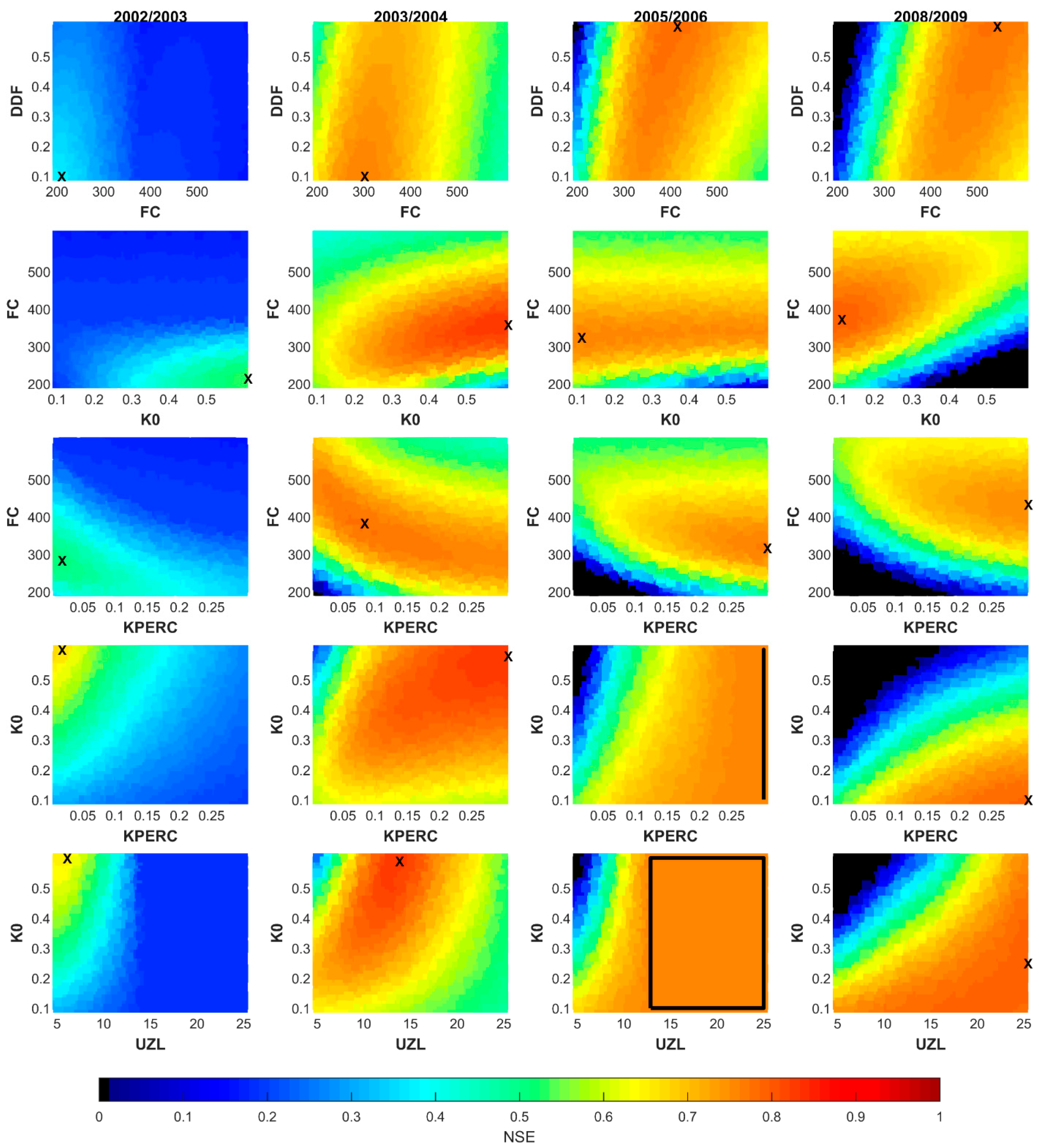
| Years | SCA [%] | Rainfall [mm] | Temperature [°C] | Streamflow [m3/s] |
|---|---|---|---|---|
| 2001/2002 | −3.78 | −57.54 | 0.38 | −3.47 |
| 2002/2003 | −3.22 | 4.96 | 0.77 | −1.75 |
| 2003/2004 | −0.96 | 163.86 | −0.17 | 3.76 |
| 2004/2005 | 0.92 | −133.64 | 0.16 | −3.94 |
| 2005/2006 | 1.60 | 31.96 | −0.28 | 1.54 |
| 2006/2007 | −2.96 | −145.04 | −0.45 | −3.57 |
| 2007/2008 | −0.03 | −75.64 | 0.18 | −2.55 |
| 2008/2009 | 10.90 | 207.91 | −1.41 | 11.66 |
| 2009/2010 | −2.48 | 258.31 | 0.83 | 16.04 |
| Parameter | Definition | Minimum | Maximum | Unit |
|---|---|---|---|---|
| BETA | Shape coefficient | 1 | 4 | - |
| ETF | Temperature correction factor | 0.01 | 0.3 | °C−1 |
| TT | Temperature threshold | 0 | 0 | °C |
| DDF | Degree day factor | 0.1 | 0.6 | mm °C−1 d−1 |
| FC | Field capacity | 200 | 600 | mm |
| K0 | Recession coefficient | 0.1 | 0.6 | d−1 |
| K1 | Recession coefficient | 0.01 | 0.2 | d−1 |
| K2 | Recession coefficient | 0.01 | 0.15 | d−1 |
| KPERC | Percolation coefficient | 0.01 | 0.3 | d−1 |
| UZL | Upper reservoir threshold | 5 | 25 | mm |
| LP | Limit for potential evapotranspiration | 0.3 | 0.7 | - |
| Title Years | Title | 2002–2003 | 2003–2004 | 2004–2005 | 2005–2006 | 2006–2007 | 2007–2008 | 2008–2009 | 2009–2010 |
|---|---|---|---|---|---|---|---|---|---|
| 2002–2003 | NSE | 0.76 | 0.69 | 0.69 | 0.32 | 0.73 | 0.67 | 0.44 | 0.57 |
| RMSE | 6.84 | 7.71 | 7.71 | 11.44 | 7.2 | 7.91 | 10.35 | 9.11 | |
| 2003–2004 | NSE | 0.84 | 0.88 | 0.87 | 0.86 | 0.87 | 0.86 | 0.8 | 0.85 |
| RMSE | 8.15 | 7.05 | 7.25 | 7.77 | 7.28 | 7.78 | 9.11 | 7.88 | |
| 2004–2005 | NSE | 0.44 | 0.44 | 0.44 | 0.43 | 0.44 | 0.44 | 0.44 | 0.44 |
| RMSE | 3.88 | 3.87 | 3.86 | 3.9 | 3.88 | 3.86 | 3.86 | 3.88 | |
| 2005–2006 | NSE | 0.58 | 0.89 | 0.9 | 0.9 | 0.79 | 0.85 | 0.84 | 0.9 |
| RMSE | 7.82 | 4.03 | 3.74 | 3.72 | 5.52 | 4.67 | 4.77 | 3.83 | |
| 2006–2007 | NSE | 0.42 | 0.42 | 0.37 | 0.36 | 0.43 | 0.41 | 0.41 | 0.42 |
| RMSE | 4.48 | 4.5 | 4.7 | 4.71 | 4.46 | 4.52 | 4.52 | 4.5 | |
| 2007–2008 | NSE | 0.64 | 0.68 | 0.68 | 0.62 | 0.68 | 0.68 | 0.67 | 0.59 |
| RMSE | 3.98 | 3.7 | 3.7 | 4.07 | 3.7 | 3.7 | 3.81 | 4.24 | |
| 2008–2009 | NSE | 0.65 | 0.78 | 0.81 | 0.81 | 0.81 | 0.81 | 0.81 | 0.62 |
| RMSE | 12.38 | 9.87 | 9.12 | 9.12 | 9.12 | 9.12 | 9.12 | 12.85 | |
| 2009–2010 | NSE | 0.83 | 0.87 | 0.87 | 0.87 | 0.86 | 0.86 | 0.79 | 0.87 |
| RMSE | 14.9 | 13.34 | 13.25 | 13.25 | 13.48 | 13.53 | 16.57 | 13.25 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouatiki, H.; Boudhar, A.; Ouhinou, A.; Beljadid, A.; Leblanc, M.; Chehbouni, A. Sensitivity and Interdependency Analysis of the HBV Conceptual Model Parameters in a Semi-Arid Mountainous Watershed. Water 2020, 12, 2440. https://doi.org/10.3390/w12092440
Ouatiki H, Boudhar A, Ouhinou A, Beljadid A, Leblanc M, Chehbouni A. Sensitivity and Interdependency Analysis of the HBV Conceptual Model Parameters in a Semi-Arid Mountainous Watershed. Water. 2020; 12(9):2440. https://doi.org/10.3390/w12092440
Chicago/Turabian StyleOuatiki, Hamza, Abdelghani Boudhar, Aziz Ouhinou, Abdelaziz Beljadid, Marc Leblanc, and Abdelghani Chehbouni. 2020. "Sensitivity and Interdependency Analysis of the HBV Conceptual Model Parameters in a Semi-Arid Mountainous Watershed" Water 12, no. 9: 2440. https://doi.org/10.3390/w12092440
APA StyleOuatiki, H., Boudhar, A., Ouhinou, A., Beljadid, A., Leblanc, M., & Chehbouni, A. (2020). Sensitivity and Interdependency Analysis of the HBV Conceptual Model Parameters in a Semi-Arid Mountainous Watershed. Water, 12(9), 2440. https://doi.org/10.3390/w12092440





