Variation in Anisotropy with Dehydration in Layered Sandstone
Abstract
:1. Introduction
2. Experimental Design
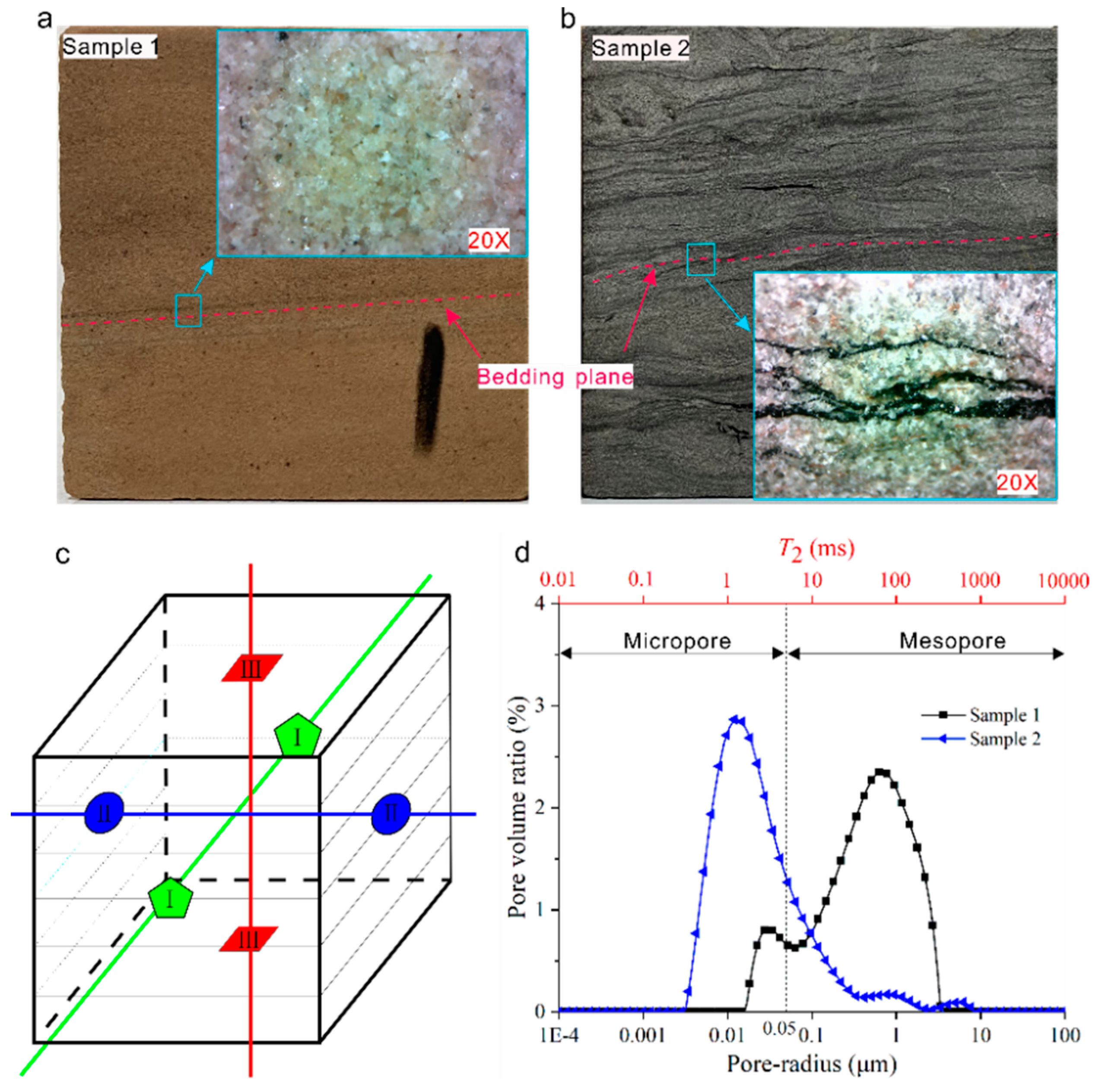
2.1. Sample Preparation
- (1)
- Sample processing and selection
- (2)
- Preparation of samples with different saturations
2.2. Principles of the NMR Tests
2.2.1. Basic Principles of NMR
2.2.2. Measurement of the Pore Structure of Rocks
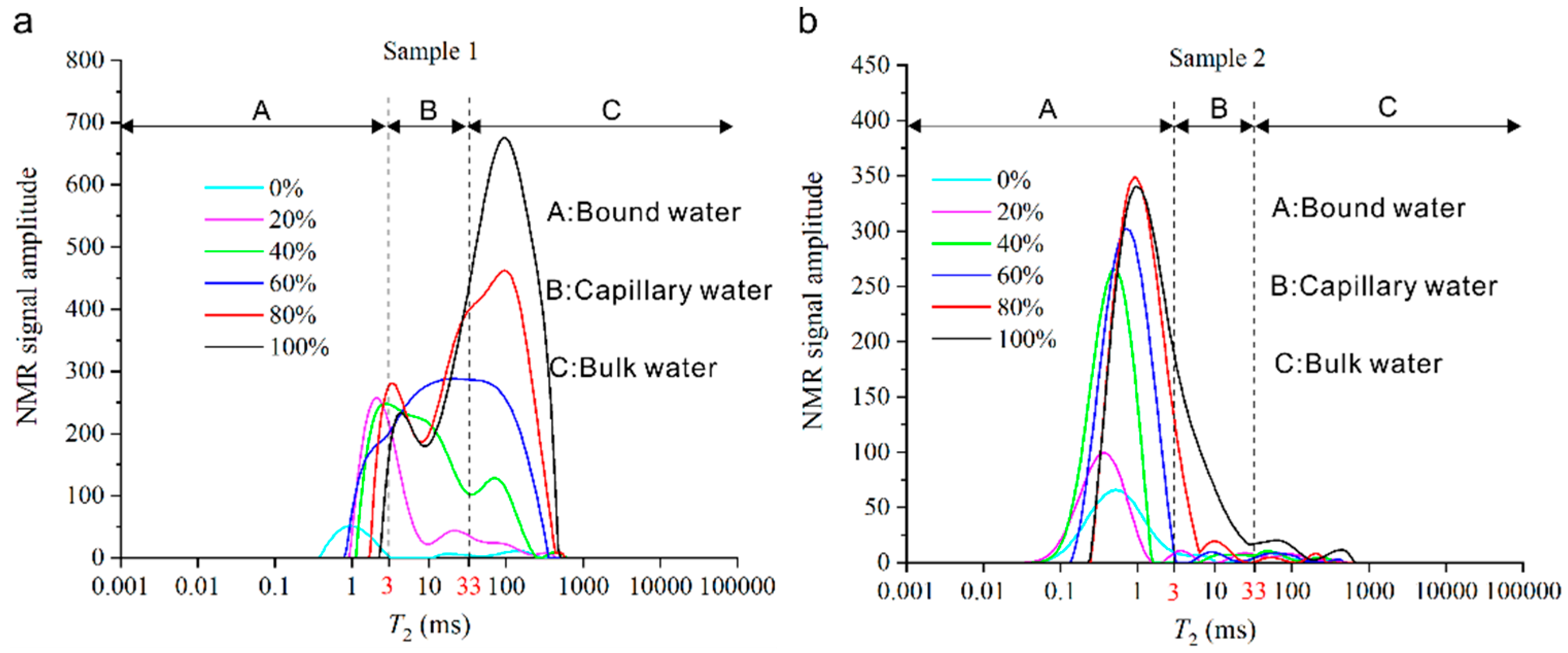
2.2.3. Categorization of Pore Water
2.3. Experimental Design
- (1)
- Ultrasonic testing of rock samples under different saturations
- (2)
- NMR testing of rock samples at different saturations
3. Results
3.1. Variation in P-Wave Velocity of Layered Sandstone during Dehydration
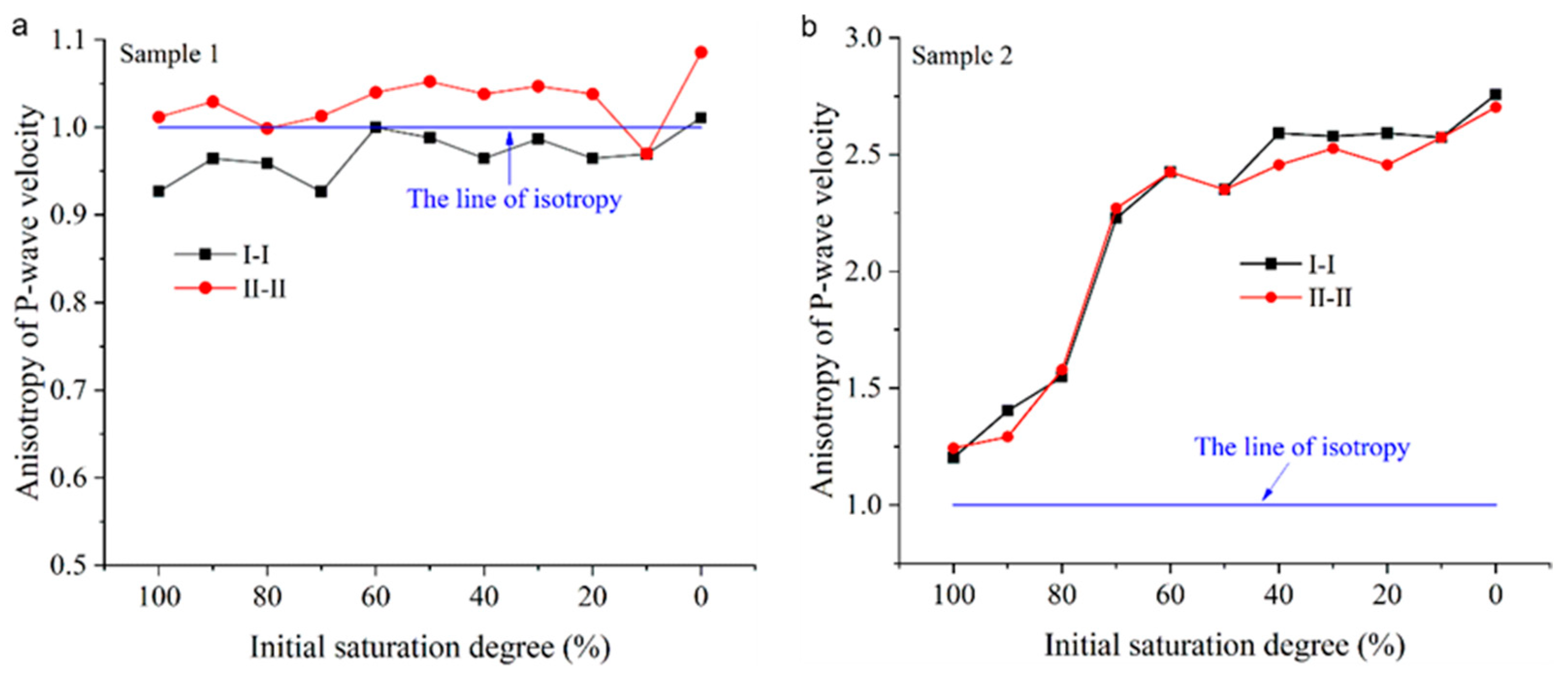
3.2. Variation in Anisotropy in Bedded Sandstone during Dehydration
3.3. Moisture State in Layered Sandstone during Dehydration
3.3.1. T2 Spectra of Rocks under Different Saturations
3.3.2. Variations in Pore Water Type with Different Saturations
4. Discussion
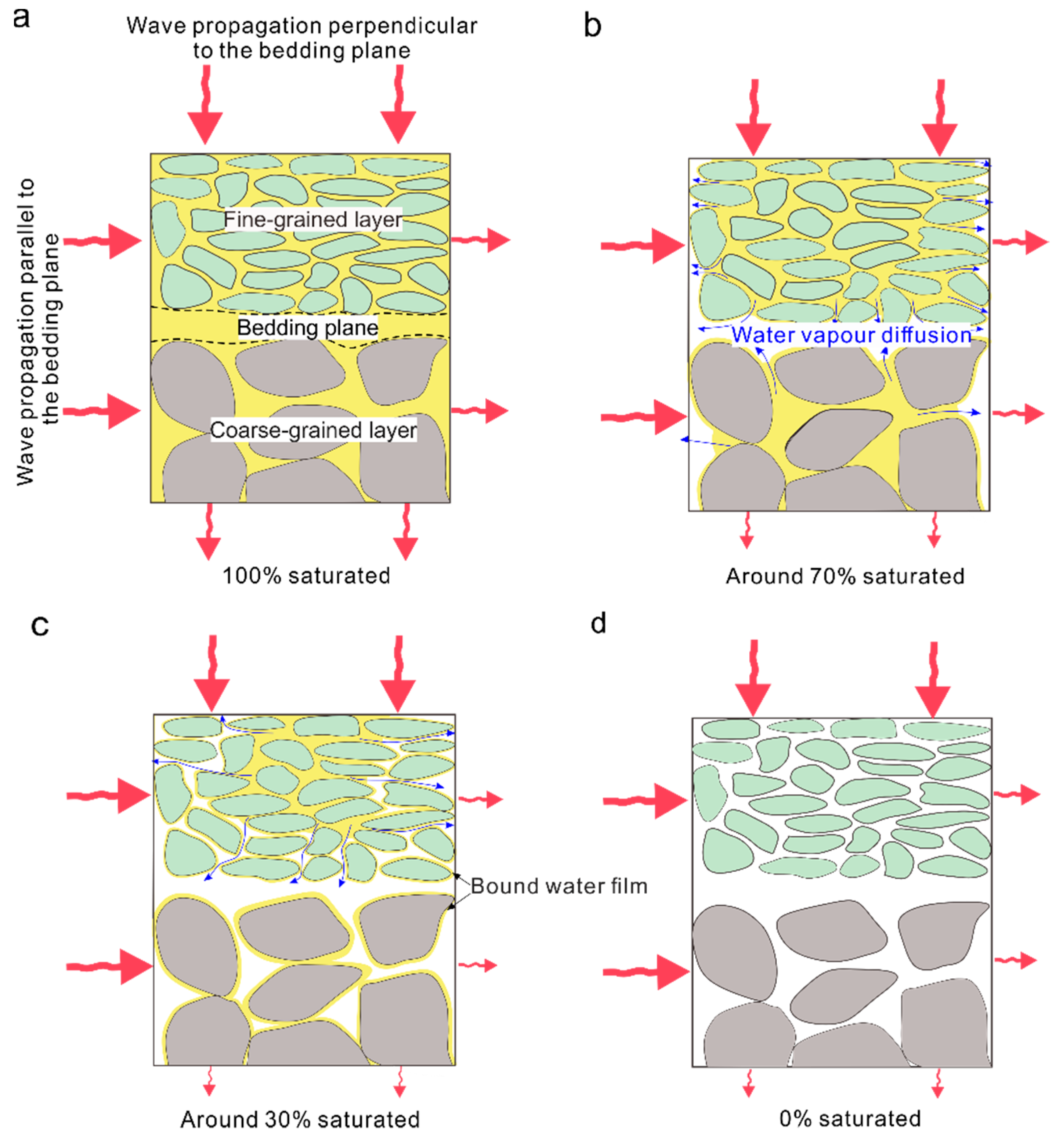
4.1. Dehydration Process of Pore Water in Bedded Sandstone
4.2. Mechanism of Dehydration Altering Anisotropy in Bedded Rocks
5. Conclusions
- (1)
- Sandstone with more obvious bedding bears stronger anisotropy. For the sandstone with no obvious bedding structure, the wave velocities in the directions parallel and perpendicular to the bedding plane were close, and both decreased gradually with dehydration. For the sandstone with an obvious bedding structure, the P-wave velocity perpendicular to the bedding plane was much lower than that in the parallel direction and the difference between them increased with dehydration.
- (2)
- In the sandstone with no obvious bedding structure, the anisotropy index fluctuated around 1 with changes in saturation. For the sandstone with the obvious bedding structure, the anisotropy showed a two-stage trend with decreases in saturation. At saturations > 70%, the anisotropy index increased rapidly from about 1.2 to about 2.3; and at saturations < 70%, it increased slightly.
- (3)
- During the dehydration process in the sandstone with no obvious bedding structure, at saturations > 50%, the decrease in pore water content was mainly due to the decreased of bulk water. At saturations of 50–10%, it was mainly caused by bulk water and capillary water. At saturation < 10%, it was mainly because of bound water. For the sandstone with an obvious bedding structure, the decrease in pore water was caused by capillary water at saturations > 70% and by bound water at saturations < 70%.
- (4)
- The bedding structure controls the dehydration process. The different dehydration rates of pore water in different directions inevitably lead to heterogeneity in moisture state that change the anisotropy of the rock, which is reflected by the non-synchronous changes in P-wave velocities in different directions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Johnston, J.E.; Christensen, N.I. Seismic anisotropy of shales. J. Geophys. Res. Solid Earth 1995, 100, 5991–6003. [Google Scholar] [CrossRef] [Green Version]
- Ademović, N.; Kurtović, A. Influence of planes of anisotropy on physical and mechanical properties of freshwater limestone (Mudstone). Constr. Build. Mater. 2021, 268, 121174. [Google Scholar] [CrossRef]
- Zhang, F.; Xie, S.Y.; Hu, D.W.; Shao, J.F.; Gatmiri, B. Effect of water content and structural anisotropy on mechanical property of claystone. Appl. Clay Sci. 2012, 69, 79–86. [Google Scholar] [CrossRef]
- Vernik, L.; Liu, X. Velocity anisotropy in shales: A petrophysical study. Geophysics 1997, 62, 521–532. [Google Scholar] [CrossRef]
- Lloret-Cabot, M.; Wheeler, S.J.; Pineda, J.A.; Romero, E.; Sheng, D. From saturated to unsaturated conditions and vice versa. Acta Geotech. 2018, 13, 15–37. [Google Scholar] [CrossRef] [Green Version]
- Du, C.; Sun, L.; Qin, B.; Xu, J.; Liu, Y. Shear Behavior and Anisotropy Characteristics of the Fracture Morphology of Sandstone with Different Water Contents. Geofluids 2020, 2020, 4543719. [Google Scholar] [CrossRef]
- Domenico, S.N. Effect of Water Saturation on Seismic Reflectivity of Sand Reservoirs Encased in Shale. Geophysics 1974, 39, 759–769. [Google Scholar] [CrossRef]
- Hamzaban, M.-T.; Buyuksagis, I.S.; Fasaghandis, M.; Touranchezadeh, A. The effect of saturation on the physical and mechanical behavior of some rock samples. Civil Eng. Limits 2021, 3, 23–31. [Google Scholar] [CrossRef]
- Zhou, Z.; Cai, X.; Cao, W.; Li, X.; Xiong, C. Influence of Water Content on Mechanical Properties of Rock in Both Saturation and Drying Processes. Rock Mech. Rock Eng. 2016, 49, 3009–3025. [Google Scholar] [CrossRef]
- Sarout, J.; Esteban, L.; Delle Piane, C.; Maney, B.; Dewhurst, D.N. Elastic anisotropy of Opalinus Clay under variable saturation and triaxial stress. Geophys. J. Int. 2014, 198, 1662–1682. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.Y.; Zhuang, L.; Yang, H.; Kim, H.; Min, K.-B. Strength Anisotropy of Berea Sandstone: Results of X-ray Computed Tomography, Compression Tests, and Discrete Modeling. Rock Mech. Rock Eng. 2016, 49, 1201–1210. [Google Scholar] [CrossRef]
- Li, X.; Lei, X.; Li, Q. Response of Velocity Anisotropy of Shale under Isotropic and Anisotropic Stress Fields. Rock Mech. Rock Eng. 2018, 51, 695–711. [Google Scholar] [CrossRef]
- Wang, P.; Cai, M.; Ren, F. Anisotropy and directionality of tensile behaviours of a jointed rock mass subjected to numerical Brazilian tests. Tunn. Undergr. Space Technol. 2018, 73, 139–153. [Google Scholar] [CrossRef]
- Jin, Z.; Li, W.; Jin, C.; Hambleton, J.; Cusatis, G. Anisotropic elastic, strength, and fracture properties of Marcellus shale. Int. J. Rock Mech. Min. Sci. 2018, 109, 124–137. [Google Scholar] [CrossRef] [Green Version]
- Ramamurthy, T.; Rao, G.V.; Singh, J. Engineering behaviour of phyllites. Eng. Geol. 1993, 33, 209–225. [Google Scholar] [CrossRef]
- Louis, L.; Baud, P.; Wong, T.-F. Microstructural Inhomogeneity and Mechanical Anisotropy Associated with Bedding in Rothbach Sandstone. In Rock Physics and Natural Hazards; Vinciguerra, S., Bernabé, Y., Eds.; Birkhäuser Basel: Basel, Switzerland, 2009; pp. 1063–1087. [Google Scholar]
- Gatelier, N.; Pellet, F.; Loret, B. Mechanical damage of an anisotropic porous rock in cyclic triaxial tests. Int. J. Rock Mech. Min. Sci. 2002, 39, 335–354. [Google Scholar] [CrossRef]
- Ding, Q.-L.; Song, S. Experimental Investigation of the Relationship between the P-Wave Velocity and the Mechanical Properties of Damaged Sandstone. Adv. Mater. Sci. Eng. 2016, 2016, 7654234. [Google Scholar] [CrossRef] [Green Version]
- Chawre, B. Correlations between ultrasonic pulse wave velocities and rock properties of quartz-mica schist. J. Rock Mech. Geotech. Eng. 2018, 10, 594–602. [Google Scholar] [CrossRef]
- Best, A.I.; McCann, C.; Sothcott, J. The relationships between the velocities, attenuations and petrophysical properties of reservoir sedimentary rocks1. Geophys. Prospect. 1994, 42, 151–178. [Google Scholar] [CrossRef]
- Ding, C.; Hu, D.; Zhou, H.; Lu, J.; Lv, T. Investigations of P-Wave velocity, mechanical behavior and thermal properties of anisotropic slate. Int. J. Rock Mech. Min. Sci. 2020, 127, 104176. [Google Scholar] [CrossRef]
- Dai, F.; Xia, K. Loading Rate Dependence of Tensile Strength Anisotropy of Barre Granite. Pure Appl. Geophys. 2010, 167, 1419–1432. [Google Scholar] [CrossRef]
- Dai, F.; Xia, K.; Zuo, J.P.; Zhang, R.; Xu, N.W. Static and Dynamic Flexural Strength Anisotropy of Barre Granite. Rock Mech. Rock Eng. 2013, 46, 1589–1602. [Google Scholar] [CrossRef]
- Shi, X.; Jing, H.; Yin, Q.; Zhao, Z.; Han, G.; Gao, Y. Investigation on physical and mechanical properties of bedded sandstone after high-temperature exposure. Bull. Eng. Geol. Environ. 2020, 79, 2591–2606. [Google Scholar] [CrossRef]
- Jia, H.; Ding, S.; Zi, F.; Li, G.; Yao, Y. Development of Anisotropy in Sandstone Subjected to Repeated Frost Action. Rock Mech. Rock Eng. 2021, 54, 1863–1874. [Google Scholar] [CrossRef]
- Zamora, M. Experimental study of acoustic anisotropy and birefringence in dry and saturated Fontainebleau sandstone. Geophysics 1990, 55, 1455–1465. [Google Scholar] [CrossRef] [Green Version]
- Ding, P.; Di, B.; Wang, D.; Wei, J.; Zeng, L. P- and S-wave velocity and anisotropy in saturated rocks with aligned cracks. Wave Motion 2018, 81, 1–14. [Google Scholar] [CrossRef]
- Do, D.-P.; Tran, N.-H.; Dang, H.-L.; Hoxha, D. Closed-form solution of stress state and stability analysis of wellbore in anisotropic permeable rocks. Int. J. Rock Mech. Min. Sci. 2019, 113, 11–23. [Google Scholar] [CrossRef]
- Jia, H.; Ding, S.; Wang, Y.; Zi, F.; Sun, Q.; Yang, G. An NMR-based investigation of pore water freezing process in sandstone. Cold Reg. Sci. Technol. 2019, 168, 102893. [Google Scholar] [CrossRef]
- Jia, H.; Ding, S.; Zi, F.; Dong, Y.; Shen, Y. Evolution in sandstone pore structures with freeze-thaw cycling and interpretation of damage mechanisms in saturated porous rocks. Catena 2020, 195, 104915. [Google Scholar] [CrossRef]
- Jia, H.; Zi, F.; Yang, G.; Li, G.; Shen, Y.; Sun, Q.; Yang, P. Influence of Pore Water (Ice) Content on the Strength and Deformability of Frozen Argillaceous Siltstone. Rock Mech. Rock Eng. 2020, 53, 967–974. [Google Scholar] [CrossRef]
- Godefroy, S.; Korb, J.P.; Fleury, M.; Bryant, R.G. Surface nuclear magnetic relaxation and dynamics of water and oil in macroporous media. Phys. Rev. E 2001, 64, 021605. [Google Scholar] [CrossRef] [PubMed]
- Matteson, A.; Tomanic, J.; Herron, M.; Allen, D.; Kenyon, W. NMR Relaxation of Clay-Brine Mixtures. SPE Reserv. Eval. Eng. 2000, 3, 408–413. [Google Scholar] [CrossRef]
- Martinez, G.A.; Davis, L.A. Petrophysical Measurements on Shales Using NMR. In SPE/AAPG Western Regional Meeting; OnePetro: Richardson, TX, USA, 2000. [Google Scholar]
- Li, X.; Zhang, L.M. Characterization of dual-structure pore-size distribution of soil. Can. Geotech. J. 2009, 46, 129–141. [Google Scholar] [CrossRef] [Green Version]
- Inoue, M.; Ohomi, M. Relation between Uniaxial Compressive Strength and Elastic Wave Velocity of Soft Rock. In Proceedings of the ISRM International Symposium, Tokyo, Japan, 9–13 September 1981. [Google Scholar]
- Deng, H.F.; Yuan, X.F.; Li, J.L.; He, M.; Luo, S.; Zhu, M. Experimental Research on Influence of Saturation Degree on Sandstone Longitudinal Wave Velocity and Strength. Chin. J. Rock Mech. Eng. 2013, 32, 1626–1631. [Google Scholar]
- Amalokwu, K.; Chapman, M.; Best, A.I.; Minshull, T.A.; Li, X.-Y. Water saturation effects on P-wave anisotropy in synthetic sandstone with aligned fractures. Geophys. J. Int. 2015, 202, 1088–1095. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, F.; Yang, L.; Jia, H. Variation in Anisotropy with Dehydration in Layered Sandstone. Water 2021, 13, 2224. https://doi.org/10.3390/w13162224
Liu F, Yang L, Jia H. Variation in Anisotropy with Dehydration in Layered Sandstone. Water. 2021; 13(16):2224. https://doi.org/10.3390/w13162224
Chicago/Turabian StyleLiu, Fujun, Liu Yang, and Hailiang Jia. 2021. "Variation in Anisotropy with Dehydration in Layered Sandstone" Water 13, no. 16: 2224. https://doi.org/10.3390/w13162224
APA StyleLiu, F., Yang, L., & Jia, H. (2021). Variation in Anisotropy with Dehydration in Layered Sandstone. Water, 13(16), 2224. https://doi.org/10.3390/w13162224





