Integrating Structural Resilience in the Design of Urban Drainage Networks in Flat Areas Using a Simplified Multi-Objective Optimization Framework
Abstract
:1. Introduction
2. Materials and Methods
2.1. Problem Formulation and the Proposed Method
2.2. Layout Generator (Hanging Gardens Algorithm)
2.3. Sizing the Network’s Components (Adaptive Algorithm)
- For each manhole, place upstream pipes at elevations higher than the downstream one;
- choose sewer diameters from the commercial list;
- maintain the minimum buried depth to prevent damages from the traffic loads and other surface activities; and
- for each manhole, assign the outlet pipe’s diameter equal to or greater than the upstream inlet pipes’ (telescopic pattern).
2.4. Simplified Cost Functions (Proposed Indices)
2.4.1. Cost of UDSs
2.4.2. Elevation Rank Index (ERI)
2.4.3. Length Area Index
2.4.4. Area Diameter Index ()
2.4.5. Structural Resilience Index (SRI)
3. Results and Discussion
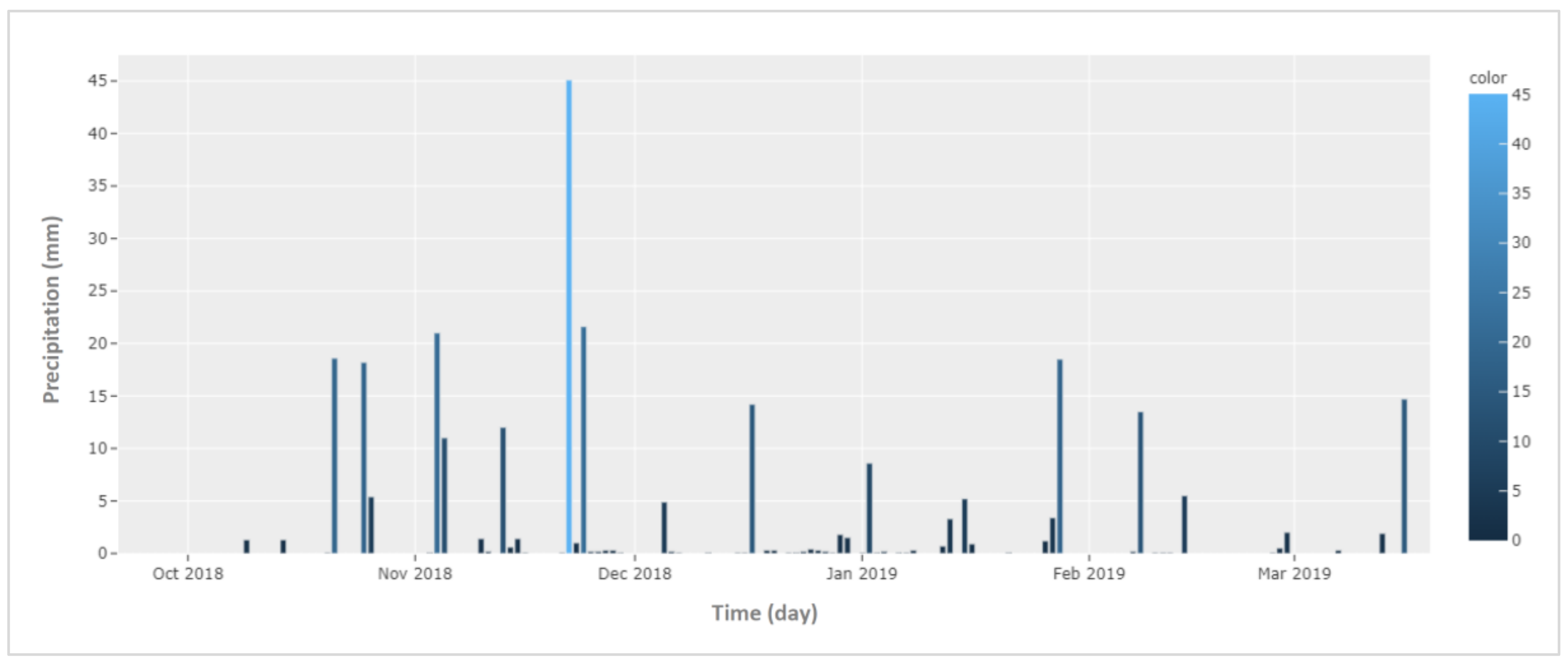
3.1. Case Study
3.2. Analyzing the Cost Indices
3.3. Introducing the Fast MOO Framework
3.4. MOO Results Analysis
3.5. Analyzing the Computational Efficiency
3.6. Analyzing the Structural Resilience
3.7. Analyzing the Functional Resilience
4. Summary and Conclusions
- The proposed framework can significantly reduce the computational effort needed for optimizing UDSs in flat areas without a noticeable sacrifice in the quality of solutions. Doing that will increase the potential of the proposed frameworks and algorithms to be incorporated into commercial UDS design software to deliver more sustainable and less expensive designs.
- As the number of required hydraulic simulations for optimizing sewers’ sizes was significantly reduced (98% in our test case), it is possible to consider different types of design storms and historical precipitation data within the proposed framework. That leads, apparently, to more robust designs.
- The proposed indicator of structural resilience can reliably evaluate the structural resilience of different UDSs. Furthermore, the proposed framework can integrate structural resilience into the UDS design procedure.
- In flat areas, the layout configuration and the degree of centralization are the most challenging and decisive problems for optimizing the UDSs, and sizing the sewers can be handled with simple optimization methods, as proposed in this study.
- There is no apparent relation between functional and structural resilience in UDSs. Therefore, to build these different types of resilience into the system, completely different strategies must be taken.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Butler, D.; Davies, J. Urban Drainage, 3rd ed.; CRC Press: London, UK, 2011; ISBN 9781315272535. [Google Scholar]
- Haghighatafshar, S.; Nordlöf, B.; Roldin, M.; Gustafsson, L.G.; Jansen, J.L.C.; Jönsson, K. Efficiency of blue-green stormwater retrofits for flood mitigation–Conclusions drawn from a case study in Malmö, Sweden. J. Environ. Manag. 2018, 207, 60–69. [Google Scholar] [CrossRef] [PubMed]
- Diogo, A.F.; Barros, L.T.; Santos, T.J.; Temido, J.S. An effective and comprehensive model for optimal rehabilitation of separate sanitary sewer systems. Sci. Total. Environ. 2018, 612, 1042–1057. [Google Scholar] [CrossRef] [PubMed]
- Butler, D.; Farmani, R.; Fu, G.; Ward, S.E.; Diao, K.; Astaraie-Imani, M. A New Approach to Urban Water Management: Safe and Sure. Procedia Eng. 2014, 89, 347–354. [Google Scholar] [CrossRef] [Green Version]
- Dong, X.; Guo, H.; Zeng, S. Enhancing future resilience in urban drainage system: Green versus grey infrastructure. Water Res. 2017, 124, 280–289. [Google Scholar] [CrossRef] [PubMed]
- Sweetapple, C.; Fu, G.; Butler, D. Reliable, Robust, and Resilient System Design Framework with Application to Wastewater-Treatment Plant Control. J. Environ. Eng. 2017, 143, 04016086. [Google Scholar] [CrossRef]
- Mugume, S.N.; Gomez, D.E.; Fu, G.; Farmani, R.; Butler, D. A global analysis approach for investigating structural resilience in urban drainage systems. Water Res. 2015, 81, 15–26. [Google Scholar] [CrossRef] [Green Version]
- Mugume, S.N.; Butler, D. Evaluation of functional resilience in urban drainage and flood management systems using a global analysis approach. Urban Water J. 2016, 14, 727–736. [Google Scholar] [CrossRef]
- Eggimann, S.; Truffer, B.; Maurer, M. To connect or not to connect? Modelling the optimal degree of centralisation for wastewater infrastructures. Water Res. 2015, 84, 218–231. [Google Scholar] [CrossRef] [Green Version]
- Eggimann, S. The Optimal Degree of Centralisation for Wastewater Infrastructures. A Model-Based Geospatial Economic Analysis. Ph.D. Thesis, ETH, Zurich, Switzerland, 2016. [Google Scholar]
- Spuhler, D.; Scheidegger, A.; Maurer, M. Generation of sanitation system options for urban planning considering novel technologies. Water Res. 2018, 145, 259–278. [Google Scholar] [CrossRef] [Green Version]
- McDonald, W.M. Drones in urban stormwater management: A review and future perspectives. Urban Water J. 2019, 16, 505–518. [Google Scholar] [CrossRef]
- McDonald, W.M.; Naughton, J.B. Stormwater management actions under regulatory pressure: A case study of southeast Wisconsin. J. Environ. Plan. Manag. 2019, 62, 2273–2294. [Google Scholar] [CrossRef]
- Haghighi, A.; Bakhshipour, A.E. Deterministic Integrated Optimization Model for Sewage Collection Networks Using Tabu Search. J. Water Resour. Plan. Manag. 2015, 141, 04014045. [Google Scholar] [CrossRef]
- Diogo, A.F.; Walters, G.A.; De Sousa, E.R.; Graveto, V.M. Three-Dimensional Optimization of Urban Drainage Systems. Comput. Civ. Infrastruct. Eng. 2000, 15, 409–425. [Google Scholar] [CrossRef]
- Diogo, A.F.; Graveto, V.M. Optimal Layout of Sewer Systems: A Deterministic versus a Stochastic Model. J. Hydraul. Eng. 2006, 132, 927–943. [Google Scholar] [CrossRef]
- Haghighi, A. Loop-by-Loop Cutting Algorithm to Generate Layouts for Urban Drainage Systems. J. Water Resour. Plan. Manag. 2013, 139, 693–703. [Google Scholar] [CrossRef]
- Haghighi, A. Intelligent Optimization of Wastewater Collection Networks. In Intelligence Systems in Environmental Man-agement: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2017; pp. 41–65. [Google Scholar]
- Tekeli, S.; Belkaya, H. Computerized Layout Generation for Sanitary Sewers. J. Water Resour. Plan. Manag. 1986, 112, 500–515. [Google Scholar] [CrossRef]
- Li, G.; Matthew, R.G.S. New Approach for Optimization of Urban Drainage Systems. J. Environ. Eng. 1990, 116, 927–944. [Google Scholar] [CrossRef]
- Moeini, R.; Afshar, M.H. Arc Based Ant Colony Optimization Algorithm for optimal design of gravitational sewer networks. Ain Shams Eng. J. 2017, 8, 207–223. [Google Scholar] [CrossRef] [Green Version]
- Moeini, R.; Afshar, M.H. Layout and size optimization of sanitary sewer network using intelligent ants. Adv. Eng. Softw. 2012, 51, 49–62. [Google Scholar] [CrossRef]
- Duque, N.; Duque, D.; Aguilar, A.; Saldarriaga, J. Sewer Network Layout Selection and Hydraulic Design Using a Mathematical Optimization Framework. Water 2020, 12, 3337. [Google Scholar] [CrossRef]
- Bakhshipour, A.E.; Bakhshizadeh, M.; Dittmer, U.; Haghighi, A.; Nowak, W. Hanging Gardens Algorithm to Generate Decentralized Layouts for the Optimization of Urban Drainage Systems. J. Water Resour. Plan. Manag. 2019, 145, 04019034. [Google Scholar] [CrossRef]
- Alves, A.; Gersonius, B.; Kapelan, Z.; Vojinovic, Z.; Sanchez, A. Assessing the Co-Benefits of green-blue-grey infrastructure for sustainable urban flood risk management. J. Environ. Manag. 2019, 239, 244–254. [Google Scholar] [CrossRef] [PubMed]
- Dhakal, K.P.; Chevalier, L.R. Urban Stormwater Governance: The Need for a Paradigm Shift. Environ. Manag. 2016, 57, 1112–1124. [Google Scholar] [CrossRef]
- Goncalves, M.L.R.; Zischg, J.; Rau, S.; Sitzmann, M.; Rauch, W.; Kleidorfer, M. Modeling the Effects of Introducing Low Impact Development in a Tropical City: A Case Study from Joinville, Brazil. Sustainability 2018, 10, 728. [Google Scholar] [CrossRef] [Green Version]
- Barron, N.J.; Kuller, M.; Yasmin, T.; Castonguay, A.C.; Copa, V.; Duncan-Horner, E.; Gimelli, F.M.; Jamali, B.; Nielsen, J.S.; Ng, K.; et al. Towards water sensitive cities in Asia: An interdisciplinary journey. Water Sci. Technol. 2017, 76, 1150–1157. [Google Scholar] [CrossRef] [Green Version]
- Porse, E. Stormwater Governance and Future Cities. Water 2013, 5, 29–52. [Google Scholar] [CrossRef] [Green Version]
- Sitzenfrei, R.; Möderl, M.; Rauch, W. Assessing the impact of transitions from centralised to decentralised water solutions on existing infrastructures–Integrated city-scale analysis with VIBe. Water Res. 2013, 47, 7251–7263. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reyes-Silva, J.D.; Bangura, E.; Helm, B.; Benisch, J.; Krebs, P. The Role of Sewer Network Structure on the Occurrence and Magnitude of Combined Sewer Overflows (CSOs). Water 2020, 12, 2675. [Google Scholar] [CrossRef]
- Hesarkazzazi, S.; Hajibabaei, M.; Reyes-Silva, J.D.; Krebs, P.; Sitzenfrei, R. Assessing Redundancy in Stormwater Structures Under Hydraulic Design. Water 2020, 12, 1003. [Google Scholar] [CrossRef] [Green Version]
- Fathy, I.; Abdel-Aal, G.M.; Fahmy, M.R.; Fathy, A.; Zelenakova, M. The Negative Impact of Blockage on Storm Water Drainage Network. Water 2020, 12, 1974. [Google Scholar] [CrossRef]
- Haghighi, A.; Bakhshipour, A.E. Optimization of Sewer Networks Using an Adaptive Genetic Algorithm. Water Resour. Manag. 2012, 26, 3441–3456. [Google Scholar] [CrossRef]
- Diogo, A.F.; Carmo, J.S.A.D. Peak Flows and Stormwater Networks Design—Current and Future Management of Urban Surface Watersheds. Water 2019, 11, 759. [Google Scholar] [CrossRef] [Green Version]
- Price, R.K.; Vojinovic, Z. Urban Hydroinformatics. Data, Models and Decision Support for Integrated Urban Water Management; IWA Publishing: London, UK, 2011; ISBN 9781780401362. [Google Scholar]
- Maier, H.R.; Razavi, S.; Kapelan, Z.; Zhu, Z.; Kasprzyk, J.R.; Tolson, B. Introductory overview: Optimization using evolutionary algorithms and other metaheuristics. Environ. Model. Softw. 2019, 114, 195–213. [Google Scholar] [CrossRef]
- Bakhshipour, A.E.; Dittmer, U.; Haghighi, A.; Nowak, W. Hybrid green-blue-gray decentralized urban drainage systems design, a simulation-optimization framework. J. Environ. Manag. 2019, 249, 109364. [Google Scholar] [CrossRef] [PubMed]
- Bakhshipour, A.E.; Dittmer, U.; Haghighi, A.; Nowak, W. Towards sustainable urban drainage infrastructure planning: A combined multiobjective optimization and multicriteria decision-making platform. J. Water Resour. Plan. Manag. Forthcom. 2021, in press. [Google Scholar] [CrossRef]
- Van Laarhoven, P.J.M.; Aarts, E.H.L. (Eds.) Simulated annealing. In Simulated Annealing: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 1987; pp. 7–15. ISBN 978-90-481-8438-5. [Google Scholar]
- Hadka, D.; Reed, P. Borg: An Auto-Adaptive Many-Objective Evolutionary Computing Framework. Evol. Comput. 2013, 21, 231–259. [Google Scholar] [CrossRef] [PubMed]
- Eckart, K.; McPhee, Z.; Bolisetti, T. Multiobjective optimization of low impact development stormwater controls. J. Hydrol. 2018, 562, 564–576. [Google Scholar] [CrossRef]
- De Villiers, N.; Van Rooyen, G.C.; Middendorf, M. Sewer network design: Heuristic algorithm for hydraulic optimisation. J. South Afr. Inst. Civ. Eng. 2017, 59, 48–56. [Google Scholar] [CrossRef] [Green Version]
- Walters, G.A.; Smith, D.K. Evolutionary design algorithm for optimal layout of tree networks. Engineering Optimization. Eng. Optim. 1995, 24, 261–281. [Google Scholar] [CrossRef]
- Haghighi, A.; Bakhshipour, A.E. Reliability-based layout design of sewage collection systems in flat areas. Urban Water J. 2015, 13, 790–802. [Google Scholar] [CrossRef]
- Bakhshipour, A.E.; Bakhshizadeh, M.; Dittmer, U.; Nowak, W.; Haghighi, A. A Graph-Theory Based Algorithm to Generate Decentralized Urban Drainage Layouts. In New Trends in Urban Drainage Modelling; Mannina, G., Ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2018; pp. 633–637. ISBN 978-3-319-99866-4. [Google Scholar]
- Zischg, J.; Rogers, B.; Gunn, A.; Rauch, W.; Sitzenfrei, R. Future trajectories of urban drainage systems: A simple exploratory modeling approach for assessing socio-technical transitions. Sci. Total. Environ. 2019, 651, 1709–1719. [Google Scholar] [CrossRef]
- Diogo, A.F.; Oliveira, M.C. A simplified approach for the computation of steady two-phase flow in inverted siphons. J. Environ. Manag. 2016, 166, 294–308. [Google Scholar] [CrossRef] [PubMed]
- Diogo, A.F.; Oliveira, M.C. A Preliminary Numerical Approach for the Study of Compressed Air Injection in Inverted Siphons. J. Hydraul. Eng. 2013, 139, 772–784. [Google Scholar] [CrossRef]
- Shao, Z.; Zhang, X.; Li, S.; Deng, S.; Chai, H. A Novel SWMM Based Algorithm Application to Storm Sewer Network Design. Water 2017, 9, 747. [Google Scholar] [CrossRef] [Green Version]






| Description | Constraint |
|---|---|
| Maximum Velocity | 4.0 m/s |
| Maximum excavation depth | 5.0 m |
| Minimum cover depth | 1.2 m |
| Minimum slope | 0.0041 if D = 200 mm |
| 0.0033 if D = 250 mm | |
| 0.0027 if D = 350 mm | |
| 0.0020 if D = 400 mm | |
| 0.0016 if D = 500 mm | |
| 0.0014 if D = 630 mm | |
| 0.0010 if D = 800 mm | |
| 0.0010 if D 1000 mm |
| Index | LCC (M. Rials) | Average Diameter (m/m) | Average Buried Depth (m) | Maximum Diameter (m) | Maximum Buried Depth (m) | DC (%) |
|---|---|---|---|---|---|---|
| LAI | 280070 | 0.68 | 2.17 | 1.5 | 5.78 | 22 |
| ADI | 250150 | 0.63 | 2.08 | 1.5 | 5.22 | 33 |
| ERI | 290947 | 0.71 | 2.25 | 2 | 5.98 | 55 |
| Diameter (m) | Maximum Impervious Connected Area (ha) |
|---|---|
| 0.25 | 0.4 |
| 0.35 | 0.8 |
| 0.40 | 1.2 |
| 0.5 | 3.2 |
| 0.63 | 4.8 |
| 0.80 | 10.4 |
| 1.0 | 32.0 |
| 1.2 | 72.0 |
| 1.5 | 96.0 |
| 2.0 | 400.0 |
| Design | LCC (M. Rials) | Structural Resilience (%) | DC (%) | Average Diameter (m/m) | Average Buried Depth (m) | Maximum Diameter (m) | Maximum Buried Depth (m) | Non-outfall(-) | Minimum Structural Resilience (%) | |
|---|---|---|---|---|---|---|---|---|---|---|
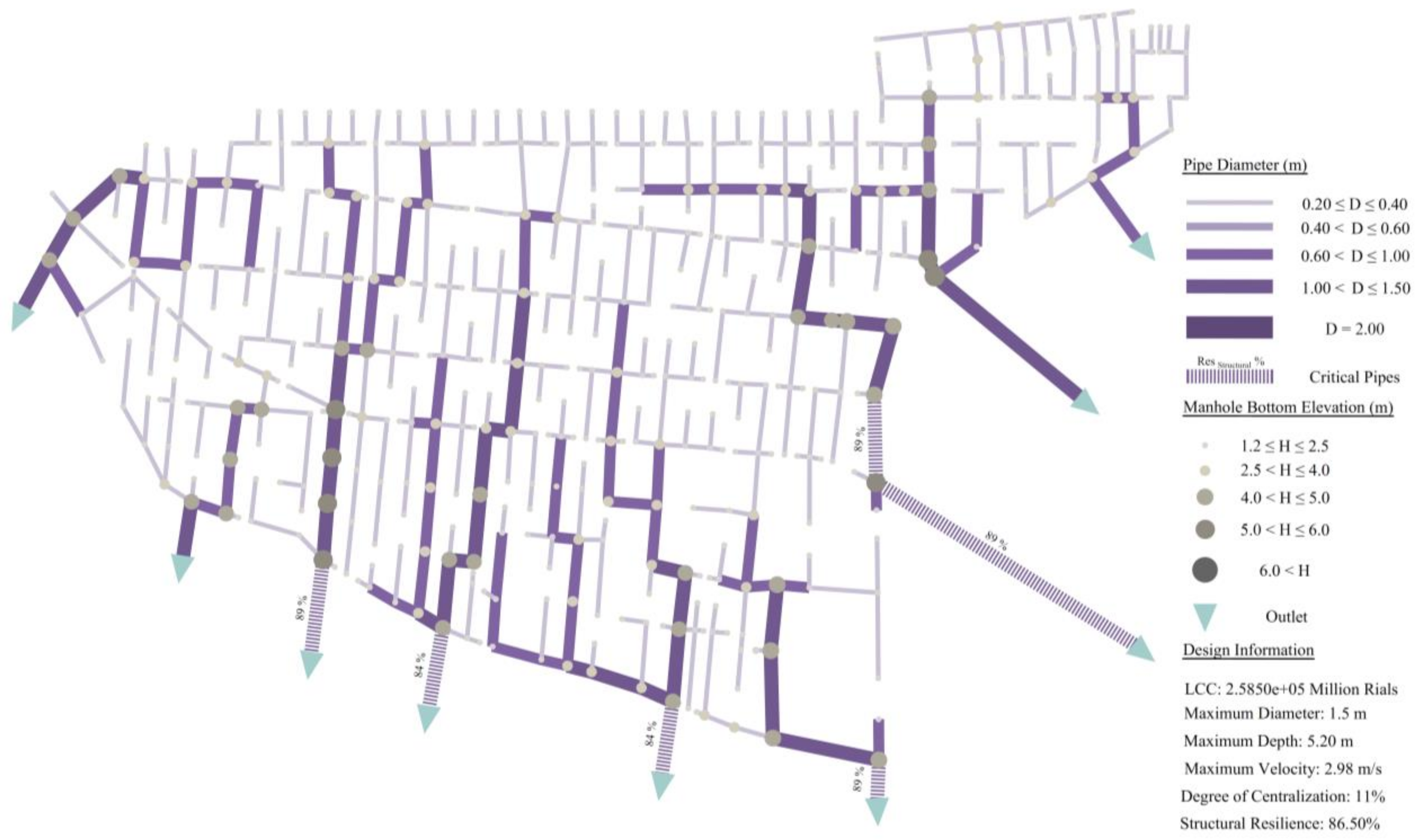
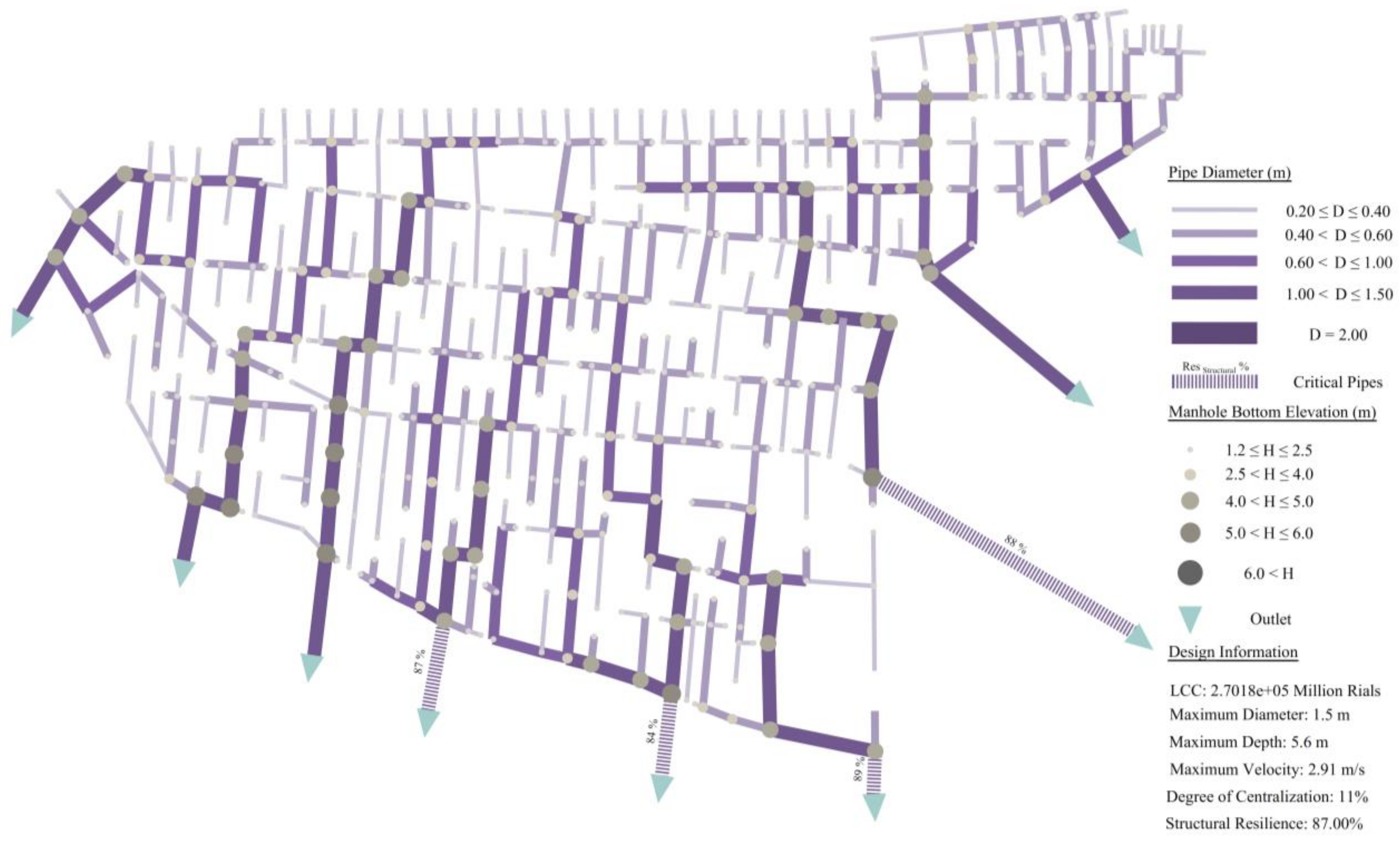
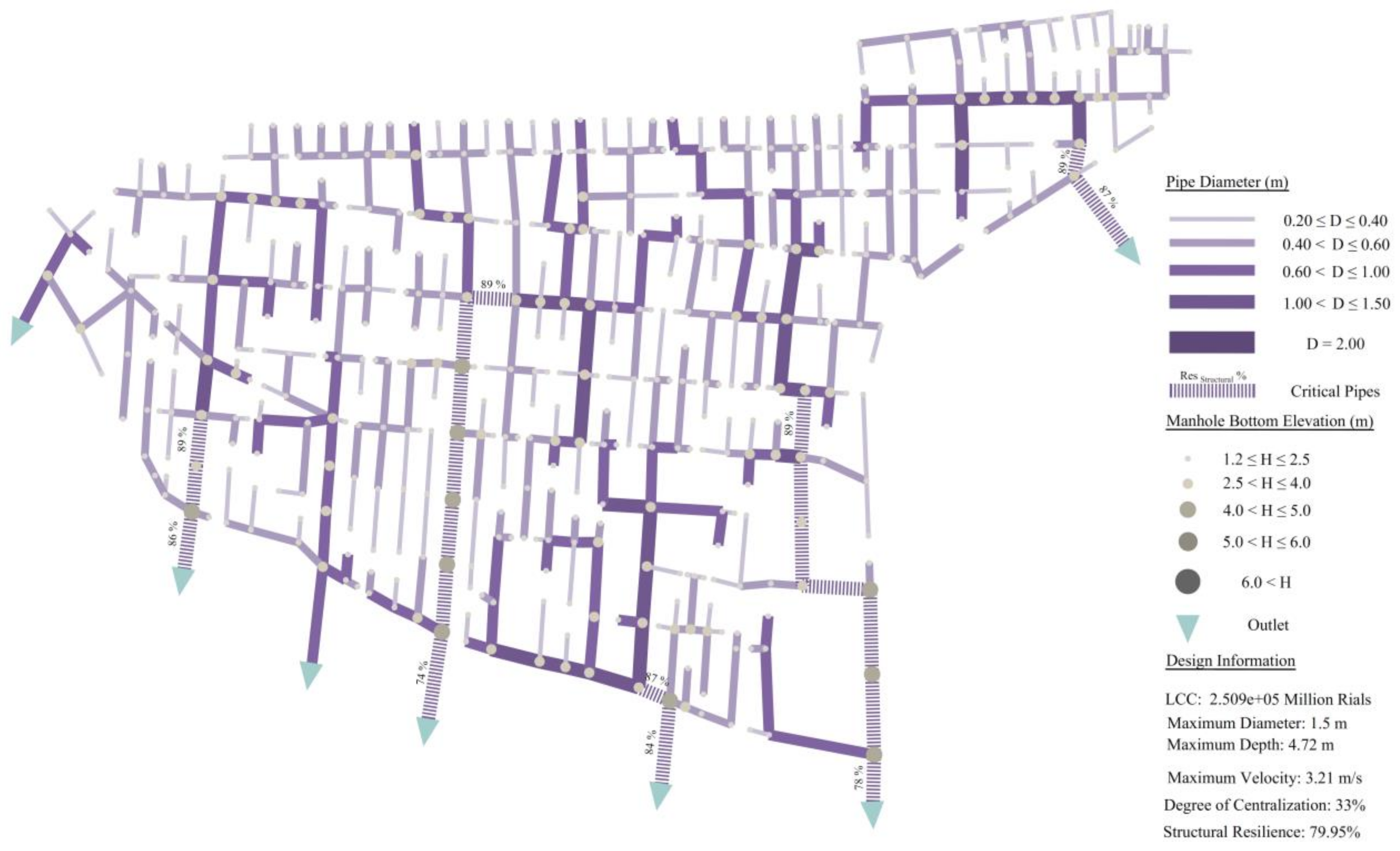
| 1 | 249630 | 85.3 | 22 | 0.56 | 2.17 | 1.5 | 5.10 | 12 | 6 | 82 |
| 2 | 258500 | 86.5 | 11 | 0.57 | 2.20 | 1.5 | 5.20 | 6 | 1 | 84 |
| 3 | 270180 | 87.0 | 11 | 0.58 | 2.26 | 1.5 | 5.60 | 4 | 0 | 84 |
| 4 | 250953 | 79.9 | 33 | 0.64 | 2.13 | 1.5 | 4.70 | 21 | 16 | 74 |
| Design | DC (%) | 10 Years (38.3 mm) | 20 Years (46.7 mm) | 25 Years (49.5 mm) | 50 Years (58.5 mm) |
|---|---|---|---|---|---|
| 1 | 22 | 97.7 | 94.0 | 92.8 | 89.2 |
| 2 | 11 | 98.1 | 94.9 | 93.8 | 90.5 |
| 3 | 11 | 98.0 | 94.4 | 93.1 | 89.5 |
| 4 | 33 | 96.97 | 91.85 | 90.01 | 84.43 |
| Optimization Problem | Centralized Layout (Flat Area) | Decentralized Layout (Flat Area) | Centralized Layout (Steep Area) | Decentralized Layout Design (Steep Area) | Sizing the Sewers (Flat Area) | Sizing the Sewers (Steep Area) | Optimization Approach |
|---|---|---|---|---|---|---|---|
| Design of sewage collection systems | Loop-by-loop algorithm [17] | Hanging gardens algorithm [24] or Forest Algorithm [15] | Engineering judgment | Hanging gardens algorithm [24], SNIP model [9], or Forest Algorithm [15] | Adaptive algorithm [34] | Adaptive algorithm [34] | Simultaneous optimization (layout and sizes) |
| Design of stormwater collection systems | Loop-by-loop algorithm [17] | Hanging gardens algorithm [24] or Forest Algorithm [15] | Engineering judgment | Hanging gardens algorithm [24], SNIP model [9], or Forest Algorithm [15] | Adaptive algorithm [34] | The method proposed in [50] | Separate optimization (first layout then sizes) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bakhshipour, A.E.; Hespen, J.; Haghighi, A.; Dittmer, U.; Nowak, W. Integrating Structural Resilience in the Design of Urban Drainage Networks in Flat Areas Using a Simplified Multi-Objective Optimization Framework. Water 2021, 13, 269. https://doi.org/10.3390/w13030269
Bakhshipour AE, Hespen J, Haghighi A, Dittmer U, Nowak W. Integrating Structural Resilience in the Design of Urban Drainage Networks in Flat Areas Using a Simplified Multi-Objective Optimization Framework. Water. 2021; 13(3):269. https://doi.org/10.3390/w13030269
Chicago/Turabian StyleBakhshipour, Amin E., Jessica Hespen, Ali Haghighi, Ulrich Dittmer, and Wolfgang Nowak. 2021. "Integrating Structural Resilience in the Design of Urban Drainage Networks in Flat Areas Using a Simplified Multi-Objective Optimization Framework" Water 13, no. 3: 269. https://doi.org/10.3390/w13030269
APA StyleBakhshipour, A. E., Hespen, J., Haghighi, A., Dittmer, U., & Nowak, W. (2021). Integrating Structural Resilience in the Design of Urban Drainage Networks in Flat Areas Using a Simplified Multi-Objective Optimization Framework. Water, 13(3), 269. https://doi.org/10.3390/w13030269









