Flood Forecasting via the Ensemble Kalman Filter Method Using Merged Satellite and Measured Soil Moisture Data
Abstract
:1. Introduction
2. Materials and Methods
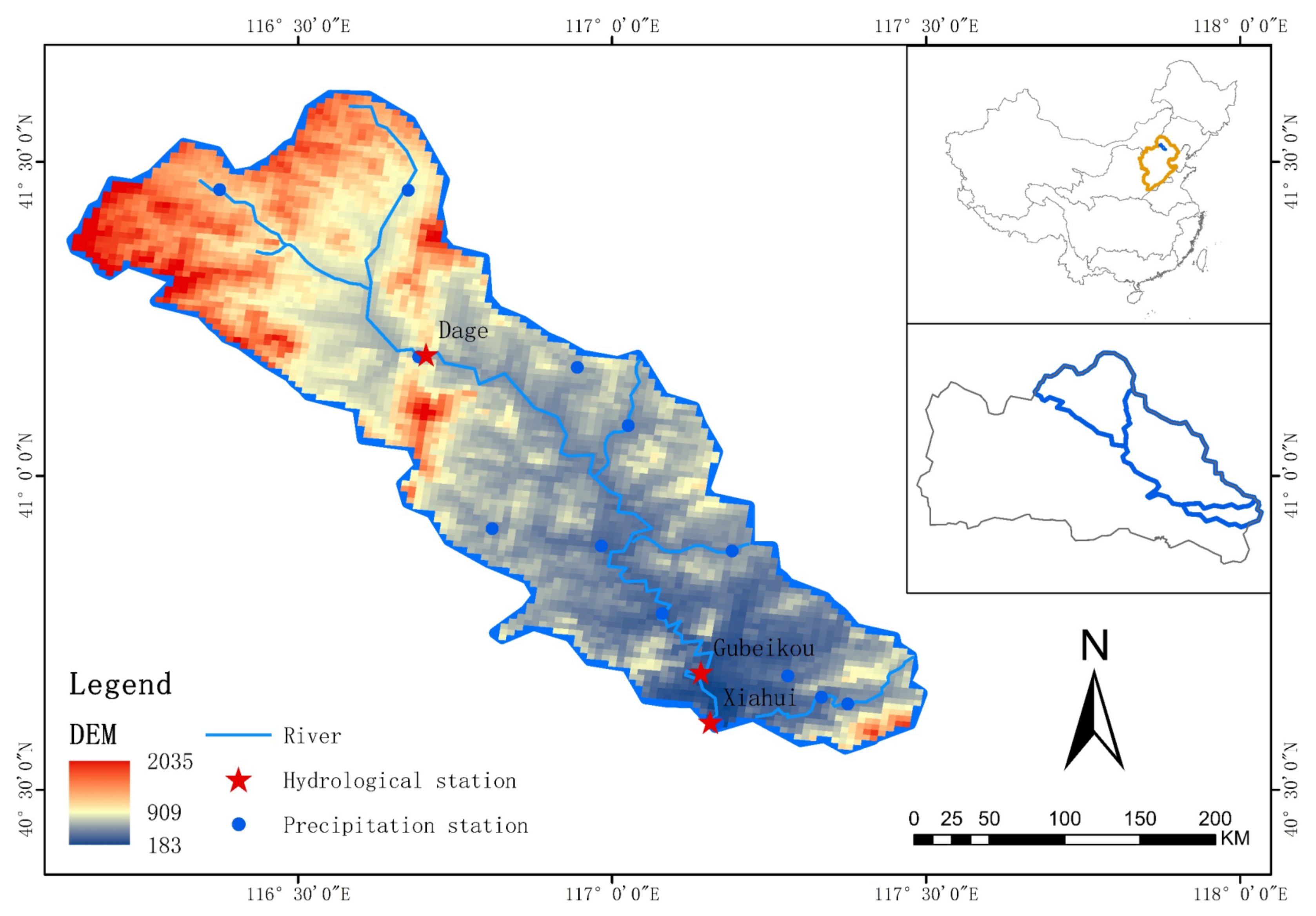
2.1. Study Area
2.2. Data
2.2.1. Precipitation and Runoff Data
2.2.2. Soil Moisture Data
2.3. Improved Xin’anjiang Model
3. Methods
3.1. Data Merging
3.2. Ensemble Kalman Filter (EnKF)
- Observation data update
3.3. Data Assimilation Setup
4. Results and Discussion
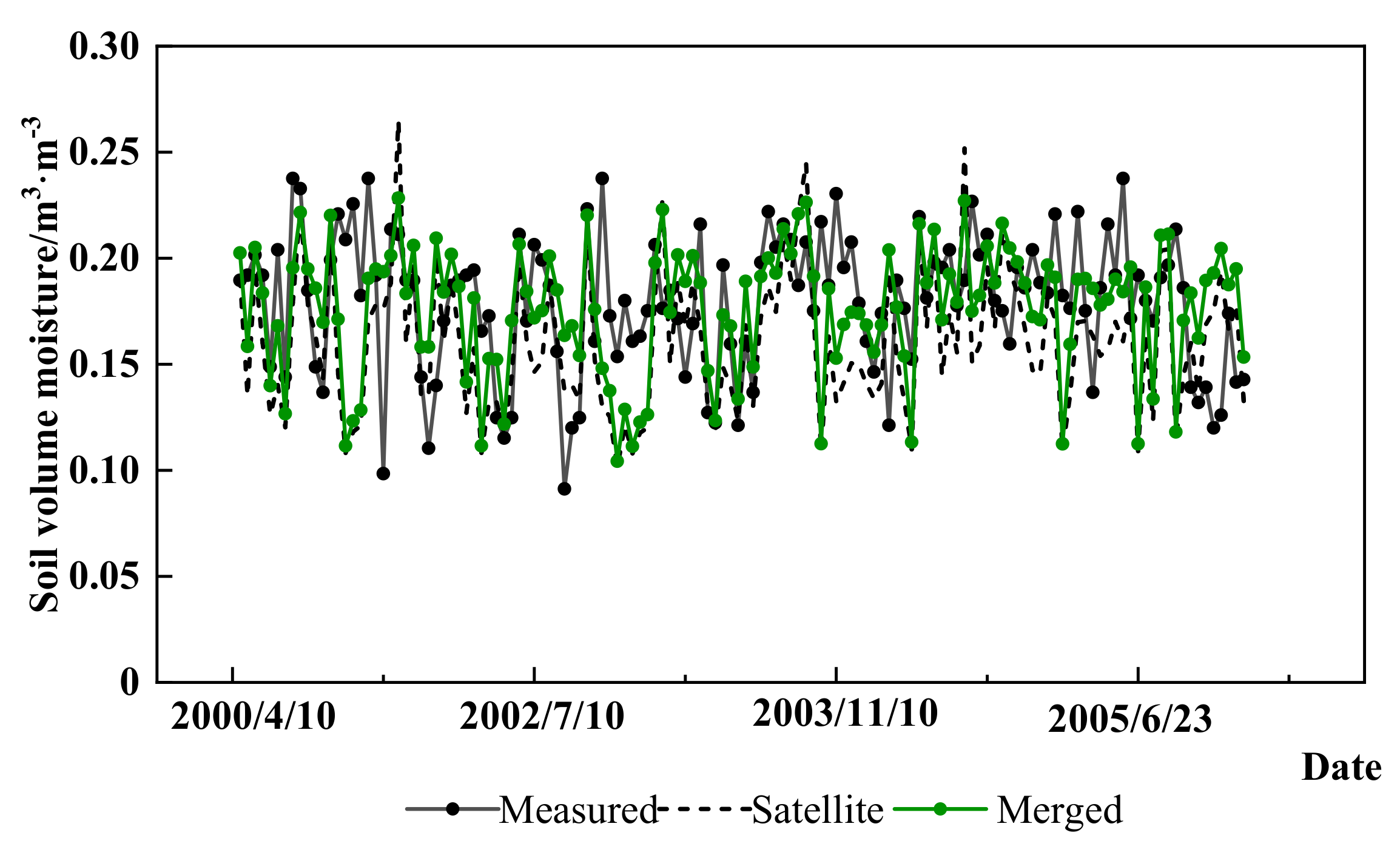
4.1. Data Merging
4.2. Data Assimilation
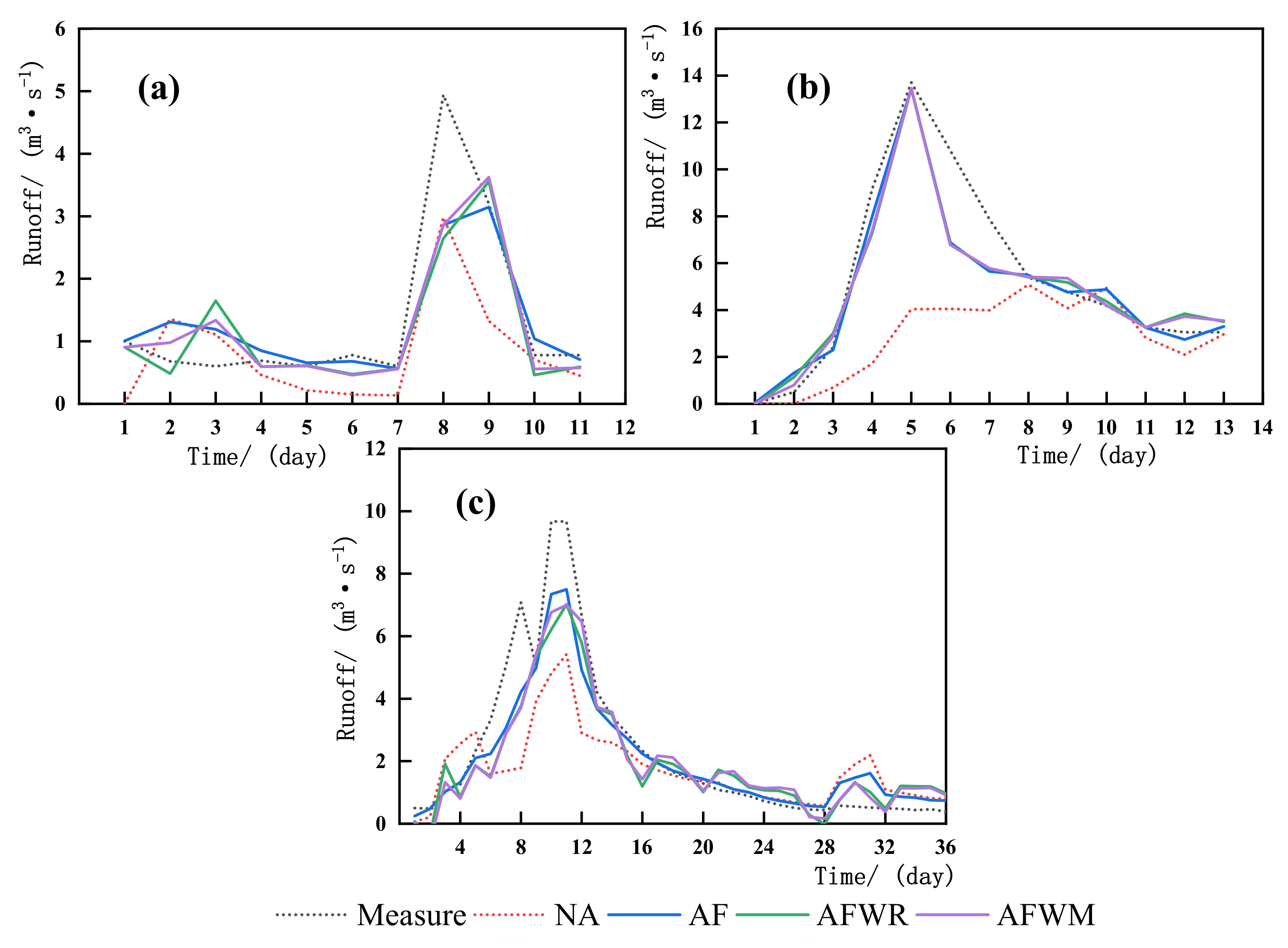
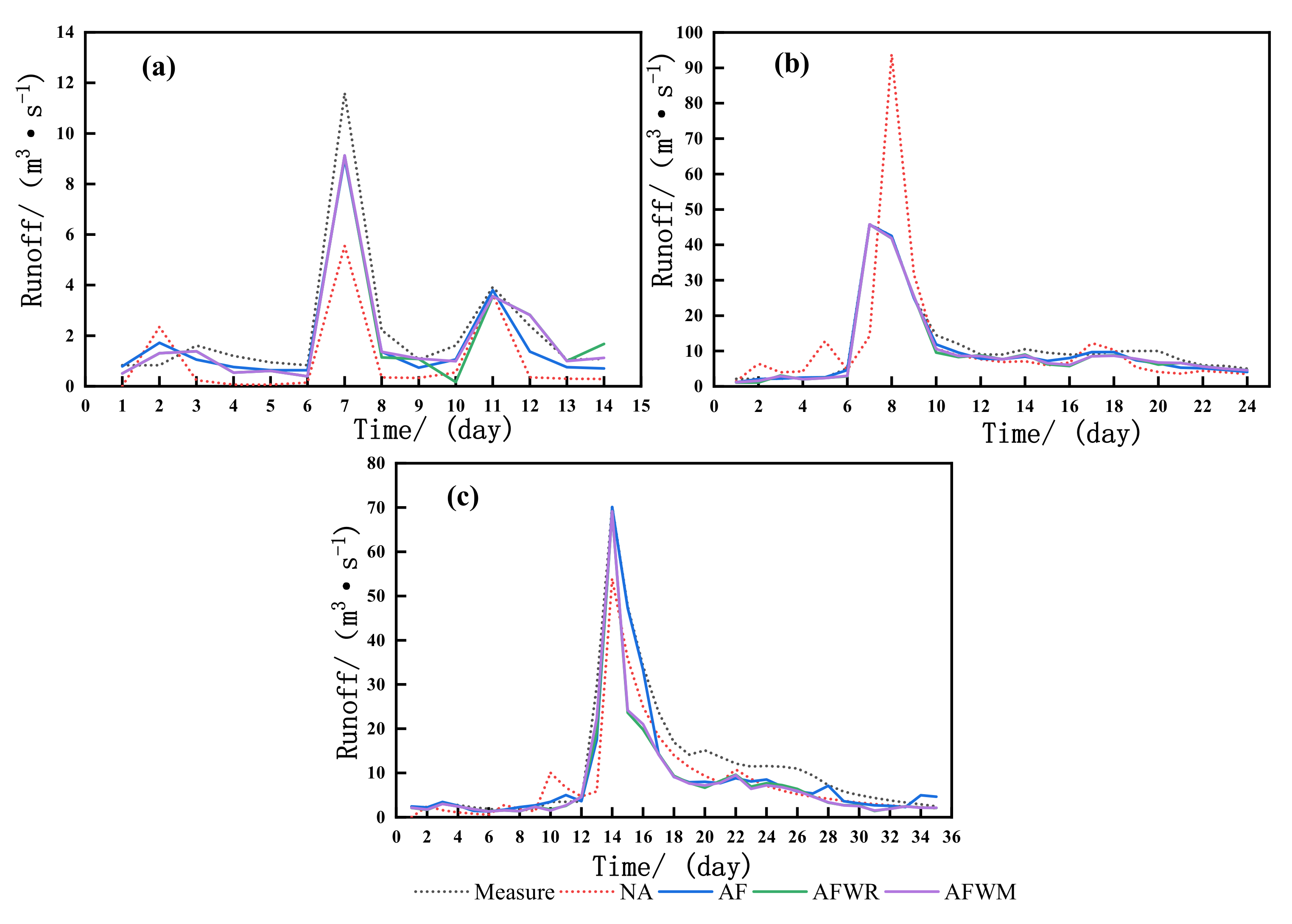
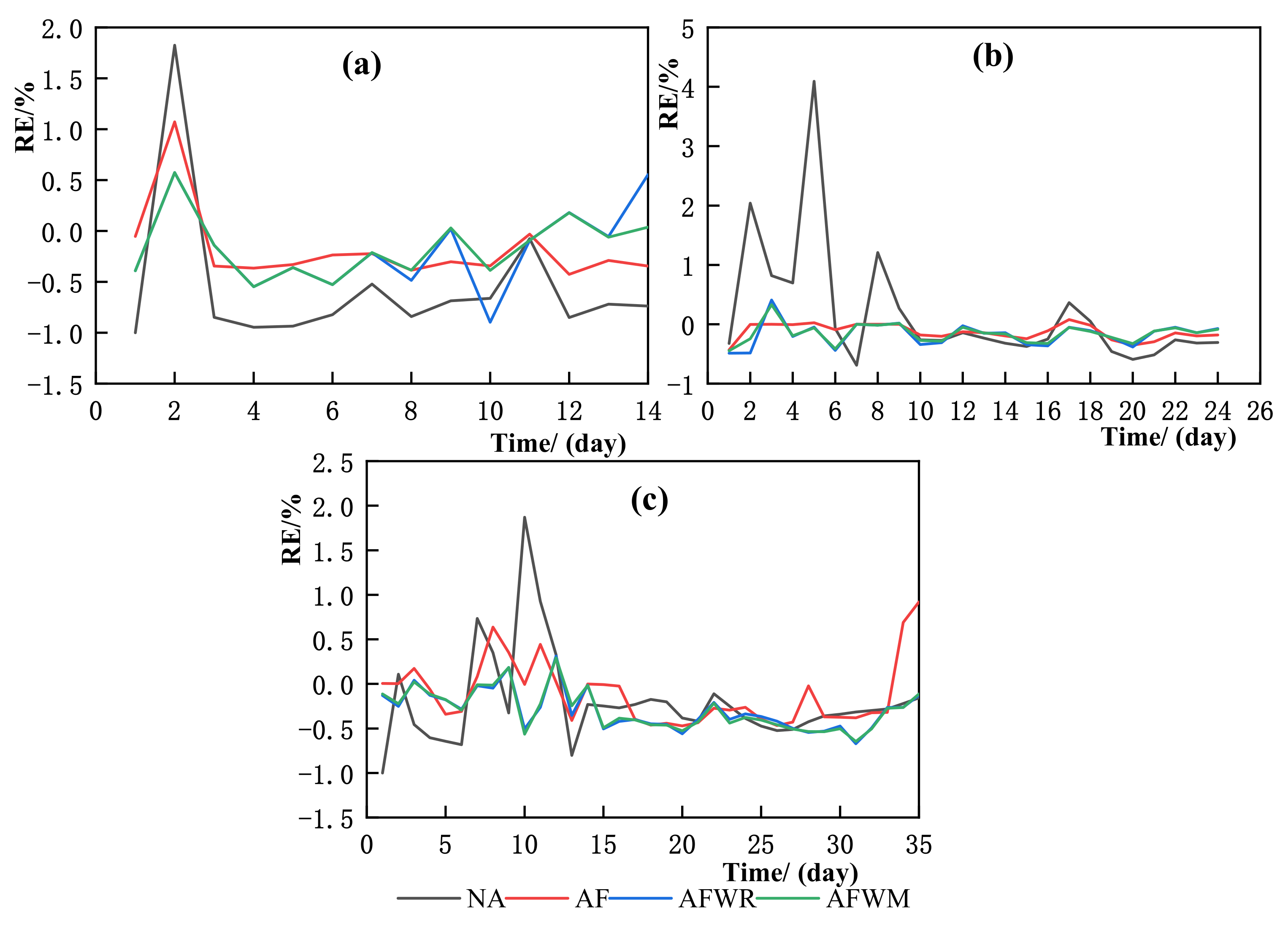
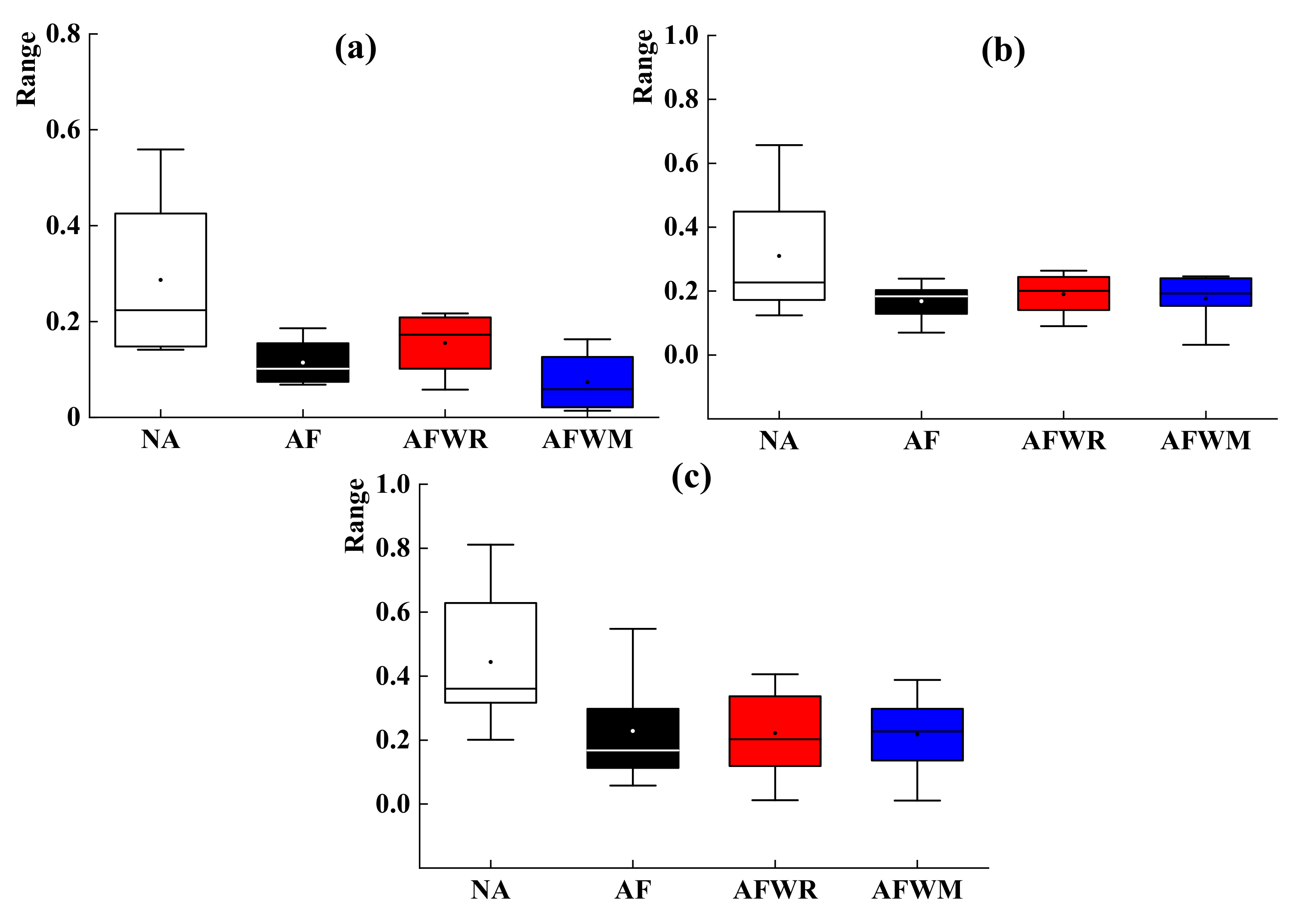
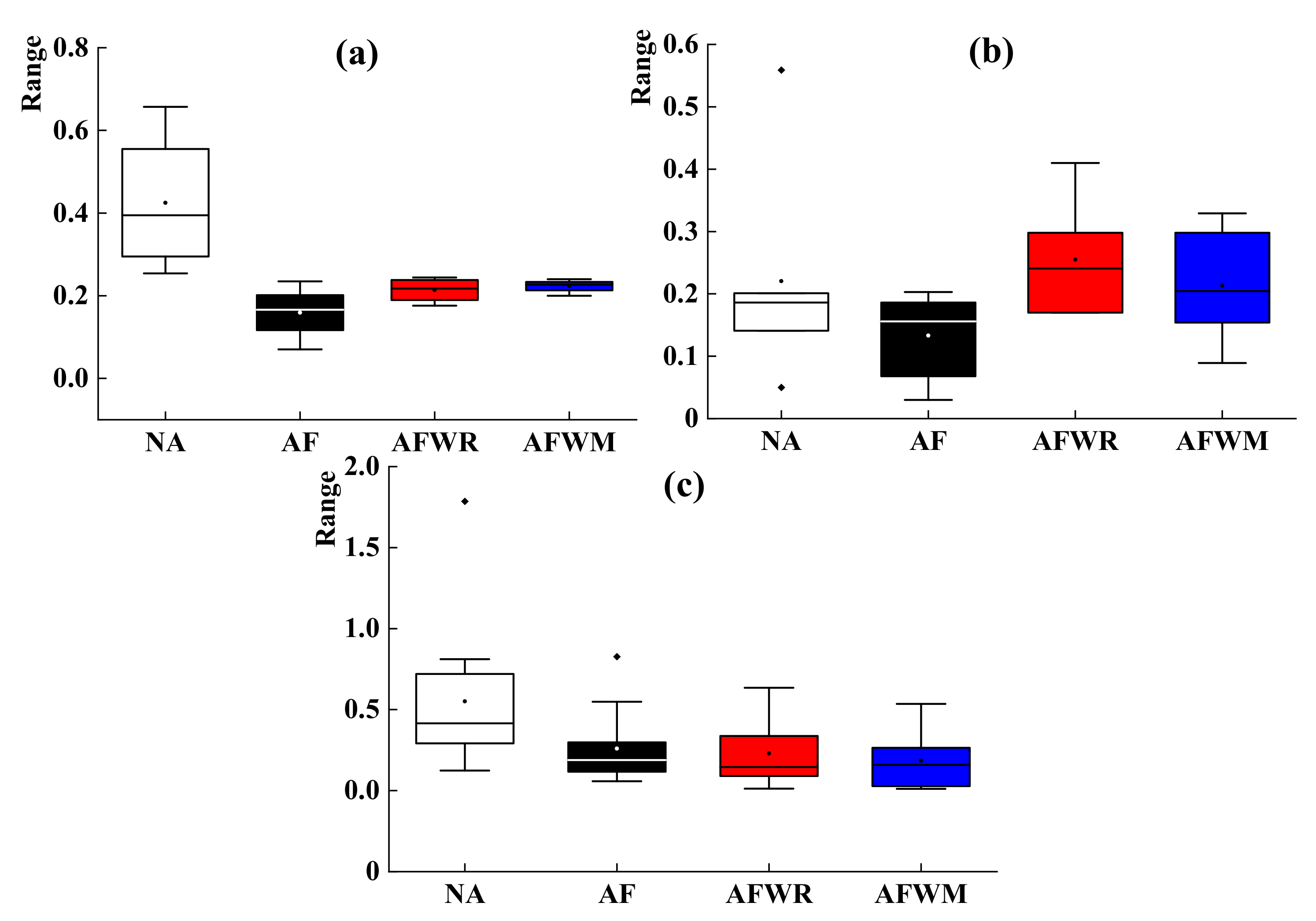
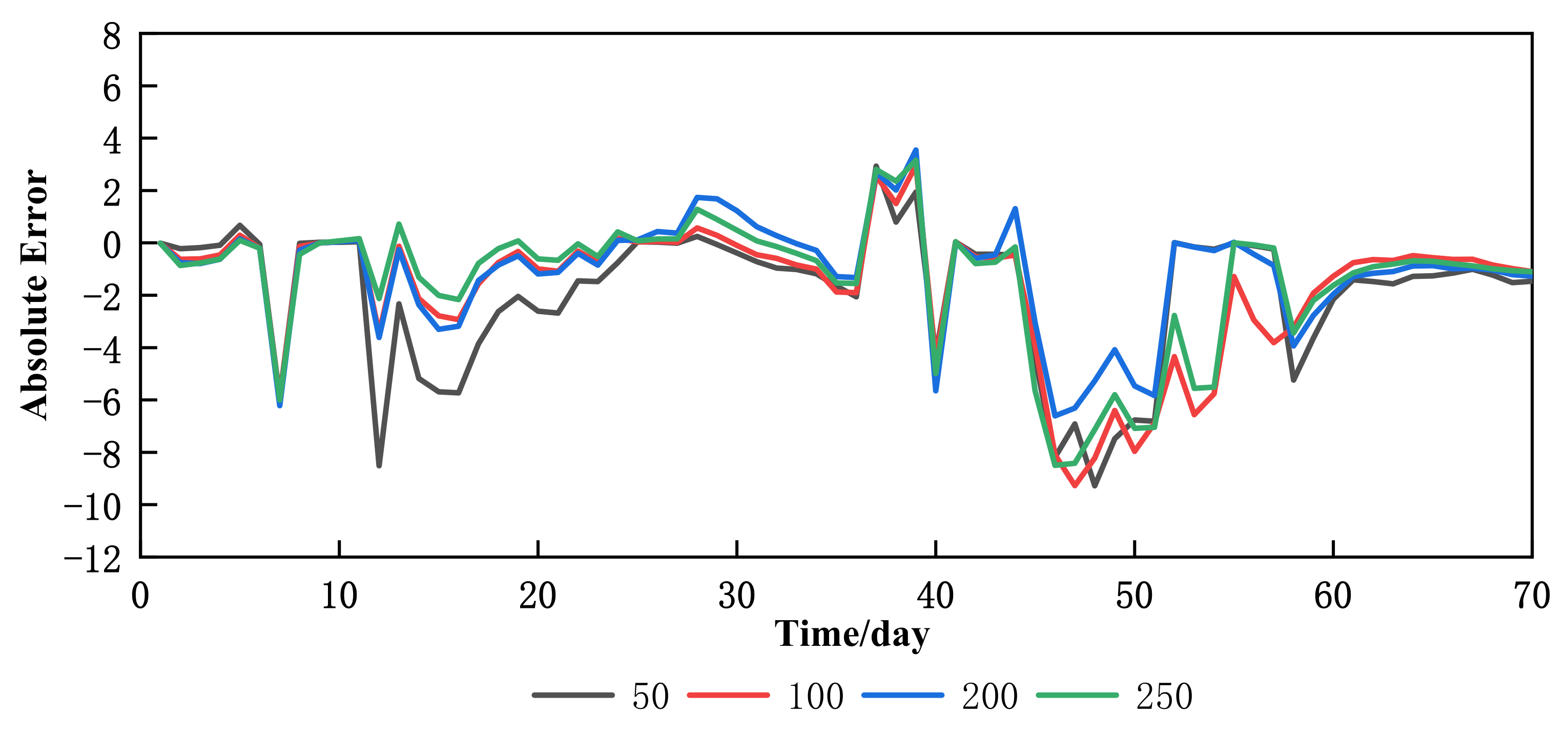
4.2.1. Small Flood
4.2.2. Medium Flood
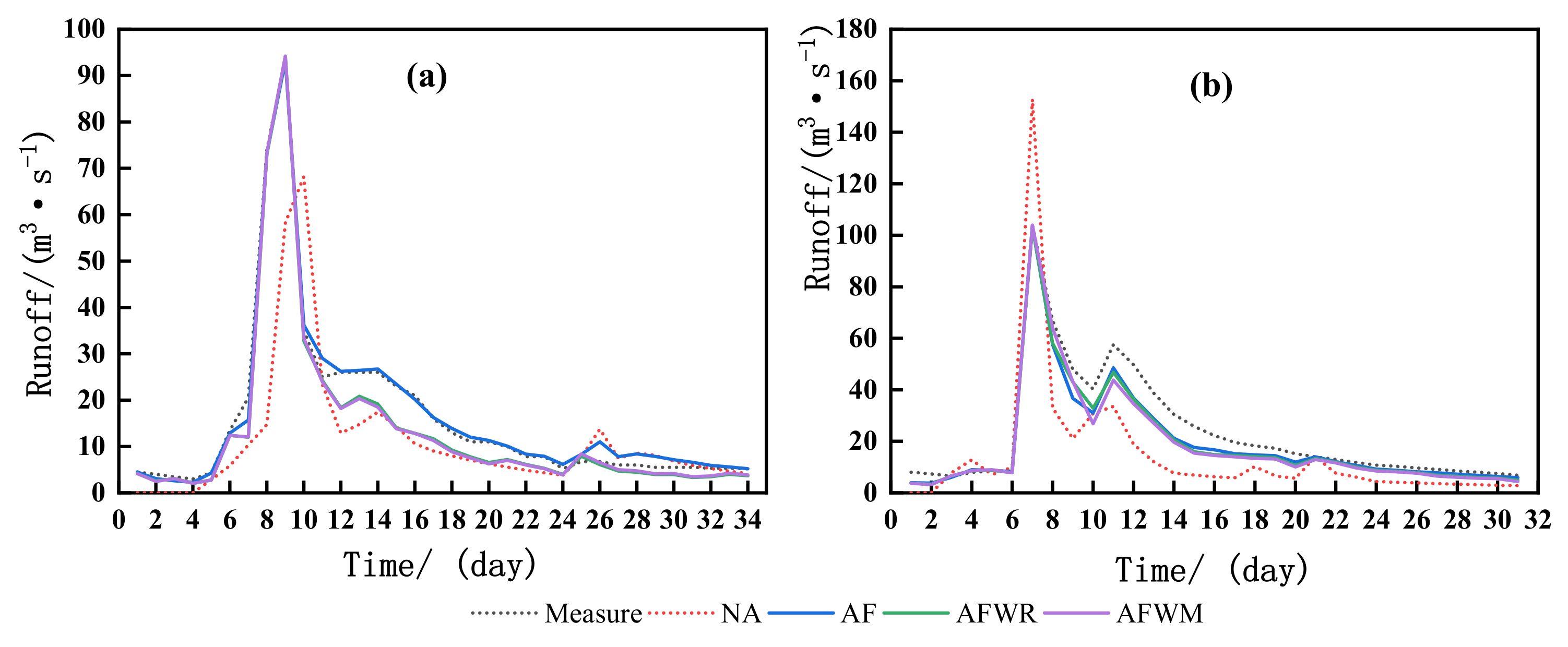
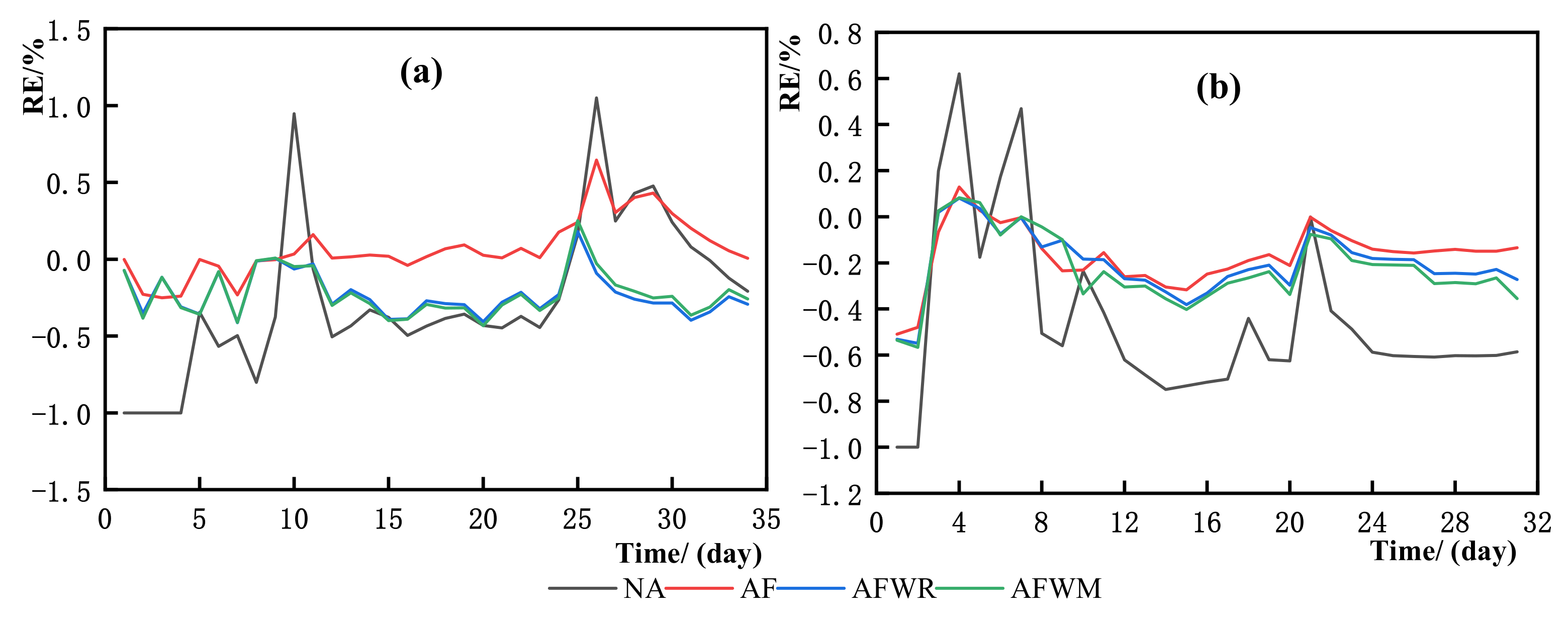
4.2.3. Large Flood
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| NA | non-assimilation |
| AF | assimilation of runoff data |
| AFWR | assimilation of runoff and satellite-based soil moisture data |
| AFWM | assimilation of runoff and merged soil moisture data |
| RE | relative error |
| SM | soil moisture |
| KF | Kalman filter |
| EKF | extended Kalman filter |
| EnKF | ensemble Kalman filter |
| DEM | digital elevation model |
| ESA | European Space Agency |
| CCI | Climate Change Initiative |
| CDF | cumulative distribution function |
| NSE | Nash–Sutcliffe efficiency coefficient |
| AE | absolute error |
| RMSE | root-mean-square error |
References
- Bahrami, A.; Goïta, K.; Magagi, R.; Davison, B.; Razavi, S.; Elshamy, M.; Princz, D. Data assimilation of satellite-based terrestrial water storage changes into a hydrology land-surface model. J. Hydrol. 2020, 597, 125744. [Google Scholar] [CrossRef]
- Liu, Y.; Gupta, H.V. Uncertainty in hydrologic modeling: Toward an integrated data assimilation framework. Water Resour. Res. 2007, 43, W07401. [Google Scholar] [CrossRef]
- Abbott, M.B.; Refsgaard, J.C. Construction, calibration and validation of hydrological models. In Distributed Hydrological Modelling; Springer: Dordrecht, The Netherlands, 1990; pp. 41–54. [Google Scholar] [CrossRef]
- Alvarez-Garreton, C.; Ryu, D.; Western, A.W.; Su, C.H.; Crow, W.T.; Robertson, D.E.; Leahy, C. Improving operational flood ensemble prediction by the assimilation of satellite soil moisture: Comparison between lumped and semi-distributed schemes. Hydrol. Earth Syst. Sci. 2015, 19, 1659–1676. [Google Scholar] [CrossRef] [Green Version]
- Samuel, J.; Rousseau, A.N.; Abbasnezhadi, K.; Savary, S. Development and evaluation of a hydrologic data-assimilation scheme for short-range flow and inflow forecasts in a data-sparse high-latitude region using a distributed model and ensemble Kalman filtering. Adv. Water Resour. 2019, 130, 198–220. [Google Scholar] [CrossRef]
- Zhu, Q.; Wang, Y.; Luo, Y. Improvement of multi-layer soil moisture prediction using support vector machines and ensemble Kalman filter coupled with remote sensing soil moisture datasets over an agriculture dominant basin in China. Hydrol. Process. 2021, 35, e14154. [Google Scholar] [CrossRef]
- Azimi, S.; Dariane, A.B.; Modanesi, S.; Bauer-Marschallinger, B.; Bindish, R.; Wagner, W.; Massari, C. Understanding the benefit of Sentinel 1 and SMAP—Era satellite soil moisture retrievals for flood forecasting in small basins: Effect of revisit time and the spatial resolution. J. Hydrol. 2019, 581, 124367. [Google Scholar] [CrossRef]
- Wood, E.F.; Andras, S. An Adaptive Algorithm for Analyzing Short-Term Structural and Parameter Changes in Hydrologic Prediction Models. Water Resour. Res. 1978, 14, 577–581. [Google Scholar] [CrossRef]
- Aubert, D.; Loumagne, C.; Oudin, L. Sequential assimilation of soil moisture and streamflow data in a conceptual rainfall–runoff model. J. Hydrol. 2003, 280, 145–161. [Google Scholar] [CrossRef]
- Evensen, G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. Atmos. 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Whitaker, J.S.; Hamill, T.M. Ensemble Data Assimilation without Perturbed Observations. Mon. Weather Rev. 2002, 130, 1913–1924. [Google Scholar] [CrossRef]
- Mehta, D.J.; Yadav, S.M. Hydrodynamic Simulation of River Ambica for Riverbed Assessment: A Case Study of Navsari Region. Lect. Notes Civ. Eng. 2020, 39, 127–140. [Google Scholar] [CrossRef]
- Wu, C.L.; Chau, K.W. Prediction of rainfall time series using modular soft computing methods. Eng. Appl. Artif. Intell. 2013, 26, 997–1007. [Google Scholar] [CrossRef] [Green Version]
- Moradkhani, H.; Sorooshian, S.; Gupta, H.V.; Houser, P.R. Dual state–parameter estimation of hydrological models using ensemble Kalman filter. Adv. Water Resour. 2005, 28, 135–147. [Google Scholar] [CrossRef] [Green Version]
- Moradkhani, H.; Hsu, K.L.; Gupta, H.; Sorooshian, S. Uncertainty assessment of hydrologic model states and parameters: Sequential data assimilation using the particle filter. Water Resour. Res. 2005, 41, 237–246. [Google Scholar] [CrossRef] [Green Version]
- Xie, X.H.; Zhang, D.X. Data assimilation for distributed hydrological catchment modeling via ensemble Kalman filter. Adv. Water Resour. 2010, 33, 678–690. [Google Scholar] [CrossRef]
- Xie, X.H.; Zhang, D.X. A partitioned update scheme for state-parameter estimation of distributed hydrologic models based on the ensemble Kalman filter. Water Resour. Res. 2013, 49, 7350–7365. [Google Scholar] [CrossRef]
- Lü, H.S.; Hou, T.; Horton, R.; Zhu, Y.H.; Chen, X.; Jia, Y.W.; Wang, W.; Fu, X.L. The streamflow estimation using the Xinanjiang rainfall runoff model and dual state-parameter estimation method. J. Hydrol. 2013, 480, 102–114. [Google Scholar] [CrossRef]
- Shi, Y.; Davis, K.J.; Zhang, F.; Duffy, C.J.; Yu, X. Parameter estimation of a physically-based land surface hydrologic model using an ensemble Kalman filter: A multivariate real-data experiment. Adv. Water Resour. 2015, 83, 421–427. [Google Scholar] [CrossRef] [Green Version]
- Khaki, M.; Hendricks Franssen, H.J.; Han, S.C. Multi-mission satellite remote sensing data for improving land hydrological models via data assimilation. Sci. Rep. 2020, 10, 18791. [Google Scholar] [CrossRef]
- Kampf, S.K.; Burges, S.J. Parameter estimation for a physics-based distributed hydrologic model using measured outflow fluxes and internal moisture states. Water Resour. Res. 2007, 43, 55–60. [Google Scholar] [CrossRef]
- Pan, M.; Wood, E.F.; Wójcik, R.; McCabe, M.F. Estimation of regional terrestrial water cycle using multi-sensor remote sensing observations and data assimilation. Remote Sens. Environ. 2008, 112, 1282–1294. [Google Scholar] [CrossRef]
- Lee, H.; Seo, D.J.; Koren, V. Assimilation of streamflow and in situ soil moisture data into operational distributed hydrologic models: Effects of uncertainties in the data and initial model soil moisture states. Adv. Water Resour. 2011, 34, 1597–1615. [Google Scholar] [CrossRef]
- Dumedah, G.; Coulibaly, P. Evolutionary assimilation of streamflow in distributed hydrologic modeling using in-situ soil moisture data. Adv. Water Resour. 2013, 53, 231–241. [Google Scholar] [CrossRef]
- Samuel, J.; Coulibaly, P.; Dumedah, G.; Moradkhan, H. Assessing model state and forecasts variation in hydrologic data assimilation. J. Hydrol. 2014, 513, 127–141. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, W.; Hu, Y. Investigating the impact of surface soil moisture assimilation on state and parameter estimation in SWAT model based on the ensemble Kalman filter in upper Huai River basin. J. Hydrol. Hydromech. 2017, 65, 123–133. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Wang, G.L. Analysis on Error Distributions of Input Data and Output Data of Flood Forecasting Model and Its Correlation. J. China Hydrol. 2022, 42, 23–28. [Google Scholar] [CrossRef]
- Entekhabi, D.; Nakamura, H.; Njoku, E.G. Solving the inverse problem for soil moisture and temperature profiles by sequential assimilation of multifrequency remotely sensed observations. IEEE Trans. Geosci. Remote Sens. 1994, 32, 438–448. [Google Scholar] [CrossRef]
- Wagner, W.; Dorigo, W.; De Jeu, R.; Fernandez, D.; Benveniste, J.; Haas, E.; Ertl, M. Fusion of active and passive microwave observations to create an essential climate variable data record on soil moisture. In Proceedings of the ISPRS Annals of Photogrammetry, Remote Sensing and Spatial Information Sciences, Melbourne, Australia, 25 August–1 September 2012; pp. 315–321. [Google Scholar] [CrossRef]
- Li, Y.K.; Mao, F.; Li, M.Y.; Li, Y.G.; Peng, Y.X. Design flood revision method based on improved Xin’anjiang model—Taking Chaohe River Basin as an example. China Flood Drought Manag. 2021, 31, 49–54. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the IEEE MHS’95—Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings, IEEE World Congress on Computational Intelligence (Cat. No.98TH8360), Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar] [CrossRef]
- Griensven, A.V.; Meixner, T.; Grunwald, S.; Bishop, T.; Diluzio, M.; Srinivasan, R. A global sensitivity analysis tool for the parameters of multi-variable catchment models. J. Hydrol. 2006, 324, 10–23. [Google Scholar] [CrossRef]
- Evensen, G. The ensemble Kalman filter: Theoretical formulation and practical implementation. Ocean. Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Predietion Problems. Trans. ASME-J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Burgers, G.; Van Leeuwen, P.J.; Evensen, G. Analysis Scheme in the Ensemble Kalman Filter. Mon. Weather Rev. 1998, 126, 1719–1724. [Google Scholar] [CrossRef]
- Reichle, R.H.; Mclaughlin, D.B.; Entekhabi, D. Hydrologic Data assimilation with the ensemble Kalman filter. Mon. Weather Rev. 2000, 130, 103–114. [Google Scholar] [CrossRef] [Green Version]
- Xie, X.H.; Meng, S.; Liang, S.; Yao, Y. Improving streamflow predictions at ungauged locations with real-time updating: Application of an EnKF-based state-parameter estimation strategy. Hydrol. Earth Syst. Sci. 2014, 18, 13441–13473. [Google Scholar] [CrossRef] [Green Version]
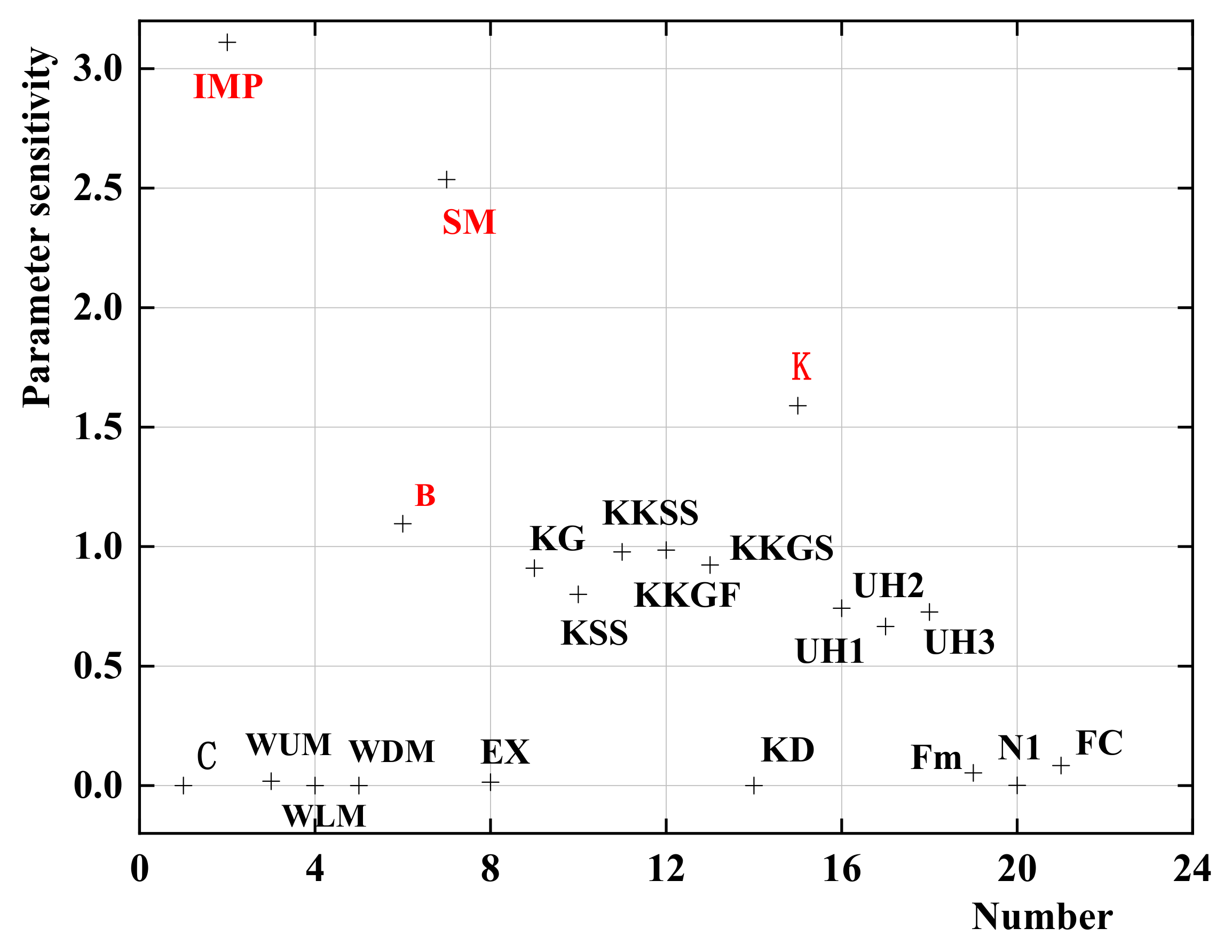




| Number | Parameter | Meaning | Lowe | Bound |
|---|---|---|---|---|
| 1 | C | Ratio of potential evapotranspiration | 0 | 0.3 |
| 2 | IMP | Ratio of the impervious area to the total area | 0.02 | 0.7 |
| 3 | WUM | Tension water capacity of the upper layer | 5 | 100 |
| 4 | WLM | Tension water capacity of the lower layer | 40 | 200 |
| 5 | WDM | Tension water capacity of the deeper layer | 5 | 100 |
| 6 | B | Exponent of the distribution of the tension water capacity | 0.1 | 0.3 |
| 7 | SM | Free water capacity | 5 | 100 |
| 8 | EX | Exponent of distribution of free water capacity | 0.5 | 2 |
| 9 | KG | Outflow coefficient of free water storage to groundwater | 0.05 | 0.65 |
| 10 | KSS | Outflow coefficient of free water storage to interflow | 0.65 | 0.8 |
| 11 | KKSS | Recession constant of interflow storage | 0.05 | 0.95 |
| 12 | KKGF | Recession constant of fast groundwater | 0 | 1 |
| 13 | KKGS | Recession constant of slow groundwater | 0 | 1 |
| 14 | KD | Division value of groundwater | 0 | 1 |
| 15 | K | Ratio of pan evaporation | 0 | 1 |
| 16 | UH(1) | First coefficient of unit graph | 0 | 1 |
| 17 | UH(2) | Second coefficient of unit graph | 0 | 1 |
| 18 | UH(3) | Third coefficient of unit graph | 0 | 1 |
| 19 | Fm | Maximum infiltration rate | 0 | 10 |
| 20 | N1 | Empirical coefficient of infiltration curve | 0 | 1 |
| 21 | FC | Stable infiltration rate | 0 | 1 |
| AE | RE | RMSE | |
|---|---|---|---|
| Before adjustment | −0.0186 | –0.0793 | 0.0391 |
| After adjustment | −0.0031 | 0.0126 | 0.0350 |
| Station | Average Error | NA | AF | AFWR | AFWM |
|---|---|---|---|---|---|
| Dage | AE | −0.524 | −0.018 | −0.193 | −0.145 |
| RE | −0.292 | 0.143 | −0.021 | 0.011 | |
| Gubeikou | AE | −2.438 | −0.47 | −0.417 | −0.43 |
| RE | −0.449 | 0.165 | −0.09 | 0.032 | |
| Xiahui | AE | −0.483 | −0.202 | −0.312 | −0.273 |
| RE | 0.317 | 0.249 | 0.119 | 0.136 |
| Station | Average Error | NA | AF | AFWR | AFWM |
|---|---|---|---|---|---|
| Dage | AE | −1.213 | 0.486 | −0.42 | −0.385 |
| RE | −0.559 | 0.186 | −0.17 | −0.163 | |
| Gubeikou | AE | 0.347 | –1.043 | −1.359 | −1.254 |
| RE | 0.172 | −0.129 | −0.17 | −0.154 | |
| Xiahui | AE | −3.313 | −2.145 | −3.752 | −3.679 |
| RE | −0.201 | −0.113 | −0.298 | −0.298 |
| Station | Average Error | NA | AF | AFWR | AFWM |
|---|---|---|---|---|---|
| Gubeikou | AE | −4.928 | 0.51 | −0.912 | −0.731 |
| RE | −0.254 | 0.07 | −0.232 | −0.226 | |
| Xiahui | AE | −8.551 | −3.817 | −4.116 | −4.547 |
| RE | −0.453 | −0.168 | −0.203 | −0.227 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Cai, S.; Tong, J.; Liao, W.; Zhang, P. Flood Forecasting via the Ensemble Kalman Filter Method Using Merged Satellite and Measured Soil Moisture Data. Water 2022, 14, 1555. https://doi.org/10.3390/w14101555
Zhang C, Cai S, Tong J, Liao W, Zhang P. Flood Forecasting via the Ensemble Kalman Filter Method Using Merged Satellite and Measured Soil Moisture Data. Water. 2022; 14(10):1555. https://doi.org/10.3390/w14101555
Chicago/Turabian StyleZhang, Chen, Siyu Cai, Juxiu Tong, Weihong Liao, and Pingping Zhang. 2022. "Flood Forecasting via the Ensemble Kalman Filter Method Using Merged Satellite and Measured Soil Moisture Data" Water 14, no. 10: 1555. https://doi.org/10.3390/w14101555
APA StyleZhang, C., Cai, S., Tong, J., Liao, W., & Zhang, P. (2022). Flood Forecasting via the Ensemble Kalman Filter Method Using Merged Satellite and Measured Soil Moisture Data. Water, 14(10), 1555. https://doi.org/10.3390/w14101555







