Statistical Roughness Properties of the Bed Surface in Braided Rivers
Abstract
:1. Introduction
2. Experimental Arrangements
3. Calculation Methods
3.1. Data Collection and Processing
3.2. Morphological Parameters
3.3. Statistical Parameters
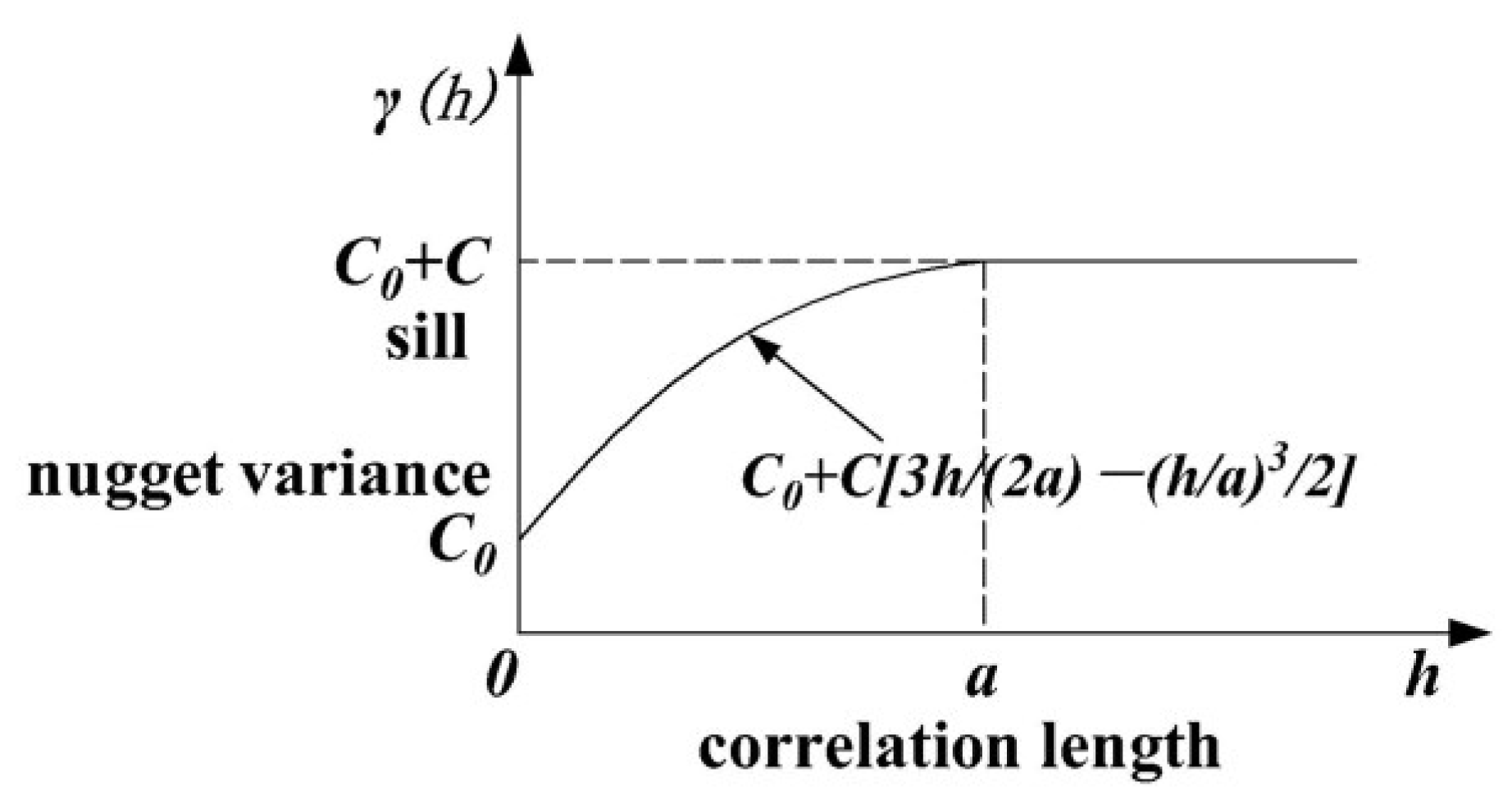
3.4. Variogram
- The nugget variance reflects the magnitude of the randomness of the regionalized variables. Theoretically, when the sampling scale , the value of should be equal to 0. However, due to the presence of microstructural variations (i.e., internal variability that occurs at scales smaller than the sampling scale ) and errors associated with sampling, measurement, and analysis, when two sampling points are very close, leading to the existence of a nugget variance.
- The sill reflects the magnitude of the variability of the regionalized variables, indicating the intensity of the variation within the study area. The ratio of the nugget variance to the sill is defined as the nugget coefficient, denoted as , which represents the proportion of spatial variability caused by the random component to the total variability, indicating the strength of spatial variability. If , it indicates strong spatial correlation of the variable; if , it indicates moderate spatial correlation; if , it indicates weak spatial correlation. A larger suggests that the variability is mainly due to random factors.
- The correlation length reflects the extent of spatial autocorrelation of the regionalized variables and represents the point where the spatial correlation transitions from existence to non-existence. When the sampling scale , there is spatial correlation and mutual influence between two points in space, with the influence decreasing as the distance between the points increases. When the sampling scale , there is no spatial correlation between the two points.
4. Results and Discussion
4.1. Morphological Parameters of Braided Rivers
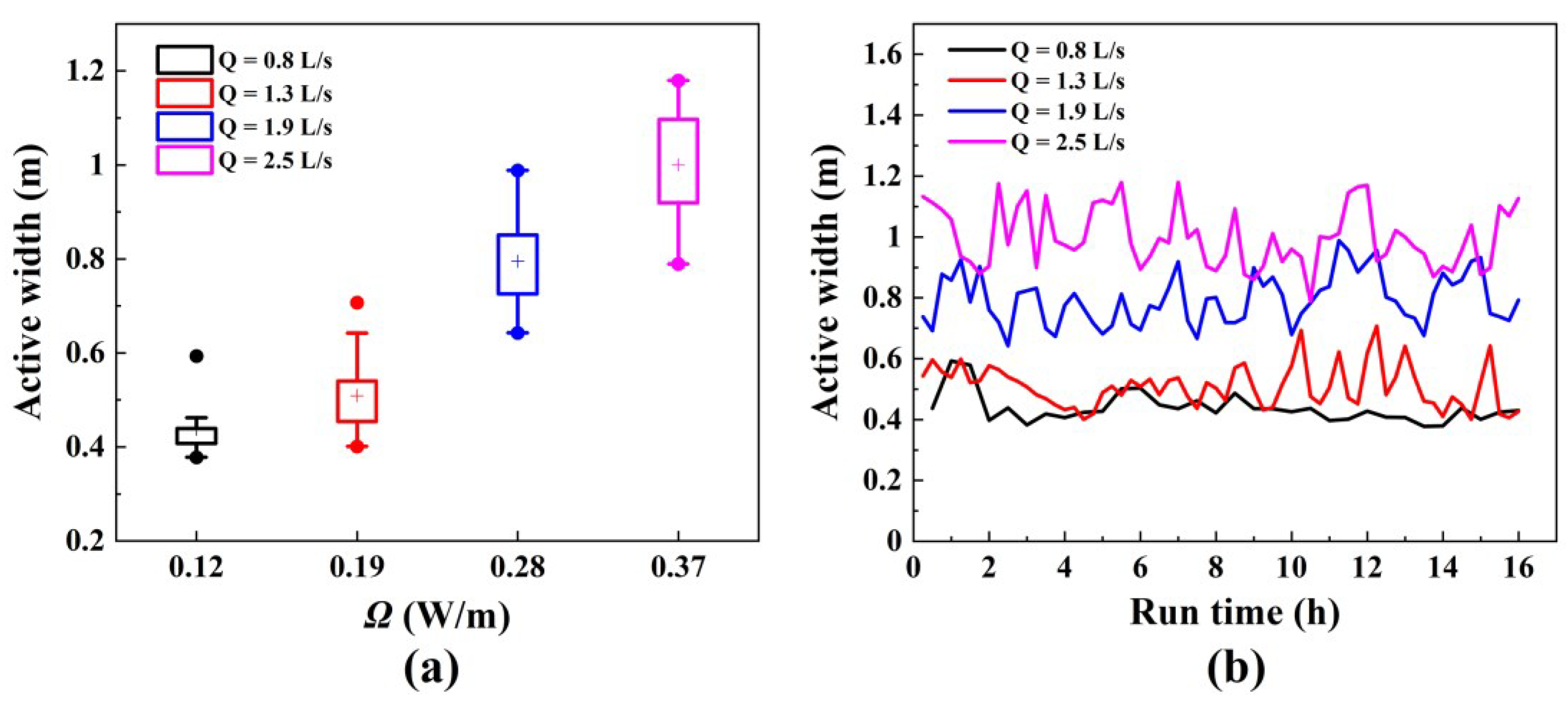
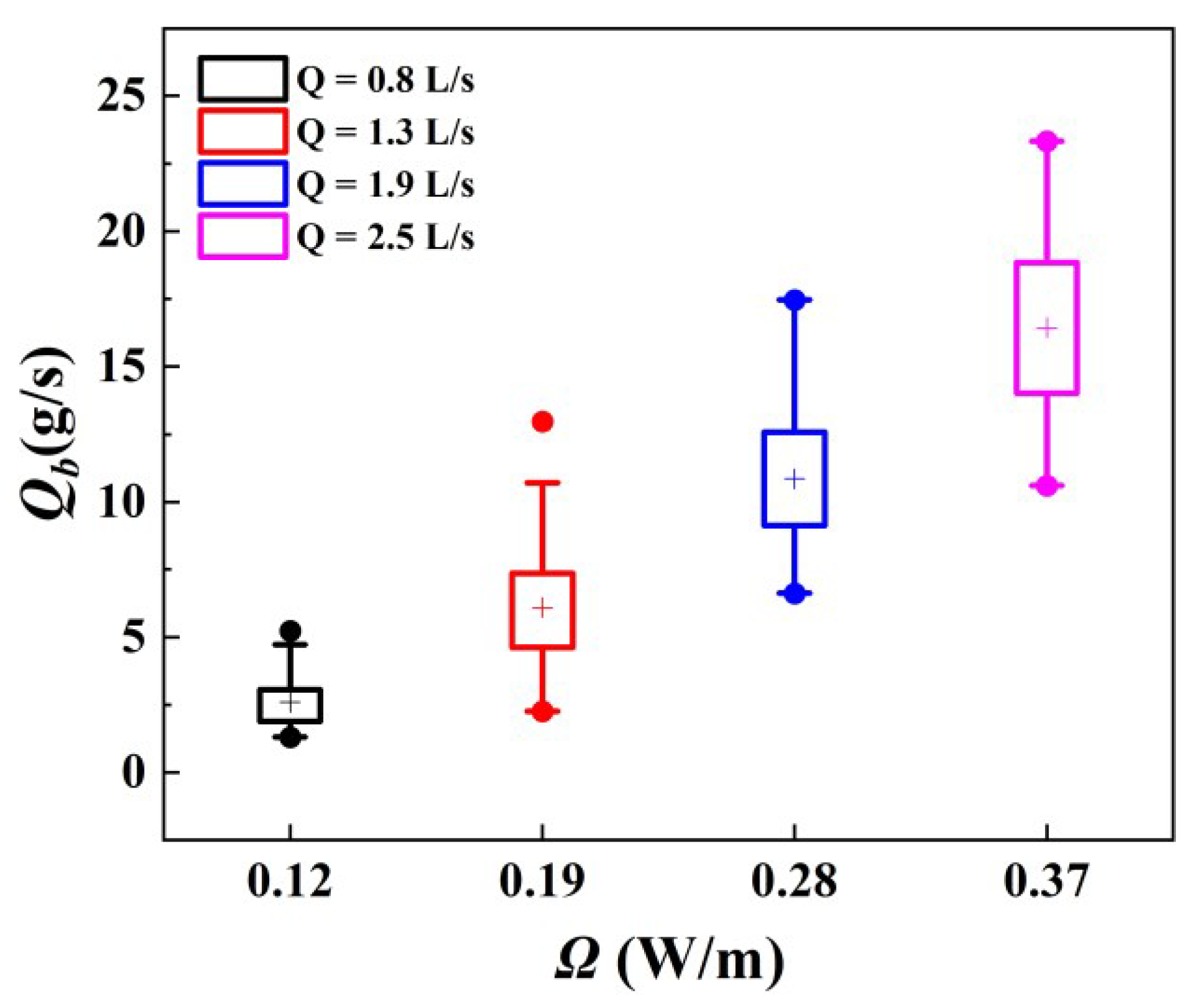
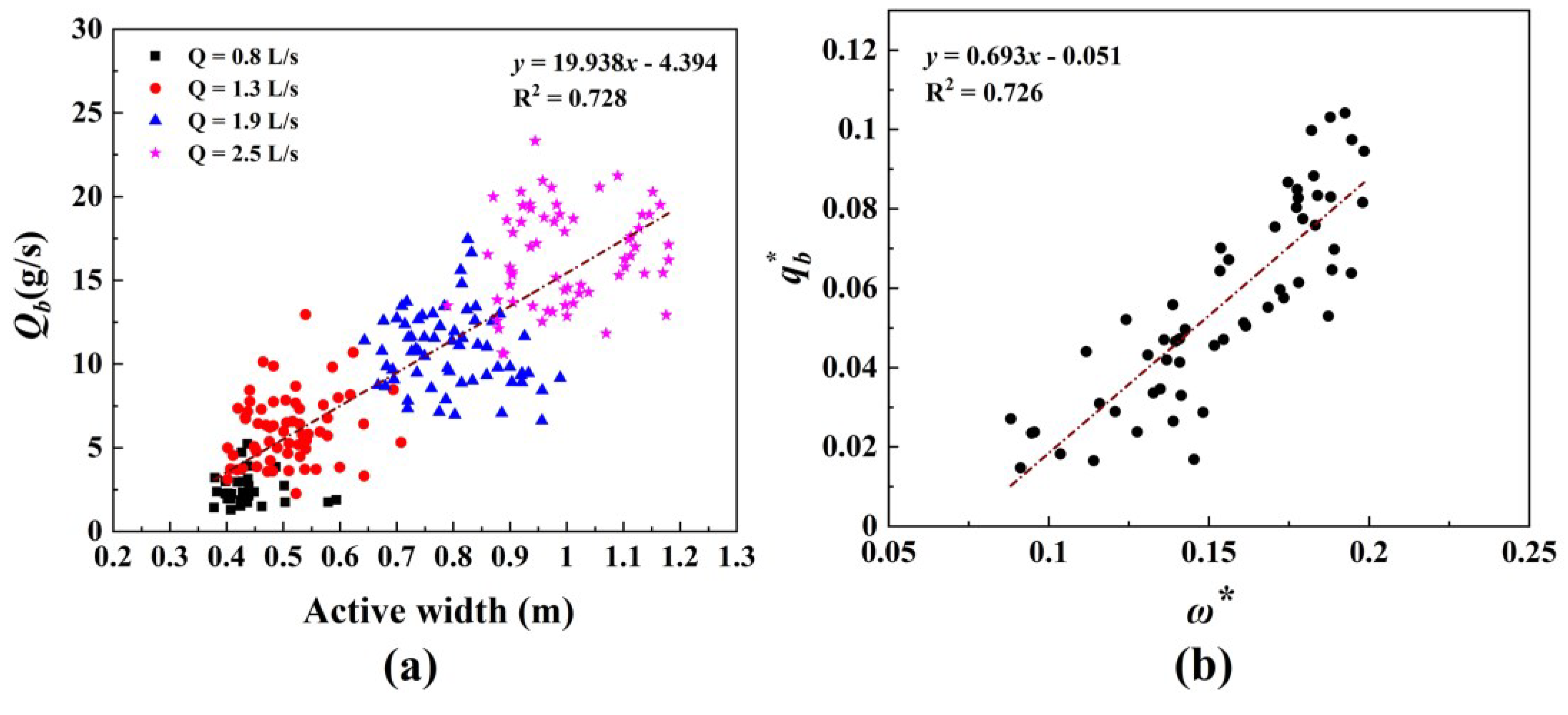
4.2. Relationship between Morphological Active Width, Stream Power, and Bedload Transport Rate
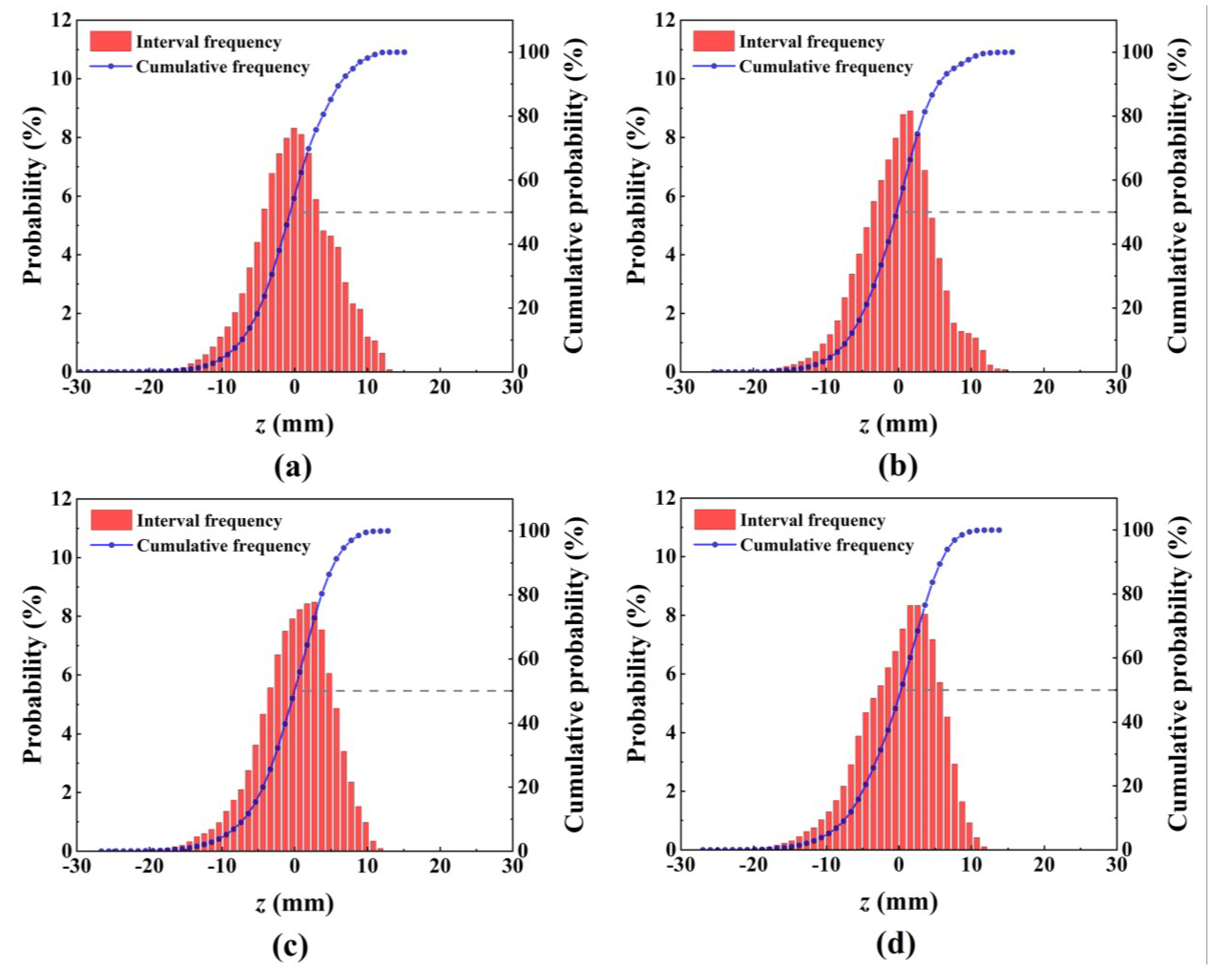
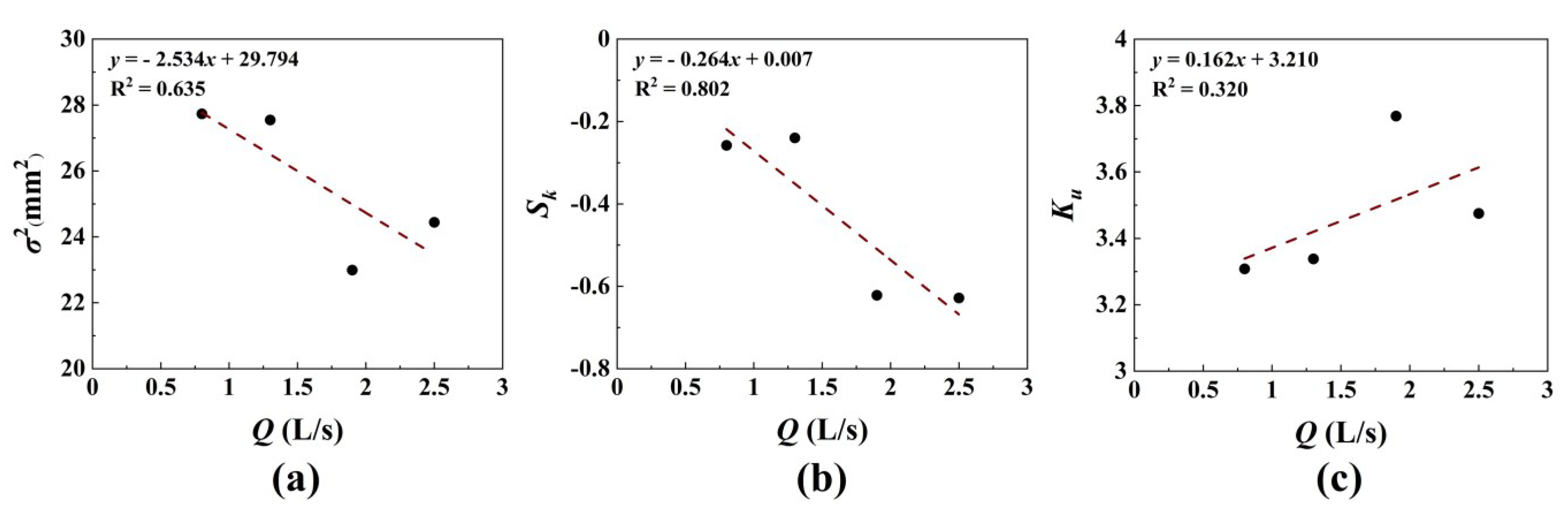
4.3. Elevation Probability Distribution and Statistical Parameters of the Bed Surface
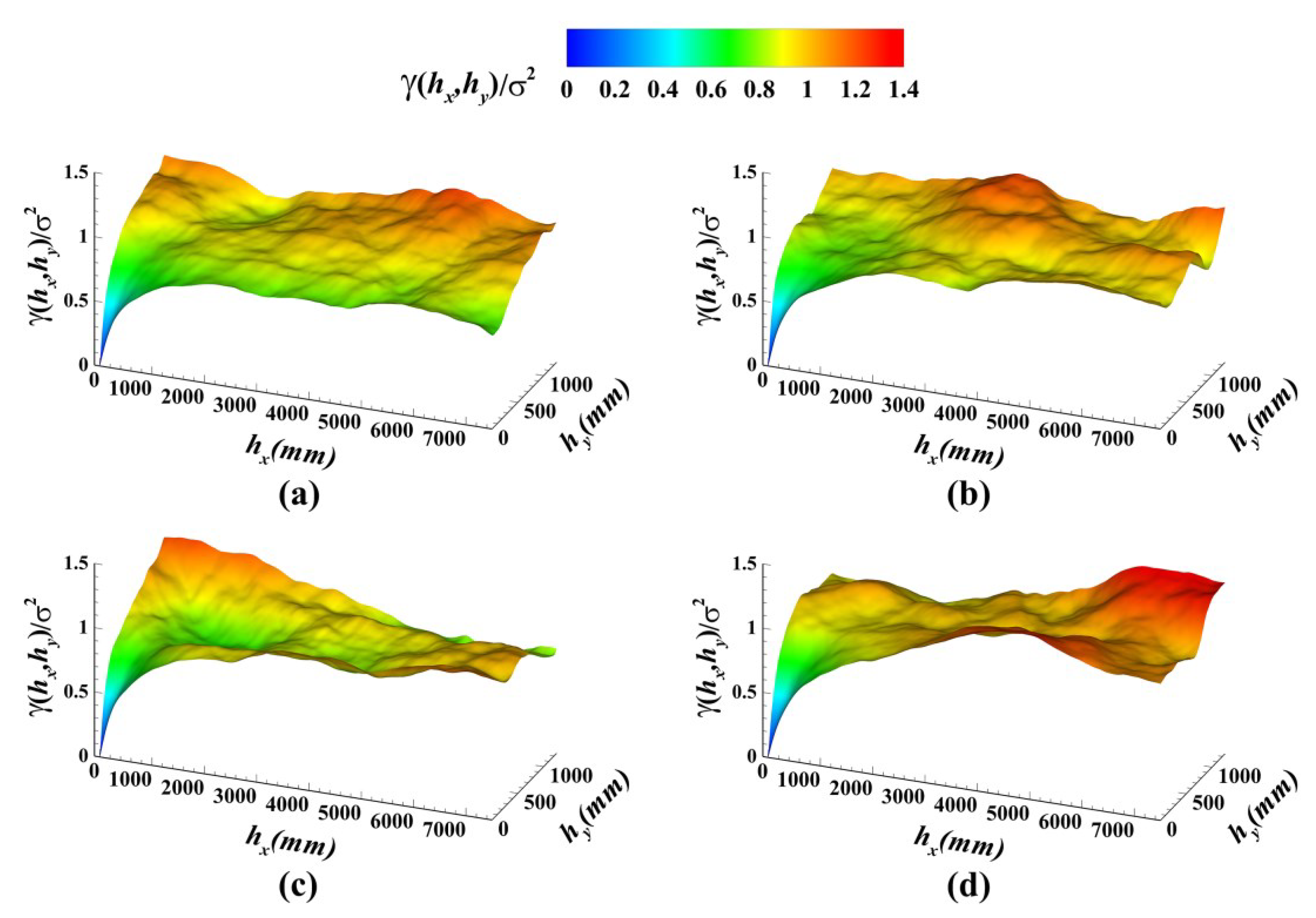
4.4. Two-Dimensional Variograms of the Bed Surface Elevations
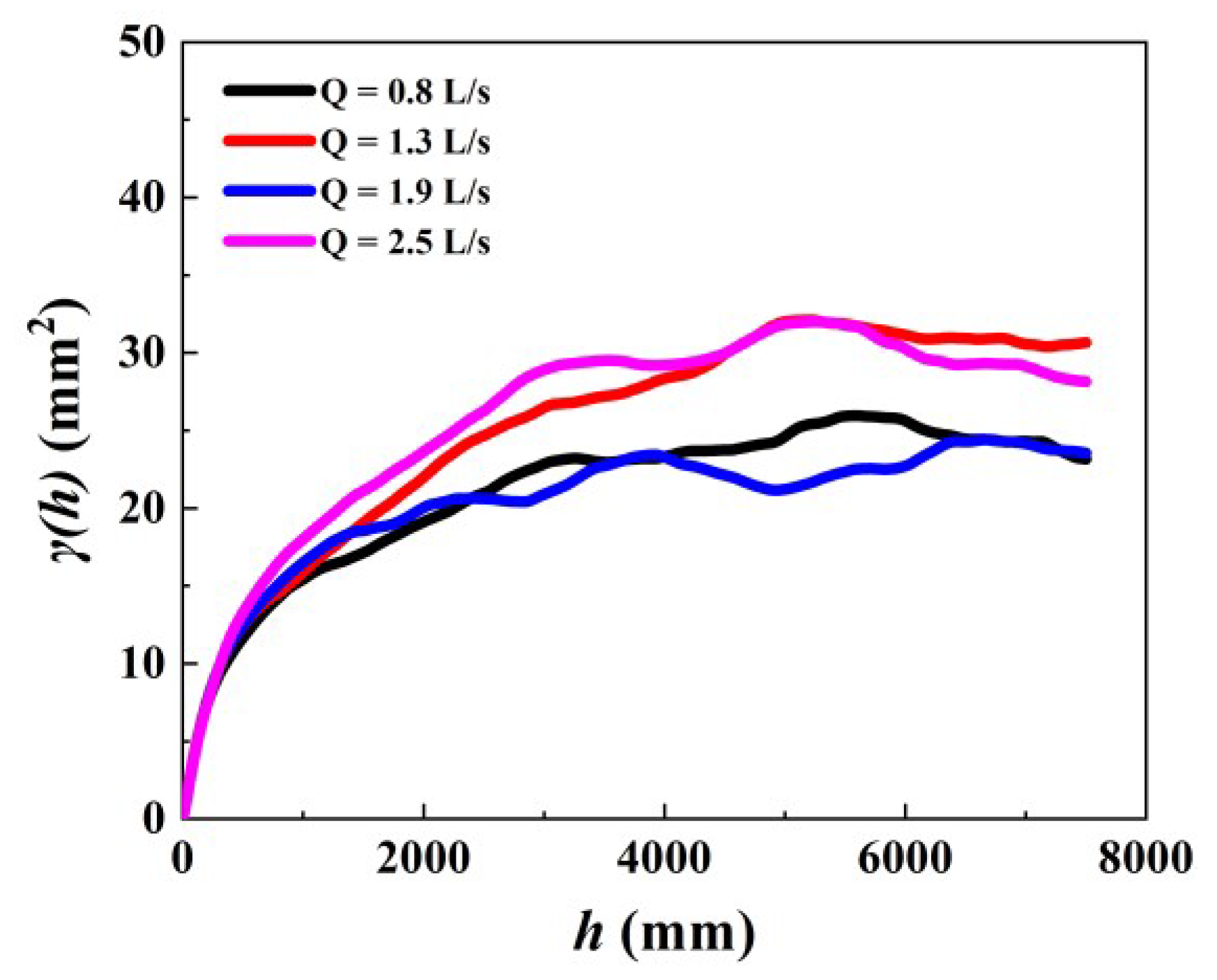
4.5. One-Dimensional Variograms of the Bed Surface Elevations
5. Conclusions
- The morphological change area of the reach becomes more continuous and extensive with increasing discharge. The average morphological active width increases, while the average morphological active depth remains almost unchanged.
- There is a significant positive correlation between the bedload transport rate and the reach-averaged morphological active width and the stream power. This indicates that the easily measured parameters such as discharge, bed surface particle size, wetted width, and active width, which characterize morphological change, can be used to predict the mass of bedload transport that is difficult to measure directly.
- The bed elevation probability distribution in braided rivers is negatively skewed and leptokurtic. There is a relatively significant correlation between skewness and the dimensionless bedload transport rate, providing a simple index for the preliminary prediction of bedload transport rate in braided rivers. The two-dimensional variogram values of the bed surface elevation differ in each direction, indicating anisotropy in bed surface roughness within the research reach.
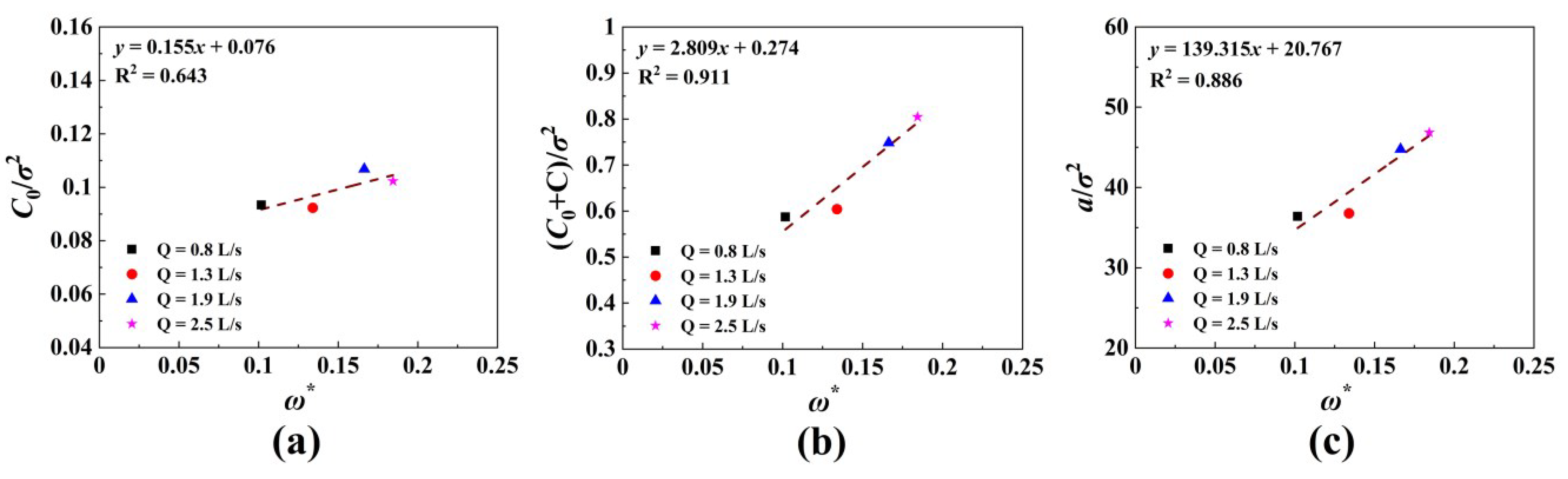
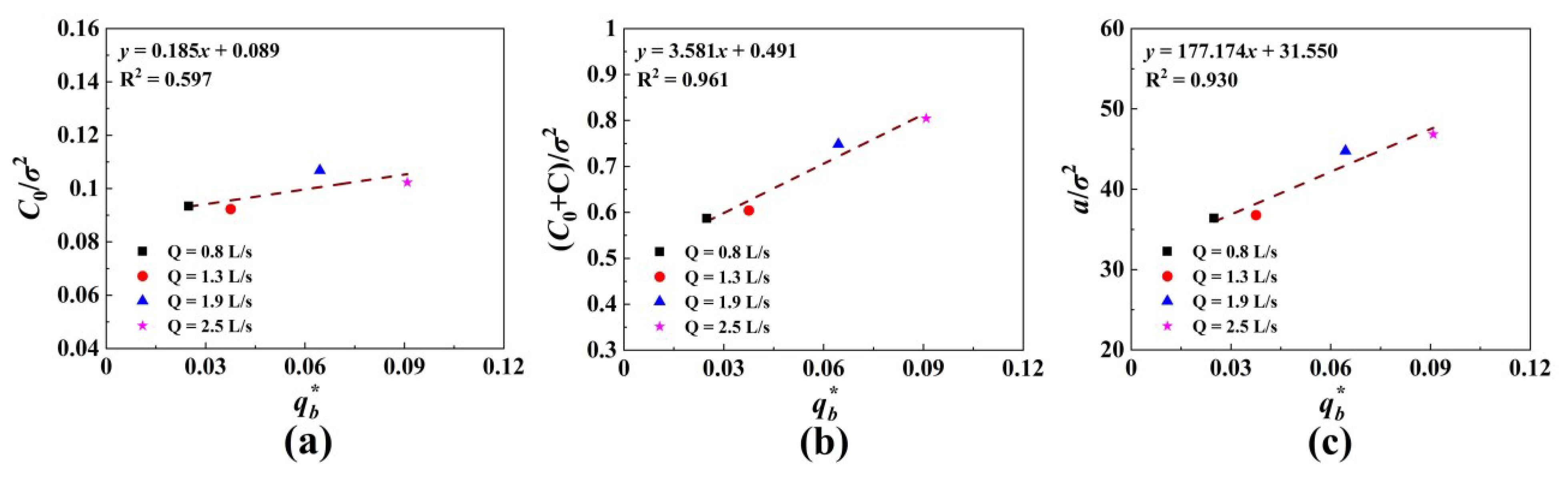
- As flow intensity increases, bed surface roughness, the corresponding sill, and correlation length increase. The bed elevation variable in the -axis direction has a strong spatial correlation, and elevation variation caused by random factors can be ignored. The sill and correlation length of the bed surface elevation variogram can be used to estimate the bedload transport rate in the constant discharge experiments of braided rivers.
- This study primarily focused on different flow intensities. In the future, more extensive and systematic research should be conducted to analyze the influence of bed surface particle sizes, slopes, and different flow and sediment conditions on the statistical roughness properties of the bed surface in braided rivers to enrich the relevant research achievements.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Surian, N. Fluvial processes in Braided Rivers. In Rivers—Physical, Fluvial and Environmental Processes; Rowiński, P., Radecki-Pawlik, A., Eds.; Springer: Cham, Switzerland, 2015; Chapter 15; pp. 403–425. [Google Scholar] [CrossRef]
- Leopold, L.B.; Wolman, M.G. River channel patterns-braided, meandering and straight. United States Geol. Surv. Prof. Paper 1957, 282A, 39–85. [Google Scholar]
- Bertoldi, W.; Zanoni, L.; Tubino, M. Planform dynamics of braided streams. Earth Surf. Process. Landf. 2009, 34, 547–557. [Google Scholar] [CrossRef]
- Ashmore, P. Morphology and Dynamics of Braided Rivers. In Treatise on Geomorphology; Shroder, J., Wohl, E., Eds.; Elsevier: San Diego, CA, USA, 2013; Volume 9, pp. 289–312. [Google Scholar] [CrossRef]
- Liu, C.; Shan, Y.Q. Impact of an emergent model vegetation patch on flow adjustment and velocity. Water Manag. 2022, 175, 55–66. [Google Scholar] [CrossRef]
- Yan, C.H.; Shan, Y.Q.; Liu, C.; Liu, X.N. Analytical model for predicting the lateral profiles of velocities through a partially vegetated channel. J. Hydrol. 2022, 612, 128137. [Google Scholar] [CrossRef]
- Liu, C.; Yan, C.H.; Sun, S.C.; Lei, J.R.; Nepf, H.; Shan, Y.Q. Velocity, turbulence, and sediment deposition in a channel partially filled with a Phragmites australis canopy. Water Resour. Res. 2022, 58, e2022WR032381. [Google Scholar] [CrossRef]
- Gui, Z.Q.; Shan, Y.Q.; Liu, C. Flow velocity evolution through a floating rigid cylinder array under unidirectional flow. J. Hydrol. 2023, 617, 128915. [Google Scholar] [CrossRef]
- Pender, G.; Hoey, T.B.; Fuller, C.; McEwan, I.K. Selective bedload transport during the degradation of a well sorted graded sediment bed. J. Hydraul. Res. 2001, 39, 269–277. [Google Scholar] [CrossRef]
- Haynes, H.; Pender, G. Stress history effects on graded bed stability. J. Hydraul. Eng. 2007, 133, 343–349. [Google Scholar] [CrossRef]
- Luo, M.; Wang, X.K.; Yan, X.F.; Huang, E. Applying the mixing layer analogy for flow resistance evaluation in gravel-bed streams. J. Hydrol. 2020, 589, 125119. [Google Scholar] [CrossRef]
- Fu, H.S.; Shan, Y.Q.; Liu, C. A model for predicting the grain size distribution of an armor layer under clear water scouring. J. Hydrol. 2023, 623, 129842. [Google Scholar] [CrossRef]
- Liu, C.; Nepf, H. Sediment deposition within and around a finite patch of model vegetation over a range of channel velocity. Water Resour. Res. 2016, 52, 600–612. [Google Scholar] [CrossRef] [Green Version]
- Ackers, P.; White, W. Sediment transport: New approach and analysis. J. Hydraul. Eng. 1973, 99, 2041–2060. [Google Scholar] [CrossRef]
- Kamphuis, J.W. Determination of sand roughness for fixed beds. J. Hydraul. Res. 1974, 12, 193–203. [Google Scholar] [CrossRef]
- Whiting, P.J.; Dietrich, W.E. Boundary shear-stress and roughness over mobile alluvial beds. J. Hydraul. Eng. 1990, 116, 1495–1511. [Google Scholar] [CrossRef]
- Powell, D.M. Flow resistance in gravel-bed rivers: Progress in research. Earth-Sci. Rev. 2014, 136, 301–338. [Google Scholar] [CrossRef]
- Robert, A. Statistical properties of sediment bed profiles in alluvial channels. Math. Geol. 1988, 20, 205–225. [Google Scholar] [CrossRef]
- Bertin, S.; Friedrich, H. Measurement of gravel-bed topography: Evaluation study applying statistical roughness analysis. J. Hydraul. Eng. 2014, 140, 269–279. [Google Scholar] [CrossRef]
- Wu, W.M.; Wang, S.S.Y.; Jia, Y.F. Nonuniform sediment transport in alluvial rivers. J. Hydraul. Res. 2000, 38, 427–434. [Google Scholar] [CrossRef]
- Bai, Y.C.; Wang, X.; Cao, Y.G. Incipient motion of non-uniform coarse grain of bedload considering the impact of two-way exposure. Sci. China Tech. Sci. 2013, 56, 1896–1905. [Google Scholar] [CrossRef]
- Xing, R.; Zhang, G.G.; Liang, Z.X.; Wu, Z.S. Study on the location characteristics of bed surface particle. J. Sediment Res. 2016, 4, 28–33. [Google Scholar] [CrossRef]
- Sapozhnikov, V.; Foufoula-Georgiou, E. Self-affinity in braided rivers. Water Resour. Res. 1996, 32, 1429–1439. [Google Scholar] [CrossRef]
- Robert, A. Fractal properties of simulated bed profiles in coarse-grained channels. Math. Geol. 1991, 23, 367–382. [Google Scholar] [CrossRef]
- Butler, J.B.; Lane, S.N.; Chandler, J.H. Characterization of the structure of riverbed gravels using two-dimensional fractal analysis. Math. Geol. 2001, 33, 301–330. [Google Scholar] [CrossRef]
- Papanicolaou, A.N.; Tsakiris, A.G.; Strom, K.B. The use of fractals to quantify the morphology of cluster microforms. Geomorphology 2012, 139, 91–108. [Google Scholar] [CrossRef]
- Aubeneau, A.F.; Martin, R.L.; Bolster, D.; Schumer, R.; Jerolmack, D.; Packman, A. Fractal patterns in riverbed morphology produce fractal scaling of water storage times. Geophys. Res. Lett. 2015, 42, 5309–5315. [Google Scholar] [CrossRef] [Green Version]
- Brasington, J.; Vericat, D.; Rychkov, I. Modeling river bed morphology, roughness, and surface sedimentology using high resolution terrestrial laser scanning. Water Resour. Res. 2012, 48, W11519. [Google Scholar] [CrossRef] [Green Version]
- Bouratsis, P.P.; Diplas, P.; Dancey, C.L.; Apsilidis, N. High-resolution 3-D monitoring of evolving sediment beds. Water Resour. Res. 2013, 49, 977–992. [Google Scholar] [CrossRef] [Green Version]
- Morgan, J.A.; Brogan, D.J.; Nelson, P.A. Application of Structure-from-Motion photogrammetry in laboratory flumes. Geomorphology 2017, 276, 125–143. [Google Scholar] [CrossRef]
- Nikora, V.I.; Goring, D.G.; Biggs, B.J.F. On gravel-bed roughness characterization. Water Resour. Res. 1998, 34, 517–527. [Google Scholar] [CrossRef]
- Nikora, V.; Walsh, J. Water-worked gravel surfaces: High-order structure functions at the particle scale. Water Resour. Res. 2004, 40, W12601. [Google Scholar] [CrossRef]
- Aberle, J.; Nikora, V. Statistical properties of armored gravel bed surfaces. Water Resour. Res. 2006, 42, W11414. [Google Scholar] [CrossRef]
- Aberle, J.; Nikora, V.; Henning, M.; Ettmer, B.; Hentschel, B. Statistical characterization of bed roughness due to bed forms: A field study in the Elbe River at Aken, Germany. Water Resour. Res. 2010, 46, W03521. [Google Scholar] [CrossRef]
- Pan, Y.W.; Liu, X.; Cai, T.; Yang, K.J. Influences of average particle size and non-uniformity on the statistical roughness characteristics of gravel-bed surfaces. Arab. J. Geosci. 2022, 15, 1021. [Google Scholar] [CrossRef]
- Pan, Y.W.; Xia, J.Q.; Yang, K.J. Statistical roughness properties of the gravel bed surfaces in a meandering channel. J. Hydrol. 2023, 617, 128966. [Google Scholar] [CrossRef]
- Egozi, R.; Ashmore, P. Defining and measuring braiding intensity. Earth Surf. Process. Landf. 2008, 33, 2121–2138. [Google Scholar] [CrossRef]
- Sarma, J.N.; Acharjee, S. A study on variation in channel width and braiding intensity of the Brahmaputra River in Assam, India. Geosciences 2018, 8, 343. [Google Scholar] [CrossRef] [Green Version]
- Das, B.C.; Islam, A. Reviewing braiding indices of the river channel in an attempt to establish alternatives. MethodsX 2023, 10, 102042. [Google Scholar] [CrossRef]

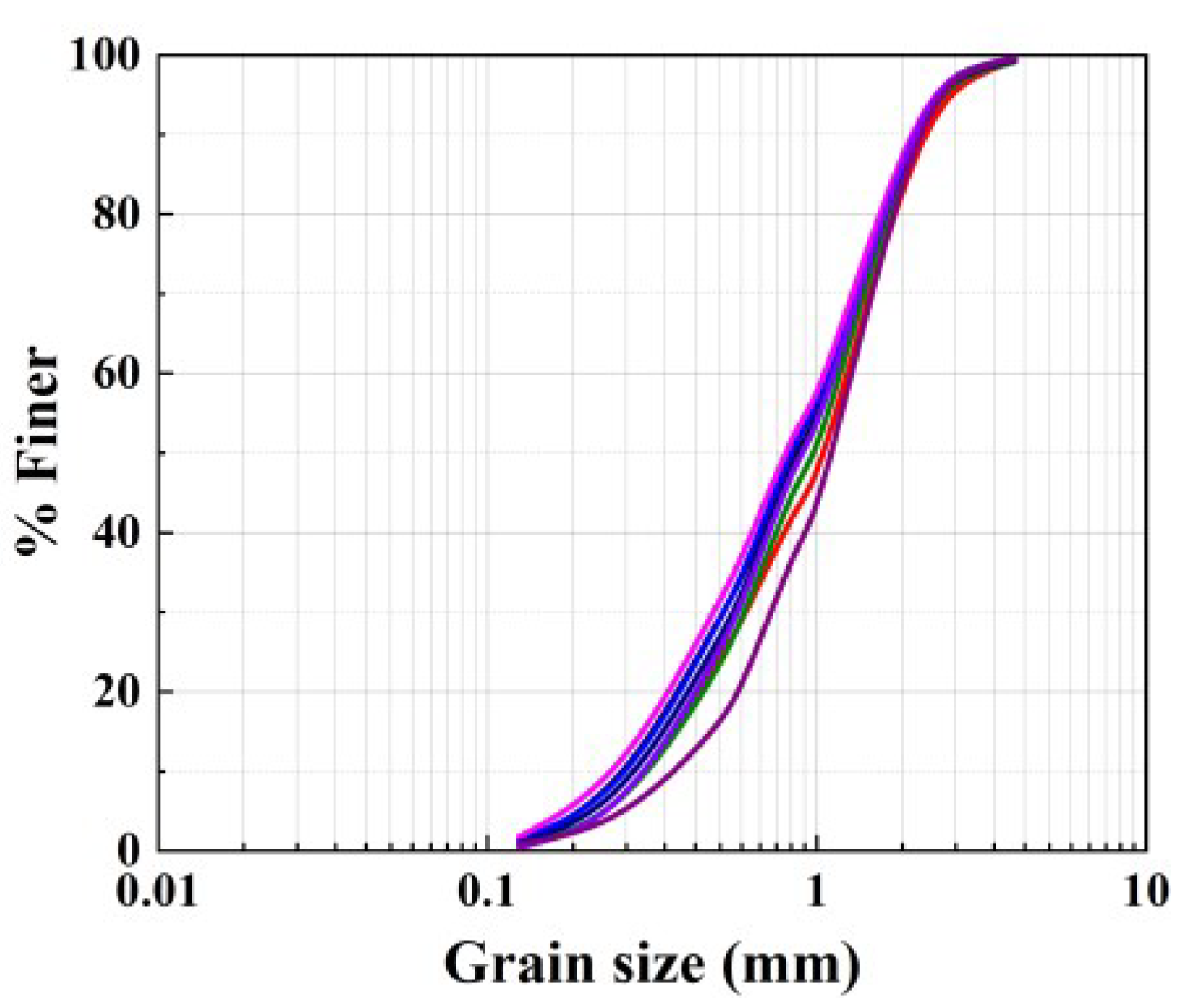



| Experiment | Slope | Discharge | Stream Power | Evolution Time | Experimental Run Time | Threshold |
|---|---|---|---|---|---|---|
| S | Q | Ω | ||||
| (%) | (L/s) | (W/m) | (h) | (h) | (mm) | |
| Run 1 | 1.5 | 0.8 | 0.12 | 15 | 16 | 2.42 |
| Run 2 | 1.5 | 1.3 | 0.19 | 15 | 16 | 2.18 |
| Run 3 | 1.5 | 1.9 | 0.28 | 12 | 16 | 1.98 |
| Run 4 | 1.5 | 2.5 | 0.37 | 10 | 16 | 1.70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, B.; Pan, Y.; Lin, X.; Yang, K. Statistical Roughness Properties of the Bed Surface in Braided Rivers. Water 2023, 15, 2612. https://doi.org/10.3390/w15142612
Ren B, Pan Y, Lin X, Yang K. Statistical Roughness Properties of the Bed Surface in Braided Rivers. Water. 2023; 15(14):2612. https://doi.org/10.3390/w15142612
Chicago/Turabian StyleRen, Baoliang, Yunwen Pan, Xingyu Lin, and Kejun Yang. 2023. "Statistical Roughness Properties of the Bed Surface in Braided Rivers" Water 15, no. 14: 2612. https://doi.org/10.3390/w15142612
APA StyleRen, B., Pan, Y., Lin, X., & Yang, K. (2023). Statistical Roughness Properties of the Bed Surface in Braided Rivers. Water, 15(14), 2612. https://doi.org/10.3390/w15142612






