Optimized Design of Sponge-Type Comprehensive Pipe Corridor Rainwater Chamber Based on NSGA-III Algorithm
Abstract
:1. Introduction
2. Materials and Methods
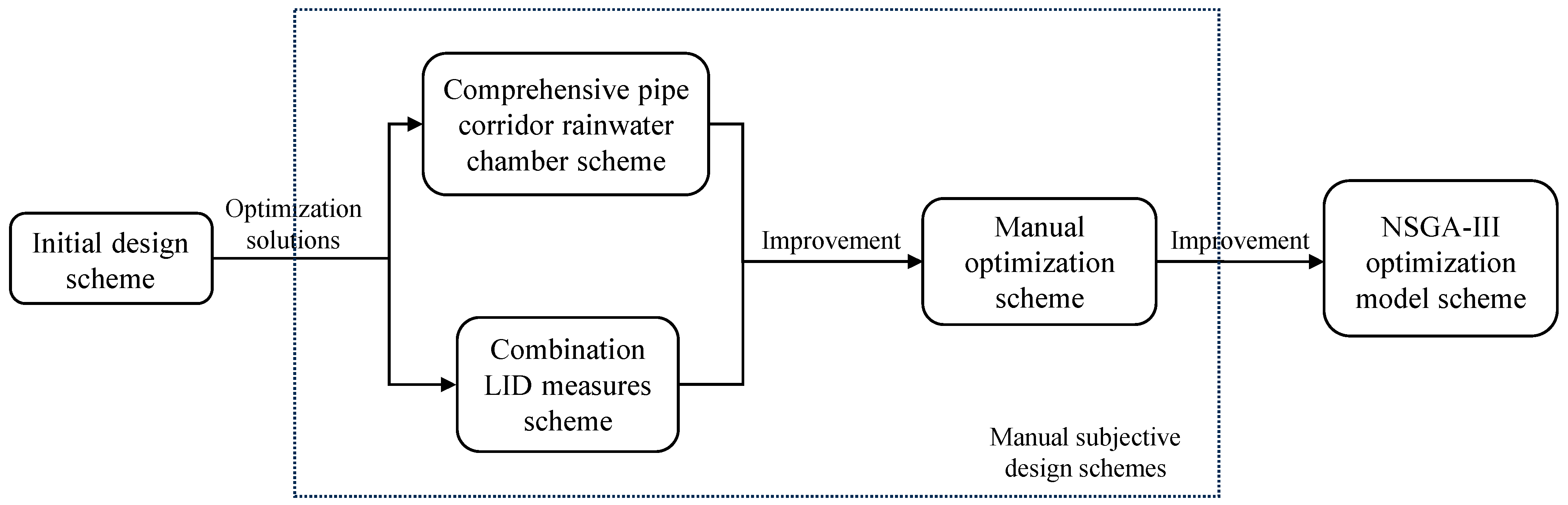
2.1. Scheme Design
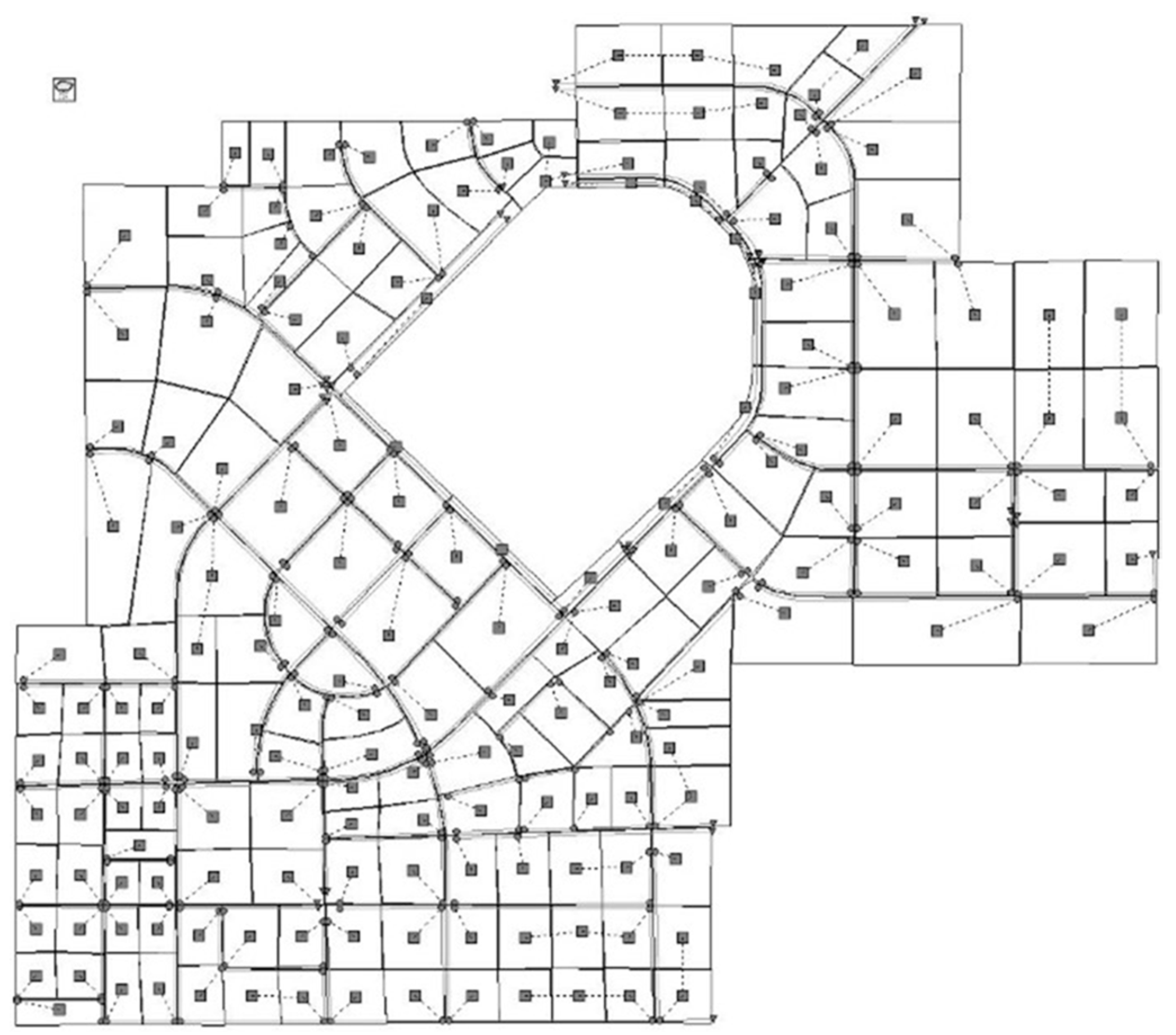
2.2. Study Area
2.3. Storm Water Management Model
2.3.1. Model Description
2.3.2. Establishment of the SWMM
2.3.3. Design Rainfall
2.3.4. SWMM Model Parameterization and Validation
2.4. Design of Manual Subjective Design Schemes
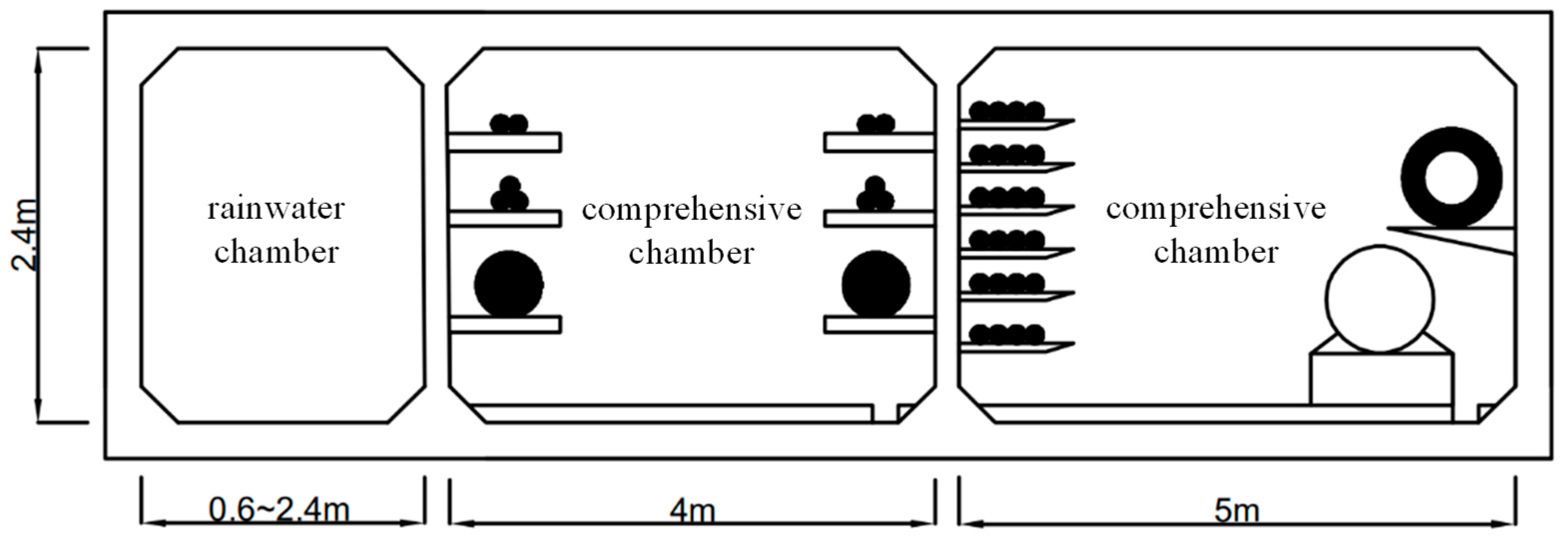
2.4.1. Comprehensive Pipe Corridor Rainwater Chamber Scheme
2.4.2. Combination LID Measure Scheme
2.4.3. Manual Optimization Scheme
2.5. Optimization Model Scheme Based on NSGA-III Algorithm
2.5.1. NSGA-III Optimization Algorithm
2.5.2. Objective Function
2.5.3. Constraints
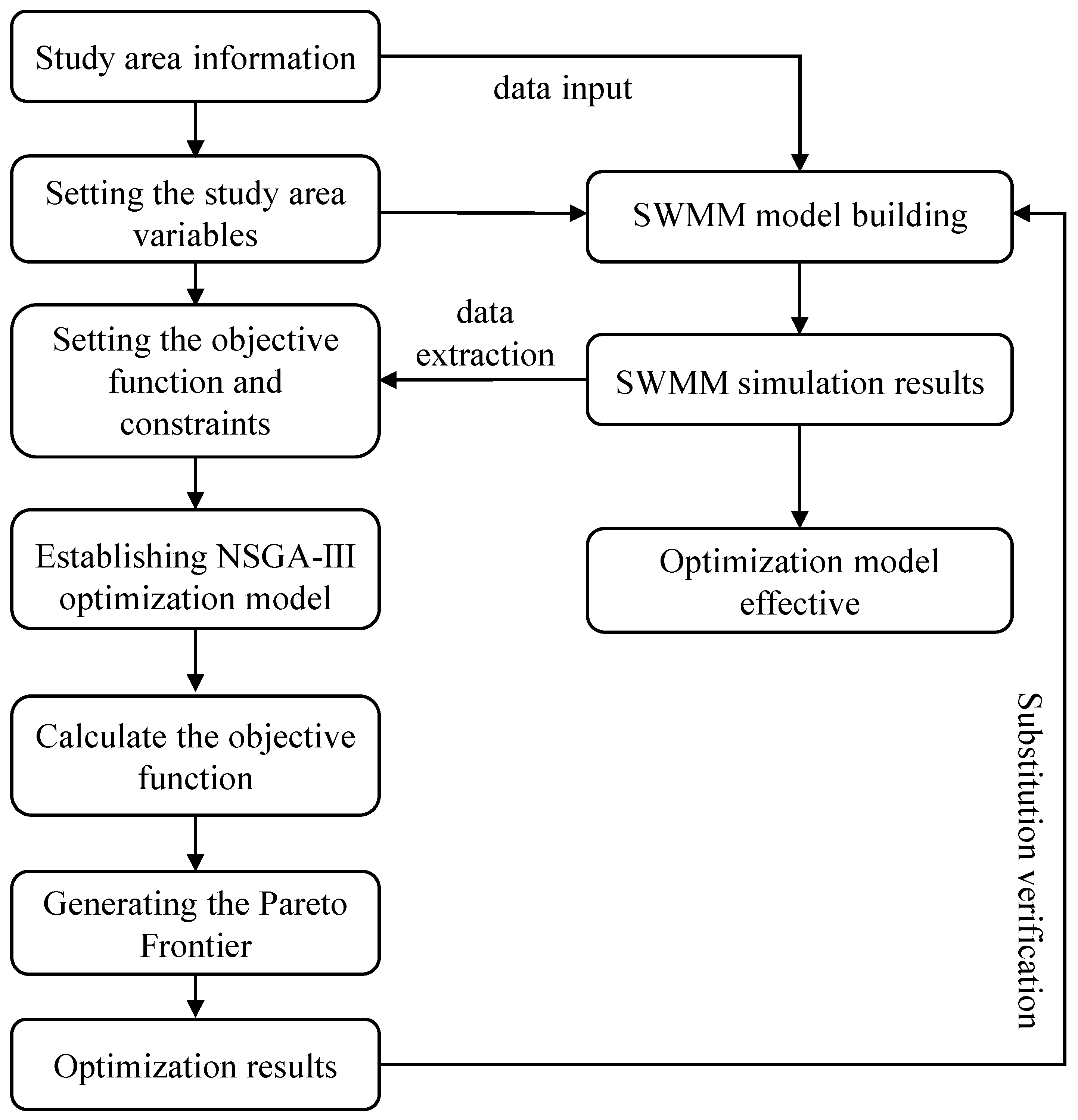
2.5.4. Optimization Model Construction
- (1)
- Model SWMM and identify the different combinations of LID measures used in each sub-catchment;
- (2)
- Dimensional information for combination LID measures with different percentages of paving and different rainwater chamber section widths was entered into the model to create SWMM models with different ratios, and 100 groups of data were obtained;
- (3)
- Multiple linear regression was used to establish linear relationships between the percentage of combined LID measures laid, the width of the rainwater chamber section, the surface runoff coefficient, pipe overload time, nodal overflow, and the total investment cost;
- (4)
- The best design scheme is obtained by optimally solving the linear relationship between several by the NSGA-III algorithm to obtain the Pareto front;
- (5)
- Substitute the individual optimal solutions in the obtained solution set into the model for checking and verifying the validity of the optimization model and the applicability of the NSGA-III algorithm.
3. Results
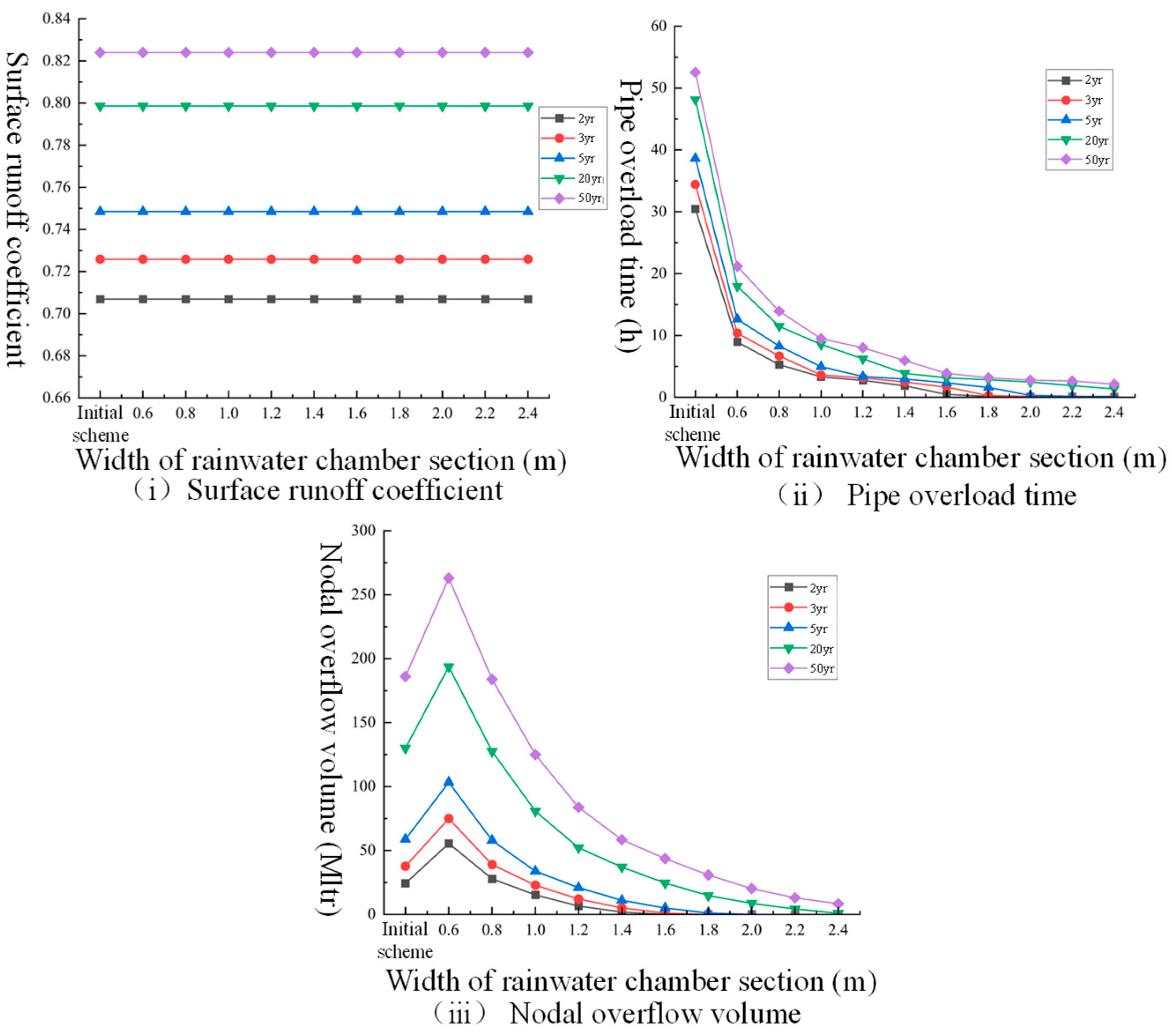
3.1. Comprehensive Pipe Corridor Rainwater Chamber Scheme
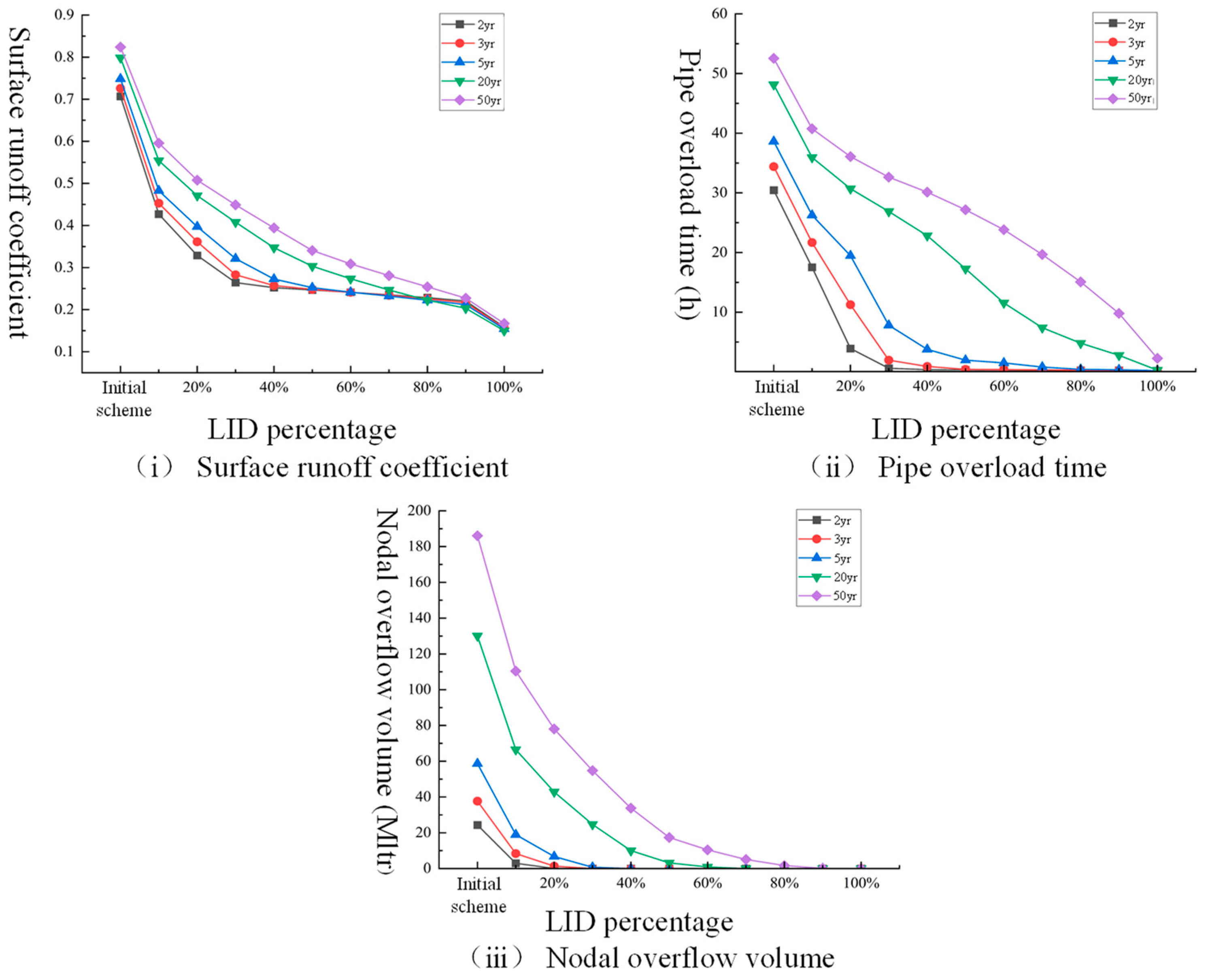
3.2. Combination LID Measures
3.3. Manual Optimization Scheme
3.4. NSGA-III Optimization Model
3.4.1. Optimal Variables
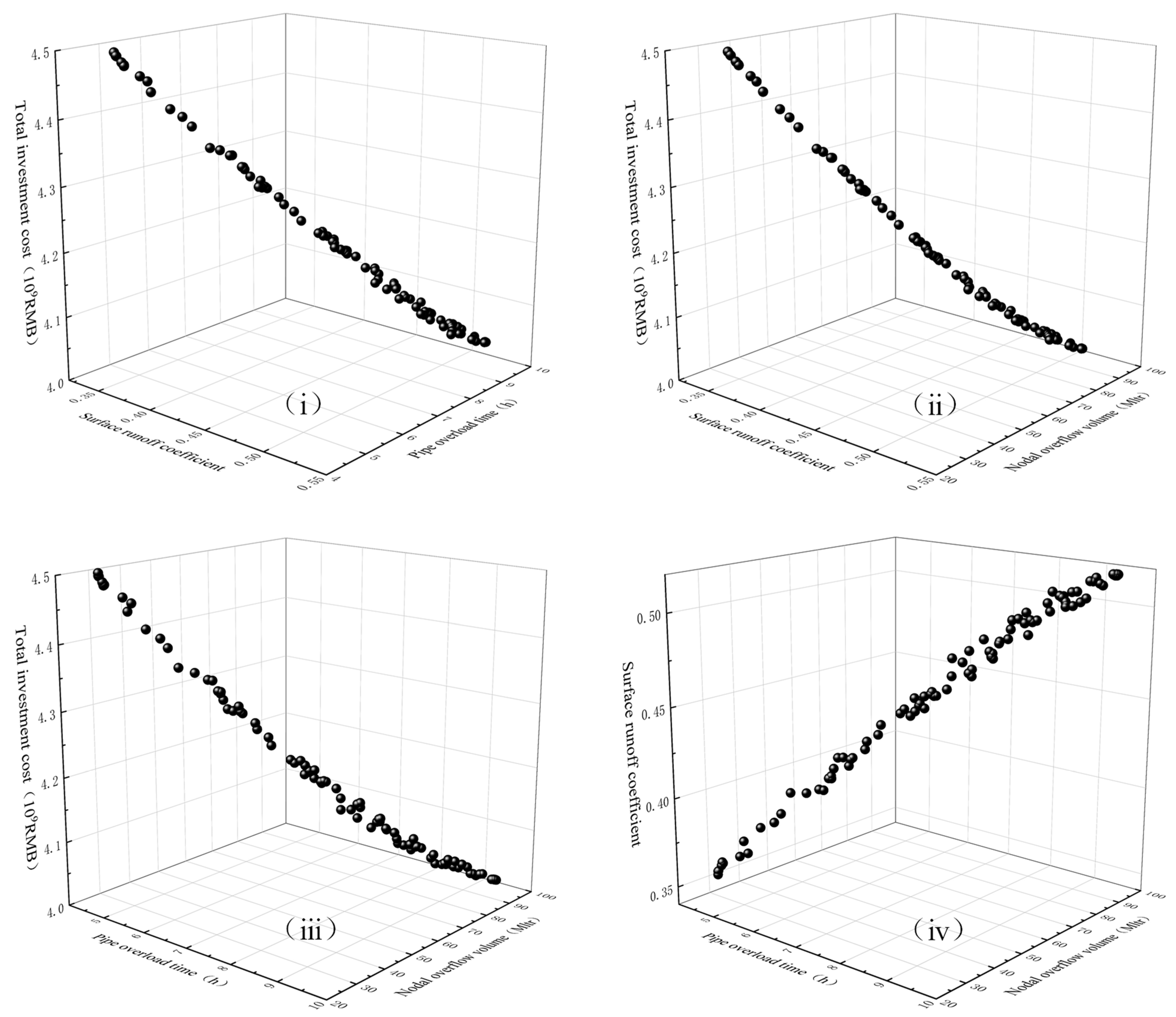
3.4.2. Pareto Frontier of the Optimizing Model
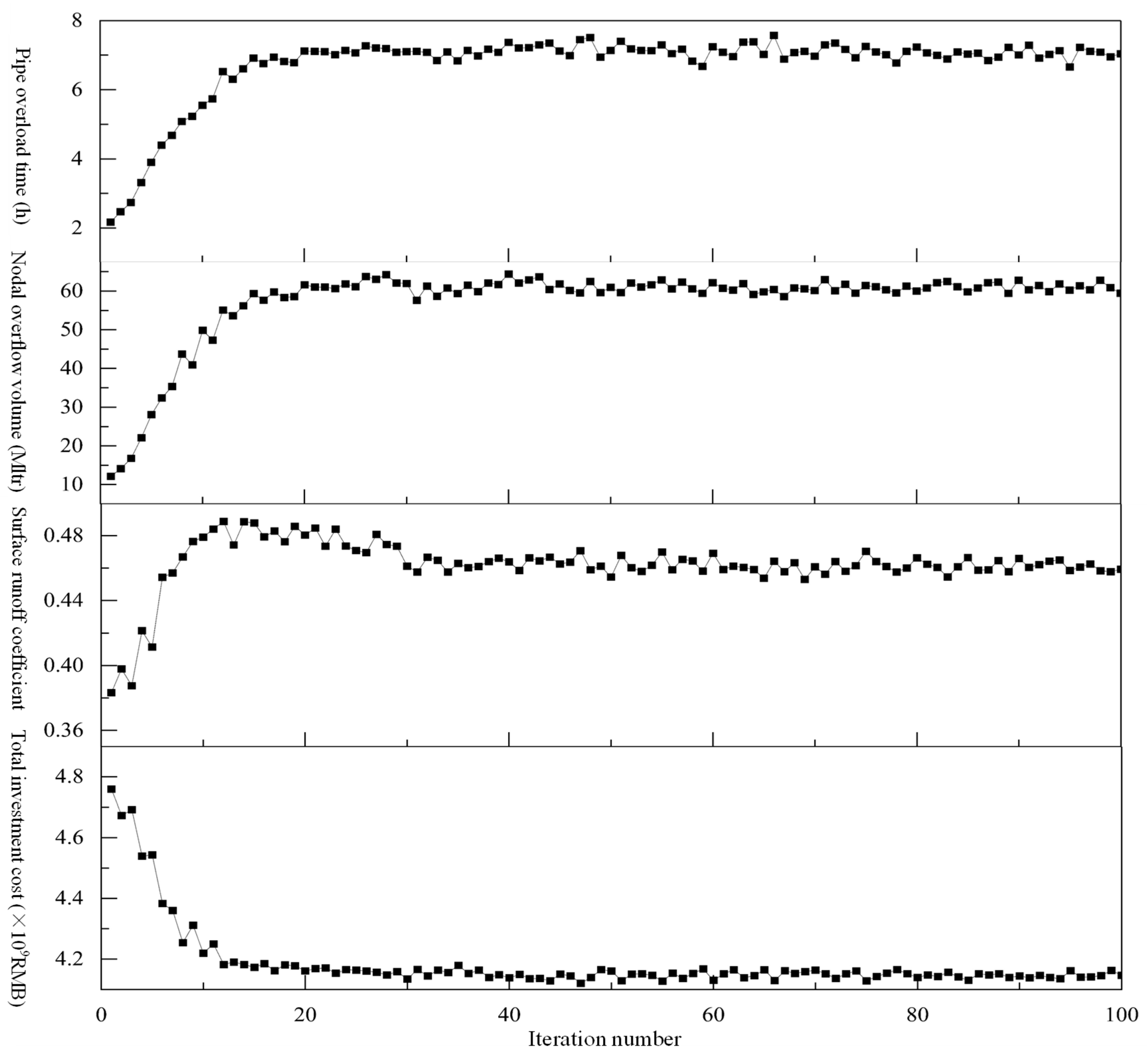
3.4.3. Optimization Model Convergence Evaluation
3.4.4. Optimization Model Validation
4. Discussion
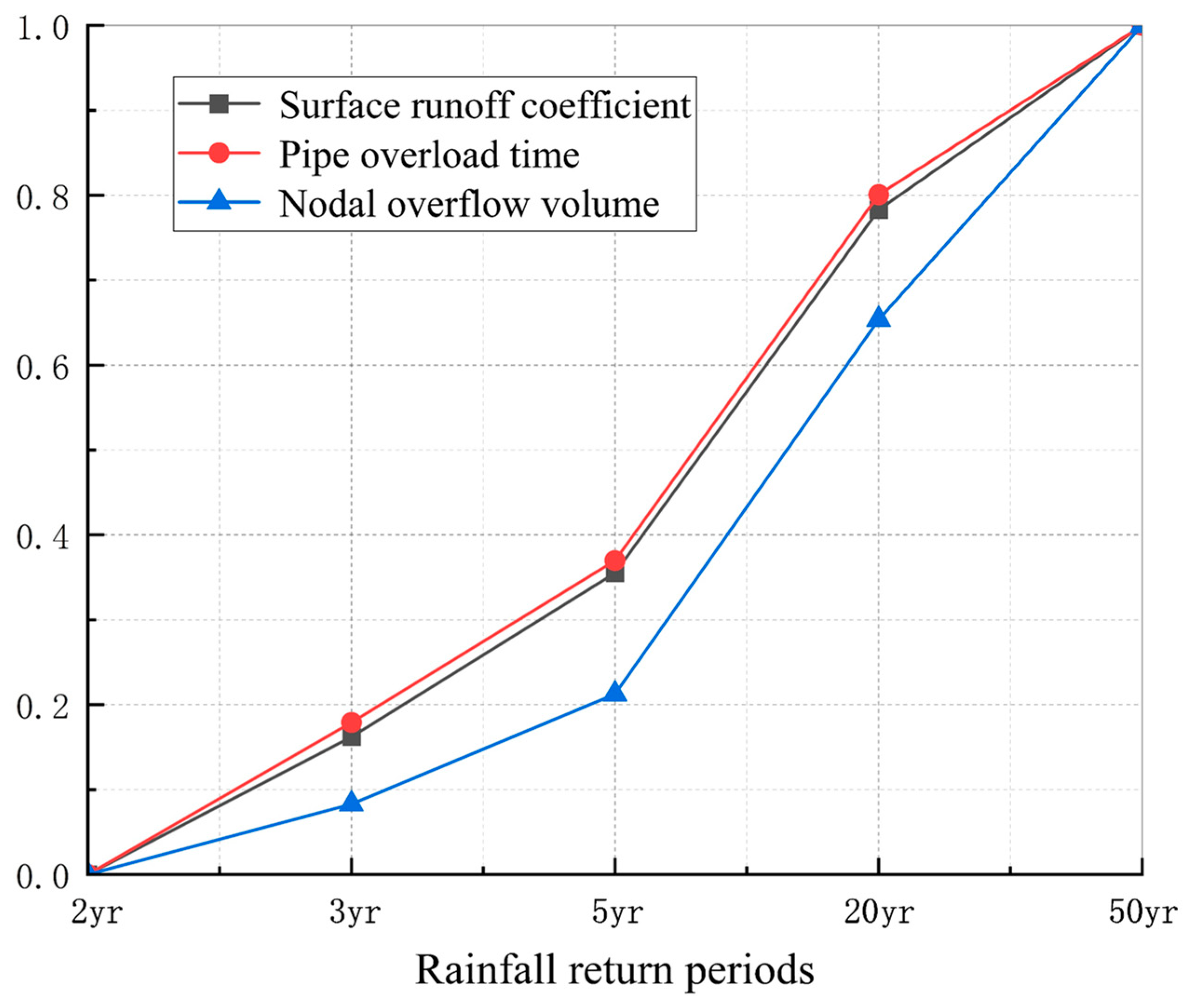
4.1. Impact of Different Rainfall Return Periods on the Three Indicators
4.2. Multi-Objective Tradeoffs
4.3. Scheme Assessment
5. Conclusions
- (1)
- A four-objective NSGA-III optimization model is established, and two traditional drainage system state indicators, surface runoff coefficient and total investment cost, are selected as the optimization objectives to be solved, and optimization schemes are obtained;
- (2)
- The NSGA-III optimization model can realize the simultaneous optimization of surface runoff coefficient, pipe overload time, node overflow, and total investment cost, which can effectively reduce the three flooding evaluation indexes and control the total investment cost. The NSGA-III optimization algorithm has high reliability and effectiveness in this field;
- (3)
- The NSGA-III optimization model has a better mitigation effect than the integrated pipe corridor rainwater tank scheme and the combined LID measure scheme and has more choice space compared with the manual optimization scheme;
- (4)
- According to the Pareto front, surface runoff coefficient, pipe overload time, and nodal overflow volume are proportional to each other, while they are inversely proportional to the total investment cost, and designers must consider the balance and priority between them.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tian, J.; Zhang, Z.; Ahmed, Z.; Zhang, L.; Su, B.; Tao, H.; Jiang, T. Projections of precipitation over China based on CMIP6 models. Stoch. Environ. Res. Risk Assess. 2021, 35, 831–848. [Google Scholar]
- Liu, Y.; Liu, Y.; Zheng, J.; Chai, F.; Ren, H. Intelligent Prediction Method for Waterlogging Risk Based on AI and Numerical Model. Water 2022, 14, 2282. [Google Scholar]
- Shi, J.; Cui, L. Characteristics of high impact weather and meteorological disaster in Shanghai, China. Nat. Hazards 2012, 60, 951–969. [Google Scholar]
- Quan, R.S.; Liu, M.; Lu, M.; Zhang, L.J.; Wang, J.J.; Xu, S.Y. Waterlogging risk assessment based on land use/cover change: A case study in Pudong New Area, Shanghai. Environ. Earth Sci. 2010, 61, 1113–1121. [Google Scholar]
- Billot, R.; Faouzi, N.E.E.; Sau, J.; De Vuyst, F. Integrating the impact of rain into traffic management: Online traffic state estimation using sequential Monte Carlo techniques. Transp. Res. Rec. 2010, 2169, 141–149. [Google Scholar]
- Tran, D.; Xu, D.; Dang, V.; Alwah, A.A.Q. Predicting Urban Waterlogging Risks by Regression Models and Internet Open-Data Sources. Water 2020, 12, 879. [Google Scholar]
- Rui, W.; Zhi, L.; Yu, L.; Xuan, J. Optimization Study of Urban Drainage System Rehabilitation Based on SWMM. Water Resour. Hydropower Eng. 2018, 49, 60–69. (In Chinese) [Google Scholar]
- Lu, T.; Jin, H.; Zhang, L.; Zhi, Y.; Qing, L. SWMM-based Bottleneck Analysis and Rehabilitation Evaluation of Urban Drainage Networks. China Water Wastewater 2018, 34, 112–117. (In Chinese) [Google Scholar]
- Saldarriaga, J.; Zambrano, J.; Herrán, J.; Iglesias-Rey, P.L. Layout Selection for an Optimal Sewer Network Design Based on Land Topography, Streets Network Topology, and Inflows. Water 2021, 13, 2491. [Google Scholar]
- Kwon, S.H.; Jung, D.; Kim, J.H. Optimal layout and pipe sizing of urban drainage networks to improve robustness and rapidity. J. Water Resour. Plan. Manag. 2021, 147, 6021003. [Google Scholar]
- Bayas-Jiménez, L.; Martínez-Solano, F.J.; Iglesias-Rey, P.L.; Mora-Meliá, D. Search Space Reduction for Genetic Algorithms Applied to Drainage Network Optimization Problems. Water 2021, 13, 2008. [Google Scholar]
- Davis, A.P.; McCuen, R.H. Stormwater Management for Smart Growth; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Livesley, S.J.; Baudinette, B.; Glover, D. Rainfall interception and stem flow by eucalypt street trees—The impacts of canopy density and bark type. Urban For. Urban Green. 2014, 13, 192–197. [Google Scholar]
- Bliss, D.J.; Neufeld, R.D.; Ries, R.J. Storm water runoff mitigation using a green roof. Environ. Eng. Sci. 2009, 26, 407–418. [Google Scholar]
- Alfredo, K.; Montalto, F.; Goldstein, A. Observed and modeled performances of prototype green roof test plots subjected to simulated low-and high-intensity precipitations in a laboratory experiment. J. Hydrol. Eng. 2010, 15, 444–457. [Google Scholar]
- Hou, J.; Sun, S.; Wang, Y.; Wang, J.; Yang, C. Comparison of runoff from low-impact development measures in arid and humid cities. In Proceedings of the Institution of Civil Engineers-Water Management; Thomas Telford Ltd.: London, UK, 2022; Volume 175, pp. 135–148. [Google Scholar]
- Huang, C.L.; Hsu, N.S.; Liu, H.J.; Huang, Y.H. Optimization of low impact development layout designs for megacity flood mitigation. J. Hydrol. 2018, 564, 542–558. [Google Scholar]
- Liu, W.; Chen, W.; Peng, C. Assessing the effectiveness of green infrastructures on urban flooding reduction: A community scale study. Ecol. Model. 2014, 291, 6–14. [Google Scholar]
- Xia, L.; Yu, L.; Guo, L. Simulation Study of Stormwater Control in Old Urban Areas Based on SWMM and Low Impact Development Patterns. Water Wastewater Eng. 2015, 51, 152–156. (In Chinese) [Google Scholar]
- Xiong, L.; Tian, T.; Xiang, C.; Xiao, Y.; Zhuo, S. Analysis of the Effectiveness of Comprehensive Pipeline Corridor Rainwater Pods in Mitigating Urban Flooding. Water Resour. Prot. 2021, 37, 20–26. (In Chinese) [Google Scholar]
- Lopes, M.D.; da Silva, G.B.L. An efficient simulation-optimization approach based on genetic algorithms and hydrologic modeling to assist in identifying optimal low impact development designs. Landsc. Urban Plan. 2021, 216, 104251. [Google Scholar]
- Hou, J.; Yuan, H. Optimal spatial layout of low-impact development practices based on SUSTAIN and NSGA-II. Desalination Water Treat 2020, 177, 227–235. [Google Scholar]
- Fang, L.; Jin, Z.; Ming, L.; Wen, P.; Qi, W.; Jing, Z. Current status and trend of research on optimization of urban low-impact development schemes. Water Conserv. Sci. Technol. Econ. 2018, 24, 7–10+26. [Google Scholar]
- Duan, H.F.; Li, F.; Yan, H. Multi-objective optimal design of detention tanks in the urban stormwater drainage system: LID implementation and analysis. Water Resour. Manag. 2016, 30, 4635–4648. [Google Scholar]
- Kumar, S.; Guntu, R.K.; Agarwal, A.; Villuri, V.G.K.; Pasupuleti, S.; Kaushal, D.R.; Gosian, A.K.; Bronstert, A. Multi-objective optimization for stormwater management by green-roofs and infiltration trenches to reduce urban flooding in central Delhi. J. Hydrol. 2022, 606, 127455. [Google Scholar]
- Yang, B.; Zhang, T.; Li, J.; Feng, P.; Miao, Y. Optimal designs of LID based on LID experiments and SWMM for a small-scale community in Tianjin, north China. J. Environ. Manag. 2023, 334, 117442. [Google Scholar]
- Long, C.; Ying, L. Optimization of Spatial Layout of Low-Impact Development Facilities Based on Stormwater Management Model and NSGA-II Algorithm—A Residential Cluster in Tongzhou, Beijing. Urban Plan. Int. 2022, 37, 42–48. (In Chinese) [Google Scholar]
- U.S. Environmental Protection Agency. Storm Water Management Model User’s Manual Version 5.2; U.S. Environmental Protection Agency: Washington, DC, USA, 2022. [Google Scholar]
- Xing, L. Calibration of urban rainfall runoff model parameters based on runoff coefficients. Water Wastewater Eng. 2009, 45, 213–217. (In Chinese) [Google Scholar]
- Zhong, Z.; Jing, C. Concise Drainage Design Manual; China Construction Industry Press: Beijing, China, 1990. [Google Scholar]
- GB/50838-2015; Standard for Technical Specification for Urban Comprehensive Pipe Corridor Engineering. Standardization Administration of China: Beijing, China, 2019. (In Chinese)
- Fan, X.; Wen, J.; Xiao, Y.; Jun, L. Key points of pipeline design for rainwater and sewage pipes in comprehensive pipeline corridors. China Water Wastewater 2018, 34, 41–46. [Google Scholar]
- Man, Z.; Ke, Z.; Ting, Z.; Jian, Z.; Ping, F. Analysis of hydrological effects of typical urban LID measures and the effectiveness of rainfall and flood control. J. Hydroelectr. Eng. 2019, 38, 57–71. [Google Scholar]
- Han, Z.; Zeng, D.; Zhao, Q.; Xin, J.; Hong, J.; Rong, C. Simulation and Evaluation of Low-Impact Development Effects in Urban Industrial Parks Based on SWMM Modeling. Water Resour. Prot. 2019, 35, 32–36. [Google Scholar]
- Shuang, H.; Jun, L.; Jia, Q. Simulation and Evaluation of the Effectiveness of Stormwater Control and Utilization of Low-Impact Development Models Based on SWMM Models. Water Resour. Power 2019, 35, 32–36. [Google Scholar]
- Liao, X.; Zheng, J.; Huang, C.; Huang, G. Approach for Evaluating LID Measure Layout Scenarios Based on Random Forest: Case of Guangzhou—China. Water 2018, 10, 894. [Google Scholar]
- Wen, X.; Zhu, J.; Yi, Y.; Meng, Z.; Ning, L.; Jia, G.; Jia, L. Flooding Analysis and LID Rehabilitation Study in Nanchang City by MIKE & SWMM. Water Resour. Power 2023, 41, 77–81+171. [Google Scholar]
- Xiang, L.; Cheng, L.; Zhao, W.; Zhao, Z.; Guang, L.; Jun, Z. Impact of LID Retrofit on Urban Flooding and Surface Source Pollution. Water Resour. Prot. 2021, 37, 131–139. [Google Scholar]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2013, 18, 577–601. [Google Scholar]
- Jain, H.; Deb, K. An evolutionary many-objective optimization algorithm using reference-point based nondominated sorting approach, part II: Handling constraints and extending to an adaptive approach. IEEE Trans. Evol. Comput. 2013, 18, 602–622. [Google Scholar]
- Ministry of Housing and Construction of China. Technical Guidelines for Sponge City Construction—Low Impact Development Stormwater System Construction (Trial); Ministry of Housing and Construction of China: Beijing, China, 2014. (In Chinese) [Google Scholar]
- Heng, W. Research on the whole process cost management of comprehensive pipeline corridor project based on BIM. Constr. Econ. 2021, 42, 53–58. [Google Scholar]
- Jemberie, M.A.; Melesse, A.M. Urban Flood Management through Urban Land Use Optimization Using LID Techniques, City of Addis Ababa, Ethiopia. Water 2021, 13, 1721. [Google Scholar]
- Kollat, J.B.; Reed, P.M.; Wagener, T. When are multiobjective calibration trade-offs in hydrologic models meaningful? Water Resour. Res. 2012, 48, W0352. [Google Scholar] [CrossRef]

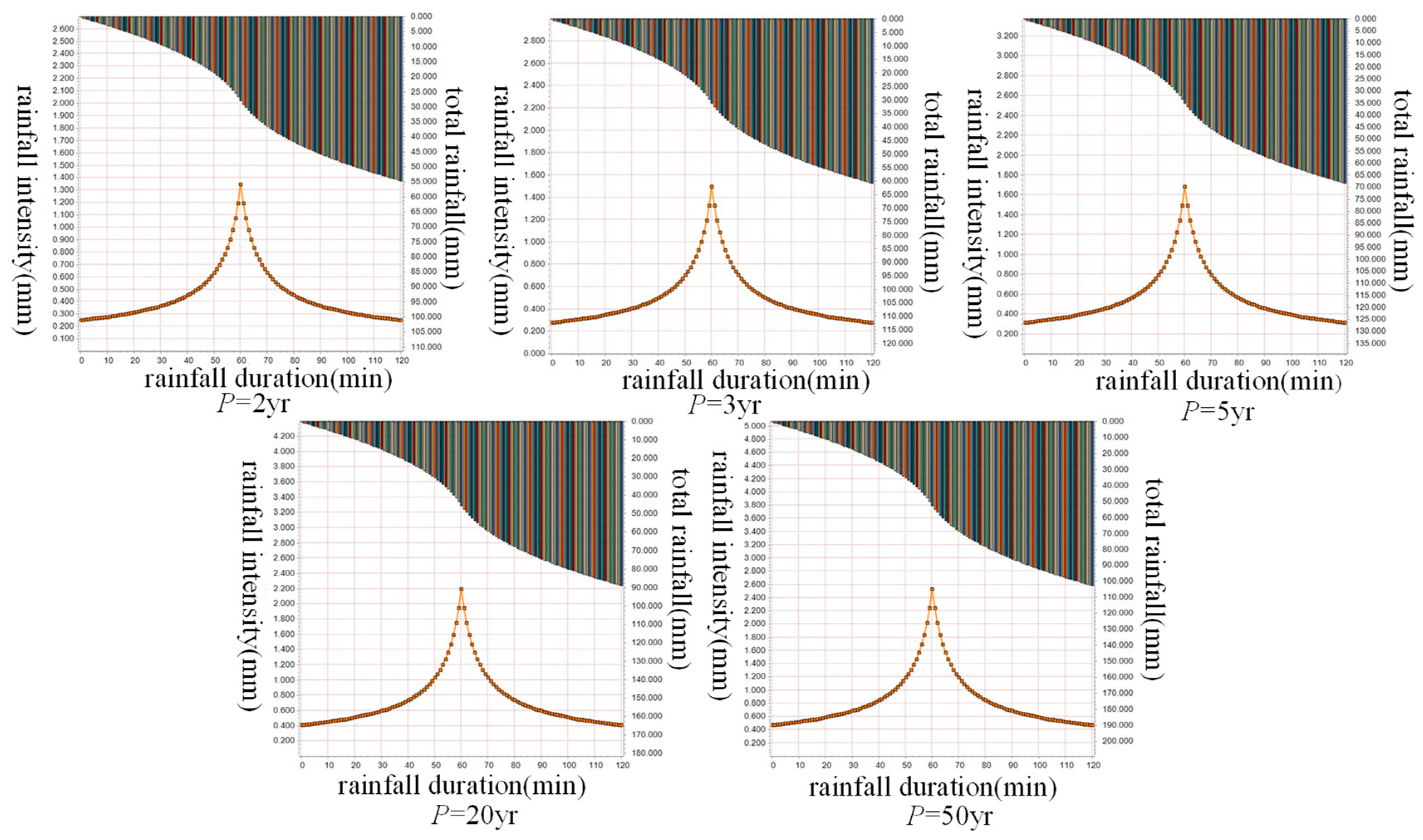

| Rains Return Period (yr) | 2 | 3 | 5 | 20 | 50 |
| Rainfall depth (mm) | 57.48 | 60.51 | 68.10 | 88.71 | 102.33 |
| Degree of Land Development | Values |
|---|---|
| Most densely built-up central area (imperviousness rate > 70%) | 0.6~0.8 |
| More densely built-up residential areas (50% < imperviousness rate < 70%) | 0.5~0.7 |
| Sparsely built-up residential areas (30% < imperviousness rate < 50%) | 0.4~0.6 |
| Sparsely populated areas (imperviousness rate < 30%) | 0.3~0.5 |
| Item | Main Parameters | Value Range | Final Value |
|---|---|---|---|
| Sub-catchments | Manning coefficients in impervious areas | 0.011~0.014 | 0.013 |
| Manning coefficients in pervious areas | 0.15 | 0.15 | |
| Depression storage in impervious areas/mm | 1.27~2.54 | 2 | |
| Depression storage in pervious areas/mm | 3~10 | 8 | |
| Pipe | Pipeline Manning’s Coefficient | 0.012~0.015 | 0.012 |
| Infiltration Data (HORTON) | Maximum infiltration rate (mm/h) | — | 75.4 |
| Minimum infiltration rate (mm/h) | — | 3.66 | |
| Infiltration decay constant (1/h) | — | 2 | |
| Drainage time/d | — | 7 |
| Land Use Type | Area (hm2) | Percentage (%) |
|---|---|---|
| residential land | 299.00 | 26.0 |
| Public administration and public service land | 113.85 | 9.9 |
| Business services facilities land | 136.85 | 11.9 |
| Industrial land | 162.15 | 14.1 |
| Logistics and warehousing land | 148.35 | 12.9 |
| Roads and Transportation Facility Land | 164.45 | 14.3 |
| Serviced land | 21.85 | 1.9 |
| Green space and plaza land | 103.50 | 9.0 |
| Total | 1150.00 | 100 |
| No. | Land Use Type | Combination |
|---|---|---|
| 1 | residential land, Public administration and public service land and Business services facilities land | 50% green roof + 30% permeable pavement +10% vegetative swale + 10% bioretention pond |
| 2 | Industrial land | 40% green roof + 40% permeable pavement +10% vegetative swale + 10% bioretention pond |
| 3 | Logistics and warehousing land | 30% green roof + 50% permeable pavement +10% vegetative swale + 10% bioretention pond |
| 4 | Roads and Transportation Facility Land | 80% permeable pavement +10% vegetative swale + 10% bioretention pond |
| 5 | Green space and plaza land | 40% permeable pavement +30% vegetative swale + 30% bioretention pond |
| LID Measures | Structural Layer | Design Parameters | Parameter Values (%) |
|---|---|---|---|
| Green roof | surface | berm height/mm | 80 |
| surface roughness | 0.25 | ||
| surface slope/% | 1 | ||
| vegetation volume fraction | 0.4 | ||
| soil | thicknesses/mm | 150 | |
| porosity | 0.18 | ||
| hydraulic conductivity/mm·h−1 | 18 | ||
| storage | thicknesses/mm | 20 | |
| porosity | 0.5 | ||
| permeable pavement | surface | berm height/mm | 20 |
| surface roughness | 0.11 | ||
| surface slope/% | 1 | ||
| pavement | thicknesses/mm | 120 | |
| void ratio | 0.5 | ||
| permeability/mm·h−1 | 300 | ||
| storage | thicknesses/mm | 250 | |
| void ratio | 0.43 | ||
| bioretention pond | surface | berm height/mm | 300 |
| surface roughness | 0.15 | ||
| surface slope/% | 1 | ||
| vegetation volume fraction | 0.4 | ||
| soil | thicknesses/mm | 500 | |
| porosity | 0.18 | ||
| hydraulic conductivity/mm·h−1 | 18 | ||
| storage | thicknesses/mm | 200 | |
| void ratio | 0.75 | ||
| vegetative swale | surface | berm height/mm | 150 |
| surface roughness | 0.2 | ||
| surface slope/% | 0.2 | ||
| swale side slope | 3 |
| Item | Items | Unit Cost (RMB/m2) | Total Unit Cost after Calculation (RMB) |
|---|---|---|---|
| LID measures | Green roof | 179 | 16,723,411.52 |
| permeable pavement | 104 | 9,716,395.52 | |
| bioretention pond | 458 | 42,789,511.04 | |
| vegetative swale | 87 | 8,128,138.56 | |
| Comprehensive pipe corridor | Comprehensive pipe corridor | 2183 | 159,512,137.45 |
| Indicators | 2 yr | 3 yr | 5 yr | 20 yr | 50 yr |
|---|---|---|---|---|---|
| Surface runoff coefficient | 0.707 | 0.726 | 0.748 | 0.799 | 0.824 |
| Pipe overload time/h | 30.450 | 34.409 | 38.625 | 48.148 | 52.552 |
| Nodal overflow/Mltr | 24.312 | 37.712 | 58.701 | 130.042 | 186.071 |
| Combination | 20.0% + 0.756 m | 20.0% + 0.762 m | 30.0% + 0.775 m | |||
|---|---|---|---|---|---|---|
| SWMM | Optimization Model | SWMM | Optimization Model | SWMM | Optimization Model | |
| Surface runoff coefficient | 0.508 | 0.508 | 0.508 | 0.508 | 0.449 | 0.449 |
| Pipe overload time (h) | 8.730 | 8.997 | 8.606 | 8.968 | 7.245 | 7.112 |
| Nodal overflow volume (Mltr) | 82.151 | 82.242 | 80.890 | 81.173 | 55.936 | 55.668 |
| Average error | 1.03% | 1.46% | 0.78% | |||
| Situation | Surface Runoff Coefficient | Pipe Overload Time (h) | Nodal Overflow Volume (Mltr) | Total Investment Cost (108 RMB) |
|---|---|---|---|---|
| Initial scheme | 0.824 | 52.552 | 186.071 | — |
| Comprehensive pipe corridor rainwater chamber scheme | 0.824 | 2.138~21.172 | 8.311~263.027 | 36.752~43.643 |
| Combination LID measures scheme | 0.167~0.596 | 2.271~40.746 | 0~110.385 | 1.602~16.020 |
| Manual optimization scheme | 0.449 | 2.497 | 10.996 | 44.620 |
| NSGA-III optimization model scheme | 0.355~0.519 | 4.501~9.702 | 27.980~90.100 | 40.311~45.009 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Y.; Zhang, H.; Wang, X.; Gu, Z.; Fu, L.; Cheng, Y. Optimized Design of Sponge-Type Comprehensive Pipe Corridor Rainwater Chamber Based on NSGA-III Algorithm. Water 2023, 15, 3319. https://doi.org/10.3390/w15183319
Ren Y, Zhang H, Wang X, Gu Z, Fu L, Cheng Y. Optimized Design of Sponge-Type Comprehensive Pipe Corridor Rainwater Chamber Based on NSGA-III Algorithm. Water. 2023; 15(18):3319. https://doi.org/10.3390/w15183319
Chicago/Turabian StyleRen, Yazheng, Huiying Zhang, Xinhua Wang, Zhanfei Gu, Linie Fu, and Yang Cheng. 2023. "Optimized Design of Sponge-Type Comprehensive Pipe Corridor Rainwater Chamber Based on NSGA-III Algorithm" Water 15, no. 18: 3319. https://doi.org/10.3390/w15183319
APA StyleRen, Y., Zhang, H., Wang, X., Gu, Z., Fu, L., & Cheng, Y. (2023). Optimized Design of Sponge-Type Comprehensive Pipe Corridor Rainwater Chamber Based on NSGA-III Algorithm. Water, 15(18), 3319. https://doi.org/10.3390/w15183319







