Application of a VOF Multiphase Flow Model for Issues concerning Floating Raft Aquaculture
Abstract
:1. Introduction
2. Materials and Methods
2.1. Hydrodynamic Model
2.2. Method for Seeking Numerical Solutions
2.3. Model Verification
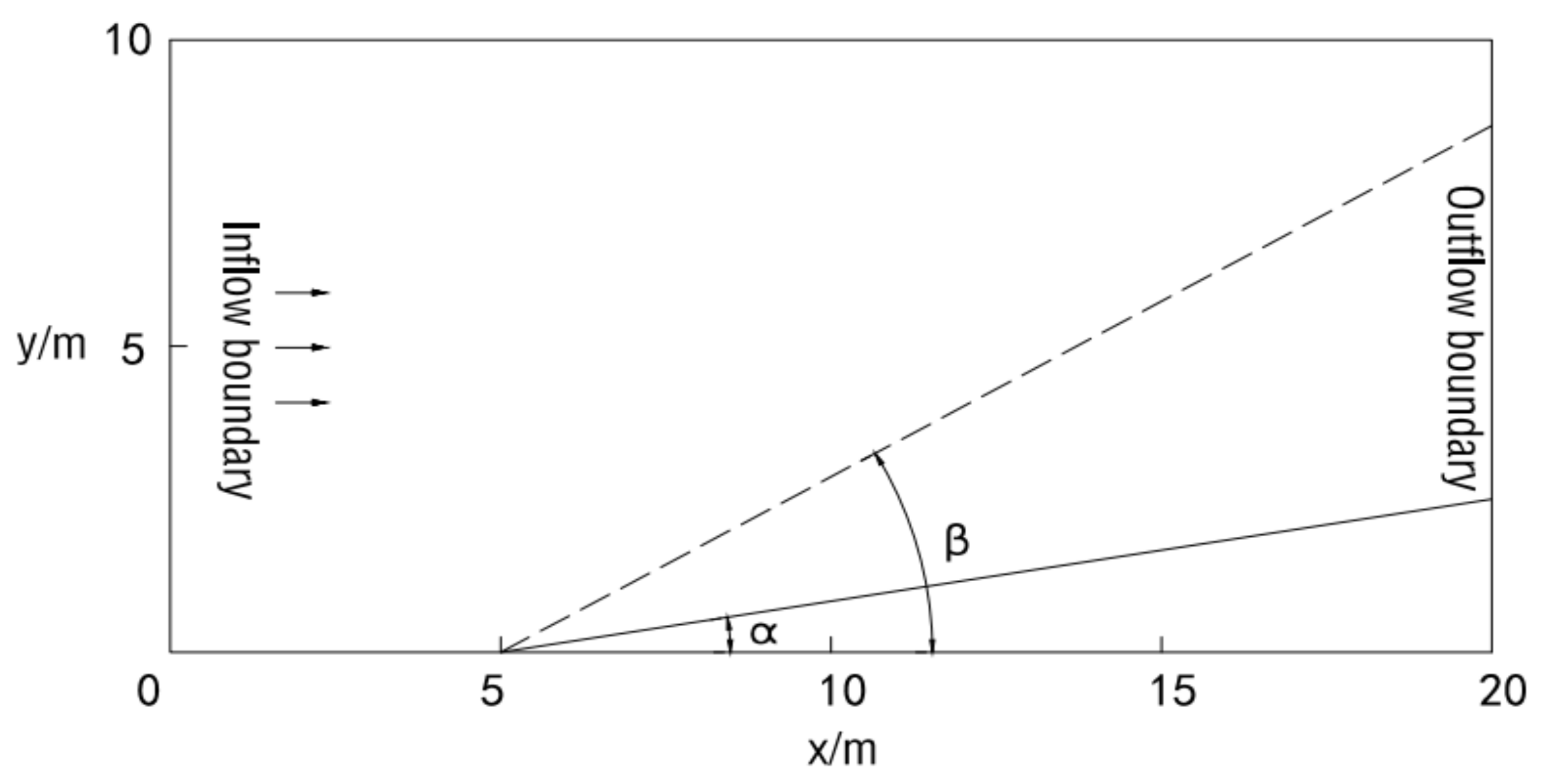
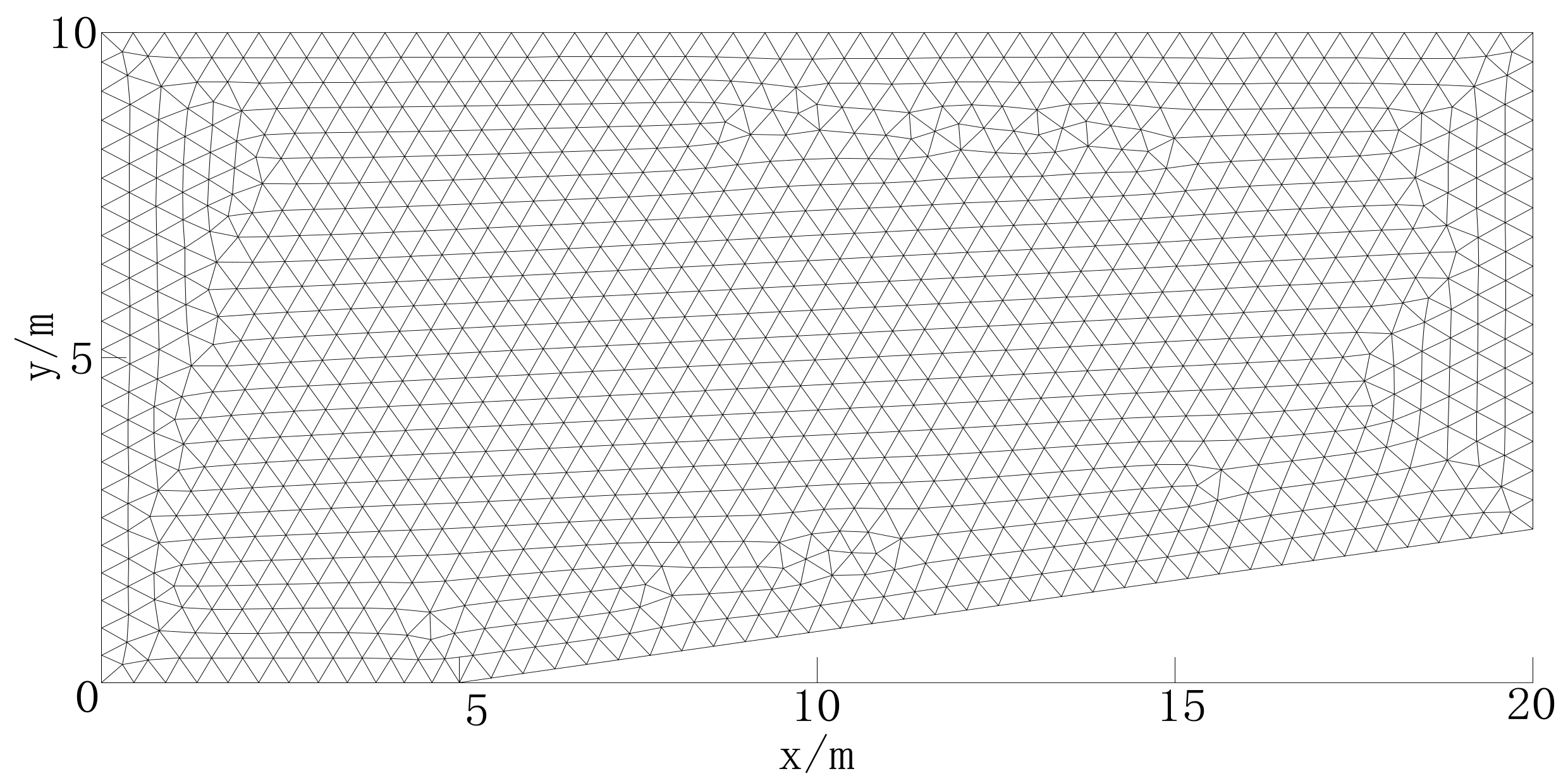
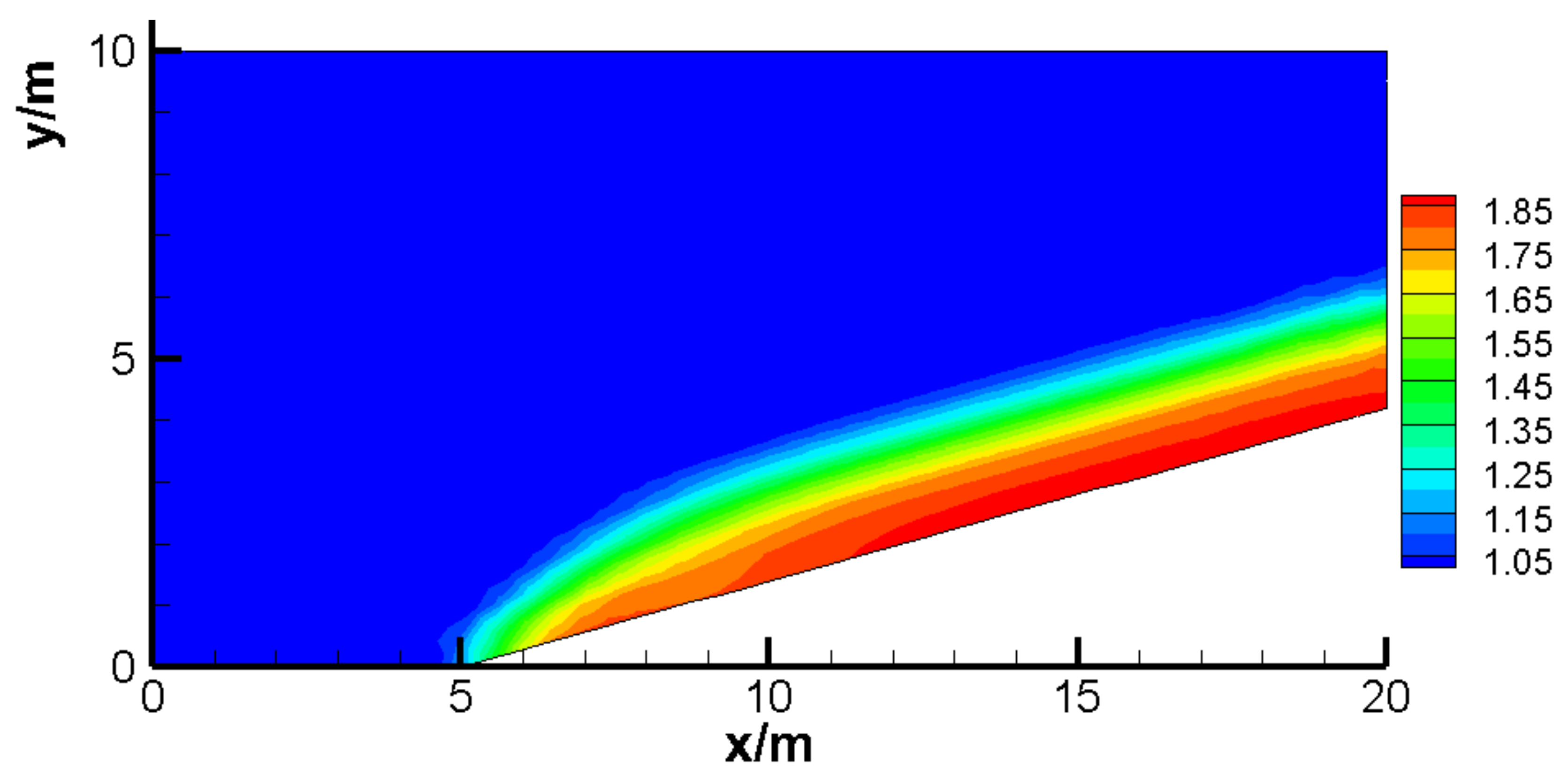
2.3.1. Oblique Hydraulic Jumps
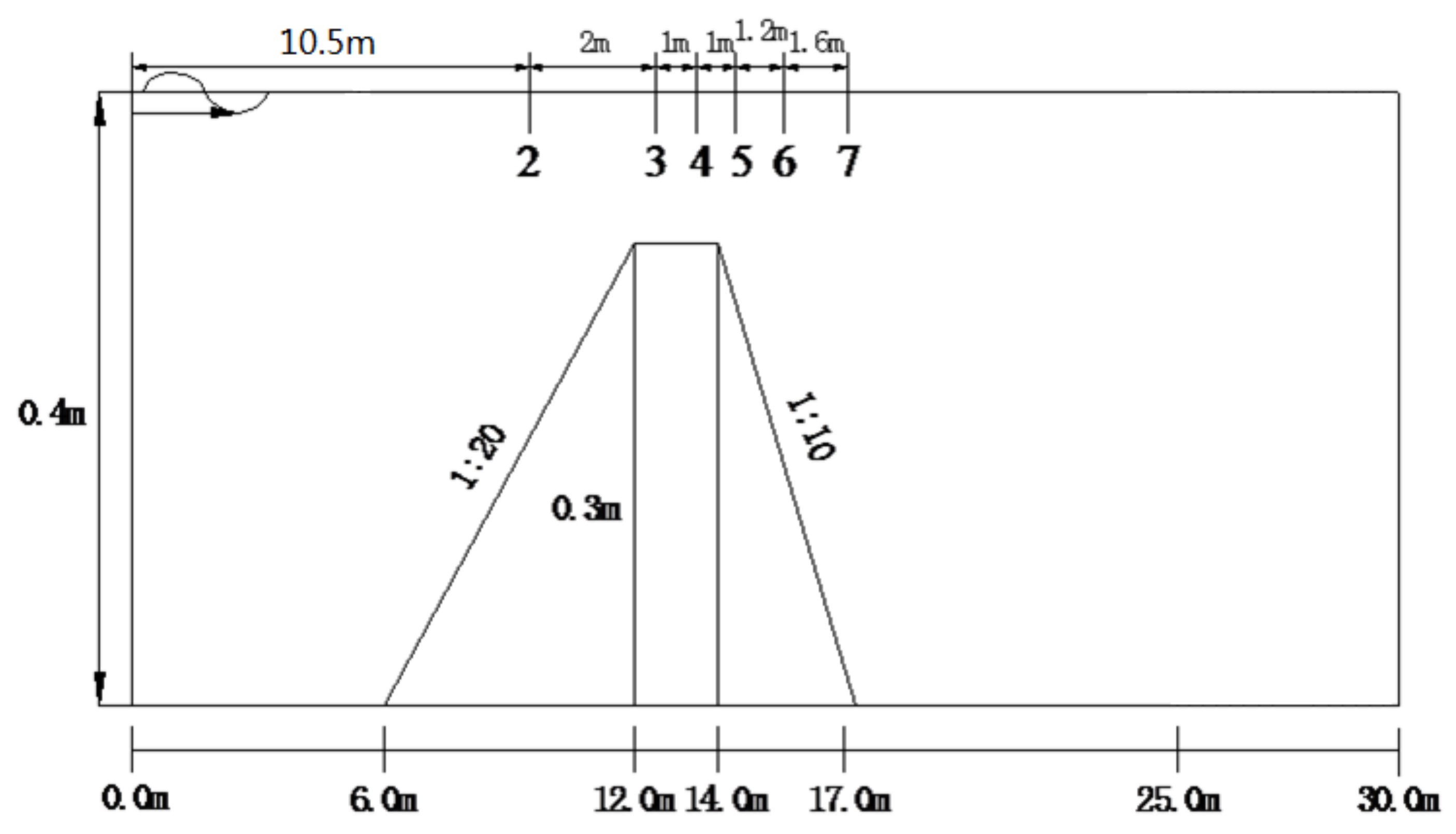
2.3.2. Passage of Generated Waves through a Submerged Bar
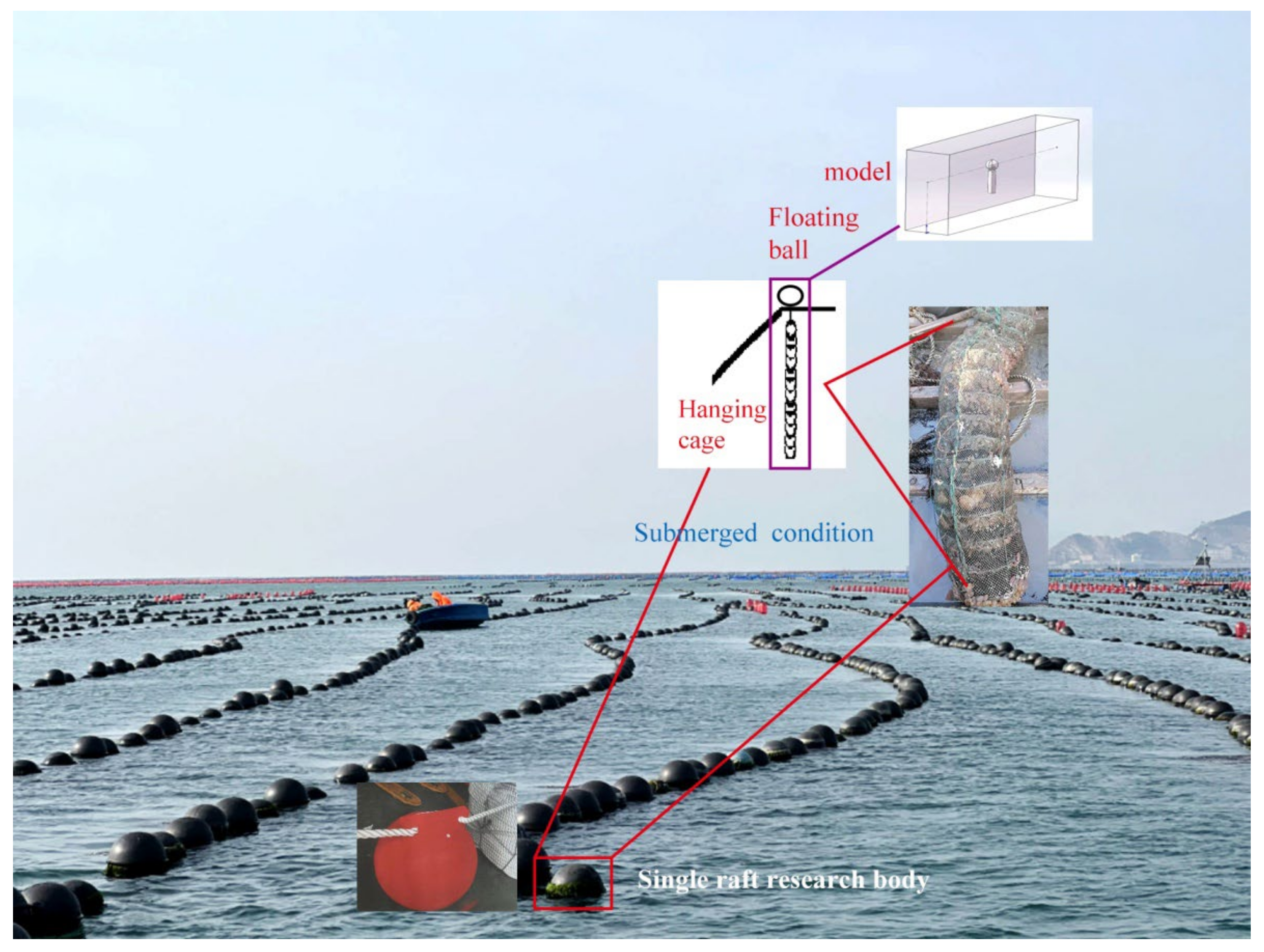
2.4. VOF Multiphase-Flow Simulation of Water Flow Movement via a Single Floating Raft Aquaculture Structure
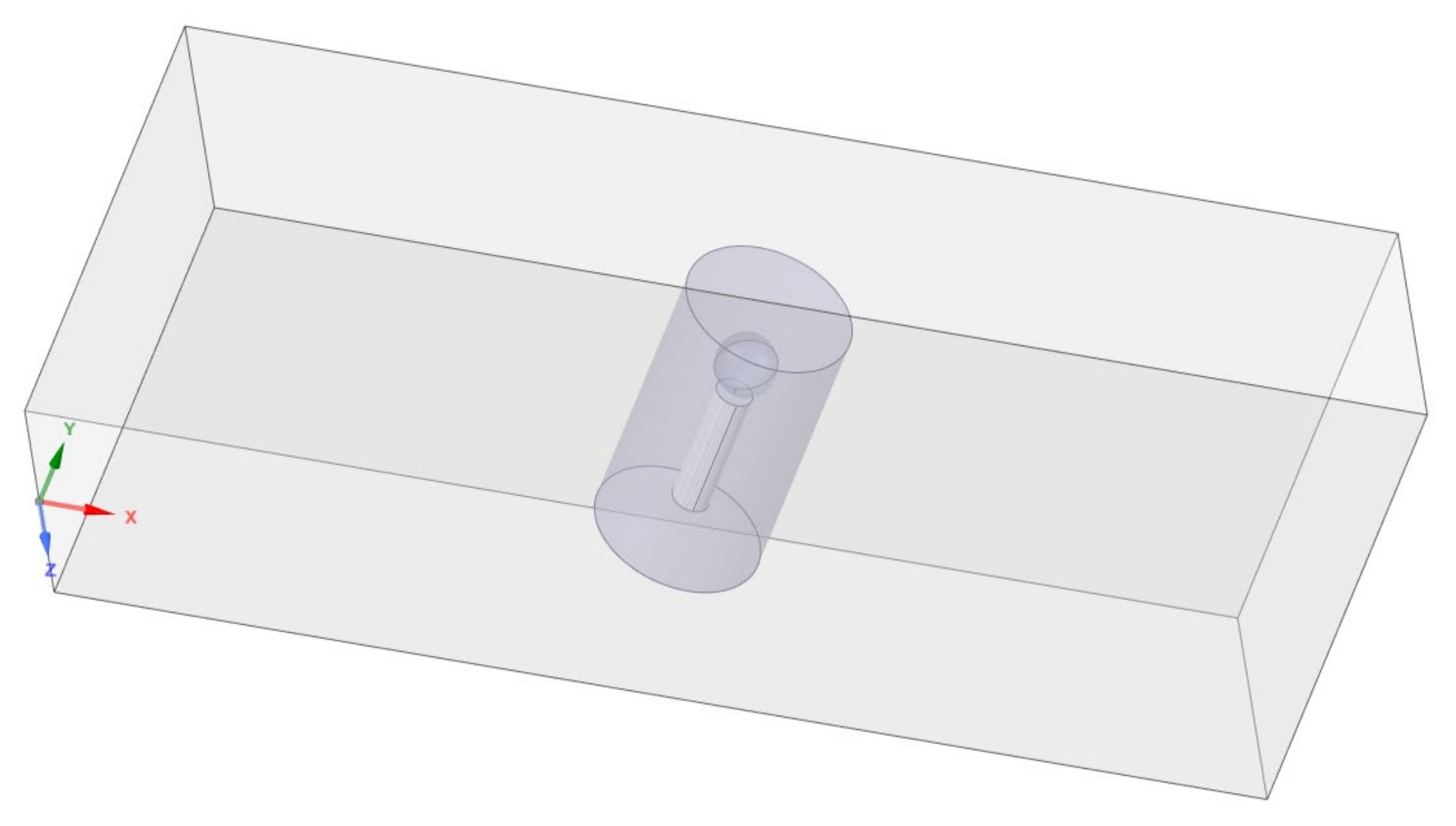
2.4.1. Modeling
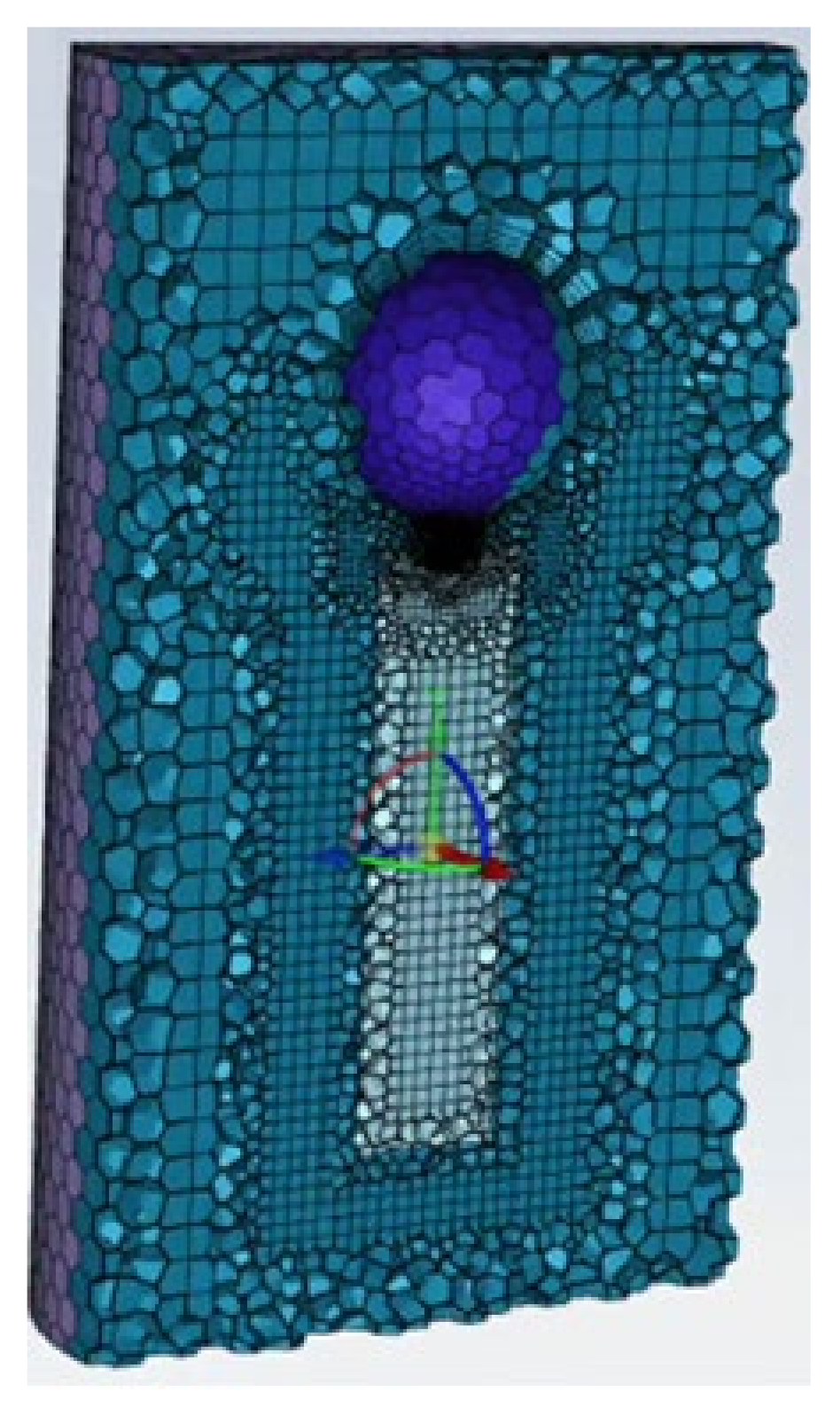
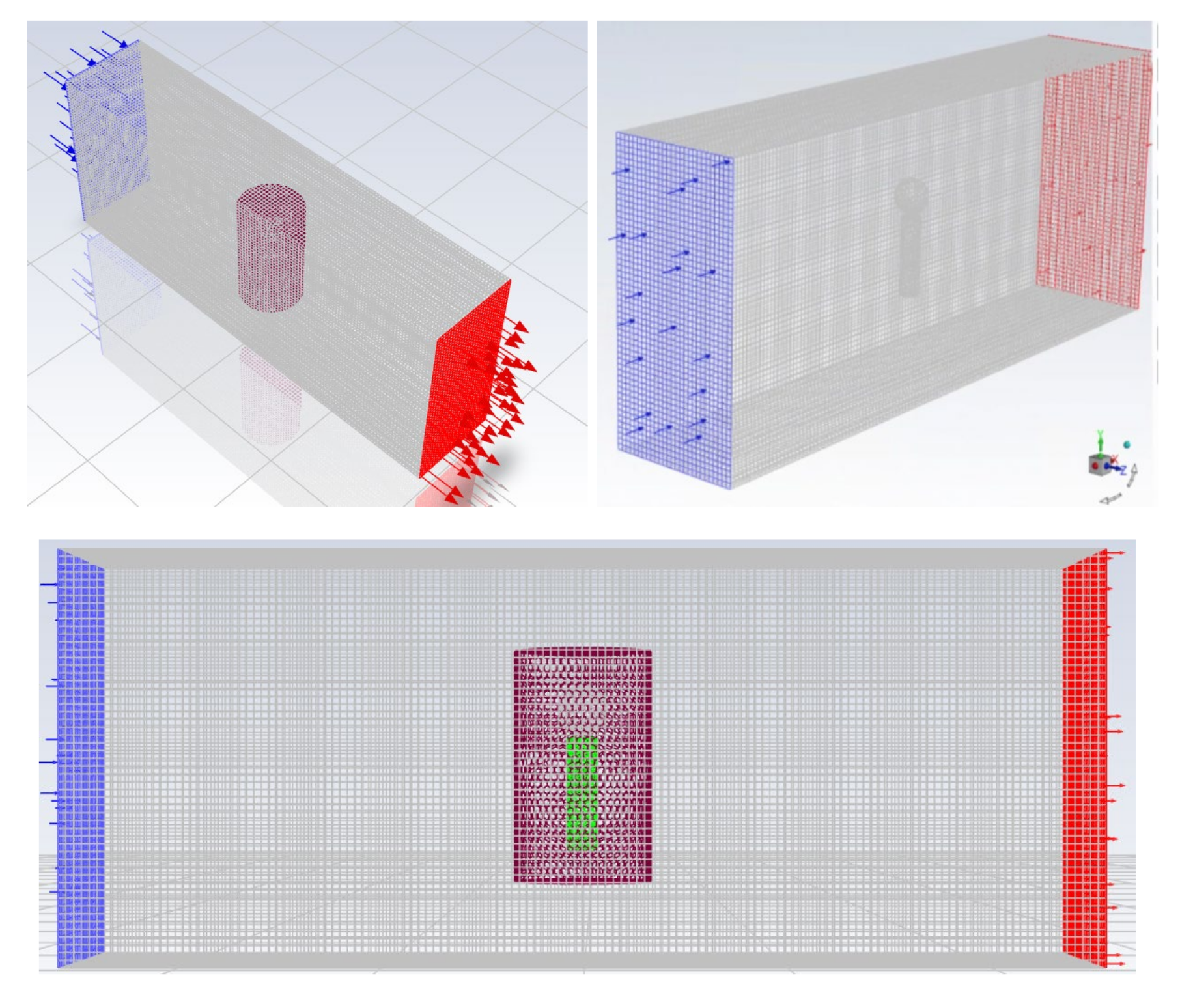
2.4.2. Meshing
2.4.3. Setting of Boundary Conditions and Parameters
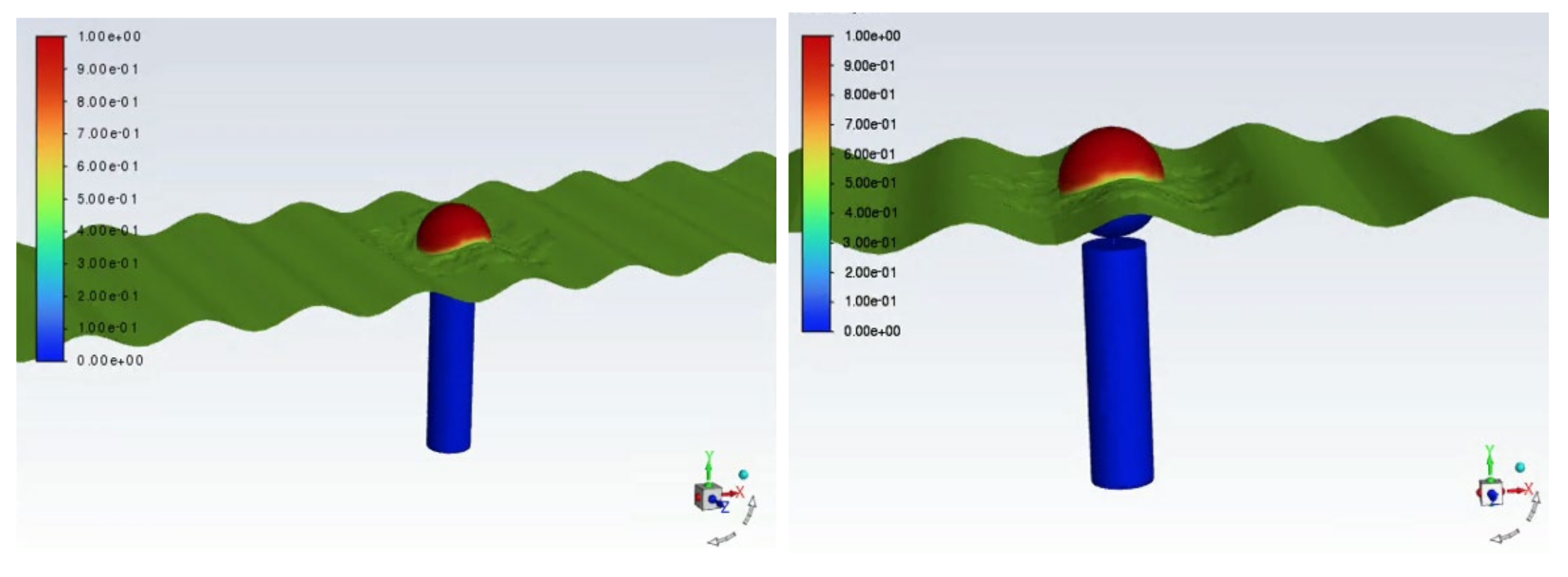
2.4.4. Model Computation Results
3. Impact of Floating Raft Aquaculture on the Hydrodynamic Environment of the Sea Area in Changhai County, Dalian
3.1. Quantitative Description of the Impact of the Resistance from Aquaculture on the Entire Floating Raft Aquaculture Area
3.2. Meshing and Other Parameter Settings
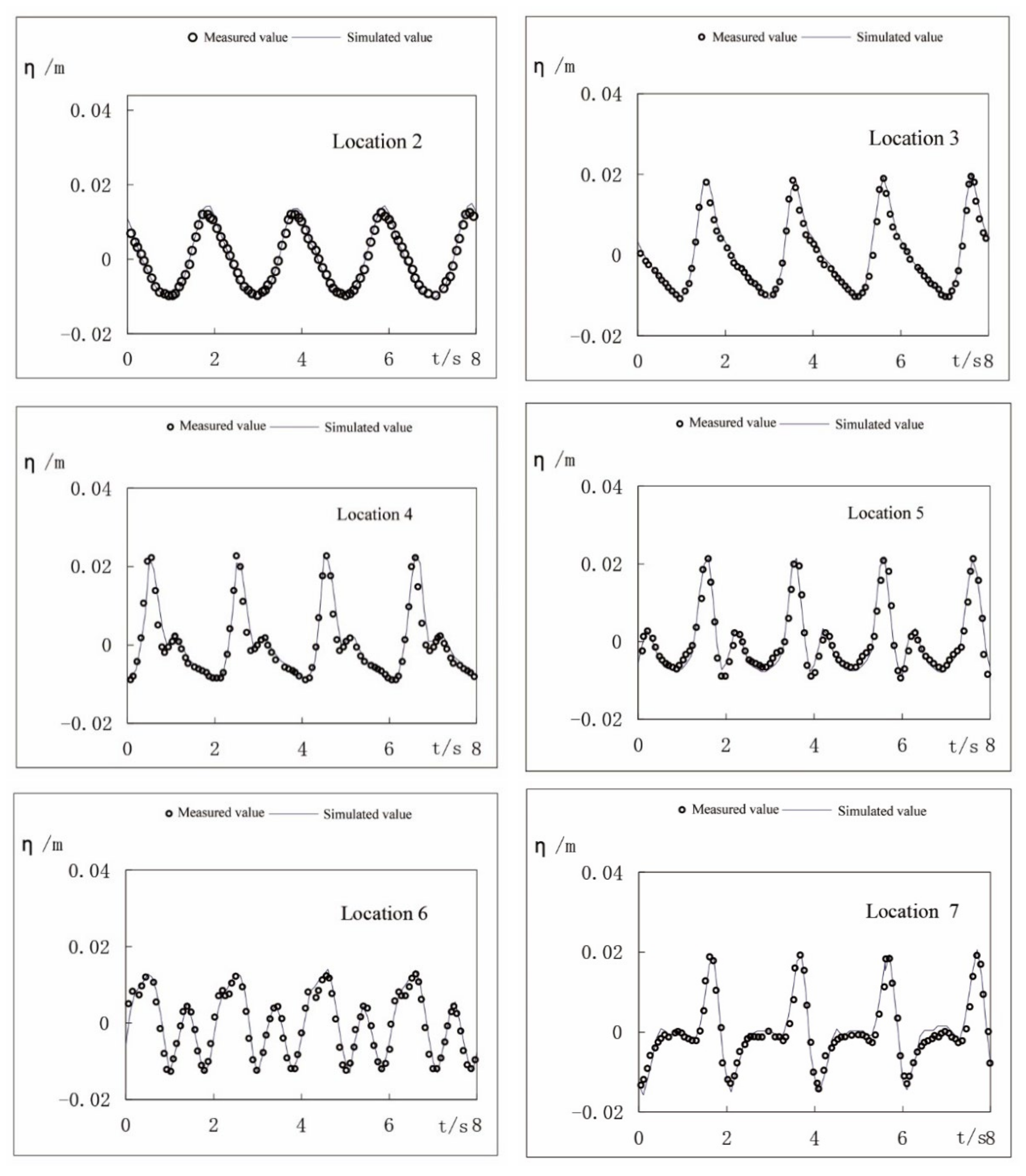
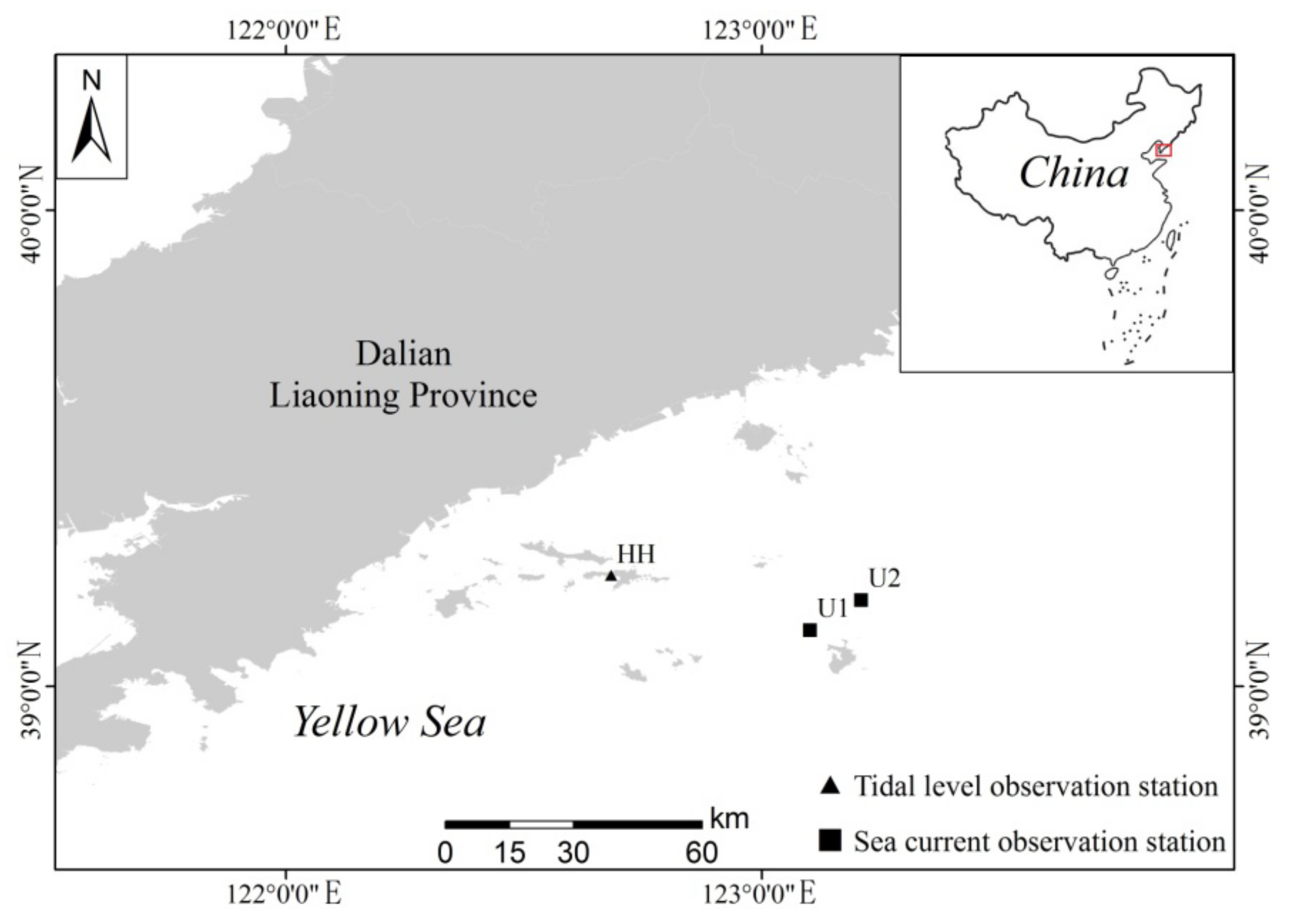
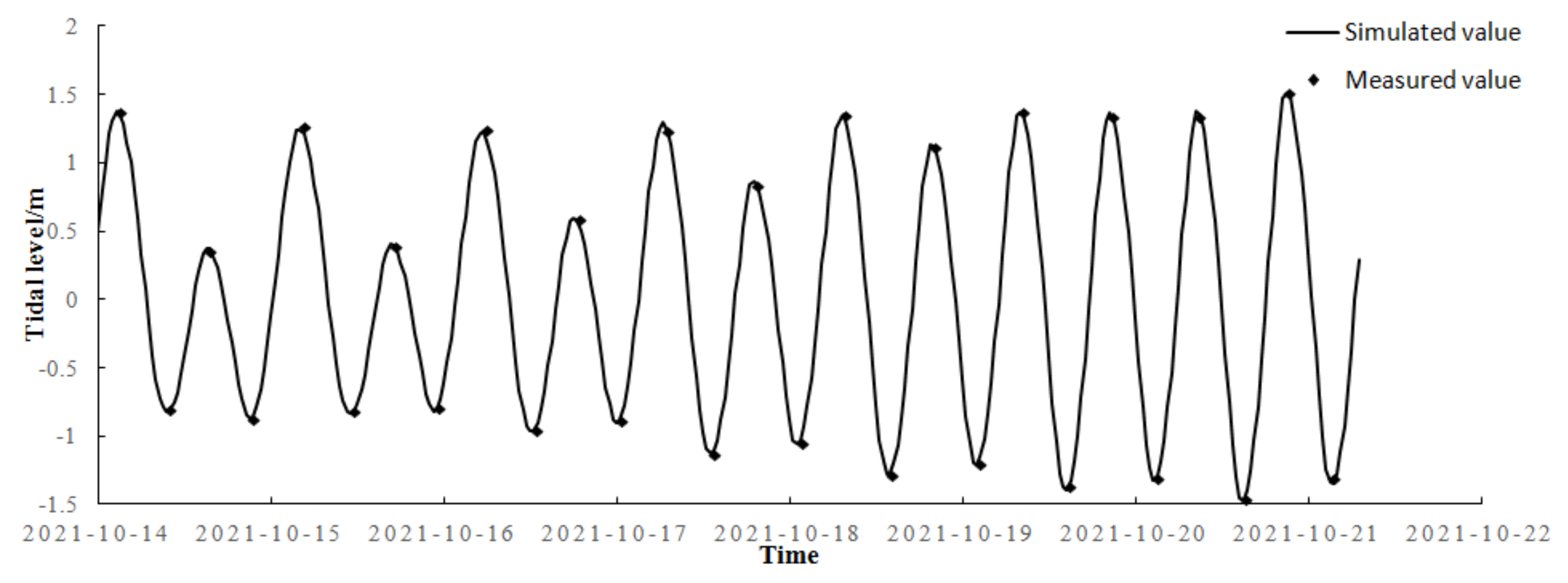
3.3. Hydrodynamic Model Verification
3.4. Simulation and Prediction Results
3.5. Analysis of Model Accuracy
4. Simulation Results of Water Exchange Performance and Analysis
5. Results and Discussion
5.1. Analysis of Calculation Results of a Single Raft
- (1)
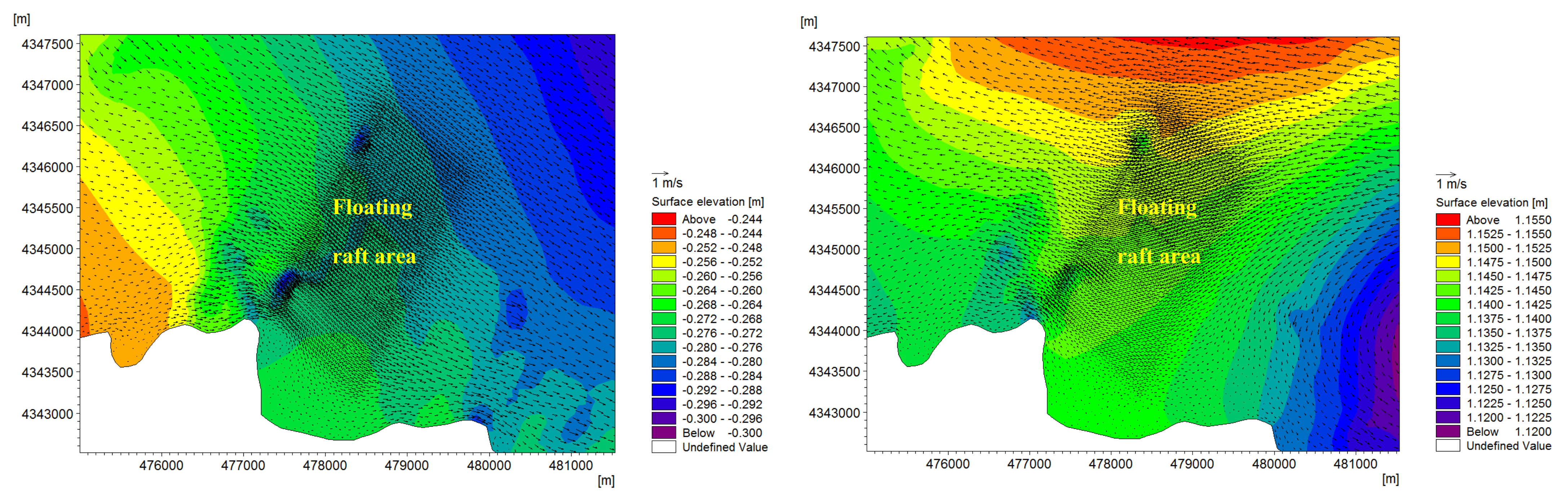
- The hydrodynamic force calculation results for a single raft in the aquaculture area show that based on a comparison between the distribution of the water level simulation results and that of the results for the raft aquaculture area, the mean water level in the raft aquaculture area was reduced by 1.05 cm compared to the mean water level in the corresponding sea area before aquaculture; the water level was reduced by at least 5.97 cm, the degree of reduction was up to about 5% and the mean flow velocity decreased by 5.24 cm/s, which indicates that this working condition was just a scenario of inflow wave generation and did not significantly affect the hydrodynamic force surrounding the raft.
- (2)
- The given flow velocity boundary of the inflow was 50 cm/s, and the other calculation conditions remained unchanged. Due to the limited space, the calculation results and analysis are described here. After the centroid of the physical structure was extracted, the mean flow velocity [27] at a distance of 2.5 m was 32.7 cm/s, and the flow resistance rate of a single raft was about 35% according to the calculation results. The quantitative parameter that reflected the impact of the raft area on the hydrodynamic force could be applied to the entire aquaculture area.
5.2. Analysis of Calculation Results of the Floating Raft Aquaculture Area
- (1)
- We quantitatively analyzed the relative error between the simulated values and the measured values by comparing them and using the relative standard deviation. It was found that the relative standard deviation of flow velocity was less than 5% and the average absolute error of tide level was less than 8 cm, indicating that the model has great accuracy, which further demonstrates that the VOF multiphase flow model used in this study accurately depicts the resistance from the facility in an aquaculture area with a single floating raft, and this quantitative damping result can be applied to large-scale simulations for actual raft areas. These results show that the simulated values are in good agreement with the measured values, which demonstrates that the model is relatively reliable.
- (2)
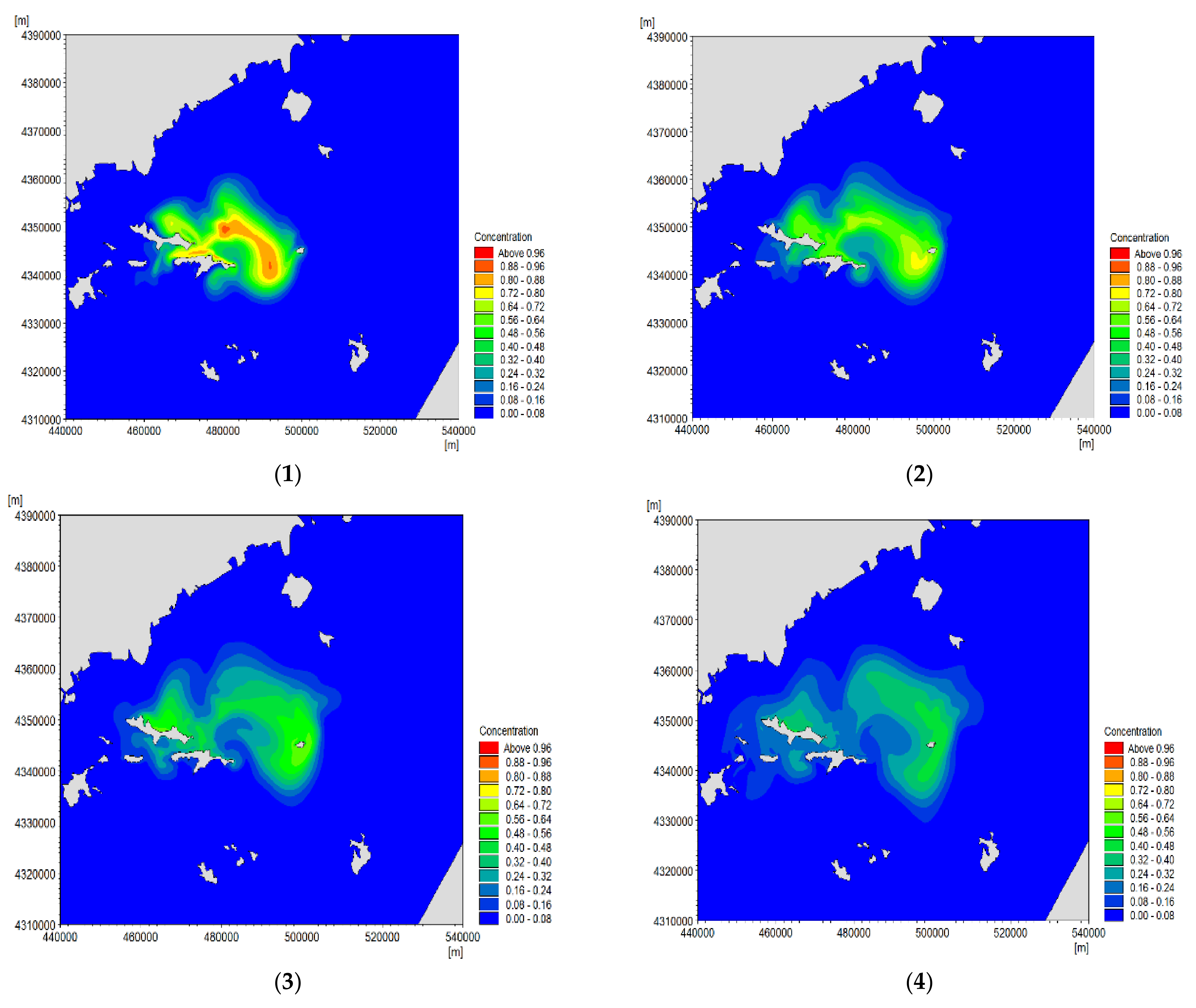
- According to the simulation results for the water exchange rate shown in Table 1, after 1 d, 5 d and 9 d of water exchange, the water exchange rates were 27.90%, 64.65% and 80.26%, respectively, when there was no floating raft, and 22.21%, 57.84% and 76.87%, respectively, when there were floating rafts, a decrease of 5.69%, 6.81% and 3.39%, respectively. The half-exchange cycles without and with floating raft aquaculture appeared on 2.3 d and 3.99 d, respectively, showing that the water exchange rates in a sea area with floating raft aquaculture were significantly reduced compared with those in a natural sea area.
6. Conclusions
- (1)
- Based on spatial modeling, wherein the impact of the floating raft facility, mainly including the floating ball, the external aquaculture net of the hanging cage and organisms, was considered, the computation results for the flow of water through a single raft show that the 3D VOF multiphase flow model described in this paper can accurately simulate the flow of water through the raft and the hydrodynamic environment of the raft aquaculture area, which demonstrates great stability and universality.
- (2)
- When the hydrodynamic force results calculated using the 3D VOF multiphase flow model were used as the background conditions, the convection–diffusion tracer method based on Euler substance transport was used to quantitatively calculate the water exchange rates in the fixed aquaculture area for statistics, which indicates that the aquaculture activities have significantly reduced the water exchange rates in this open-sea area during different periods. In addition, the half-exchange cycles of the water further showed that the existence of floating raft aquaculture activities has reduced the water exchange performance of this sea area. The exact extent of this impact depends on the density, size, scope and location of rafts in an aquaculture area.
- (3)
- Even floating raft aquaculture facilities located in open-sea areas, such as the sea area in Changhai County, have a certain impact on water exchange performance, and the specific extent of this impact varies with the density, size, scope and location of rafts in the aquaculture area, which should absolutely be brought to the attention of workers engaging in fishery, aquaculture and marine environment protection. In addition, only after accurately determining the impact of a raft area on the hydrodynamic environment can aquaculture workers select a reasonable site and install bait feeding and distribution devices in an area where biological nutrients are scarce, thereby helping increase the yield and efficiency of raft aquaculture, ensuring stable income for aquaculture operators and improving the social and economic benefits provided by the floating raft aquaculture areas in Changhai County and other open-sea floating raft aquaculture areas.
- (4)
- In future studies, the law of flow velocity attenuation in the downstream area for floating rafts should be considered when cages and the water flow direction are at different angles of attack. Furthermore, in addition to the impact of floating rafts in aquaculture facilities on the hydrodynamic force, the impact of cultured organisms in hanging cages and the biomasses of different aquaculture cycles on the hydrodynamic environment should also be taken into account. Such studies would further provide technical methods for the precise layout of actual raft areas and technical support for the development of the industry.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gao, J.; Lyu, J.; Wang, J.; Zhang, J.; Liu, Q.; Zang, J.; Zou, T. Study on transient gap resonance with consideration of the motion of floating body. China Ocean Eng. 2022, 36, 994–1006. [Google Scholar] [CrossRef]
- Weng, L.X.; Xu, J.N.; Hu, Z.X. Analysis and Evaluation of Wind Turbine Flow Field and Noise Simulation Based on CFD Software. Appl. Mech. Mater. 2014, 716–717, 755–759. [Google Scholar] [CrossRef]
- Gao, J.; Shi, H.; Zang, J.; Liu, Y. Mechanism analysis on the mitigation of harbor resonance by periodic undulating topography. Ocean Eng. 2023, 281, 114923. [Google Scholar] [CrossRef]
- Sharma, S.L.; Ishii, M.; Hibiki, T.; Schlegel, J.P.; Liu, Y.; Buchanan, J.R., Jr. Beyond Bubbly Two-Phase Flow Investigation using a CFD Three-Field Two-Fluid Model. Int. J. Multiph. Flow 2019, 113, 1–15. [Google Scholar] [CrossRef]
- Gao, J.; He, Z.; Huang, X.; Liu, Q.; Zang, J.; Wang, G. Effects of free heave motion on wave resonance inside a narrow gap between two boxes under wave actions. Ocean Eng. 2021, 224, 108753. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Dong, G.; Chen, H.; Liu, Q.; Zang, J. Investigation on the effects of Bragg reflection on harbor oscillations. Coast. Eng. 2021, 170, 103977. [Google Scholar] [CrossRef]
- Jalaluddin, M.I. CFD Simulation of 3-D Flow Field over Clean and Loaded Wing; Universiti Teknologi Petronas: Perak, Malaysia, 2014; pp. 1–30. [Google Scholar]
- Aly, E.A.; Habashi, W.G. Accurate marine propellers flow field CFD through anisotropic mesh optimization. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 3148–3168. [Google Scholar]
- Xie, H.; Yang, J.; Hu, Y.; Zhang, H.; Yang, Y.; Zhang, K.; Zhu, X.; Li, Y.; Yang, C. Simulation of flow field and sludge settling in a full-scale oxidation ditch by using a two-phase flow CFD model. Chem. Eng. Sci. 2014, 109, 296–305. [Google Scholar] [CrossRef]
- Yang, Y.; Li, D.; Ma, Y.; Zhang, M. Refinement three-dimensional simulation of effect of floodplain vegetation on hydrodynamic characteristics in compound open channel based on Fluent soft ware. J. Dalian Ocean Univ. 2021, 36, 317–324. [Google Scholar]
- Gallerano, F.; Cannata, G.; Barsi, L.; Scarpone, S. Numerical Investigation of Fluid-Structure Interaction for Long-Span Bridge Decks; WIT Press: Torquay, UK, 2016; Volume 105, pp. 15–26. [Google Scholar]
- Hessenthaler, A.; Roehrle, O.; Nordsletten, D. Validation of a non-conforming monolithic fluid-structure interaction method using phase-contrast MRI. Commun. Numer. Methods Eng. 2017, 33, e2845. [Google Scholar] [CrossRef]
- Lindgren, J.; Karlsson, H. Fluid-Structure Interaction; Numerical Modelling and Experimental Comparison. Struct. Mech. 2017, 3–49. [Google Scholar]
- Habeeb, L.J.; Saleh, F.A.; Maajel, B.M. Numerical Simulation of 3-D One-Way Fluid-Structure Interaction in a Tube with Twisted Tape under Laminar and Turbulent Flow Regime. Int. J. Appl. Eng. Res. 2018, 13, 1–10. [Google Scholar]
- Sangalli, L.A.; Braun, A.L. A fluid-structure interaction model for numerical simulation of bridge flutter using sectional models with active control devices. Preliminary results. J. Sound Vib. 2020, 477, 115338. [Google Scholar] [CrossRef]
- Kassiotis, C.; Ibrahimbegovic, A.; Matthies, H. Partitioned solution to fluid-structure interaction problems in application to free-surface flows. Eur. J. Mech. B Fluids 2010, 29, 510–521. [Google Scholar] [CrossRef]
- He, Y.; Huang, D.; Zeng, D.; Qiao, X. The impact of raft kelp aquaculture on the vertical structure of tidal currents in Sanggou Bay. J. Mar. Sci. 2016, 34, 20–27. [Google Scholar]
- Klebert, P.; Su, B. Turbulence and flow field alterations inside a fish sea cage and its wake. Appl. Ocean Res. 2020, 98, 102113. [Google Scholar] [CrossRef]
- Ji, R.; Mao, X.; Zhu, M. The impact of shellfish farming on the bay ecosystem. Huanghai Sea Bohai Sea 1998, 16, 21–27. [Google Scholar]
- Scott, C.; James, F.O. Drag coefficient parameter estimation for aquaculture systems. Environ. Fluid Mech. 2019, 19, 989–1003. [Google Scholar]
- Wang, K.; Li, N.; Wang, Z.; Song, G.; Du, J.; Song, L.; Jiang, H.; Wu, J. The Impact of Floating Raft Aquaculture on the Hydrodynamic Environment of an Open Sea Area in Liaoning Province, China. Water 2022, 14, 3125. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, H.; Liu, Y.; Bi, H.; Yan, L. Numerical study of hydrodynamic conditions and sedimentary environments of the suspended kelp aquaculture area in Heini Bay. Estuarine. Coast. Shelf Sci. 2020, 232, 106492. [Google Scholar] [CrossRef]
- ANSYS, Inc. ANSYS Fluent Theory Guide; ANSYS: Canonsburg, PA, USA, 2018. [Google Scholar]
- Wang, K.; Jin, S.; Liu, G. Numerical modelling of free-surface flows with bottom and surface-layer pressure treatment. J. Hydrodyn. 2009, 21, 352–359. [Google Scholar] [CrossRef]
- Salih, S.M.; Jalil, J.M.; Najim, S.I. Experimental and numerical analysis of a double-pass solar air heater with PCM. Renew. Energy 2019, 143, 1053–1066. [Google Scholar] [CrossRef]
- Liu, X.; Cheng, L. A K-ε two-equation turbulence model for the solid-liquid two-phase flows. Appl. Math. Mech. 1996, 17, 523–531. [Google Scholar]
- Liu, C. Study on Characteristics of Flow Distribution around Marine Cage Culture Area; Tianjin University: Tianjin, China, 2020. [Google Scholar]
- Wu, H.; Wang, J. A high-resolution finite volume method for solving two-dimensional shallow water equations. Commun. Appl. Math. Comput. 2006, 20, 83–88. [Google Scholar]
- Pan, C.; Xu, K. To solve two-dimensional shallow water equations in the form of KFVS with triangular meshes. J. Hydraul. Eng. 2006, 3, 858–864. [Google Scholar]
- Casulli, V. Semi-Implicit Numerical Modeling of Nonhydrostatic Free-Surface Flows for Environmental Problems. Math. Comput. Model. 2002, 36, 1131–1149. [Google Scholar] [CrossRef]
- Liu, F.; Huang, K.; Jiang, Y.; Song, S.; Gu, B. Analytical Description for Solid-State Phase Transformation Kinetics: Extended Works from a Modular Model, a Review. J. Mater. Sci. Technol. 2016, 32, 97–120. [Google Scholar] [CrossRef]





| Station | Longitude | Latitude |
|---|---|---|
| HH | 122°41.000′ E | 39°14.000′ N |
| U1 | 123°06.098′ E | 39°07.111′ N |
| U2 | 123°12.539′ E | 39°10.895′ N |
| Working Condition | Number of Days | |||||
|---|---|---|---|---|---|---|
| 0d | 1d | 3d | 5d | 7d | 9d | |
| Without floating rafts | 0.00 | 27.90% | 56.80% | 64.65% | 73.87% | 80.26% |
| With floating rafts | 0.00 | 22.21% | 45.69% | 57.84% | 69.31% | 76.87% |
| Previous research results | 0.00 | 22.90% | 48.20% | 60.37% | 72.13% | 79.07% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Li, N.; Song, L.; Wu, J.; Jiang, H. Application of a VOF Multiphase Flow Model for Issues concerning Floating Raft Aquaculture. Water 2023, 15, 3450. https://doi.org/10.3390/w15193450
Wang K, Li N, Song L, Wu J, Jiang H. Application of a VOF Multiphase Flow Model for Issues concerning Floating Raft Aquaculture. Water. 2023; 15(19):3450. https://doi.org/10.3390/w15193450
Chicago/Turabian StyleWang, Kun, Nan Li, Lun Song, Jinhao Wu, and Hengzhi Jiang. 2023. "Application of a VOF Multiphase Flow Model for Issues concerning Floating Raft Aquaculture" Water 15, no. 19: 3450. https://doi.org/10.3390/w15193450
APA StyleWang, K., Li, N., Song, L., Wu, J., & Jiang, H. (2023). Application of a VOF Multiphase Flow Model for Issues concerning Floating Raft Aquaculture. Water, 15(19), 3450. https://doi.org/10.3390/w15193450





