Numerical and Experimental Analysis of Vortex Pump with Various Axial Clearances
Abstract
1. Introduction
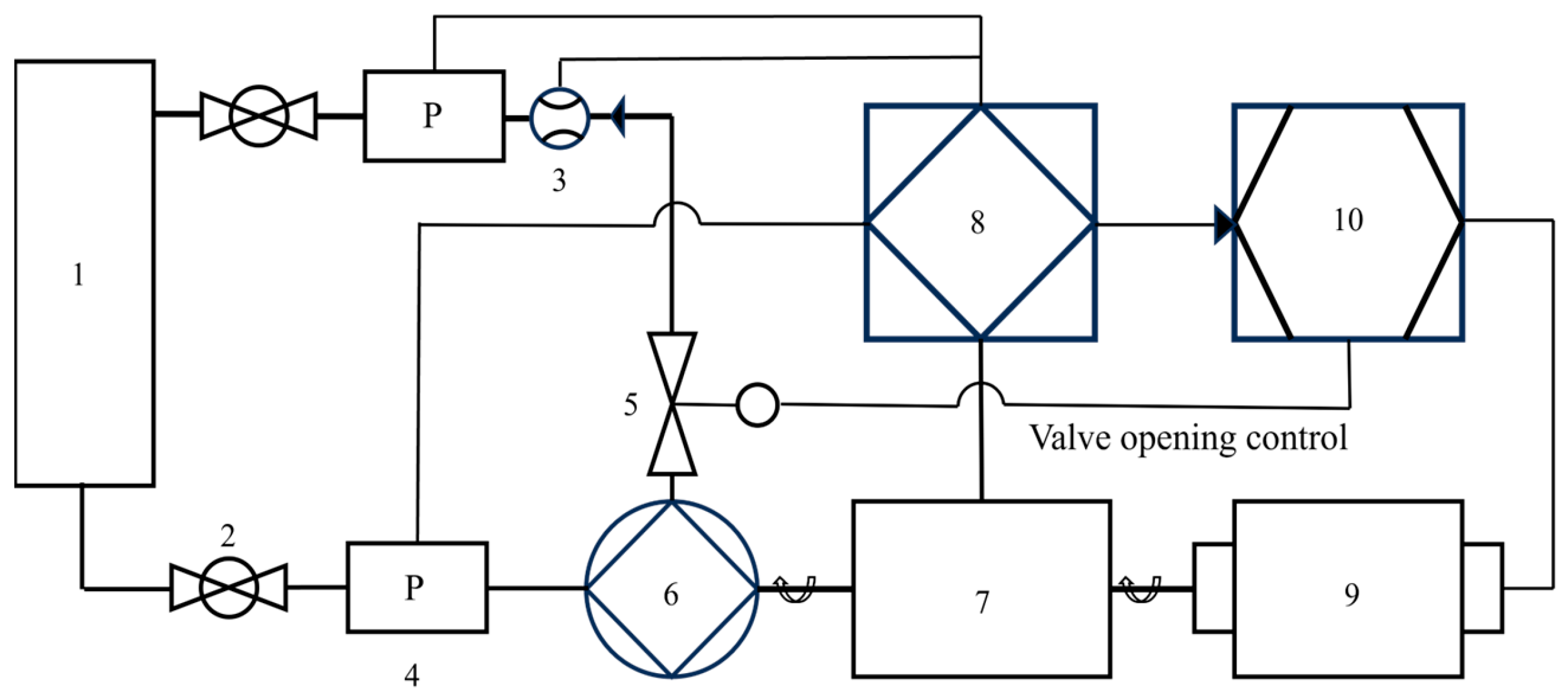
2. Numerical Simulation and Experimental Validation
2.1. Turbulence Model and Boundary Conditions
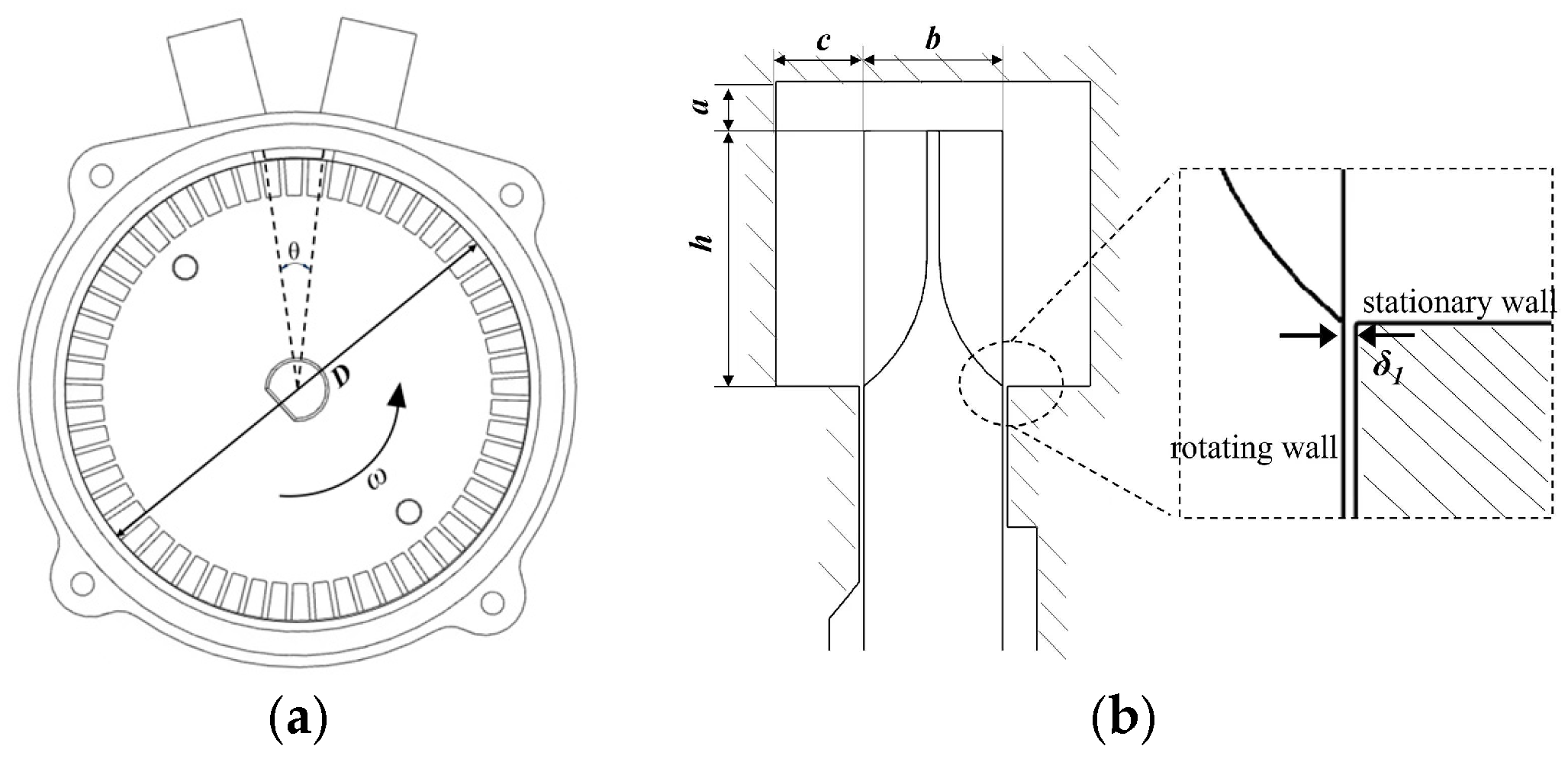
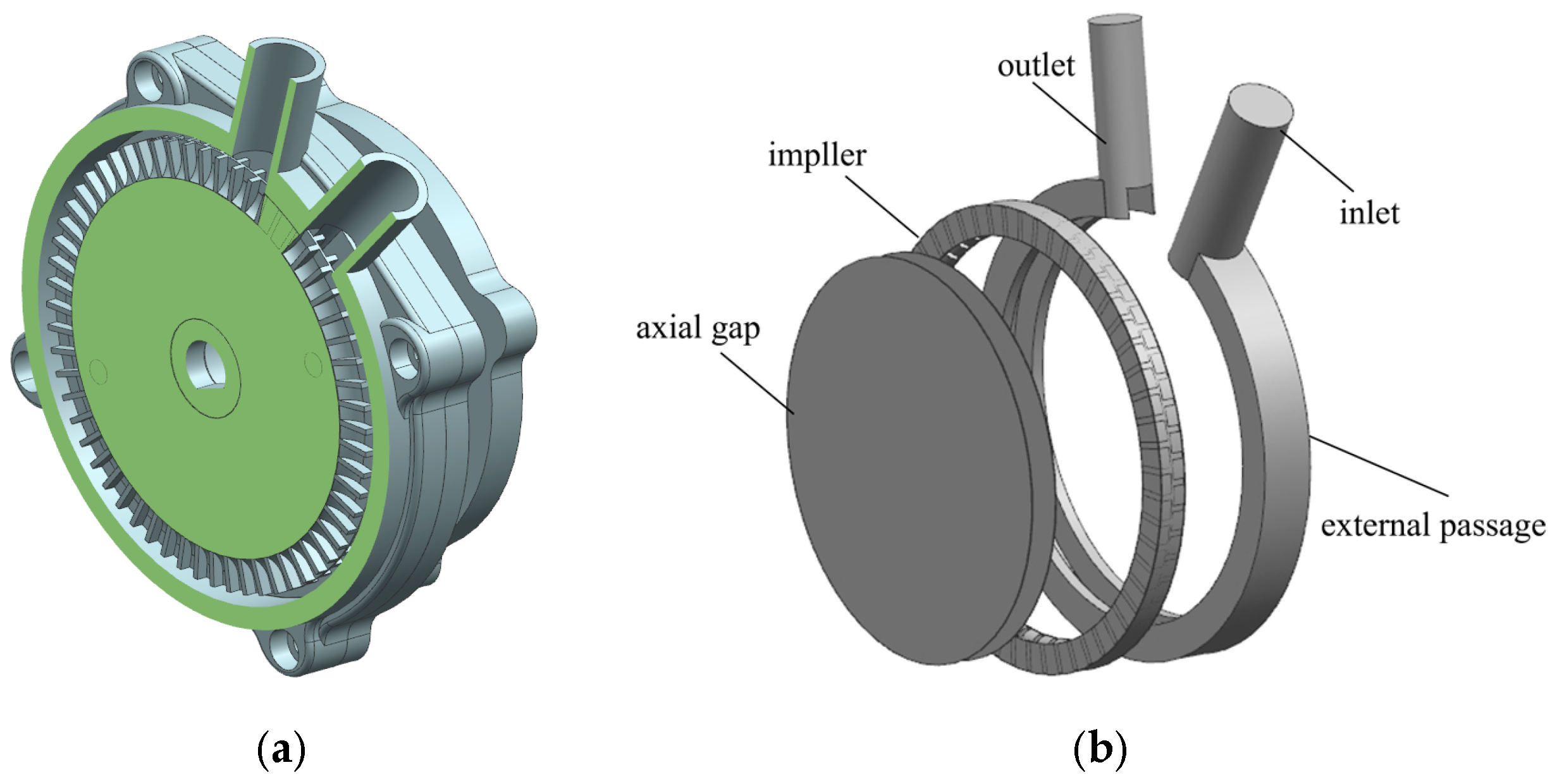
2.2. Geometric Model
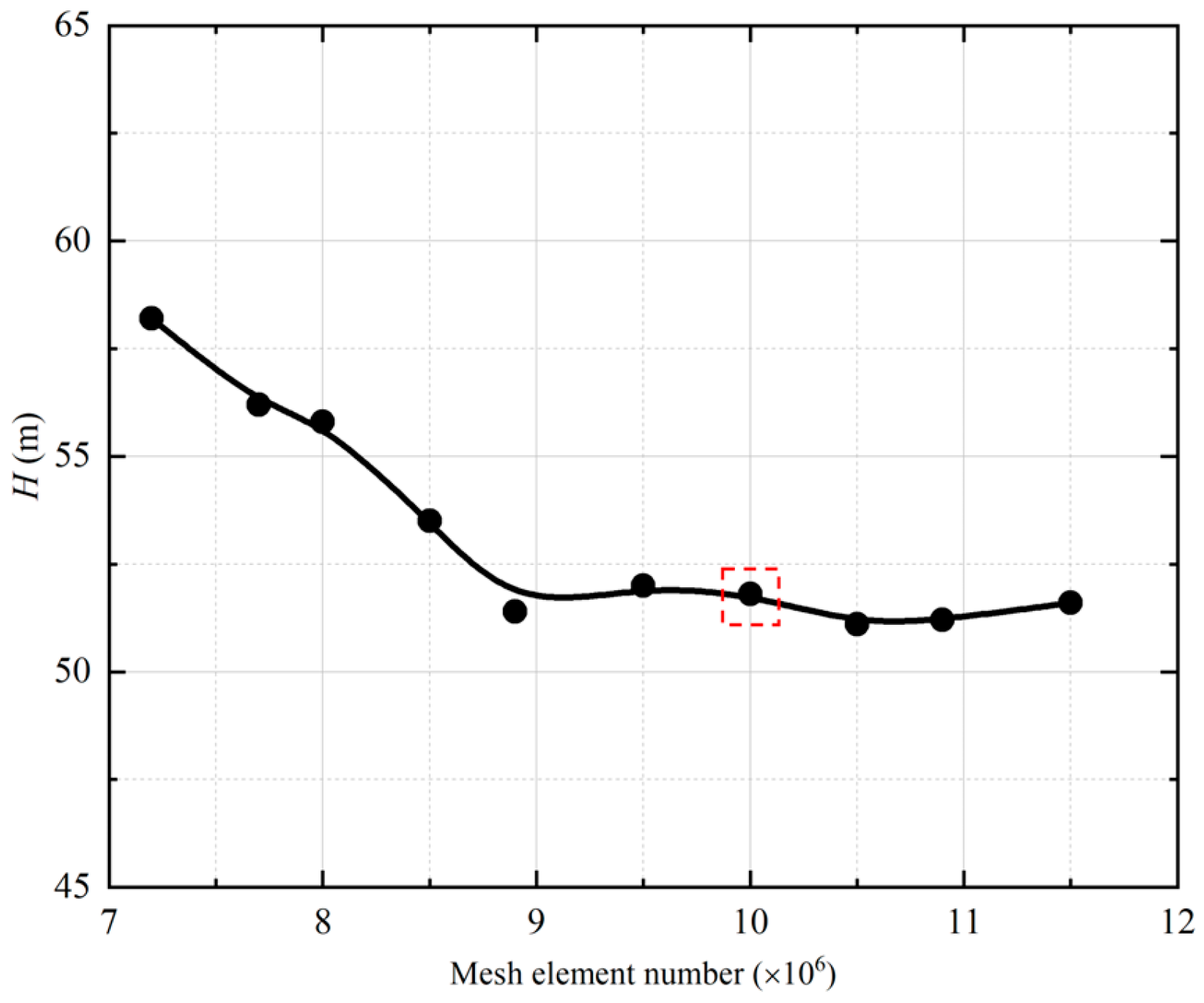
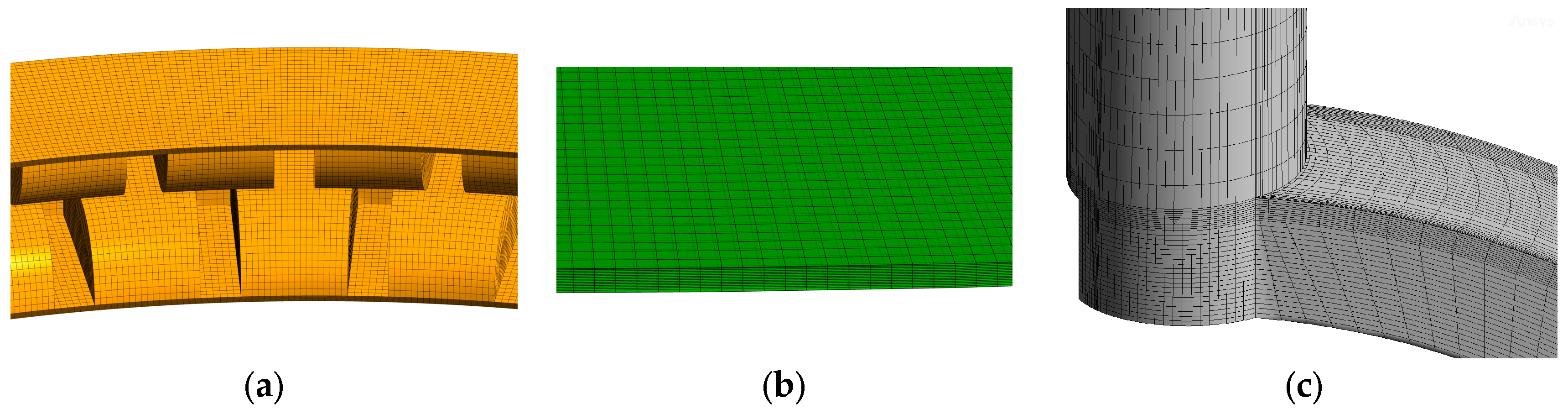
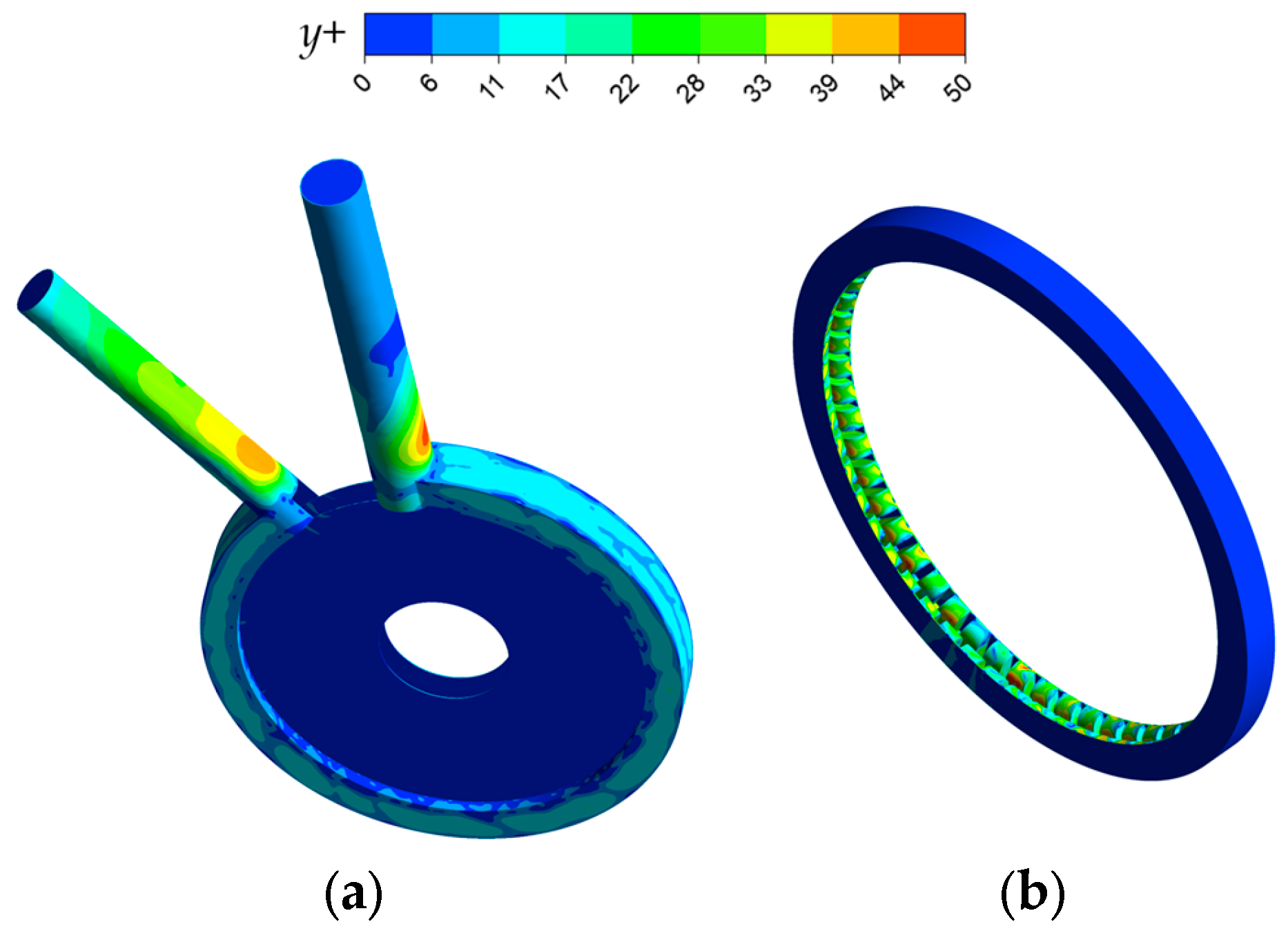
2.3. Grid Generation
2.4. Experimental Procedure and Validation by Numerical Simulation
3. Results and Discussion
3.1. External Characteristics Comparison
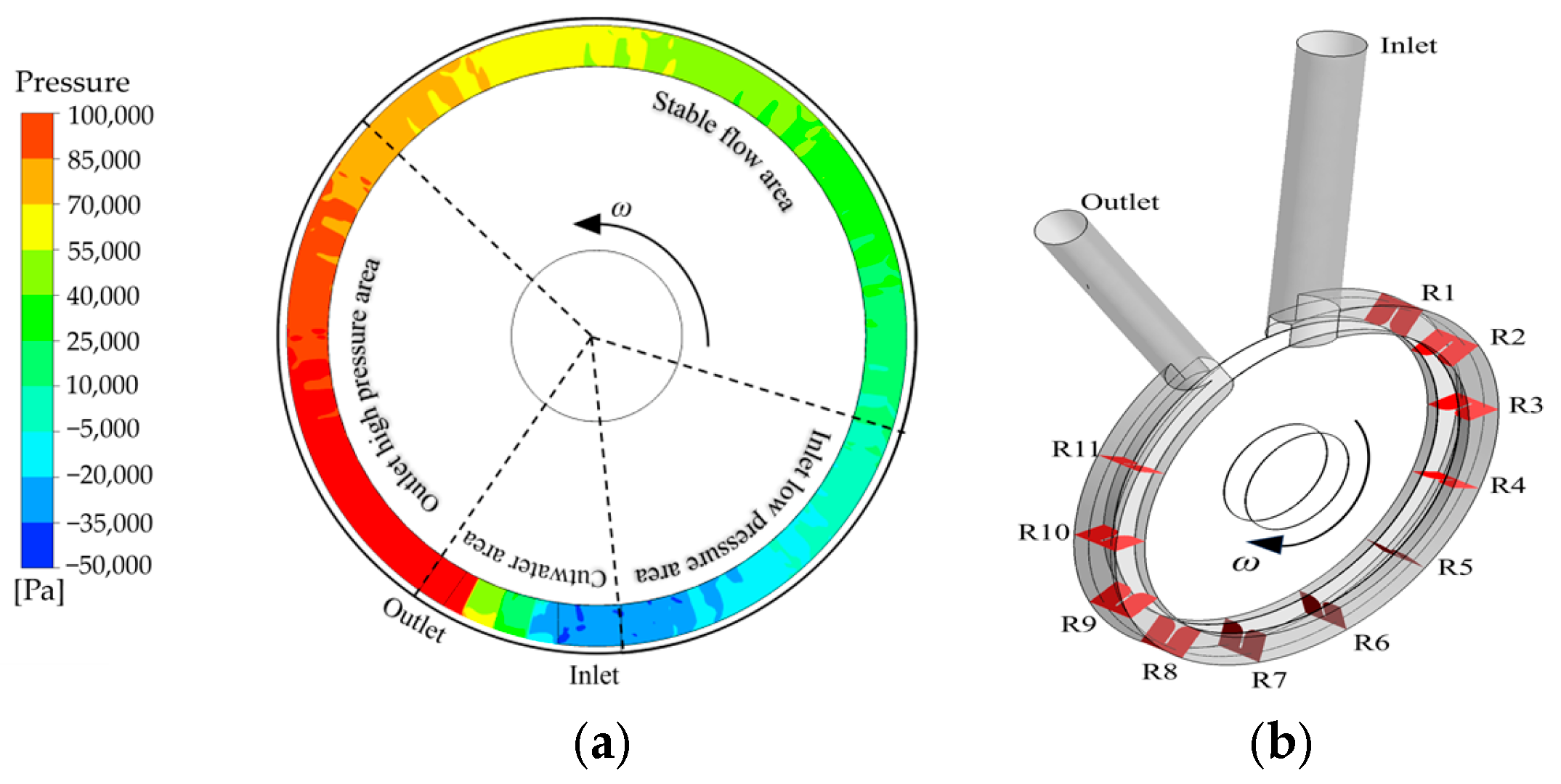
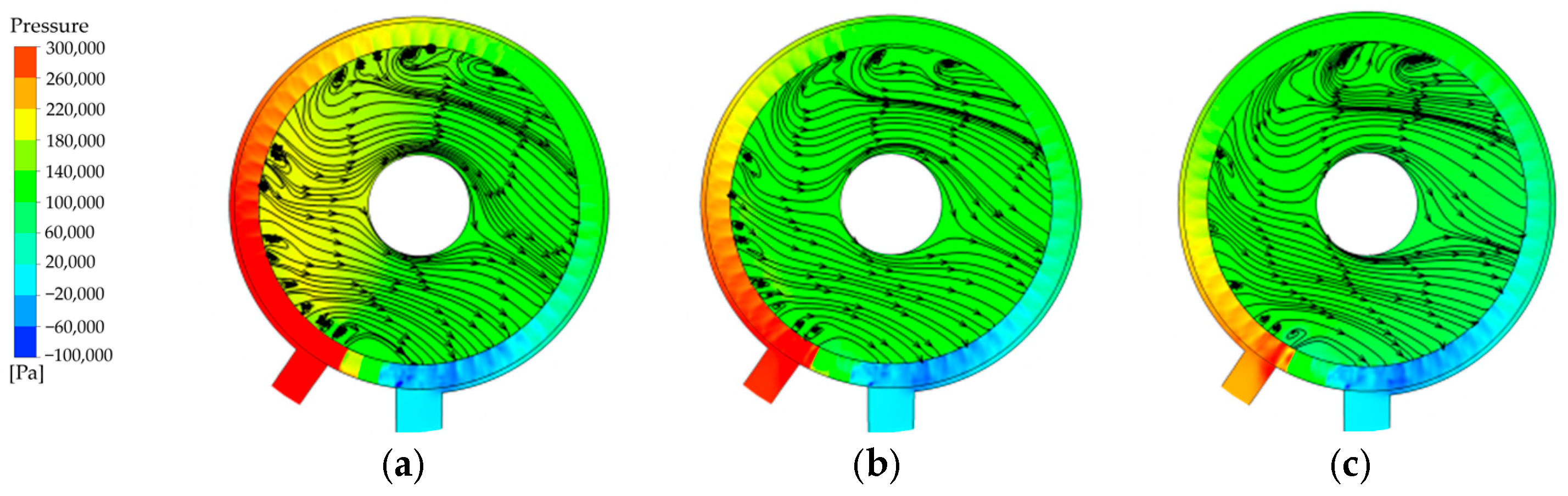
3.2. Internal Flow Field Analysis
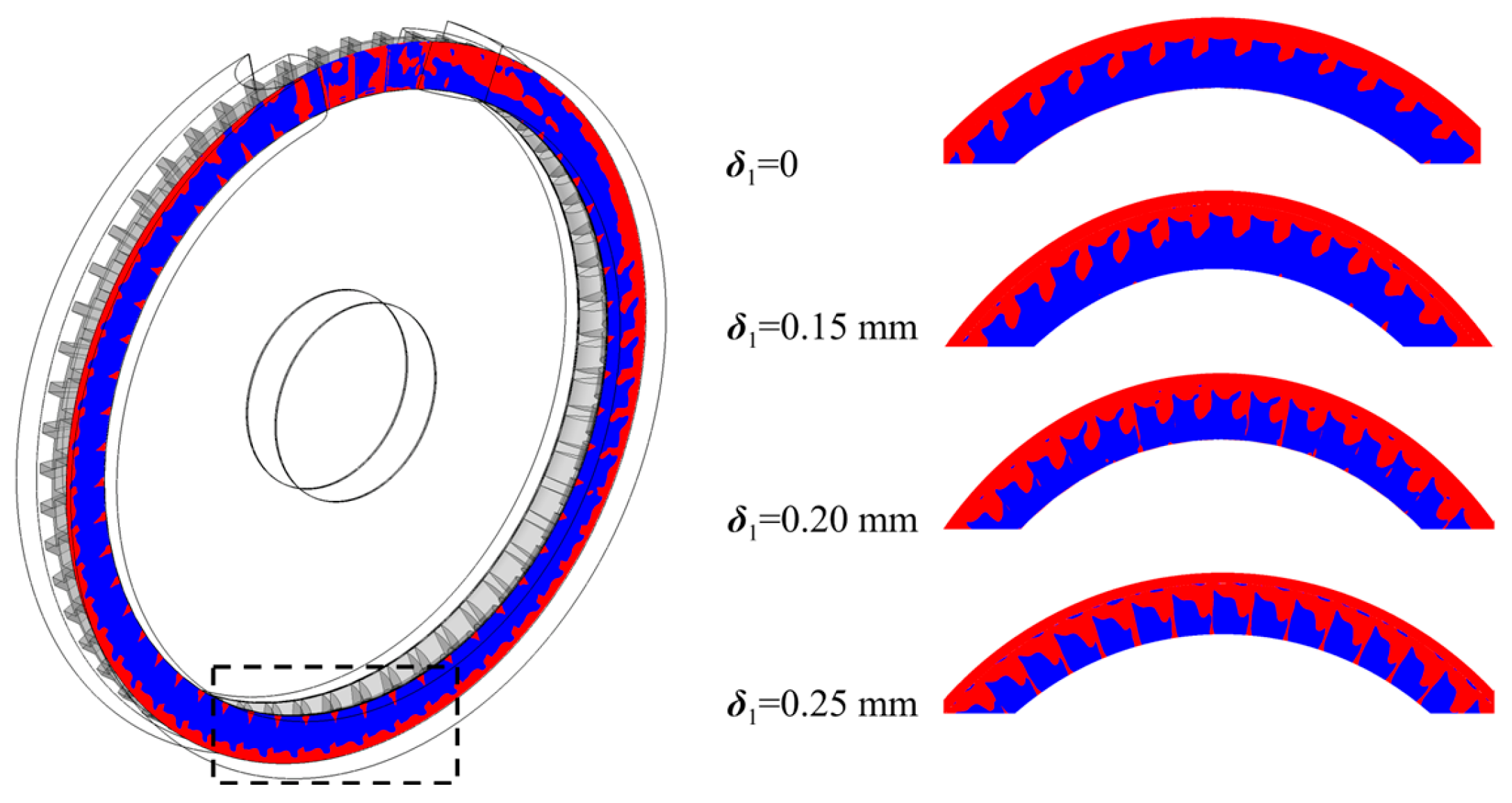
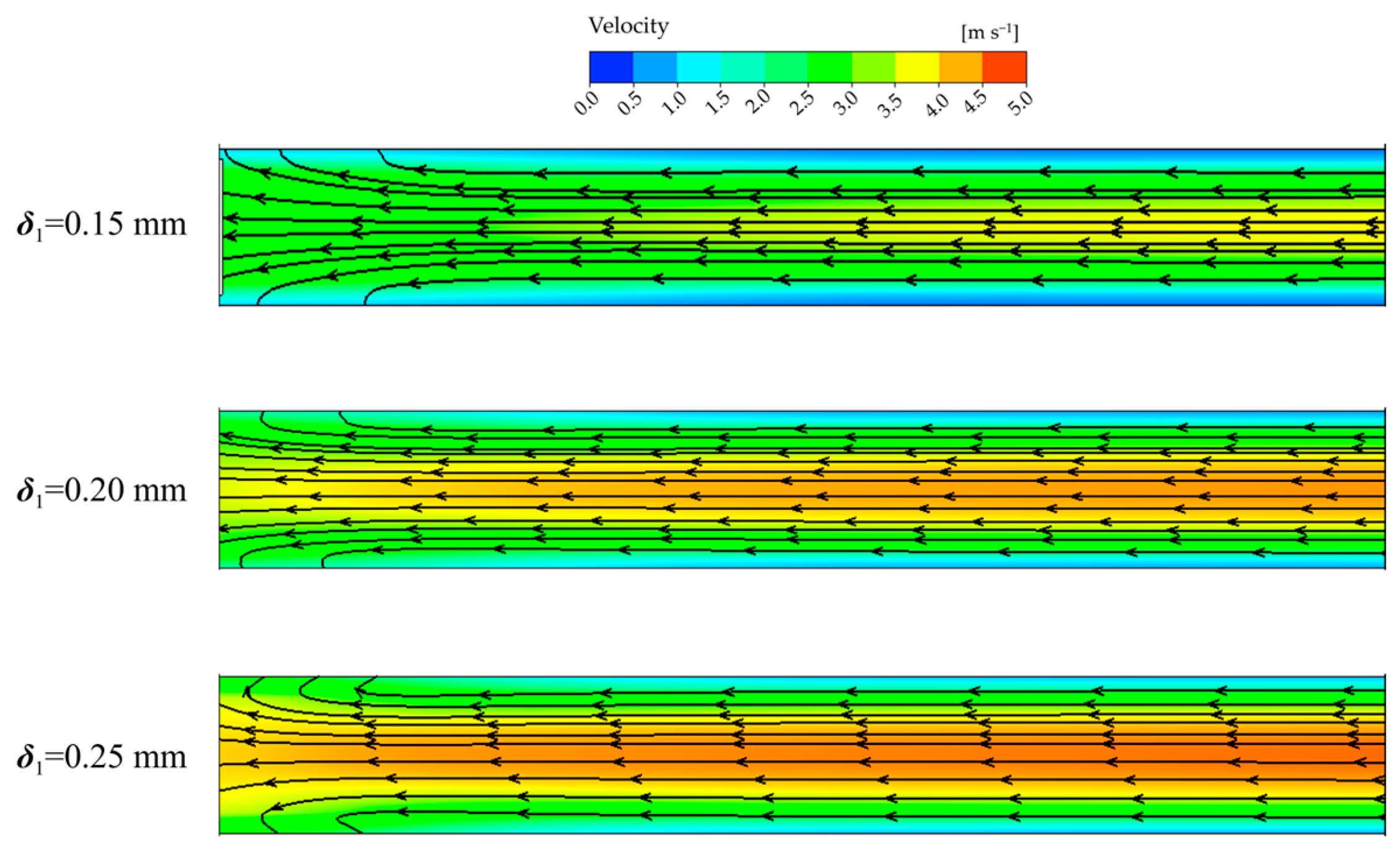
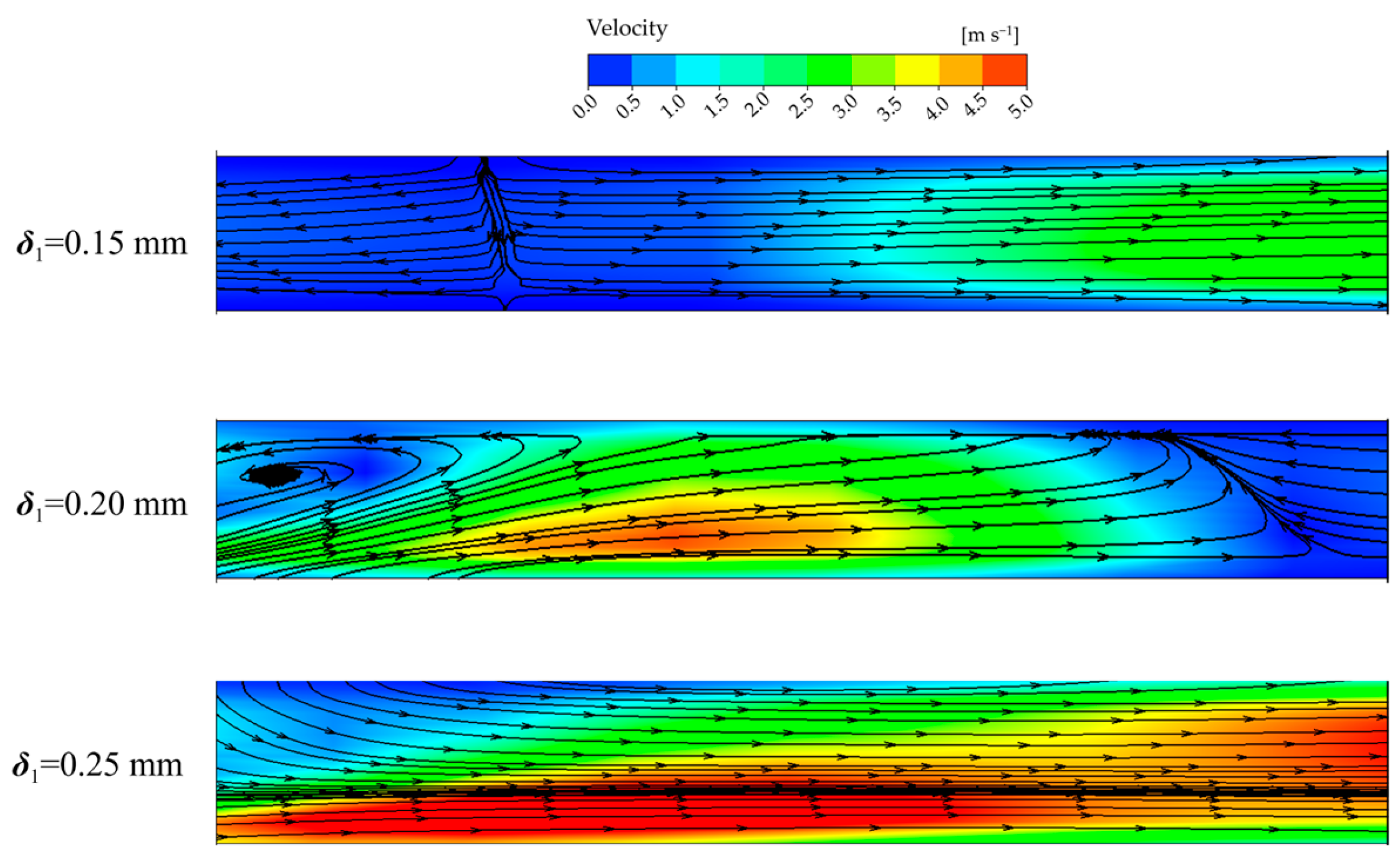
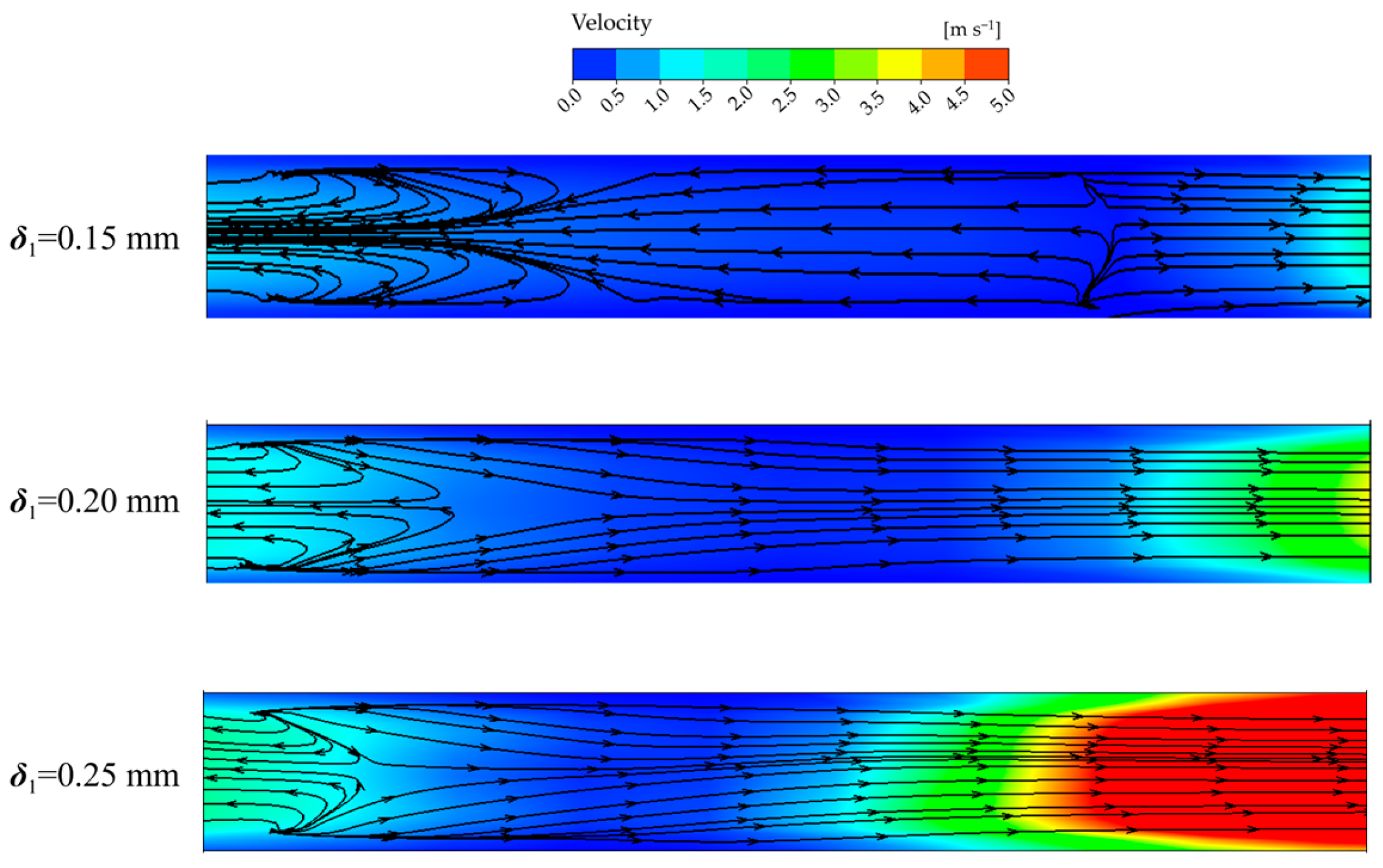
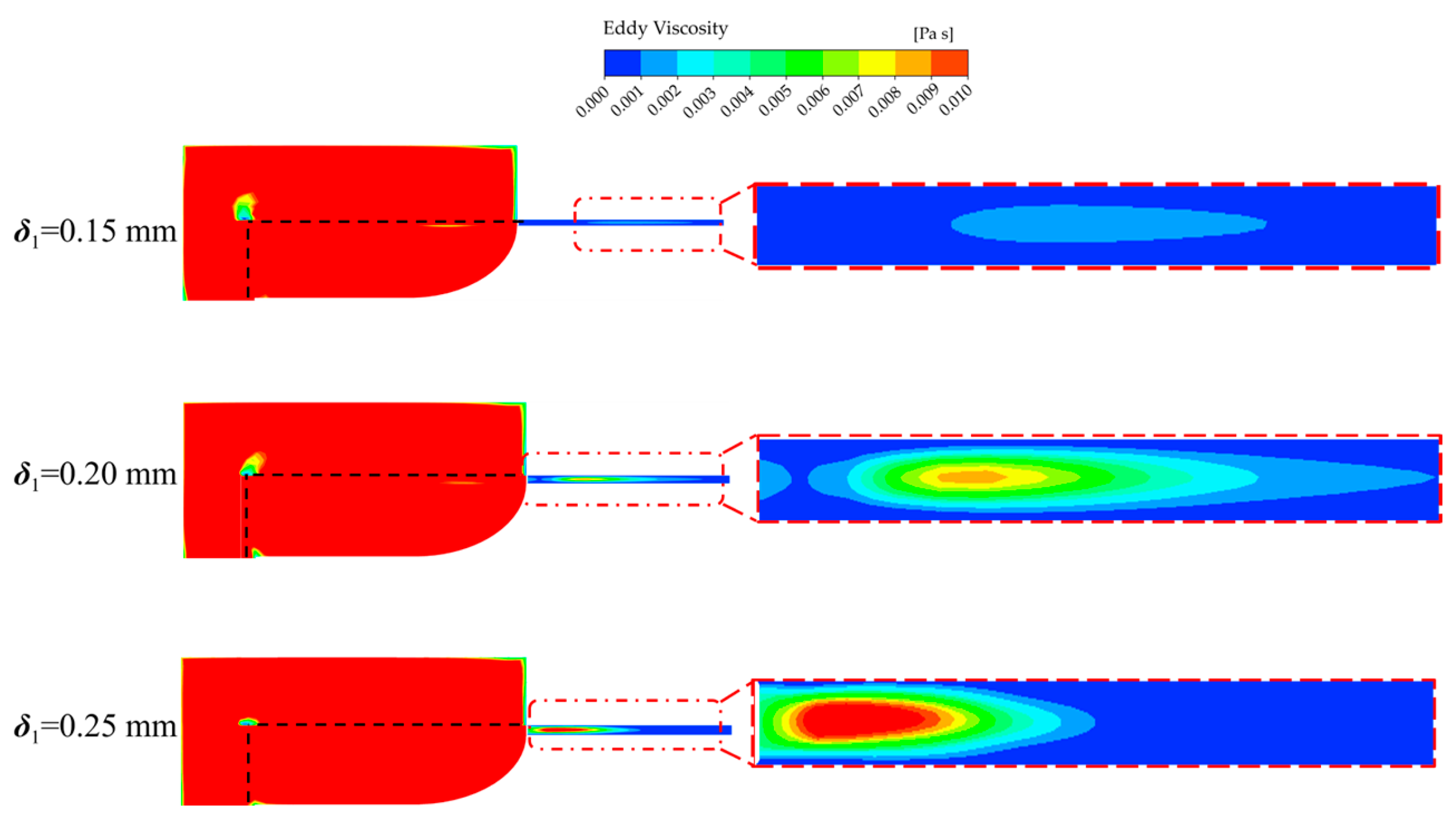
3.3. Clearance Flow Characteristics Analysis
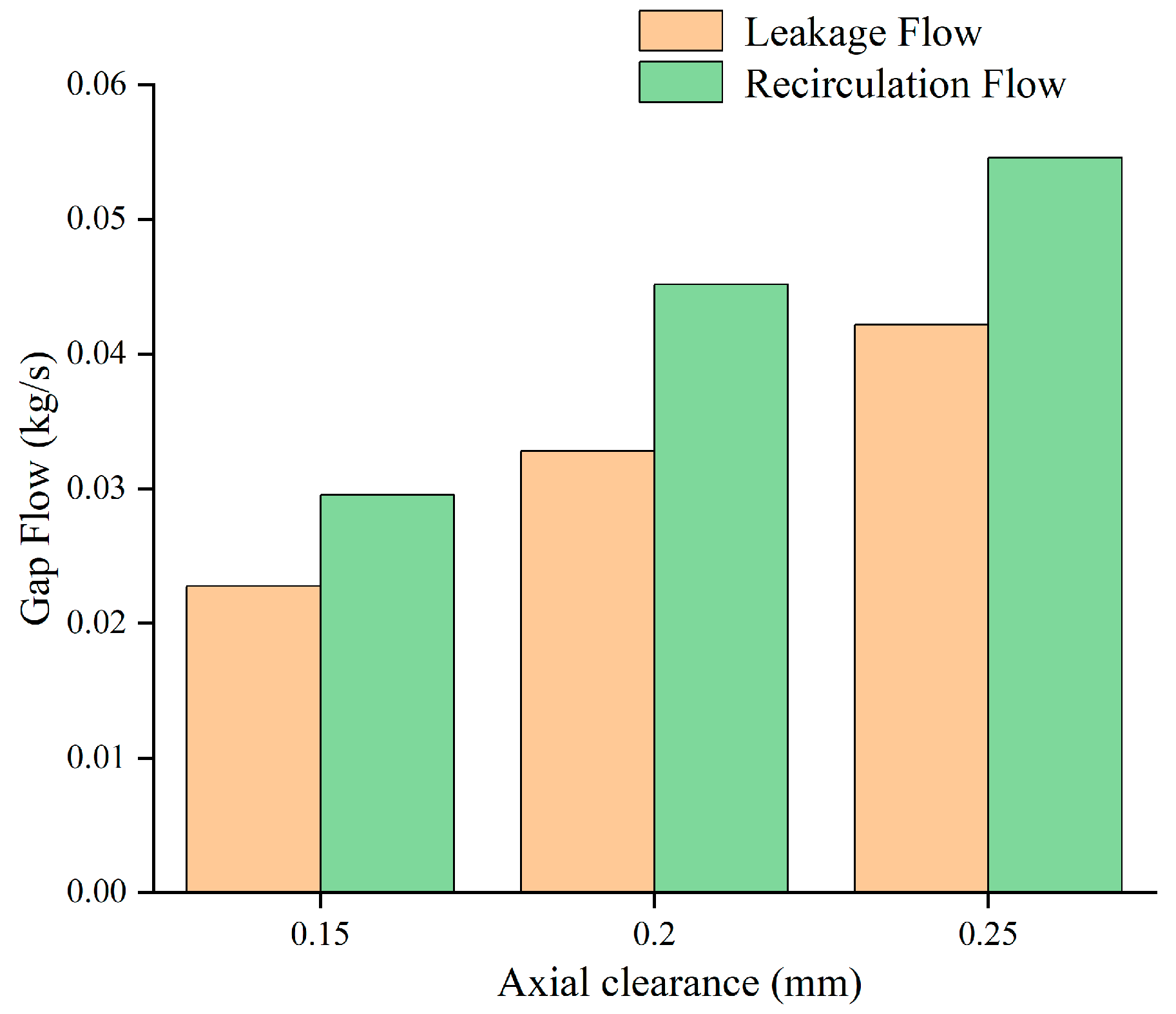
3.4. Leakage Analysis
4. Conclusions
- Axial clearance has a significant impact on the external characteristics of the vortex pump, with a rapid decline in performance as the clearance size increases. The pump head index is more sensitive to clearance scale under low flow conditions, while the pump efficiency index is more sensitive to clearance scale under high flow conditions.
- In the axial clearance of the vortex pump, there is a significant phenomenon of fluid recirculation. The fluid from the main flow path leaks from the high-pressure area at the outlet and recirculates back to the main flow path in the low-pressure area at the inlet. Both the leakage flow and the recirculation flow cause considerable energy dissipation.
- As the clearance increases, the flow resistance in the clearance region decreases, leading to an increase in both the clearance leakage and recirculation flow. This results in a higher intensity of fluid recirculation within the clearance region, consuming more energy. Simultaneously, the increased clearance affects the internal vortices of the pump, leading to a decrease in vortex intensity that consequently reduces the intensity of the momentum exchange between the fluid inside and outside the impeller. These two factors are the main reasons for the decline in the external characteristics of the vortex pump caused by an increase in clearance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guan, X. Modern Pump Theory and Design; China Aerospace Press: Beijing, China, 2011. [Google Scholar]
- Wang, H.; Mao, W.; Zhang, Y.; Li, C.; Shen, Y. Design and experiment of online drug mixing system based on synchronous control of water and pesticide flow. J. Jiangsu Univ. (Nat. Sci. Ed.) 2022, 43, 737–744. [Google Scholar]
- Möttönen, M.; Pietilä, V.; Virtanen, S.M.M. Vortex pump for dilute Bose-Einstein condensates. Phys. Rev. Lett. 2007, 99, 250406. [Google Scholar] [CrossRef] [PubMed]
- Deng, X.; Harrison, G.; Roger, F.; Houston, W. Methodology of turbulence parameter correction in water-lubricated thrust bearings. ASME J. Fluids Eng. 2019, 141, 071104. [Google Scholar] [CrossRef]
- El-Emam, M.; Zhou, L.; Yasser, E.; Bai, L.; Shi, W. Computational methods of erosion wear in centrifugal pump: A state-of-the-art review. Arch. Comput. Methods Eng. 2022, 29, 3789–3814. [Google Scholar] [CrossRef]
- Senoo, Y. Theoretical Research on Friction Pump; Reports of the Research Institute for Fluid Engineering; Research Institute for Fluid Engineering, Kyushu University: Fukuoka, Japan, 1948; Volume 5, pp. 23–38. [Google Scholar]
- Senoo, Y. Researches on Peripheral Pump; Reports of the Research Institute for Applied Mechanics; Research Institute for Applied Mechanics, Kyushu University: Fukuoka, Japan, 1954; Volume 3, pp. 53–113. [Google Scholar]
- Iversen, H. Performance of the periphery pump. Trans. Am. Soc. Mech. Eng. 1970, 77, 19–28. [Google Scholar] [CrossRef]
- Weinig, F. Analysis of traction pumps. Hydraul. Div. ASME 1955, 2, 21–23. [Google Scholar]
- Pfleiderer, C. Centrifugal Pump for Liquids and Gases; Springer: Berlin, Germany, 1949. [Google Scholar]
- Wilson, W.; Santalo, M.; Oelrich, J. A theory of the fluid-dynamic mechanism of regenerative pumps. Trans. Am. Soc. Mech. Eng. 1955, 7, 1303–1316. [Google Scholar] [CrossRef]
- Grabow, G. Effect of Blade Shape on the Characteristic Behavior of Peripheral and Side Channel Pumps and Hydrodynamic Fluid Couplings. Doctoral Thesis, Technical University of Magdeburg, Magdeburg, Germany, 1971. [Google Scholar]
- Quail, F.; Scanlon, T.; Baumgartner, A. Design study of a regenerative pump using one-dimensional and three-dimensional numerical techniques. Eur. J. Mech. B-Fluid 2012, 31, 181–187. [Google Scholar] [CrossRef]
- Karlsen-Davies, N.D.; Aggidis, G.A. Regenerative liquid ring pumps review and advances on design and performance. Appl. Energy 2016, 164, 815–825. [Google Scholar] [CrossRef]
- Fleder, A.; Böhle, M. A systematical study of the influence of blade number on the performance of a side channel pump. J. Fluids Eng. 2019, 141, 109–111. [Google Scholar] [CrossRef]
- Choi, W.C.; Yoo, I.S.; Park, M.R.; Chung, M.K. Experimental study on the effect of blade angle on regenerative pump performance. Proc. Inst. Mech. Eng. Part A J. Power Energy 2013, 227, 585–592. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.C.; Cao, P.Y.; Liu, Y.; Lü, Z. Analysis of the influence of M-section runner on the performance of vortex pump. Trans. Chin. Soc. Agric. Mach. 2014, 45, 77–82. [Google Scholar]
- Mosshammer, M.; Benigni, H.; Jaberg, H.; Konrad, J. Maximum efficiency despite lowest specific speed—Simulation and optmisation of a side channel pump. Int. J. Turbomach. Propuls. Power 2019, 4, 6. [Google Scholar] [CrossRef]
- Pei, J.; Zhang, F.; Appiah, D.; Hu, B.; Yuan, S.; Chen, K.; Asomani, S.N. Performance prediction based on effects of wrapping angle of a side channel pump. Energies 2019, 12, 139. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Z. Axial clearance of vortex pump. Pump Technol. 1991, 22–26. [Google Scholar]
- Shi, G.; Liu, D. Vortex pump impeller backlash adjustment technology. Pump Technol. 2009, 14, 29–31. [Google Scholar]
- Zhu, Z.; Wang, L.; Huang, D.; Jin, Q. Theoretical design and experimental study of low flow vortex pump. J. Eng. Thermophys. 2001, 22, 450–452. [Google Scholar]
- Wang, J.; Zhang, F.; Zhang, J.; Chen, K.; Hong, Q. Internal flow characteristics of single-stage and multi-stage side channel pumps. J. Drain. Irrig. Mach. Eng. 2023, 41, 133–139. [Google Scholar]
- Fleder, A.; Bohle, M. A Systematical Study of the Influence of Blade Length, Blade Width and Side Channel Height on the Performance of a Side Channel Pump. ASME J. Fluids Eng. 2015, 137, 121102. [Google Scholar] [CrossRef]
- Qiu, Z.; Zhou, L.; Bai, L.; El-Emam, M.A.; Agarwal, R. Empirical and numerical advancements in gas-liquid separation technology: A review. Geoenergy Sci. Eng. 2024, 233, 212577. [Google Scholar] [CrossRef]
- Zhou, L.; Hang, J.; Bai, L.; Krzemianowski, Z.; El-Emam, M.A.; Yasser, E.; Agarwal, R. Application of entropy production theory for energy losses and other investigation in pumps and turbines: A review. Appl. Energy 2022, 318, 119211. [Google Scholar] [CrossRef]
- Song, M.; Liu, R.; Chen, K.; Wang, Y.; Zhang, F. Influence of clocking effect on pressure pulsation of multistage side channel pump. J. Drain. Irrig. Mach. Eng. 2023, 41, 993–998. [Google Scholar]
- Li, Y.; Bai, C.; Qiao, H.; Yang, Y. Flow characteristics of viscous oil in rotor cavity of cam pump. J. Jiangsu Univ. (Nat. Sci. Ed.) 2022, 43, 464–471. [Google Scholar]
- Li, Q. Research on Energy Exchange and Pressure Pulsation Mechanism of Vortex Pump. Doctoral Thesis, Zhejiang University, Hangzhou, China, 2021. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, L.; Zhou, C.; Bai, L.; Agarwal, R. Numerical and Experimental Analysis of Vortex Pump with Various Axial Clearances. Water 2024, 16, 1602. https://doi.org/10.3390/w16111602
Zhou L, Zhou C, Bai L, Agarwal R. Numerical and Experimental Analysis of Vortex Pump with Various Axial Clearances. Water. 2024; 16(11):1602. https://doi.org/10.3390/w16111602
Chicago/Turabian StyleZhou, Ling, Chuan Zhou, Ling Bai, and Ramesh Agarwal. 2024. "Numerical and Experimental Analysis of Vortex Pump with Various Axial Clearances" Water 16, no. 11: 1602. https://doi.org/10.3390/w16111602
APA StyleZhou, L., Zhou, C., Bai, L., & Agarwal, R. (2024). Numerical and Experimental Analysis of Vortex Pump with Various Axial Clearances. Water, 16(11), 1602. https://doi.org/10.3390/w16111602







