Computational Simulation of Monopile Scour under Tidal Flow Considering Suspended Energy Dissipation
Abstract
:1. Introduction
2. Tidal Flow Bridge-Scour Simulation Model
2.1. Hydrodynamic Model
2.2. Sediment Transport Model
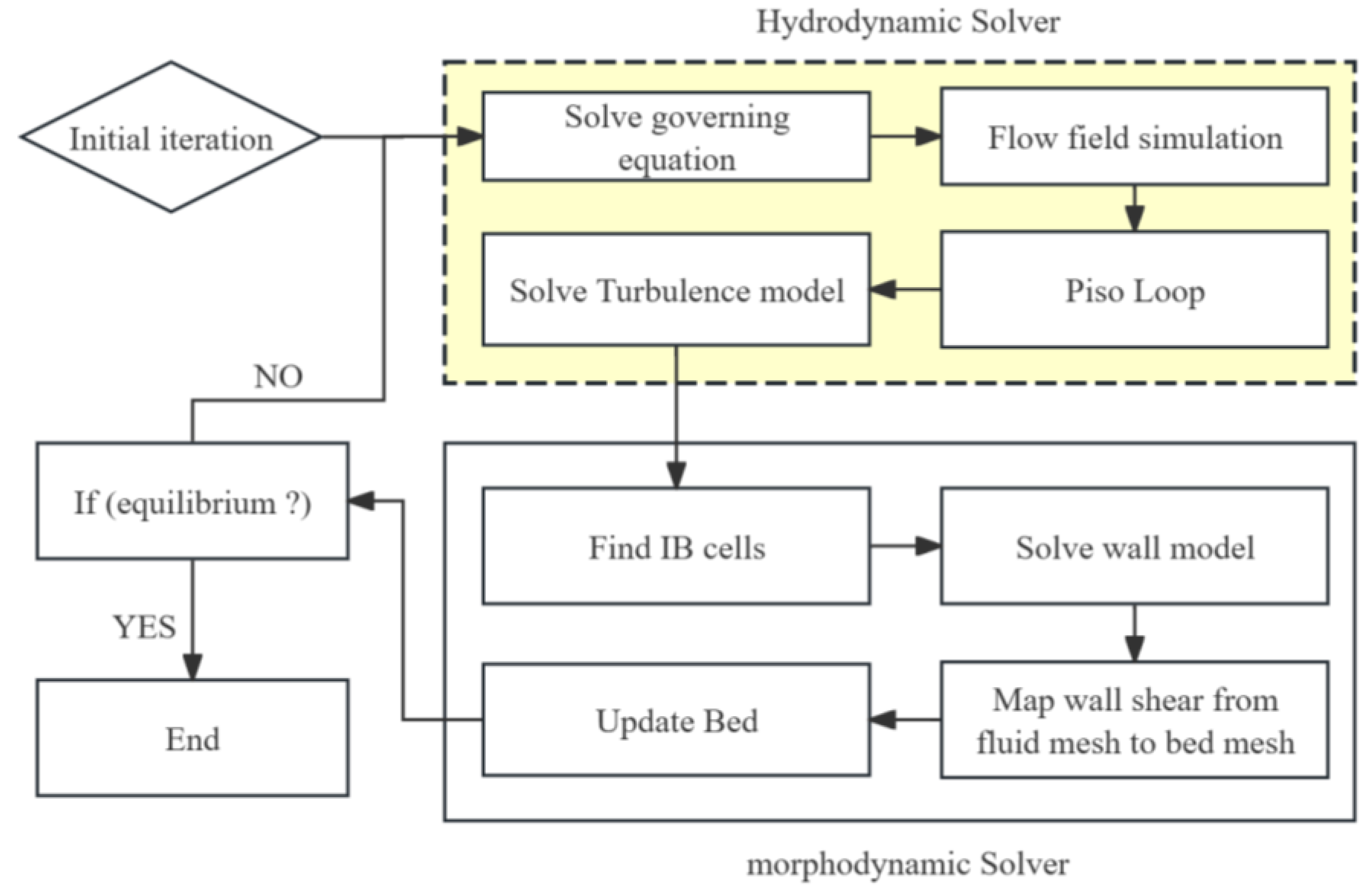
2.3. Model Coupling
- At the beginning of each time step, initial iterations are conducted. The hydrodynamic module computes the fully developed flow field to obtain the fluid’s velocity and pressure fields.
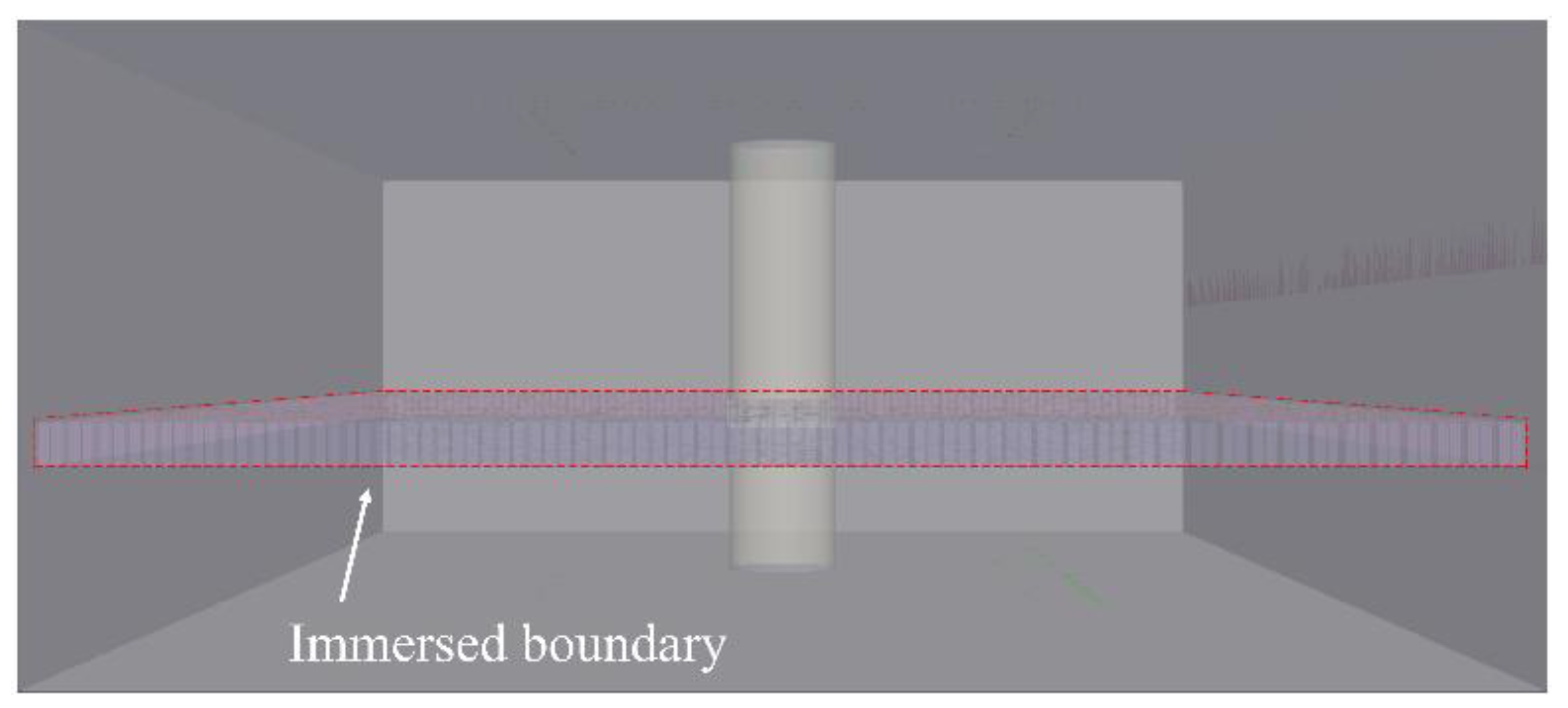
- Wall shear stresses at the immersed boundaries are obtained through the wall function model, and the wall shear forces at the riverbed mesh centers are determined via interpolation.
- The sediment transport equation is calculated to obtain the sediment transport rate, and the Exner equation is solved to update the riverbed elevation.
- After obtaining the new riverbed surface, the above process is repeated until the scour reaches equilibrium.
3. Validation of the Tidal Flow Model
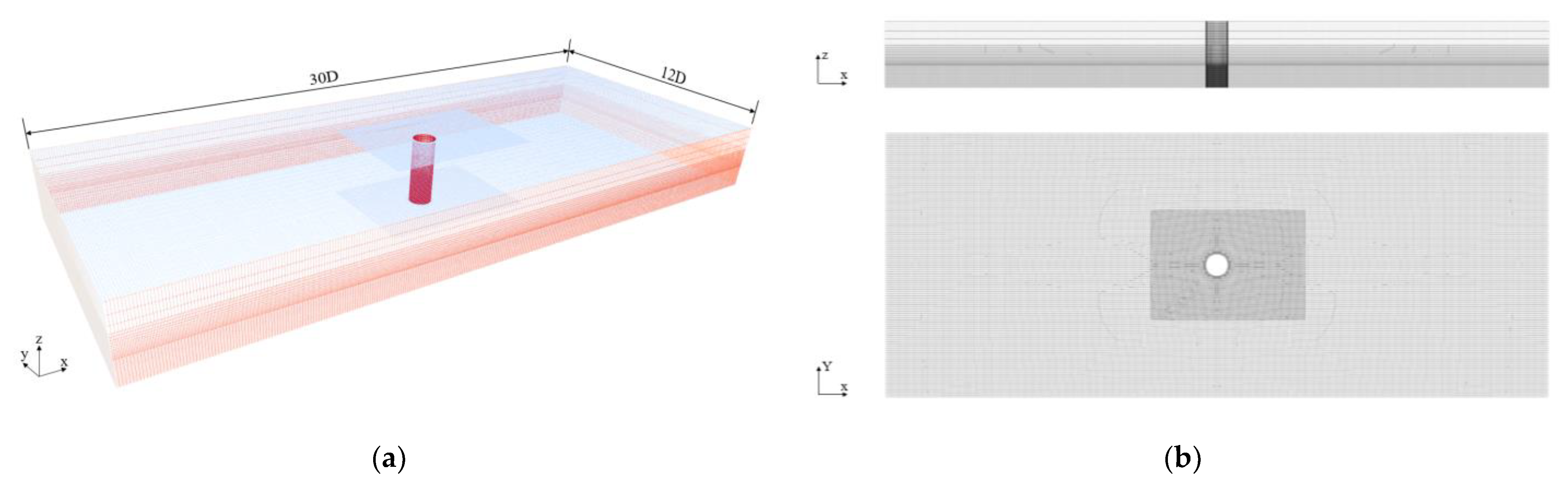
3.1. Mesh Setup
3.2. Model Mesh Settings
3.2.1. Boundary Conditions
- At the inlet, the velocities in the y-direction and z-direction are set to zero, and for pressure p, turbulent kinetic energy k, and turbulent viscosity μ, a zero-gradient condition is applied. In this study, the OpenFOAM plugin swak4Foam with the funkySetFields function is used to define the initial flow velocity, which can be used to set up an initial flow field with a certain spatial distribution. The velocity profile is determined based on the logarithmic law, as follows:
- 2.
- At the outlet boundary, except for the pressure, all quantities are specified with a zero gradient condition , and pressure is specified with the total pressure condition .
- 3.
- At the top surface, the slip condition is specified for the velocity, and zero gradient conditions are specified for p, v, and k.
- 4.
- At the bottom and pile wall surfaces, a no-slip condition is specified for the velocity , and zero gradient conditions are specified for p. The boundary conditions are specified using the wall function in OpenFOAM.
- 5.
- At the sidewall surface, a symmetry condition was set for all variables.
3.2.2. Tidal Flow Realization
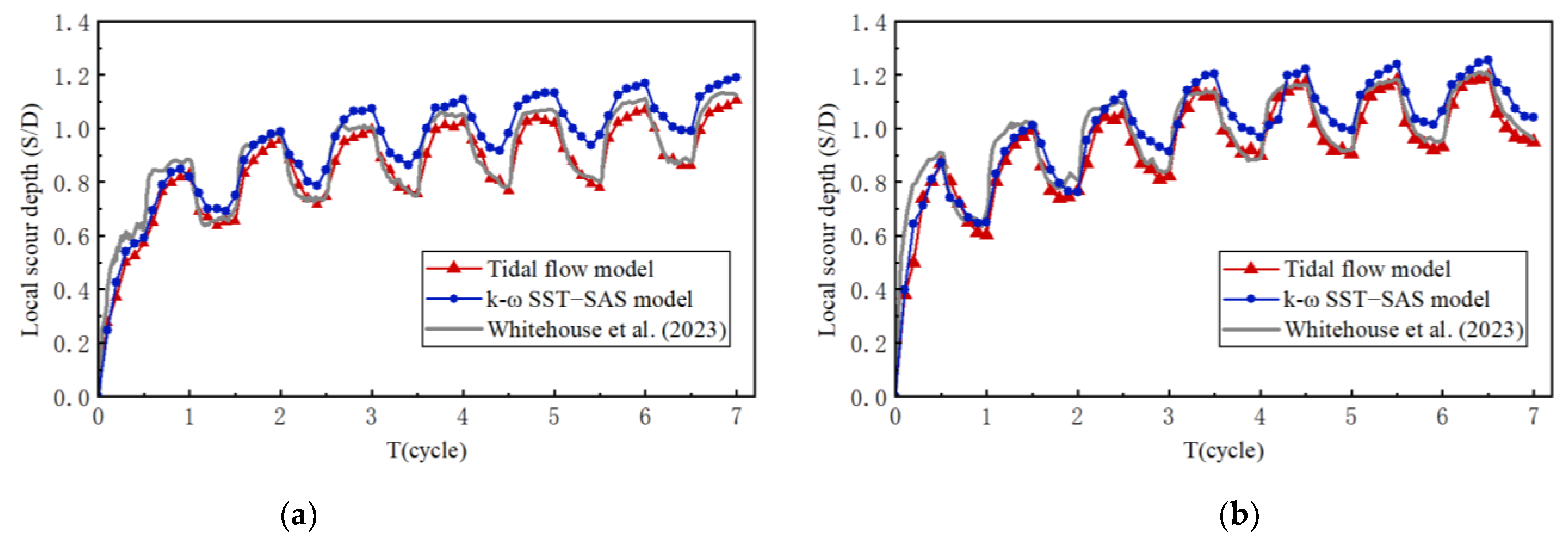
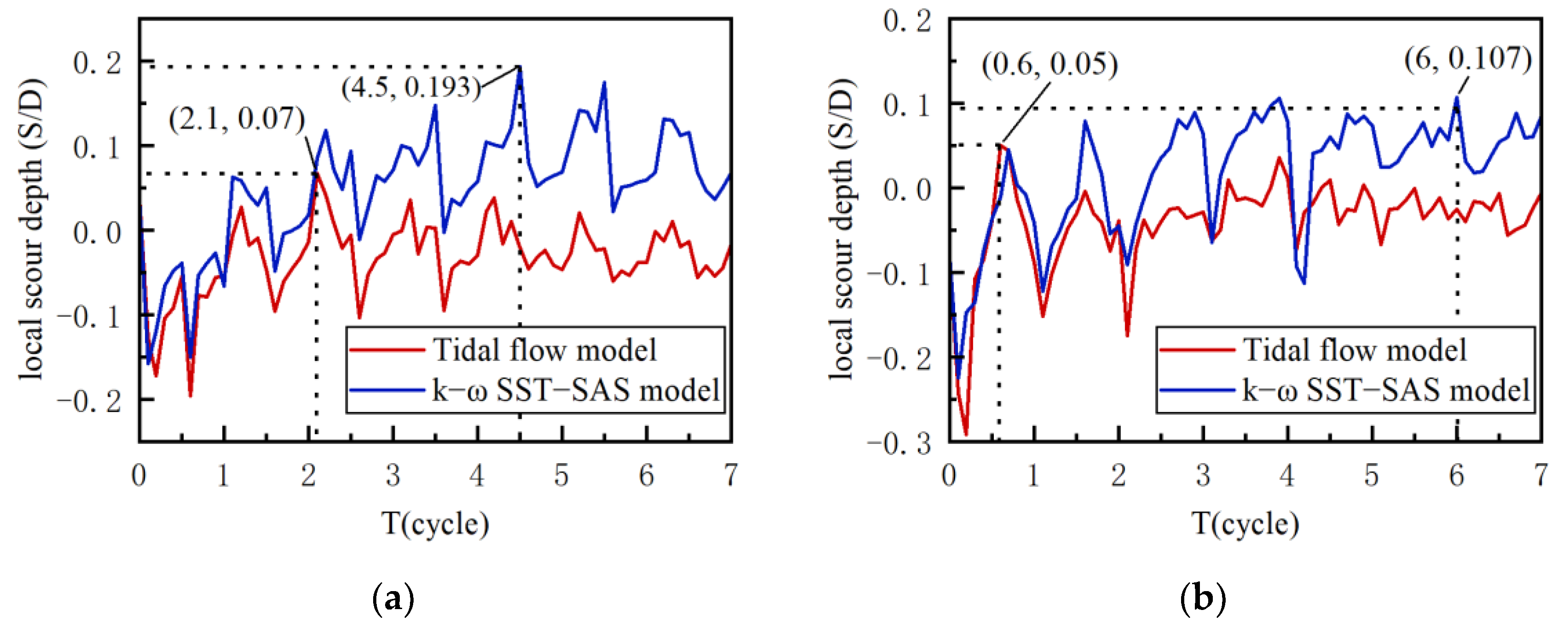
3.3. Verification of Local Scour Depth
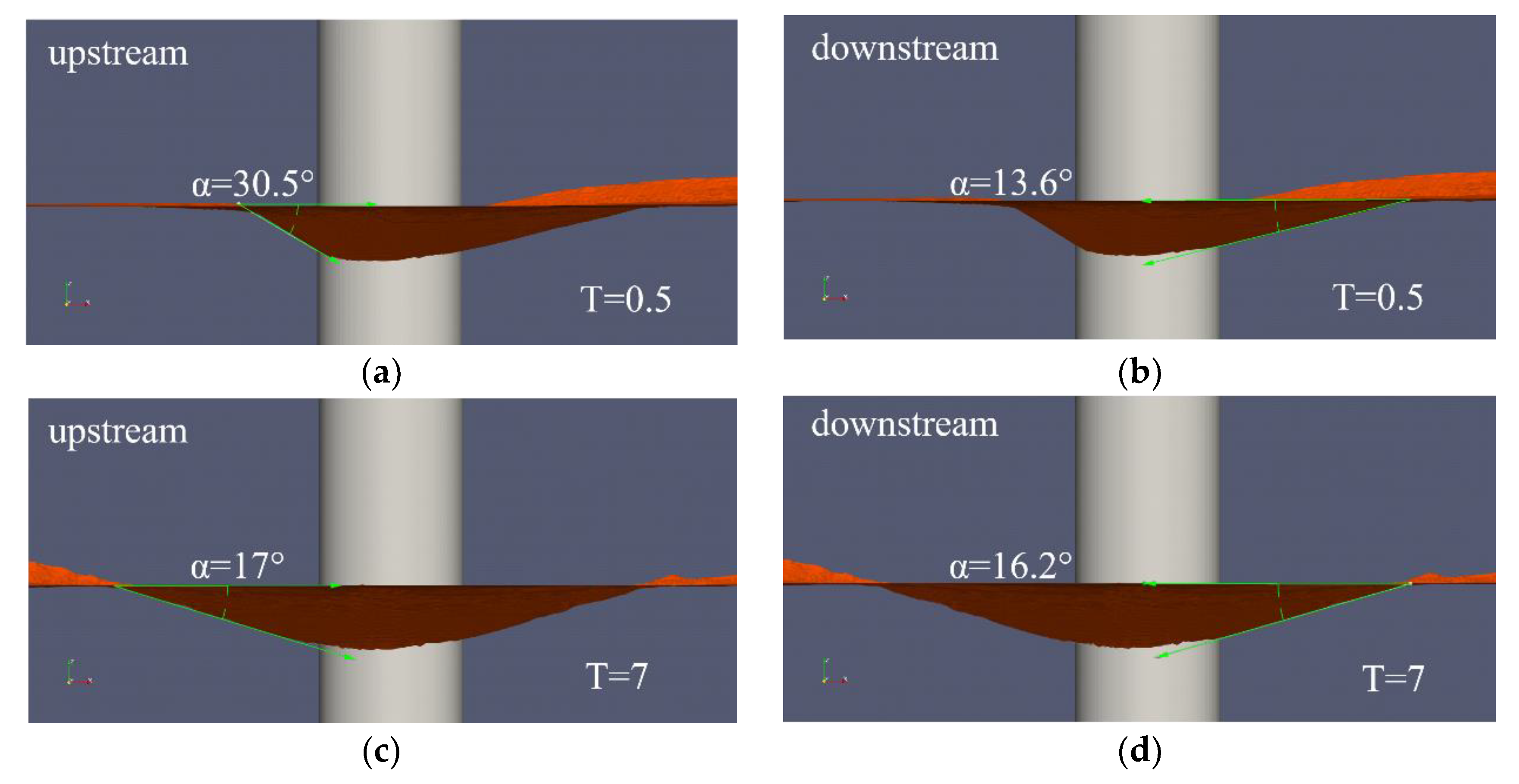
- Similar to unidirectional flow, the location of maximum localized scour in a single cycle under tidal flow conditions occurs in front of the pile. The scour depth in front of the pile is always greater than in the rear of the pile in almost every net cycle. The relative scour depths in front of the pile and in the rear of the pile are not exactly “mirror images”, although the flow velocity varies over the same period of time in the simulation, which may be due to the hysteresis of the flow velocity change. Although the experiments changed the flow velocity at the same time intervals, the change in flow velocity did not lead to an immediate change in the flow direction, and according to the setup in Chapter 2, the fluctuation of the previous flow direction still had an effect on the sediment in the current flow direction. Therefore, this phenomenon clearly indicates the existence of a correlation between flow intensity and scour depth.
- The phenomenon of scour valley/peak ratio increasing with time development was observed both before and in the rear of the pile, which indicated that the development of maximum scour depth under tidal flow conditions was not at the same rate as that of backfilling sediment.
- The development of the scour prior to scour under tidal flow is rapid, and the scour depth can reach about 70% of the maximum scour depth in the first cycle.
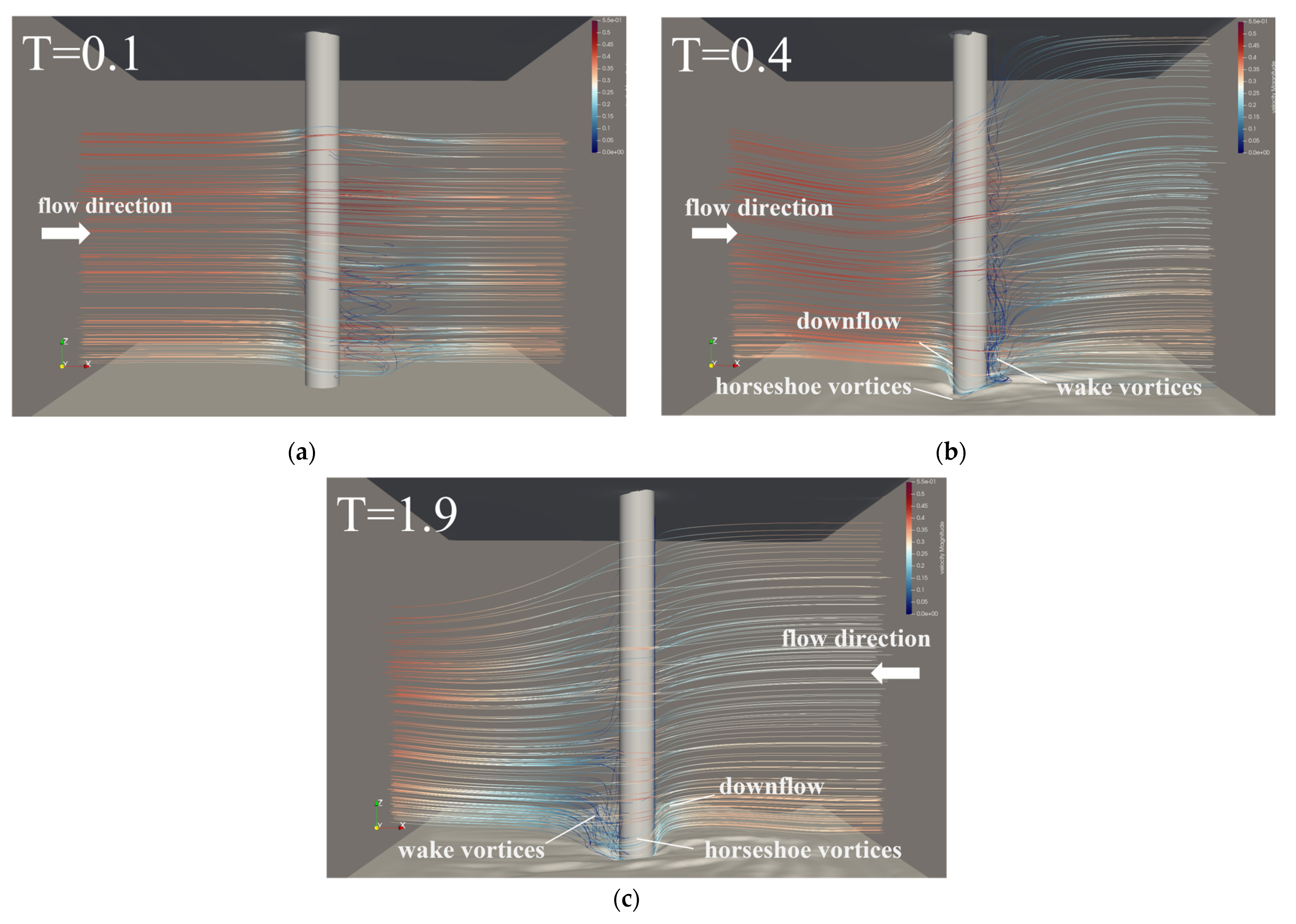
3.4. Verification of Flow Field
4. Experimental Setup
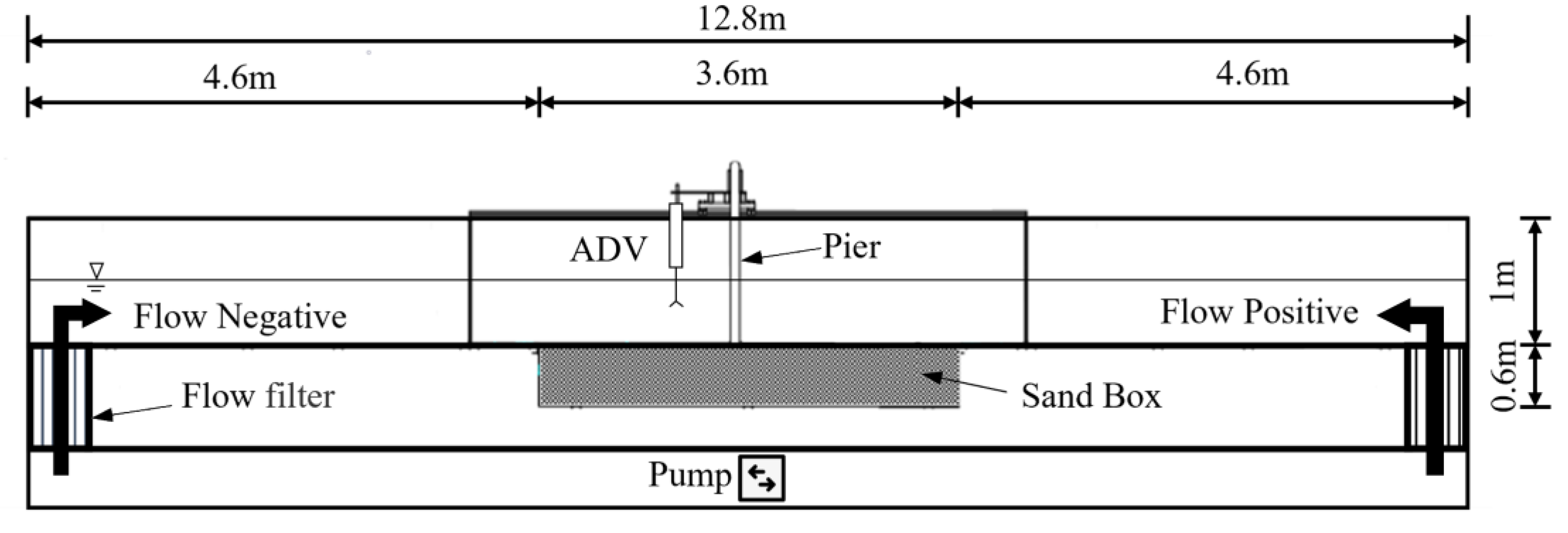
4.1. Experimental Equipment
4.2. Test Conditions and Methods
- Pre-preparation stage: Wash the sand to remove impurities, and screen the sand with a sieve to ensure the uniformity of particles. First, install the pile under test conditions on the base of the sedimentation box by bolts to make sure it is firm. Then, spread the sand over the box and inject a small amount of water into the box with the valve open to allow it to soak for 24 h to ensure that it is saturated with sand; then, smooth the sand bed using a scraper.
- Recalibrate the sand bed for levelness prior to the start of each test, and record sediment elevation readings at this time; protect the bed from early scour by pressing two PVC boards into the bed around the abutment prior to water injection.
- Slowly inject water from both sides of the sediment bed to the test water depth H, and dynamically control the flow rate V in the tank by simultaneously controlling the pumps and valves in the tank to achieve the test conditions.
- Carefully remove the PVC covers around the abutments while recording the test start time. The flow rate change cycle is 30 min for each set of tests, and each set of tests is conducted for 8 h. Record the scour depths in the four directions of 0°, 90°, 180°, and 270° from the pile in the direction of incoming flow at 10 min intervals for the first 30 min of scour initiation, and take readings at 30 min intervals thereafter. Subtract the initial scale value from the reading at each moment to obtain the scour depth at that moment.
- At the end of the test, slowly drain the water from the flume, and take final measurements of the local scour holes around the pile.
- Remove sediment in the flume that washed out of the caisson, replace the pile model, and replenish quartz sand upstream of the scour hole in preparation for the next set of tests.
5. Results and Discussion
5.1. Tidal Flow Experimentation
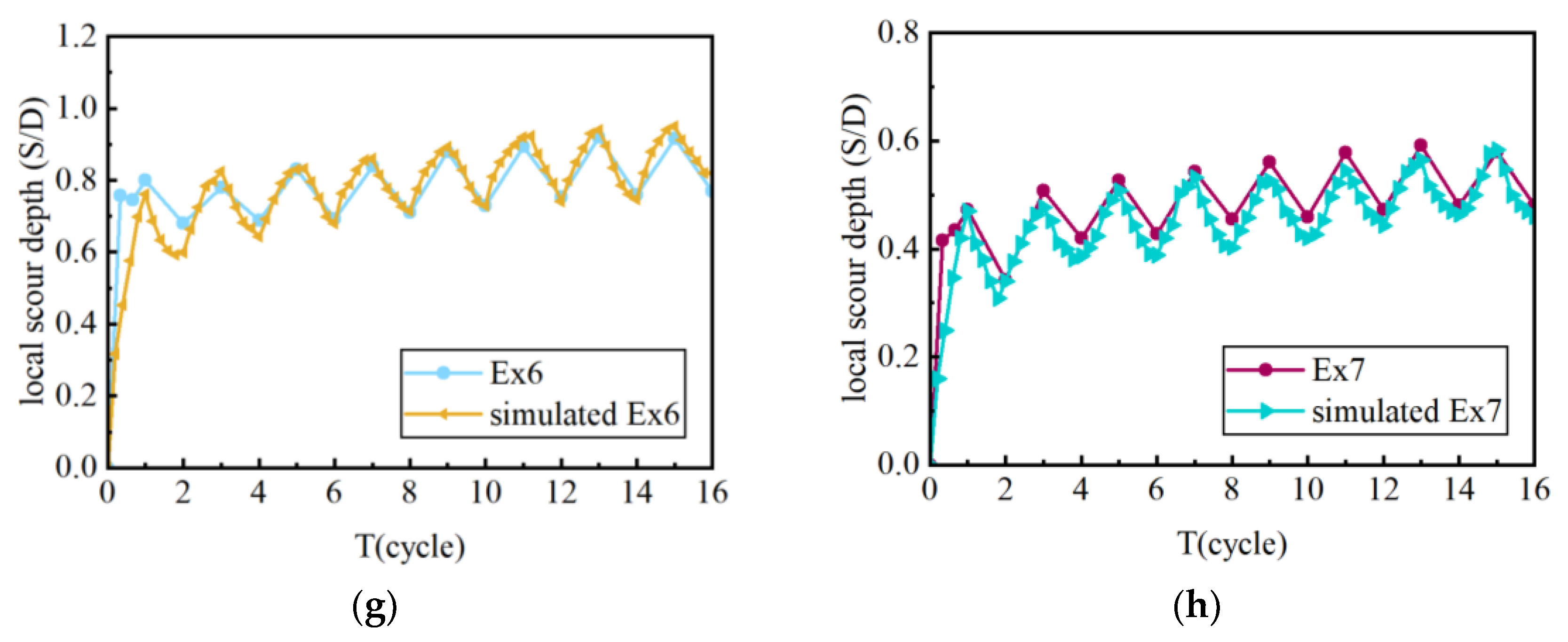
5.2. Verification of Scour Hole Morphology
6. Conclusions
- Cylindrical scour under tidal flow conditions can be regarded as a unidirectional flow scour pattern for a monopile local scour at this stage when the flow direction has not changed, when the scour value upstream of the pile is greater than that at the downstream location. When the flow direction is changed, the scour depth in the former upstream direction of the pile decreases due to sediment backfilling in the former downstream direction, while the scour depth in the former downstream direction of the pile continues to develop until the flow direction is changed again.
- Regarding different abutment diameters, the scour depth and scour hole morphology are symmetrically developed in the direction of water flow about the center of the abutment in the initial stages of scour development; the depth of scour develops more rapidly, whereas in the later stages it progresses more slowly. Under the condition of dynamic bed scour, the scour depth is negatively correlated with the diameter of the abutment; the smaller the diameter of the abutment is, the easier it is to achieve dynamic scour equilibrium. The scour depth can reach about 70% of the maximum scour depth in the first cycle.
- The phenomenon of scour valley/peak ratio increasing with time development was observed both before and in the rear of the pile, which indicated that the development of maximum scour depth under tidal flow conditions was not at the same rate as that of backfilling sediment.
- The computational results show that the solver can well simulate the changing characteristics of the flow field distribution and the evolution of the scour hole morphology at different time periods under tidal flow. However, the differences between the initial results and the later ones in the shape characteristics need to be further analyzed to establish the reasons for this phenomenon. The solver is not currently effective for this part, which can be a subject for further research.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ma, L.L.; Wang, L.Z.; Guo, Z.; Jiang, H.Y.; Gao, Y.Y. Time development of scour around pile groups in tidal currents. Ocean Eng. 2018, 163, 400–418. [Google Scholar] [CrossRef]
- Whitehouse, R. Scour at Marine Structures; Thomas Telford: London, UK, 1998. [Google Scholar]
- Harris, J.M.; Whitehouse, R.J.S.; Benson, T. The time evolution of scour around offshore structures. Maritime Eng. 2015, 163, 3–17. [Google Scholar] [CrossRef]
- Escarameia, M.; May, R.W.P. Scour Around Structures in Tidal Flows; HR Wallingford: Wallingford, UK, 1999. [Google Scholar]
- Jensen, M.; Larsen, B.; Frigaard, P.; De Vos, L.; Christensen, E.; Asp, E.; Solberg, T.; Hjertager, B.; Bove, S. Offshore wind turbines situated in areas with strong currents. 2006.Report NO. 6004RE01ER1. Offshore Centre Denmark, page 79–96.
- McGovern, D.J.; Ilic, S.; Folkard, A.M.; McLelland, S.J.; Murphy, B.J. Time Development of Scour around a Cylinder in Simulated Tidal Currents. J. Hydraul. Eng. 2014, 140, 04014014. [Google Scholar] [CrossRef]
- Schendel, A.; Hildebrandt, A.; Goseberg, N.; Schlurmann, T. Processes and evolution of scour around a monopile induced by tidal currents. Coast. Eng. 2018, 139, 65–84. [Google Scholar] [CrossRef]
- Sumer, B.M.; Fredsøe, J.; Christiansen, N. Scour Around Vertical Pile in Waves. J. Waterw. Port Coast. Ocean. Eng. 1992, 118, 15–31. [Google Scholar] [CrossRef]
- Whitehouse, R.J.S.; Stroescu, E.I. Scour depth development at piles of different height under the action of cyclic (tidal) flow. Coast. Eng. 2023, 179, 104225. [Google Scholar] [CrossRef]
- Williamson, C.H.K. Sinusoidal flow relative to circular cylinders. J. Fluid Mech. 2006, 155, 141–174. [Google Scholar] [CrossRef]
- Obasaju, E.D.; Bearman, P.W.; Graham, J.M.R. A study of forces, circulation and vortex patterns around a circular cylinder in oscillating flow. J. Fluid Mech. 2006, 196, 467–494. [Google Scholar] [CrossRef]
- Khosronejad, A.; Kang, S.; Sotiropoulos, F. Experimental and computational investigation of local scour around bridge piers. Adv. Water Resour. 2012, 37, 73–85. [Google Scholar] [CrossRef]
- Kim, H.S.; Nabi, M.; Kimura, I.; Shimizu, Y. Numerical investigation of local scour at two adjacent cylinders. Adv. Water Resour. 2014, 70, 131–147. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, X.-L.; Wang, J.-H. Numerical investigation of local scour around three adjacent piles with different arrangements under current. Ocean. Eng. 2017, 142, 625–638. [Google Scholar] [CrossRef]
- Chauchat, J.; Cheng, Z.; Nagel, T.; Bonamy, C.; Hsu, T.-J. SedFoam-2.0: A 3-D two-phase flow numerical model for sediment transport. Geosci. Model Dev. 2017, 10, 4367–4392. [Google Scholar] [CrossRef]
- Sun, R.; Xiao, H. SediFoam: A general-purpose, open-source CFD–DEM solver for particle-laden flow with emphasis on sediment transport. Comput. Geosci. 2016, 89, 207–219. [Google Scholar] [CrossRef]
- Yazdanfar, Z.; Lester, D.; Robert, D.; Setunge, S. A novel CFD-DEM upscaling method for prediction of scour under live-bed conditions. Ocean Eng. 2021, 220, 108442. [Google Scholar] [CrossRef]
- Zhang, S.; Li, B.; Ma, H. Numerical investigation of scour around the monopile using CFD-DEM coupling method. Coast. Eng. 2023, 183, 104334. [Google Scholar] [CrossRef]
- Song, Y.; Xu, Y.; Ismail, H.; Liu, X. Scour modeling based on immersed boundary method: A pathway to practical use of three-dimensional scour models. Coast. Eng. 2022, 171, 104037. [Google Scholar] [CrossRef]
- Greenshields, C. OpenFOAM v6 User Guide; The OpenFOAM Foundation: London, UK, 2018. [Google Scholar]
- Jasak, H.; Rigler, D.; Tuković, Ž. Design and implementation of Immersed Boundary Method with discrete forcing approach for boundary conditions. In Proceedings of the 6th European Conference on Computational Fluid Dynamics, Barcelona, Spain, 20–25 July 2014. [Google Scholar]
- Soulsby, R.L. Dynamics of marine sands: A manual for practical applications. Oceanogr. Lit. Rev. 1997, 9, 947. [Google Scholar]
- Burcharth, H.F.; Andersen, O.K. On the one-dimensional steady and unsteady porous flow equations. Coast. Eng. 1995, 24, 233–257. [Google Scholar] [CrossRef]
- Schiller, L.; Naumann, A. A drag coefficient correlation. Z. Des Ver. Dtsch. Ingenieure 1935, 77, 51–86. [Google Scholar]
- Di Felice, R. The voidage function for fluid-particle interaction systems. Int. J. Multiph. Flow 1994, 20, 153–159. [Google Scholar] [CrossRef]
- Egorov, Y.; Menter, F. Development and Application of SST-SAS Turbulence Model in the DESIDER Project; Springer: Berlin/Heidelberg, Germany, 2008; pp. 261–270. [Google Scholar]
- Yoshizawa, A.; Horiuti, K. A Statistically-Derived Subgrid-Scale Kinetic Energy Model for the Large-Eddy Simulation of Turbulent Flows. J. Phys. Soc. Jpn. 1985, 54, 2834–2839. [Google Scholar] [CrossRef]
- Engelund, F.; Fredsøe, J. A Sediment Transport Model for Straight Alluvial Channels. Hydrol. Res. 1976, 7, 293–306. [Google Scholar] [CrossRef]
- Akhtaruzzaman Sarker, M. Flow measurement around scoured bridge piers using Acoustic-Doppler Velocimeter (ADV). Flow Meas. Instrum. 1998, 9, 217–227. [Google Scholar] [CrossRef]
- Kumar, A.; Kothyari, U.C. Three-Dimensional Flow Characteristics within the Scour Hole around Circular Uniform and Compound Piers. J. Hydraul. Eng. 2012, 138, 420–429. [Google Scholar] [CrossRef]
- Dwivedi, A.; Melville, B.; Shamseldin, A.Y. Hydrodynamic Forces Generated on a Spherical Sediment Particle during Entrainment. J. Hydraul. Eng. 2010, 136, 756–769. [Google Scholar] [CrossRef]
- Dwivedi, A.; Melville, B.W.; Shamseldin, A.Y.; Guha, T.K. Flow structures and hydrodynamic force during sediment entrainment. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Ettema, R. Scour at Bridge Piers; Department of Civil Engineering, University of Auckland: Auckland, New Zealand, 1980. [Google Scholar]
- Yao, W.; An, H.; Draper, S.; Cheng, L.; Harris, J.M. Experimental investigation of local scour around submerged piles in steady current. Coast. Eng. 2018, 142, 27–41. [Google Scholar] [CrossRef]
- Sumer, B.M.; Christiansen, N.; Fredsoe, J. Time Scale Of Scour Around A Vertical Pile. In Proceedings of the Second International Offshore and Polar Engineering Conference, San Francisco, CA, USA, 14–19 June 1992. [Google Scholar]
- Kim, S.-C.; Friedrichs, C.T.; Maa, J.P.-Y.; Wright, L.D. Estimating Bottom Stress in Tidal Boundary Layer from Acoustic Doppler Velocimeter Data. J. Hydraul. Eng. 2000, 126, 399–406. [Google Scholar] [CrossRef]
- Melville, B.W.; Chiew, Y.-M. Time Scale for Local Scour at Bridge Piers. J. Hydraul. Eng. 1999, 125, 59–65. [Google Scholar] [CrossRef]




| Simulation Parameters | Value |
|---|---|
| Sediment Density | 2650 Kg/m3 |
| Sediment Diameter | 0.17 mm |
| Shape Factor | 1 |
| Fluid Density | 1000 Kg/m3 |
| Fluid Dynamic Viscosity | 8.90 e−4 Pa·s |
| Time Step | 2 × 10 −4 s |
| Experiment | H (m) | V (m·s−1) | (m) | (mm) | T (min) |
|---|---|---|---|---|---|
| 1 | 0.3 | 0.35 | 0.06 | 0.16 | 30 |
| 2 | 0.3 | 0.4 | 0.06 | 0.16 | 30 |
| 3 | 0.3 | 0.4 | 0.08 | 0.16 | 30 |
| 4 | 0.35 | 0.25 | 0.06 | 0.16 | 30 |
| 5 | 0.35 | 0.3 | 0.06 | 0.16 | 30 |
| 6 | 0.35 | 0.35 | 0.06 | 0.16 | 30 |
| 7 | 0.35 | 0.25 | 0.08 | 0.16 | 30 |
| Experimental Case | Measured S/D | Simulated S/D | Error (%) |
|---|---|---|---|
| 1 | 0.836 | 0.834 | −0.01 |
| 2 | 1.089 | 1.041 | −4.41 |
| 3 | 0.902 | 0.851 | −5.65 |
| 4 | 0.621 | 0.583 | −6.12 |
| 5 | 0.890 | 0.857 | −3.71 |
| 6 | 1.052 | 1.010 | −3.99 |
| 7 | 0.521 | 0.487 | −6.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Lu, J.; Liang, Z. Computational Simulation of Monopile Scour under Tidal Flow Considering Suspended Energy Dissipation. Water 2024, 16, 1940. https://doi.org/10.3390/w16141940
Liu J, Lu J, Liang Z. Computational Simulation of Monopile Scour under Tidal Flow Considering Suspended Energy Dissipation. Water. 2024; 16(14):1940. https://doi.org/10.3390/w16141940
Chicago/Turabian StyleLiu, Jiawei, Junliang Lu, and Zejun Liang. 2024. "Computational Simulation of Monopile Scour under Tidal Flow Considering Suspended Energy Dissipation" Water 16, no. 14: 1940. https://doi.org/10.3390/w16141940
APA StyleLiu, J., Lu, J., & Liang, Z. (2024). Computational Simulation of Monopile Scour under Tidal Flow Considering Suspended Energy Dissipation. Water, 16(14), 1940. https://doi.org/10.3390/w16141940






