Multivariate Geostatistics for Mapping of Transmissivity and Uncertainty in Karst Aquifers
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Hydrogeological Conditions
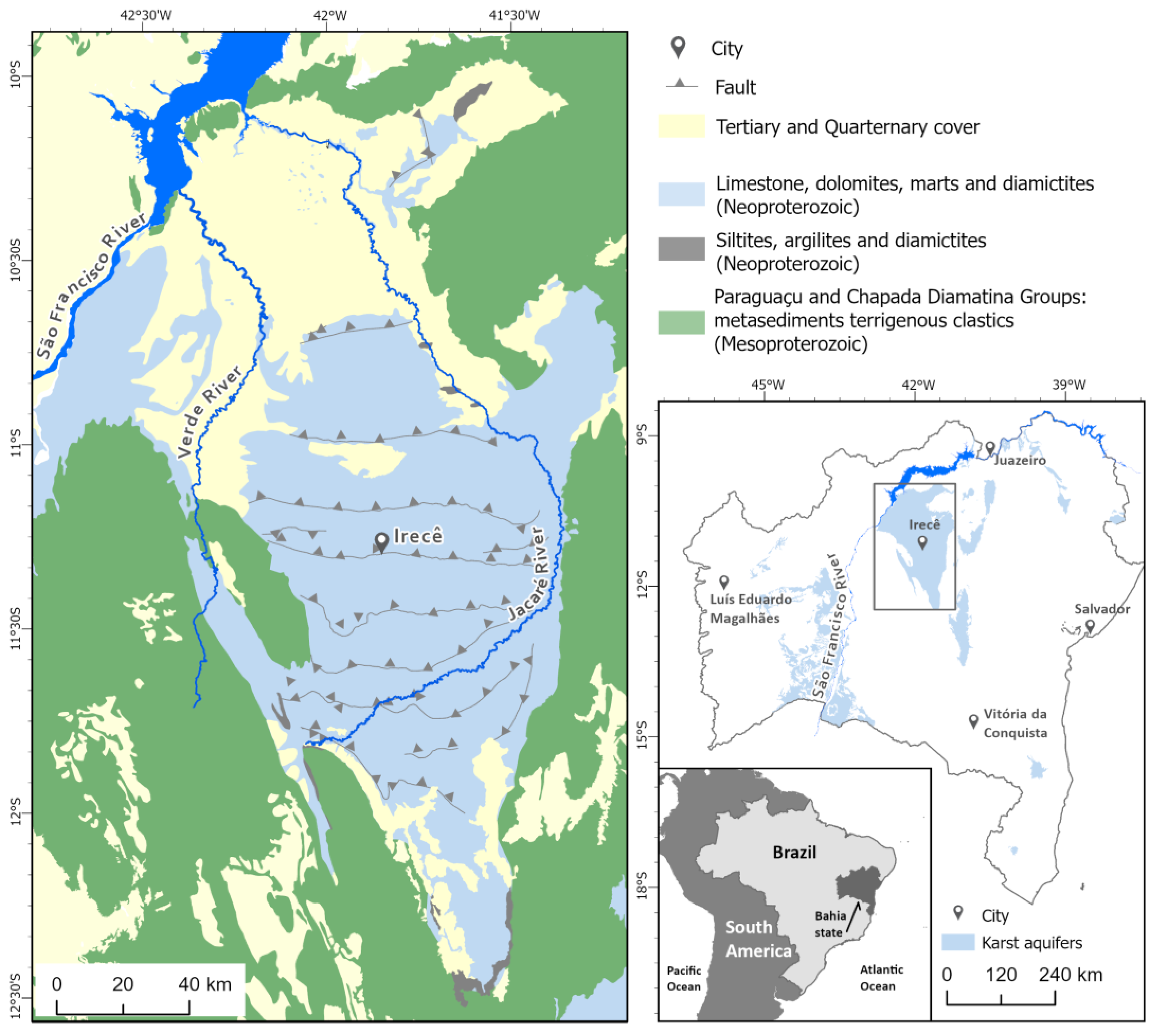
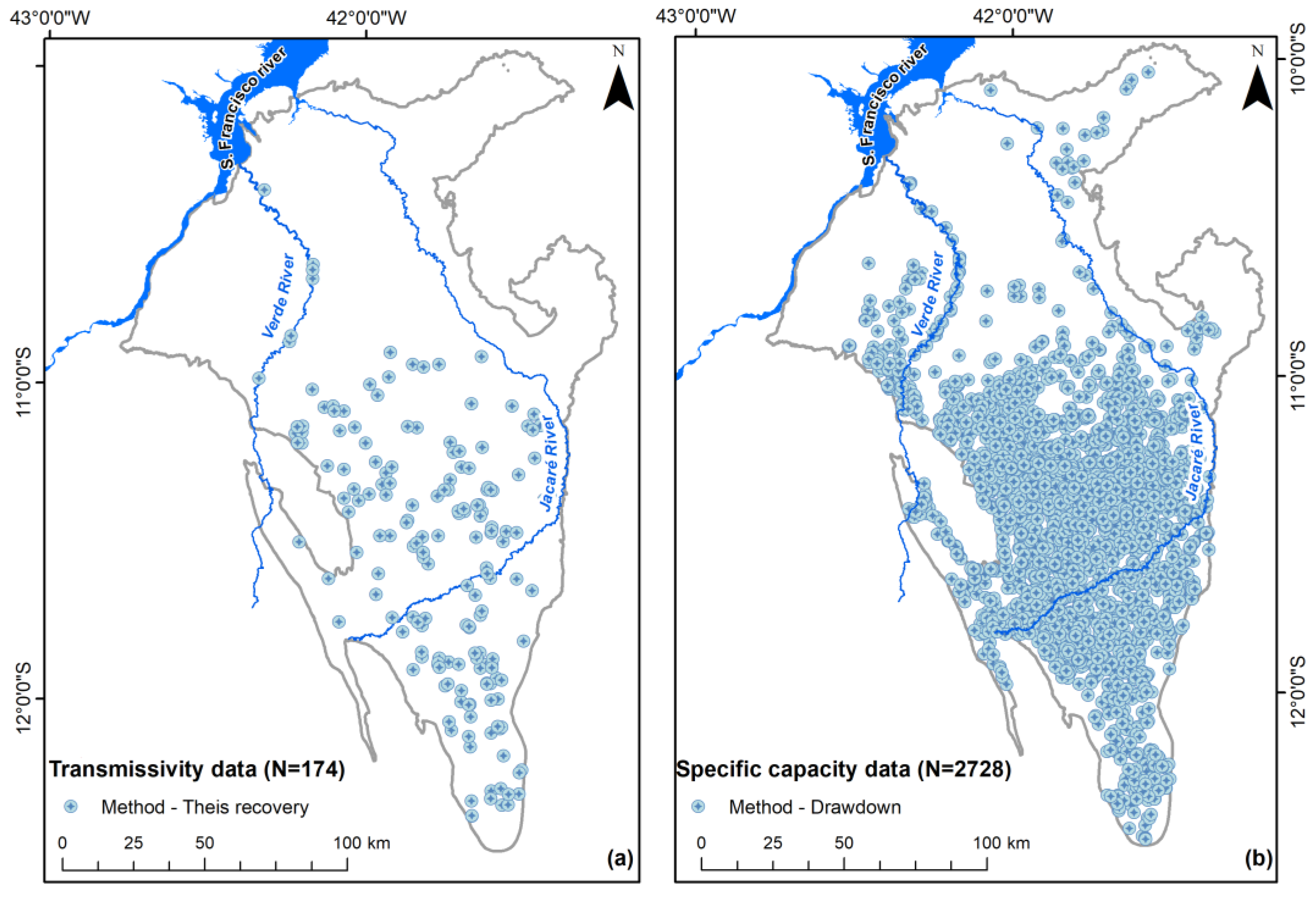
2.2. Data and Well Characteristics
2.3. Linear Correlation
2.4. Cross-Variogram
2.5. Linear Model of Coregionalization
2.6. Ordinary Co-Kriging
2.7. Conditional Gaussian Co-Simulation
3. Results
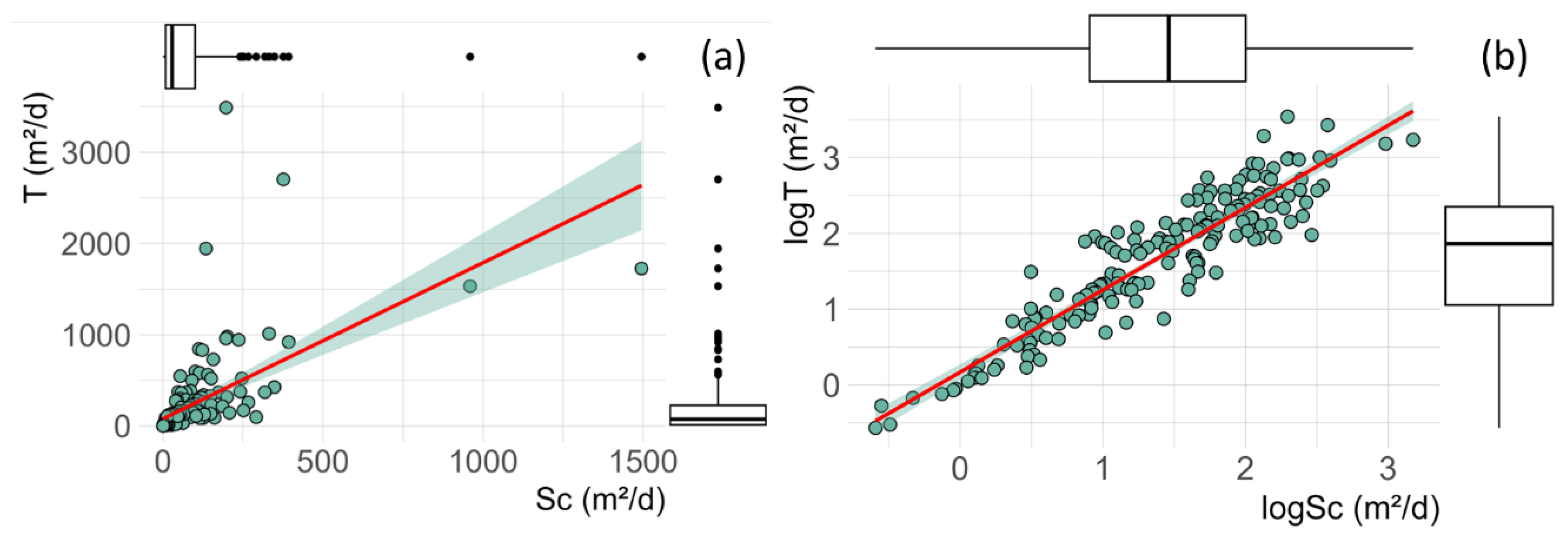
3.1. Linear Correlation between logSc and logT
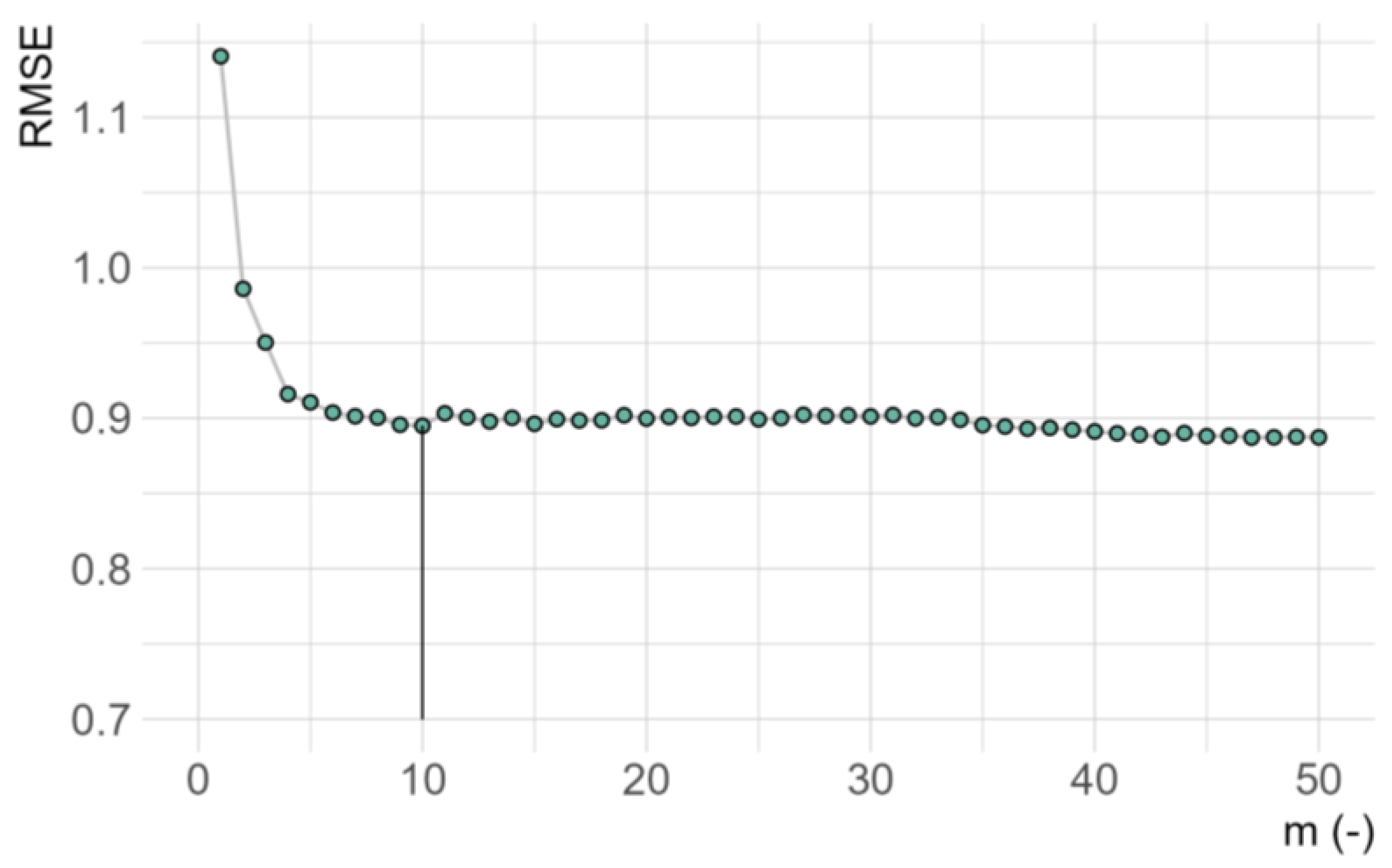
3.2. Spatial Structure and Linear Model of Coregionalization
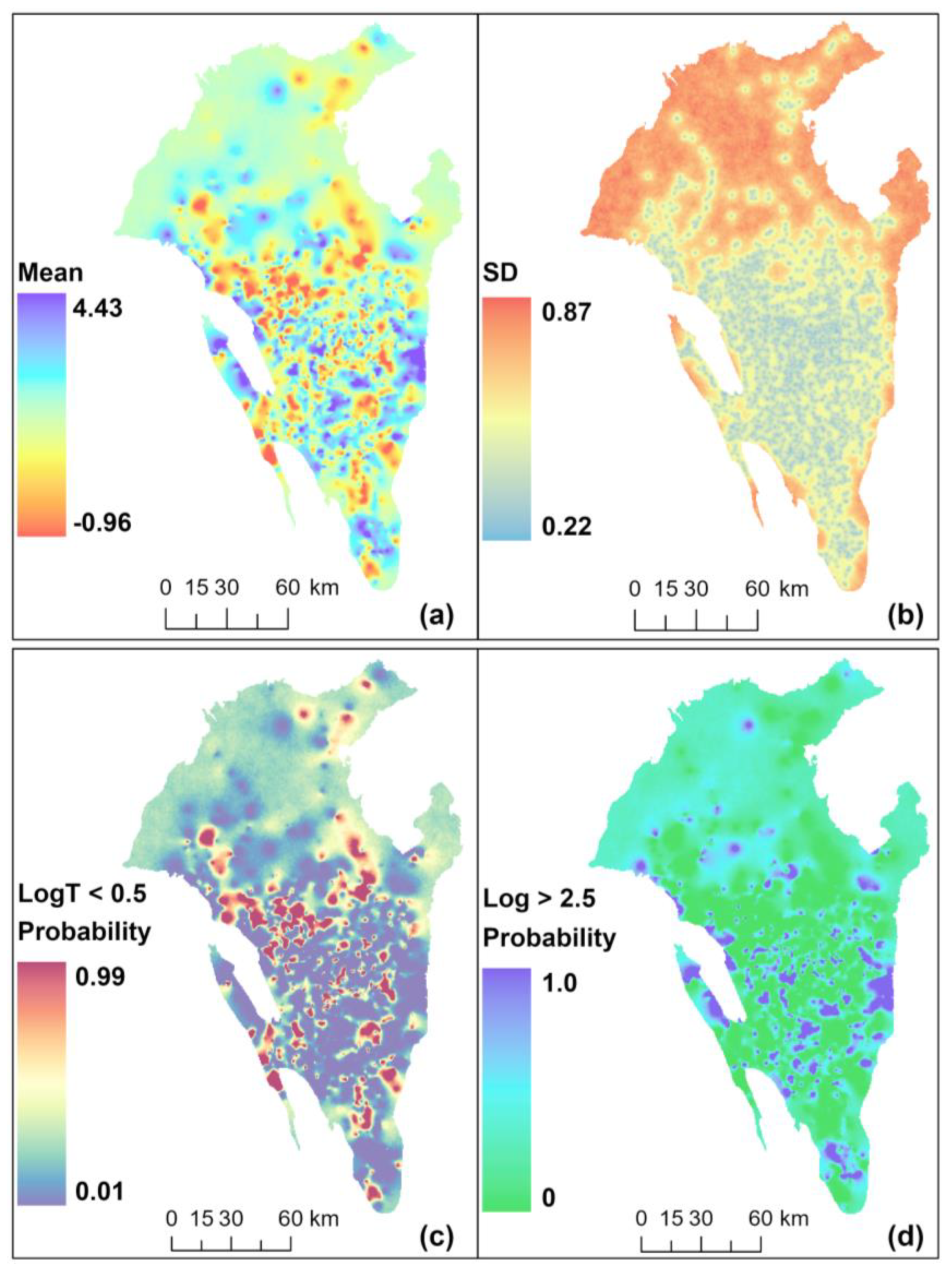
3.3. Interpolation and Uncertainty
3.4. Co-Simulation and Probability Maps
4. Discussion
4.1. Regression and Co-Kriging
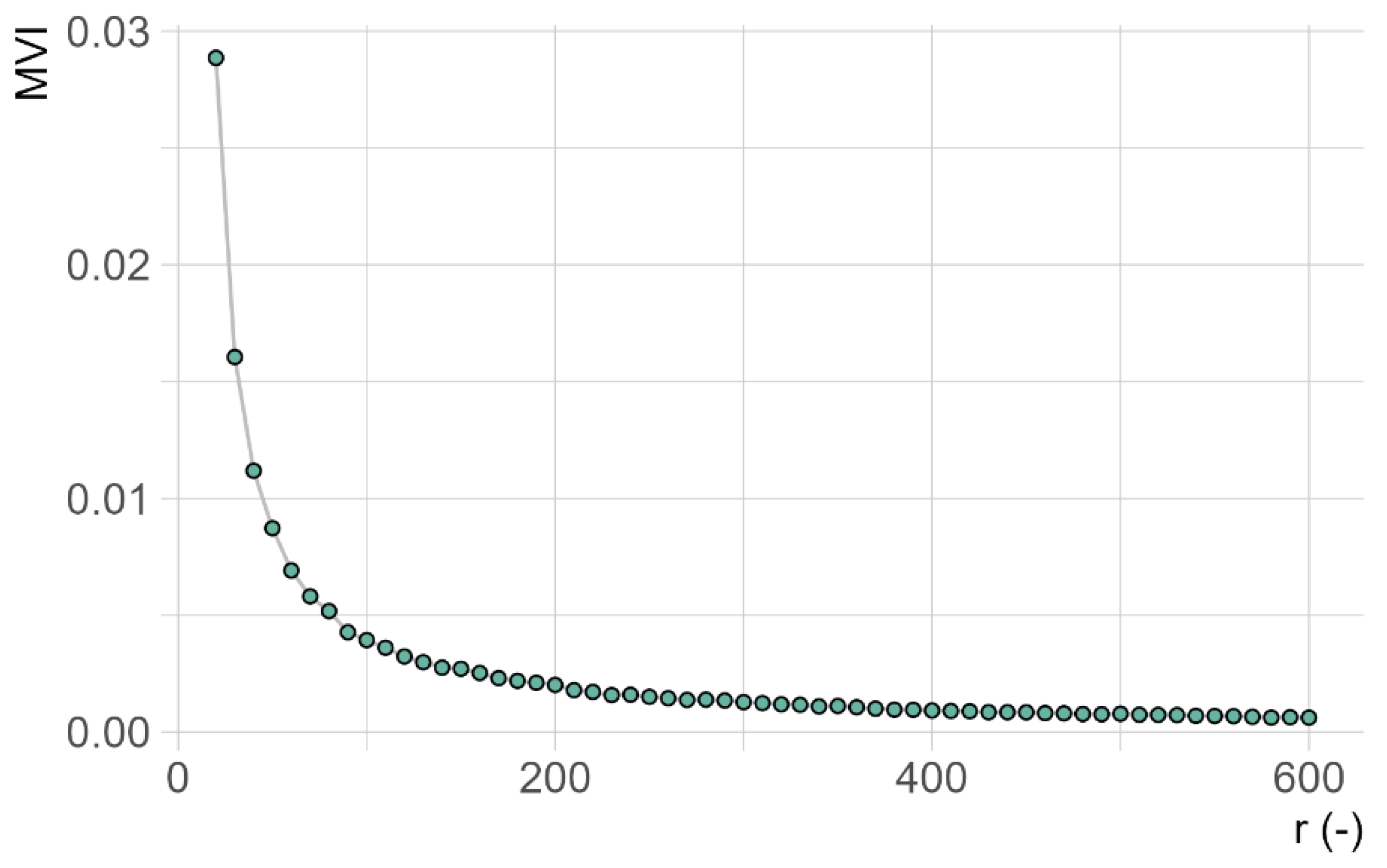
4.2. Cross-Variogram and Multivariate Interpolation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stevanović, Z. Karst Waters in Potable Water Supply: A Global Scale Overview. Environ. Earth Sci. 2019, 78, 662. [Google Scholar] [CrossRef]
- Ford, D.; Williams, P. Karst Hydrogeology and Geomorphology, 1st ed.; Wiley: Hoboken, NJ, USA, 2007; ISBN 9780470849965. [Google Scholar]
- Theis, C.V. The Relation between the Lowering of the Piezometric Surface and the Rate and Duration of Discharge of a Well Using Ground-water Storage. Eos Trans. AGU 1935, 16, 519–524. [Google Scholar] [CrossRef]
- Bouwer, H.; Rice, R.C. A Slug Test for Determining Hydraulic Conductivity of Unconfined Aquifers with Completely or Partially Penetrating Wells. Water Resour. Res. 1976, 12, 423–428. [Google Scholar] [CrossRef]
- Barker, J.A. A Generalized Radial Flow Model for Hydraulic Tests in Fractured Rock. Water Resour. Res. 1988, 24, 1796–1804. [Google Scholar] [CrossRef]
- Mace, R.E. Determination of Transmissivity from Specific Capacity Tests in a Karst Aquifer. Groundwater 1997, 35, 738–742. [Google Scholar] [CrossRef]
- Razack, M.; Lasm, T. Geostatistical Estimation of the Transmissivity in a Highly Fractured Metamorphic and Crystalline Aquifer (Man-Danane Region, Western Ivory Coast). J. Hydrol. 2006, 325, 164–178. [Google Scholar] [CrossRef]
- Srivastav, S.K.; Lubczynski, M.W.; Biyani, A.K. Upscaling of Transmissivity, Derived from Specific Capacity: A Hydrogeomorphological Approach Applied to the Doon Valley Aquifer System in India. Hydrogeol. J. 2007, 15, 1251–1264. [Google Scholar] [CrossRef]
- Galvão, P.; Halihan, T.; Hirata, R. Transmissivity of Aquifer by Capture Zone Method: An Application in the Sete Lagoas Karst Aquifer, MG, Brazil. An. Acad. Bras. Ciênc. 2017, 89, 91–102. [Google Scholar] [CrossRef]
- Gonçalves, T.S. Quantitative Models for Estimating Transmissivity in the Salitre Aquifer in the Region of Irecê–Ba, Brazil. Master’s Thesis, Institute of Geosciences, Federal University of Bahia, Salvador, Brazil, 2017. (In Portuguese with English Abstract). [Google Scholar]
- Gonçalves, T.S.; Leal, L.R.B. Potencialidades Hídricas No Aquífero Carstico Salitre Na Região de Irecê, Bahia. R. Águas Subter. 2018, 32, 191–199, (In Portuguese with English Abstract). [Google Scholar] [CrossRef]
- Gonçalves, T.S.; Klammler, H.; Bastos Leal, L.R. Geospatial Analysis of Transmissivity and Uncertainty in a Semi-Arid Karst Region. Water 2024, 16, 780. [Google Scholar] [CrossRef]
- Kitanidis, P.K. Introduction to Geostatistics: Applications to Hydrogeology; Cambridge University Press: Cambridge, UK; New York, NY, USA, 1997; ISBN 9780521583121. [Google Scholar]
- Aboufirassi, M.; Mariño, M.A. Cokriging of Aquifer Transmissivities from Field Measurements of Transmissivity and Specific Capacity. Math. Geol. 1984, 16, 19–35. [Google Scholar] [CrossRef]
- Ahmed, S.; De Marsily, G. Comparison of Geostatistical Methods for Estimating Transmissivity Using Data on Transmissivity and Specific Capacity. Water Resour. Res. 1987, 23, 1717–1737. [Google Scholar] [CrossRef]
- Wackernagel, H. Multivariate Geostatistics; Springer: Berlin/Heidelberg, Germany, 2003; ISBN 9783642079115. [Google Scholar]
- Gloaguen, E.; Chouteau, M.; Marcotte, D.; Chapuis, R. Estimation of hydraulic conductivity of an unconfined aquifer using cokriging of GPR and hydrostratigraphic data. J. Appl. Geophys. 2001, 47, 135–152. [Google Scholar] [CrossRef]
- Zangeneh, D.K.; Amanipoor, H.; Battaleb-Looie, S. Evaluation of heavy metal contamination using cokriging geostatistical methods (case study os Abteymour oilfield in southern Iran). Appl. Water Sci. 2023, 13, 200. [Google Scholar] [CrossRef]
- Journel, A.G.; Rossi, M.E. When Do We a Trend Model in kriging? Math. Geol. 1989, 21, 715–739. [Google Scholar] [CrossRef]
- Larocque, G.; Dutilleul, P.; Pelletier, B.; Fyles, J.W. Conditional Gaussian Co-Simulation of Regionalized Components of Soil Variation. Geoderma 2006, 134, 1–16. [Google Scholar] [CrossRef]
- Schiavo, M. Numerical impact of variable volumes of Monte Carlo simulations of heterogeneous conductivity fields in groundwater flow models. J. Hydrol. 2024, 634, 131072. [Google Scholar] [CrossRef]
- Aliouache, M.; Jourde, H. Influence of structural properties and connectivity of initial fracture network on incipient karst genesis. J. Hydrol. 2024, 640, 131684. [Google Scholar] [CrossRef]
- 2022 Demographic Census of Brazil-IBGE. Available online: https://www.ibge.gov.br/censo2022 (accessed on 26 July 2024).
- Salles, L.Q.; Bastos Leal, L.R.; Pereira, R.G.F.D.A.; Laureano, F.V.; Gonçalves, T.S. Influence of the Hydrogeological Aspects of Karst Aquifers on Landscape Evolution: Central Portion of the Diamantina Plateau, Bahia, Brazil. Rev. Bras. Geomorfol. 2018, 19, 93–106, (In Portuguese with English Abstract). [Google Scholar] [CrossRef]
- Silva, H.M. Geographic Information System of the Karst Aquifer of the Microregion of Irecê, Bahia: Subsidy for the Inte-Grated Management of the Water Resources of the Verde and Jacaré River Basins. Master’s Thesis, Federal University of Bahia, Salvador, Brazil, 2005. [Google Scholar]
- Guerra, A.M. Karstification Processes and Hydrogeology of Bambuí Group at Irecê Region, Bahia. Doctoral Thesis, University of São Paulo, São Paulo, Brazil, 1986. (In Portuguese with English Abstract). [Google Scholar]
- Bastos Leal, L.R.; Dutton, A.R.; Luz, J.G.; Barbosa, J.S.F. Hydrogeology and hydrochemistry of a Precambrian karst aquifer in a semi-arid region from Bahia, Brazil. In Proceedings of the Geological Society of America, Annual Meeting 2006, Philadelphia, PA, USA, 22–25 October 2006; p. 286. [Google Scholar]
- Misi, A.; Kaufman, A.J.; Azmy, K.; Dardenne, M.A.; Sial, A.N.; De Oliveira, T.F. Chapter 48 Neoproterozoic Successions of the São Francisco Craton, Brazil: The Bambuí, Una, Vazante and Vaza Barris/Miaba Groups and Their Glaciogenic Deposits. Memoirs 2011, 36, 509–522. [Google Scholar] [CrossRef]
- Feitosa, F.A.C.; Diniz, J.A.O.; Kirchheim, R.E.; Kiang, C.H.; Feitosa, E.C. Assessment of Groundwater Resources in Brazil: Current Status of Knowledge. In Groundwater Assessment, Modeling, and Management; CRC Press: Boca Raton, FL, USA, 2016; Available online: https://www.routledgehandbooks.com/doi/10.1201/9781315369044-5 (accessed on 5 August 2023).
- Laipelt, L.; Comini de Andrade, B.; Collischonn, W.; de Amorim Teixeira, A.; Paiva, R.C.D.d.; Ruhoff, A. ANADEM: A Digital Terrain Model for South America. Remote Sens. 2024, 16, 232. [Google Scholar] [CrossRef]
- Pedreira, A.J. The Espinhaço Supergroup in the Central-Eastern Chapada Dia mantina, Bahia: Sedimentology, Stratigraphy and Tectonics. Doctoral Thesis, University of São Paulo, São Paulo, Brazil, 2004. (In Portuguese with English Abstract). [Google Scholar]
- Souza, S.L.; Brito, P.C.R.; Silva, R.W.S.; Pedreira, A.J. Stratigraphy, Sedimentology and Mineral Resources of the Salitre Formation in the Irecê Basin, Bahia; Arquivos Abertos; CBPM: Salvador, Brazil, 1993; Volume 2. (In Portuguese) [Google Scholar]
- Misi, A.; Veizer, J. Neoproterozoic Carbonate Sequences of the Una Group, Irecê Basin, Brazil: Chemostratigraphy, Age and Correlations. Precambrian Res. 1998, 89, 87–100. [Google Scholar] [CrossRef]
- Bastos Leal, L.R.; Silva, H.P. Hydrologic Model and Management of the Aquifer-River Sistem on the Verde and Jacaré Rivers–Semi-Arid Region of the Bahia State, Brazil; SRH/UFBA: Salvador, Brazil, 2004. (In Portuguese) [Google Scholar]
- Furtado, C.P.Q.; Borges, S.V.F.; Bezerra, F.H.R.; De Castro, D.L.; Maia, R.P.; Teixeira, W.L.E.; Souza, A.M.; Auler, A.S.; Lima-Filho, F.P. The Fracture-Controlled Carbonate Brejões Karst System Mapped with UAV, LiDAR, and Electroresistivity in the Irecê Basin-Brazil. J. S. Am. Earth Sci. 2022, 119, 103986. [Google Scholar] [CrossRef]
- Kuchenbecker, M.; Reis, H.L.S.; Fragoso, D.G.C. Structural Characterization and Considerations on the Tectonic Evolution of the Salitre Formation in the Central Portion of the Irecê Basin, North of the São Francisco Craton (BA). Geonomos 2011, 19, 42–49. (In Portuguese) [Google Scholar] [CrossRef]
- Furtado, C.P.Q.; Medeiros, W.E.; Borges, S.V.; Lopes, J.A.G.; Bezerra, F.H.R.; Lima-Filho, F.P.; Maia, R.P.; Bertotti, G.; Auler, A.S.; Teixeira, W.L.E. The influence of subseismic-scale fracture interconnectivity on fluid flow in fracture corridors of the Brejões carbonate karst system, Brazil. Mar. Pet. Geol. 2022, 141, 105689. [Google Scholar] [CrossRef]
- Auler, A.S.; Smart, P.L. The Influence of Bedrock-derived Acidity in the Development of Surface and Underground Karst: Evidence from the Precambrian Carbonates of Semi-arid Northeastern Brazil. Earth Surf. Process. Landf. 2003, 28, 157–168. [Google Scholar] [CrossRef]
- Ennes-Silva, R.A.; Bezerra, F.H.R.; Nogueira, F.C.C.; Balsamo, F.; Klimchouk, A.; Cazarin, C.L.; Auler, A.S. Superposed Folding and Associated Fracturing Influence Hypogene Karst Development in Neoproterozoic Carbonates, São Francisco Craton, Brazil. Tectonophysics 2016, 666, 244–259. [Google Scholar] [CrossRef]
- Meteorological Database of INMET. Available online: https://bdmep.inmet.gov.br/# (accessed on 17 July 2024).
- Chagas, V.B.P.; Chaffer, P.L.B.; Addor, N.; Fan, F.M.; Fleischmann, A.S.; Paiva, R.C.D.; Siqueira, V.A. CAMELS-BR: Hydrometeorological time series and landscap attributes for 897 catchments in Brasil. Earth Syst. Data. 2020, 12, 2075–2096. [Google Scholar] [CrossRef]
- de Paiva, A.Q. Carbonate-Phosphate Soils of the Irecê Plateau, BA: Genesis, Mineralogy and Geochemistry. Doctoral Thesis, Federal University of Viçosa, Viçosa, Brazil, 2010. (In Portuguese with English Abstract). [Google Scholar]
- Salles, L.Q.; Galvão, P.; Bastos Leal, L.R.; De Araujo Pereira, R.G.F.; Purificação, C.G.C.; Laureano, F.V. Evaluation of Susceptibility for Terrain Collapse and Subsidence in Karst Areas, Municipality of Iraquara, Chapada Diamantina (BA), Brazil. Environ. Earth Sci. 2018, 77, 593. [Google Scholar] [CrossRef]
- Maia, P.H.P.; Neto, B.D.; Corrêa-Gomes, L.C. Geological and Structural Analysis of Fissures and Subsidence in Lapão Karst. Águas Subterrâneas 2010, 7, 112–121. (In Portuguese) [Google Scholar]
- Ramos, S.O.; Araújo, H.A.D.; Leal, L.R.B.; Luz, J.A.G.D.; Dutton, A.R. Temporal Variation of the Water Table in the Karst Aquifer of Irecê-Bahia: Contribution to the Use and Management of Groundwater in the Semi-Arid Region. RBG 2007, 37, 227–233. (In Portuguese) [Google Scholar] [CrossRef]
- Geological Database of Geological Survey of Brazil (GSB). Available online: https://geoportal.sgb.gov.br/geosgb/# (accessed on 21 May 2024).
- Shapiro, S.S.; Wilk, M.B. An Analysis of Variance Test for Normality (Complete Samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Volfová, A.; Šmejkal, M. Geostatistical Methods in R. Geoinformatics FCE CTU 2012, 8, 29–54. [Google Scholar] [CrossRef] [PubMed]
- Pardo-Igúzquiza, E.; Dowd, P.A.; Luque-Espinar, J.A.; Chica-Olmo, M. Increasing Knowledge of the Transmissivity Field of a Detrital Aquifer by Geostatistical Merging of Different Sources of Information. Hydrogeol. J. 2023, 31, 1505–1524. [Google Scholar] [CrossRef]
- de Lima, R.F.G. Hydrogeology and Vuknerability of Salitre Karst Aquifer at Una-Utinga, Bahia. Doctoral Thesis, Federal University of Bahia, Salvador, Brazil, 2019. (In Portuguese). [Google Scholar]
- Al-Murad, M.; Zubari, W.K.; Uddin, S. Geostatistical Characterization of the Transmissivity: An Example of Kuwait Aquifers. Water 2018, 10, 828. [Google Scholar] [CrossRef]
- Castro, D.L.; Bezerra, F.H.R.; Oliveira Jr, J.G. Integrated Geophysical Approach for Detection and Size-Geometry Characterization of a Multiscale Karst System in Carbonate Units, Semiarid Brazil. Open Geosci. 2024, 16, 20220606. [Google Scholar] [CrossRef]
- Assunção, P.; Galvão, P.; Lucon, T.; Doi, B.; Marshall Fleming, P.; Marques, T.; Costa, F. Hydrodynamic and Hydrodispersive Behavior of a Highly Karstified Neoproterozoic Hydrosystem Indicated by Tracer Tests and Modeling Approach. J. Hydrol. 2023, 619, 129300. [Google Scholar] [CrossRef]
- Magnabosco, R.; Galvão, P.; De Carvalho, A.M. An Approach to Map Karst Groundwater Potentiality in an Urban Area, Sete Lagoas, Brazil. Hydrol. Sci. J. 2020, 65, 2482–2498. [Google Scholar] [CrossRef]
- Hughson, L.; Huntley, D.; Razack, M. Cokriging Limited Transmissivity Data Using Widely Sampled Specific Capacity from Pump Tests in an Alluvial Aquifer. Groundwater 1996, 34, 12–18. [Google Scholar] [CrossRef]


| Parameters | Min 1 | Max 2 | Mean | Median | SD 3 | CV 4 |
|---|---|---|---|---|---|---|
| Pumping rate (m3/d) | 2 | 8544 | 383 | 288 | 452 | 1 |
| Water table depth (m) | 0 | 147 | 26 | 20 | 21 | 1 |
| Water entrance depths (m) | 4.5 | 196 | 62 | 54 | 37 | 0.6 |
| Well depth (m) | 0 | 294 | 105 | 100 | 40 | 0.4 |
| Attributes | Min 1 | Max 2 | Mean | Median | SD 3 | CV 4 |
|---|---|---|---|---|---|---|
| Sc | 0.25 | 1495 | 77.7 | 29 | 152.7 | 1.94 |
| logSc | −0.59 | 3.17 | 1.89 | 1.46 | 2.18 | 0.29 |
| T | 0.27 | 3.49 | 211.48 | 73.45 | 433.96 | 2.05 |
| logT | −0.56 | 3.54 | 2.3 | 1.87 | 0.89 | 0.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonçalves, T.d.S.; Klammler, H.; Leal, L.R.B.; de Queiroz Salles, L. Multivariate Geostatistics for Mapping of Transmissivity and Uncertainty in Karst Aquifers. Water 2024, 16, 2430. https://doi.org/10.3390/w16172430
Gonçalves TdS, Klammler H, Leal LRB, de Queiroz Salles L. Multivariate Geostatistics for Mapping of Transmissivity and Uncertainty in Karst Aquifers. Water. 2024; 16(17):2430. https://doi.org/10.3390/w16172430
Chicago/Turabian StyleGonçalves, Thiago dos Santos, Harald Klammler, Luíz Rogério Bastos Leal, and Lucas de Queiroz Salles. 2024. "Multivariate Geostatistics for Mapping of Transmissivity and Uncertainty in Karst Aquifers" Water 16, no. 17: 2430. https://doi.org/10.3390/w16172430
APA StyleGonçalves, T. d. S., Klammler, H., Leal, L. R. B., & de Queiroz Salles, L. (2024). Multivariate Geostatistics for Mapping of Transmissivity and Uncertainty in Karst Aquifers. Water, 16(17), 2430. https://doi.org/10.3390/w16172430






