Evaluation of Water System Connectivity Based on Node Centrality in the Tarim River Basin, Xinjiang, China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Sources and Methods
2.2.1. Data Sources
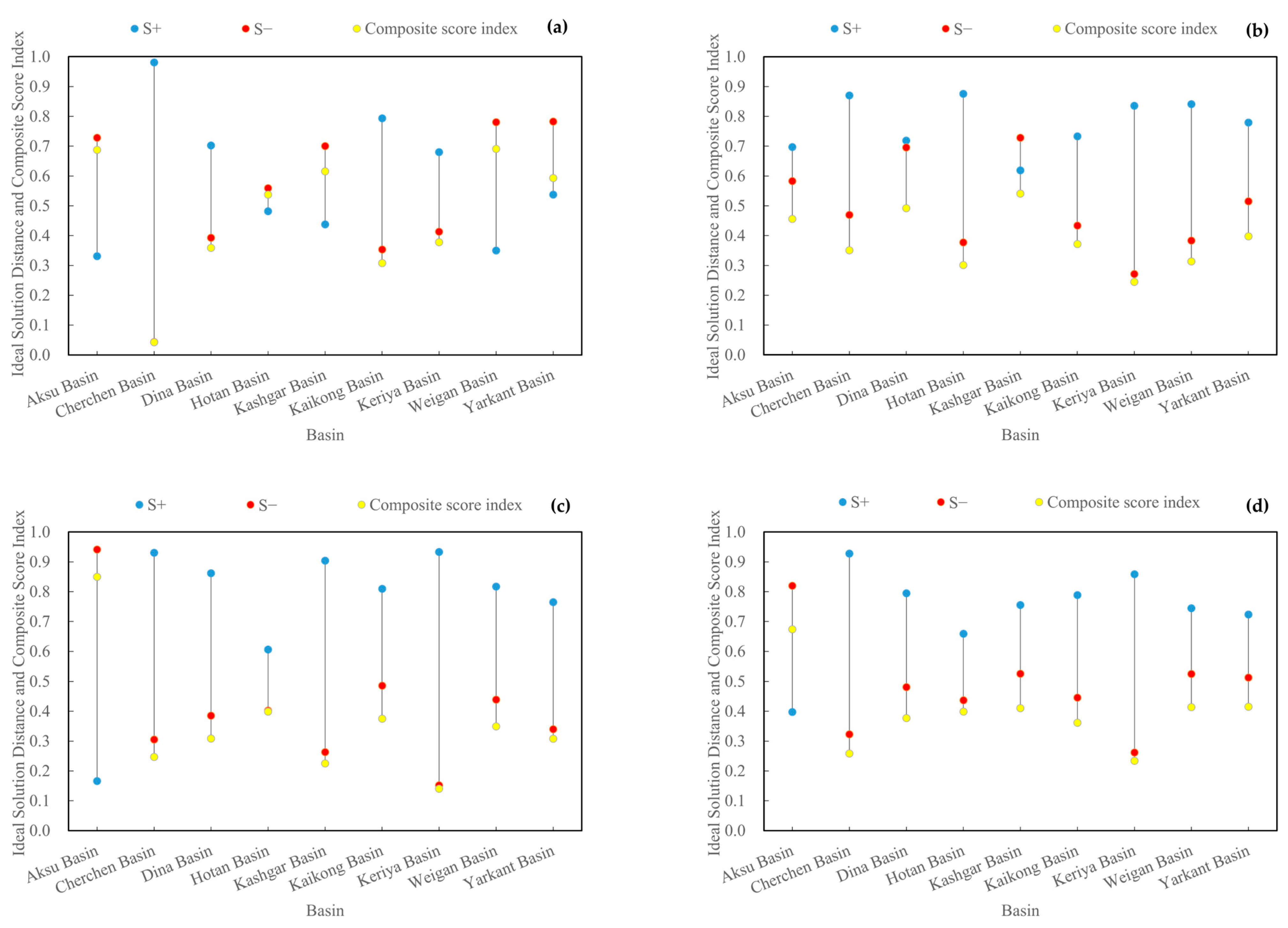
2.2.2. TOPSIS Comprehensive Evaluation Method
- (1)
- In order to eliminate the effect of the scale between the different evaluation indicators, a matrix with a sample size of m and n indicators was standardized as follows:
- (2)
- The positive ideal solutionand negative ideal solutionfor different water system connectivity evaluation metrics were calculated as follows:
- (3)
- The Euclidean distancesandwere calculated between each headwater basin and the positive ideal solution and the negative ideal solution as follows:where is the combined weight of indicator j using the analytic hierarchy process and the entropy weight method [20]. The analytic hierarchy process is a subjective empowerment method that breaks the problem down into three layers—namely, the target layer, normative layer and indicator layer—and systematically analyzes the relative importance of each evaluation indicator. The entropy weight method is an objective weighting method that utilizes the principle of information entropy to determine the weight of each evaluation index. The combination of the two methods can make the final result more scientific and reasonable.
- (4)
- Calculation of proximity :
2.2.3. Complex Network Analysis (CNA)
- (1)
- Betweenness centrality:
- (2)
- Eigenvector centrality:
2.2.4. Evaluation Indicator System
3. Results
3.1. Evaluation of Water System Connectivity
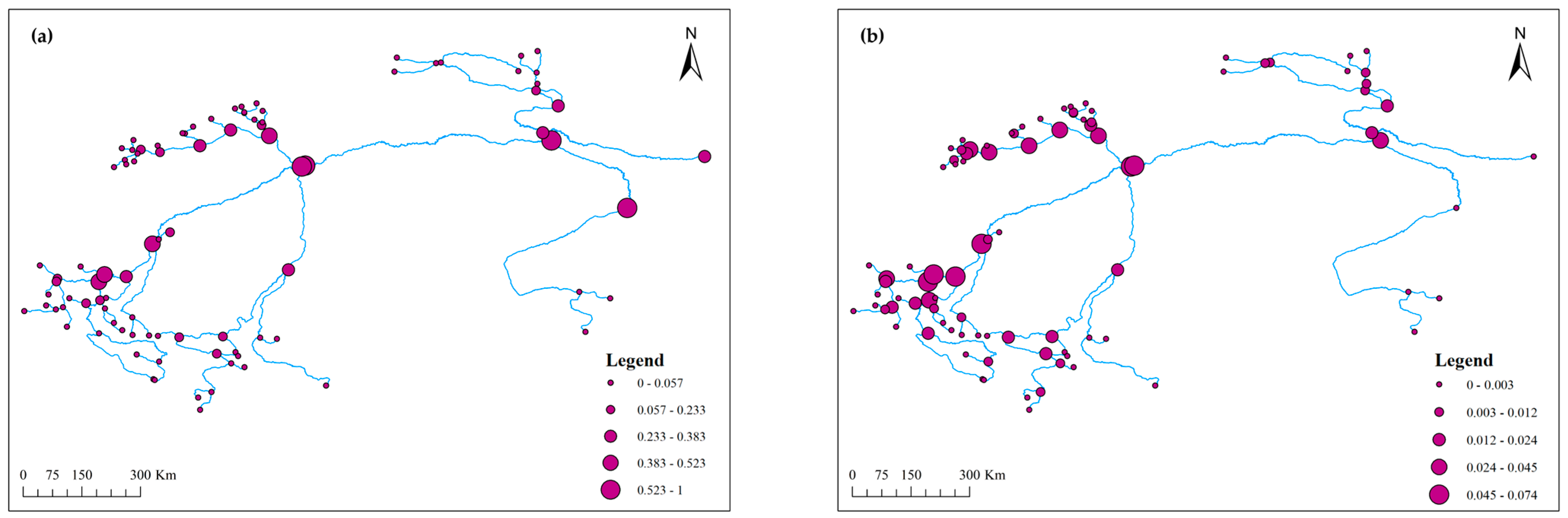
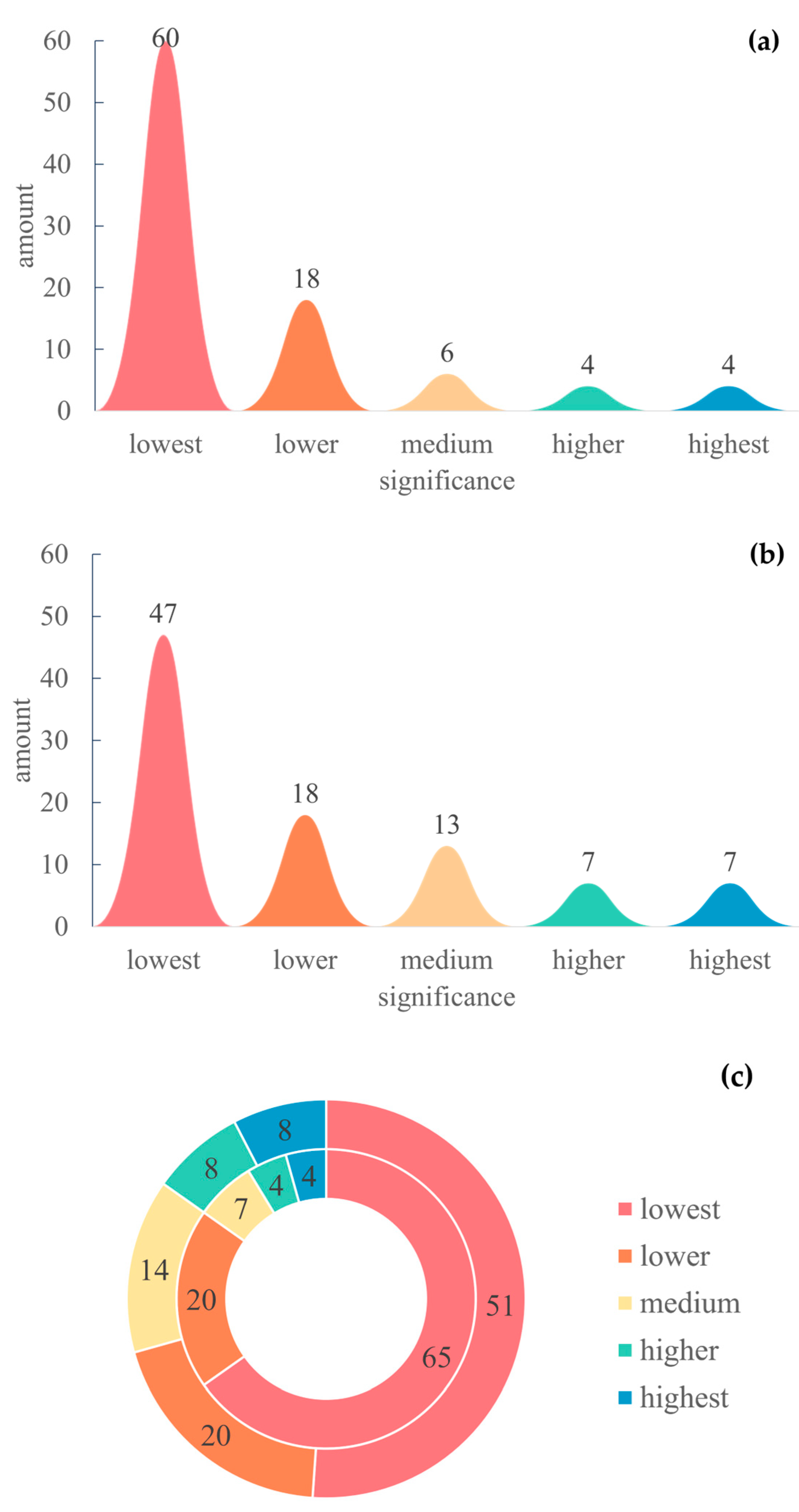
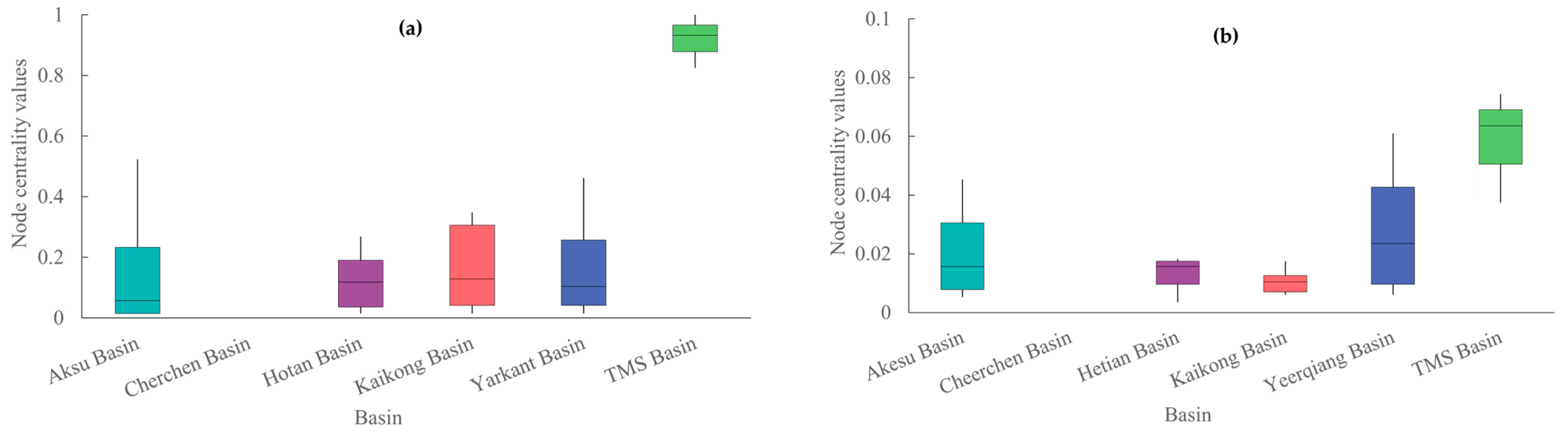
3.2. Centrality Analysis of Nodes in the Water System Network
4. Discussion
5. Conclusions and Recommendations
- (1)
- The article only compared the connectivity of different headwater basins in the Tarim River Basin and lacked a time-scale comparison.
- (2)
- The analytic hierarchy process required the decision-maker to have an in-depth understanding of the problem in order to accurately construct the judgment matrix.
- (3)
- Betweenness centrality heavily relied on the shortest path of the river. However, in actual watersheds, the flow may be affected by a variety of factors such as the topography, vegetation and soil type.
- (4)
- Eigenvector centrality emphasized the connection relationship between nodes and important nodes, but may have ignored the contribution of the node’s own characteristics (e.g., water quantity and water quality) to the connectivity of the watershed.
- (1)
- The connectivity and importance of the nodes could be comprehensively assessed and other network analysis metrics and methods such as closeness centrality and clustering coefficients could be explored.
- (2)
- The watershed system has complexity and uncertainty; an uncertainty analysis could be introduced in the future to assess the impact of different parameters and assumptions on the results.
- (3)
- A demonstration project could be conducted to verify the validity and feasibility of the research results.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xia, J.; Gao, Y.; Zuo, Q.; Liu, X.; Chen, Q.; Dou, M. Characteristics of Interconnected Rivers System and Its Ecological Effects on Water Environment. Prog. Geogr. 2012, 31, 26–31. [Google Scholar]
- Xu, Z.; Pang, B.; Leng, L. Research on the construction of river-lake system connectivity and national water network. South North Water Transf. Water Sci. Technol. 2022, 20, 757–764. [Google Scholar] [CrossRef]
- Jin, F.; Ye, Z.; Chen, Z.; Ma, L. National Water Network Construction for Serving the Chinese Path to Modernization: Development Direction and Strategic Approach. Econ. Geogr. 2024, 44, 148–156. [Google Scholar] [CrossRef]
- Lu, M.; Xu, Y.; Gao, B.; Zhou, C. Variations of hydrological connectivity regulated by sluices in a delta plain. Acta Geogr. Sin. 2021, 76, 2685–2696. [Google Scholar]
- Yin, L.; Zhang, J.; Jiang, J.; Zhang, P.; Gu, X.; Dong, J.; Guo, P.; Yang, B.; Li, Y. Issues and countermeasures on water resources in the Southern Xinjiang. China Geol. 2023, 50, 1–12. [Google Scholar]
- Liu, C.; Chen, Y.; Fang, G.; Zhou, H.; Huang, W.; Liu, Y.; Wang, X.; Li, Z. Hydrological Connectivity Improves the Water-Related Environment in a Typical Arid Inland River Basin in Xinjiang, China. Remote Sens. 2022, 14, 4977. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.; Liu, D. Intermittency of Endorheic Rivers in the Tarim River Basin. J. Basic Sci. Eng. 2023, 31, 257–267. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Y.; Chen, K. Index system of water system connectivity and its application. J. Hydraul. Eng. 2020, 51, 1080–1088+1100. [Google Scholar] [CrossRef]
- Gao, X.; Hu, Z.; Yan, C.; Sun, B. Construction and application of water system connectivity evaluation index system considering hydraulic connectivity. Water Res. Protect. 2022, 38, 41–47. [Google Scholar]
- Bu, J.; Zhang, S.; Li, C.; Xu, X.; Wang, X.; Liu, Q.; Wang, X. A Longitudinal Functional Connectivity Comprehensive Index for Multi-Sluice Flood Control System in Plain Urban River Networks. J. Hydrol. 2022, 613, 128362. [Google Scholar] [CrossRef]
- Zhang, C.; Kuai, S.; Tang, C.; Zhang, S. Evaluation of Hydrological Connectivity in a River Floodplain System and Its Influence on the Vegetation Coverage. Ecol. Indic. 2022, 144, 109445. [Google Scholar] [CrossRef]
- Fang, S.; Chen, M.; Li, J.; Zhang, L.; Zhang, Y.; Yang, C.; Wang, H. Evaluation and Optimization of Urban Hydrological Connectivity Based on Graph Theory: A Case Study in Chengdu, China. Ecol. Inform. 2024, 82, 102749. [Google Scholar] [CrossRef]
- Hajibabaei, M.; Hesarkazzazi, S.; Minaei, A.; Dastgir, A.; Sitzenfrei, R. Using Complex Network Theory for Missing Data Reconstruction in Water Distribution Networks. Sust. Cities Soc. 2024, 101, 105114. [Google Scholar] [CrossRef]
- Spence, C.; Phillips, R.W. Refining Understanding of Hydrological Connectivity in a Boreal Catchment. Hydrol. Process. 2015, 29, 3491–3503. [Google Scholar] [CrossRef]
- Halverson, M.J.; Fleming, S.W. Complex Network Theory, Streamflow, and Hydrometric Monitoring System Design. Hydrol. Earth Syst. Sci. 2015, 19, 3301–3318. [Google Scholar] [CrossRef]
- Chen, Y.; Hao, X.; Chen, Y.; Zhu, C. Study on Water System Connectivity and Ecological Protection Countermeasures of Tarim River Basin in Xinjiang. Bull. Chin. Acad. Sci. 2019, 34, 1156–1164. [Google Scholar] [CrossRef]
- Wang, Y.; Zi, F.; Lu, S.; Li, M.; Zhou, J.; Yang, X.; Wang, W.; Niu, R. Analysis of surface-groundwater changes in the Tarim River Basin of Xinjiang from 1989 to 2019. Sci. Geogr. Sin. 2023, 43, 899–909. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S. Exploration of Eco-Environment and Urbanization Changes Based on Multi-Source Remote Sensing Data-A Case Study of Yangtze River Delta Urban Agglomeration. Sustainability 2024, 16, 5903. [Google Scholar] [CrossRef]
- Zuo, Q.; Zhang, Z.; Wu, B. Evaluation of water resources carrying capacity of nine provinces in Yellow River Basin based on combined weight TOPSIS model. Water Res. Protect. 2020, 36, 1–7. [Google Scholar]
- Liang, X.; Ju, W.; Sun, B.; Hu, Z.; Gao, X.; Zhang, J.; Zhao, J. Water system connectivity evaluation in plain urban river network based on AHP-entropy weight method: A case study of Langfang City. South North Water Transf. Water Sci. Technol. 2022, 20, 352–364. [Google Scholar] [CrossRef]
- Li, F.; Zhao, Y. Evaluation of water network connectivity using complex network method based on node-subbasin double layer structure. J. Water Resour. Water Eng. 2023, 34, 16–26. [Google Scholar]
- Ren, X.; Lü, L. Review of ranking nodes in complex networks. Chin. Sci. Bull. 2014, 59, 1175–1197. [Google Scholar] [CrossRef]
- Dou, M.; Yu, J.; Guan, J.; Yang, L.; Wang, C.; Li, G. Study on relationship between water system development and connectivity in China based on water resource zoning. Adv. Water Sci. 2023, 34, 877–886. [Google Scholar] [CrossRef]
- Wang, Y. The connectivity evaluation of Shanghai urban landscape eco-network. Geogr. Res. 2009, 28, 284–292. [Google Scholar]
- Fu, C.; Deng, J.; Ouyang, H.; Fu, Y.; Zhang, J. Layout and Optimization of Urban Water System Connectivity Based on the Graph Theory. Sci. Geogr. Sin. 2022, 42, 2028–2038. [Google Scholar] [CrossRef]
- Gao, T.; Yin, X.; He, S.; Zhao, Y. Structural Connectivity Evaluation of the Baiyangdian Lake Water System. J. Hydroecol. 2020, 41, 63–69. [Google Scholar] [CrossRef]
- Hu, R.; Chang, J.; Deng, M.; Zhou, H.; Guo, A.; Wang, Y. Multi-dimensional response of hydrological connectivity to ecological water conveyance project. J. Hydraul. Eng. 2023, 54, 1359–1370. [Google Scholar] [CrossRef]
- Dörnhöfer, K.; Oppelt, N. Remote Sensing for Lake Research and Monitoring–Recent Advances. Ecol. Indic. 2016, 64, 105–122. [Google Scholar] [CrossRef]
- Juwana, I.; Muttil, N.; Perera, B.J.C. Indicator-Based Water Sustainability Assessment—A Review. Sci. Total Environ. 2012, 438, 357–371. [Google Scholar] [CrossRef]
- Zhao, Z.-Y.; Zuo, J.; Zillante, G. Transformation of Water Resource Management: A Case Study of the South-to-North Water Diversion Project. J. Clean Prod. 2017, 163, 136–145. [Google Scholar] [CrossRef]
- Jacinto, E.; Fangue, N.A.; Cocherell, D.E.; Kiernan, J.D.; Moyle, P.B.; Rypel, A.L. Increasing Stability of a Native Freshwater Fish Assemblage Following Flow Rehabilitation. Ecol. Appl. 2023, 33, e2868. [Google Scholar] [CrossRef] [PubMed]
- Basuki, T.M.; Nugroho, H.Y.S.H.; Indrajaya, Y.; Pramono, I.B.; Nugroho, N.P.; Supangat, A.B.; Indrawati, D.R.; Savitri, E.; Wahyuningrum, N.; Purwanto; et al. Improvement of Integrated Watershed Management in Indonesia for Mitigation and Adaptation to Climate Change: A Review. Sustainability 2022, 14, 9997. [Google Scholar] [CrossRef]
- Cai, Y.; Liang, J.; Zhang, P.; Wang, Q.; Wu, Y.; Ding, Y.; Wang, H.; Fu, C.; Sun, J. Review on Strategies of Close-to-Natural Wetland Restoration and a Brief Case Plan for a Typical Wetland in Northern China. Chemosphere 2021, 285, 131534. [Google Scholar] [CrossRef] [PubMed]

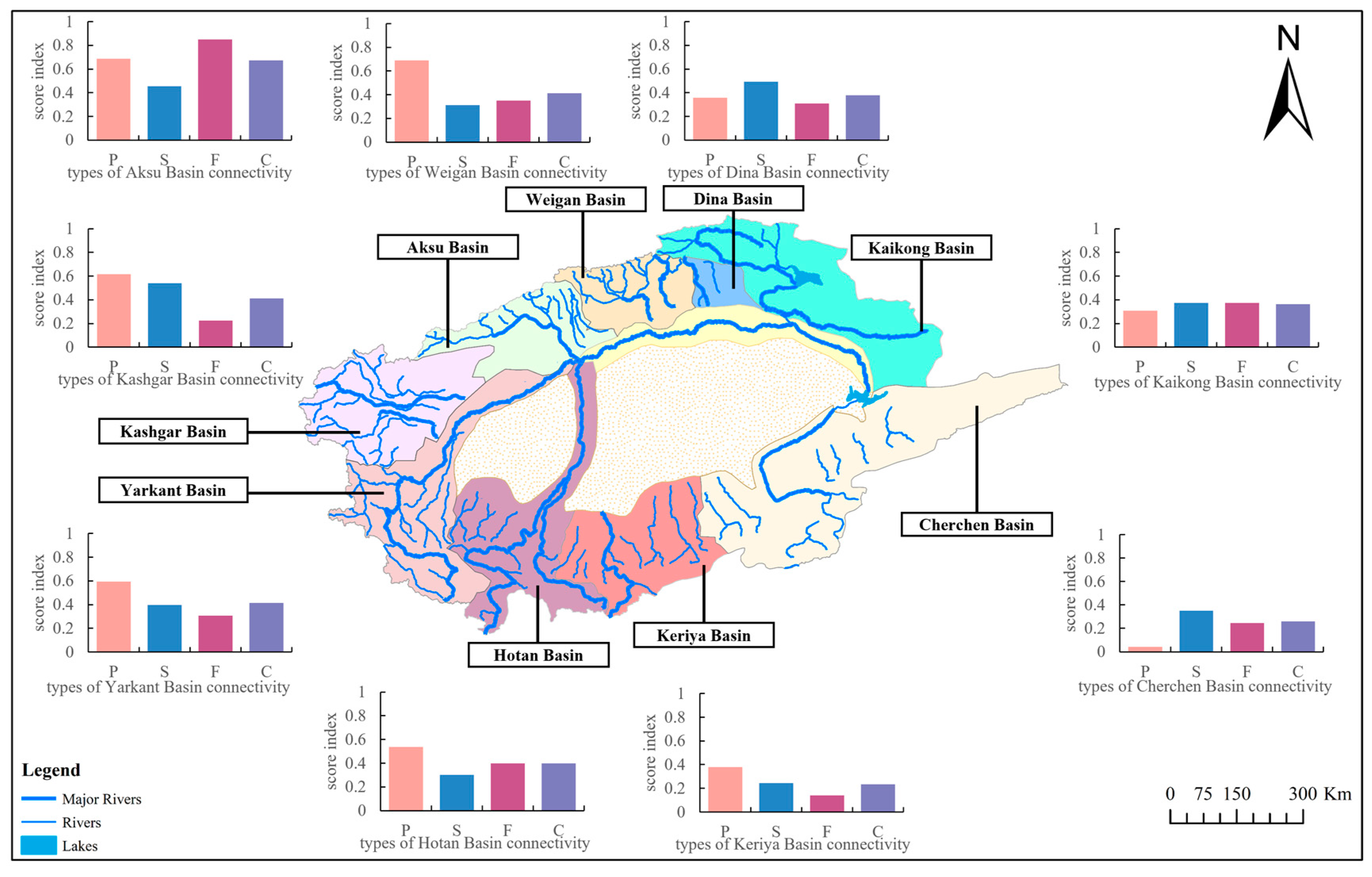
| Target Layer | Normative Layer | Indicator Layer | Calculation Formula |
|---|---|---|---|
| Water system connectivity evaluation program | Pattern connectivity | Drainage density(km/km2) | 1 |
| Growth index | 2 | ||
| River density(km−2) | 3 | ||
| Ecological connectivity | 4 | ||
| Structural connectivity | Circuitry of river network connectivity | 5 | |
| Node connection rate | 6 | ||
| Network connectivity | 7 | ||
| Degree of node connectivity | 8 | ||
| Functional connectivity | Surface runoff index(m3/km2) | 9 | |
| Average annual runoff guarantee rate | 10 | ||
| Fractional vegetation cover | 11 | ||
| Water delivery rate to main stream | 12 |
| Normative Layer | Indicator Layer | AB | CB | DB | HB | KAB | KKB | KEB | WB | YB * |
|---|---|---|---|---|---|---|---|---|---|---|
| Pattern connectivity | 0.036 | 0.015 | 0.027 | 0.032 | 0.037 | 0.022 | 0.027 | 0.032 | 0.041 | |
| 9.340 | 0.474 | 0.325 | 5.242 | 3.766 | 0.286 | 0.616 | 15.159 | 0.923 | ||
| (10−4) | 3.648 | 1.076 | 2.438 | 2.137 | 3.262 | 7.580 | 1.901 | 3.658 | 2.288 | |
| 0.997 | 0.648 | 0.892 | 1.070 | 1.118 | 1.038 | 1 | 0.926 | 1.284 | ||
| Structural connectivity | 0.026 | 0 | 0 | 0 | 0.043 | 0 | 0 | 0 | 0.014 | |
| 2 | 1.500 | 1.500 | 1.889 | 2 | 1.833 | 1.750 | 1.889 | 2 | ||
| 0.367 | 0.500 | 0.500 | 0.354 | 0.389 | 0.367 | 0.389 | 0.354 | 0.352 | ||
| 0.042 | 0.052 | 0.267 | 0.044 | 0.044 | 0.167 | 0.055 | 0.071 | 0.044 | ||
| Functional connectivity | 0.169 | 0.006 | 0.031 | 0.065 | 0.055 | 0.045 | 0.014 | 0.087 | 0.099 | |
| 0.322 | 0.421 | 0.361 | 0.303 | 0.191 | 0.440 | 0.290 | 0.396 | 0.276 | ||
| 0.205 | 0.061 | 0.216 | 0.104 | 0.180 | 0.234 | 0.099 | 0.205 | 0.169 | ||
| 0.625 | 0.013 | 0 | 0.266 | 0 | 0.028 | 0 | 0 | 0.069 |
| Importance | Range of Eigenvector Centrality | Range of Betweenness Centrality |
|---|---|---|
| Lowest | 0–0.057 | 0–0.003 |
| Lower | 0.057–0.233 | 0.003–0.012 |
| Medium | 0.233–0.383 | 0.012–0.024 |
| Higher | 0.383–0.523 | 0.024–0.045 |
| Highest | 0.523–1 | 0.045–0.074 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Chen, Y.; Zhu, C.; Di, Y.; Li, Z.; Fang, G.; Liu, C.; Zou, B.; Lyu, H. Evaluation of Water System Connectivity Based on Node Centrality in the Tarim River Basin, Xinjiang, China. Water 2024, 16, 3031. https://doi.org/10.3390/w16213031
Yu J, Chen Y, Zhu C, Di Y, Li Z, Fang G, Liu C, Zou B, Lyu H. Evaluation of Water System Connectivity Based on Node Centrality in the Tarim River Basin, Xinjiang, China. Water. 2024; 16(21):3031. https://doi.org/10.3390/w16213031
Chicago/Turabian StyleYu, Junyuan, Yaning Chen, Chenggang Zhu, Yanfeng Di, Zhi Li, Gonghuan Fang, Chuanxiu Liu, Bin Zou, and Haodong Lyu. 2024. "Evaluation of Water System Connectivity Based on Node Centrality in the Tarim River Basin, Xinjiang, China" Water 16, no. 21: 3031. https://doi.org/10.3390/w16213031
APA StyleYu, J., Chen, Y., Zhu, C., Di, Y., Li, Z., Fang, G., Liu, C., Zou, B., & Lyu, H. (2024). Evaluation of Water System Connectivity Based on Node Centrality in the Tarim River Basin, Xinjiang, China. Water, 16(21), 3031. https://doi.org/10.3390/w16213031










