Analysis of Land Use Change and Hydrogeological Parameters in the Andean Semiarid Region of Ecuador
Abstract
:1. Introduction
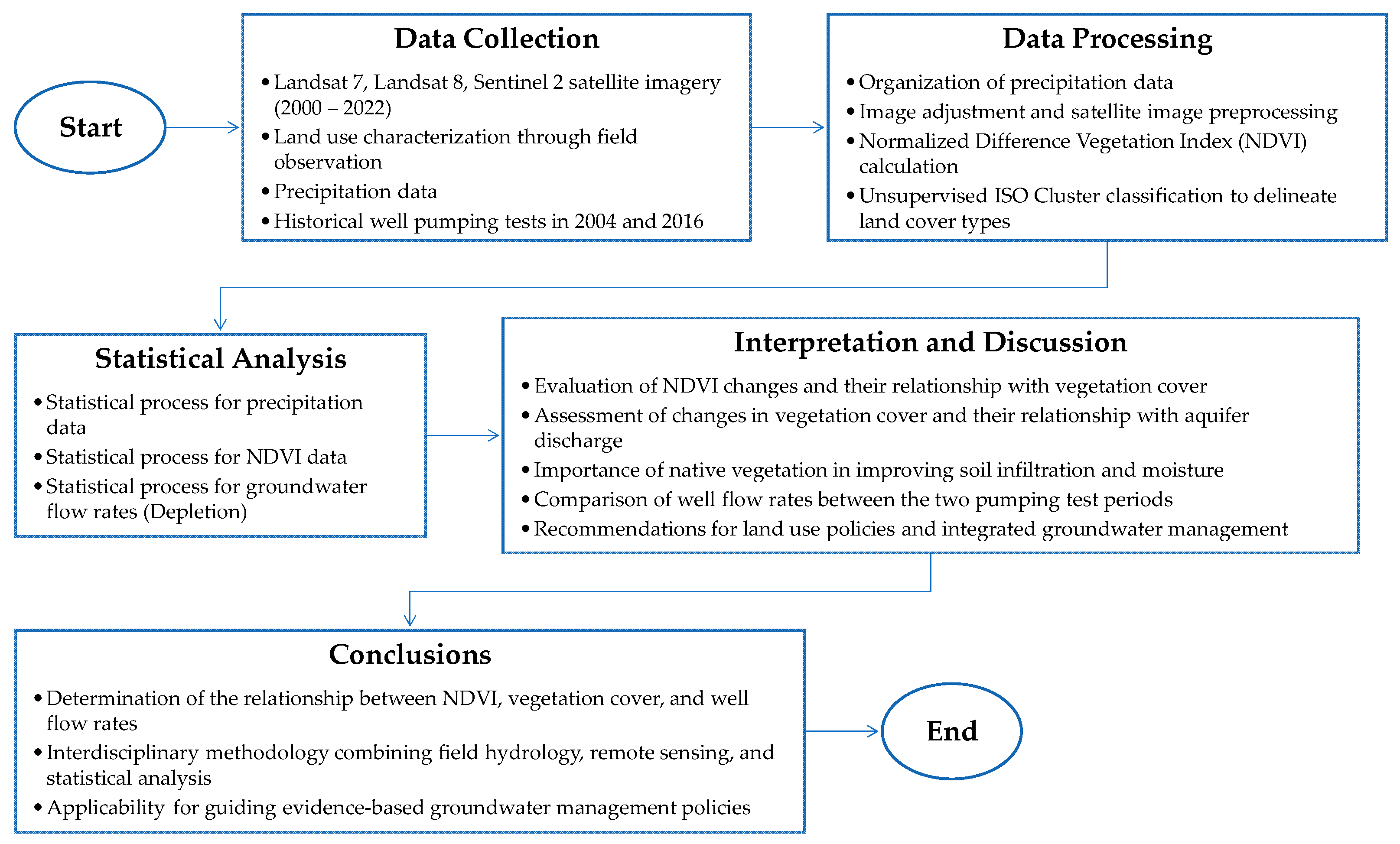
2. Materials and Methods
2.1. Study Area
2.2. Field Methods
2.3. Satellite Data Analysis
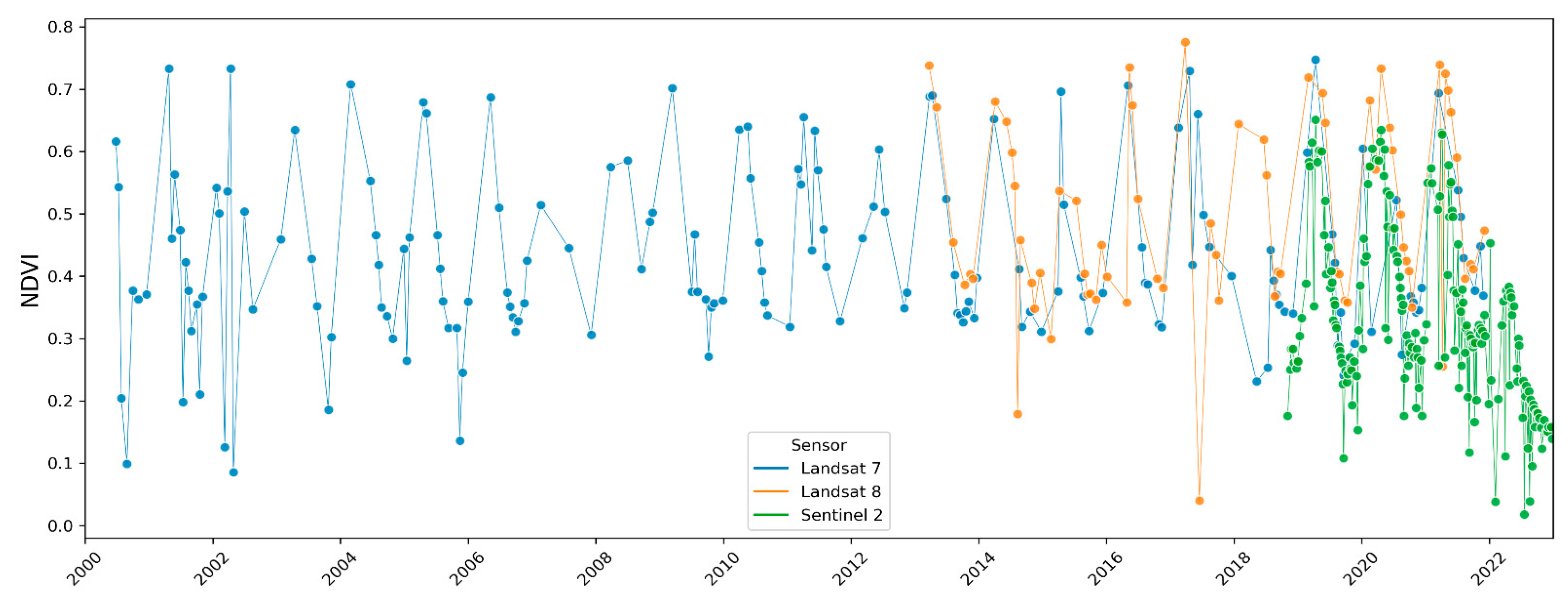
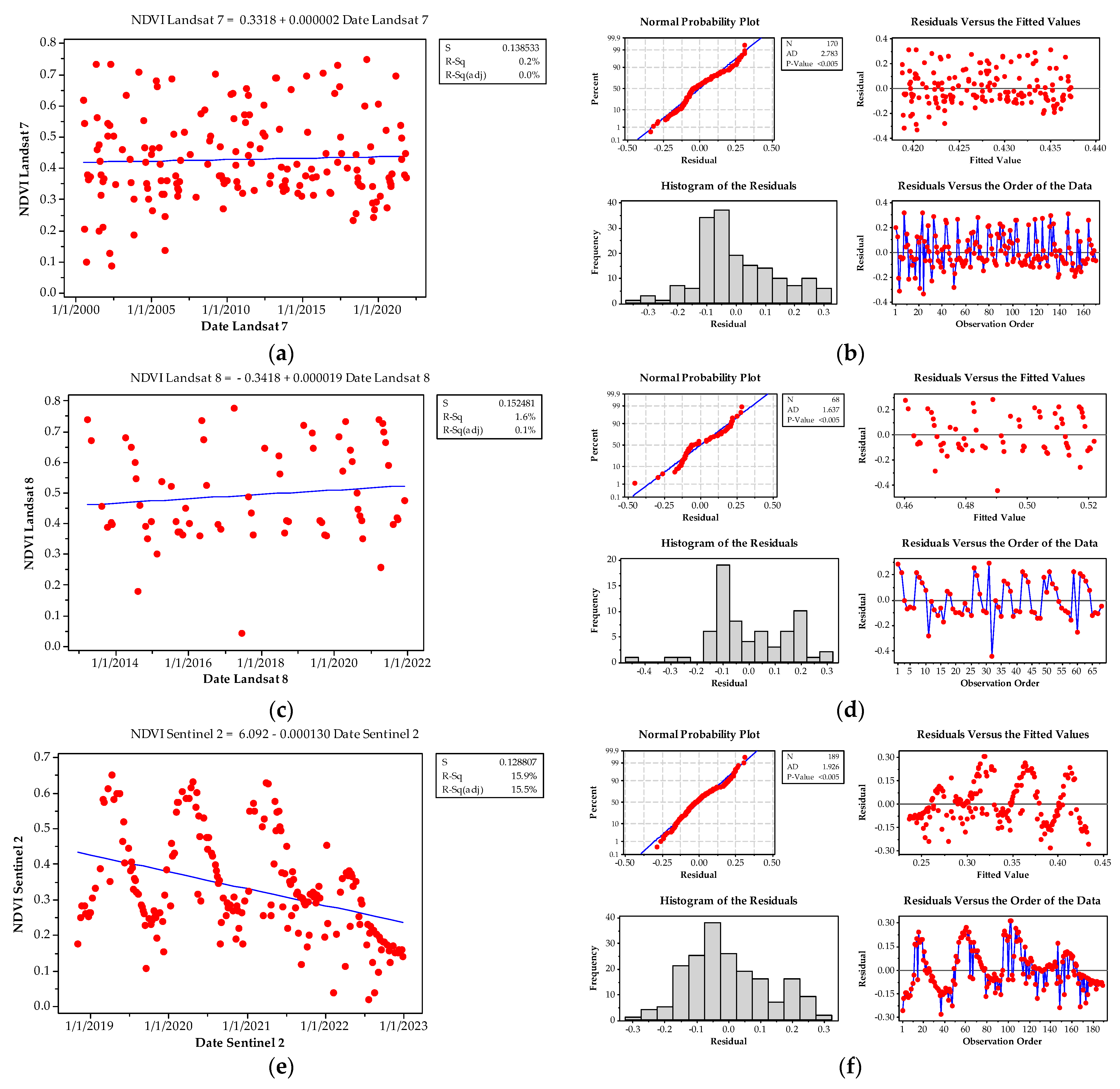
2.4. Calculation of Vegetation Index
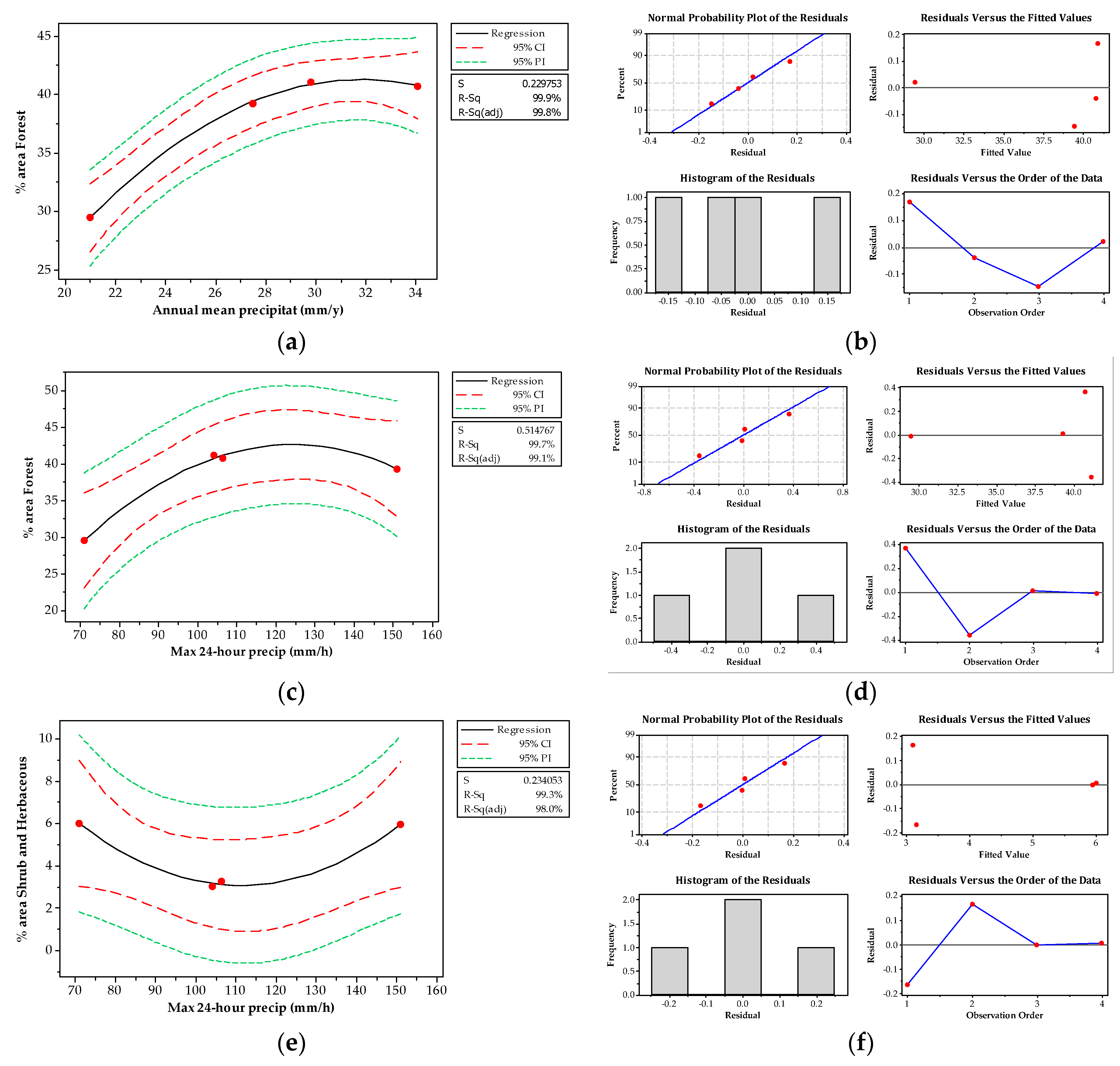
2.5. Statistical Analysis
2.6. Groundwater Recharge
2.6.1. Theis and Hantush Solution for a Pumping Test in a Confined Aquifer
2.6.2. Solution Method of Butler
3. Results
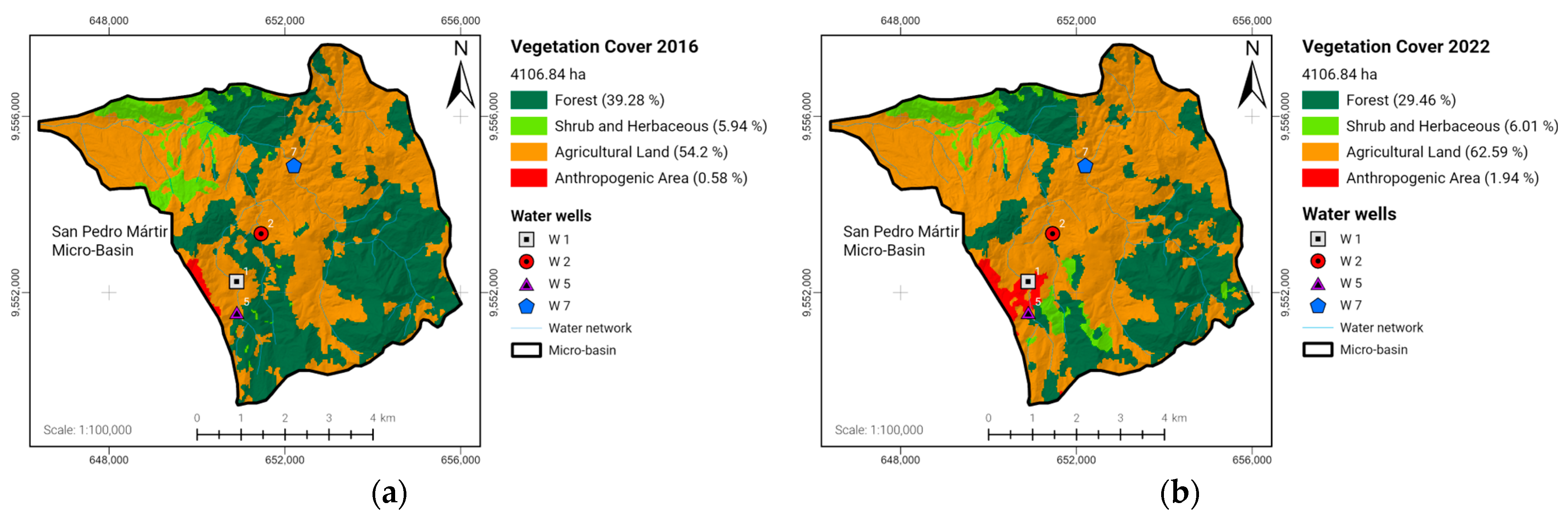
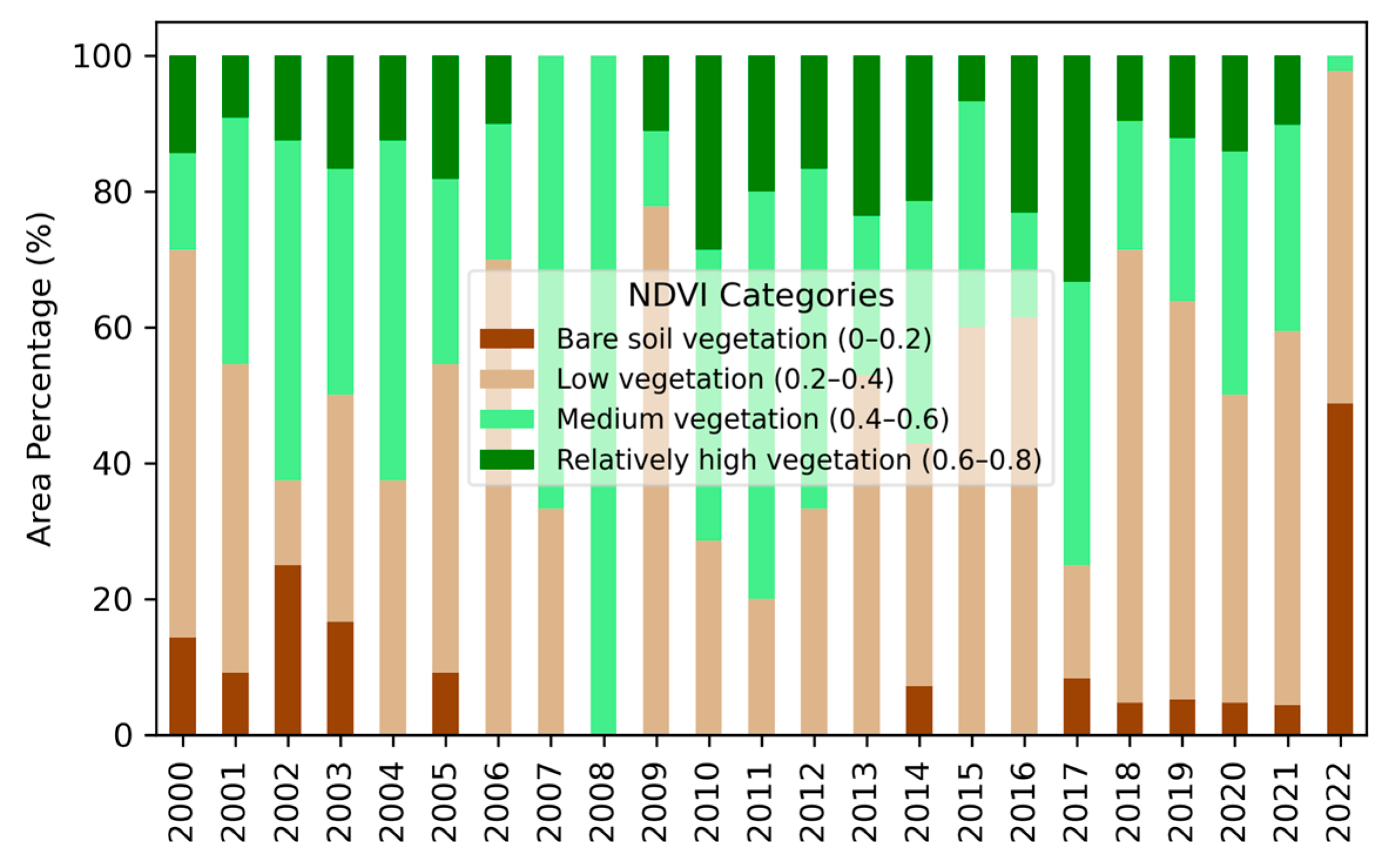
3.1. Land Cover Changes
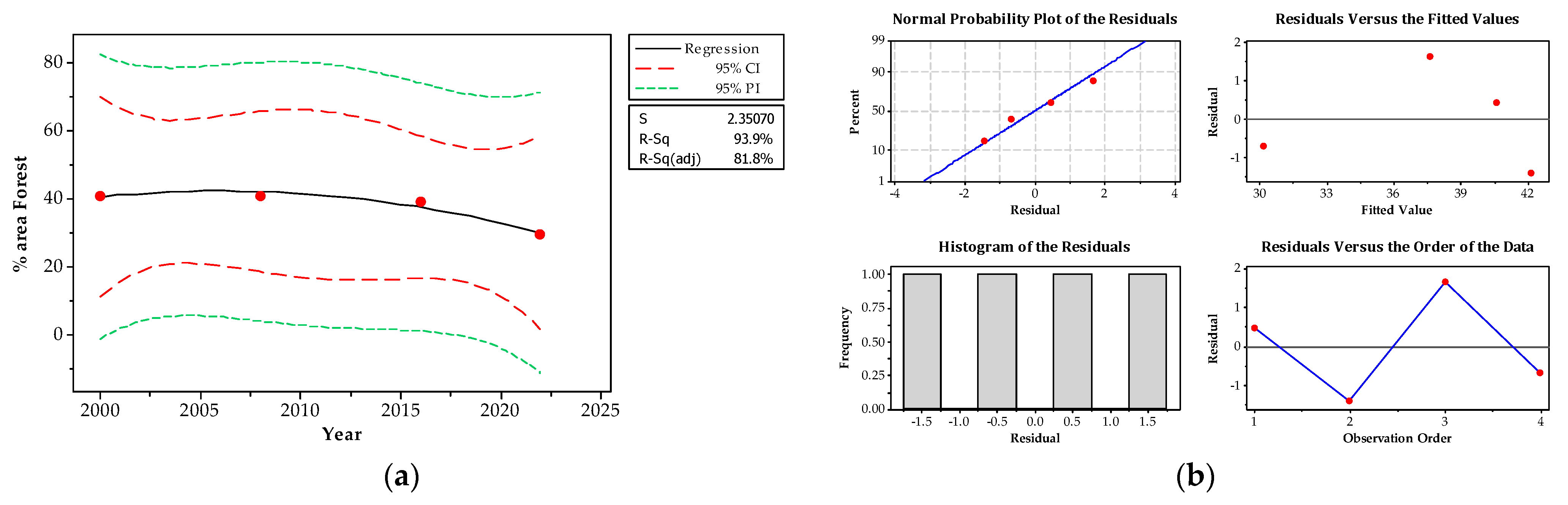
3.2. Vegetation Changes
3.3. Groundwater Level Changes
3.3.1. Stratigraphic Description of the Project Coverage Zone
3.3.2. The Lithological Well Profiles
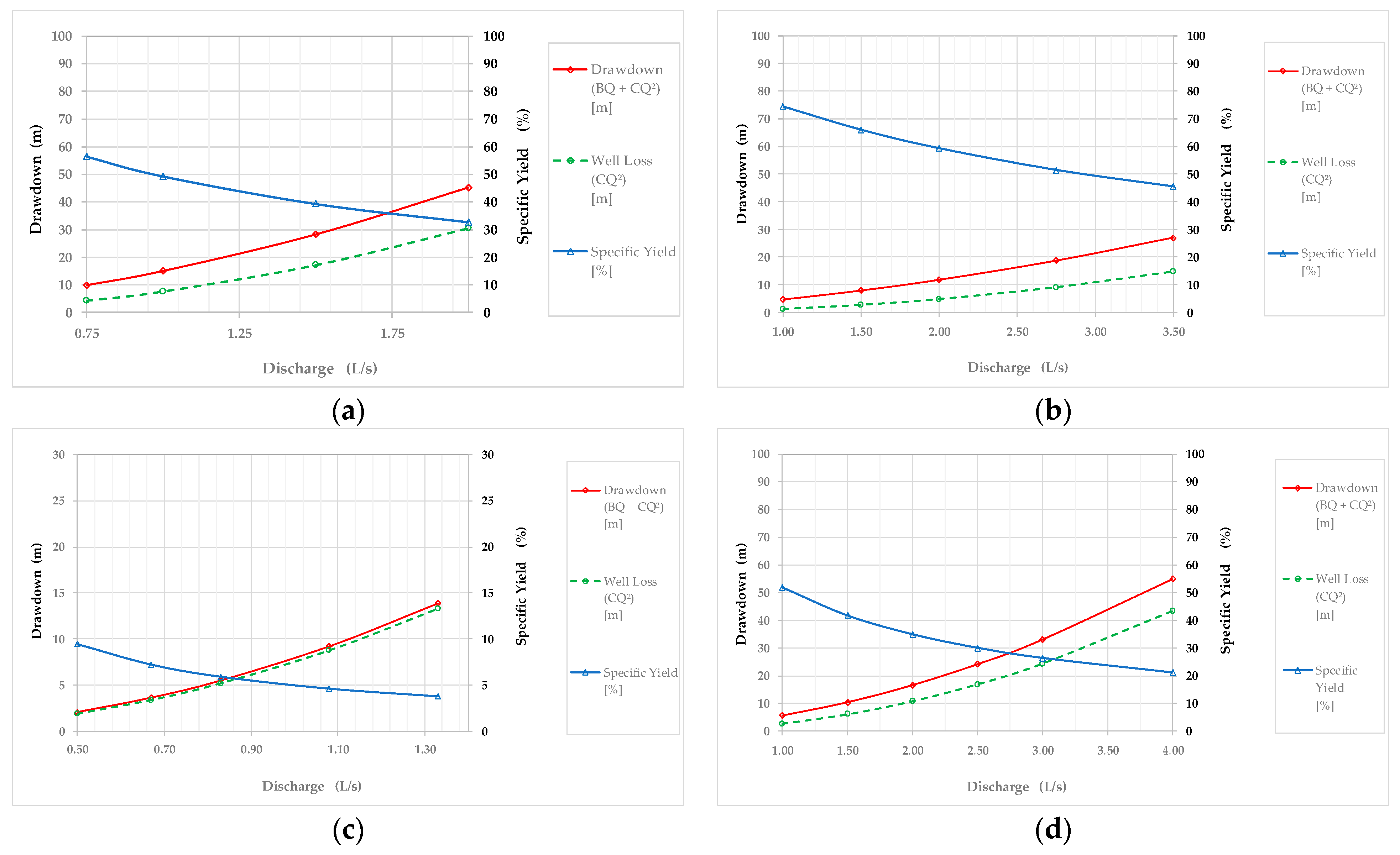
3.4. Groundwater Depletion and Recovery Dynamics
4. Discussion
5. Conclusions
6. Limitations
7. Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Foster, S.; Hirata, R.; Gomes, D.; Delia, M.; Paris, M. Groundwater Quality Protection: A Guide for Water Utilities, Municipal Authorities, and Environment Agencies; The World Bank: Washington, DC, USA, 2003. [Google Scholar]
- Pastore, N.; Cherubini, C.; Giasi, C.I. Integrated Hydrogeological Modelling for Sustainable Management of the Brindisi Plain Aquifer (Southern Italy). Water 2023, 15, 2943. [Google Scholar] [CrossRef]
- Meixner, T.; Manning, A.H.; Stonestrom, D.A.; Allen, D.M.; Ajami, H.; Blasch, K.W.; Brookfield, A.E.; Castro, C.L.; Clark, J.F.; Gochis, D.J.; et al. Implications of projected climate change for groundwater recharge in the western United States. J. Hydrol. 2016, 534, 124–138. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Healy, R.W.; Cook, P.G. Choosing Appropriate Techniques for Quantifying Groundwater Recharge. Hydrogeol. J. 2002, 10, 18–39. [Google Scholar] [CrossRef]
- López, G.C.; Stigter, T.Y.; de Melo, M.T.C.; Werner, M. Análisis de los procesos de recarga y las interacciones agua superficial-subterránea en la cuenca Bolo del río Cauca, Colombia. Boletín Geológico Y Min. 2021, 132, 115–125. [Google Scholar]
- Hendrickx, J.M.; Walker, G.R. Recharge from Precipitation. In Recharge of Phreatic Aquifers in (Semi-) Arid Areas; Routledge: London, UK, 2017; pp. 19–111. [Google Scholar]
- Cook, P.G.; Favreau, G.; Dighton, J.C.; Tickell, S. Determining Natural Groundwater Influx to a Tropical River Using Radon, Chlorofluorocarbons, and Ionic Environmental Tracers. J. Hydrol. 2003, 277, 74–88. [Google Scholar] [CrossRef]
- De Vries, J.J.; Simmers, I. Groundwater Recharge: An Overview of Processes and Challenges. Hydrogeol. J. 2002, 10, 5–17. [Google Scholar] [CrossRef]
- Crosbie, R.S.; McCallum, J.L.; Walker, G.R.; Chiew, F.H. Modelling Climate-Change Impacts on Groundwater Recharge in the Murray-Darling Basin, Australia. Hydrogeol. J. 2010, 18, 1639–1656. [Google Scholar] [CrossRef]
- Glenn, E.P.; Nagler, P.L.; Huete, A.R. Vegetation Index Methods for Estimating Evapotranspiration by Remote Sensing. Surv. Geophys. 2010, 31, 531–555. [Google Scholar] [CrossRef]
- Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A Simple Method for Reconstructing a High-Quality NDVI Time-Series Dataset Based on the Savitzky-Golay Filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Santoni, C.S.; Jobbágy, E.G.; Contreras, S. Vadose Zone Transport in Dry Forests of Central Argentina: Role of Land Use. Water Resour. Res. 2010, 46, 1–12. [Google Scholar] [CrossRef]
- Kizito, F.; Dragila, M.; Sene, M.; Lufafa, A.; Diedhiou, I.; Dick, R.P.; Selker, J.S.; Dossa, E.; Badiane, A.; Ndiaye, S. Seasonal Soil Water Variation and Root Patterns Between Two Semi-Arid Shrubs Co-existing with Pearl Millet in Senegal, West Africa. J. Arid. Environ. 2006, 67, 436–455. [Google Scholar] [CrossRef]
- Leaney, F.W.; Herczeg, A.L.; Walker, G.R. Salinization of a Fresh Palaeo-groundwater Resource by Enhanced Recharge. Groundwater 2011, 49, 84–92. [Google Scholar]
- Gücker, B.; Brauns, M.; Pusch, M.T. Effects of Wastewater Treatment Plant Discharge on Ecosystem Structure and Function of Lowland Streams. J. N. Am. Benthol. Soc. 2009, 28, 313–329. [Google Scholar] [CrossRef]
- Scalenghe, R.; Marsan, F.A. The Anthropogenic Sealing of Soils in Urban Areas. Landsc. Urban Plan. 2009, 90, 1–10. [Google Scholar] [CrossRef]
- Pyne, R.D.G. Groundwater Recharge and Wells: A Guide to Aquifer Storage Recovery; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Solano, A.; Correa, V. Study of the Main Water Supply Sources for Human Consumption in the Main Towns of Paltas Canton; Universidad Técnica Particular de Loja: Loja, Ecuador, 2013. [Google Scholar]
- INEC. Population and Housing Census 2010; Instituto Nacional de Estadística y Censos: Quito, Ecuador, 2010. [Google Scholar]
- Ortiz, J.; Chalan, L. Vegetation Cover and Current Land Use in Loja Province; Amazonas Graphs: Loja, Ecuador, 2010. [Google Scholar]
- Salas, J. Hydrology of Arid and Semi-Arid Regions. Ing. Agua 2000, 7, 409–429. [Google Scholar] [CrossRef]
- Alvarado, L. Understanding the Architectural Work Represented by the Houses that Make Up the Cultural Heritage of the City of Catacocha, Paltas Canton, Loja Province, as a Path to Establish Regional Architecture; (Technical Report, Architecture); Universidad Técnica Particular de Loja: Loja, Ecuador, 2008. [Google Scholar]
- INAMHI. Ecuador Meteorological Yearbook. Anuario Meteorológico del Ecuador; Instituto Nacional de Meteorología e Hidrología: Quito, Ecuador, 2019. [Google Scholar]
- Criollo, W. Municipal Development and Land-Use Planning Plan of the Paltas Municipal Government. In Plan de Desarrollo y Ordenamiento Territorial del GAD Municipal de Paltas; GADM Paltas: Loja, Ecuador, 2015. [Google Scholar]
- Burbano, M. The Hydrogeology of Ecuador; Instituto Nacional de Meteorología e Hidrología: Quito, Ecuador, 2011. [Google Scholar]
- HCPL. Evaluation and Operational Testing of the Potable Water System in the City of Catacocha; H. Provincial Council of Loja, Groundwater Development Project for the Province of Loja: Catacocha, Ecuador, 2017. [Google Scholar]
- Kruseman, G.P.; de Ridder, N.A. Analysis and Evaluation of Pumping Test Data; International Institute for Land Reclamation and Improvement: Wageningen, The Netherlands, 1990. [Google Scholar]
- Zhao, Z.; Illman, W.A.; Zha, Y.; Yeh, T.C.J.; Mok, C.M.B.; Berg, S.J.; Han, D. Transient Hydraulic Tomography Analysis of Fourteen Pumping Tests at a Highly Heterogeneous Multiple Aquifer–Aquitard System. Water 2019, 11, 1864. [Google Scholar] [CrossRef]
- Matsushita, B.; Yang, W.; Chen, J.; Onda, Y.; Qiu, G. Sensitivity of the Enhanced Vegetation Index (EVI) and Normalized Difference Vegetation Index (NDVI) to topographic effects: A case study in high-density cypress forest. Sensors 2007, 7, 2636–2651. [Google Scholar] [CrossRef]
- Kruseman, G.P.; de Ridder, N.A. Analysis and Evaluation of Pumping Test Data, 2nd ed.; International Institute for Land Reclamation and Improvement: Wageningen, The Netherlands, 1994. [Google Scholar]
- Karami, G.H.; Younger, P.L. Analysing step-drawdown tests in heterogeneous aquifers. Q. J. Eng. Geol. Hydrogeol. 2002, 35, 295–303. [Google Scholar] [CrossRef]
- Olson, P.R. Novel Remediation Schemes for Groundwater and Urban Runoff. Ph.D. Dissertation, Ohio University, Athens, OH, USA, June 2011. [Google Scholar]
- Misstear, B.; Banks, D.; Clark, L. Water Wells and Boreholes; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Custodio, E.; Llamas, M.R. Hidrología Subterránea, 2nd ed.; Tomo, I., Ed.; Ediciones Omega, S.A.: Barcelona, Spain, 2001; pp. 826–835, 1138. [Google Scholar]
- Schultz, M.; Clevers, J.G.; Carter, S.; Verbesselt, J.; Avitabile, V.; Quang, H.V.; Herold, M. Performance of Vegetation Indices from Landsat Time Series in Deforestation Monitoring. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 318–327. [Google Scholar] [CrossRef]
- Yeneneh, N.; Elias, E.; Feyisa, G.L. Detection of Land Use/Land Cover and Land Surface Temperature Change in the Suha Watershed, North-Western Highlands of Ethiopia. Environ. Chall. 2022, 7, 100523. [Google Scholar] [CrossRef]
- Belay, T.; Melese, T.; Senamaw, A. Impacts of Land Use and Land Cover Change on Ecosystem Service Values in the Afroalpine Area of Guna Mountain, Northwest Ethiopia. Heliyon 2022, 8, e12246. [Google Scholar] [CrossRef] [PubMed]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The Climate Hazards Infrared Precipitation with Stations—A New Environmental Record for Monitoring Extremes. Sci. Data 2015, 2, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Zhou, M.; Li, D.; Liao, K.; Lu, D. Integration of Landsat Time-Series Vegetation Indices Improves Consistency of Change Detection. Int. J. Digit. Earth 2023, 16, 1276–1299. [Google Scholar] [CrossRef]
- Perez, M.; Vitale, M. Landsat-7 ETM+, Landsat-8 OLI, and Sentinel-2 MSI Surface Reflectance Cross-Comparison and Harmonization over the Mediterranean Basin Area. Remote Sens. 2023, 15, 4008. [Google Scholar] [CrossRef]
- Li, P.; Jiang, L.; Feng, Z. Cross-Comparison of Vegetation Indices Derived from Landsat-7 Enhanced Thematic Mapper Plus (ETM+) and Landsat-8 Operational Land Imager (OLI) Sensors. Remote Sens. 2014, 6, 310–329. [Google Scholar] [CrossRef]
- Song, C.; Woodcock, C.E.; Seto, K.C.; Lenney, M.P.; Macomber, S.A. Classification and Change Detection Using Landsat TM Data: When and How to Correct Atmospheric Effects? Remote Sens. Environ. 2001, 75, 230–244. [Google Scholar] [CrossRef]
- Wang, Q.; Moreno-Martínez, Á.; Muñoz-Marí, J.; Campos-Taberner, M.; Camps-Valls, G. Estimation of Vegetation Traits with Kernel NDVI. ISPRS J. Photogramm. Remote Sens. 2023, 195, 408–417. [Google Scholar] [CrossRef]
- Donovan, G.H.; Gatziolis, D.; Derrien, M.; Michael, Y.L.; Prestemon, J.P.; Douwes, J. Shortcomings of the Normalized Difference Vegetation Index as an Exposure Metric. Nat. Plants 2022, 8, 617–622. [Google Scholar] [CrossRef]
- Kiptala, J.; Mohamed, Y.; Mul, M.; Cheema, M.; Van der Zaag, P. Land Use and Land Cover Classification Using Phenological Variability from MODIS Vegetation in the Upper Pangani River Basin, Eastern Africa. Phys. Chem. Earth, Parts A/B/C 2013, 66, 112–122. [Google Scholar] [CrossRef]
- Andualem, Z.A.; Meshesha, D.T.; Hassen, E.E. Impacts of Watershed Management on Land Use/Cover Changes and Landscape Greenness in Yezat Watershed, North West, Ethiopia. Environ. Sci. Pollut. Res. 2023, 30, 64377–64398. [Google Scholar] [CrossRef] [PubMed]
- Mendonça dos Santos, F.; Proença de Oliveira, R.; Augusto Di Lollo, J. Effects of Land Use Changes on Streamflow and Sediment Yield in Atibaia River Basin—SP, Brazil. Water 2020, 12, 1711. [Google Scholar] [CrossRef]
- Souza, V.A.S.D.; Moreira, D.M.; Rotunno Filho, O.C.; Rudke, A.P.; Andrade, C.D.; Araujo, L.M.N.D. Spatio-temporal Analysis of Remotely Sensed Rainfall Datasets Retrieved for the Transboundary Basin of the Madeira River in Amazonia. Atmósfera 2022, 35, 39–66. [Google Scholar] [CrossRef]
- de Andrade, J.M.; Neto, A.R.; Bezerra, U.A.; Moraes, A.C.C.; Montenegro, S.M.G.L. A Comprehensive Assessment of Precipitation Products: Temporal and Spatial Analyses over Terrestrial Biomes in Northeastern Brazil. Remote Sens. Appl. Soc. Environ. 2022, 28, 100842. [Google Scholar] [CrossRef]
- Duan, Z.; Bastiaanssen, W.G.M. First Results from Version 7 TRMM 3B43 Precipitation Product in Combination with a New Downscaling–Calibration Procedure. Remote Sens. Environ. 2013, 131, 1–13. [Google Scholar] [CrossRef]
- Xue, J.; Su, B. Significant Remote Sensing Vegetation Indices: A Review of Developments and Applications. J. Sens. 2017, 2017, 1353691. [Google Scholar] [CrossRef]
- Richards, J.A.; Richards, J.A. Remote Sensing Digital Image Analysis; Springer: Berlin/Heidelberg, Germany, 2022; Volume 5. [Google Scholar]
- de Lange, N. Remote Sensing and Digital Image Processing. In Geoinformatics in Theory and Practice: An Integrated Approach to Geoinformation Systems, Remote Sensing and Digital Image Processing; Springer: Berlin/Heidelberg, Germany, 2023; pp. 435–510. [Google Scholar]
- Key, C.H.; Benson, N.C. Landscape Assessment (LA). In FIREMON: Fire Effects Monitoring and Inventory System; Lutes, D.C., Keane, R.E., Caratti, J.F., Key, C.H., Benson, N.C., Sutherland, S., Gangi, L.J., Eds.; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2006; pp. LA-1–LA-55. Available online: https://www.fs.usda.gov/research/treesearch/24066 (accessed on 11 November 2023)Gen. Tech. Rep. RMRS-GTR-164-CD.
- Rouse, J., Jr.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. NASA Spec. Publ. 1974, 351, 309. [Google Scholar]
- Lillesand, T.; Kiefer, R.W.; Chipman, J. Remote Sensing and Image Interpretation; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Huete, A.R. Vegetation Indices, Remote Sensing and Forest Monitoring. Geogr. Compass 2012, 6, 513–532. [Google Scholar] [CrossRef]
- Lee-Rodgers, J.; Nicewander, W.A. Thirteen Ways to Look at the Correlation Coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Kutner, M.H.; Nachtsheim, C.J.; Neter, J.; Li, W. Applied Linear Statistical Models; McGraw-Hill Irwin: New York, NY, USA, 2005; Volume 5. [Google Scholar]
- Bivand, R.S.; Pebesma, E.; Gómez-Rubio, V. Applied Spatial Data Analysis with R, 2nd ed.; Springer: New York, NY, USA, 2013; pp. 263–318. [Google Scholar] [CrossRef]
- Yun, S.M.; Jeon, H.T.; Cheong, J.Y.; Kim, J.; Hamm, S.Y. Combined Analysis of Net Groundwater Recharge Using Water Budget and Climate Change Scenarios. Water 2023, 15, 571. [Google Scholar] [CrossRef]
- Giglou, A.N.; Nazari, R.R.; Jazaei, F.; Karimi, M. Numerical Analysis of Surface Hydrogeological Water Budget to Estimate Unconfined Aquifers Recharge. J. Environ. Manag. 2023, 346, 118892. [Google Scholar] [CrossRef]
- Suk, H.; Park, E. Numerical Solution of the Kirchhoff-Transformed Richards Equation for Simulating Variably Saturated Flow in Heterogeneous Layered Porous Media. J. Hydrol. 2019, 579, 124213. [Google Scholar] [CrossRef]
- Rabinovich, A.; Guy, D. Equivalent Hydraulic Conductivity of Heterogeneous Aquifers Estimated by Multi-Frequency Oscillatory Pumping. Sustainability 2023, 15, 13124. [Google Scholar] [CrossRef]
- Theis, C.V. The Relation Between the Lowering of the Piezometric Surface and the Rate and Duration of Discharge of a Well Using Groundwater Storage. Am. Geophys. Union Trans. 1935, 16, 519–524. [Google Scholar] [CrossRef]
- Hantush, M.S. Drawdown around a partially penetrating well. J. Hydraul. Div. Proc. Am. Soc. Civ. Eng. 1961, 87, 83–98. [Google Scholar] [CrossRef]
- Butler, J.J., Jr. The Design, Performance, and Analysis of Slug Tests; Lewis Publishers: Boca Raton, FL, USA, 1998; 252p. [Google Scholar]
- Butler, J.J., Jr. A Simple Correction for Slug Tests in Small-Diameter Wells. Ground Water 2002, 40, 303–307. [Google Scholar] [CrossRef]
- IGM Instituto Geográfico Militar—IGM. Geographic Information Basic Layers from IGM Freely Accessible; (UTF-8 Encoding); Spatial Data Infrastructure for Military Geographic Institute: Quito, Ecuador, 2017; Available online: http://www.geoportaligm.gob.ec/portal/index.php/descargas (accessed on 20 November 2023).
- MAATE. Ministerio del Ambiente, Agua y Transición Ecológica. Apache Tomcat/9.0.79. Available online: http://ide.ambiente.gob.ec:8080/mapainteractivo/ (accessed on 5 January 2024).
- Google, L.L.C. Google Earth Engine Platform. [Data Processing Platform: Landsat 7, Landsat 8, Sentinel-2]. Available online: https://earthengine.google.com/ (accessed on 5 February 2024).
- Lambin, E.F.; Meyfroidt, P. Land use transitions: Socio-ecological feedback versus socio-economic change. Land Use Policy 2010, 27, 108–118. [Google Scholar] [CrossRef]
- MAE. National Forest Restoration Plan 2014–2017; Ministerio del Ambiente: Quito, Ecuador, 2014. [Google Scholar]
- Zhang, J.; Felzer, B.S.; Troy, T.J. Extreme precipitation drives groundwater recharge: The northern high plains aquifer, central United States, 1950–2010. Hydrol. Process. 2016, 30, 2533–2545. [Google Scholar] [CrossRef]
- Owor, M.; Taylor, R.G.; Tindimugaya, C.; Mwesigwa, D. Rainfall intensity and groundwater recharge: Empirical evidence from the Upper Nile Basin. Environ. Res. Lett. 2009, 4, 035009. [Google Scholar] [CrossRef]
- Throop, H.L.; Archer, S.R.; McClaran, M.P. Soil organic carbon in drylands: Shrub encroachment and vegetation management effects dwarf those of livestock grazing. Ecol. Appl. 2020, 30, 7. [Google Scholar] [CrossRef]
- Tietjen, B.; Jeltsch, F.; Zehe, E.; Classen, N.; Groengroeft, A.; Schiffers, K.; Oldeland, J. Effects of climate change on the coupled dynamics of water and vegetation in drylands. Ecohydrol. Ecosyst. Land Water Process Interact. Ecohydrogeomorphol. 2010, 3, 226–237. [Google Scholar] [CrossRef]
- GAD Paltas. Final Studies and Designs of the Regional Drinking Water Master Plan for the City of Catacocha-Paltas. Consulting Study for GAD-Paltas; First Phase Report: Evaluation and Diagnosis; GAD Paltas: Catacocha, Loja, Ecuador, 2016. [Google Scholar]
- Gonzaga, S.L.; Serrano, J.A.; Benavides-Muñoz, H.M. University Research and Outreach. Groundwater Management in the Catacocha Community. Investigación y Extensión Universitaria. Gestión de Aguas Subterráneas en la Comunidad de Catacocha, Ecuador. Rev. De Extensión Univ. + E 2017, 7, 280–289. [Google Scholar]
- Gómez, J.; López, J. Joint Use and Artificial Recharge Initiatives Aimed at Improving Environmental Management and Sustainable Use of Aquifers Connected to the Transversal Artery of Mallorca Island; Instituto Geológico y Minero de España: Madrid, Spain, 2007. [Google Scholar]
- Kopec, D.; Michalska-Hejduk, D.; Krogulec, E. The Relationship Between Vegetation and Groundwater Levels as an Indicator of Spontaneous Wetland Restoration. Ecol. Eng. 2013, 57, 242–251. [Google Scholar] [CrossRef]
- Jasechko, S.; Kirchner, J.W.; Welker, J.M.; McDonnell, J.J. Substantial Proportion of Global Streamflow Less Than Three Months Old. Nat. Geosci. 2014, 9, 126–129. [Google Scholar] [CrossRef]
- Wang, W.; Chen, Y.; Wang, W.; Chen, Y.; Hou, Y. Groundwater Level Dynamics Impacted by Land-Cover Change in the Desert Regions of Tarim Basin, Central Asia. Water 2023, 15, 3601. [Google Scholar] [CrossRef]
- SENAGUA & UTPL. Technical Report: Socio-Economic and Environmental Survey for the Drinking Water System of Catacocha; Secretaría Nacional del Agua, Universidad Técnica Particular de Loja: Loja, Ecuador, 2016. [Google Scholar]
- Chen, Z.; Grasby, S.; Osadetz, K. Relation between Climate Variability and Groundwater Levels in the Upper Carbonate Aquifer, Southern Manitoba, Canada. J. Hydrol. 2004, 290, 43–62. [Google Scholar] [CrossRef]







| Well Number | Coordinates | Altitude | Drill Depth | Specific Yield | |
|---|---|---|---|---|---|
| Longitude | Latitude | m a.s.l. | m | (Discharge L/s) % | |
| Well 1 Consacola | −79.64222 | −4.04675 | 1776 | 200 | (2.00 L/s) 32.67% |
| Well 2 Chapango | −79.63567 | −4.03995 | 1691 | 130 | (2.00 L/s) 59.29% |
| Well 5 Santa Marianita | −79.64060 | −4.05577 | 1795 | 170 | (1.08 L/s) 32.67% |
| Well 7 San Pedro Mártir | −79.62659 | −4.01992 | 1640 | 142 | (2.00 L/s) 34.93% |
| Well | Discharge [L/s] | Aquifer Loss (BQ) [m] | Well Loss (CQ²) [m] | Drawdown (BQ + CQ²) [m] | Specific Yield [%] | Specific Capacity [m³/d/m] |
|---|---|---|---|---|---|---|
| 1 | 0.75 | 5.53 | 4.28 | 9.81 | 56.41 | 6.60 |
| Consacola | 1.00 | 7.38 | 7.60 | 14.98 | 49.25 | 5.77 |
| B = 8.54 × 10−2 | 1.50 | 11.07 | 17.11 | 28.18 | 39.28 | 4.60 |
| C = 1.02 × 10−3 | 2.00 | 14.76 | 30.42 | 45.18 | 32.67 | 3.83 |
| 2 | 1.00 | 3.51 | 1.20 | 4.71 | 74.44 | 18.33 |
| Chapango | 1.50 | 5.26 | 2.71 | 7.97 | 66.01 | 16.25 |
| 2.00 | 7.02 | 4.82 | 11.84 | 59.29 | 14.60 | |
| B = 4.06 × 10−2 | 2.75 | 9.65 | 9.11 | 18.76 | 51.44 | 12.66 |
| C = 1.61 × 10−4 | 3.50 | 12.28 | 14.76 | 27.04 | 45.42 | 11.18 |
| 5 | 0.50 | 0.20 | 1.88 | 2.08 | 9.41 | 20.79 |
| Sta. Marianita | 0.67 | 0.26 | 3.38 | 3.64 | 7.20 | 15.89 |
| 0.83 | 0.32 | 5.19 | 5.51 | 5.89 | 13.01 | |
| B = 4.53 × 10−3 | 1.08 | 0.42 | 8.78 | 9.21 | 4.59 | 10.14 |
| C = 1.01 × 10−3 | 1.33 | 0.52 | 13.32 | 13.84 | 3.76 | 8.30 |
| 7 | 1.00 | 2.90 | 2.71 | 5.61 | 51.78 | 15.40 |
| San Pedro | 1.50 | 4.36 | 6.09 | 10.44 | 41.72 | 12.41 |
| Mártir | 2.00 | 5.81 | 10.82 | 16.63 | 34.93 | 10.39 |
| 2.50 | 7.26 | 16.91 | 24.17 | 30.04 | 8.94 | |
| B = 3.36 × 10−2 | 3.00 | 8.71 | 24.35 | 33.06 | 26.36 | 7.84 |
| C = 3.62 × 10−4 | 4.00 | 11.62 | 43.29 | 54.91 | 21.16 | 6.29 |
| Well | Vegetation Type | 2004 | 2016 | Change over the Period (%) |
|---|---|---|---|---|
| Area (ha) | Area (ha) | |||
| Well 1 | Shrubland | 15.21 | 8.85 | −41.81 |
| Consacola | Urban area and bare soil | 8.23 | 68.40 | 731.11 |
| Cropland | 56.59 | 96.36 | 70.28 | |
| Natural vegetation | 65.00 | 20.72 | −68.12 | |
| Reforestation | 98.43 | 49.13 | −50.09 | |
| Well 2 | Shrubland | 58.27 | 70.12 | 20.34 |
| Chapango | Urban area and bare soil | 9.26 | 121.80 | 1215.33 |
| Cropland | 108.64 | 109.20 | 0.52 | |
| Natural vegetation | 96.91 | 7.90 | −91.85 | |
| Reforestation | 71.90 | 35.96 | −49.99 | |
| Well 5 | Shrubland | 14.85 | 4.15 | −72.05 |
| Santa Marianita | Urban area and bare soil | 6.46 | 54.77 | 747.83 |
| Cropland | 52.35 | 72.21 | 37.94 | |
| Natural vegetation | 46.74 | 20.32 | −56.53 | |
| Reforestation | 61.94 | 30.89 | −50.13 | |
| Well 7 | Shrubland | 398.97 | 558.19 | 39.91 |
| San Pedro Mártir | Urban area and bare soil | 71.05 | 468.80 | 559.82 |
| Cropland | 365.15 | 222.61 | −39.04 | |
| Natural vegetation | 275.24 | 27.61 | −89.97 | |
| Reforestation | 333.65 | 166.85 | −50.00 |
| Well | Number | Time (minutes) | Period | Flow (L/s) |
|---|---|---|---|---|
| Consacola | 1 | 16 | 2004 | 4.50 |
| 2016 | 4.57 | |||
| Chapango | 2 | 90 | 2004 | 2.42 |
| 2016 | 2.31 | |||
| Santa Marianita | 5 | 90 | 2004 | 1.50 |
| 2016 | 1.96 | |||
| San Pedro Mártir | 7 | 90 | 2004 | 2.50 |
| 2016 | 2.76 |
| Well | Year | Coefficient of Losses in the Well C | Interpretation of Coefficient C |
|---|---|---|---|
| 1 | 2004 | 0.0010 | Well properly constructed and developed |
| Consacola | 2016 | 0.0100 | Initiation of encrustations on wellbore screens |
| 2 | 2004 | 0.0002 | Well properly constructed and developed |
| Chapango | 2016 | 0.0022 | Initiation of encrustations on wellbore screens |
| 5 | 2004 | 0.0010 | Well properly constructed and developed |
| Sta Marianita | 2016 | 0.0052 | Initiation of encrustations on wellbore screens |
| 7 | 2004 | 0.0034 | Initiation of encrustations on wellbore screens |
| San Pedro Mártir | 2016 | 0.0170 | Initiation of encrustations on wellbore screens |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benavides-Muñoz, H.M.; Correa-Escudero, V.; Pucha-Cofrep, D.; Pucha-Cofrep, F. Analysis of Land Use Change and Hydrogeological Parameters in the Andean Semiarid Region of Ecuador. Water 2024, 16, 892. https://doi.org/10.3390/w16060892
Benavides-Muñoz HM, Correa-Escudero V, Pucha-Cofrep D, Pucha-Cofrep F. Analysis of Land Use Change and Hydrogeological Parameters in the Andean Semiarid Region of Ecuador. Water. 2024; 16(6):892. https://doi.org/10.3390/w16060892
Chicago/Turabian StyleBenavides-Muñoz, Holger Manuel, Verónica Correa-Escudero, Darwin Pucha-Cofrep, and Franz Pucha-Cofrep. 2024. "Analysis of Land Use Change and Hydrogeological Parameters in the Andean Semiarid Region of Ecuador" Water 16, no. 6: 892. https://doi.org/10.3390/w16060892
APA StyleBenavides-Muñoz, H. M., Correa-Escudero, V., Pucha-Cofrep, D., & Pucha-Cofrep, F. (2024). Analysis of Land Use Change and Hydrogeological Parameters in the Andean Semiarid Region of Ecuador. Water, 16(6), 892. https://doi.org/10.3390/w16060892







