Variability of Double-Porosity Flow, Interporosity Flow Coefficient λ and Storage Ratio ω in Dolomites
Abstract
:1. Introduction
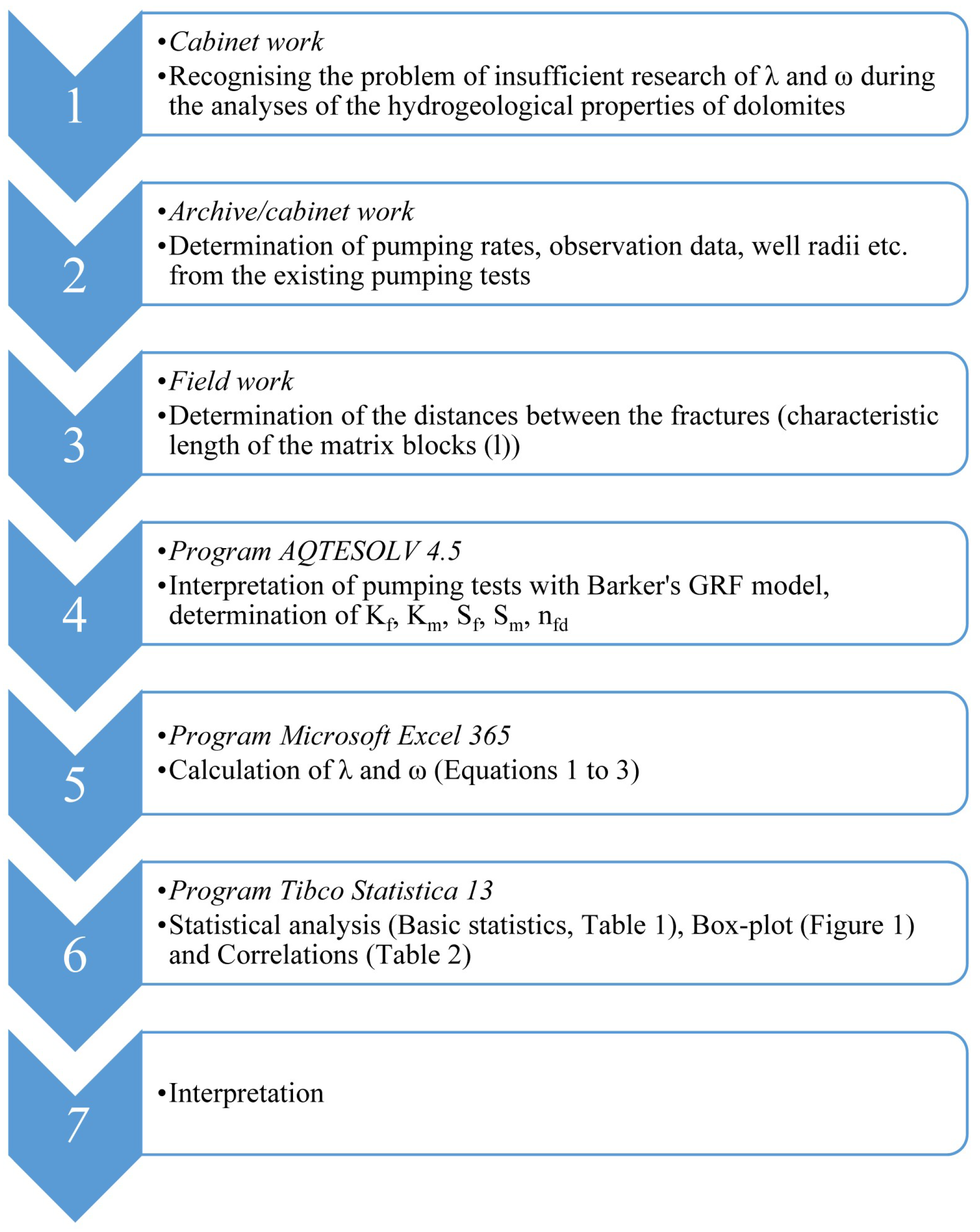
2. Materials and Methods
2.1. Dolomites in Slovenia
2.2. Pumping Test Data
2.3. Interporosity Flow Coefficient (λ)
2.4. Ratio between Storage in Fractures and Storage in the Whole System (ω)—‘Storage Ratio’
3. Results and Discussion
| Dolomite | N | λ-GM [-] | λMIN [-] | λMAX [-] | ω-GM [-] | ω MIN [-] | ω MAX [-] | Kf-GM [m/s] | Km-GM [m/s] | Sf-GM [-] | Sm-GM [-] | nfd [-] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Anisian | 11 | 9.05 × 10−2 | 1.22 × 10−5 | 3.57 × 10−4 | 4.85 × 10−4 | 9.51 × 10−12 | 1.00 × 100 | 4.13 × 10−6 | 2.75 × 10−9 | 1.49 × 10−5 | 1.63 × 10−2 | 2.22 |
| Main | 37 | 1.68 × 10−1 | 3.12 × 10−6 | 7.86 × 10−8 | 1.10 × 10−3 | 5.56 × 10−13 | 1.00 × 100 | 4.21 × 10−6 | 4.06 × 10−9 | 2.18 × 10−7 | 9.01 × 10−5 | 2.11 |
| Scythian | 6 | 1.15 × 10−1 | 3.39 × 10−5 | 7.10 × 10−3 | 3.38 × 10−3 | 1.02 × 10−5 | 2.20 × 10−1 | 3.14 × 10−6 | 2.15 × 10−9 | 2.13 × 10−5 | 1.79 × 10−2 | 1.96 |
| Cordevolian | 14 | 6.53 × 10−1 | 4.07 × 10−6 | 1.24 × 10−6 | 4.73 × 10−2 | 3.42 × 10−4 | 9.81 × 10−1 | 2.48 × 10−5 | 9.65 × 10−8 | 2.04 × 10−4 | 7.22 × 10−3 | 2.34 |
| Bača | 3 | 2.21 × 10−2 | 3.24 × 10−3 | 3.24 × 10−1 | 1.80 × 10−3 | 7.64 × 10−5 | 2.85 × 10−2 | 2.83 × 10−5 | 2.83 × 10−9 | 6.07 × 10−4 | 1.00 × 100 | 2.19 |
| All Groups | 71 | 1.77 × 10−1 | 3.12 × 10−6 | 7.86 × 10−8 | 2.29 × 10−3 | 5.56 × 10−13 | 1.00 × 100 | 6.29 × 10−6 | 6.66 × 10−9 | 3.33 × 10−6 | 1.11 × 10−3 | 2.16 |
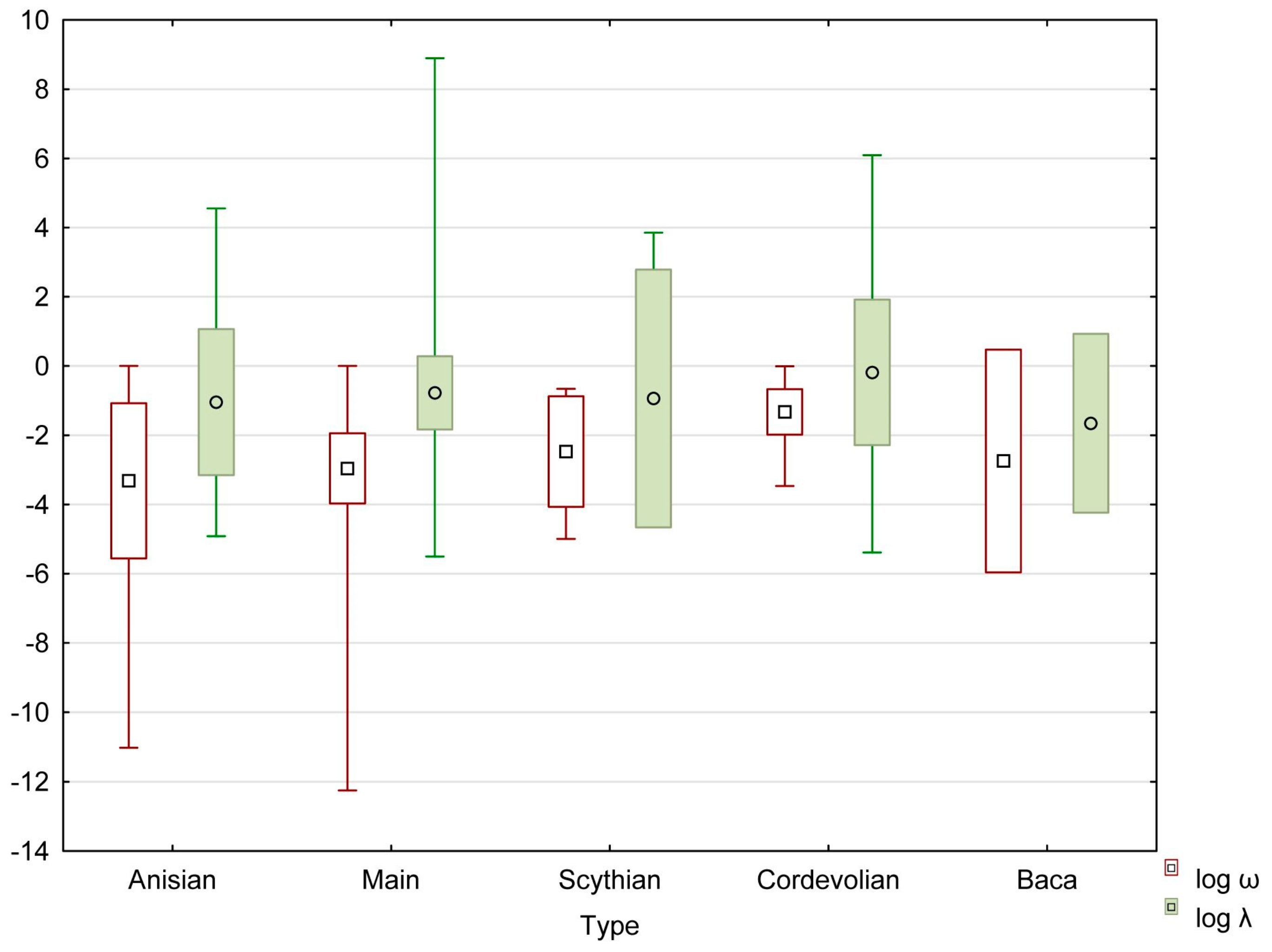
3.1. Interporosity Flow Coefficient (λ)
3.2. Ratio between Storage in the Fractures and Storage in the Whole System (ω)
3.3. Correlations between the Hydrogeological Parameters
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Barenblatt, G.I.; Zheltov, I.P.; Kochina, I.N. Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks. J. Appl. Math. Mech. 1960, 24, 1286–1303. [Google Scholar] [CrossRef]
- Warren, J.E.; Root, P.J. The Behavior of Naturally Fractured Reservoirs. Soc. Pet. Eng. J. 1963, 3, 245–255. [Google Scholar] [CrossRef]
- Bourdet, D.; Gringarten, A. Determination of Fissure Volume and Block Size in Fractured Reservoirs by Type-Curve Analysis. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 23–25 September 1980. [Google Scholar]
- Mavor, M.J.; Cinco-Ley, H. Transient Pressure Behavior Of Naturally Fractured Reservoirs. In Proceedings of the SPE California Regional Meeting, Ventura, CA, USA, 18–20 April 1979. [Google Scholar]
- Kruseman, G.P.; Ridder, N.A.D. Analysis and Evaluation of Pumping Test Data, 2nd ed.; International Institute for Land Reclamation and Improvement: Wageningen, The Netherlands, 2000; p. 275. [Google Scholar]
- Pulido, H.; Samaniego, V.F.; Rivera, J.; Díaz, F.; Galicia, G. On a Well-Test Pressure Theory of Analysis for Naturally Fractured Reservoirs, Considering Transient Interporosity Matrix, Microfractures, Vugs, and Fractures Flow. In Proceedings of the International Oil Conference and Exhibition in Mexico, Cancun, Mexico, 31 August–2 September 2006. [Google Scholar]
- Liu, J.; Bodvarsson, G.S.; Wu, Y.-S. Analysis of flow behavior in fractured lithophysal reservoirs. J. Contam. Hydrol. 2003, 62–63, 189–211. [Google Scholar] [CrossRef]
- Najurieta, H.L. A Theory for Pressure Transient Analysis in Naturally Fractured Reservoirs. J. Petrol. Technol. 1980, 32, 1241–1250. [Google Scholar] [CrossRef]
- Odeh, A.S. Unsteady-State Behavior of Naturally Fractured Reservoirs. Soc. Pet. Eng. J. 1965, 5, 60–66. [Google Scholar] [CrossRef]
- Kazemi, H. Pressure Transient Analysis of Naturally Fractured Reservoirs with Uniform Fracture Distribution. Soc. Pet. Eng. J. 1969, 9, 451–462. [Google Scholar] [CrossRef]
- Kazemi, H.; Seth, M.S.; Thomas, G.W. The Interpretation of Interference Tests in Naturally Fractured Reservoirs with Uniform Fracture Distribution. Soc. Pet. Eng. J. 1969, 9, 463–472. [Google Scholar] [CrossRef]
- de Swaan, O.A. Analytic Solutions for Determining Naturally Fractured Reservoir Properties by Well Testing. Soc. Pet. Eng. J. 1976, 16, 117–122. [Google Scholar] [CrossRef]
- Serra, K.; Reynolds, A.C.; Raghavan, R. New Pressure Transient Analysis Methods for Naturally Fractured Reservoirs (includes associated papers 12940 and 13014). J. Petrol. Technol. 1983, 35, 2271–2283. [Google Scholar] [CrossRef]
- Moench, A.F. Double-Porosity Models for a Fissured Groundwater Reservoir with Fracture Skin. Water Resour. Res. 1984, 20, 831–846. [Google Scholar] [CrossRef]
- Gringarten, A.C. Flow-Test Evaluation of Fractured Reservoirs. In Recent Trends in Hydrogeology; Geological Society of America Special Papers; Geological Society of America: Boulder, CO, USA, 1982; pp. 237–264. [Google Scholar]
- Huang, S.; Ma, X.; Yong, R.; Wu, J.; Zhang, J.; Wu, T. Transient Interporosity Flow in Shale/Tight Oil Reservoirs: Model and Application. ACS Omega 2022, 7, 14746–14755. [Google Scholar] [CrossRef]
- Al-Bemani, A.S.; Ershaghi, I. Two-Phase Flow Interporosity Effects on Pressure Transient Test Response in Naturally Fractured Reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 6–9 October 1991. [Google Scholar]
- Ogorelec, B.; Dolenec, T.; Pezdič, J. Isotope composition of O and C in Mesosoic carbonate rocks of Slovenia—Effect of facies and diagenesis. Geologija 1999, 42, 171–205. [Google Scholar] [CrossRef]
- Verbovšek, T.; Veselič, M. Factors influencing the hydraulic properties of wells in dolomite aquifers of Slovenia. Hydrogeol. J. 2008, 16, 779–795. [Google Scholar] [CrossRef]
- Verbovšek, T. Estimation of transmissivity and hydraulic conductivity from specific capacity and specific capacity index in dolomite aquifers. J. Hydrol. Eng. 2008, 13, 817–823. [Google Scholar] [CrossRef]
- Verbovšek, T. Diagenetic effects on the well yield of dolomite aquifers in Slovenia. Environ. Geol. 2008, 53, 1173–1182. [Google Scholar] [CrossRef]
- Verbovšek, T. Hydraulic conductivities of fractures and matrix in Slovenian carbonate aquifers. Geologija 2008, 51, 245–255. [Google Scholar] [CrossRef]
- Verbovšek, T. Influences of Aquifer Properties on Flow Dimensions in Dolomites. Ground Water 2009, 47, 660–668. [Google Scholar] [CrossRef]
- Barker, J.A. A Generalized Radial Flow Model for Hydraulic Tests in Fractured Rock. Water Resour. Res. 1988, 24, 1796–1804. [Google Scholar] [CrossRef]
- Hamm, S.-Y.; Bidaux, P. Dual-Porosity Fractal Models for Transient Flow Analysis in Fissured Rocks. Water Resour. Res. 1996, 32, 2733. [Google Scholar] [CrossRef]
- Hydrosolve. AQTESOLV for Windows; Version 4.5; Hydrosolve Inc.: Reston, VA, USA, 2006. [Google Scholar]
- StatSoft GmbH. Tibco Statistica; Version 13.3; StatSoft GmbH: Hamburg, Germany, 2019. [Google Scholar]
- Lim, K.T.; Aziz, K. Matrix-fracture transfer shape factors for dual-porosity simulators. J. Petrol. Sci. Eng. 1995, 13, 169–178. [Google Scholar] [CrossRef]
- Lai, K.S.; Pao, W.K.S. Assessment of Different Matrix-fracture Shape Factor in Double Porosity Medium. J. Appl. Sci. 2013, 13, 308–314. [Google Scholar] [CrossRef]
- Bauer, H.; Schröckenfuchs, T.C.; Decker, K. Hydrogeological properties of fault zones in a karstified carbonate aquifer (Northern Calcareous Alps, Austria). Hydrogeol. J. 2016, 24, 1147–1170. [Google Scholar] [CrossRef]
- Čar, J. Geostructural mapping of karstified limestones. Geologija 2018, 61, 133–162. [Google Scholar] [CrossRef]
- Caine, J.S.; Evans, J.P.; Forster, C.B. Fault zone architecture and permeability structure. Geology 1996, 24, 1025–1028. [Google Scholar] [CrossRef]
- Pavičić, I.; Duić, Ž.; Vrbaški, A.; Dragičević, I. Fractal Characterization of Multiscale Fracture Network Distribution in Dolomites: Outcrop Analogue of Subsurface Reservoirs. Fractal Fract. 2023, 7, 676. [Google Scholar] [CrossRef]
- Verbovšek, T. Extrapolation of fractal dimensions of natural fracture networks from one to two dimensions in dolomites of Slovenia. Geosci. J. 2009, 13, 343–351. [Google Scholar] [CrossRef]
- Verbovšek, T.; Kanduč, T. Isotope Geochemistry of Groundwater from Fractured Dolomite Aquifers in Central Slovenia. Aquat. Geochem. 2015, 22, 131–151. [Google Scholar] [CrossRef]
- Uldrich, D.O.; Ershaghi, I. A Method for Estimating the Interporosity Flow Parameter in Naturally Fractured Reservoirs. Soc. Pet. Eng. J. 1979, 19, 324–332. [Google Scholar] [CrossRef]
- Crawford, G.E.; Hagedorn, A.R.; Pierce, A.E. Analysis of Pressure Buildup Tests in a Naturally Fractured Reservoir. J. Petrol. Technol. 1976, 28, 1295–1300. [Google Scholar] [CrossRef]
- Rebolledo, L.C.; Ershaghi, I. Errors in Estimating Interporosity Flow Coefficient in Naturally Fractured Reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 28–30 September 2015. [Google Scholar]
- Gringarten, A.C. Interpretation of Tests in Fissured and Multilayered Reservoirs With Double-Porosity Behavior: Theory and Practice. J. Petrol. Technol. 1984, 36, 549–564. [Google Scholar] [CrossRef]
- de Sá, M.; Joaquim, P. Applied Statistics Using SPSS, STATISTICA, MATLAB and R.; Springer: Berlin, Germany, 2007; p. 505. [Google Scholar]
- Negra, M.H.; Purser, B.H.; M’Rabet, A. Permeability and Porosity Evolution in Dolomitized Upper Cretaceous Pelagic Limestones of Central Tunisia. In Dolomites; Blackwell Publishing Ltd.: London, UK, 2009; pp. 309–323. [Google Scholar]
- Warren, J. Dolomite: Occurrence, evolution and economically important associations. Earth-Sci. Rev. 2000, 52, 1–81. [Google Scholar] [CrossRef]
- Stearns, D.W.; Friedman, N. Reservoirs in Fractured Rock. In AAPG Memoir 16: Stratigraphic Oil and Gas Fields—Classification, Exploration Methods, and Case Histories; Gould, H.R., Ed.; American Association of Petroleum Geologists (AAPG): Tulsa, OK, USA, 1972; Volume 16, pp. 82–106. [Google Scholar]
- Aguilera, R. Naturally Fractured Reservoirs; PennWell Books: Tulsa, OK, USA, 1980. [Google Scholar]
- Gaswirth, S.B.; Budd, D.A.; Crawford, B.R. Textural and stratigraphic controls on fractured dolomite in a carbonate aquifer system, Ocala limestone, west-central Florida. Sediment. Geol. 2006, 184, 241–254. [Google Scholar] [CrossRef]

| Duration [min] | Q [L/s] | Kf [m/s] | Sf [-] | Km [m/s] | Sm [-] | rw [m] | ω [-] | λ [-] | |
|---|---|---|---|---|---|---|---|---|---|
| Duration [min] | 1.000 | 0.070 | 0.179 | 0.174 | −0.025 | 0.081 | −0.026 | 0.130 | −0.093 |
| Q [L/s] | 0.070 | 1.000 | 0.563 * | 0.058 | 0.149 | −0.080 | 0.022 | 0.060 | 0.004 |
| Kf [m/s] | 0.179 | 0.563 * | 1.000 | 0.132 | 0.087 | −0.060 | −0.058 | 0.157 | −0.209 |
| Sf [-] | 0.174 | 0.058 | 0.132 | 1.000 | 0.341 * | 0.418 * | −0.190 | 0.521 * | 0.284 * |
| Km [m/s] | −0.025 | 0.149 | 0.087 | 0.341 * | 1.000 | 0.084 | 0.033 | 0.227 | 0.940 * |
| Sm [-] | 0.081 | −0.080 | −0.060 | 0.418 * | 0.084 | 1.000 | −0.028 | −0.430 * | 0.096 |
| rw [m] | −0.026 | 0.022 | −0.058 | −0.190 | 0.033 | −0.028 | 1.000 | −0.136 | 0.064 |
| ω [-] | 0.130 | 0.060 | 0.157 | 0.521 * | 0.227 | −0.430 * | −0.136 | 1.000 | 0.179 |
| λ [-] | −0.093 | 0.004 | −0.209 | 0.284 * | 0.940 * | 0.096 | 0.064 | 0.179 | 1.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verbovšek, T. Variability of Double-Porosity Flow, Interporosity Flow Coefficient λ and Storage Ratio ω in Dolomites. Water 2024, 16, 1072. https://doi.org/10.3390/w16081072
Verbovšek T. Variability of Double-Porosity Flow, Interporosity Flow Coefficient λ and Storage Ratio ω in Dolomites. Water. 2024; 16(8):1072. https://doi.org/10.3390/w16081072
Chicago/Turabian StyleVerbovšek, Timotej. 2024. "Variability of Double-Porosity Flow, Interporosity Flow Coefficient λ and Storage Ratio ω in Dolomites" Water 16, no. 8: 1072. https://doi.org/10.3390/w16081072






