Spatial Coupling Analysis of Urban Waterlogging Depth and Value Based on Land Use: Case Study of Beijing
Abstract
1. Introduction
2. Materials and Methods
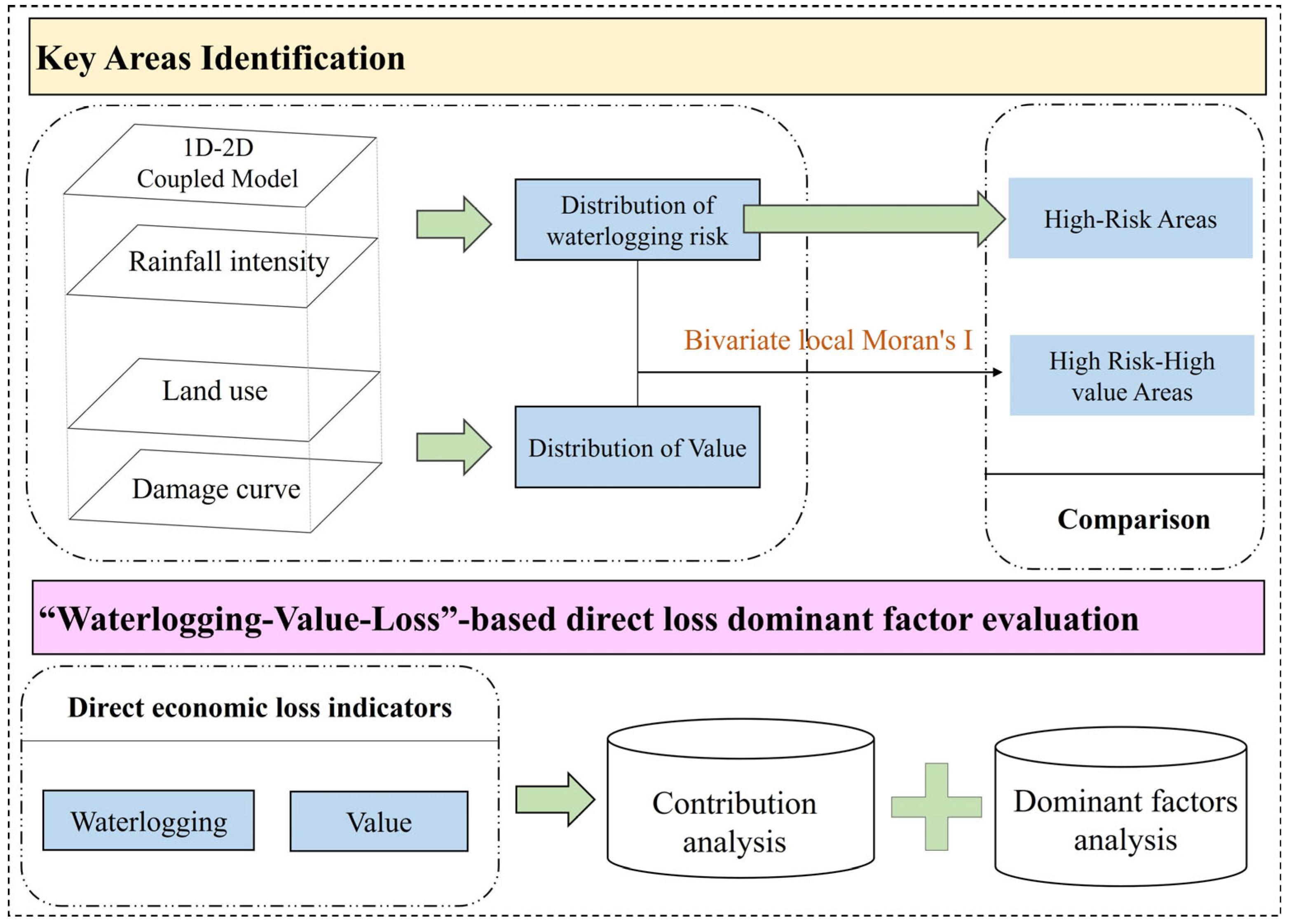
2.1. Research Framework
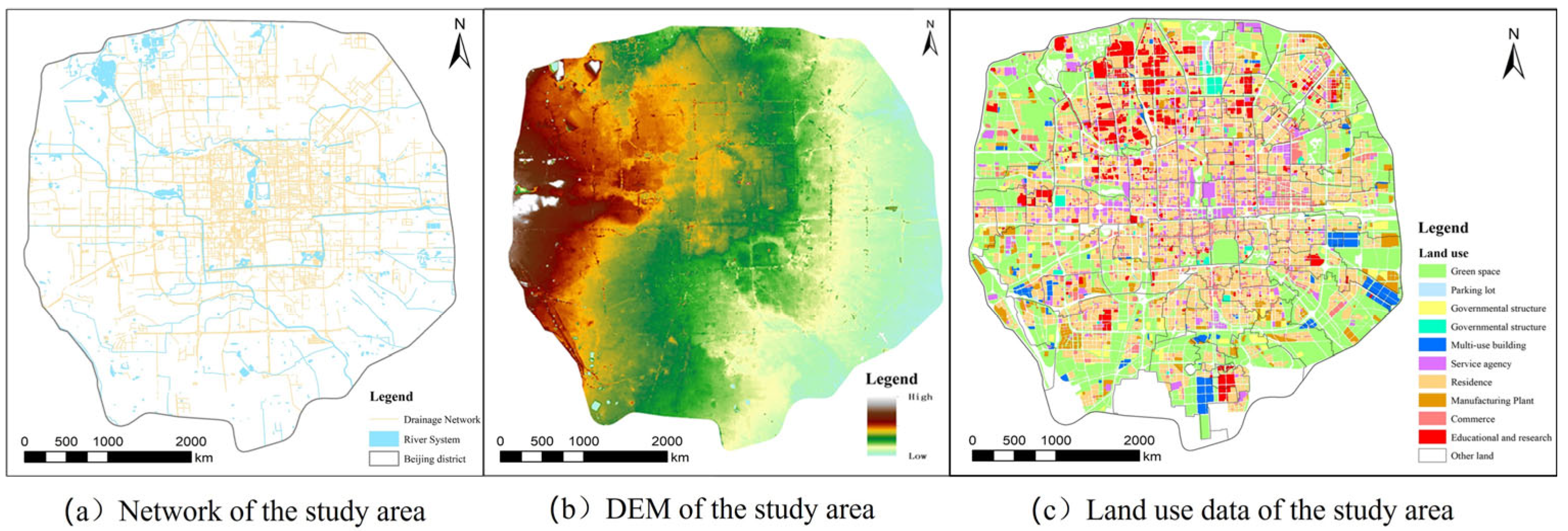
2.2. Study Area
2.3. Urban Waterlogging Model Construction
2.3.1. Model Construction
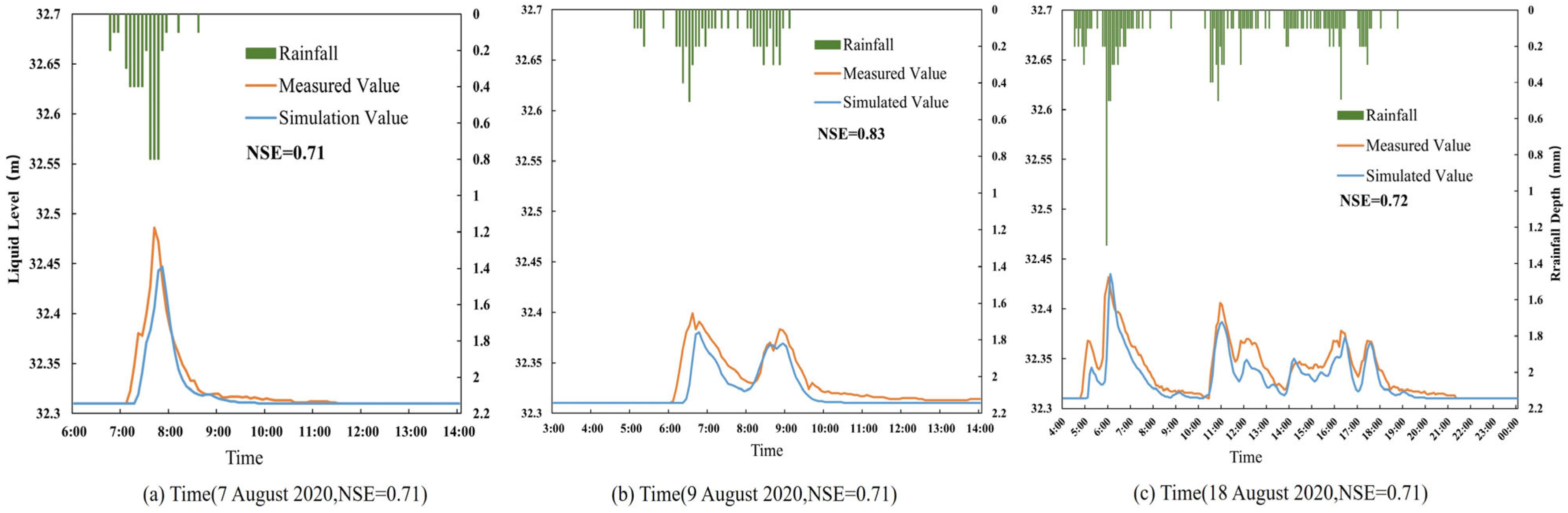
2.3.2. Model Accuracy Verification
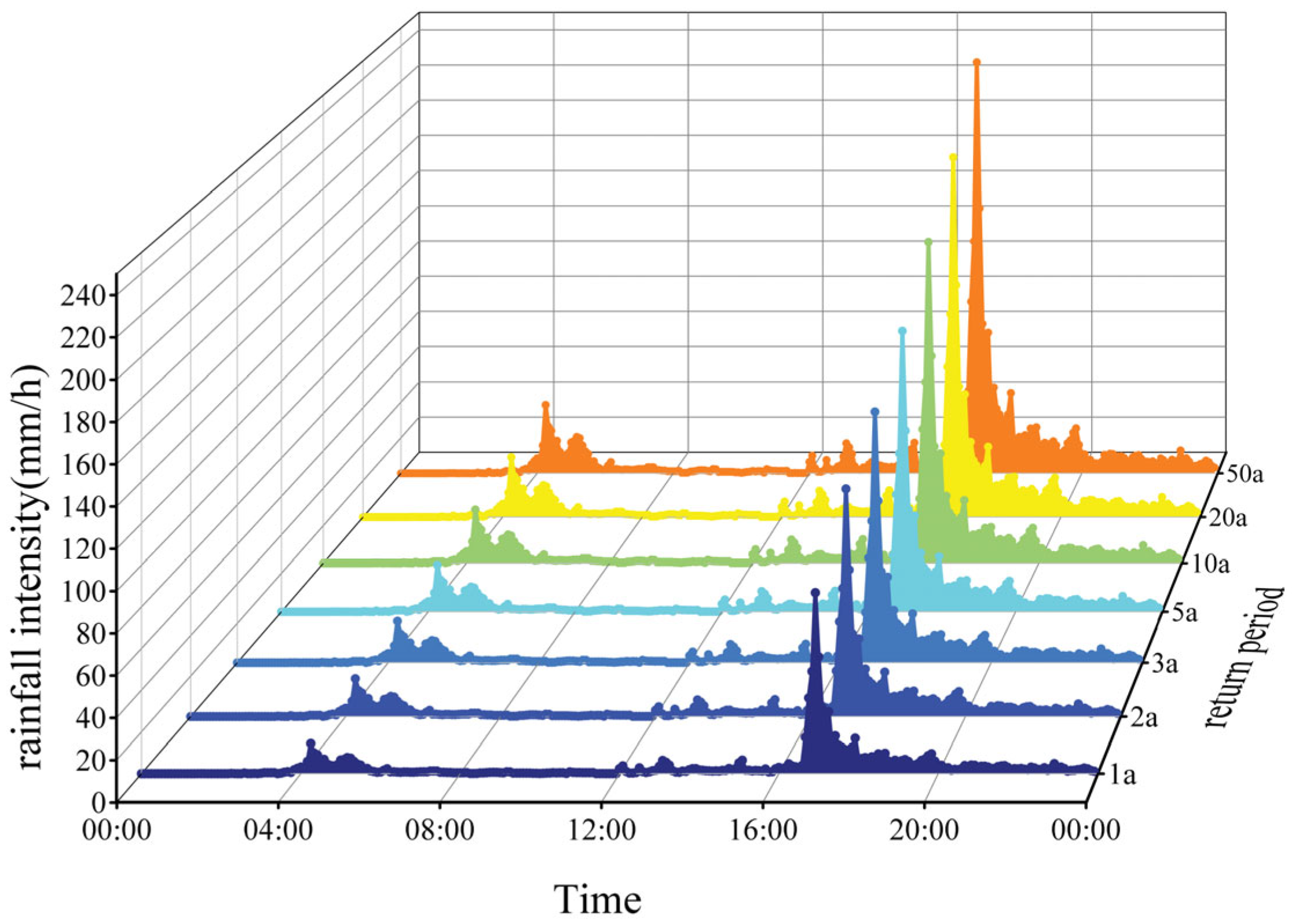
2.3.3. Design Rainfall Scenarios
2.4. Land Use Value Assessment Based on the Integration Method
2.5. Local Spatial Autocorrelation Analysis Based on Local Moran’s I
2.6. Contribution Analysis
2.6.1. Urban Flooding Loss Analysis
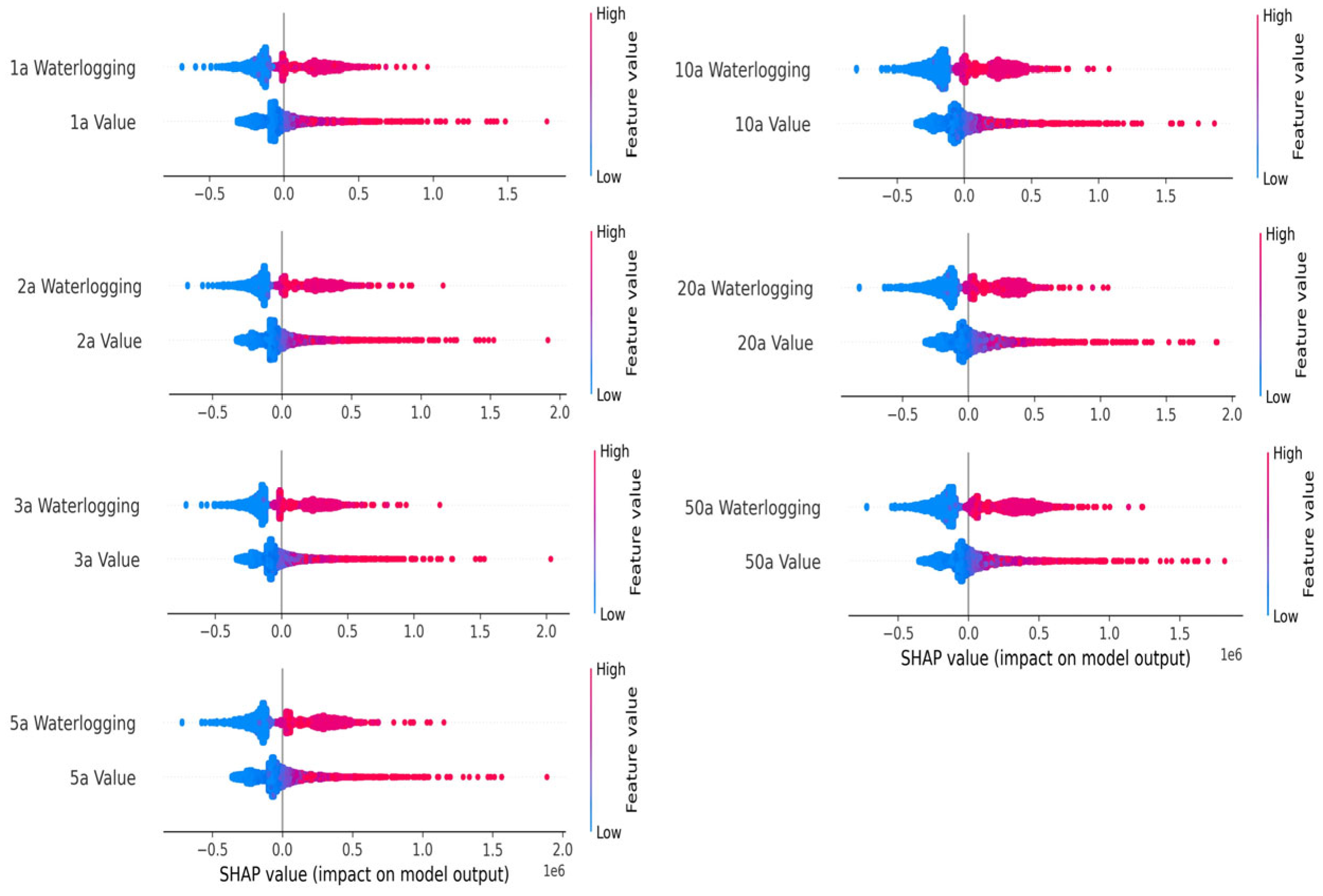
2.6.2. Relative Contribution Analysis Based on Shapley Value
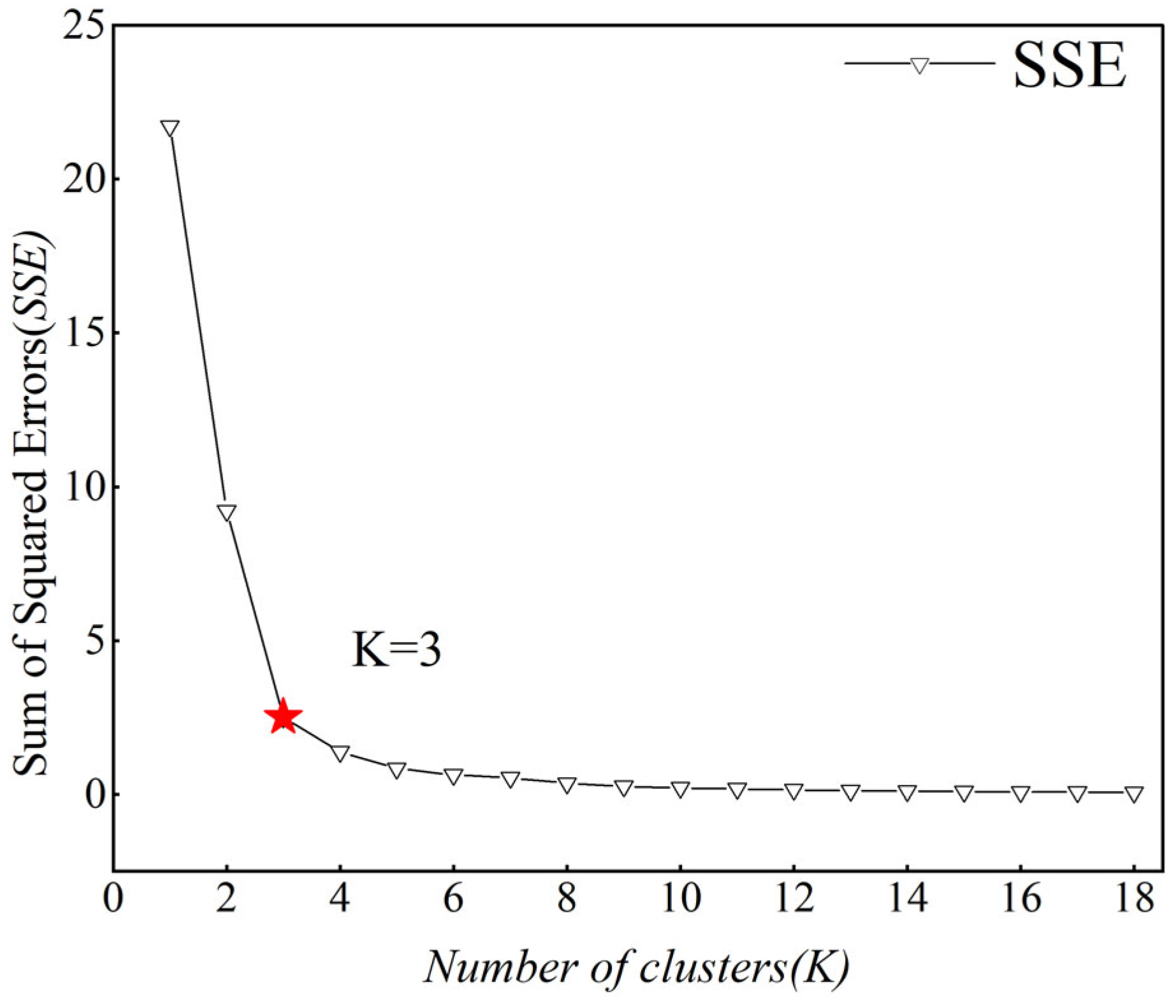
2.6.3. Dominant Factor Analysis Based on the Birch-K-Means Combined Algorithm
3. Results
3.1. Urban Waterlogging Risk and Value Analysis
3.1.1. Urban Waterlogging Risk Analysis
3.1.2. Value Analysis of Land Use
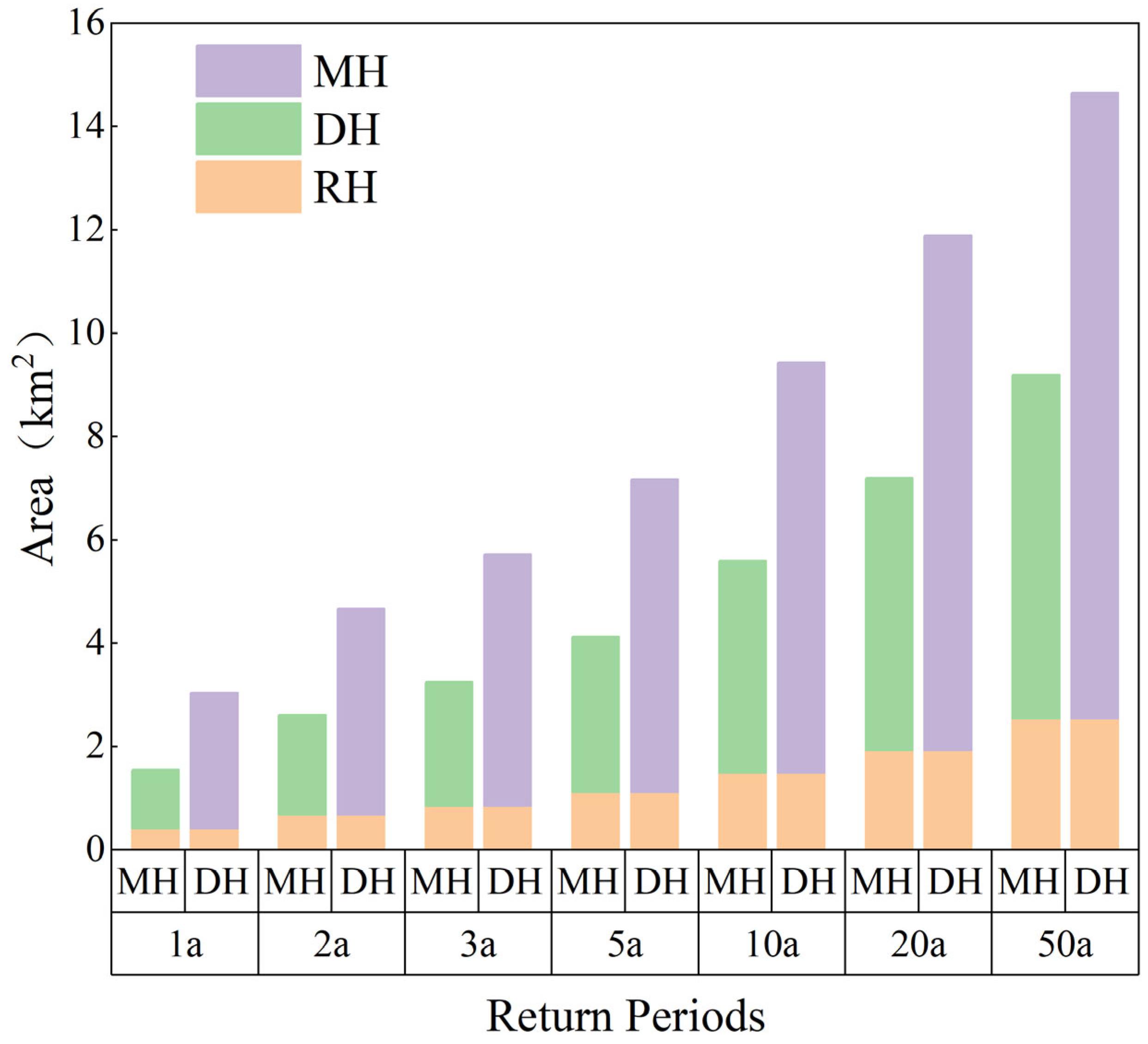
3.2. Analysis of the Spatial Overlap Between Urban Waterlogging Risk and Land Value
3.3. Contribution Analysis
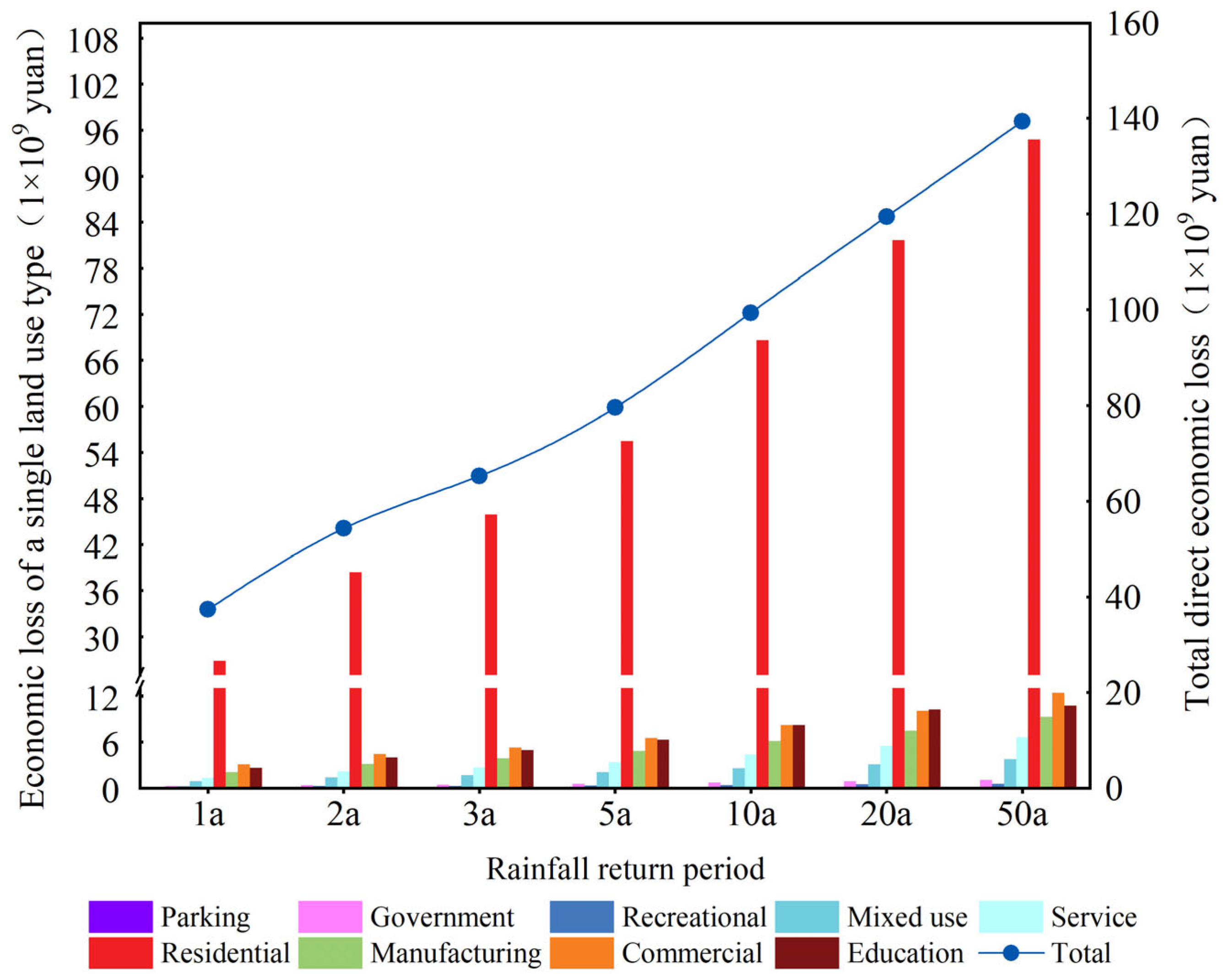
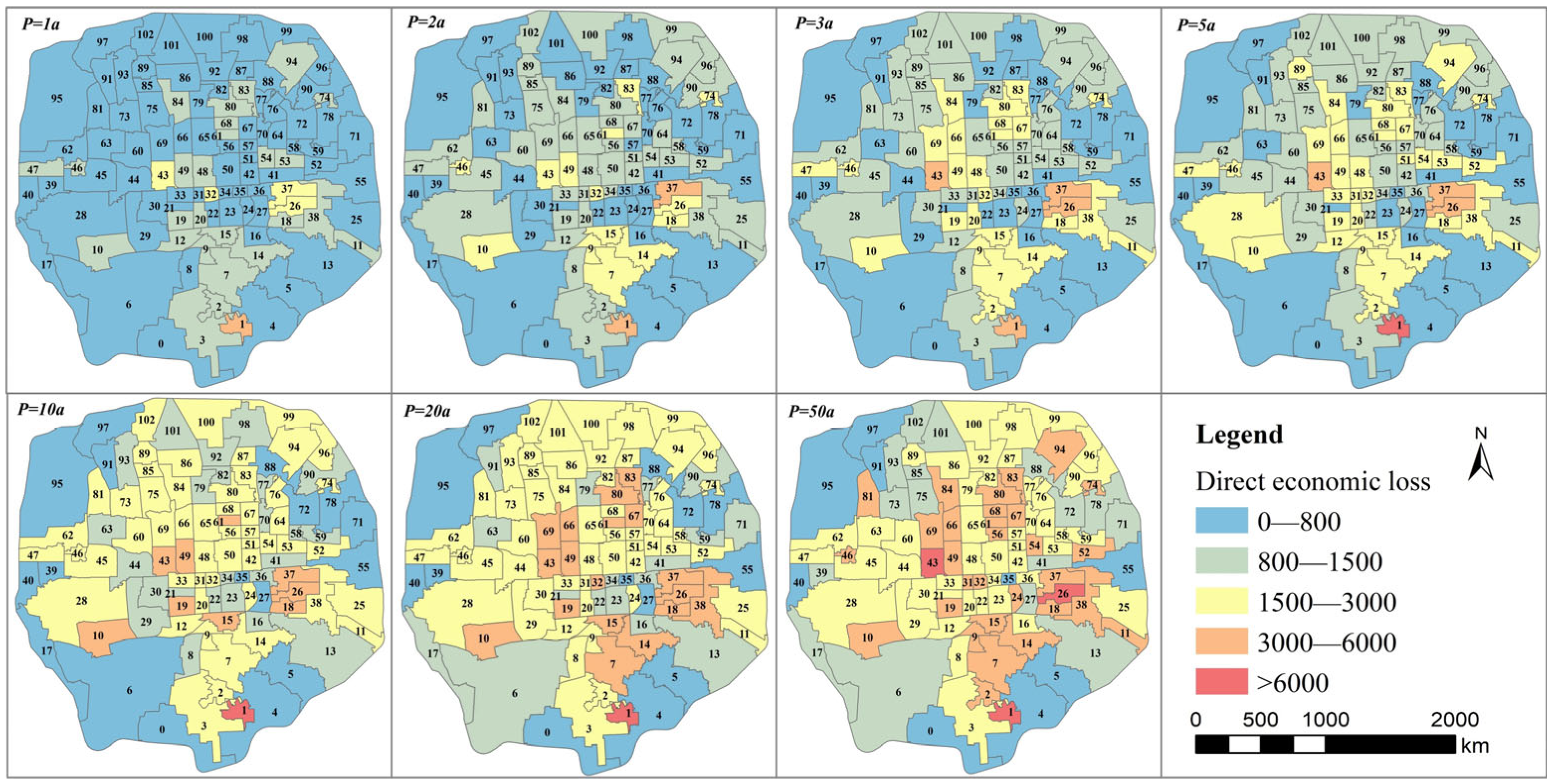
3.3.1. Waterlogging Loss Analysis
3.3.2. Dominant Factor Analysis
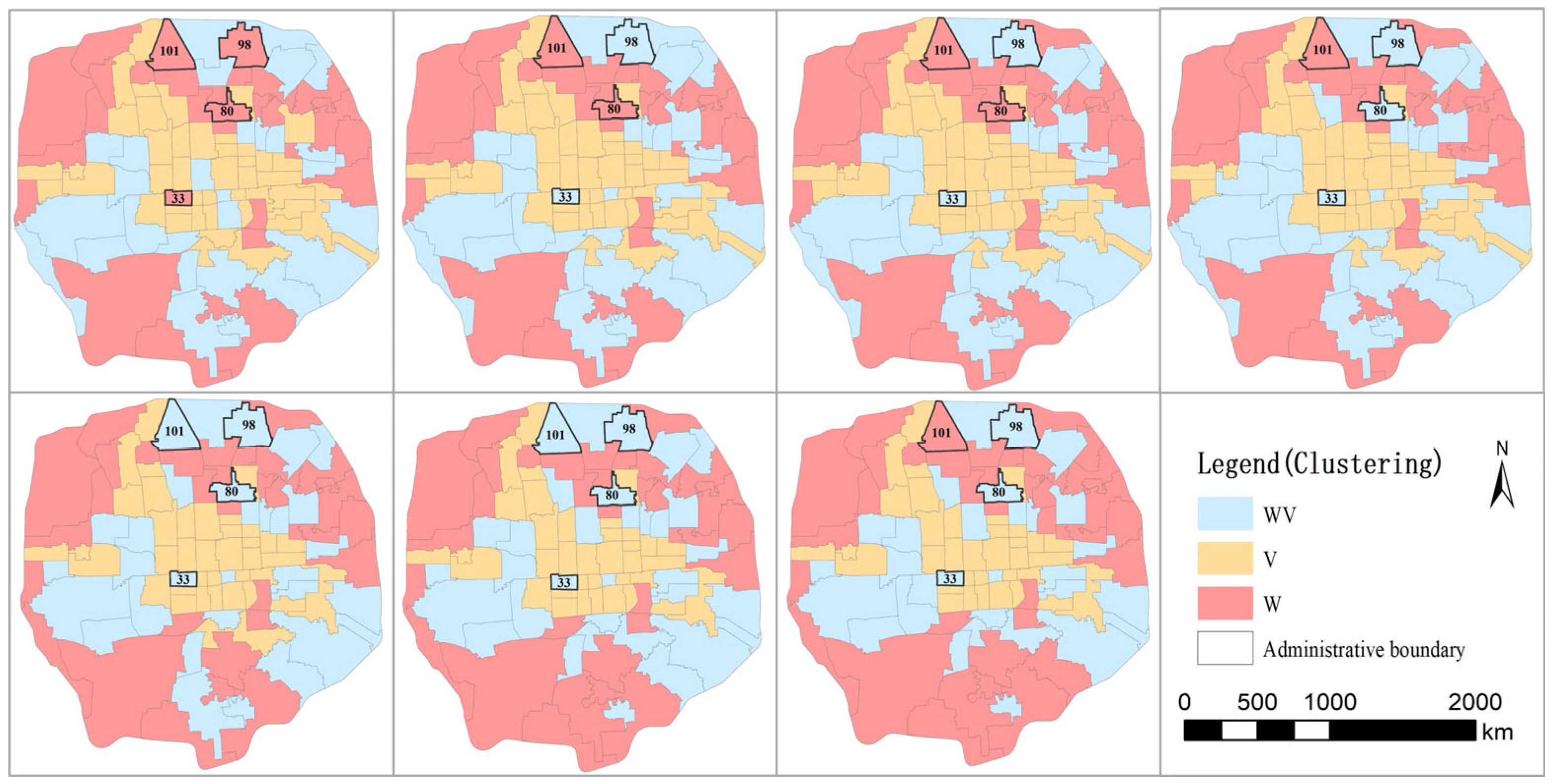
3.3.3. Clustering Analysis
4. Discussion
4.1. Spatial Coupling Characteristics of Waterlogging, Value, and Loss
4.2. Analysis of Factors Influencing Urban Waterlogging Losses
4.3. Urban Disaster Prevention and Mitigation Strategies Based on Risk and Value
- (1)
- This study, based on the spatial coupling relationship between urban value and waterlogging risk, categorizes urban waterlogging risk into five types, prioritizing high-risk, high-value lands. Although these lands account for only 1.5% of the affected areas, they contribute to 35% of flood losses. To mitigate risks in these areas, it is necessary to strengthen infrastructure development by adding new branch pipelines and constructing reservoirs to enhance drainage and storage capacity, reducing sewer overflow. Simultaneously, optimize spatial layout by transforming underutilized spaces into landscaped green areas, such as designing sunken plazas in commercial districts. For low-waterlogging, high-value areas, proactive flood prevention measures are essential, including issuing flood warnings, protecting or relocating critical assets, and safeguarding entrances to basements and underground parking lots. In high-waterlogging, low-value lands, measures should be tailored to different land-use types. For instance, the development of parks and green spaces should be restricted to enhance their stormwater ecological functions.
- (2)
- Based on the spatial distribution characteristics of waterlogging losses at the street scale and the clustering results, differentiated prevention and control strategies should be developed. For waterlogging-dominated streets, priority should be given to enhancing the drainage network capacity and adding decentralized storage facilities. For value-dominated streets, the focus should be on strengthening asset protection systems and improving insurance mechanisms. For waterlogging-value co-dominated streets, systematic governance should be carried out in conjunction with regional characteristics to improve disaster prevention and mitigation efficiency. It is worth noting that for streets prone to type migration with increasing return periods, a dynamic monitoring and evaluation system should be established to adjust prevention and control measures in a timely manner.
5. Conclusions
- (1)
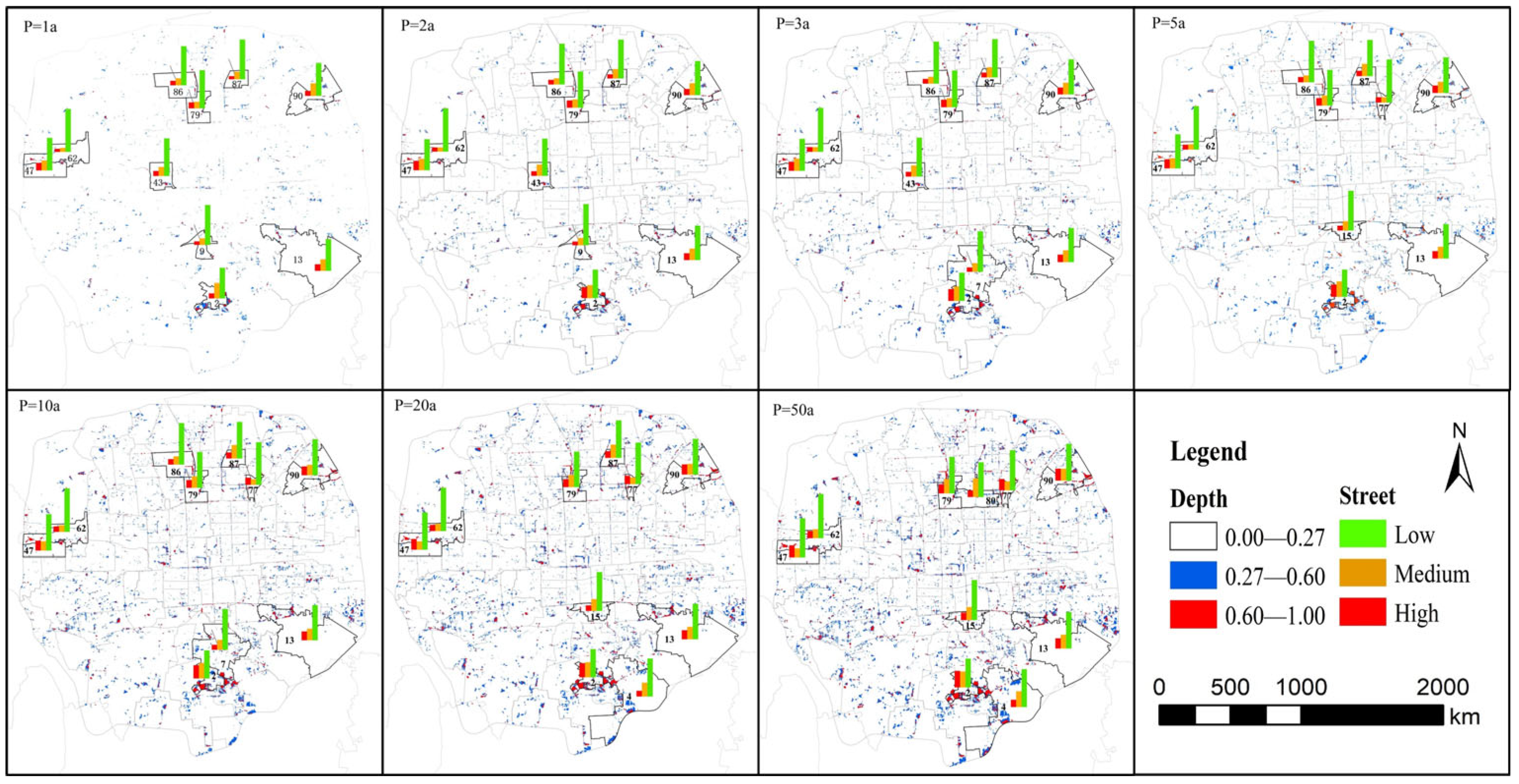
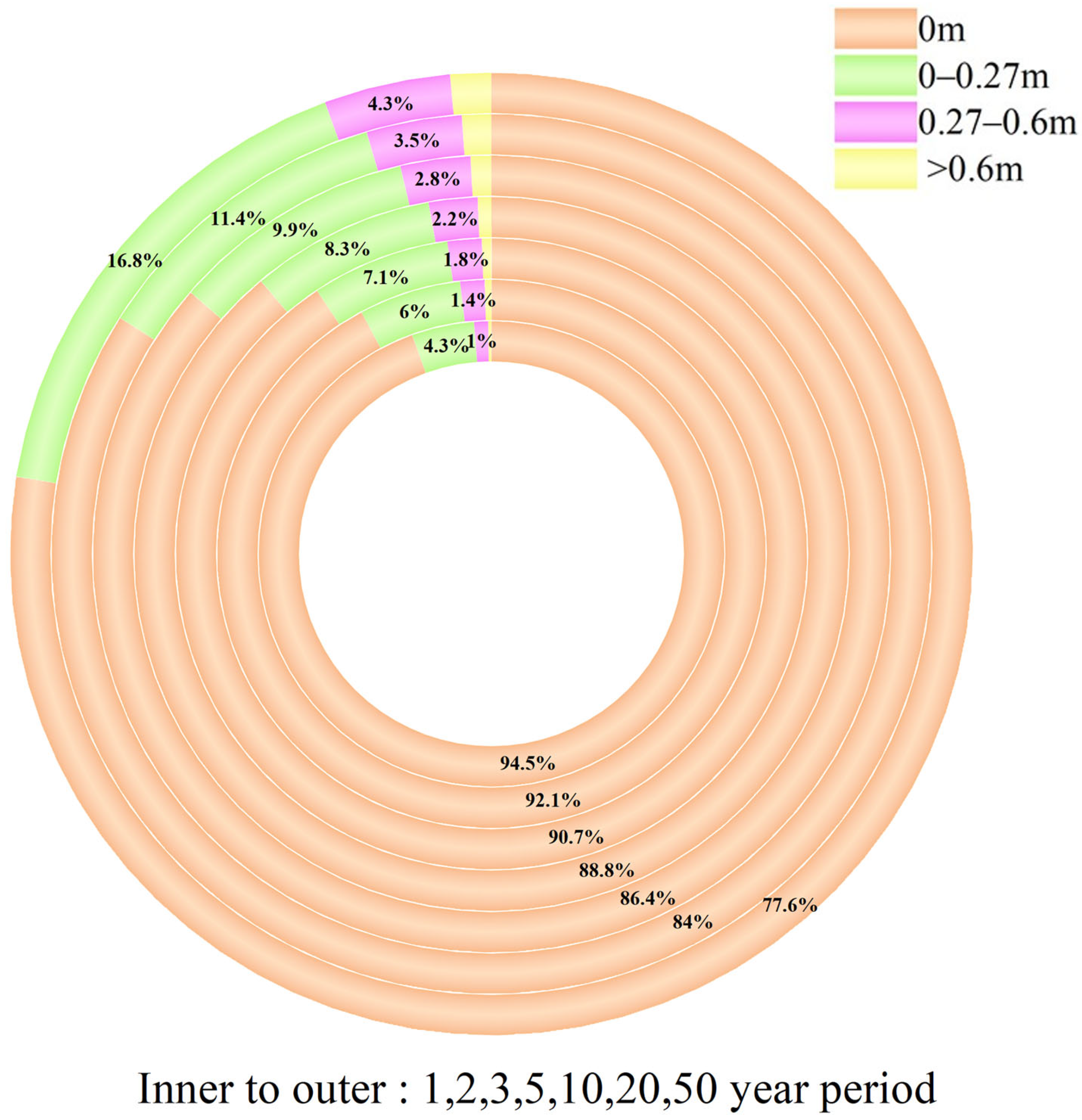
- The urban waterlogging coupling model can effectively identify areas at risk of waterlogging and, when combined with disaster loss curves, can quantitatively assess the economic losses caused by waterlogging. The study reveals that waterlogging hotspots are primarily concentrated in areas outside the Fourth Ring Road with sparse drainage networks. As the rainfall return period increases, waterlogging depth gradually rises, and the affected area expands from 5.5% to 22.4%. Economic losses also grow from CNY 3.73 billion to CNY 13.93 billion, with the most significant losses occurring in educational and research land, commercial land, and residential land.
- (2)
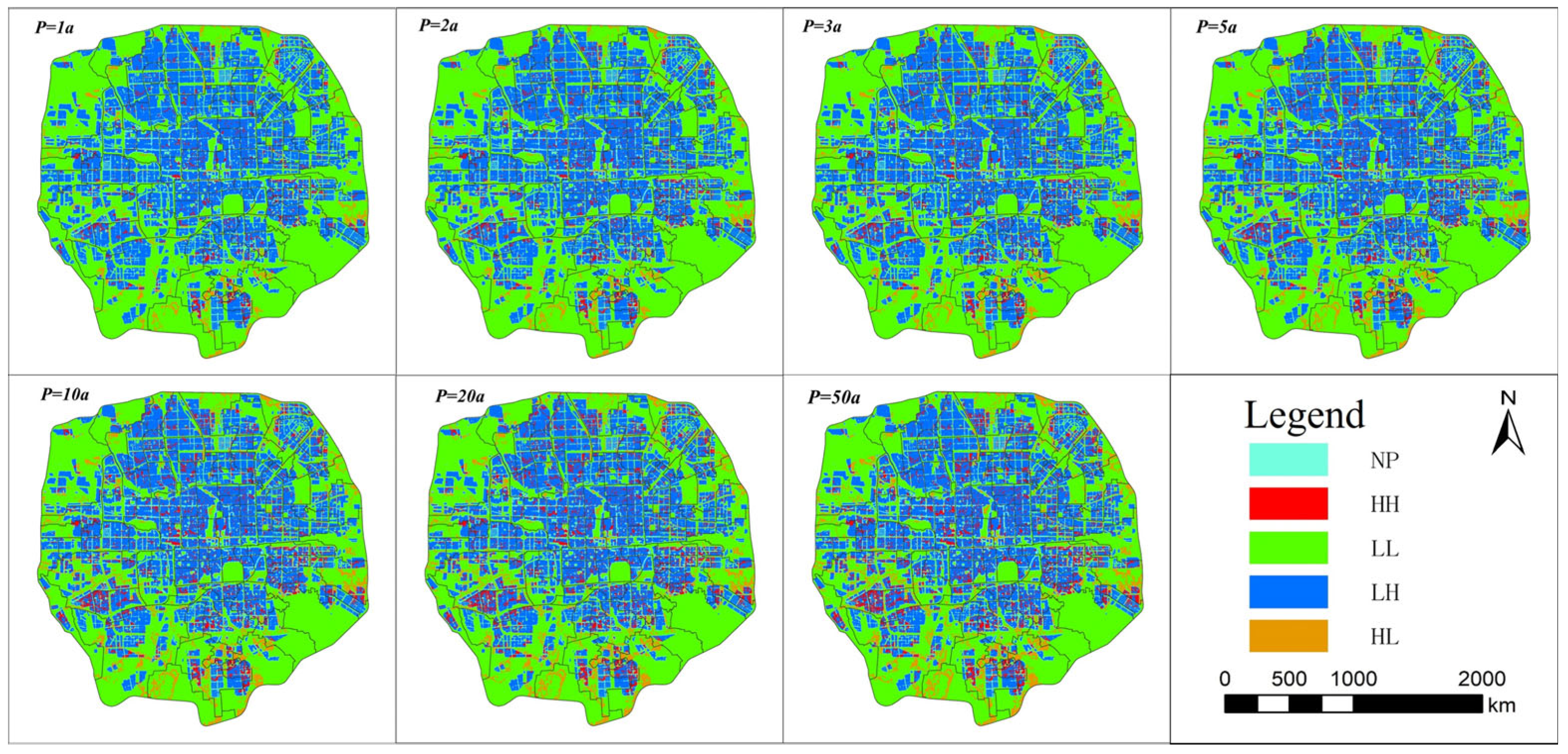
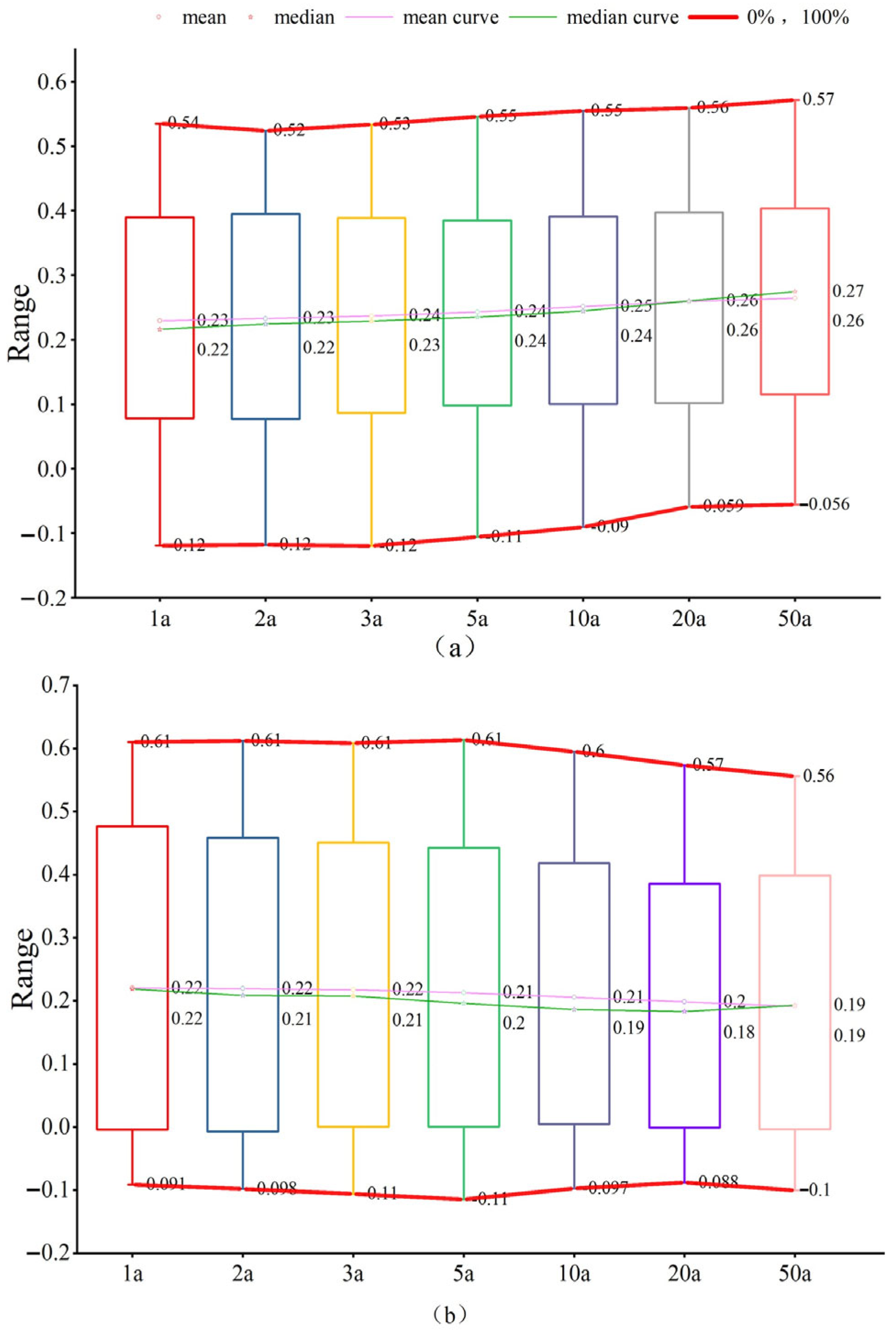
- The use of bivariate spatial correlation analysis has significantly improved the accuracy of identifying key areas of concern for urban waterlogging. The spatial distribution of urban waterlogging risk and value exhibits significant heterogeneity, characterized by relatively lower waterlogging risks in areas with higher value. By comprehensively considering both value and risk, it is possible to more precisely identify priority areas. Based on the 1-year return period scenario, 66% of the areas identified as key concern zones based solely on waterlogging risk were overlooked in the bivariate spatial correlation analysis. On the other hand, 2.61 km2 of areas, due to their higher land-use value, were prioritized in the results of the bivariate spatial correlation analysis.
- (3)
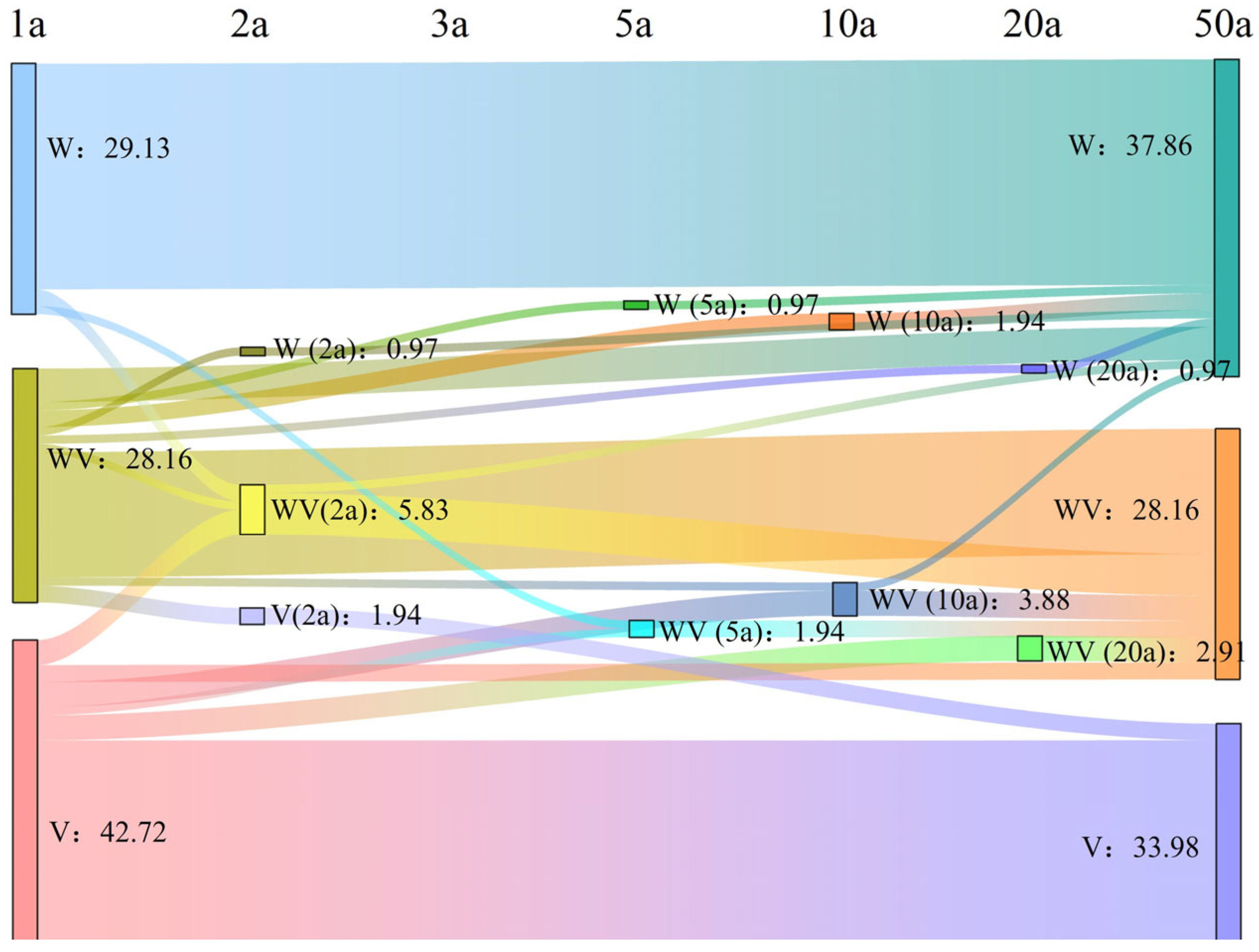
- The “Waterlogging-Value-Loss” assessment framework effectively reveals the changing characteristics of the relative contributions of water depth and value to waterlogging losses. The study found that as the return period increases, the relative contribution of water depth rises from 66% to 75%, while the relative contribution of value gradually decreases. Additionally, the dominant factors of loss across different streets also change with the return period, with 22.23% of streets experiencing a shift in factor type, demonstrating a clear temporal transition characteristic. For example, the proportion of W-type streets decreased from 43% to 34%, while the proportion of V-type streets increased from 29% to 38%. This dynamic nature requires that prevention and control measures be tailored to regional characteristics and return periods to enhance the precision and effectiveness of disaster prevention and mitigation efforts.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chocat, B.; Ashley, R.; Marsalek, J.; Matos, M.R.; Rauch, W.; Schilling, W.; Urbonas, B. Toward the Sustainable Management of Urban Storm-Water. Indoor Built Environ. 2007, 16, 273–285. [Google Scholar] [CrossRef]
- Güneralp, B.; Reba, M.; Hales, B.U.; Wentz, E.A.; Seto, K.C. Trends in Urban Land Expansion, Density, and Land Transitions from 1970 to 2010: A Global Synthesis. Environ. Res. Lett. 2020, 15, 044015. [Google Scholar] [CrossRef]
- Sun, S.; Zhai, J.; Li, Y.; Huang, D.; Wang, G. Urban Waterlogging Risk Assessment in Well-Developed Region of Eastern China. Phys. Chem. Earth Parts ABC 2020, 115, 102824. [Google Scholar] [CrossRef]
- Su, X.; Shao, W.; Liu, J.; Jiang, Y.; Wang, K. Dynamic Assessment of the Impact of Flood Disaster on Economy and Population under Extreme Rainstorm Events. Remote Sens. 2021, 13, 3924. [Google Scholar] [CrossRef]
- Lewis, J.A.; Zipperer, W.C.; Ernstson, H.; Bernik, B.; Hazen, R.; Elmqvist, T.; Blum, M.J. Socioecological Disparities in New Orleans Following Hurricane Katrina. Ecosphere 2017, 8, e01922. [Google Scholar] [CrossRef]
- Compilation Group of China Flood and Drought Disaster Prevention Bulletin. Summary of China Flood and Drought Disaster Prevention Bulletin 2020. China Flood Drought Manag. 2021, 31, 26–32. [Google Scholar]
- Sun, R.; An, D.; Lu, W.; Shi, Y.; Wang, L.; Zhang, C.; Zhang, P.; Qi, H.; Wang, Q. Impacts of a Flash Flood on Drinking Water Quality: Case Study of Areas Most Affected by the 2012 Beijing Flood. Heliyon 2016, 2, e00071. [Google Scholar] [CrossRef]
- Yang, M.; Mohammad Yusoff, W.F.; Mohamed, M.F.; Jiao, S.; Dai, Y. Flood Economic Vulnerability and Risk Assessment at the Urban Mesoscale Based on Land Use: A Case Study in Changsha, China. J. Environ. Manag. 2024, 351, 119798. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Jiang, R.; Yang, M.; Xie, J.; Wang, Y.; Li, W. Urban Rainstorm and Waterlogging Scenario Simulation Based on SWMM under Changing Environment. Environ. Sci. Pollut. Res. 2023, 30, 123351–123367. [Google Scholar] [CrossRef] [PubMed]
- Tan, K.M.; Seow, W.K.; Wang, C.L.; Kew, H.J.; Parasuraman, S.B. Evaluation of Performance of Active, Beautiful and Clean (ABC) on Stormwater Runoff Management Using MIKE URBAN: A Case Study in a Residential Estate in Singapore. Urban Water J. 2019, 16, 156–162. [Google Scholar] [CrossRef]
- Yang, H.; Tong, X.; Gou, D. Study on the Waterlogging Operation Effects of InfoWorks ICM Dispatching Strategies. E3S Web Conf. 2021, 228, 01009. [Google Scholar] [CrossRef]
- Guo, W.; Zhai, M.; Lei, X.; Huang, H.; Long, Y.; Li, S. Two-Dimensional Hydrodynamic Simulation of the Effect of Stormwater Inlet Blockage on Urban Waterlogging. Water 2024, 16, 2029. [Google Scholar] [CrossRef]
- Ji, X.; Dong, W.; Wang, W.; Dai, X.; Huang, H. Impacts of Climate Change on Extreme Precipitation Events and Urban Waterlogging: A Case Study of Beijing. Nat. Hazards Rev. 2024, 25, 05023014. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, P.; Dai, S.; Han, Y.; Chang, X. Urban HydroConnect: Harnessing SWMM for Dynamic Waterway Management Assessment. Water Resour. Manag. 2024, 38, 4473–4498. [Google Scholar] [CrossRef]
- Haq, M.; Akhtar, M.; Muhammad, S.; Paras, S.; Rahmatullah, J. Techniques of Remote Sensing and GIS for Flood Monitoring and Damage Assessment: A Case Study of Sindh Province, Pakistan. Egypt. J. Remote Sens. Space Sci. 2012, 15, 135–141. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Q.; Lin, K.; Liu, Z.; Liang, Y.; Liu, Y.; Li, C. A Novel Framework for Urban Flood Risk Assessment: Multiple Perspectives and Causal Analysis. Water Res. 2024, 256, 121591. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Wang, D.; Zhang, L.; Guo, H.; Ma, J.; Gao, W. Flood Risk Assessment of Wuhan, China, Using a Multi-Criteria Analysis Model with the Improved AHP-Entropy Method. Environ. Sci. Pollut. Res. 2023, 30, 96001–96018. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zheng, A.; Guo, W.; Bandyopadhyay, N.; Zhang, Y.; Wang, Q. Urban Flood Risk Assessment Based on DBSCAN and K-Means Clustering Algorithm. Geomat. Nat. Hazards Risk 2023, 14, 2250527. [Google Scholar] [CrossRef]
- Yoshida, Y.; Banba, M. Flood Disaster Mitigation Measures Through Land Use Management in the UK and France. In Land Use Management in Disaster Risk Reduction: Practice and Cases from a Global Perspective; Banba, M., Shaw, R., Eds.; Springer: Tokyo, Japan, 2017; pp. 405–448. ISBN 978-4-431-56442-3. [Google Scholar]
- King, D.; Gurtner, Y.; Firdaus, A.; Harwood, S.; Cottrell, A. Land Use Planning for Disaster Risk Reduction and Climate Change Adaptation: Operationalizing Policy and Legislation at Local Levels. Int. J. Disaster Resil. Built Environ. 2016, 7, 158–172. [Google Scholar] [CrossRef]
- Adnan, M.S.G.; Abdullah, A.Y.M.; Dewan, A.; Hall, J.W. The Effects of Changing Land Use and Flood Hazard on Poverty in Coastal Bangladesh. Land Use Policy 2020, 99, 104868. [Google Scholar] [CrossRef]
- European Commission; Joint Research Centre. Global Flood Depth-Damage Functions: Methodology and the Database with Guidelines; European Commission: Luxembourg, 2016. [Google Scholar]
- Jongman, B.; Kreibich, H.; Apel, H.; Barredo, J.I.; Bates, P.D.; Feyen, L.; Gericke, A.; Neal, J.; Aerts, J.C.J.H.; Ward, P.J. Comparative Flood Damage Model Assessment: Towards a European Approach. Nat. Hazards Earth Syst. Sci. 2012, 12, 3733–3752. [Google Scholar] [CrossRef]
- Strauss, R.; Pfeifer, C.; Ulmer, H.; Mu, V. Spatial Analysis of Percutaneous Transluminal Coronary Angioplasty (PTCA) in Austria. Eur. J. Epidemiol. 1999, 15, 451–459. [Google Scholar] [CrossRef]
- Peng, B.; Zhang, X.; Elahi, E.; Wan, A. Evolution of Spatial–Temporal Characteristics and Financial Development as an Influencing Factor of Green Ecology. Environ. Dev. Sustain. 2022, 24, 789–809. [Google Scholar] [CrossRef]
- Wu, X.; Li, B.; Li, M.; Guo, M.; Zang, S.; Zhang, S. Examining the Relationship Between Spatial Configurations of Urban Impervious Surfaces and Land Surface Temperature. Chin. Geogr. Sci. 2019, 29, 568–578. [Google Scholar] [CrossRef]
- Qin, M.; Zhu, W.; Pan, J.; Li, S.; Qiu, S. Research on the Formation Mechanism of Product Contribution in Online Product Communities: Content Contribution as a Mediating Variable. Aslib J. Inf. Manag. 2024, 76, 329–352. [Google Scholar] [CrossRef]
- Liu, J.; Kang, H.; Tao, W.; Li, H.; He, D.; Ma, L.; Tang, H.; Wu, S.; Yang, K.; Li, X. A Spatial Distribution—Principal Component Analysis (SD-PCA) Model to Assess Pollution of Heavy Metals in Soil. Sci. Total Environ. 2023, 859, 160112. [Google Scholar] [CrossRef]
- Liang, L.; Yu, L.; Wang, Z. Identifying the Dominant Impact Factors and Their Contributions to Heatwave Events over Mainland China. Sci. Total Environ. 2022, 848, 157527. [Google Scholar] [CrossRef] [PubMed]
- Ryu, Y.-H.; Min, S.-K. Leveraging Physics-Based and Explainable Machine Learning Approaches to Quantify the Relative Contributions of Rain and Air Pollutants to Wet Deposition. Sci. Total Environ. 2024, 931, 172980. [Google Scholar] [CrossRef]
- Wang, X.; Bai, Y. The Global Minmax K-Means Algorithm. SpringerPlus 2016, 5, 1665. [Google Scholar] [CrossRef] [PubMed]
- Sinaga, K.P.; Yang, M.-S. Unsupervised K-Means Clustering Algorithm. IEEE Access 2020, 8, 80716–80727. [Google Scholar] [CrossRef]
- Liu, Y.; Li, B. Bayesian Hierarchical K-Means Clustering. Intell. Data Anal. 2020, 24, 977–992. [Google Scholar] [CrossRef]
- Huang, X.; Ye, Y.; Xiong, L.; Lau, R.Y.K.; Jiang, N.; Wang, S. Time Series k-Means: A New k-Means Type Smooth Subspace Clustering for Time Series Data. Inf. Sci. 2016, 367–368, 1–13. [Google Scholar] [CrossRef]
- Kaur, J.; Singh, H. Performance Evaluation of a Novel Hybrid Clustering Algorithm Using Birch and K-Means. In Proceedings of the 2015 Annual IEEE India Conference (INDICON), New Delhi, India, 17–20 December 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–6. [Google Scholar]
- Jiang, X.; Yuan, H.; Xue, M.; Chen, X.; Tan, X. Analysis of a Heavy Rainfall Event over Beijing during 21–22 July 2012 Based on High Resolution Model Analyses and Forecasts. J. Meteorol. Res. 2014, 28, 199–212. [Google Scholar] [CrossRef]
- Xie, Y.; Xing, J.; Shi, J.; Dou, Y.; Lei, Y. Impacts of Radiance Data Assimilation on the Beijing 7.21 Heavy Rainfall. Atmos. Res. 2016, 169, 318–330. [Google Scholar] [CrossRef]
- Yang, W.; Zheng, C.; Jiang, X.; Wang, H.; Lian, J.; Hu, D.; Zheng, A. Study on Urban Flood Simulation Based on a Novel Model of SWTM Coupling D8 Flow Direction and Backflow Effect. J. Hydrol. 2023, 621, 129608. [Google Scholar] [CrossRef]
- Lin, F.; Chen, X.; Yao, H. Evaluating the Use of Nash-Sutcliffe Efficiency Coefficient in Goodness-of-Fit Measures for Daily Runoff Simulation with SWAT. J. Hydrol. Eng. 2017, 22, 05017023. [Google Scholar] [CrossRef]
- DB11/T 2074–2022; Technical Specification for Construction and Application of Mathematical Model of Urban Flooding Prevention and Control System. Beijing Municipal Commission of Planning and Natural Resources; Beijing Municipal Bureau of Market Supervision and Administration: Beijing, China, 2022.
- Wu, Z.; Lv, H.; Meng, Y.; Guan, X.; Zang, Y. The Determination of Flood Damage Curve in Areas Lacking Disaster Data Based on the Optimization Principle of Variation Coefficient and Beta Distribution. Sci. Total Environ. 2021, 750, 142277. [Google Scholar] [CrossRef]
- GB 51222-2017; Technical Code for Urban Flooding Prevention and Control. Ministry of Housing and Urban-Rural Development: Beijing, China, 2017.
- Liu, K.; Wang, S.; Chen, B.; Wang, H. Quantifying the Direct and Indirect Impacts of Urban Waterlogging Using Input–output Analysis. J. Environ. Manag. 2024, 352, 120068. [Google Scholar] [CrossRef]

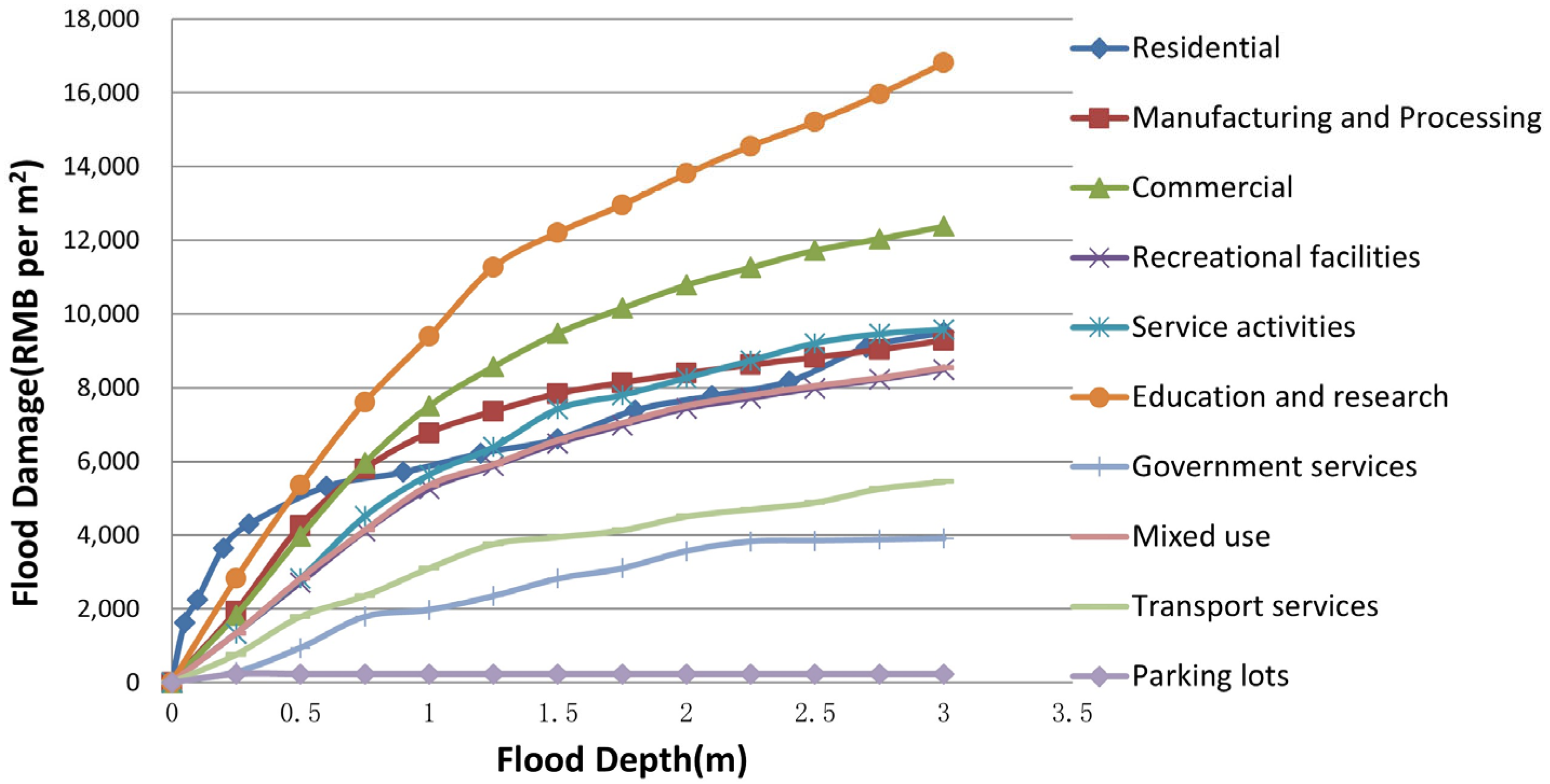


| Land Use | Fitting Function | Loss (RMB per m2) | Normalization |
|---|---|---|---|
| Residential | 5381.72 | 0.62 | |
| Transport services | 2760.30 | 0.30 | |
| Service activities | 5006.76 | 0.57 | |
| Commercial | 6611.67 | 0.77 | |
| Parking lots | 224.73 | 0.01 | |
| Recreational facilities | 4556.71 | 0.52 | |
| Manufacturing and Processing | 5799.97 | 0.67 | |
| Education and research | 8554.82 | 0.99 | |
| Government services | 1898.77 | 0.20 | |
| Mixed use | 4618.37 | 0.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Zhang, S.; Wang, H.; Ding, Y. Spatial Coupling Analysis of Urban Waterlogging Depth and Value Based on Land Use: Case Study of Beijing. Water 2025, 17, 529. https://doi.org/10.3390/w17040529
Zhou J, Zhang S, Wang H, Ding Y. Spatial Coupling Analysis of Urban Waterlogging Depth and Value Based on Land Use: Case Study of Beijing. Water. 2025; 17(4):529. https://doi.org/10.3390/w17040529
Chicago/Turabian StyleZhou, Jinjun, Shuxun Zhang, Hao Wang, and Yi Ding. 2025. "Spatial Coupling Analysis of Urban Waterlogging Depth and Value Based on Land Use: Case Study of Beijing" Water 17, no. 4: 529. https://doi.org/10.3390/w17040529
APA StyleZhou, J., Zhang, S., Wang, H., & Ding, Y. (2025). Spatial Coupling Analysis of Urban Waterlogging Depth and Value Based on Land Use: Case Study of Beijing. Water, 17(4), 529. https://doi.org/10.3390/w17040529








