Deep Learning Downscaling of Precipitation Projection over Central Asia
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Research Data
2.3. Research Methodology
3. Results
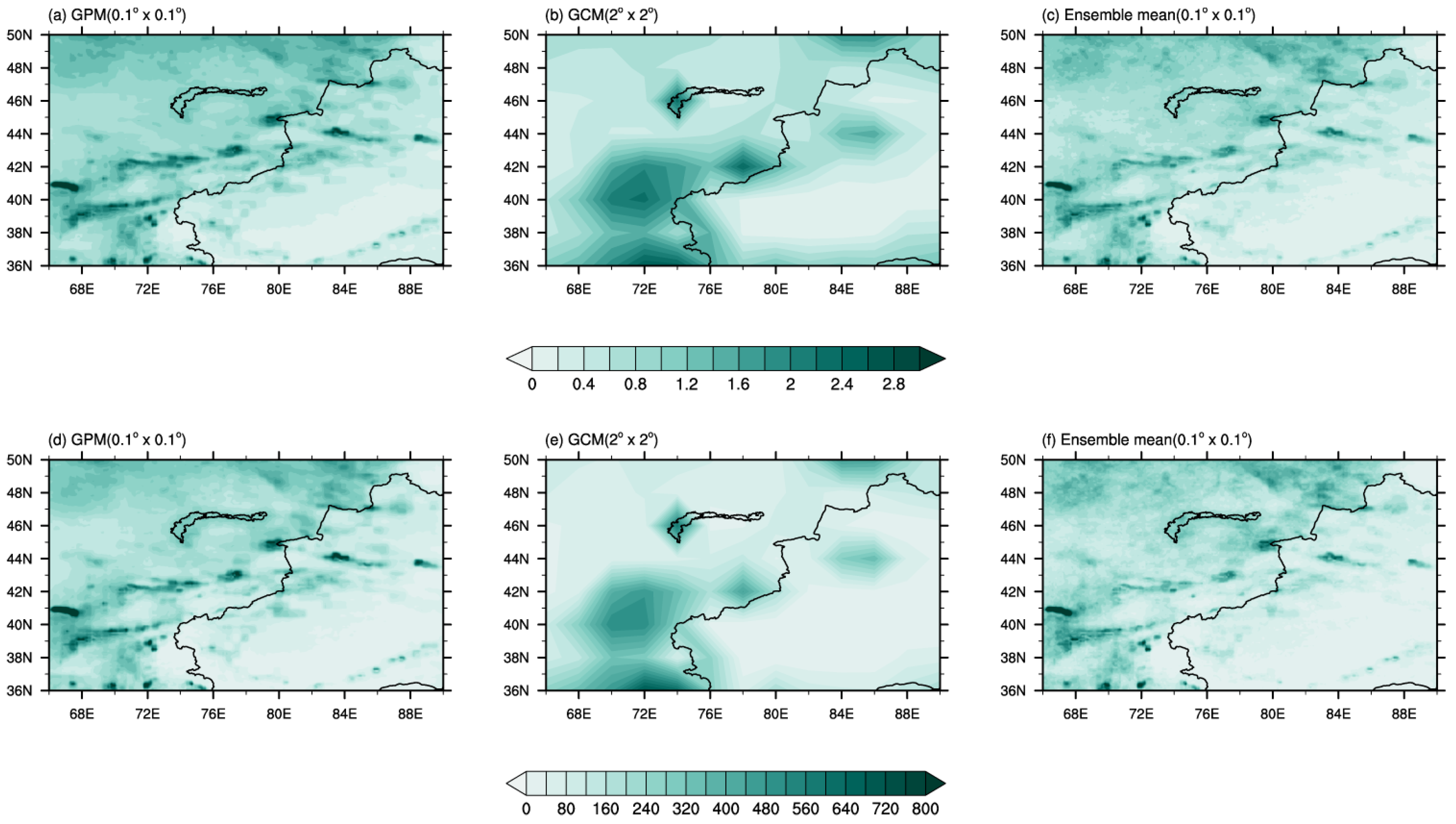
3.1. Validation of Precipitation Simulations from Deep Learning Models
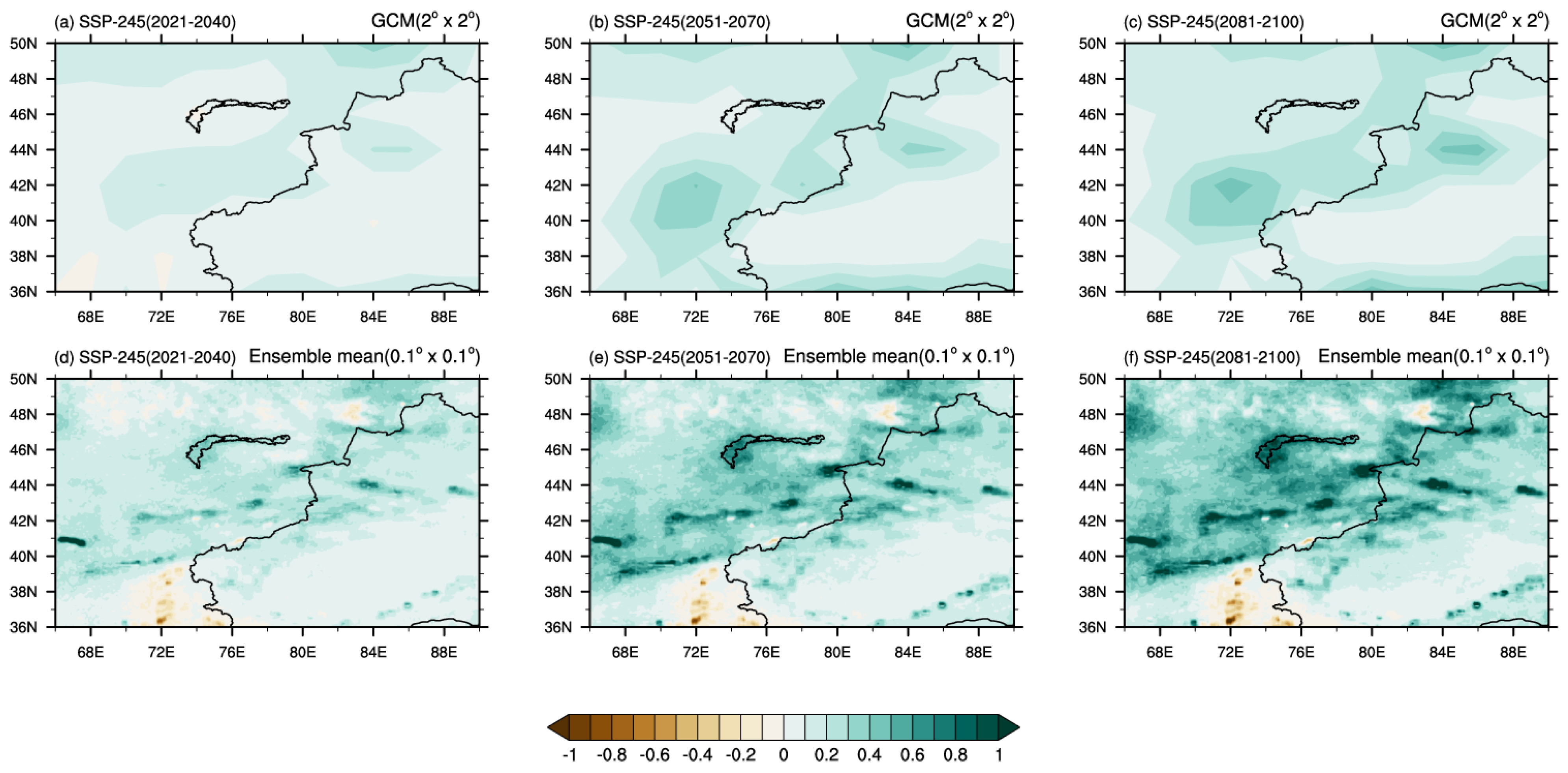
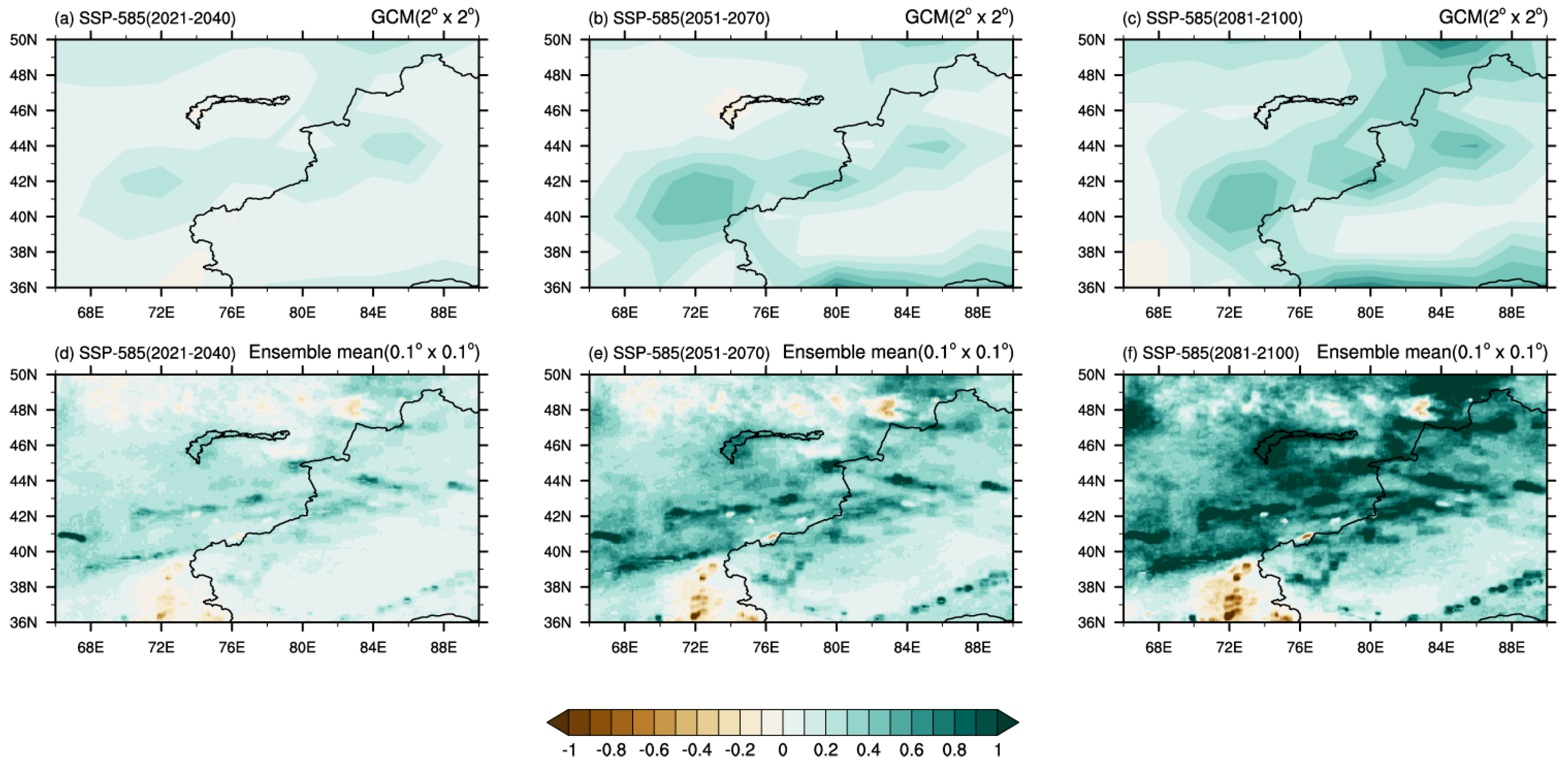
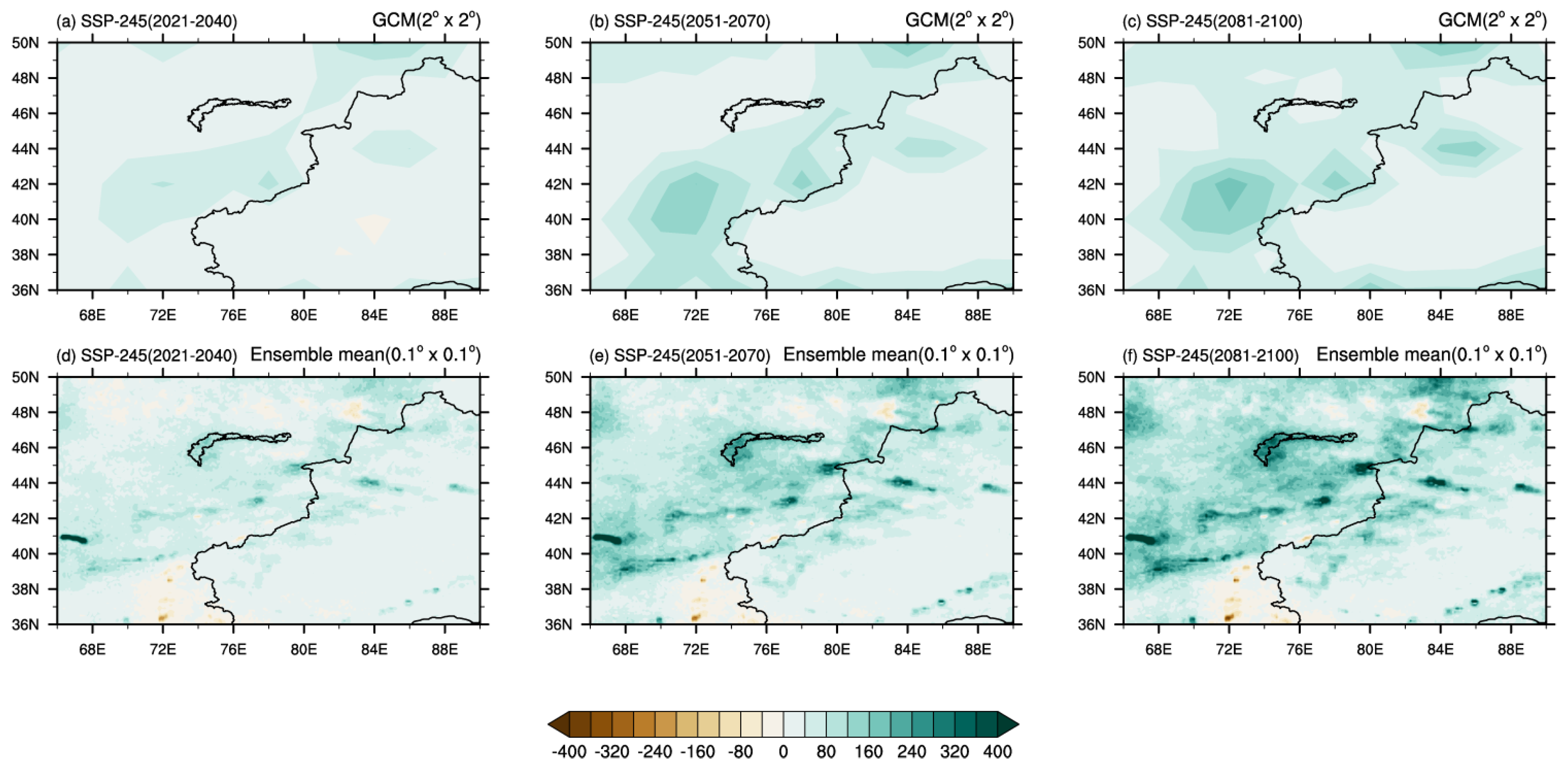
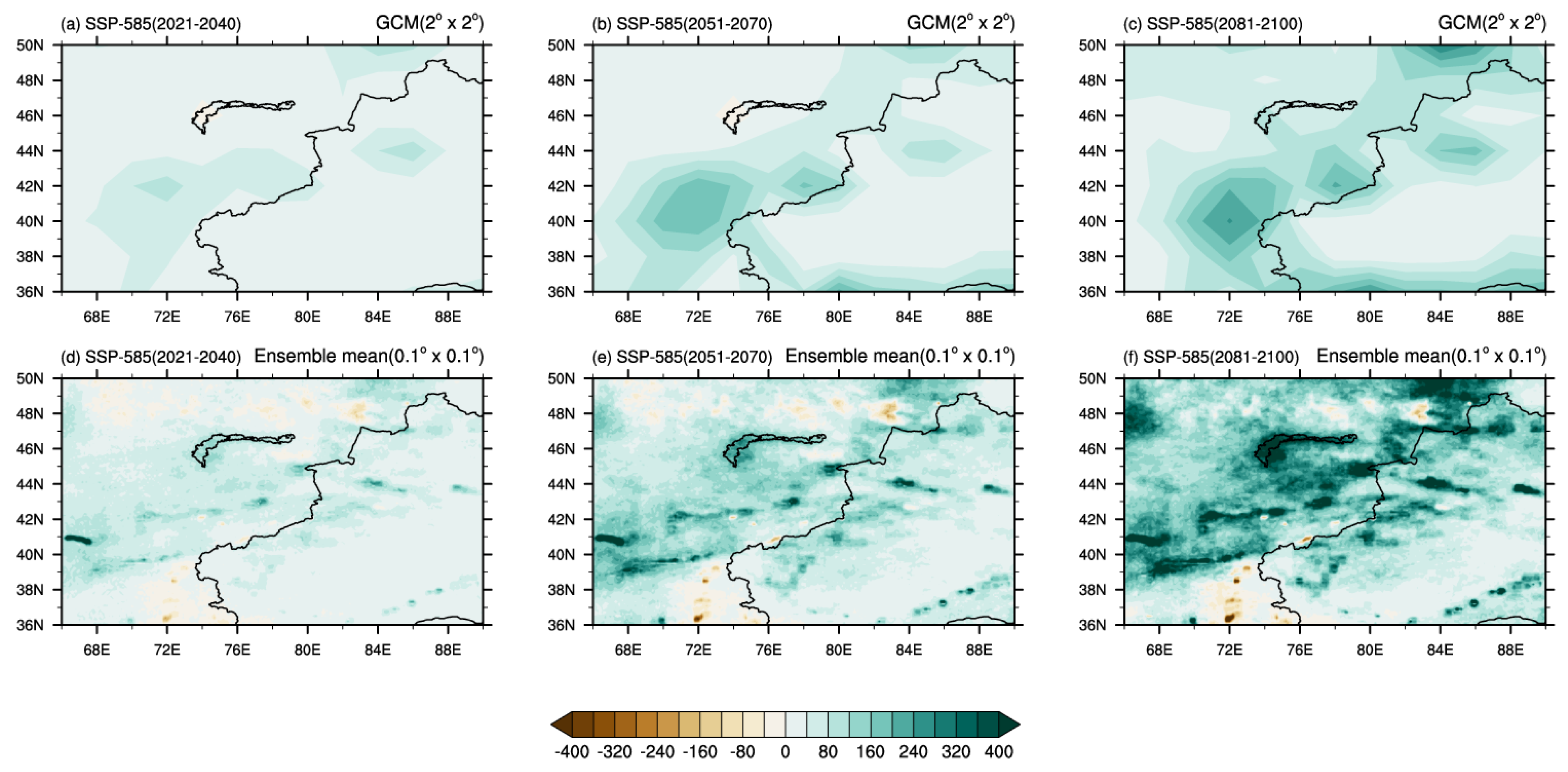
3.2. Future Precipitation Changes Simulated by Deep Learning Models
3.2.1. Annual Mean Precipitation
3.2.2. Extreme Precipitation
3.3. Interannual Variability of Future Precipitation
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gessner, U.; Naeimi, V.; Klein, I.; Kuenzer, C.; Klein, D.; Dech, S. The relationship between precipitation anomalies and satellite-derived vegetation activity in Central Asia. Glob. Planet. Chang. 2013, 110, 74–87. [Google Scholar] [CrossRef]
- Huang, J.; Yu, H.; Han, D.; Zhang, G.; Wei, Y.; Huang, J.; An, L.; Liu, X.; Ren, Y. Declines in global ecological security under climate change. Ecol. Indic. 2020, 117, 106651. [Google Scholar] [CrossRef]
- Peng, D.; Zhou, T. Why was the arid and semiarid northwest China getting wetter in the recent decades? J. Geophys. Res. Atmos. 2017, 122, 9060–9075. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, Q.; Chen, H.; Zhao, S.; Chen, Z. Increasing warm-season precipitation in Asian drylands and response to reducing spring snow cover over the Tibetan Plateau. J. Clim. 2021, 34, 3129–3144. [Google Scholar] [CrossRef]
- Jiang, J.; Zhou, T.; Chen, X.; Zhang, L. Future changes in precipitation over Central Asia based on CMIP6 projections. Environ. Res. Lett. 2020, 15, 054009. [Google Scholar]
- Dike, V.N.; Lin, Z.; Fei, K.; Langendijk, G.S.; Nath, D. Evaluation and multimodel projection of seasonal precipitation extremes over central Asia based on CMIP6 simulations. Int. J. Clim. 2022, 42, 7228–7251. [Google Scholar]
- Huang, X.; Wang, Y.; Ma, X. Simulation of extreme precipitation changes in Central Asia using CMIP6 under different climate scenarios. Theor. Appl. Climatol. 2024, 155, 3203–3219. [Google Scholar] [CrossRef]
- Sillmann, J.; Kharin, V.V.; Zhang, X.; Zwiers, F.W.; Bronaugh, D. Climate extremes indices in the CMIP5 multimodel ensemble: Part 1. Model evaluation in the present climate. J. Geophys. Res. Atmos. 2013, 118, 1716–1733. [Google Scholar]
- Jiang, Z.; Li, W.; Xu, J.; Li, L. Extreme precipitation indices over China in CMIP5 models. Part I: Model evaluation. J. Clim. 2015, 28, 8603–8619. [Google Scholar]
- Zarrin, A.; Dadashi-Roudbari, A. Projection of future extreme precipitation in Iran based on CMIP6 multi-model ensemble. Theor. Appl. Climatol. 2021, 144, 643–660. [Google Scholar]
- Misra, S.; Sarkar, S.; Mitra, P. Statistical downscaling of precipitation using long short-term memory recurrent neural networks. Theor. Appl. Climatol. 2018, 134, 1179–1196. [Google Scholar] [CrossRef]
- Anaraki, M.V.; Farzin, S.; Mousavi, S.F.; Karami, H. Uncertainty analysis of climate change impacts on flood frequency by using hybrid machine learning methods. Water Resour. Manag. 2021, 35, 199–223. [Google Scholar] [CrossRef]
- Wang, K.; Deng, L.; Shangguan, Z.; Chen, Y.; Lin, X. Sustainability of eco-environment in semi-arid regions: Lessons from the Chinese Loess Plateau. Environ. Sci. Policy 2021, 125, 126–134. [Google Scholar] [CrossRef]
- Sha, Y.; Gagne, D.J., II; West, G.; Stull, R. Deep-learning-based gridded downscaling of surface meteorological variables in complex terrain. Part I: Daily maximum and minimum 2-m temperature. J. Appl. Meteorol. Climatol. 2020, 59, 2057–2073. [Google Scholar] [CrossRef]
- Sha, Y.; Gagne, D.J., II; West, G.; Stull, R. Deep-learning-based gridded downscaling of surface meteorological variables in complex terrain. Part II: Daily precipitation. J. Appl. Meteorol. Climatol. 2020, 59, 2075–2092. [Google Scholar] [CrossRef]
- Sun, L.; Lan, Y. Statistical downscaling of daily temperature and precipitation over China using deep learning neural models: Localization and comparison with other methods. Int. J. Climatol. 2021, 41, 1128–1147. [Google Scholar] [CrossRef]
- Baño-Medina, J.; Manzanas, R.; Gutiérrez, J.M. Configuration and intercomparison of deep learning neural models for statistical downscaling. Geosci. Model Dev. 2020, 13, 2109–2124. [Google Scholar] [CrossRef]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual dense network for image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2472–2481. [Google Scholar]
- Fu, H.; Guo, J.; Deng, C.; Liu, H.; Wu, J.; Shi, Z.; Wang, C.; Xie, X. Deep-learning-based downscaling of precipitation in the middle reaches of the Yellow River using residual-based CNNs. Q. J. R. Meteorol. Soc. 2024, 150, 3290–3304. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Baño-Medina, J.; Manzanas, R.; Cimadevilla, E.; Fernández, J.; González-Abad, J.; Cofiño, A.S.; Gutiérrez, J.M. Downscaling multi-model climate projection ensembles with deep learning (DeepESD): Contribution to CORDEX EUR-44. Geosci. Model Dev. 2022, 15, 6747–6758. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Xie, P.; Yoo, S.H. NASA global precipitation measurement (GPM) integrated multi-satellite retrievals for GPM (IMERG). Algorithm Theor. Basis Doc. (ATBD) Version 2015, 4, 30. [Google Scholar]
- Döscher, R.; Acosta, M.; Alessandri, A.; Anthoni, P.; Arneth, A.; Arsouze, T.; Bergmann, T.; Bernadello, R.; Bousetta, S.; Caron, L.P.; et al. The EC-Earth3 Earth system model for the Coupled Model Intercomparison Project 6. Geosci. Model Dev. 2022, 15, 2973–3020. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar] [CrossRef]
- Bedia, J.; Baño-Medina, J.; Legasa, M.N.; Iturbide, M.; Manzanas, R.; Herrera, S.; Casanueva, A.; San-Martín, D.; Cofiño, A.S.; Gutiérrez, J.M. Statistical downscaling with the downscaleR package (v3.1.0): Contribution to the VALUE intercomparison experiment. Geosci. Model Dev. 2020, 13, 1711–1735. [Google Scholar] [CrossRef]
- Sillmann, J.; Kharin, V.V.; Zwiers, F.W.; Zhang, X.; Bronaugh, D. Climate extremes indices in the CMIP5 multimodel ensemble: Part 2. Future climate projections. J. Geophys. Res. Atmos. 2013, 118, 2473–2493. [Google Scholar]
- Palmer, T. Climate forecasting: Build high-resolution global climate models. Nature 2014, 515, 338–339. [Google Scholar]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat, F. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar]
- Irrgang, C.; Boers, N.; Sonnewald, M.; Barnes, E.A.; Kadow, C.; Staneva, J.; Saynisch-Wagner, J. Towards neural Earth system modelling by integrating artificial intelligence in Earth system science. Nat. Mach. Intell. 2021, 3, 667–674. [Google Scholar]
- Mardani, M.; Brenowitz, N.; Cohen, Y.; Pathak, J.; Chen, C.Y.; Liu, C.C.; Vahdat, A.; Nabian, M.A.; Ge, T.; Subramaniam, A.; et al. Residual corrective diffusion modeling for km-scale atmospheric downscaling. Commun. Earth Environ. 2025, 6, 124. [Google Scholar] [CrossRef]
- Rastogi, D.; Kao, S.C.; Ashfaq, M. How may the choice of downscaling techniques and meteorological reference observations affect future hydroclimate projections? Earth’s Future 2022, 10, e2022EF002734. [Google Scholar] [CrossRef]
- Hall, A.; Rahimi, S.; Norris, J.; Ban, N.; Siler, N.; Leung, L.R.; Ullrich, P.; Reed, K.A.; Prein, A.F.; Qian, Y. An evaluation of dynamical downscaling methods used to project regional climate change. J. Geophys. Res. Atmos. 2024, 129, e2023JD040591. [Google Scholar] [CrossRef]
- Gao, S. Dynamical downscaling of surface air temperature and precipitation using RegCM4 and WRF over China. Clim. Dyn. 2020, 55, 1283–1302. [Google Scholar]
- Han, Z.; Zhou, B.; Xu, Y.; Wu, J.; Shi, Y. Projected changes in haze pollution potential in China: An ensemble of regional climate model simulations. Atmos. Chem. Phys. 2017, 17, 10109–10123. [Google Scholar] [CrossRef]
- Wu, J.; Han, Z.Y.; Yan, Y.P.; Sun, C.Y.; Xu, Y.; Shi, Y. Future changes in wind energy potential over China using RegCM4 under RCP emission scenarios. Adv. Clim. Chang. Res. 2021, 12, 596–610. [Google Scholar] [CrossRef]
- Zhang, W.; Zhou, T.; Wu, P. Anthropogenic amplification of precipitation variability over the past century. Science 2024, 385, 427–432. [Google Scholar] [CrossRef]

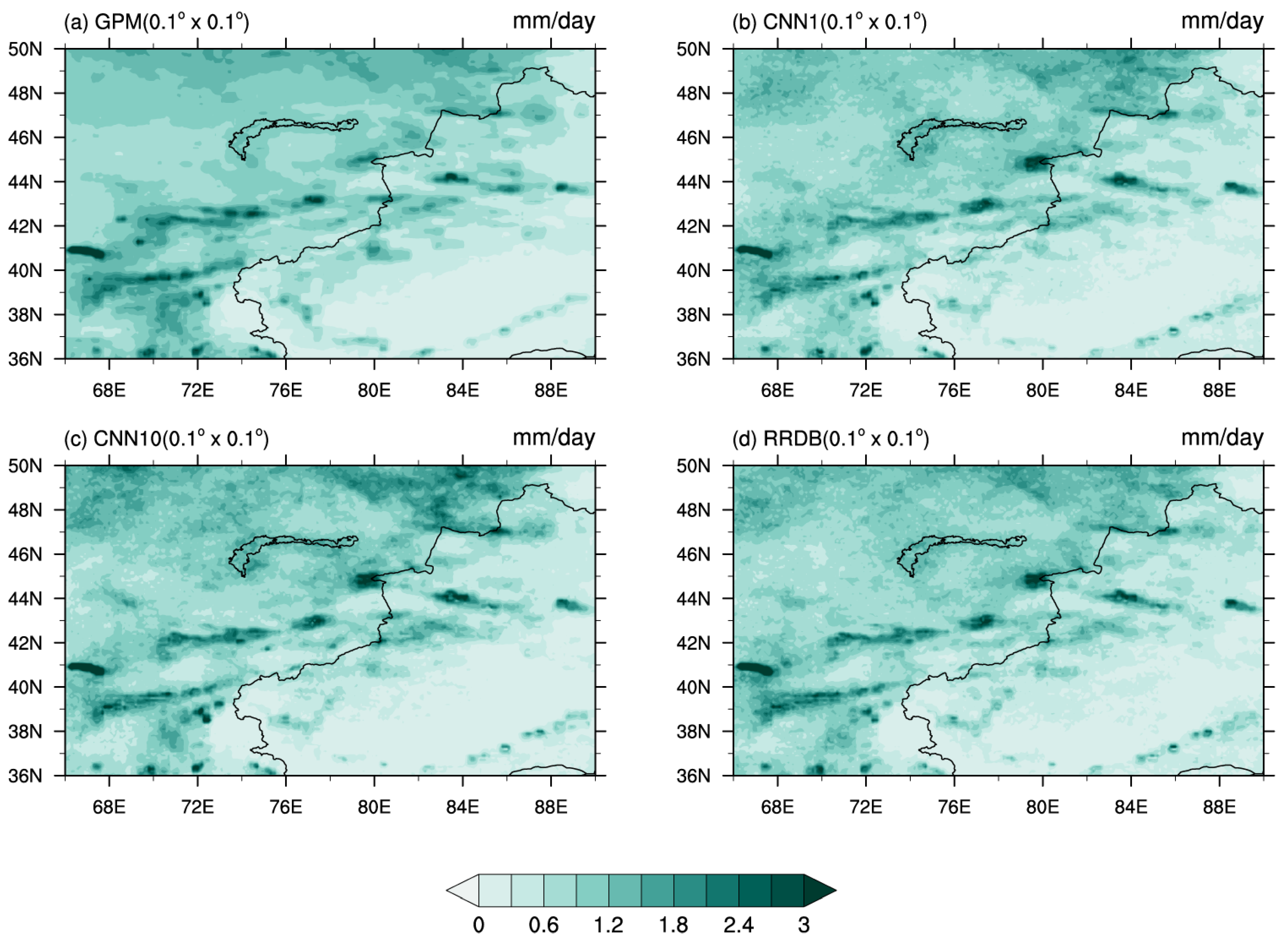




| Models | Difference | RMSE | CC |
|---|---|---|---|
| CNN1 | −0.05 | 0.35 | 0.80 |
| CNN10 | −0.03 | 0.38 | 0.80 |
| RRDB | −0.05 | 0.36 | 0.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Guo, J.; Fan, L.; Sun, H.; Xie, X. Deep Learning Downscaling of Precipitation Projection over Central Asia. Water 2025, 17, 1089. https://doi.org/10.3390/w17071089
Jiang Y, Guo J, Fan L, Sun H, Xie X. Deep Learning Downscaling of Precipitation Projection over Central Asia. Water. 2025; 17(7):1089. https://doi.org/10.3390/w17071089
Chicago/Turabian StyleJiang, Yichang, Jianing Guo, Lei Fan, Hui Sun, and Xiaoning Xie. 2025. "Deep Learning Downscaling of Precipitation Projection over Central Asia" Water 17, no. 7: 1089. https://doi.org/10.3390/w17071089
APA StyleJiang, Y., Guo, J., Fan, L., Sun, H., & Xie, X. (2025). Deep Learning Downscaling of Precipitation Projection over Central Asia. Water, 17(7), 1089. https://doi.org/10.3390/w17071089








