Study on the Impact of Climate Change on Water Cycle Processes in Cold Mountainous Areas—A Case Study of Water Towers in Northeastern China
Abstract
:1. Introduction
2. Materials and Methods
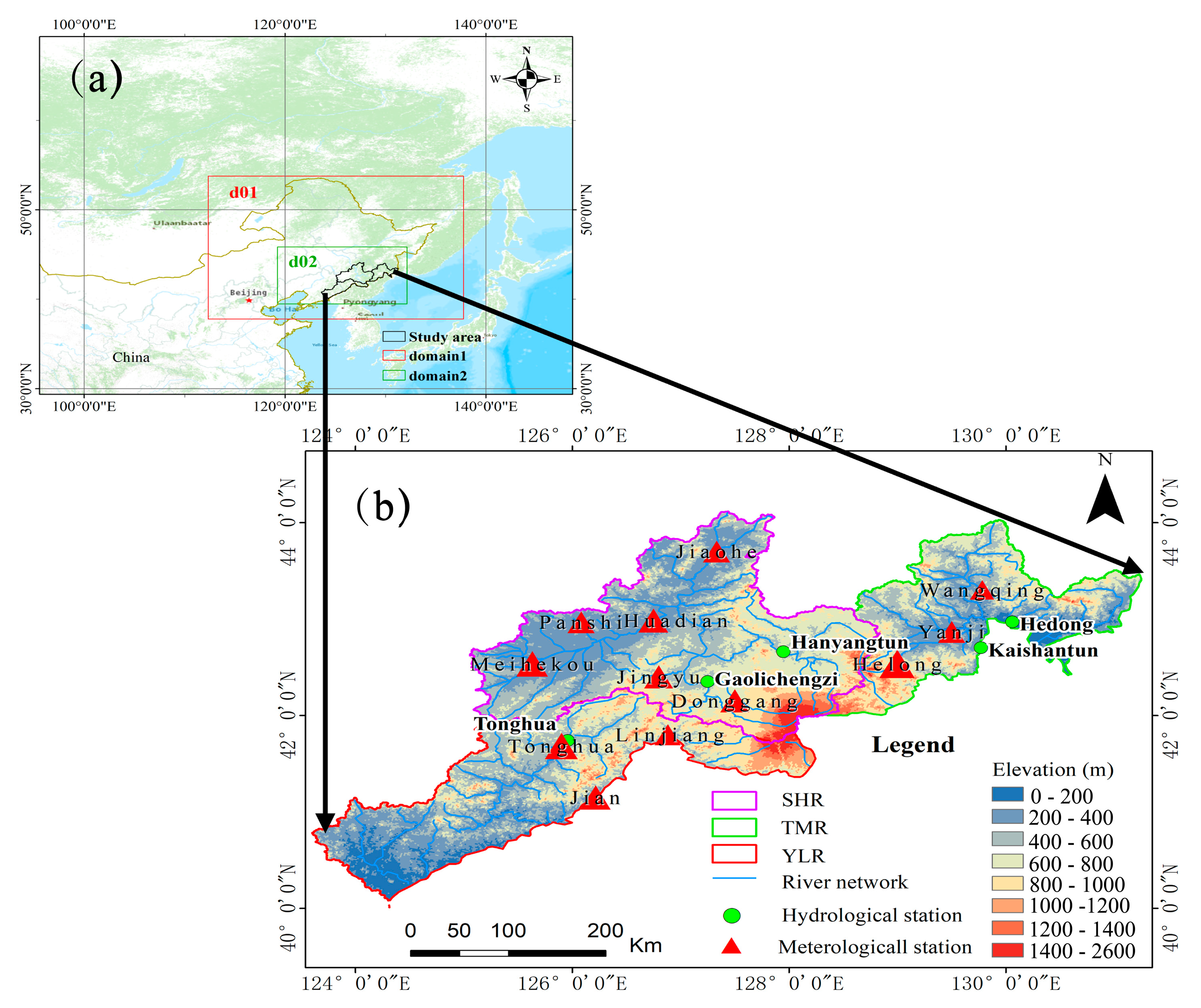
2.1. Study Area
2.2. Data
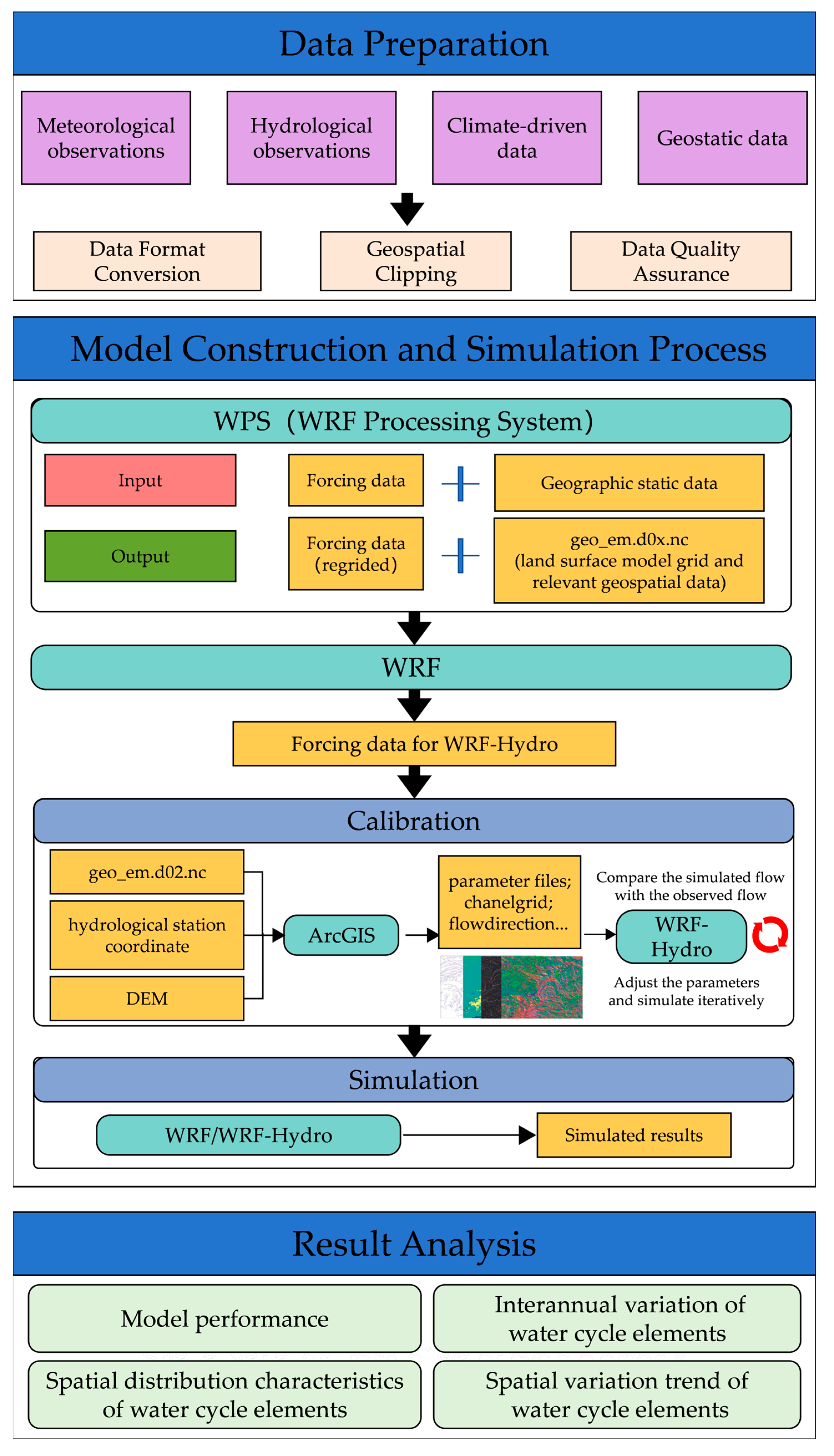
2.3. Models
2.4. Model Calibration
2.5. Static Method
3. Results
3.1. Model Performance
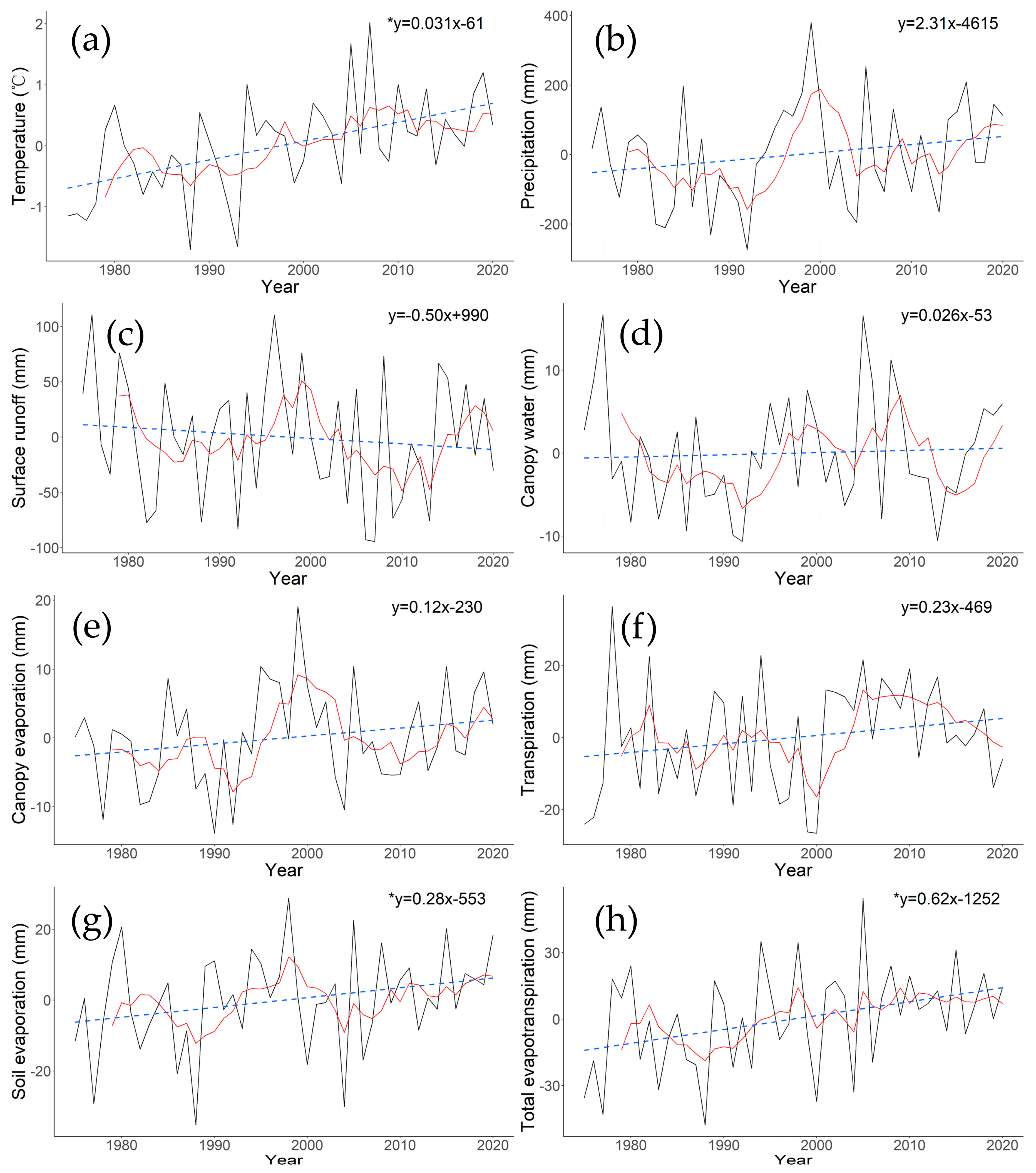
3.2. Interannual Variation of Water Cycle Elements
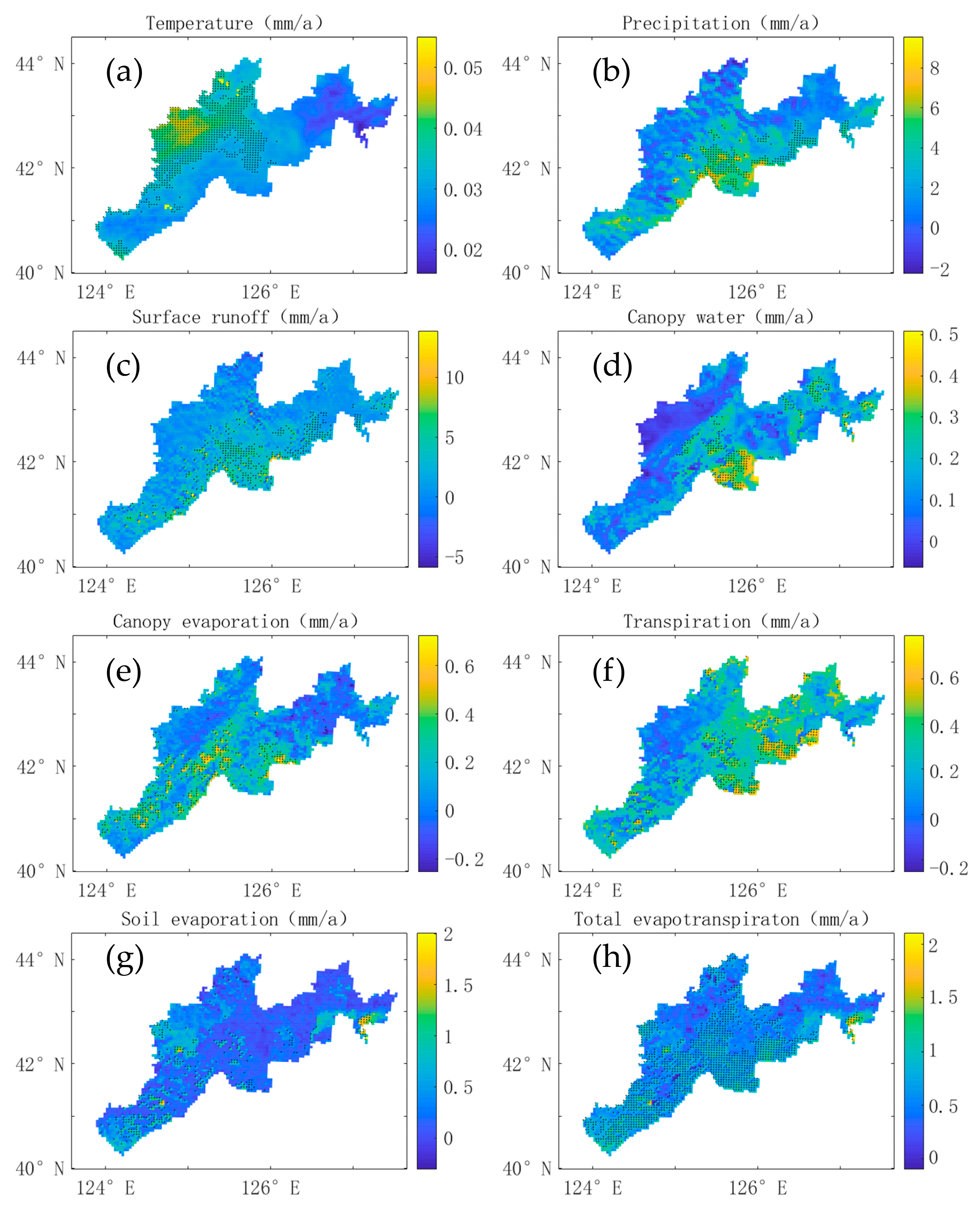
3.3. Spatial Distribution Characteristics of Water Cycle Elements
3.4. Spatial Variation Trend of Water Cycle Elements
4. Discussions
4.1. Analysis of Model Uncertainties
4.2. The Hydrological Response to Climate Change
4.3. The Impact on Water Cycle Process
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arnault, J.; Wei, J.; Rummler, T.; Fersch, B.; Zhang, Z.; Jung, G.; Wagner, S.; Kunstmann, H. A Joint Soil-vegetation-atmospheric Water Tagging Procedure with WRF-hydro: Implementation and Application to the Case of Precipitation Partitioning in the Upper Danube River Basin. Water Resour. Res. 2019, 55, 6217–6243. [Google Scholar] [CrossRef]
- Special Report on Climate Change and Land—IPCC Site. Available online: https://www.ipcc.ch/srccl/ (accessed on 19 March 2025).
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2021—The Physical Science Basis: Working Group I Contribution to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, 1st ed.; Cambridge University Press: Cambridge, UK, 2023; ISBN 978-1-009-15789-6. [Google Scholar]
- Zhou, T. New Physical Science behind Climate Change: What Does IPCC AR6 Tell Us? Innovation 2021, 2, 100173. [Google Scholar] [CrossRef] [PubMed]
- Climate and Hydrologic Ensembling Lead to Differing Streamflow and Sediment Yield Predictions/Climatic Change. Available online: https://link.springer.com/article/10.1007/s10584-021-03011-5 (accessed on 19 March 2025).
- Stergiadi, M.; Di Marco, N.; Avesani, D.; Righetti, M.; Borga, M. Impact of Geology on Seasonal Hydrological Predictability in Alpine Regions by a Sensitivity Analysis Framework. Water 2020, 12, 2255. [Google Scholar] [CrossRef]
- Nie, Y.; Pritchard, H.D.; Liu, Q.; Hennig, T.; Wang, W.; Wang, X.; Liu, S.; Nepal, S.; Samyn, D.; Hewitt, K.; et al. Glacial Change and Hydrological Implications in the Himalaya and Karakoram. Nat. Rev. Earth Environ. 2021, 2, 91–106. [Google Scholar] [CrossRef]
- Viviroli, D.; Dürr, H.H.; Messerli, B.; Meybeck, M.; Weingartner, R. Mountains of the World, Water Towers for Humanity: Typology, Mapping, and Global Significance. Water Resour. Res. 2007, 43, 2006WR005653. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Lutz, A.F.; Andrade, M.; Bahl, A.; Biemans, H.; Bolch, T.; Hyde, S.; Brumby, S.; Davies, B.J.; Elmore, A.C.; et al. Importance and Vulnerability of the World’s Water Towers. Nature 2020, 577, 364–369. [Google Scholar] [CrossRef]
- Yagbasan, O.; Demir, V.; Yazicigil, H. Trend Analyses of Meteorological Variables and Lake Levels for Two Shallow Lakes in Central Turkey. Water 2020, 12, 414. [Google Scholar] [CrossRef]
- Norbiato, D.; Borga, M.; Merz, R.; Blöschl, G.; Carton, A. Controls on Event Runoff Coefficients in the Eastern Italian Alps. J. Hydrol. 2009, 375, 312–325. [Google Scholar] [CrossRef]
- Chen, Y.; Chang, Z.; Xu, S.; Qi, P.; Tang, X.; Song, Y.; Liu, D. Altitudinal Gradient Characteristics of Spatial and Temporal Variations of Snowpack in the Changbai Mountain and Their Response to Climate Change. Water 2021, 13, 3580. [Google Scholar] [CrossRef]
- Zhou, Z.; Shi, H.; Fu, Q.; Li, T.; Gan, T.Y.; Liu, S.; Liu, K. Is the Cold Region in Northeast China Still Getting Warmer under Climate Change Impact? Atmos. Res. 2020, 237, 104864. [Google Scholar] [CrossRef]
- Singh, P.; Wu, J.Q.; McCool, D.K.; Dun, S.; Lin, C.-H.; Morse, J.R. Winter Hydrologic and Erosion Processes in the U.S. Palouse Region: Field Experimentation and WEPP Simulation. Vadose Zone J. 2009, 8, 426–436. [Google Scholar] [CrossRef]
- Han, P.; Long, D.; Han, Z.; Du, M.; Dai, L.; Hao, X. Improved Understanding of Snowmelt Runoff from the Headwaters of China’s Yangtze River Using Remotely Sensed Snow Products and Hydrological Modeling. Remote Sens. Environ. 2019, 224, 44–59. [Google Scholar] [CrossRef]
- Stewart, I.T.; Cayan, D.R.; Dettinger, M.D. Changes in Snowmelt Runoff Timing in Western North America under a ‘business as Usual’ Climate Change Scenario. Clim. Change 2004, 62, 217–232. [Google Scholar] [CrossRef]
- Demand, D.; Selker, J.S.; Weiler, M. Influences of Macropores on Infiltration into Seasonally Frozen Soil. Vadose Zone J. 2019, 18, 1–14. [Google Scholar] [CrossRef]
- Bayard, D.; Stähli, M.; Parriaux, A.; Flühler, H. The Influence of Seasonally Frozen Soil on the Snowmelt Runoff at Two Alpine Sites in Southern Switzerland. J. Hydrol. 2005, 309, 66–84. [Google Scholar] [CrossRef]
- Daniel, E.B. Watershed Modeling and Its Applications: A State-of-the-Art Review. Open Hydrol. J. 2011, 5, 26–50. [Google Scholar] [CrossRef]
- Devia, G.K.; Ganasri, B.P.; Dwarakish, G.S. A Review on Hydrological Models. Aquat. Procedia 2015, 4, 1001–1007. [Google Scholar] [CrossRef]
- Zeng, F.; Ma, M.-G.; Di, D.-R.; Shi, W.-Y. Separating the Impacts of Climate Change and Human Activities on Runoff: A Review of Method and Application. Water 2020, 12, 2201. [Google Scholar] [CrossRef]
- Pietroniro, A.; Soulis, E.; Snelgrove, K.; Kouwen, N. A Framework for Coupling Atmospheric and Hydrological Models. In Proceedings of the International Symposium, Held During the Sixth IAHS Scientific Assembly, Maastricht, The Netherlands, 18–27 July 2001; pp. 27–34. [Google Scholar]
- Majone, B.; Avesani, D.; Zulian, P.; Fiori, A.; Bellin, A. Analysis of High Streamflow Extremes in Climate Change Studies: How Do We Calibrate Hydrological Models? Hydrol. Earth Syst. Sci. 2022, 26, 3863–3883. [Google Scholar] [CrossRef]
- Maxwell, R.M.; Chow, F.K.; Kollet, S.J. The Groundwater–Land-Surface–Atmosphere Connection: Soil Moisture Effects on the Atmospheric Boundary Layer in Fully-Coupled Simulations. Adv. Water Resour. 2007, 30, 2447–2466. [Google Scholar] [CrossRef]
- Tang, C.; Dennis, R.L. How Reliable Is the Offline Linkage of Weather Research & Forecasting Model (WRF) and Variable Infiltration Capacity (VIC) Model? Glob. Planet. Change 2014, 116, 1–9. [Google Scholar] [CrossRef]
- Wagner, S.; Fersch, B.; Yuan, F.; Yu, Z.; Kunstmann, H. Fully Coupled Atmospheric-hydrological Modeling at Regional and Long-term Scales: Development, Application, and Analysis of WRF-HMS. Water Resour. Res. 2016, 52, 3187–3211. [Google Scholar] [CrossRef]
- Givati, A.; Gochis, D.; Rummler, T.; Kunstmann, H. Comparing One-Way and Two-Way Coupled Hydrometeorological Forecasting Systems for Flood Forecasting in the Mediterranean Region. Hydrology 2016, 3, 19. [Google Scholar] [CrossRef]
- Xia, Q.; Fan, Y.; Zhang, H.; Jiang, C.; Wang, Y.; Hua, X.; Liu, D. A Review on the Development of Two-Way Coupled Atmospheric-Hydrological Models. Sustainability 2023, 15, 2803. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, J.; Li, C.; Yu, F.; Wang, W.; Qiu, Q. Parameter Sensitivity Analysis of the WRF-Hydro Modeling System for Streamflow Simulation: A Case Study in Semi-Humid and Semi-Arid Catchments of Northern China. Asia-Pac. J. Atmos. Sci. 2021, 57, 451–466. [Google Scholar] [CrossRef]
- Wang, W.; Liu, J.; Li, C.; Liu, Y.; Yu, F.; Yu, E. An Evaluation Study of the Fully Coupled WRF/WRF-Hydro Modeling System for Simulation of Storm Events with Different Rainfall Evenness in Space and Time. Water 2020, 12, 1209. [Google Scholar] [CrossRef]
- Wang, W.; Liu, J.; Xu, B.; Li, C.; Liu, Y.; Yu, F. A WRF/WRF-Hydro Coupling System with an Improved Structure for Rainfall-Runoff Simulation with Mixed Runoff Generation Mechanism. J. Hydrol. 2022, 612, 128049. [Google Scholar] [CrossRef]
- Naabil, E.; Kouadio, K.; Lamptey, B.; Annor, T.; Chukwudi Achugbu, I. Tono Basin Climate Modeling, the Potential Advantage of Fully Coupled WRF/WRF-Hydro Modeling System. Model. Earth Syst. Environ. 2023, 9, 1669–1679. [Google Scholar] [CrossRef]
- Sarkar, S.; Himesh, S. Evaluation of the Skill of a Fully-Coupled Atmospheric–Hydrological Model in Simulating Extreme Hydrometeorological Event: A Case Study over Cauvery River Catchment. Pure Appl. Geophys. 2021, 178, 1063–1086. [Google Scholar] [CrossRef]
- Bruyere, C.; Monaghan, A.; Steinhoff, D.; Yates, D. Bias-Corrected CMIP5 CESM Data in WRF/MPAS Intermediate File Format; UCAR/NCAR: Boulder, CO, USA, 2015. [Google Scholar]
- Lehner, B.; Verdin, K.; Jarvis, A. New Global Hydrography Derived from Spaceborne Elevation Data. EoS Trans. 2008, 89, 93–94. [Google Scholar] [CrossRef]
- Ek, M.B.; Mitchell, K.E.; Lin, Y.; Rogers, E.; Grunmann, P.; Koren, V.; Gayno, G.; Tarpley, J.D. Implementation of Noah Land Surface Model Advances in the National Centers for Environmental Prediction Operational Mesoscale Eta Model. J. Geophys. Res. 2003, 108, 2002JD003296. [Google Scholar] [CrossRef]
- Ensemble Data Assimilation for Flood Forecasting in Operational Settings: From Noah-MP to WRF-Hydro and the National Water Model|Semantic Scholar. Available online: https://www.semanticscholar.org/paper/Ensemble-Data-Assimilation-for-Flood-Forecasting-in-Zarekarizi/aed531e9ca2297e089daae98a31547fa67e86dde (accessed on 19 March 2025).
- Ma, Y.; Chandrasekar, V.; Chen, H.; Cifelli, R. Quantifying the Potential of AQPI Gap-Filling Radar Network for Streamflow Simulation through a WRF-Hydro Experiment. J. Hydrometeorol. 2021, 22, 1869–1882. [Google Scholar] [CrossRef]
- Yang, Y.; Yuan, H.; Yu, W. Uncertainties of 3D Soil Hydraulic Parameters in Streamflow Simulations Using a Distributed Hydrological Model System. J. Hydrol. 2018, 567, 12–24. [Google Scholar] [CrossRef]
- Mane, D.; Chandrasekar, A. Evaluation of a Stand-Alone WRF-Hydro Modeling System Using Different Rainfall Forcing Data: Case Study over the Godavari River Basin, India. Pure Appl. Geophys. 2022, 179, 3807–3826. [Google Scholar] [CrossRef]
- He, B.; Sun, Q.; Yu, E.; Wang, H.; Zhang, M.; Hua, W. Numerical simulation of the influence of topography of the Greater Khingan Mountains and Changbai Mountains on summer precipitation in northeast China. Clim. Environ. Stud. 2020, 25, 268–280. [Google Scholar]
- Yu, E. High-Resolution Numerical Simulation of Seasonal Snowfall in Northeast China. Chin. Sci. Bull. 2013, 58, 690–698. [Google Scholar] [CrossRef]
- Yucel, I.; Onen, A.; Yilmaz, K.K.; Gochis, D.J. Calibration and Evaluation of a Flood Forecasting System: Utility of Numerical Weather Prediction Model, Data Assimilation and Satellite-Based Rainfall. J. Hydrol. 2015, 523, 49–66. [Google Scholar] [CrossRef]
- Niu, G.-Y.; Yang, Z.-L.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E.; et al. The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J. Geophys. Res. Atmos. 2011, 116, D12109. [Google Scholar] [CrossRef]
- Xue, Z.G.; Gochis, D.J.; Yu, W.; Keim, B.D.; Rohli, R.V.; Zang, Z.; Sampson, K.; Dugger, A.; Sathiaraj, D.; Ge, Q. Modeling Hydroclimatic Change in Southwest Louisiana Rivers. Water 2018, 10, 596. [Google Scholar] [CrossRef]
- Eltahir, E.A.B.; Bras, R.L. Precipitation Recycling. Rev. Geophys. 1996, 34, 367–378. [Google Scholar] [CrossRef]
- Baig, M.A.; Zaman, Q.; Baig, S.A.; Qasim, M.; Khalil, U.; Khan, S.A.; Ismail, M.; Muhammad, S.; Ali, S. Regression Analysis of Hydro-Meteorological Variables for Climate Change Prediction: A Case Study of Chitral Basin, Hindukush Region. Sci. Total Environ. 2021, 793, 148595. [Google Scholar] [CrossRef] [PubMed]
- Wan, H.; Bian, J.; Zhang, H.; Li, Y. Assessment of Future Climate Change Impacts on Water-Heat-Salt Migration in Unsaturated Frozen Soil Using CoupModel. Front. Environ. Sci. Eng. 2021, 15, 10. [Google Scholar] [CrossRef]
- Sofokleous, I.; Bruggeman, A.; Camera, C.; Eliades, M. Grid-Based Calibration of the WRF-Hydro with Noah-MP Model with Improved Groundwater and Transpiration Process Equations. J. Hydrol. 2023, 617, 128991. [Google Scholar] [CrossRef]
- Mohammed, K.; Leconte, R.; Trudel, M. Impacts of Spatiotemporal Gaps in Satellite Soil Moisture Data on Hydrological Data Assimilation. Water 2023, 15, 321. [Google Scholar] [CrossRef]
- Dixit, A.; Sahany, S.; Kanta Mishra, S. Modeling the Climate Change Impact on Hydroclimate Fluxes over the Beas Basin Using a High-Resolution Glacier-Atmosphere-Hydrology Coupled Setup. J. Hydrol. 2023, 627, 130219. [Google Scholar] [CrossRef]
- Du, Q.; Zhang, M.; Wang, S.; Che, C.; Ma, R.; Ma, Z. Changes in Air Temperature over China in Response to the Recent Global Warming Hiatus. J. Geogr. Sci. 2019, 29, 496–516. [Google Scholar] [CrossRef]
- Silva, D.G.; Silva Junior, J.R.D.D.; Souza, F.M.D.; Ramos, D.N.D.S.; Silva, A.R.; Santos, T.S.D.; Moreira, D.M. WRF-Hydro for Streamflow Simulation in the MATOPIBA Region within the Tocantins/Araguaia River Basin—Brazil: Implications for Water Resource Management. Water 2023, 15, 3902. [Google Scholar] [CrossRef]
- Pasquier, U.; Vahmani, P.; Jones, A.D. Quantifying the City-Scale Impacts of Impervious Surfaces on Groundwater Recharge Potential: An Urban Application of WRF–Hydro. Water 2022, 14, 3143. [Google Scholar] [CrossRef]
- Wang, J.; Liu, D.; Tian, S.; Ma, J.; Wang, L. Coupling Reconstruction of Atmospheric Hydrological Profile and Dry-up Risk Prediction in a Typical Lake Basin in Arid Area of China. Sci. Rep. 2022, 12, 6535. [Google Scholar] [CrossRef]
- Towler, E.; Foks, S.S.; Dugger, A.L.; Dickinson, J.E.; Essaid, H.I.; Gochis, D.; Viger, R.J.; Zhang, Y. Benchmarking High-Resolution Hydrologic Model Performance of Long-Term Retrospective Streamflow Simulations in the Contiguous United States. Hydrol. Earth Syst. Sci. 2023, 27, 1809–1825. [Google Scholar] [CrossRef]
- Zhang, Z.-Q.; Wu, Q.-B.; Hou, M.-T.; Tai, B.-W.; An, Y.-K. Permafrost Change in Northeast China in the 1950s–2010s. Adv. Clim. Change Res. 2021, 12, 18–28. [Google Scholar] [CrossRef]
- Guo, S.; Tian, L.; Chen, S.; Liang, J.; Tian, J.; Cao, B.; Wang, X.; He, C. Analysis of Effects of Vegetation Cover and Elevation on Water Yield in an Alpine Basin of the Qilian Mountains in Northwest China by Integrating the WRF-Hydro and Budyko Framework. J. Hydrol. 2024, 629, 130580. [Google Scholar] [CrossRef]
- Yin, D.; Xue, Z.G.; Bao, D.; RafieeiNasab, A.; Huang, Y.; Morales, M.; Warner, J.C. Understanding the Role of Initial Soil Moisture and Precipitation Magnitude in Flood Forecast Using a Hydrometeorological Modelling System. Hydrol. Process. 2022, 36, e14710. [Google Scholar] [CrossRef]
- Feng, M.; Zhang, W.; Zhang, S.; Sun, Z.; Li, Y.; Huang, Y.; Wang, W.; Qi, P.; Zou, Y.; Jiang, M. The Role of Snowmelt Discharge to Runoff of an Alpine Watershed: Evidence from Water Stable Isotopes. J. Hydrol. 2022, 604, 127209. [Google Scholar] [CrossRef]
- Mehboob, M.S.; Kim, Y. Impact of Climate Change on the Hydrological Projections over a Western Himalayan River Basin and the Associated Uncertainties. J. Hydrol. 2024, 628, 130460. [Google Scholar] [CrossRef]
- Li, C.; Yu, G.; Wang, J.; Horton, D.E. Toward Improved Regional Hydrological Model Performance Using State-of-the-science Data-informed Soil Parameters. Water Resour. Res. 2023, 59, e2023WR034431. [Google Scholar] [CrossRef]
- Li, X.; He, H.S.; Li, N.; Yu, H.; Zong, S.; Wu, Z.; Du, H. Season-Dependent Climate Sensitivity of the Surface Runoff of Major Rivers in Changbai Mountain. J. Hydrol. 2024, 643, 131936. [Google Scholar] [CrossRef]




| Type | Rivers | Site | Coordinates | Period of Record (Year) | Source | |
|---|---|---|---|---|---|---|
| Longitude | Latitude | |||||
| Meterological Station | SHR | Jiaohe | 127°33′ E | 43°70′ N | 1975–2020 | China Meteorological Data Network (http://data.cma.cn/, accessed on 1 January 2023) of the China Meteorological Administration |
| Huadian | 126°76′ E | 42°98′ N | 1975–2020 | |||
| Jingyu | 126°79′ E | 42°40′ N | 1975–2020 | |||
| Donggang | 127°50′ E | 42°15′ N | 1975–2020 | |||
| Panshi | 126°08′ E | 42°96′ N | 1975–2020 | |||
| Meihekou | 125°66′ E | 42°53′ N | 1975–2020 | |||
| TMR | Wangqing | 129°79′ E | 43°30′ N | 1975–2020 | ||
| Yanji | 129°50′ E | 42°87′ N | 1975–2020 | |||
| Helong | 129°00′ E | 42°53′ N | 1975–2020 | |||
| YLR | Linjiang | 126°90′ E | 41°80′ N | 1975–2020 | ||
| Tonghua | 125°92′ E | 41°72′ N | 1975–2020 | |||
| Jian | 126°22′ E | 41°15′ N | 1975–2020 | |||
| Hydrological Station | SHR | Hanyangtun | 127°57′ E | 42°39′ N | 1975–2020 | Jilin Provincial Hydrological Bureau and the Songliao Water Resources Commission |
| Gaolichengzi | 127°14′ E | 42°21′ N | 1975–2020 | |||
| TMR | Hedong | 130°03′E | 42°58′ N | 1975,1980–2020 | ||
| Kaishantun | 129°46′ E | 42°42′ N | 1975,1980–2020 | |||
| YLR | Tonghua | 125°56′E | 41°43′N | 1980–2018 | ||
| Categories | Selected Option |
|---|---|
| Microphysics | WRF Singel-Moment 6class scheme (WSM6) |
| Cumulus parameterization | Kain-Fritsch |
| Planetary boundary layer | Yonsei University |
| Longwave radiation | Rapid Radiative Transfer Model (RRTM) |
| Shortwave radiation | Dudhia |
| Land surface model | Noah_MP |
| Prameter | Description | Units |
|---|---|---|
| REFKDT | A tunable parameter that significantly impacts surface infiltration and hence the partitioning of total runoff into surface and subsurface runoff. | unitless |
| RETDEPRTFAC | Multiplier on maximum retention depth before flow is routed as overland flow. | unitless |
| SLOPE | A coefficient that modifies the drainage out the bottom of the last soil layer. | unitless |
| OVROUGHRTFAC | A multiplier on Manning’s roughness for overland flow | unitless |
| MannN | Manning’s roughness coefficient. | s/m1/3 |
| Zmax | A bucket model coefficient of the maximum storage in the bucket before “spilling” occurs. | unitless |
| SMCMAX | Maximum soil moisture content for each soil type. | m3/m3 |
| LKSATFAC | Multiplier on saturated hydraulic conductivity in lateral flow direction. | m/s |
| Stations | Calibration Period (40%) | Validation Period (60%) | ||||
|---|---|---|---|---|---|---|
| CC | NSE | RSR | CC | NSE | RSR | |
| Hanyangtun | 0.84 | 0.67 | 0.57 | 0.78 | 0.57 | 0.65 |
| Gaolichengzi | 0.86 | 0.68 | 0.57 | 0.85 | 0.58 | 0.65 |
| Tonghua | 0.85 | 0.61 | 0.62 | 0.85 | 0.61 | 0.62 |
| Kaishantun | 0.78 | 0.57 | 0.68 | 0.80 | 0.60 | 0.64 |
| Hedong | 0.68 | 0.38 | 0.83 | 0.76 | 0.55 | 0.67 |
| Elements | Mutational Point | Cr | Tr1 | Tr2 | Tr | p |
|---|---|---|---|---|---|---|
| Temperature (Temp) | 2002 | 27.5% | 0.036 °C/a | 0.0068 °C/a | 0.031 °C/a | 0.001 |
| Precipitation (Prcp) | 2002 | 2.1% | 4.59 mm/a | 9.72 mm/a | 2.31 mm/a | 0.13 |
| Surface runoff (Sfr) | 1995 | −1.2% | −2.00 mm/a | −1.01 mm/a | −0.50 mm/a | 0.83 |
| Canopy water (Cw) | 2003 | 4.2% | −0.09 mm/a | −0.05 mm/a | 0.026 mm/a | 0.66 |
| Canopy evaporation (Ecan) | 2001 | 0.6% | 0.38 mm/a | 0.36 mm/a | 0.12 mm/a | 0.23 |
| Transpiration (Etr) | 1995 | 1.8% | 0.44 mm/a | 0.35 mm/a | 0.23 mm/a | 0.04 |
| Soil evaporation (Es) | 2007 | 2.7% | 0.16 mm/a | 0.37 mm/a | 0.28 mm/a | 0.16 |
| Total evapotranspiration (Et) | 2002 | 2.3% | 0.80 mm/a | 0.26 mm/a | 0.63 mm/a | 0.06 |
| Sub-Basin | Temp (°C/a) | Prcp (mm/a) | Sfr (mm/a) | Cw (mm/a) | Ecan (mm/a) | Etr (mm/a) | Es (mm/a) | Et (mm/a) |
|---|---|---|---|---|---|---|---|---|
| TMR | 0.029 | 1.846 | −1.285 | −0.016 | 0.067 | 0.194 | 0.258 | 0.573 |
| SHR | 0.032 | 2.257 | −0.217 | 0.054 | 0.097 | 0.271 | 0.283 | 0.597 |
| YLR | 0.031 | 3.297 | 0.094 | 0.056 | 0.212 | 0.243 | 0.279 | 0.734 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Cao, L.; Sun, F.; Ye, H.; Duan, Y.; Liu, Z. Study on the Impact of Climate Change on Water Cycle Processes in Cold Mountainous Areas—A Case Study of Water Towers in Northeastern China. Water 2025, 17, 969. https://doi.org/10.3390/w17070969
Li Z, Cao L, Sun F, Ye H, Duan Y, Liu Z. Study on the Impact of Climate Change on Water Cycle Processes in Cold Mountainous Areas—A Case Study of Water Towers in Northeastern China. Water. 2025; 17(7):969. https://doi.org/10.3390/w17070969
Chicago/Turabian StyleLi, Zhaoyang, Lei Cao, Feihu Sun, Hongsheng Ye, Yucong Duan, and Zhenxin Liu. 2025. "Study on the Impact of Climate Change on Water Cycle Processes in Cold Mountainous Areas—A Case Study of Water Towers in Northeastern China" Water 17, no. 7: 969. https://doi.org/10.3390/w17070969
APA StyleLi, Z., Cao, L., Sun, F., Ye, H., Duan, Y., & Liu, Z. (2025). Study on the Impact of Climate Change on Water Cycle Processes in Cold Mountainous Areas—A Case Study of Water Towers in Northeastern China. Water, 17(7), 969. https://doi.org/10.3390/w17070969






