Influencing Factors and Prediction of Turbine Sediment Concentration in Pure Pumped-Storage Power Stations on Sediment-Laden Rivers
Abstract
:1. Introduction
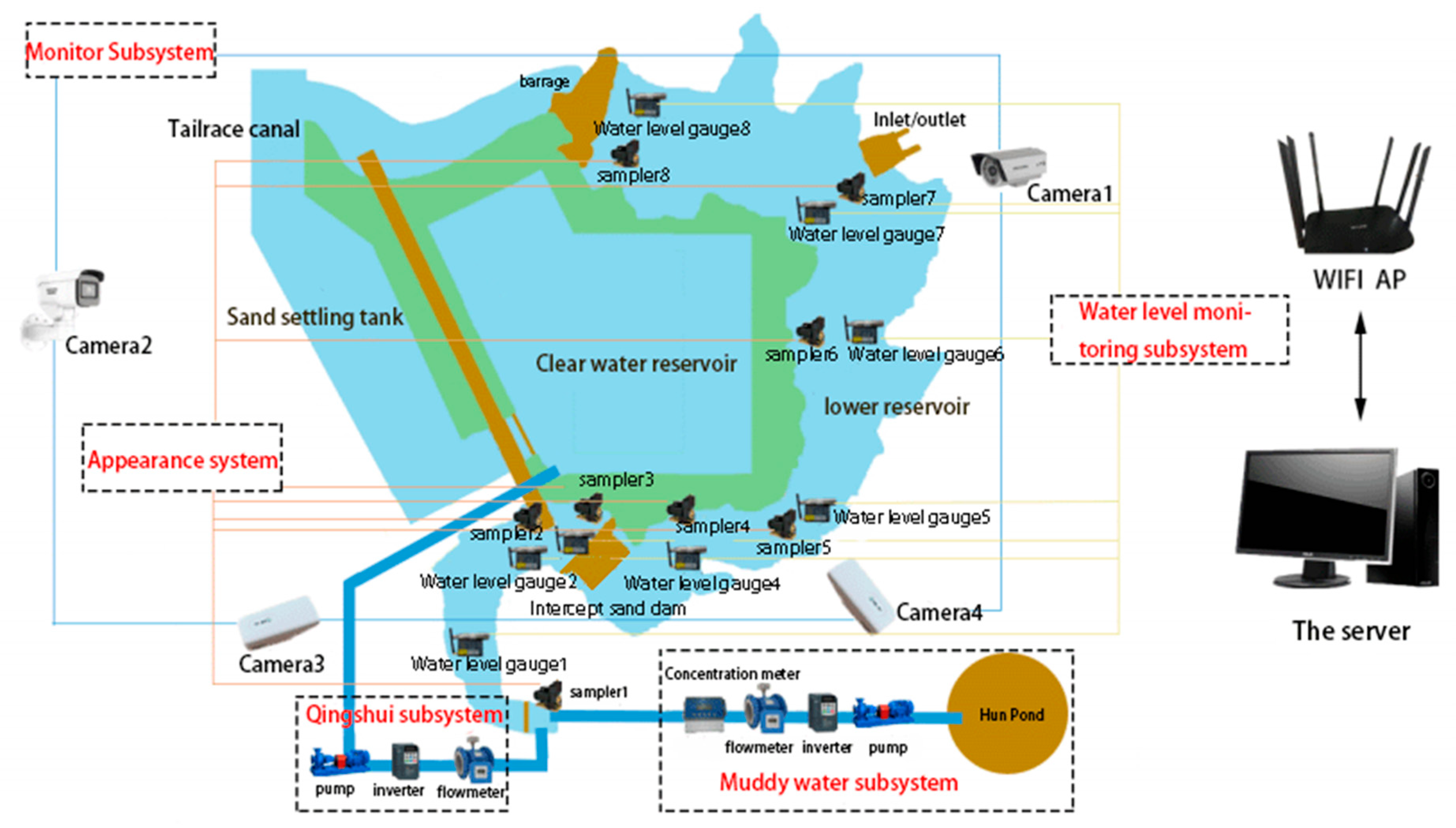
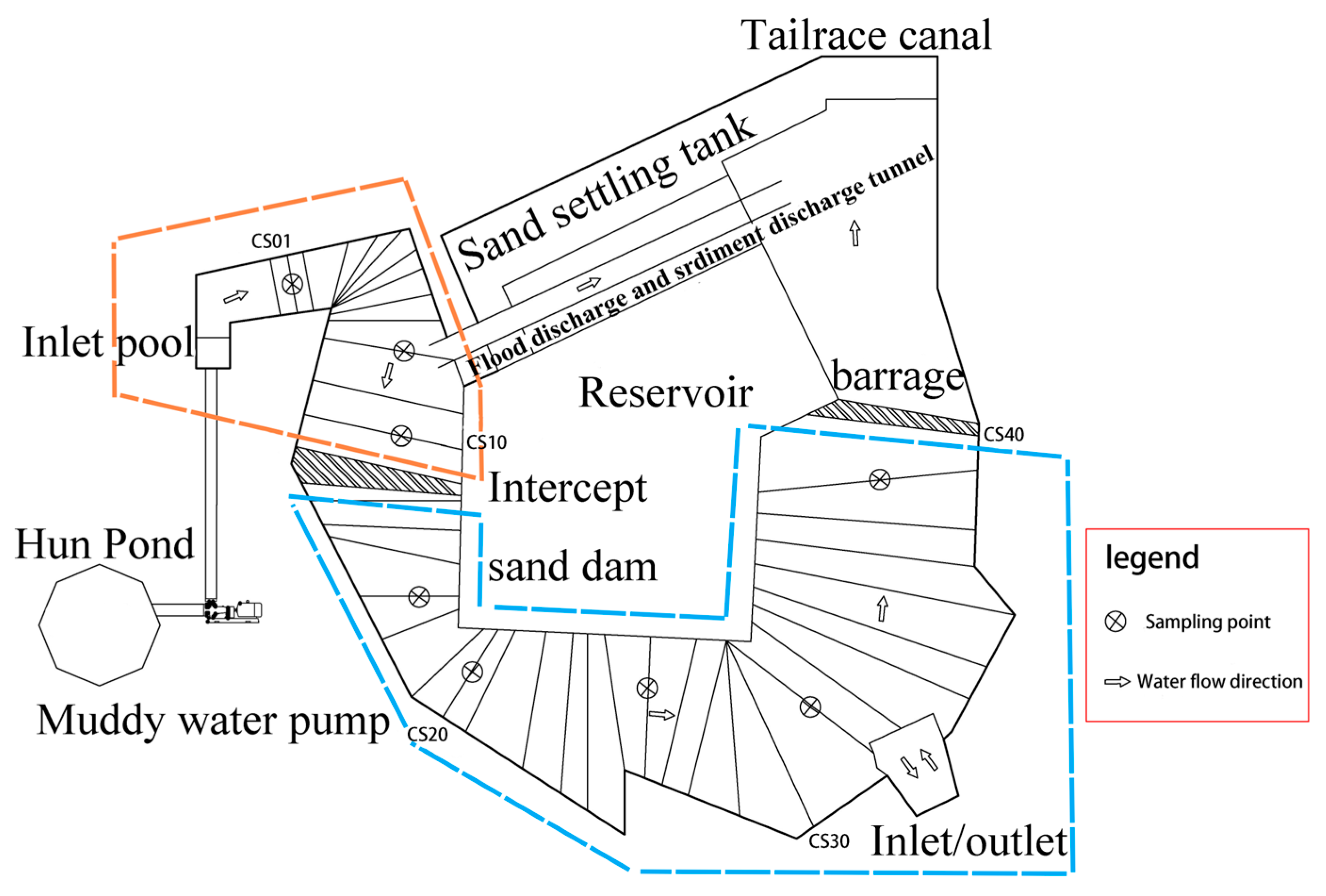
2. Materials and Methods
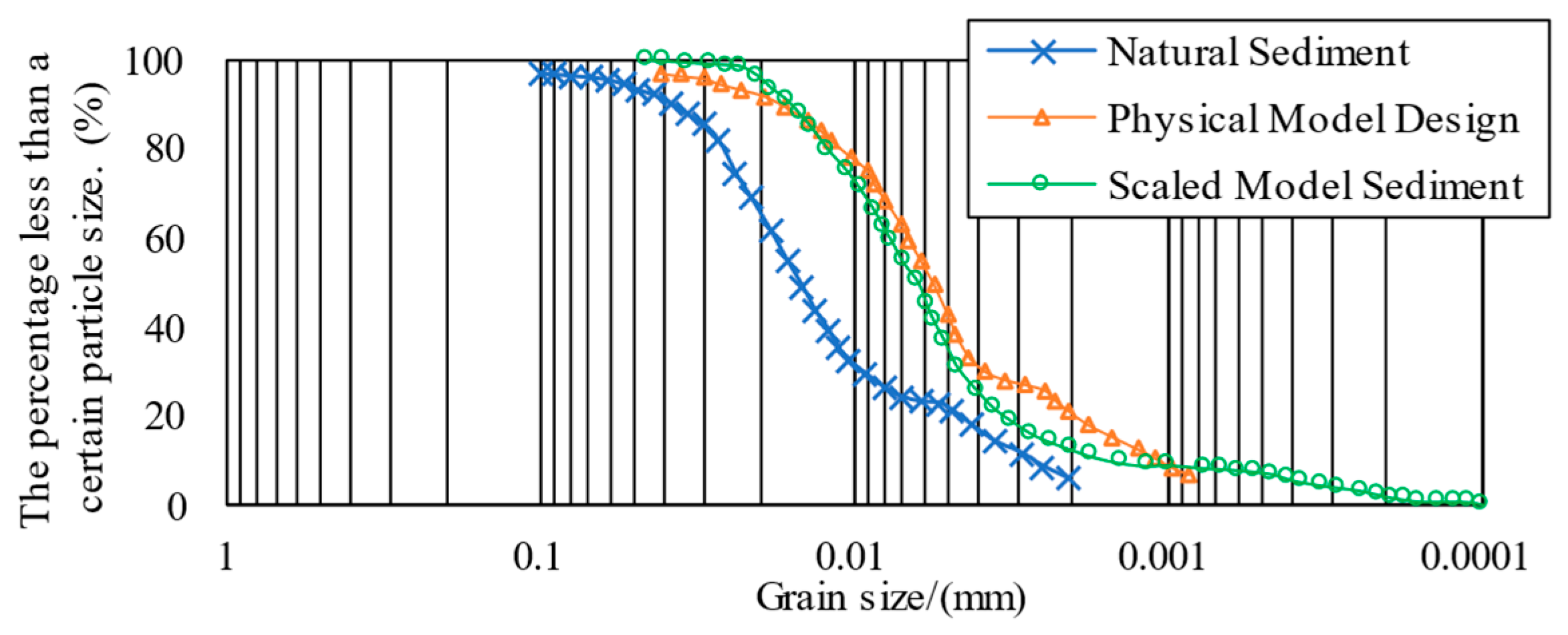
2.1. Model Design
2.2. Boundary Conditions for Model Experiments
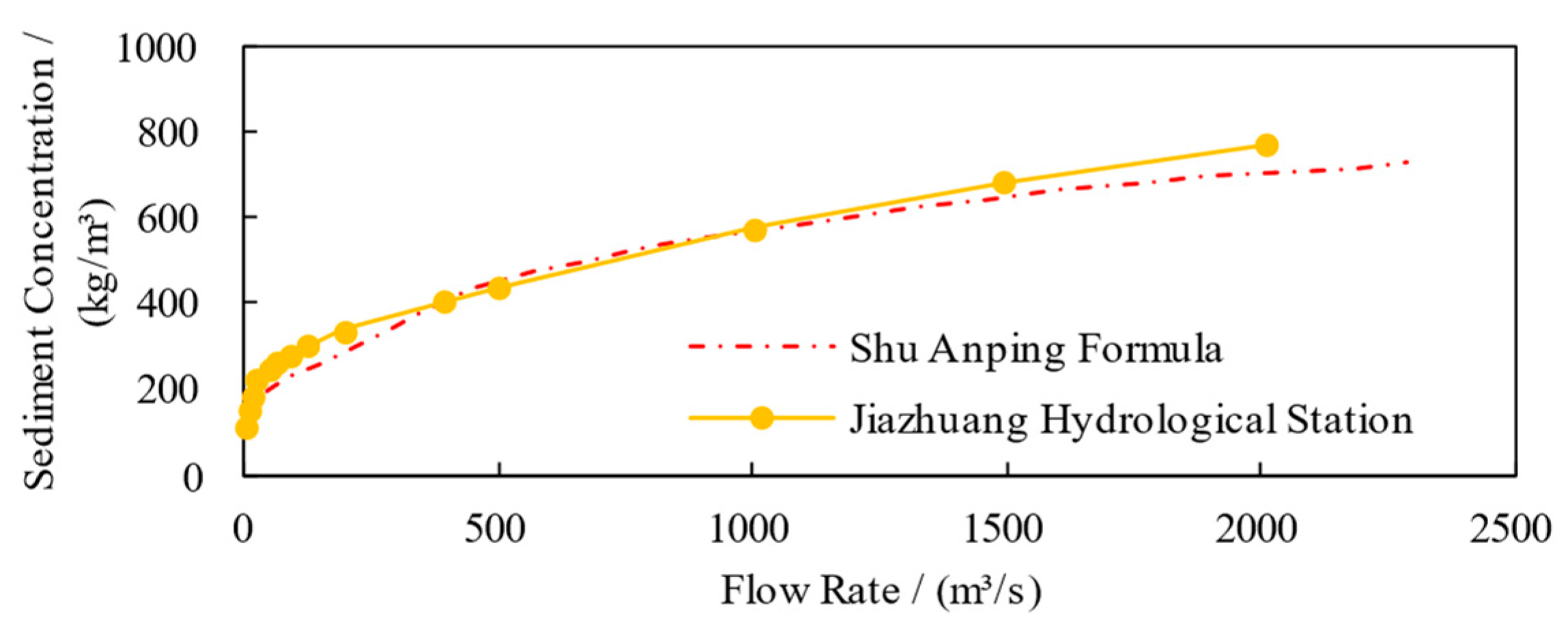
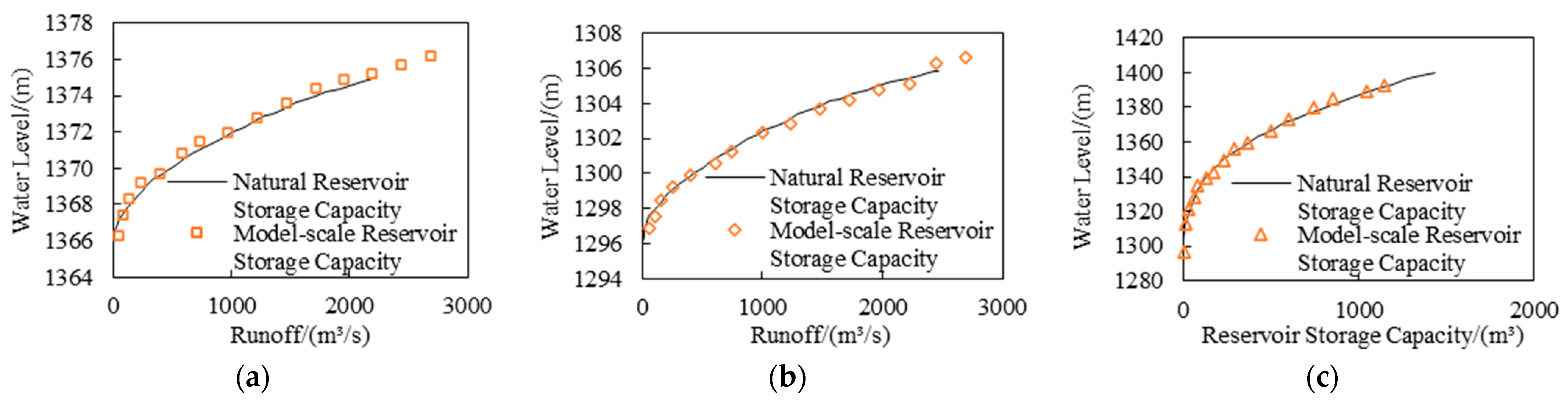
2.3. Model Calibration
2.4. Pearson Correlation Coefficient
2.5. Experimental Program
3. Results
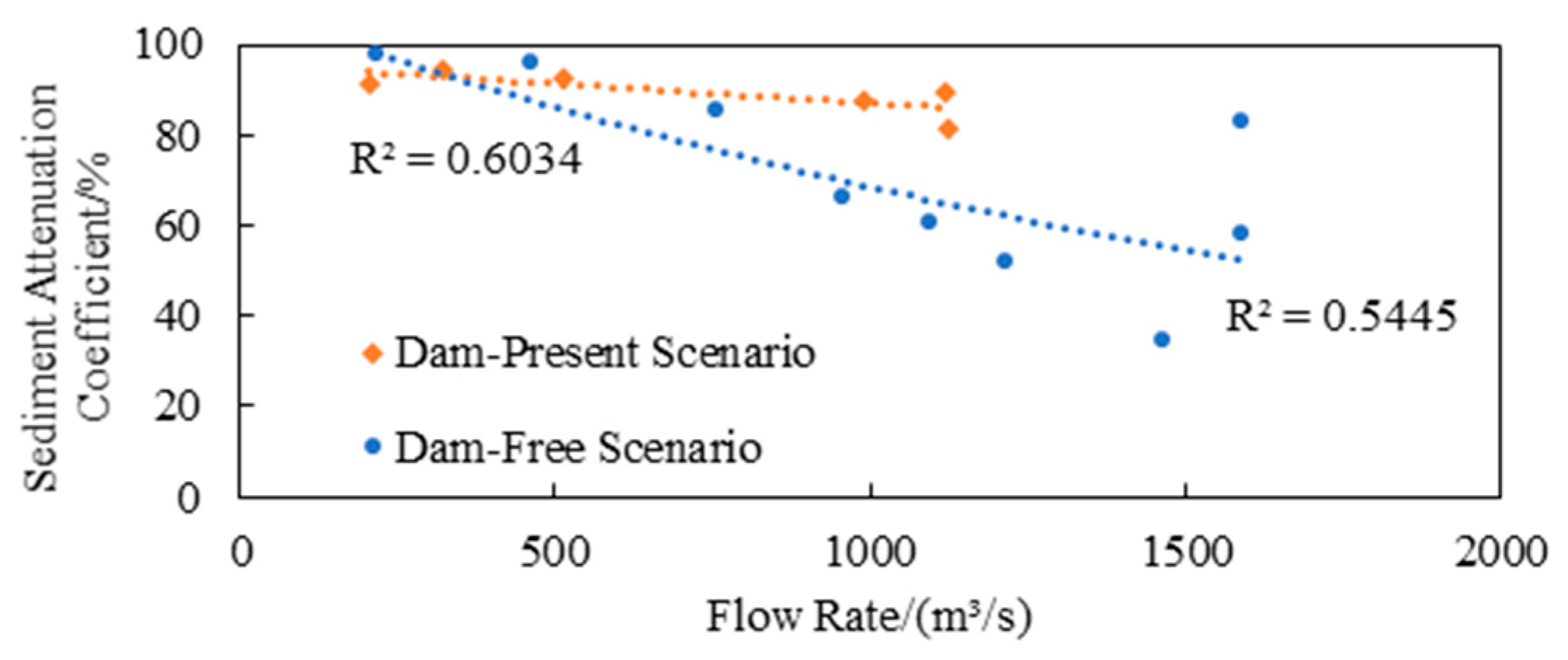
3.1. The Relationship Between Inflow Discharge and Turbine Sediment Concentration (TSC)
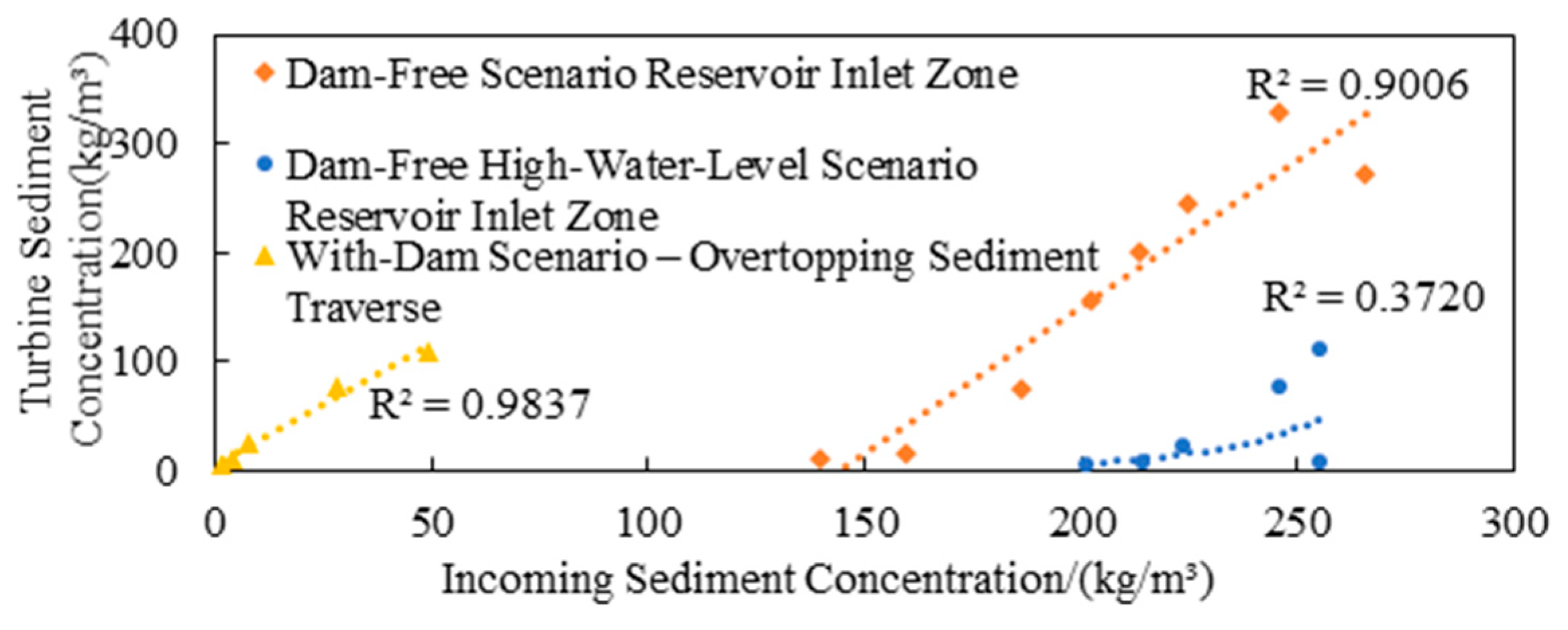
3.2. The Relationship Between the Incoming Sediment Concentration and the Turbine Sediment Concentration
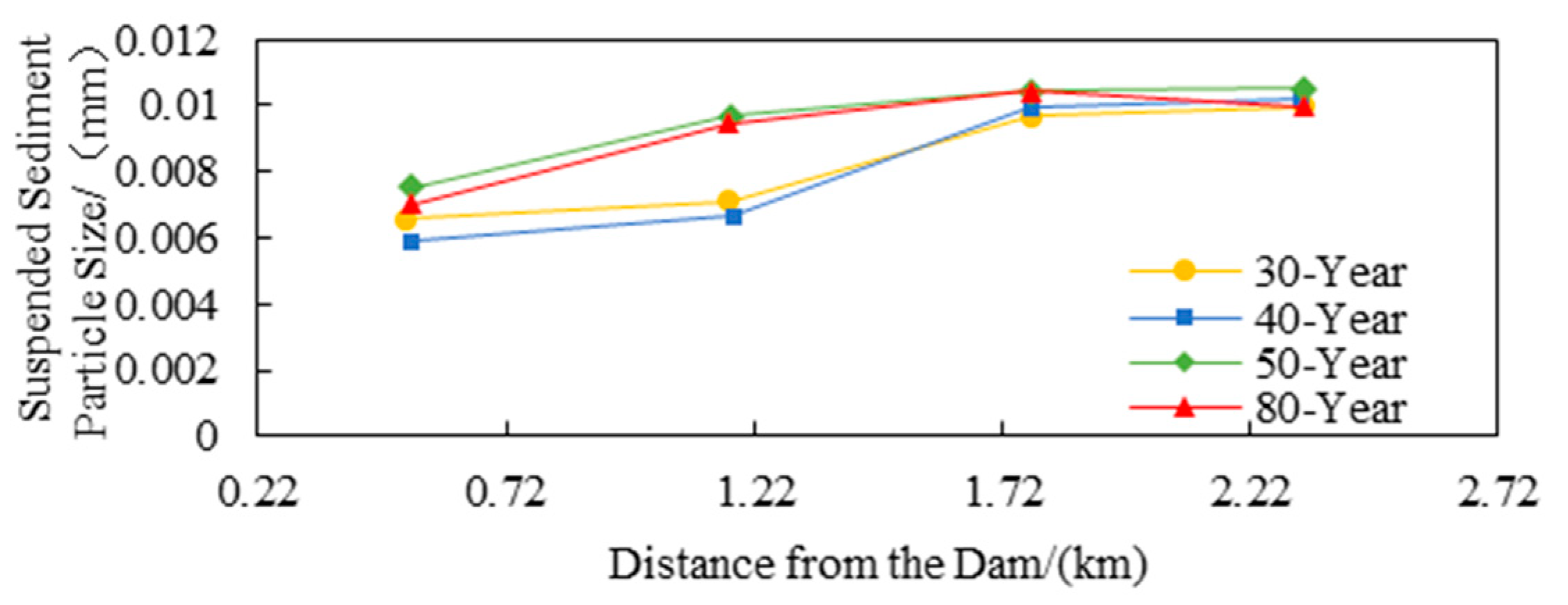
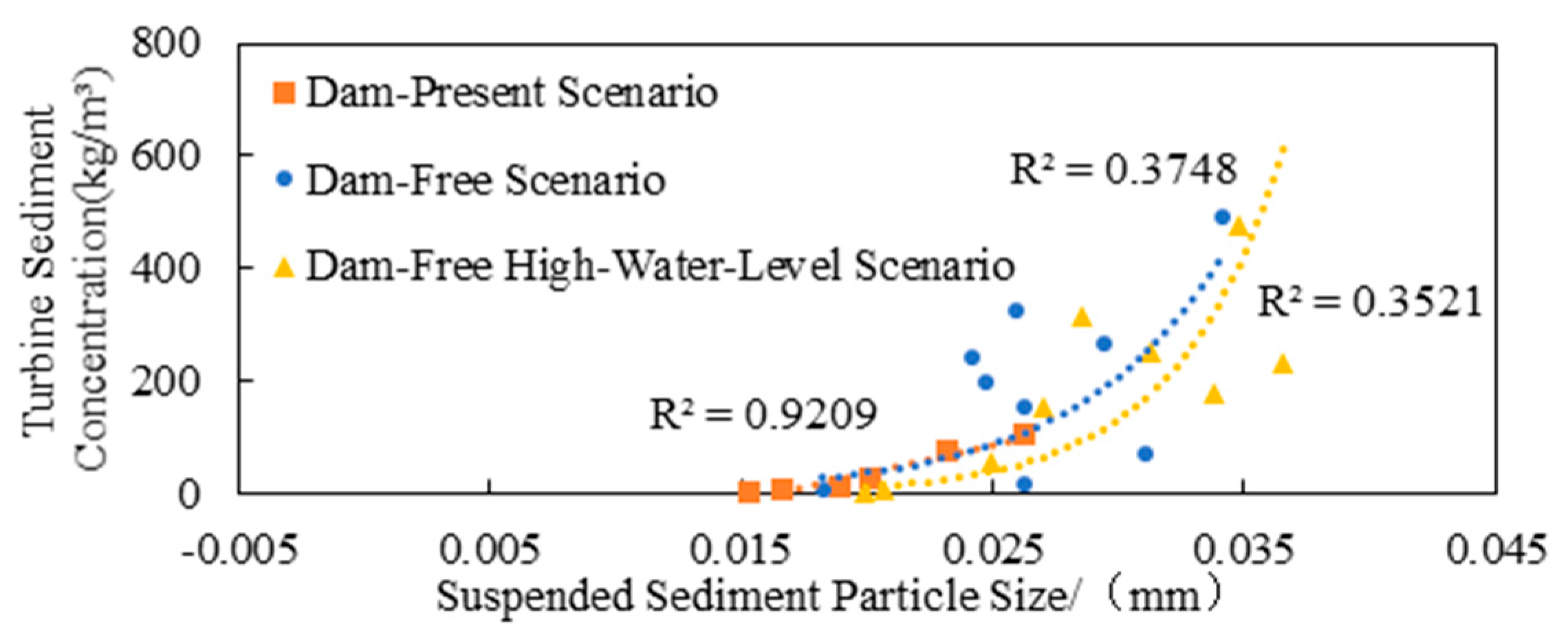
3.3. The Relationship Between the Particle Size of Incoming Sediment and the Turbine Sediment Concentration
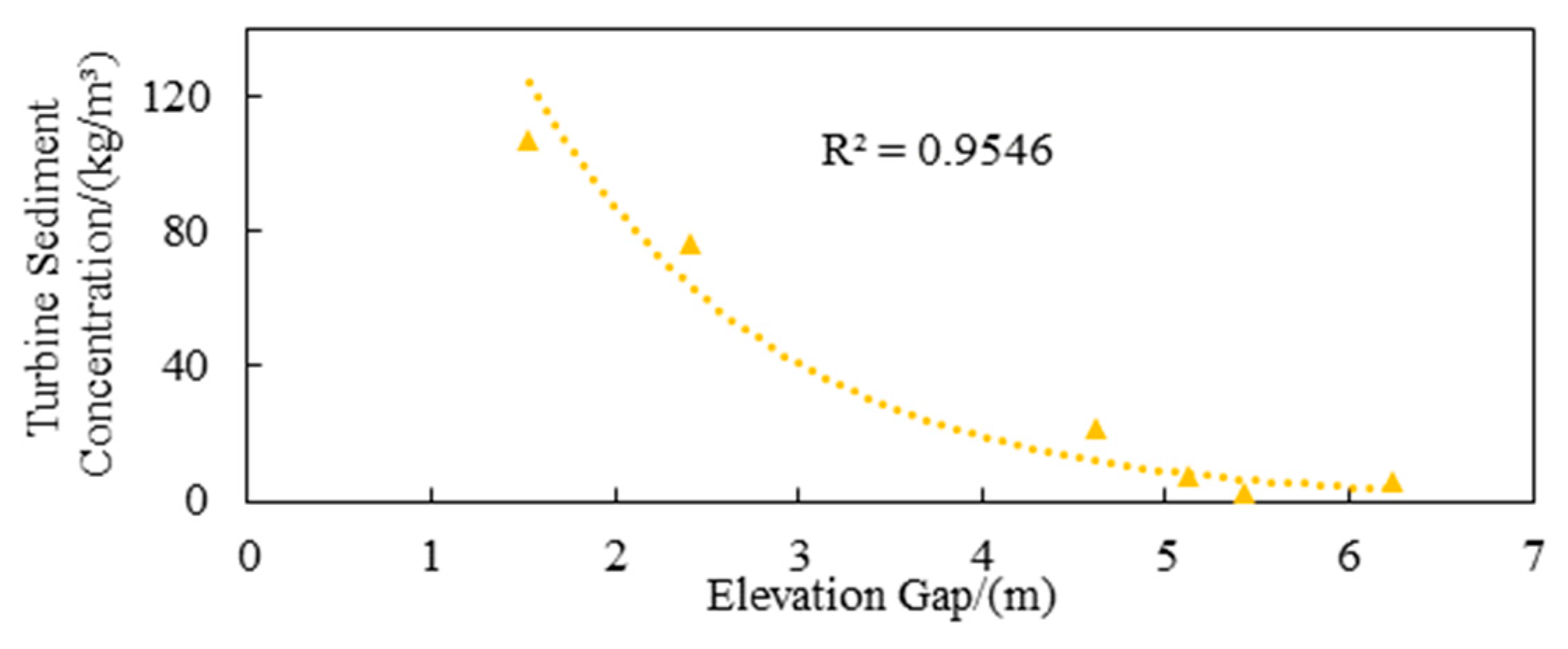
3.4. The Relationship Between the Elevation Difference (Inlet/Outlet vs. Sediment Bed) and Turbine Sediment Concentration
4. Discussion
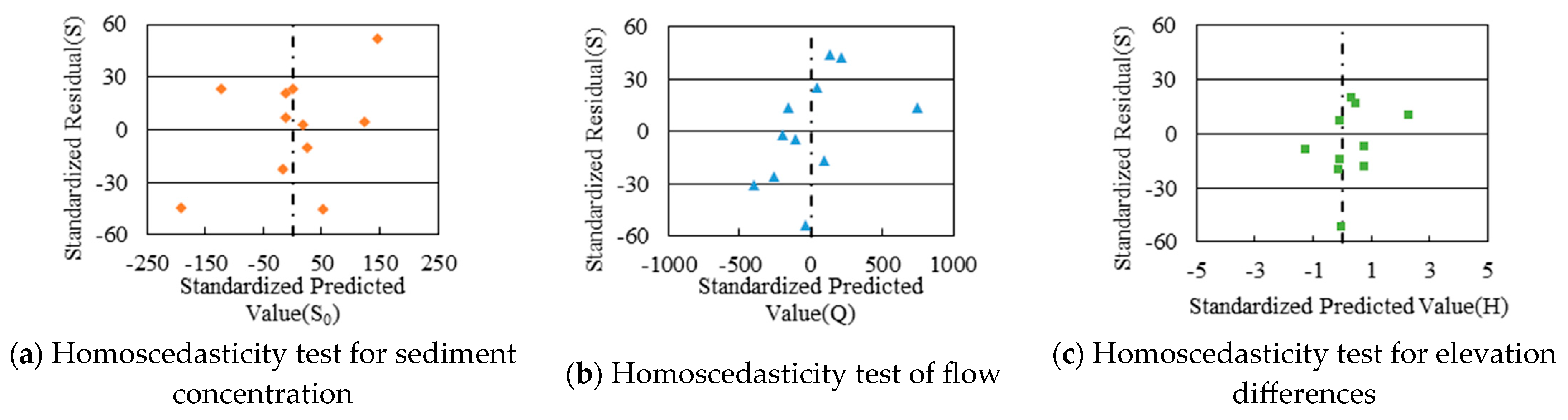
4.1. Precondition Testing for Pearson Correlation and Regression Analysis
4.2. Analysis of Linear Regression Results
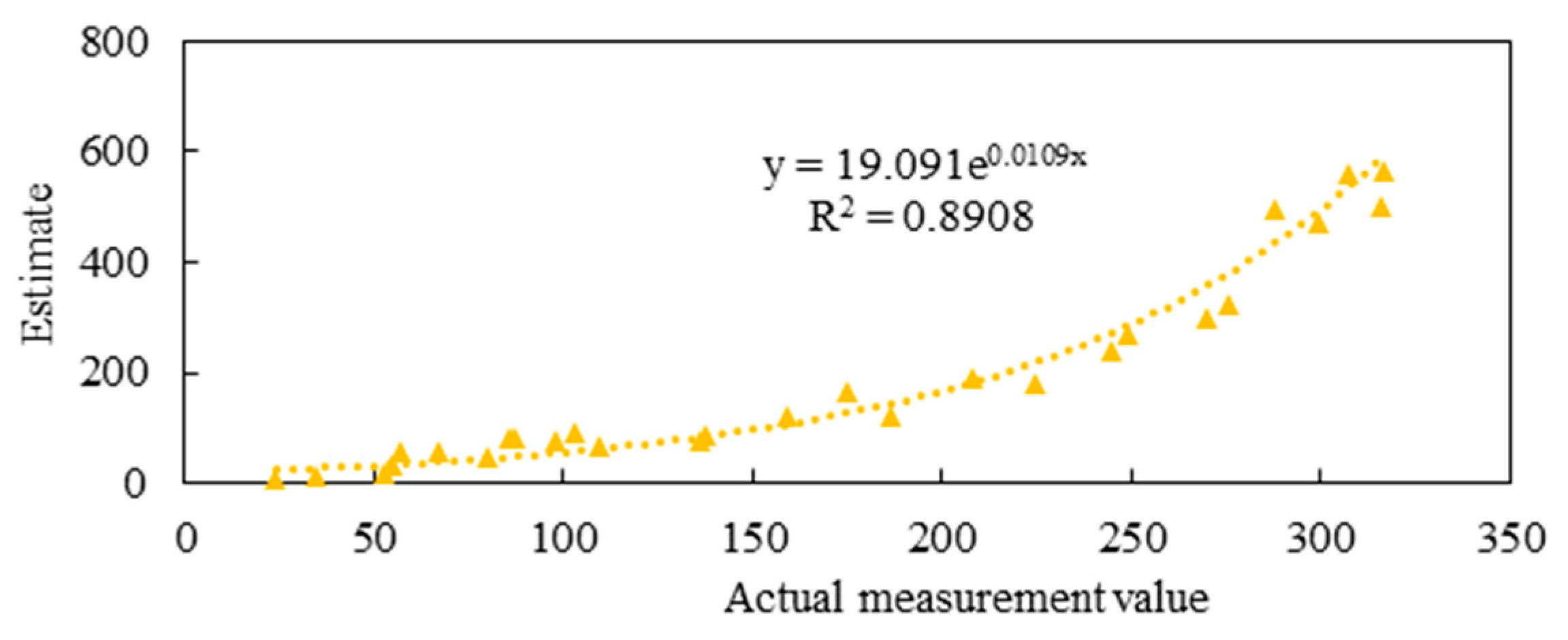
4.3. Analysis of Nonlinear Regression Results
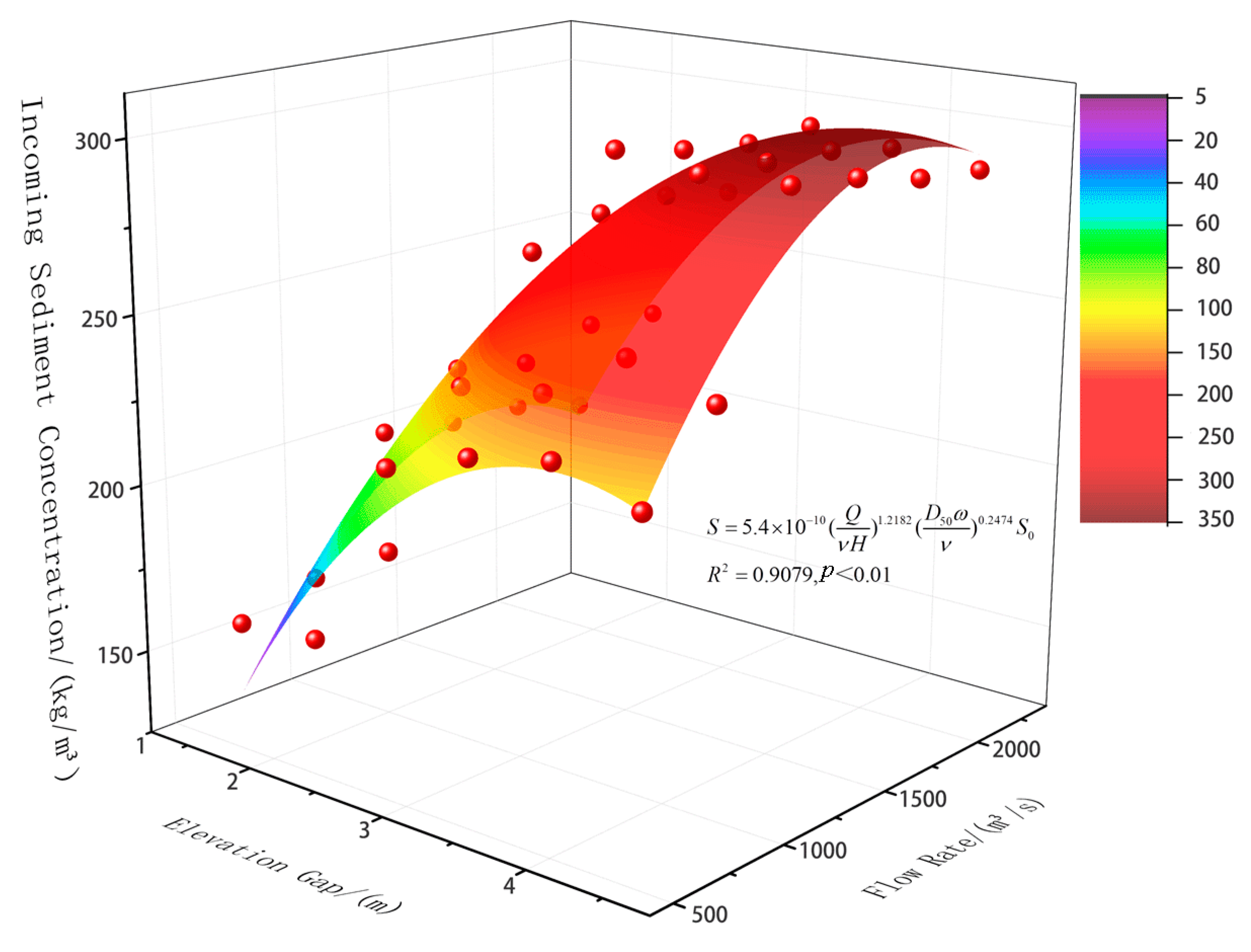
4.4. Turbine Sediment Concentration Formula Fitting
5. Conclusions
- (1)
- The test results indicate that, under constant conditions of reservoir length and other parameters, the inflow discharge significantly affects the attenuation efficiency of sediment concentration from the reservoir inflow to the power station’s inlet and outlet: in the low discharge range (Q < 500 m3/s), the sediment concentration attenuation rate generally exceeds 90%; in the medium discharge range (500~1200 m3/s), the attenuation rate decreases to between 80% and 90%; and under high discharge conditions (Q > 1200 m3/s), the sediment concentration exhibits a sharp attenuation, with the attenuation rate ranging from 30% to 80%, leading to an increase in the sediment concentration at the power station’s inlet and outlet. This suggests that a sudden change in the longitudinal hydraulic gradient occurs at an inflow discharge of 1200 m3/s, marking a critical inflection point in sediment transport efficiency.
- (2)
- The lower boundary of the median particle size adjustment range for suspended load gradually increases with the flood return period, rising from 0.006 mm for 30 and 40-year events to 0.009 mm for an 80-year event. Furthermore, during an 80-year event, the particle size fluctuation range approaches a high-level narrow distribution of 0.009~0.011 mm.
- (3)
- The linear regression model constructed using the inflow sediment concentration, inflow discharge, and the elevation difference between the inlet/outlet and the nearby riverbed has an R2 value of 0.8, indicating that these three factors can explain 80% of the variation in the sediment concentration at the turbine for pumped storage power stations. Moreover, based on the absolute values of the standardized coefficients, the importance of each factor is ranked as follows: inflow sediment concentration (0.36) > inflow discharge (0.345) > elevation difference between the inlet/outlet and the nearby riverbed (0.319).
- (4)
- Using multiple factors influencing sediment concentration in turbines as independent variables, a TSC prediction formula was derived through dimensional analysis. The parameters were calibrated via multivariate regression, fitting a formula based on the sediment-carrying capacity theory. The results were then validated through engineering analogy, demonstrating favorable predictive accuracy.
- (5)
- Future research could integrate Large Eddy Simulation (LES) and phase-resolving modeling techniques to accurately capture the transient impact effects of turbulence on sediment entrainment at the bed interface. Simultaneously, machine learning algorithms (e.g., LSTM, Physics-Informed Neural Networks, PINNs) could be introduced to optimize the dynamic inversion and prediction of sediment-laden flow boundary conditions. This can facilitate a technological leap from theoretical mechanism analysis to intelligent engineering control, thereby providing scientific decision-making support for long-term reservoir capacity optimization and safe operation of pumped-storage power stations.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Pure-PSPS | Pure pumped-storage power stations |
| TSC | Turbine sediment concentration |
References
- Li, J.; Yi, C.; Gao, S. Prospect of new pumped-storage power station. Glob. Energy Interconnect. 2019, 2, 235–243. [Google Scholar] [CrossRef]
- Ji, L.; Li, X.; Huang, W.; Dong, J.; Bai, M.; Li, C. Study on site selection combination evaluation of pumped-storage power station based on cycle elimination—Based on the empirical analysis of North China. J. Energy Storage 2022, 52, 104824. [Google Scholar] [CrossRef]
- Kong, Y.; Kong, Z.; Liu, Z.; Wei, C.; Zhang, J.; An, G. Pumped storage power stations in China: The past, the present, and the future. Renew. Sustain. Energy Rev. 2017, 71, 720–731. [Google Scholar] [CrossRef]
- Storli, P.T. Overview of Pumped Hydro Resource. In Advances in Energy Storage: Latest Developments from R&D to the Market; Wiley: Hoboken, NJ, USA, 2022; pp. 211–238. [Google Scholar]
- Mao, X.; Hu, J.; Pan, Z.; Zhong, P.; Zhang, N. A Brief Review of Recent Research on Reversible Francis Pump Turbines in Pumped Storage Plants. Energies 2025, 18, 394. [Google Scholar] [CrossRef]
- Taniguchi, H.; Nagao, T.; Higasa, H. Development of a pumped-storage power station model for power system stability study. Electr. Eng. Jpn. 1992, 112, 50–62. [Google Scholar] [CrossRef]
- Zhang, F.; Ni, J.B.; Liu, R. Unit stability analysis for Jixi pumped-storage hydropower station. J. Hydroelectr. Eng. 2021, 40, 112–123. [Google Scholar]
- Shen, Z.Z.; Zhang, L.; Xu, L.Q. Optimization of seepage prevention form of the Zhen’an Pumped Storage Power Station. Appl. Mech. Mater. 2015, 724, 180–184. [Google Scholar] [CrossRef]
- Zeng, W.; Beck, M.B. Development and evaluation of a mathematical model for the study of sediment-related water quality issues. Water Sci. Technol. 2001, 43, 47–54. [Google Scholar] [CrossRef]
- Zhang, C.L.; Zhu, H.H.; Zhong, W.Q.; Huang, Z.M. Experimental research on inlet/outlet hydraulics of pump storage power plants. J. Hydroelectr. Eng. 2005, 24, 60–63. [Google Scholar]
- Guan, B.; Hou, J.; Lv, J.; Li, D.; Chen, G.; Fang, Y.; Shi, L. Numerical Simulation of Dam-Break Flood Routing in Pumped Storage Power Stations with Multi-Conditions and Disaster Impact Analysis. Water Resour. Manag. 2024, 39, 741–757. [Google Scholar] [CrossRef]
- Papanicolaou, A.N.; Elhakeem, M.; Krallis, G.; Prakash, S.; Edinger, J. Sediment transport modeling review—Current and future developments. J. Hydraul. Eng. 2008, 134, 1–14. [Google Scholar] [CrossRef]
- Bo, Y.; Tao, Z.; Kexun, Z.; Shuangying, Z.; Xiao, H.; Senlin, W.; Shiwan, C. Enclosed Karst Depression Identification and Analysis for the Pumped Storage Power Station Reservoir Construction Using DEM. Geofluids 2023, 2023, 4794665. [Google Scholar] [CrossRef]
- Yang, X.; Lian, J.; Wang, H.; Zhang, Z.; Hu, Y. Forced vibration analysis model for pumped storage power station based on the 1D–3D coupling and pipe walls vibration. Earthq. Eng. Resil. 2022, 1, 393–409. [Google Scholar] [CrossRef]
- Liu, C.; Yu, M.; He, X.; Wang, K.; Shao, Y. Numerical Simulation and Sensitivity Analysis of Sediment Issues in Pumped Storage Power Stations: Sediment Conveyance of Turbine and Sedimentation of Reservoirs. Water 2023, 15, 3531. [Google Scholar] [CrossRef]
- Budinski, L.; Spasojević, M. 2D modeling of flow and sediment interaction: Sediment mixtures. J. Waterw. Port Coast. Ocean. Eng. 2014, 140, 199–209. [Google Scholar] [CrossRef]
- Montaseri, H.; Tavakoli, K.; Evangelista, S.; Omidvar, P. Sediment transport and bed evolution in a 180° curved channel with lateral intake: Numerical simulations using Eulerian and Discrete Phase models. Int. J. Mod. Phys. C Comput. Phys. Phys. Comput. 2020, 31, 2050113. [Google Scholar] [CrossRef]
- Mehnifard, M.; Dalfardi, S.; Baghdadi, H.; Seirfar, Z. Simulation of local scour caused by submerged horizontal jets with Flow-3D numerical model. Desert 2015, 20, 47–55. [Google Scholar]
- Tarek, A.S. Three-dimensional numerical study for determining the optimum diversion angle of bifurcating channels. Ain Shams Eng. J. 2023, 14, 241–249. [Google Scholar]
- Jin, M. Numerical Analysis of Flow Characteristics in a Braided River with Diversion Weirs; Shenyang Agricultural University: Shenyang, China, 2017. [Google Scholar]
- Wu, T.; Wei, Z.; Zhan, Y. A prediction method for sediment passing through pumped storage power stations. Hongshui River 2006, 12, 78–81. [Google Scholar]
- Pan, J.; Ma, J.; Han, J.; Zhou, Y.; Wu, L.; Zhang, W. Prediction of sediment wear of francis turbine with high head and high sediment content. Front. Energy Res. 2023, 10, 1117606. [Google Scholar] [CrossRef]
- Li, J.; He, X.; Wei, J.; Bao, Y.; Tang, Q.; de Dieu Nambajimana, J.; Nsabimana, G. Multifractal features of the particle-size distribution of suspended sediment in the Three Gorges Reservoir, China. Int. J. Sediment Res. 2021, 36, 489–500. [Google Scholar] [CrossRef]
- Li, J.; Cao, Z.; Liu, Q. Waves and sediment transport due to granular landslides impacting reservoirs. Water Resour. Res. 2019, 55, 495–518. [Google Scholar] [CrossRef]
- Fu, Y.; Bellerby, R.G.J.; Ji, H.; Chen, S.; Fan, Y.; Li, P. Impacts of riverine floods on morphodynamics in the yellow river delta. Water 2023, 15, 1568. [Google Scholar] [CrossRef]
- Fitri, A.; Hashim, R.; Abolfathi, S.; Abdul Maulud, K.N. Dynamics of sediment transport and erosion-deposition patterns in the locality of a detached low-crested breakwater on a cohesive coast. Water 2019, 11, 1721. [Google Scholar] [CrossRef]
- Alvarez, L.V.; Grams, P.E. An Eddy-Resolving Numerical Model to Study Turbulent Flow, Sediment, and Bed Evolution Using Detached Eddy Simulation in a Lateral Separation Zone at the Field-Scale. J. Geophys. Res. Earth Surf. 2021, 126, e2021JF006149. [Google Scholar] [CrossRef]
- Hu, P.; Tao, J.; Ji, A.; Li, W.; He, Z. A computationally efficient shallow water model for mixed cohesive and non-cohesive sediment transport in the Yangtze Estuary. Water 2021, 13, 1435. [Google Scholar] [CrossRef]
- Imanshoar, F.; Jahangirzadeh, A.; Basser, H.; Akib, S.; Kamali, B.; Tabatabaei, M.R.M.; Kakouei, M. Reservoir sedimentation based on uncertainty analysis. In Abstract and Applied Analysis; Hindawi Publishing Corporation: London, UK, 2014; Volume 2014, p. 367627. [Google Scholar]
- Tsai, C.W.; Yeh, T.G.; Hsu, Y.; Wu, K.T.; Liu, W.J. Risk analysis of reservoir sedimentation under non-stationary flows. J. Flood Risk Manag. 2021, 14, e12706. [Google Scholar] [CrossRef]
- Stefanidis, P.; Stefanidis, S. Reservoir sedimentation and mitigation measures. Lakes Reserv. Res. Manag. 2012, 17, 113–117. [Google Scholar] [CrossRef]
- Lajczak, A. Modelling the long-term course of non-flushed reservoir sedimentation and estimating the life of dams. Earth Surf. Process. Landf. 1996, 21, 1091–1107. [Google Scholar] [CrossRef]
- Mustapha, M.K.; Abodunrin, I.A. Is siltation affecting the limnology and gradually eroding the functions of Agba reservoir, Ilorin, Nigeria?—An old tropical African drinking water reservoir. Lakes Reserv. Res. Manag. 2021, 26, e12366. [Google Scholar]
- Yang, Y.; Zheng, J.; Zhang, H.; Chai, Y.; Zhu, Y.; Wang, C. Impact of the Three Gorges Dam on riverbed scour and siltation of the middle reaches of the Yangtze River. Earth Surf. Process. Landf. 2022, 47, 1514–1531. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, F.; Zhang, X.; Lin, B.; Yang, Z.; Yuan, B.; Falconer, R.A. Severely declining suspended sediment concentration in the heavily dammed Changjiang fluvial system. Water Resour. Res. 2021, 57, e2021WR030370. [Google Scholar] [CrossRef]
- Eidmann, J.S.; Rathburn, S.L.; White, D.; Huson, K. Channel response and reservoir delta evolution from source to sink following an extreme flood. J. Geophys. Res. Earth Surf. 2022, 127, e2020JF006013. [Google Scholar] [CrossRef]
- Wang, T.; Tang, H.; Chen, H.; Ma, D.; Wang, Y.; Fan, H. Numerical Evaluation on Massif Vibration of Pumped Storage Power Plant in Hydraulic Transients. Energies 2025, 18, 222. [Google Scholar] [CrossRef]
- Xu, L. A new load grouping control method for pumped storage power stations in the planning curve mode. J. Phys. Conf. Ser. 2025, 2935, 012012. [Google Scholar] [CrossRef]
- Lin, J.; Zhu, Y.; Hou, J.; Pan, B.; Chu, W.; Huang, W. Equivalent Continuum Coupling-Based Slope Stability Analysis of Zhouning Pumped Storage Power Station. Geofluids 2021, 2021, 9926751. [Google Scholar] [CrossRef]
- Yang, L.; Wang, H.; Yang, X.; Li, H. Study of the inhibitory effect of a soft cushion on the propagation of pressure pulsation in pumped storage power stations. Earthq. Eng. Resil. 2023, 2, 301–315. [Google Scholar] [CrossRef]
- Tian, J.; Xu, P.; Hu, H.; Liang, D.; Wang, Y.; Shang, Y. Hydrodynamic Optimization of Non-Pressurized Tunnel Intersection of Pumped Storage Power Station. Water 2025, 17, 471. [Google Scholar] [CrossRef]
- Fan, H.; Wu, H.; Li, S.; Han, S.; Ren, J.; Huang, S.; Zou, H. Optimal Scheduling Method of Combined Wind–Photovoltaic–Pumped Storage System Based on Improved Bat Algorithm. Processes 2025, 13, 101. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Q.; Kong, S.; Li, W.; Luo, J.; Huang, T. Analysis of renewable energy consumption and economy considering the joint optimal allocation of “renewable energy+ energy storage+ synchronous condenser”. Sci. Rep. 2023, 13, 20376. [Google Scholar] [CrossRef]
- Pikl, F.G.; Richter, W.; Zenz, G. Pumped storage technology combined with thermal energy storage–Power station and pressure tunnel concept: Pumpspeichertechnologie kombiniert mit thermischer Energiespeicherung–Kraftwerks-und Druckstollenkonzept. Geomech. Tunn. 2017, 10, 611–619. [Google Scholar] [CrossRef]
- Huang, H.; Zhou, M.; Zhang, L.; Li, G.; Sun, Y. Joint generation and reserve scheduling of wind-solar-pumped storage power systems under multiple uncertainties. Int. Trans. Electr. Energy Syst. 2019, 29, e12003. [Google Scholar] [CrossRef]
- Zhang, L.; Xin, H.; Wu, J.; Ju, L.; Tan, Z. A multiobjective robust scheduling optimization mode for multienergy hybrid system integrated by wind power, solar photovoltaic power, and pumped storage power. Math. Probl. Eng. 2017, 2017, 9485127. [Google Scholar] [CrossRef]
- Gao, J.; Zheng, Y.; Li, J.; Zhu, X.; Kan, K. Optimal Model for Complementary Operation of a Photovoltaic-Wind-Pumped Storage System. Math. Probl. Eng. 2018, 2018, 5346253. [Google Scholar] [CrossRef]
- Shen, J.; Wang, Y.; Hao, T.; Cheng, C. Pumped-storage renovation for grid-scale, long-duration energy storage. Nat. Rev. Electr. Eng. 2025, 2, 79–80. [Google Scholar] [CrossRef]
- Pang, J.; Liu, H.; Liu, X.; Yang, H.; Peng, Y.; Zeng, Y.; Yu, Z. Study on sediment erosion of high head Francis turbine runner in Minjiang River basin. Renew. Energy 2022, 192, 849–858. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.H.; Zhang, S.L.; Zhang, Q.J. Influence of Imported Water and Sediment on the Sediment Concentration in a Pumped Storage Power Station. Pearl River 2018, 39, 45–49. [Google Scholar]
- Zou, X.; Wang, C.; Song, H.; Han, Z.; Ma, Z.; Hu, W. Applications of ultrasound imaging system for measuring water-sand parameters during sediment transport process in hydraulic model experiments. J. Hydroinformatics 2018, 20, 410–423. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China, State Administration for Market Regulation. GB/T 50180—2018 Standard for Design of Engineering Sediment in China; China Standards Press: Beijing, China, 2018. [Google Scholar]
- Ministry of Water Resources of the People’s Republic of China. SL 99—2012 Standard for River Model Test; China Water & Power Press: Beijing, China, 2012. [Google Scholar]
- Zhang, R.J. River Dynamics; China Water Power Press: Beijing, China, 1998; pp. 182–186. [Google Scholar]
- Shu, A.P.; Fei, X.J. Sediment transport capacity of hyperconcentrated flow. Sci. China Ser. G Phys. Mech. Astron. 2008, 51, 961–975. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. A reliable convergent Adomian decomposition method for heat transfer through extended surfaces. Int. J. Numer. Methods Heat Fluid Flow 2018, 28, 2551–2566. [Google Scholar] [CrossRef]



| Year | 2016 | 2017 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Month | June | July | August | September | Annual | June | July | August | September | Annual |
| Sand volume (t) | 783 | 4935 | 8497 | 435 | 14,651 | 495 | 6580 | 6059 | 889 | 14,024 |
| Proportion of sediment during flood season | 5.33% | 33.7% | 58% | 2.97% | 100% | 3.53% | 46.9% | 43.2% | 6.34% | 100% |
| Category | Scale Name | Symbol | Scale Value |
|---|---|---|---|
| Geometric Similarity | Horizontal Scale | λL | 75 |
| Vertical Scale | λH | 75 | |
| Hydrodynamic Similarity | Flow Velocity Scale | λv | 8.66 |
| Discharge Scale | λQ | 48,714 | |
| Suspended Load Similarity | Sediment-Carrying Capacity Scale | λs | 2.8 |
| Suspended Load Particle Size Scale | λds | 2.4 | |
| Scour-Siltation Time Scale | λt | 22.3 | |
| Bed Load Similarity | Bed Load Particle Size Scale | λd | 4.11 |
| Bed Load Transport Rate Scale | λqs | 546.42 |
| Flood Return Period | Peak Discharge/(m3/s) | Sand Content/(kg/m3) | Flood Volume/ (1 × 10⁴ m3) | Sediment Load/ (1 × 104 t) | Transfer Quality/ (1 × 104 t) |
|---|---|---|---|---|---|
| 100 | 1580 | 712 | 1060 | 755 | 227 |
| 80 | 1460 | 684 | 987 | 675 | 203 |
| 50 | 1210 | 626 | 823 | 515 | 155 |
| 40 | 1090 | 598 | 749 | 448 | 134 |
| 30 | 950 | 565 | 657 | 371 | 111 |
| 20 | 753 | 519 | 524 | 272 | 82 |
| 10 | 455 | 449 | 327 | 147 | 44 |
| 5 | 217 | 390 | 163 | 64 | 19 |
| Scenario Designations | Water-Sediment Return Period Year Configuration | Initial Topography | River Dam | Sediment Control Dam |
|---|---|---|---|---|
| Dam-Free Scenario | 5-, 10-, and 20-Year | Designed Riverbed | During flood overtopping, first open the mid-level bottom outlets; open the surface spillways when the water level exceeds 1382 m; open the side bottom outlets when the water level exceeds 1388.5 m | No |
| 100-Year | Designed Riverbed | |||
| 30-Year | 100-Year Riverbed | |||
| 40-Year | 100 + 30-Year Riverbed | |||
| 50-Year | 100 + 30 + 40-Year Riverbed | |||
| 80-Year | 100 + 30 + 40 + 50-Year Riverbed | |||
| 100-Year | 100 + 30 + 40 + 50 + 80-Year Riverbed | |||
| Dam-Free High-Water-Level Scenario | 5-, 10-, and 20-Year | Designed Riverbed | Control the water level at 1389 m | No |
| 100-Year | Designed Riverbed | |||
| 30-Year | 100-Year Riverbed | |||
| 40-Year | 100 + 30-Year Riverbed | |||
| 50-Year | 100 + 30 + 40-Year Riverbed | |||
| 80-Year | 100 + 30 + 40 + 50-Year Riverbed | |||
| 100-Year | 100 + 30 + 40 + 50 + 80-Year Riverbed | |||
| Dam-Present Scenario | 100-Year | Designed Riverbed | The operating method is the same as the Dam-Free Scenario | Yes |
| 30-Year | 100-Year Riverbed | |||
| 40-Year | 100 + 30-Year Riverbed | |||
| 50-Year | 100 + 30 + 40-Year Riverbed | |||
| 80-Year | 100 + 30 + 40 + 50-Year Riverbed | |||
| 100-Year | 100 + 30 + 40 + 50 + 80-Year Riverbed |
| Water-Sediment Series | Elevation Gap/(m) | Over-Dam Sediment Concentration/(kg/m3) | Hydro-Turbine Sediment Concentration/(kg/m3) | Attenuation Rate/(%) |
|---|---|---|---|---|
| 80-Year | 4.61 | 405.55 | 77.07 | 81.00% |
| 100-Year | 3.59 | 434.67 | 107.24 | 75.33% |
| Parameter h | Residual Res(hk) | Series Truncation Error |
|---|---|---|
| −1.0 | 8.9 × 10−4 | 12% |
| −0.6 | 2.1 × 10−4 | 7% |
| −0.43 | 3.7 × 10−5 | <1% |
| Types of Methods | Correlation Coefficient R2 | Maximum Residual |
|---|---|---|
| Linear Regression | 0.9546 | 0.53 |
| Optimize OADM | 0.9862 | 0.14 |
| Independent Variables | Correlation Coefficient (γ) | Variance Inflation Factor | Durbin-Watson Statistic |
|---|---|---|---|
| Inflow Sediment Concentration (S0) | 0.84 | 3.681 | 1.9 |
| Inflow Discharge (Q) | 0.75 | 2.097 | |
| Elevation gap (H) | −0.75 | 2.424 |
| Parameter Names | Standardized Coefficients (β) | - | Tolerance |
|---|---|---|---|
| S0 | 0.36 | - | 0.308 |
| Q | 0.345 | - | 0.495 |
| H | −0.319 | - | 0.471 |
| R2 | - | 0.8 | - |
| Adjusted R-squared | - | 0.715 | - |
| Durbin-Watson Statistic | - | 1.875 | - |
| Iteration Count | Training Set MSE | Validation Set MSE | Maximum Weight Oscillation | Convergence State |
|---|---|---|---|---|
| 0 | 0.100 | 0.108 | - | Not Converged |
| 5 | 0.028 | 0.035 | <2% | Rapid Descent |
| 10 | 0.007 | 0.012 | <5% | Deceleration and Tuning |
| 15 | 0.0004 | 0.0006 | <1% | Approaching Steady State |
| 18 | 0.00009 | 0.00015 | - | Convergence Achieved |
| Key Parameters for Comparison | Fengning Pumped-Storage Power Station | This Study’s Research Subject |
|---|---|---|
| Average daily pumping duration (h) | 7 | 7 |
| Multi-year average sediment concentration (kg/m3) | 59.42 | 45.4 |
| Pumping flow rate (m3/s) | 212.0 | 104.5 |
| Distance between lower reservoir intake/outlet and dam site (km) | 1.5 | 0.60 |
| Normal storage capacity of lower reservoir (×104 m3) | 5344 | 4587 |
| Median particle size of suspended load (mm) | 0.028 | 0.016 |
| Reservoir sediment capacity ratio | 18.7 | 15.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Dong, Z.; Wang, Z. Influencing Factors and Prediction of Turbine Sediment Concentration in Pure Pumped-Storage Power Stations on Sediment-Laden Rivers. Water 2025, 17, 1254. https://doi.org/10.3390/w17091254
Liu L, Dong Z, Wang Z. Influencing Factors and Prediction of Turbine Sediment Concentration in Pure Pumped-Storage Power Stations on Sediment-Laden Rivers. Water. 2025; 17(9):1254. https://doi.org/10.3390/w17091254
Chicago/Turabian StyleLiu, Lei, Zhandi Dong, and Zhiguo Wang. 2025. "Influencing Factors and Prediction of Turbine Sediment Concentration in Pure Pumped-Storage Power Stations on Sediment-Laden Rivers" Water 17, no. 9: 1254. https://doi.org/10.3390/w17091254
APA StyleLiu, L., Dong, Z., & Wang, Z. (2025). Influencing Factors and Prediction of Turbine Sediment Concentration in Pure Pumped-Storage Power Stations on Sediment-Laden Rivers. Water, 17(9), 1254. https://doi.org/10.3390/w17091254





