How Different Are Population Movements between Weekdays and Weekends: A Complex-Network-Based Analysis on 36 Major Chinese Cities
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.2. Methods
2.2.1. Metrics for the Network
- (1)
- Degree centrality
- (2)
- Betweenness centrality
- (3)
- Network Diversity
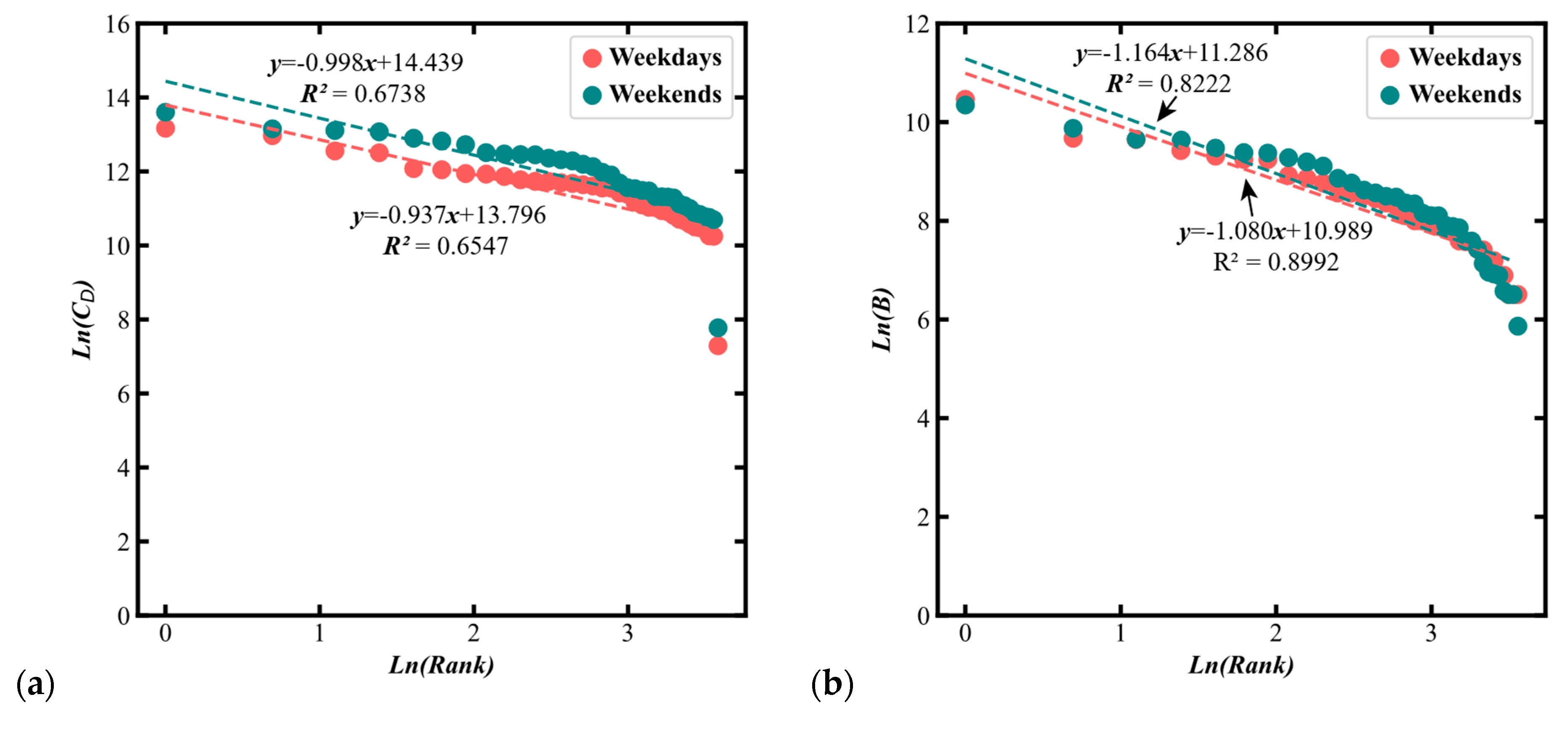
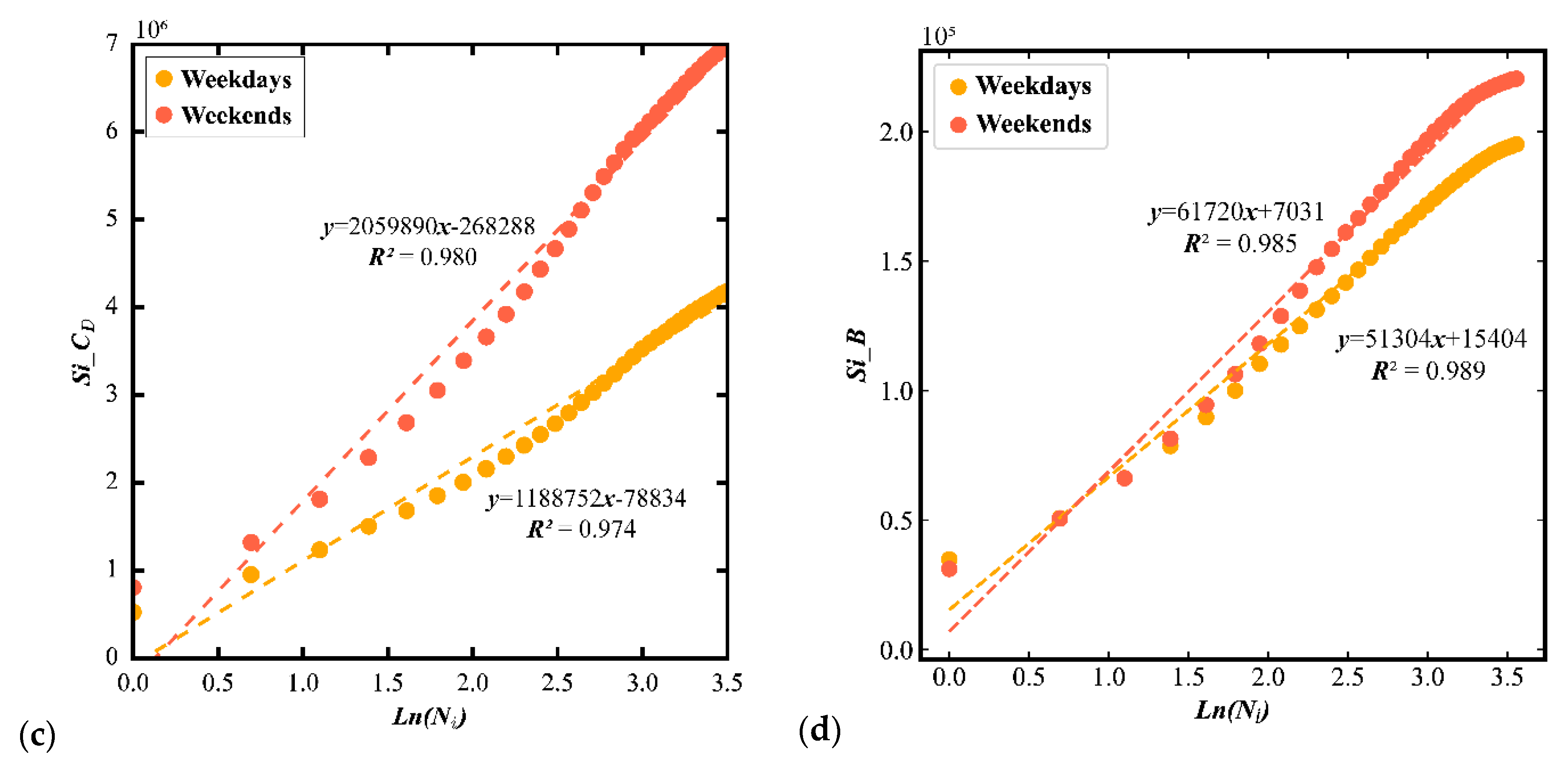
2.2.2. Power Law Examination of City-Related Metrics
3. Results
3.1. Structural Properties of the 36 Cities on Weekdays and Weekends
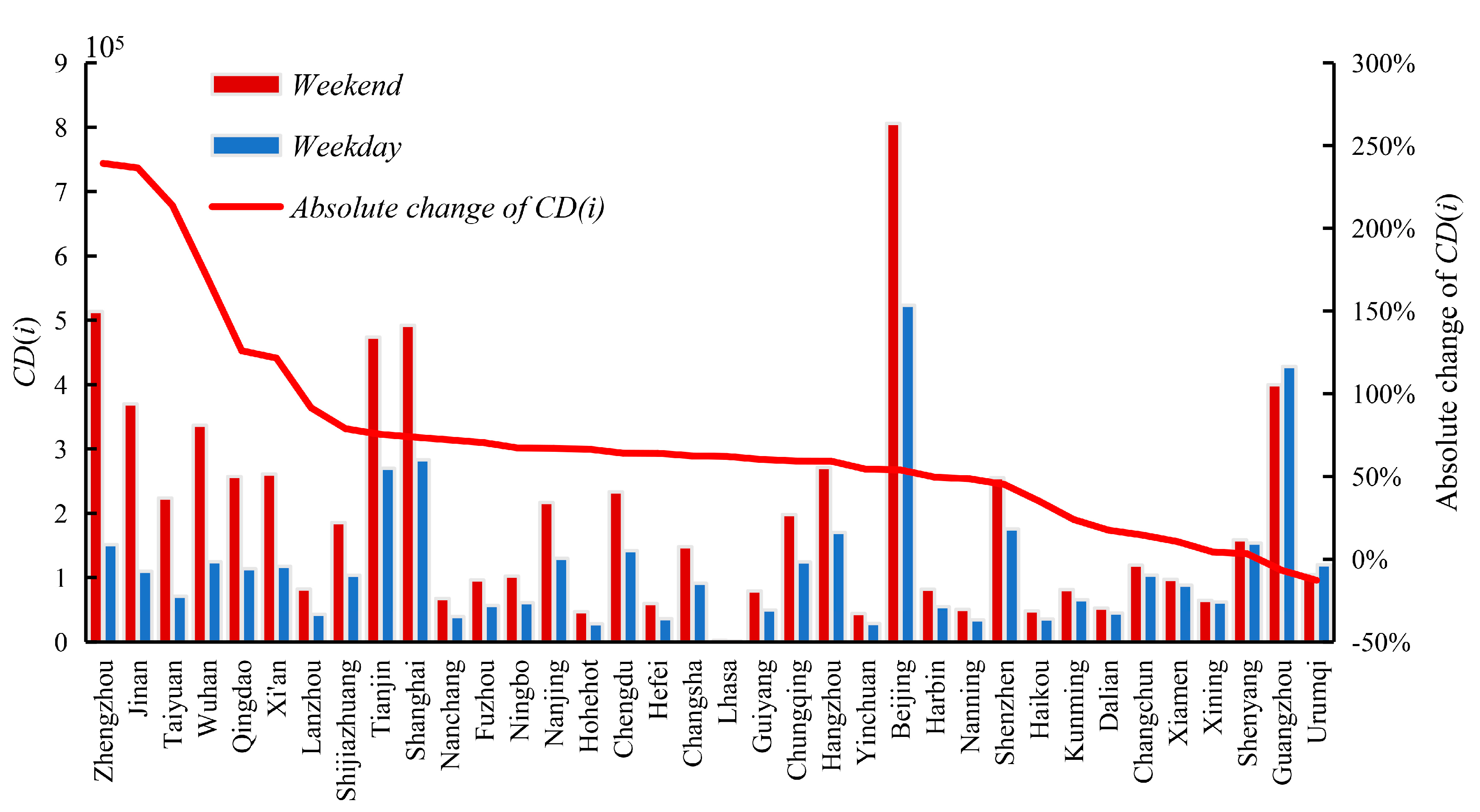
3.2. The Diversity of the Population Flows across 36 Cities
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Rank | City |
|---|---|
| First-tier cities | Beijing, Shanghai, Guangzhou, Shenzhen Beijing, Shanghai, Guangzhou, Shenzhen |
| New First-tier cities | Changsha, Chengdu, Tianjin, Shenyang, Wuhan, Xi’an, Qingdao, Chungqing, Nanjing, Hangzhou, Zhengzhou, Hefei |
| Second-tier cities | Lanzhou, Jinan, Guiyang, Xiamen, Nanning, Kunming, Taiyuan, Shijiazhuang, Ningbo, Harbin, Nanchang, Dalian, Fuzhou, Changchun |
| Third-Tier City | Yinchuan, Haikou, Hohehot, Urumqi |
| Fourth-Tier City | Xining |
References
- Yu, Z.; Lin, L. Continuity and change in the transition from the first to the second generation of migrants in China: Insights from a survey in Fujian. Habitat Int. 2014, 42, 147–154. [Google Scholar]
- Li, Q.; Chang, X.; Shaw, S.-l.; Yan, K.; Yue, Y.; Chen, B. Characteristics of micro-blog inter-city social interactions in China: Characteristics of micro-blog inter-city social interactions in China. J. Shenzhen Univ. Sci. Eng. 2013, 30, 441–449. [Google Scholar] [CrossRef]
- Barabási, A.-L.; Albert, R. Emergence of Scaling in Random Networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- de Haas, H. Migration and Development: A Theoretical Perspective. Int. Migr. Rev. 2010, 44, 227–264. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shumway, J.M.; Otterstrom, S.M. Spatial Patterns of Migration and Income Change in the Mountain West: The Dominance of Service-Based, Amenity-Rich Counties. Prof. Geogr. 2001, 53, 492–502. [Google Scholar] [CrossRef]
- Zhang, W.; Chong, Z.; Li, X.; Nie, G. Spatial patterns and determinant factors of population flow networks in China: Analysis on Tencent Location Big Data. Cities 2020, 99, 102640. [Google Scholar] [CrossRef]
- González, M.C.; Hidalgo, C.A.; Barabási, A.-L. Understanding individual human mobility patterns. Nature 2008, 453, 779–782. [Google Scholar] [CrossRef]
- Bengtsson, L.; Gaudart, J.; Lu, X.; Moore, S.; Wetter, E.; Sallah, K.; Rebaudet, S.; Piarroux, R. Using Mobile Phone Data to Predict the Spatial Spread of Cholera. Sci. Rep. 2015, 5, 8923. [Google Scholar] [CrossRef]
- Gariazzo, C.; Pelliccioni, A. A Multi-City Urban Population Mobility Study Using Mobile Phone Traffic Data. Appl. Spat. Anal. Policy 2019, 12, 753–771. [Google Scholar] [CrossRef]
- Lee, K.-S.; You, S.Y.; Eom, J.K.; Song, J.; Min, J.H. Urban spatiotemporal analysis using mobile phone data: Case study of medium- and large-sized Korean cities. Habitat Int. 2018, 73, 6–15. [Google Scholar] [CrossRef]
- Yang, X.; Zhao, Z.; Lu, S. Exploring Spatial-Temporal Patterns of Urban Human Mobility Hotspots. Sustainability 2016, 8, 674. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Ye, Q.; Deng, X.; Liu, Y.; Liu, Y. Spatial-Temporal Analysis on Spring Festival Travel Rush in China Based on Multi-source Big Data. Sustainability 2016, 8, 1184. [Google Scholar] [CrossRef] [Green Version]
- Cui, C.; Wu, X.; Liu, L.; Zhang, W. The spatial-temporal dynamics of daily intercity mobility in the Yangtze River Delta: An analysis using big data. Habitat Int. 2020, 106, 102174. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ’small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Bu, D.; Zhao, Y.; Cai, L.; Xue, H.; Zhu, X.; Lu, H.; Zhang, J.; Sun, S.; Ling, L.; Zhang, N.; et al. Topological structure analysis of the protein-protein interaction network in budding yeast. Nucleic Acids Res. 2003, 31, 2443–2450. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Watts, D.J.; Dodds, P.S.; Newman, M.E.J. Identity and Search in Social Networks. Science 2002, 296, 1302–1305. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Taylor, P.J.; Derudder, B.; Witlox, F. Comparing Airline Passenger Destinations with Global Service Connectivities: A Worldwide Empirical Study of 214 Cities. Urban Geogr. 2007, 28, 232–248. [Google Scholar] [CrossRef]
- Jackson, M.O. Social and Economic Networks; Princeton University Press: Princeton, NJ, USA, 2010; p. 648. [Google Scholar]
- Estrada, E. Quantifying network heterogeneity. Phys. Rev. E 2010, 82, 066102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, J.K.; Choi, J.; Kim, C.; Kim, Y. Social Media, Network Heterogeneity, and Opinion Polarization. J. Commun. 2014, 64, 702–722. [Google Scholar] [CrossRef]
- Xiaolong, R.; Linyuan, L. Review of ranking nodes in complex networks. Chin. Sci. Bull. 2014, 59, 1175–1197. [Google Scholar]
- Strano, E.; Shai, S.; Dobson, S.A.; Barthelemy, M. Multiplex networks in metropolitan areas: Generic features and local effects. J. R. Soc. Interface 2015, 12, 20150651. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bonato, P.; Cintia, P.; Fabbri, F.; Fadda, D.; Giannotti, F.; Lopalco, P.L.; Mazzilli, S.; Nanni, M.; Pappalardo, L.; Pedreschi, D.; et al. Mobile phone data analytics against the COVID-19 epidemics in Italy: Flow diversity and local job markets during the national lockdown. arXiv 2020, arXiv:2004.11278. [Google Scholar]
- Eagle, N.; Macy, M.; Claxton, R. Network Diversity and Economic Development. Science 2010, 328, 1029–1031. [Google Scholar] [CrossRef] [PubMed]
- Jiang, B.; Jia, T. Zipf’s law for all the natural cities in the United States: A geospatial perspective. Int. J. Geogr. Inf. Sci. 2011, 25, 1269–1281. [Google Scholar] [CrossRef]
- Jiang, B.; Yin, J.; Liu, Q. Zipf’s law for all the natural cities around the world. Int. J. Geogr. Inf. Sci. 2015, 29, 498–522. [Google Scholar] [CrossRef]
- Jiang, B.; Miao, Y. The Evolution of Natural Cities from the Perspective of Location-Based Social Media. Prof. Geogr. 2015, 67, 295–306. [Google Scholar] [CrossRef] [Green Version]
- Hao, Z.D.Y. A New Method for Analyzing the Size Structure of Urban System: Rank Cumulative Size Model. Sci. Geogr. Sin. 2017, 37, 825–832. [Google Scholar]
- Sanders, R. The pareto principle: Its use and abuse. J. Serv. Mark. 1987, 1, 37–40. [Google Scholar] [CrossRef]
- Dunford, R.; Su, Q.; Tamang, E. The Pareto Principle; University of Plymouth: Plymouth, UK, 2014. [Google Scholar]
- Xu, J.; Li, A.; Li, D.; Liu, Y.; Du, Y.; Pei, T.; Ma, T.; Zhou, C. Difference of urban development in China from the perspective of passenger transport around Spring Festival. Appl. Geogr. 2017, 87, 85–96. [Google Scholar] [CrossRef]
- Liu, J.; Hao, J.; Sun, Y.; Shi, Z. Network analysis of population flow among major cities and its influence on COVID-19 transmission in China. Cities 2021, 112, 103138. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Xue, C. Spatio-temporal characteristics and influencing factors of urban floating population in China from 2011 to 2015. Chin. J. Popul. Resour. Environ. 2019, 17, 359–373. [Google Scholar] [CrossRef]
- Wei, Y.; Xiu, C.; Liu, Z.; Chen, W. Spatial pattern of city network in transitional China based on the population flows in ‘Chunyun’period. Sci. Geogr. Sin. 2016, 36, 1654–1660. [Google Scholar]
- Li, T.; Wang, J.; Huang, J.; Gao, X. Exploring temporal heterogeneity in an intercity travel network: A comparative study between weekdays and holidays in China. J. Geogr. Sci. 2020, 30, 1943–1962. [Google Scholar] [CrossRef]
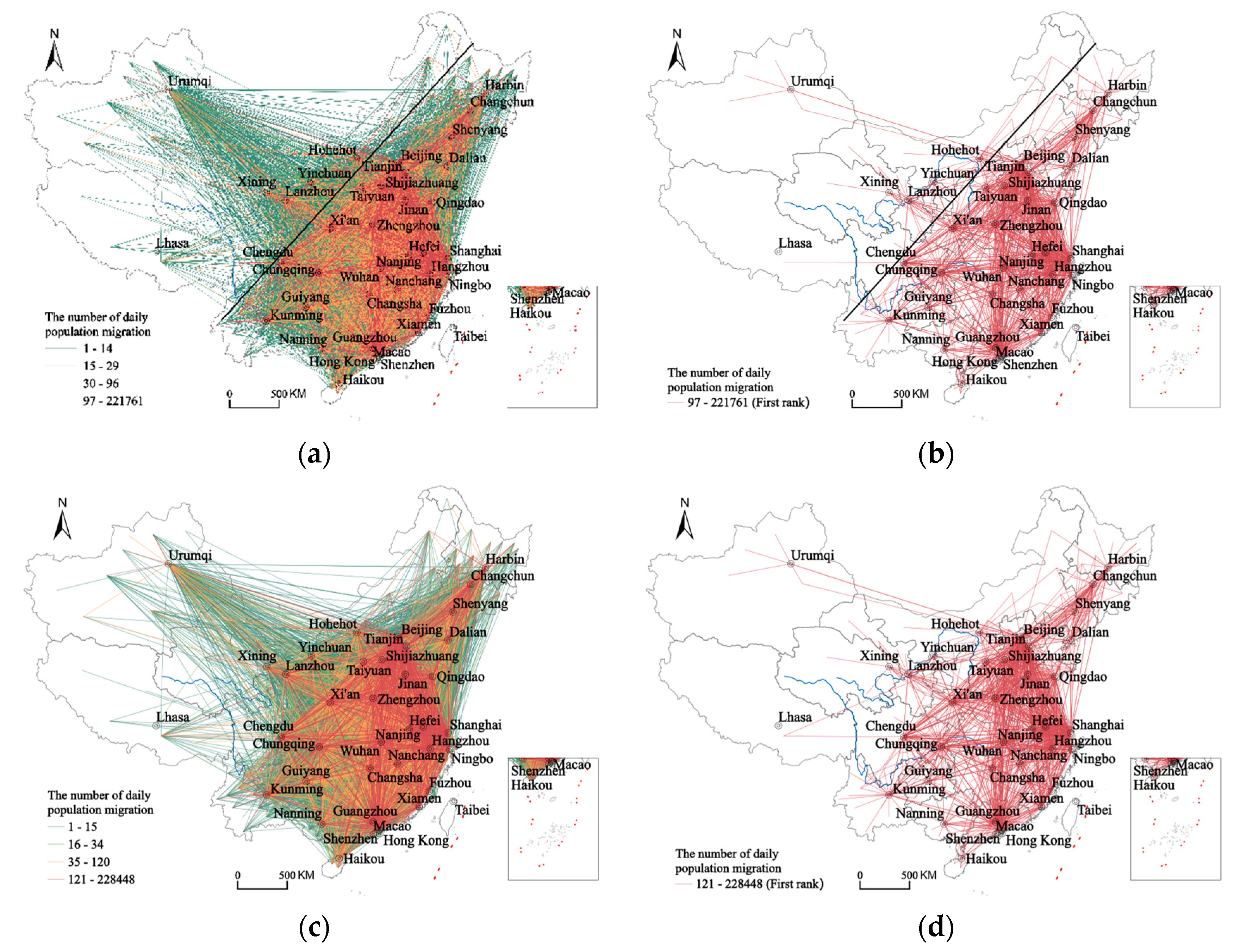

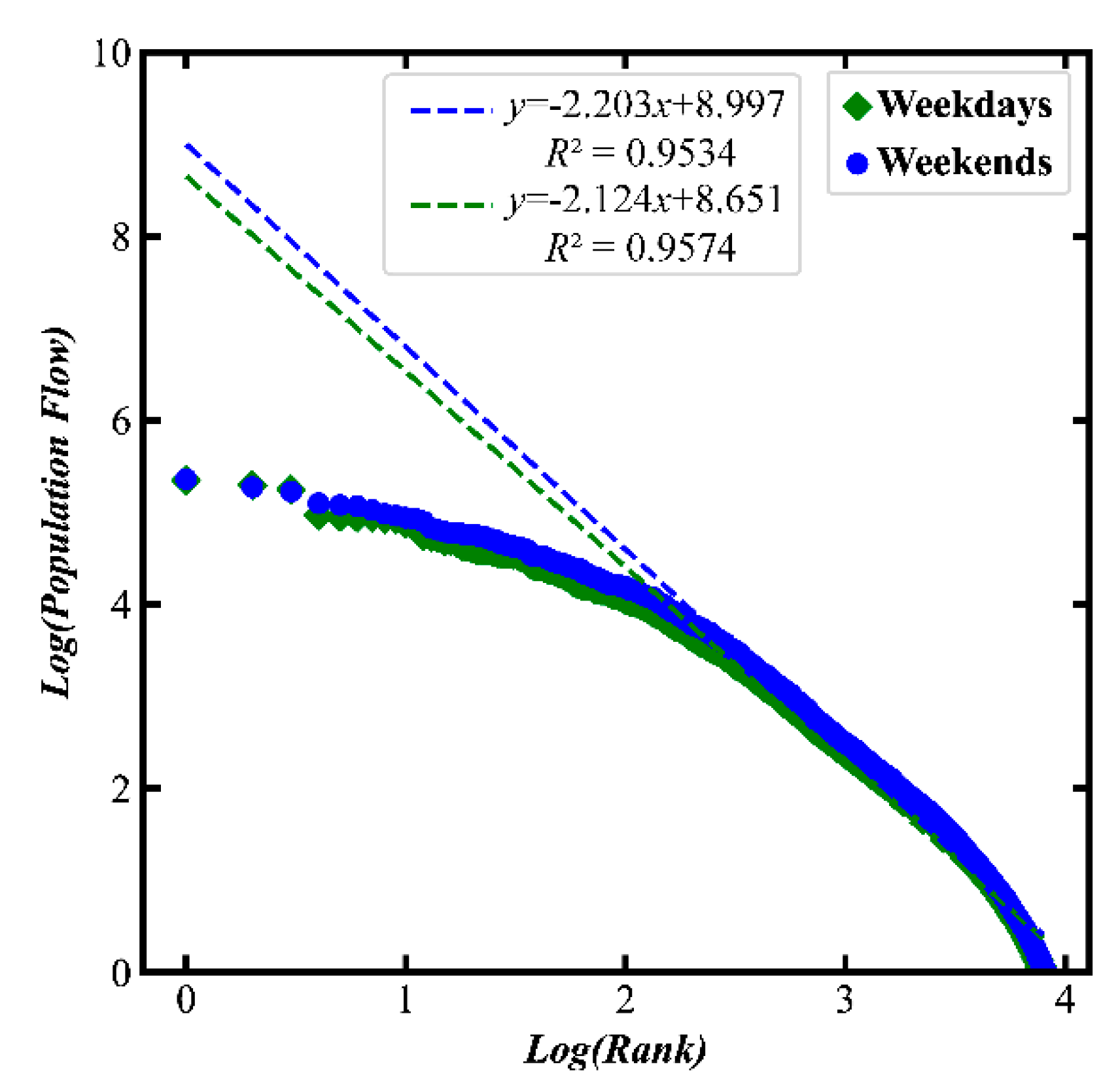
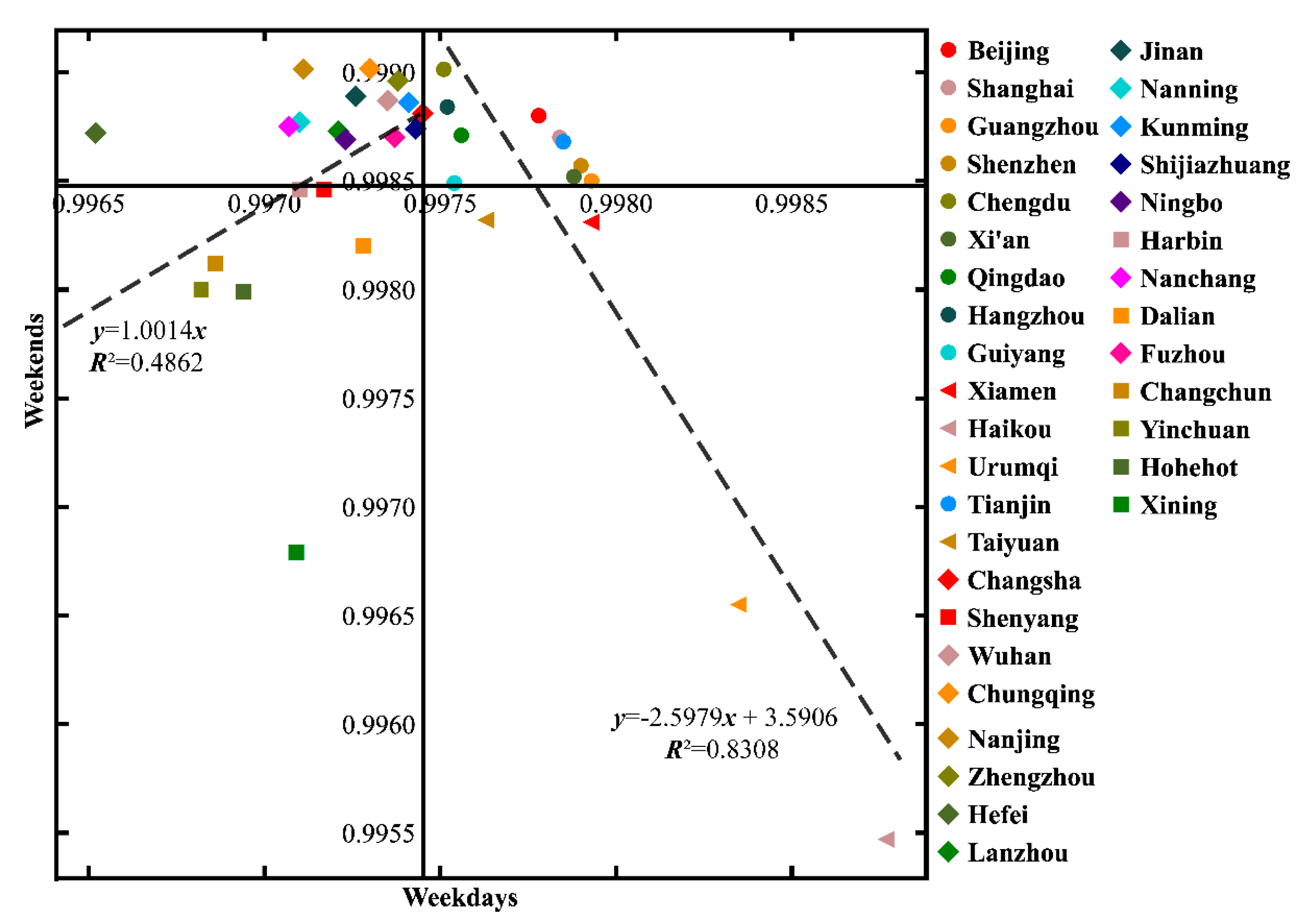
| Periods | Numbers of Nodes | Total Flow Value | Average | Maximum | Minimum |
|---|---|---|---|---|---|
| Weekdays | 337 | 5107191 | 535 | 221761 | 1 |
| Weekends | 337 | 6563026 | 687 | 228448 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Li, M.; Ma, D.; Guo, R. How Different Are Population Movements between Weekdays and Weekends: A Complex-Network-Based Analysis on 36 Major Chinese Cities. Land 2021, 10, 1160. https://doi.org/10.3390/land10111160
Zhang C, Li M, Ma D, Guo R. How Different Are Population Movements between Weekdays and Weekends: A Complex-Network-Based Analysis on 36 Major Chinese Cities. Land. 2021; 10(11):1160. https://doi.org/10.3390/land10111160
Chicago/Turabian StyleZhang, Chengyue, Minmin Li, Ding Ma, and Renzhong Guo. 2021. "How Different Are Population Movements between Weekdays and Weekends: A Complex-Network-Based Analysis on 36 Major Chinese Cities" Land 10, no. 11: 1160. https://doi.org/10.3390/land10111160
APA StyleZhang, C., Li, M., Ma, D., & Guo, R. (2021). How Different Are Population Movements between Weekdays and Weekends: A Complex-Network-Based Analysis on 36 Major Chinese Cities. Land, 10(11), 1160. https://doi.org/10.3390/land10111160







