Evaluation of a Multivariate Calibration Model for the WET Sensor That Incorporates Apparent Dielectric Permittivity and Bulk Soil Electrical Conductivity
Abstract
:1. Introduction
2. Materials and Methods
2.1. The WET Sensor
2.2. Experimental Soils and the Characterization of Their Physical Properties
2.3. Measurements of Volumetric Soil Water Content, Apparent Dielectric Permittivity, and ECb under Different Salinity Levels (ECi)
2.4. Calibration Models of Volumetric Water Content for WET Sensor
2.4.1. Manufacturer Calibration (Manuf)
2.4.2. Univariate Calibration Model (CAL)
2.4.3. Multivariate Calibration Model Considering the ECb Effects
2.5. Performance Evaluation Criteria
3. Results and Discussion
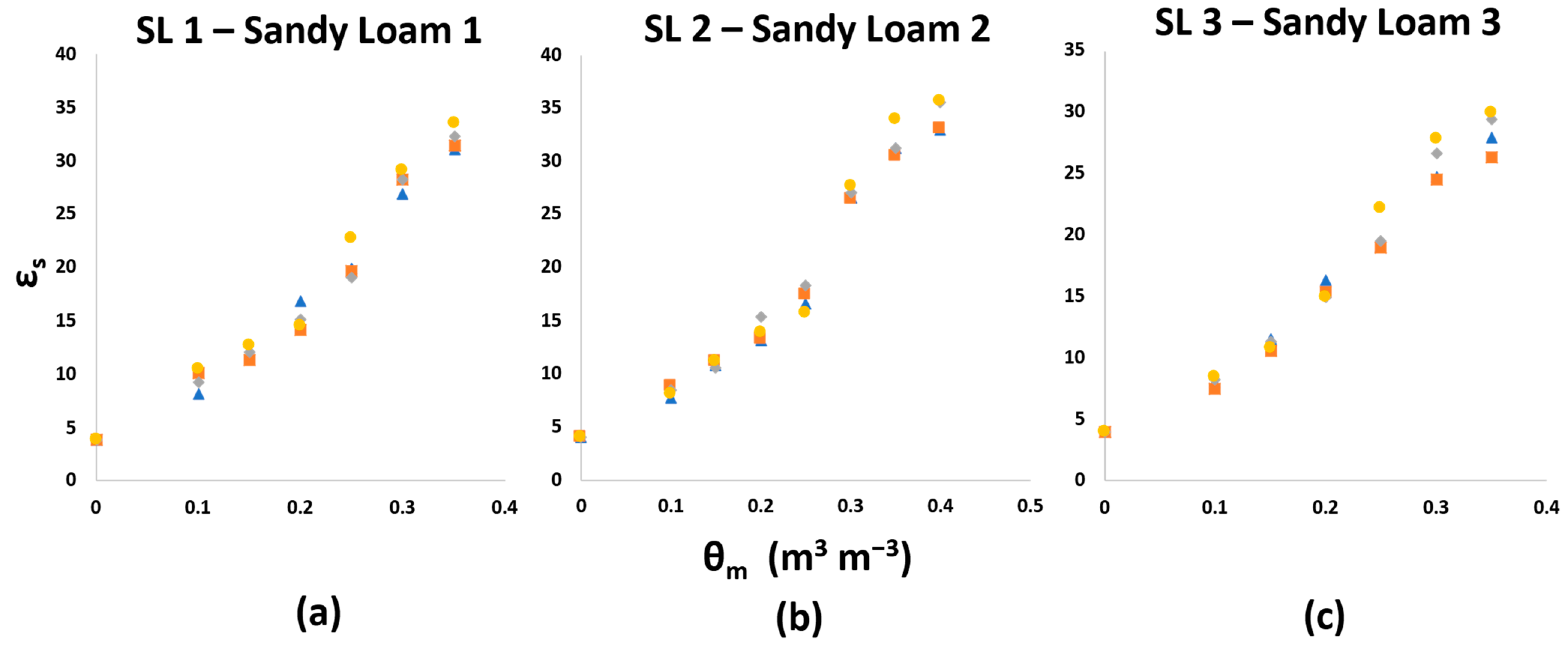
3.1. Relationship of Apparent Dielectric Permittivity and Volumetric Water Content
3.2. Evaluation of the Multivariate Model in Comparison to Manuf and CAL Calibration for the Prediction of θ
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hardie, M. Review of Novel and Emerging Proximal Soil Moisture Sensors for Use in Agriculture. Sensors 2020, 20, 6934. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Wang, C.; Gu, X.; Zhou, X.; Ma, M.; Li, L.; Feng, Z.; Ding, T.; Li, X.; Jiang, T.; et al. Accuracy Calibration and Evaluation of Capacitance-Based Soil Moisture Sensors for a Variety of Soil Properties. Agric. Water Manag. 2022, 273, 107913. [Google Scholar] [CrossRef]
- Xu, X.; Wang, H.; Qu, X.; Li, C.; Cai, B.; Peng, G. Study on the Dielectric Properties and Dielectric Constant Model of Laterite. Front. Earth Sci. 2022, 10, 1035692. [Google Scholar] [CrossRef]
- Patrignani, A.; Knapp, M.; Redmond, C.; Santos, E. Technical Overview of the Kansas Mesonet. J. Atmos. Ocean. Technol. 2020, 37, 2167–2183. [Google Scholar] [CrossRef]
- Robinson, D.A.; Jones, S.B.; Wraith, J.M.; Or, D.; Friedman, S.P. A Review of Advances in Dielectric and Electrical Conductivity Measurement in Soils Using Time Domain Reflectometry. Vadose Zone J. 2003, 2, 444–475. [Google Scholar] [CrossRef]
- Kelleners, T.J.; Paige, G.B.; Gray, S.T. Measurement of the Dielectric Properties of Wyoming Soils Using Electromagnetic Sensors. Soil Sci. Soc. Am. J. 2009, 73, 1626–1637. [Google Scholar] [CrossRef]
- Caldwell, T.G.; Bongiovanni, T.; Cosh, M.H.; Halley, C.; Young, M.H. Field and Laboratory Evaluation of the CS655 Soil Water Content Sensor. Vadose Zone J. 2018, 17, 170214. [Google Scholar] [CrossRef]
- Blonquist, J.M., Jr.; Jones, S.B.; Robinson, D.A. Standardizing Characterization of Electromagnetic Water Content Sensors: Part 2. Evaluation of Seven Sensing Systems. Vadose Zone J. 2005, 4, 1059–1069. [Google Scholar] [CrossRef]
- Seyfried, M.S.; Grant, L.E.; Du, E.; Humes, K. Dielectric Loss and Calibration of the Hydra Probe Soil Water Sensor. Vadose Zone J. 2005, 4, 1070–1079. [Google Scholar] [CrossRef]
- Silva, F.F.; Wallach, R.; Polak, A. Measuring Water Content of Soil Substitutes with Time-Domain Reflectometry (TDR). J.-Am. Soc. Hortic. Sci. 1998, 123, 734–737. [Google Scholar] [CrossRef]
- Abdulraheem, M.I.; Chen, H.; Li, L.; Moshood, A.Y.; Zhang, W.; Xiong, Y.; Zhang, Y.; Taiwo, L.B.; Farooque, A.A.; Hu, J. Recent Advances in Dielectric Properties-Based Soil Water Content Measurements. Remote Sens. 2024, 16, 1328. [Google Scholar] [CrossRef]
- Topp, G.C.; Davis, J.L.; Annan, A.P. Electromagnetic Determination of Soil Water Content: Measurements in Coaxial Transmission Lines. Water Resour. Res. 1980, 16, 574–582. [Google Scholar] [CrossRef]
- He, H.; Aogu, K.; Li, M.; Xu, J.; Sheng, W.; Jones, S.B.; González-Teruel, J.D.; Robinson, D.A.; Horton, R.; Bristow, K.; et al. A Review of Time Domain Reflectometry (TDR) Applications in Porous Media. Adv. Agron. 2021, 168, 83–155. [Google Scholar]
- Vaz, C.M.P.; Jones, S.; Meding, M.; Tuller, M. Evaluation of Standard Calibration Functions for Eight Electromagnetic Soil Moisture Sensors. Vadose Zone J. 2013, 12, vzj2012.0160. [Google Scholar] [CrossRef]
- Mane, S.; Das, N.; Singh, G.; Cosh, M.; Dong, Y. Advancements in Dielectric Soil Moisture Sensor Calibration: A Comprehensive Review of Methods and Techniques. Comput. Electron. Agric. 2024, 218, 108686. [Google Scholar] [CrossRef]
- Kelleners, T.J.; Seyfried, M.S.; Blonquist, J.M., Jr.; Bilskie, J.; Chandler, D.G. Improved Interpretation of Water Content Reflectometer Measurements in Soils. Soil Sci. Soc. Am. J. 2005, 69, 1684–1690. [Google Scholar] [CrossRef]
- Ledieu, J.; De Ridder, P.; De Clerck, P.; Dautrebande, S. A Method of Measuring Soil Moisture by Time-Domain Reflectometry. J. Hydrol. 1986, 88, 319–328. [Google Scholar] [CrossRef]
- Whalley, W.R. Considerations on the Use of Time-Domain Reflectometry (TDR) for Measuring Soil Water Content. J. Soil Sci. 1993, 44, 1–9. [Google Scholar] [CrossRef]
- Heimovaara, T.J.; Bouten, W.; Verstraten, J.M. Frequency Domain Analysis of Time Domain Reflectometry Waveforms: 2. A Four-Component Complex Dielectric Mixing Model for Soils. Water Resour. Res. 1994, 30, 201–209. [Google Scholar] [CrossRef]
- Topp, G.C.; Reynolds, W.D. Time Domain Reflectometry: A Seminal Technique for Measuring Mass and Energy in Soil. Soil Tillage Res. 1998, 47, 125–132. [Google Scholar] [CrossRef]
- Wilson, T.B.; Kochendorfer, J.; Diamond, H.J.; Meyers, T.P.; Hall, M.; Lee, T.R.; Saylor, R.D.; Krishnan, P.; Leeper, R.D.; Palecki, M.A. Evaluation of Soil Water Content and Bulk Electrical Conductivity across the U.S. Climate Reference Network Using Two Electromagnetic Sensors. Vadose Zone J. 2024, 23, e20336. [Google Scholar] [CrossRef]
- Topp, G.C.; Zegelin, S.; White, I. Impacts of the Real and Imaginary Components of Relative Permittivity on Time Domain Reflectometry Measurements in Soils. Soil Sci. Soc. Am. J. 2000, 64, 1244–1252. [Google Scholar] [CrossRef]
- Campbell, J.E. Dielectric Properties and Influence of Conductivity in Soils at One to Fifty Megahertz. Soil Sci. Soc. Am. J. 1990, 54, 332–341. [Google Scholar] [CrossRef]
- Kelleners, T.J.; Verma, A.K. Measured and Modeled Dielectric Properties of Soils at 50 Megahertz. Soil Sci. Soc. Am. J. 2010, 74, 744–752. [Google Scholar] [CrossRef]
- Kargas, G.; Persson, M.; Kanelis, G.; Markopoulou, I.; Kerkides, P. Prediction of Soil Solution Electrical Conductivity by the Permittivity Corrected Linear Model Using a Dielectric Sensor. J. Irrig. Drain Eng. 2017, 143, 04017030. [Google Scholar] [CrossRef]
- Regalado, C.M.; Ritter, A.; Rodríguez-González, R.M. Performance of the Commercial WET Capacitance Sensor as Compared with Time Domain Reflectometry in Volcanic Soils. Vadose Zone J. 2007, 6, 244–254. [Google Scholar] [CrossRef]
- Bouksila, F.; Persson, M.; Berndtsson, R.; Bahri, A. Soil Water Content and Salinity Determination Using Different Dielectric Methods in Saline Gypsiferous Soil/Détermination de La Teneur En Eau et de La Salinité de Sols Salins Gypseux à l’aide de Différentes Méthodes Diélectriques. Hydrol. Sci. J. 2008, 53, 253–265. [Google Scholar] [CrossRef]
- Visconti, F.; Martínez, D.; Molina, M.J.; Ingelmo, F.; Miguel De Paz, J. A Combined Equation to Estimate the Soil Pore-Water Electrical Conductivity: Calibration with the WET and 5TE Sensors. Soil Res. 2014, 52, 419. [Google Scholar] [CrossRef]
- Zemni, N.; Bouksila, F.; Slama, F.; Persson, M.; Berndtsson, R.; Bouhlila, R. Evaluation of Modified Hilhorst Models for Pore Electrical Conductivity Estimation Using a Low-Cost Dielectric Sensor. Arab. J. Geosci. 2022, 15, 1089. [Google Scholar] [CrossRef]
- Kargas, G.; Kerkides, P.; Seyfried, M.S. Response of Three Soil Water Sensors to Variable Solution Electrical Conductivity in Different Soils. Vadose Zone J. 2014, 13, vzj2013.09. [Google Scholar] [CrossRef]
- Rosenbaum, U.; Huisman, J.A.; Vrba, J.; Vereecken, H.; Bogena, H.R. Correction of Temperature and Electrical Conductivity Effects on Dielectric Permittivity Measurements with ECH2O Sensors. Vadose Zone J. 2011, 10, 582–593. [Google Scholar] [CrossRef]
- Kelleners, T.J.; Robinson, D.A.; Shouse, P.J.; Ayars, J.E.; Skaggs, T.H. Frequency Dependence of the Complex Permittivity and Its Impact on Dielectric Sensor Calibration in Soils. Soil Sci. Soc. Am. J. 2005, 69, 67–76. [Google Scholar] [CrossRef]
- Robinson, D.A.; Gardner, C.M.K.; Cooper, J.D. Measurement of Relative Permittivity in Sandy Soils Using TDR, Capacitance and Theta Probes: Comparison, Including the Effects of Bulk Soil Electrical Conductivity. J. Hydrol. 1999, 223, 198–211. [Google Scholar] [CrossRef]
- Kargas, G.; Soulis, K.X. Performance Evaluation of a Recently Developed Soil Water Content, Dielectric Permittivity, and Bulk Electrical Conductivity Electromagnetic Sensor. Agric. Water Manag. 2019, 213, 568–579. [Google Scholar] [CrossRef]
- Zemni, N.; Bouksila, F.; Persson, M.; Slama, F.; Berndtsson, R.; Bouhlila, R. Laboratory Calibration and Field Validation of Soil Water Content and Salinity Measurements Using the 5TE Sensor. Sensors 2019, 19, 5272. [Google Scholar] [CrossRef]
- Evett, S.; Tolk, J.; Howell, T. Time Domain Reflectometry Laboratory Calibration in Travel Time, Bulk Electrical Conductivity, and Effective Frequency. Vadose Zone J. 2005, 4, 1020. [Google Scholar] [CrossRef]
- Patrignani, A.; Ochsner, T.E.; Feng, L.; Dyer, D.; Rossini, P.R. Calibration and Validation of Soil Water Reflectometers. Vadose Zone J. 2022, 21, e20190. [Google Scholar] [CrossRef]
- Hilhorst, M.A. A Pore Water Conductivity Sensor. Soil Sci. Soc. Am. J. 2000, 64, 1922–1925. [Google Scholar] [CrossRef]
- Kargas, G.; Londra, P.; Anastasatou, M.; Moustakas, N. The Effect of Soil Iron on the Estimation of Soil Water Content Using Dielectric Sensors. Water 2020, 12, 598. [Google Scholar] [CrossRef]
- WET-User_Manual_v1.6.Pdf. Available online: https://delta-t.co.uk/wp-content/uploads/2019/06/WET-User_Manual_v1.6.pdf (accessed on 27 July 2024).
- Burnham, K.P.; Anderson, D.R. (Eds.) Model Selection and Multimodel Inference; Springer: New York, NY, USA, 2004; ISBN 978-0-387-95364-9. [Google Scholar]

| Soil | Sand | Silt | Clay | Bulk Density (ρb) |
|---|---|---|---|---|
| (%) | (%) | (%) | (g cm−1) | |
| SL 1—Sandy Loam 1 | 57.0 | 26.5 | 16.5 | 1.44 |
| SL 2—Sandy Loam 2 | 51.8 | 30.0 | 18.2 | 1.38 |
| SL 3—Sandy Loam 3 | 67.8 | 16.0 | 16.2 | 1.52 |
| CL—Clay Loam | 35.8 | 36.0 | 28.2 | 1.25 |
| S—Sand | 100 | - | - | 1.68 |
| L—Loam | 40.6 | 35.6 | 23.8 | 1.15 |
| C—Clay | 24.5 | 20.5 | 55.0 | 1.16 |
| Soil | ECi (dSm−1) | CAL | Multivariate | Max ECb (dSm−1) | |||||
|---|---|---|---|---|---|---|---|---|---|
| a | b | Adj. R2 | a | b | c | Adj. R2 | |||
| SL 1—Sandy Loam 1 | 0.28 | 0.094 | −0.176 | 0.993 | 0.129 | −0.255 | −0.146 | 0.995 | 0.81 |
| 1.2 | 0.094 | −0.177 | 0.975 | 0.117 | −0.232 | −0.087 | 0.976 | 0.94 | |
| 3 | 0.093 | −0.175 | 0.986 | 0.117 | −0.232 | −0.072 | 0.987 | 1.18 | |
| 6 | 0.090 | −0.174 | 0.979 | 0.098 | −0.194 | −0.018 | 0.979 | 1.63 | |
| SL 2—Sandy Loam 2 | 0.28 | 0.097 | −0.171 | 0.971 | 0.230 | −0.469 | −0.894 | 0.990 | 0.52 |
| 1.2 | 0.100 | −0.187 | 0.978 | 0.146 | −0.295 | −0.221 | 0.980 | 0.74 | |
| 3 | 0.096 | −0.176 | 0.988 | 0.118 | −0.232 | −0.077 | 0.988 | 1.12 | |
| 6 | 0.091 | −0.156 | 0.960 | 0.129 | −0.252 | −0.090 | 0.964 | 1.56 | |
| SL 3—Sandy Loam 3 | 0.28 | 0.102 | −0.200 | 0.993 | 0.188 | −0.378 | −0.572 | 0.994 | 0.48 |
| 1.2 | 0.103 | −0.196 | 0.986 | 0.157 | −0.313 | −0.287 | 0.987 | 0.56 | |
| 3 | 0.097 | −0.184 | 0.991 | 0.126 | −0.251 | −0.105 | 0.993 | 0.90 | |
| 6 | 0.093 | −0.172 | 0.981 | 0.112 | −0.218 | −0.047 | 0.981 | 1.38 | |
| CL—Clay Loam | 0.28 | 0.097 | −0.165 | 0.938 | 0.201 | −0.419 | −0.544 | 0.964 | 0.74 |
| 1.2 | 0.100 | −0.180 | 0.948 | 0.158 | −0.194 | −0.260 | 0.952 | 0.90 | |
| 3 | 0.101 | −0.182 | 0.964 | 0.146 | −0.299 | −0.155 | 0.970 | 1.20 | |
| 6 | 0.092 | −0.160 | 0.963 | 0.130 | −0.266 | −0.090 | 0.969 | 1.78 | |
| S—Sand | 0.28 | 0.133 | −0.207 | 0.996 | 0.165 | −0.265 | −0.921 | 0.999 | 0.09 |
| 1.2 | 0.123 | −0.191 | 0.997 | 0.150 | −0.244 | −0.271 | 0.998 | 0.29 | |
| 3 | 0.119 | −0.193 | 0.998 | 0.124 | −0.204 | −0.025 | 0.999 | 0.72 | |
| L—Loam | 0.28 | 0.095 | −0.162 | 0.962 | 0.159 | −0.314 | −0.486 | 0.973 | 0.52 |
| 1.2 | 0.091 | −0.154 | 0.977 | 0.140 | −0.274 | −0.273 | 0.990 | 0.73 | |
| 3 | 0.090 | −0.164 | 0.980 | 0.119 | −0.237 | −0.103 | 0.985 | 1.18 | |
| 6 | 0.086 | −0.153 | 0.966 | 0.111 | −0.222 | −0.066 | 0.970 | 1.77 | |
| C—Clay | 0.28 | 0.109 | −0.254 | 0.985 | 0.182 | −0.450 | −0.505 | 0.988 | 0.59 |
| 1.2 | 0.112 | −0.259 | 0.976 | 0.162 | −0.396 | −0.266 | 0.980 | 0.82 | |
| 3 | 0.108 | −0.243 | 0.970 | 0.144 | −0.349 | −0.131 | 0.972 | 1.28 | |
| 6 | 0.097 | −0.228 | 0.986 | 0.100 | −0.238 | −0.007 | 0.987 | 1.95 | |
| Soil | ECi (dSm−1) | Manuf | CAL | Multivariate | |||
|---|---|---|---|---|---|---|---|
| RMSE (m3m−3) | Average | RMSE (m3m−3) | Average | RMSE (m3m−3) | Average | ||
| SL 1—Sandy Loam 1 | 0.28 | 0.021 | 0.028 | 0.008 | 0.013 | 0.006 | 0.012 |
| 1.2 | 0.026 | 0.016 | 0.015 | ||||
| 3 | 0.026 | 0.012 | 0.011 | ||||
| 6 | 0.037 | 0.015 | 0.014 | ||||
| SL 2—Sandy Loam 2 | 0.28 | 0.020 | 0.021 | 0.020 | 0.018 | 0.011 | 0.014 |
| 1.2 | 0.018 | 0.017 | 0.015 | ||||
| 3 | 0.018 | 0.013 | 0.012 | ||||
| 6 | 0.028 | 0.023 | 0.020 | ||||
| SL 3—Sandy Loam 3 | 0.28 | 0.013 | 0.016 | 0.008 | 0.011 | 0.007 | 0.010 |
| 1.2 | 0.013 | 0.012 | 0.010 | ||||
| 3 | 0.016 | 0.010 | 0.008 | ||||
| 6 | 0.024 | 0.014 | 0.013 | ||||
| CL—Clay Loam | 0.28 | 0.031 | 0.029 | 0.031 | 0.027 | 0.022 | 0.022 |
| 1.2 | 0.029 | 0.028 | 0.025 | ||||
| 3 | 0.024 | 0.024 | 0.020 | ||||
| 6 | 0.031 | 0.025 | 0.021 | ||||
| S *—Sand | 0.28 | 0.013 | 0.019 | 0.007 | 0.006 | 0.004 | 0.003 |
| 1.2 | 0.015 | 0.006 | 0.002 | ||||
| 3 | 0.028 | 0.004 | 0.004 | ||||
| L—Loam | 0.28 | 0.024 | 0.036 | 0.024 | 0.020 | 0.018 | 0.016 |
| 1.2 | 0.022 | 0.018 | 0.011 | ||||
| 3 | 0.053 | 0.017 | 0.014 | ||||
| 6 | 0.043 | 0.022 | 0.020 | ||||
| C—Clay | 0.28 | 0.048 | 0.042 | 0.025 | 0.025 | 0.023 | 0.022 |
| 1.2 | 0.039 | 0.020 | 0.014 | ||||
| 3 | 0.049 | 0.027 | 0.025 | ||||
| 6 | 0.029 | 0.021 | 0.021 | ||||
| Soil | CAL | Multivariate | ΔAICc CAL * | ΔAICc Multivariate * |
|---|---|---|---|---|
| AICc | AICc | |||
| SL 1—Sandy Loam 1 | −36.92 | −35.40 | 2 | 0 |
| SL 2—Sandy Loam 2 | −38.68 | −35.83 | 3 | 0 |
| SL 3—Sandy Loam 3 | −39.62 | −37.58 | 2 | 0 |
| CL—Clay Loam | −32.97 | −30.33 | 3 | 0 |
| S—Sand | −41.64 | −38.72 | 3 | 0 |
| L—Loam | −61.31 | −54.29 | 7 | 0 |
| C—Clay | −33.96 | −32.15 | 2 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petsetidi, P.A.; Kargas, G. Evaluation of a Multivariate Calibration Model for the WET Sensor That Incorporates Apparent Dielectric Permittivity and Bulk Soil Electrical Conductivity. Land 2024, 13, 1490. https://doi.org/10.3390/land13091490
Petsetidi PA, Kargas G. Evaluation of a Multivariate Calibration Model for the WET Sensor That Incorporates Apparent Dielectric Permittivity and Bulk Soil Electrical Conductivity. Land. 2024; 13(9):1490. https://doi.org/10.3390/land13091490
Chicago/Turabian StylePetsetidi, Panagiota Antonia, and George Kargas. 2024. "Evaluation of a Multivariate Calibration Model for the WET Sensor That Incorporates Apparent Dielectric Permittivity and Bulk Soil Electrical Conductivity" Land 13, no. 9: 1490. https://doi.org/10.3390/land13091490
APA StylePetsetidi, P. A., & Kargas, G. (2024). Evaluation of a Multivariate Calibration Model for the WET Sensor That Incorporates Apparent Dielectric Permittivity and Bulk Soil Electrical Conductivity. Land, 13(9), 1490. https://doi.org/10.3390/land13091490








