Development of a Differential Spatial Economic Modeling Method for Improved Land Use and Multimodal Transportation Planning
Abstract
1. Introduction
2. Methodological Framework
2.1. Development of Aggregate Economic Flow Table
2.2. Analytical Framework for Identifying Regional Technology Pattern Disparity
2.2.1. Technical Coefficients for Different Regions
- —
- is the input from industry i to industry j.
- —
- is the total output of industry j.
2.2.2. Gini Index
- —
- = TCs for one period.
- —
- = TCs in second period.
- —
- N = number of sectors.
2.2.3. K-Means Clustering
- Initialization: Randomly select ‘k’ cluster centers.
- Assignment and Update: Assign each data point to the nearest cluster center based on the Euclidean distance and recalculate the cluster centers as the mean of the assigned points. This iterative process is repeated until the change in the cluster centers becomes negligible, thereby minimizing the WCSS.
- The WCSS, a key metric in K-means, measures the squared error between each data point and its corresponding cluster center by summing these across all clusters (Equation (6)).
- Euclidean distance plays a critical role in determining the proximity of data points to cluster centers. This measure determines the shortest path between a given data point and the cluster center. For the two vectors the Euclidean distance, denoted as, was calculated using Equation (7).
2.3. Economic and Demographic Forecast Model
- —
- = forecasted total for economic activity type (where = 1, 2…n, e.g., farming, forestry) in province at time .
- —
- K is the asymptote of the logistic function representing the maximum carrying capacity of the corresponding activity (where K > 0).
- —
- is the growth rate parameter.
- —
- β is the inflection point, which is the time at which the growth rate is highest (midpoint of the S-curve).
- —
- is the time variable (e.g., years from the start of the forecast period).
- —
- = forecasted total for economic activity type in province at time ,
- —
- = observed value at current time point ,
- —
- = forecasted value for activity type in province from the previous time point ,
- —
- = smoothing constant, with values between 0 and 1, determining the weight assigned to the observed data versus the previous forecast.
2.4. Differential Spatial Activity Allocation Method
2.4.1. Production Activity Allocation
2.4.2. Differential Technology Allocation
2.4.3. Production and Consumption Quantities (Exchange Locations)
- —
- is the quantity of commodity consumed in zone by activity , aggregated over all technology options.
Buying and Selling Allocation
2.5. Space Development Model
2.6. Integrated Multimodal Freight Assignment Based on a Supernetwork
- —
- : Total cost (RMB) of transporting commodity from TAZ to via route .
- —
- : Loading fee for commodity at transfer link . Note: d is the set of all transfer links, either highway-to-waterway or highway-to-railway.
- —
- : Weight of transporting commodity c from TAZ to in tons via route r.
- —
- : Length (km) of road or rail link for mode .
- —
- Base travel cost per kilometer in for transporting commodity via mode . Note: = 1,2,3 for highway, railway, and waterway, respectively.
- —
- Transfer cost of commodity at link
- —
- : Value of commodity per ton.
- —
- : Annualized rate of return.
- —
- : Loading time (h) for commodity at links .
- —
- Travel time (hour) on for mode .
- —
- Transfer time (hour) at link
- —
- ASC: Alternative-specific constant representing unobservable factors.
- —
- N denotes the total number of links (k,l) and d represents the sum of the transfer links (a,b), where n,d ∈ r.
- —
- is the flow assigned to route between origin i and destination j,
- —
- Qij is the total freight demand (or total flow) from origin i to destination j.
- —
- : Flow on link ,
- —
- : binary indicator, 1 if link is part of route otherwise.
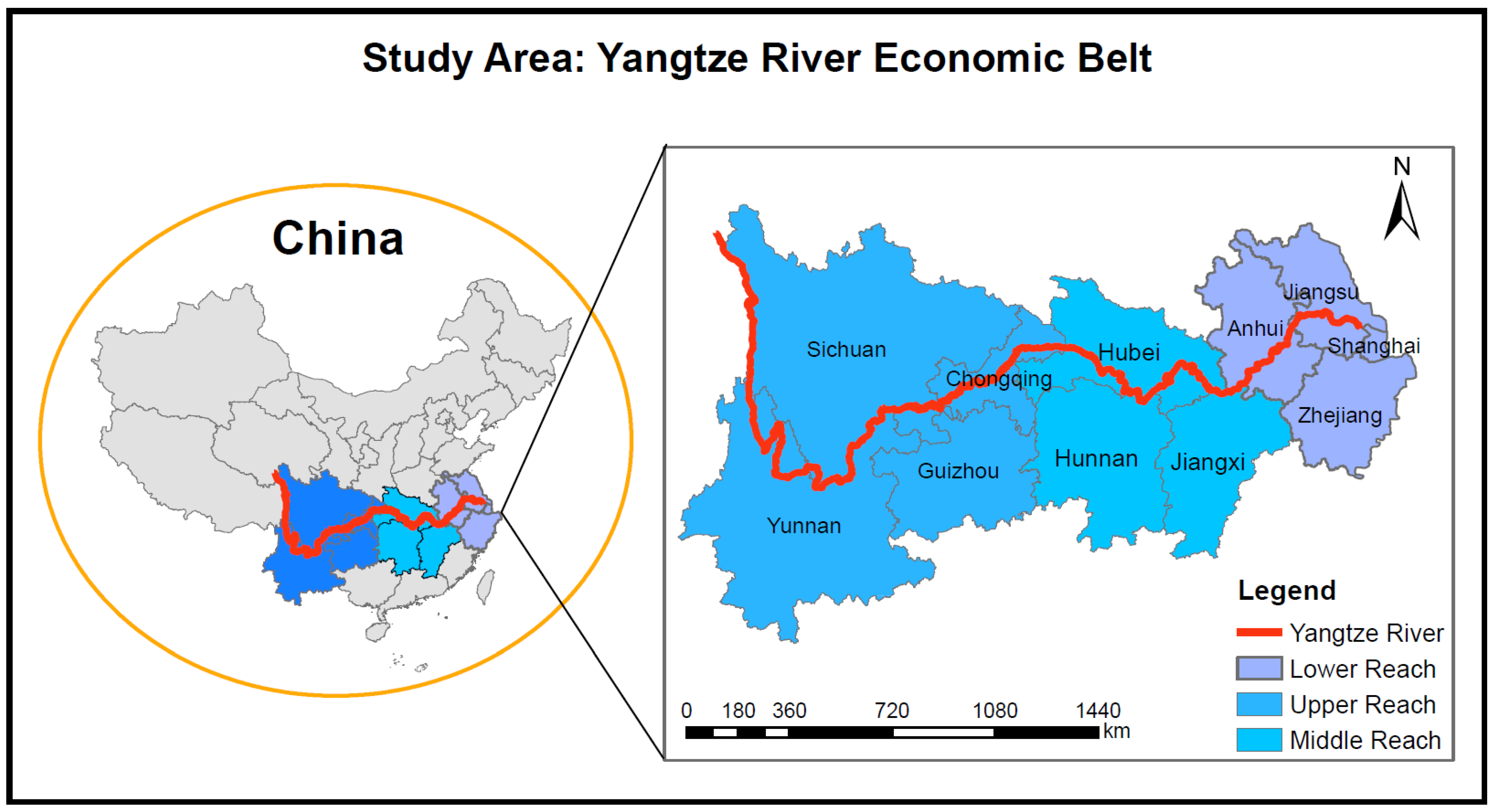
3. Study Area and Data Preparation
3.1. Data Preparation and Sources
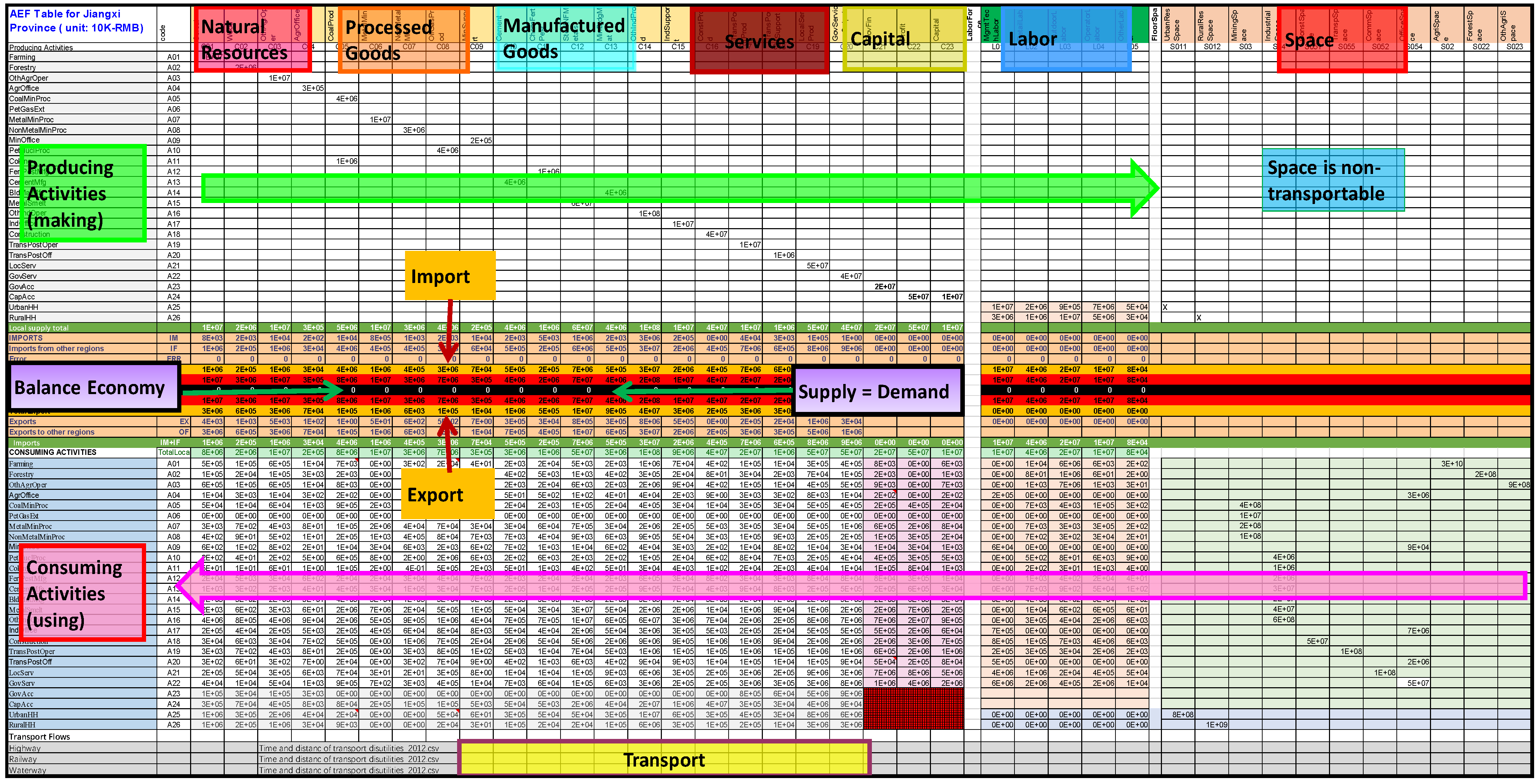
3.2. Development of Aggregate Economic Flow Table for YREB
3.3. Calculation of Technical Coefficients
4. Case Study Analysis
4.1. Results of Gini Index
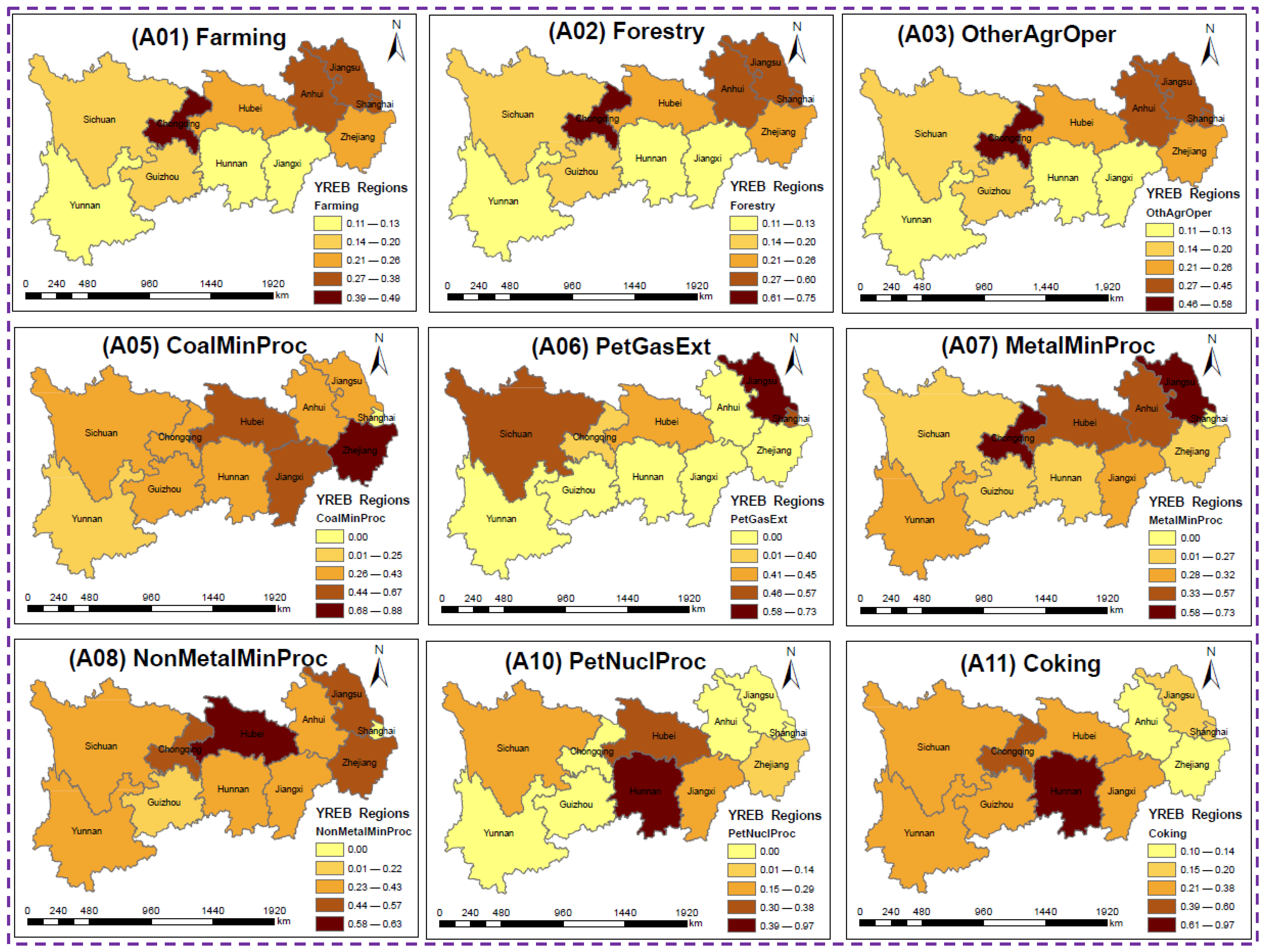
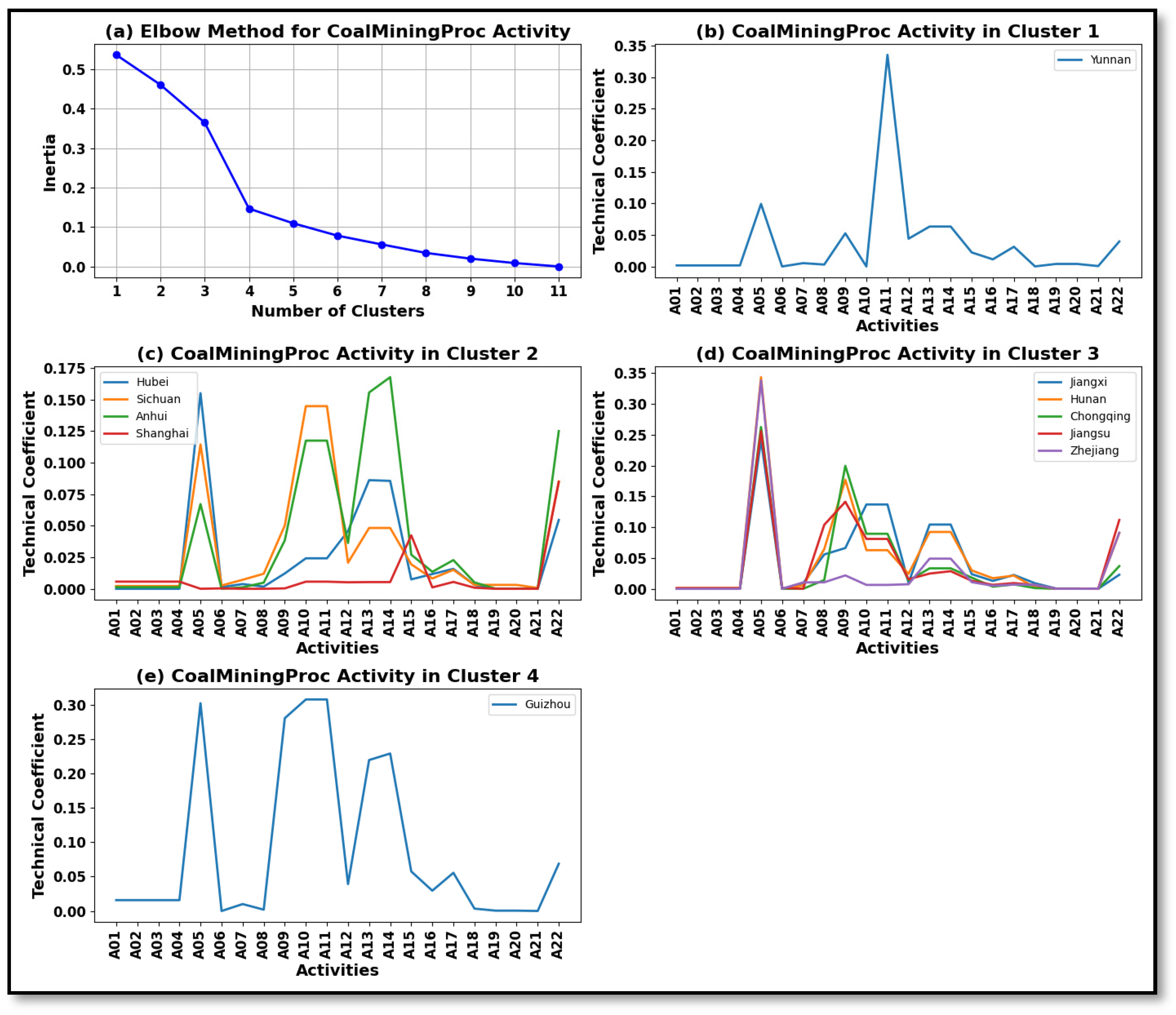
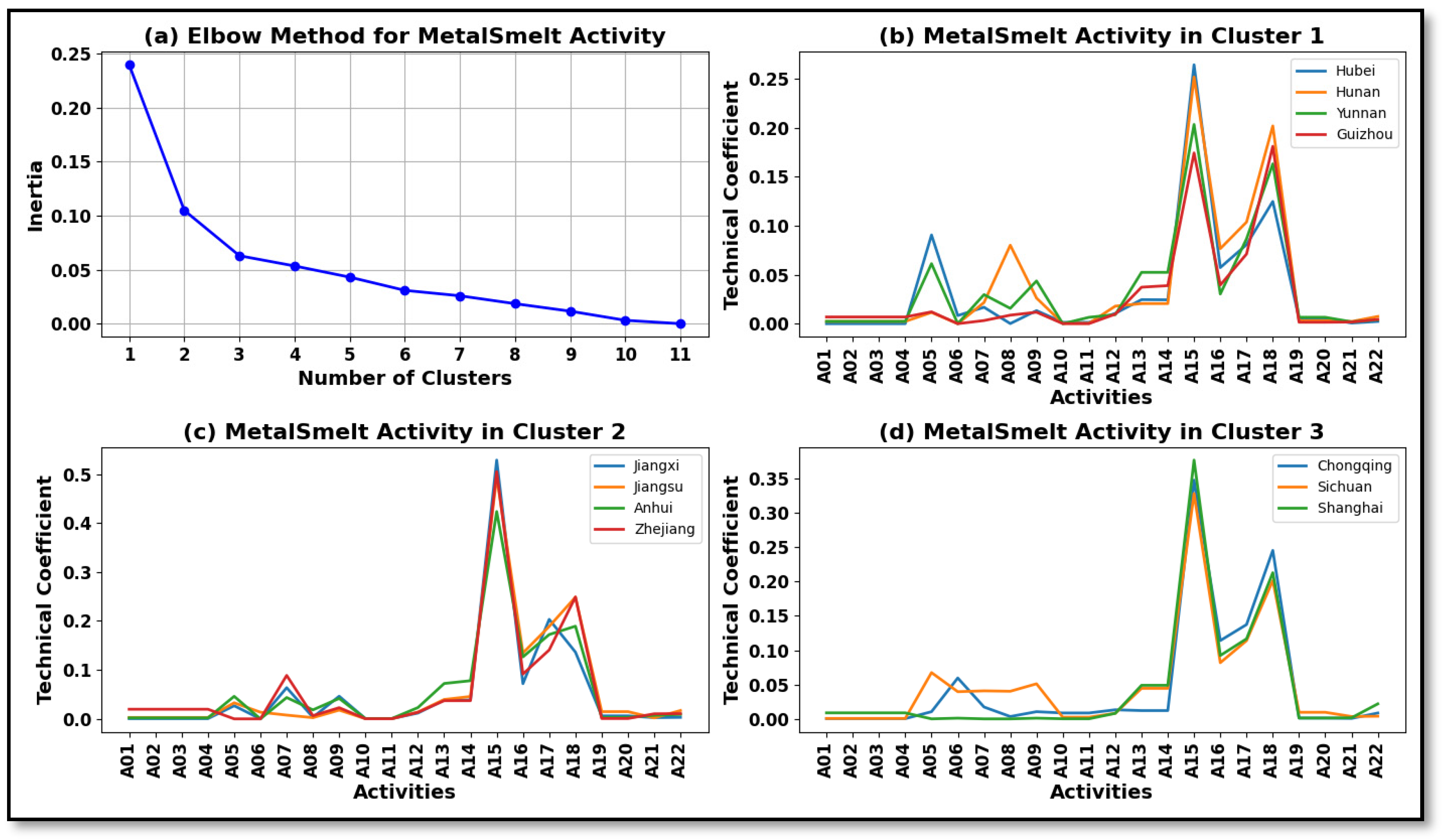
4.2. Results of K-Means Clustering
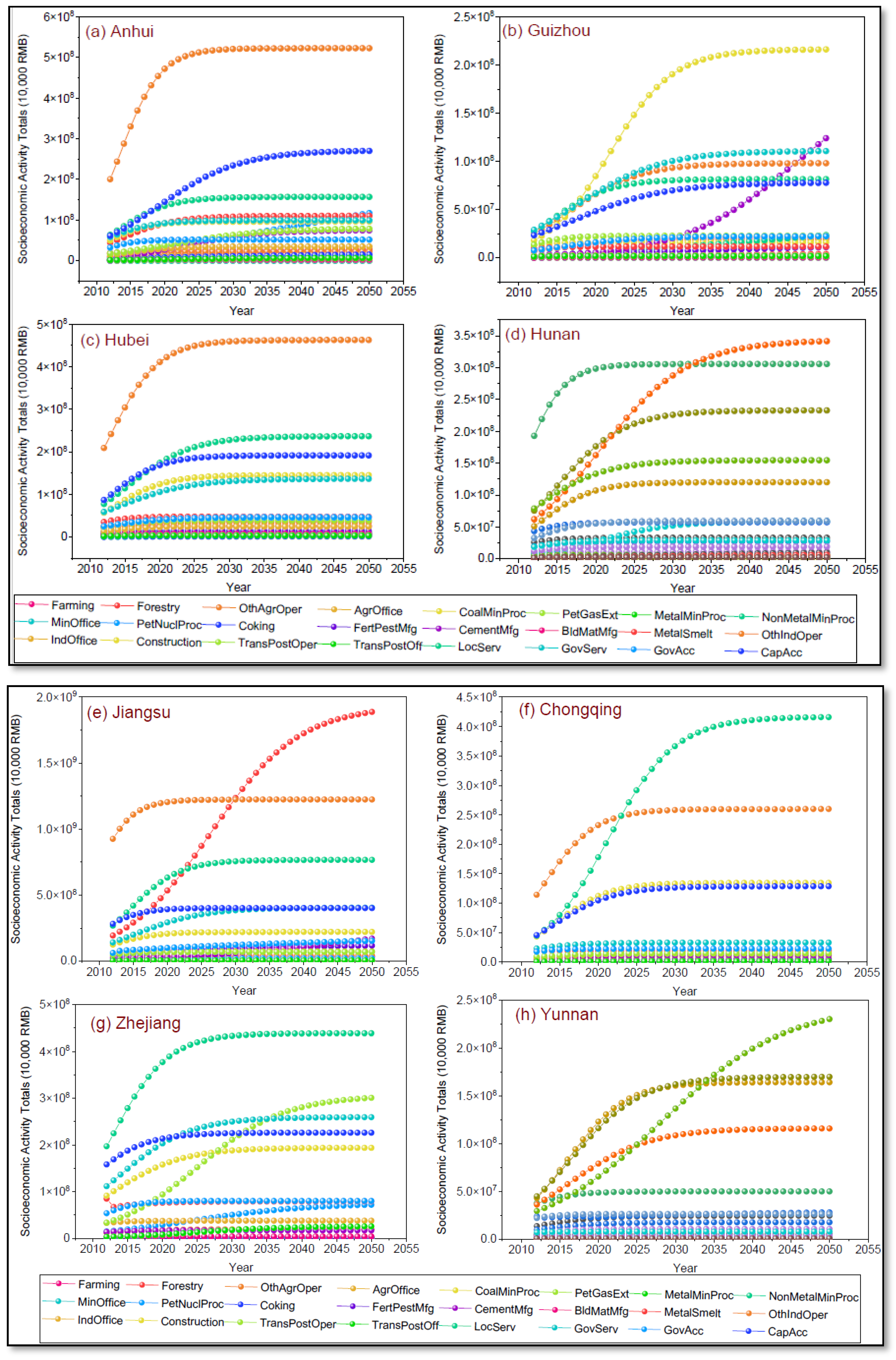
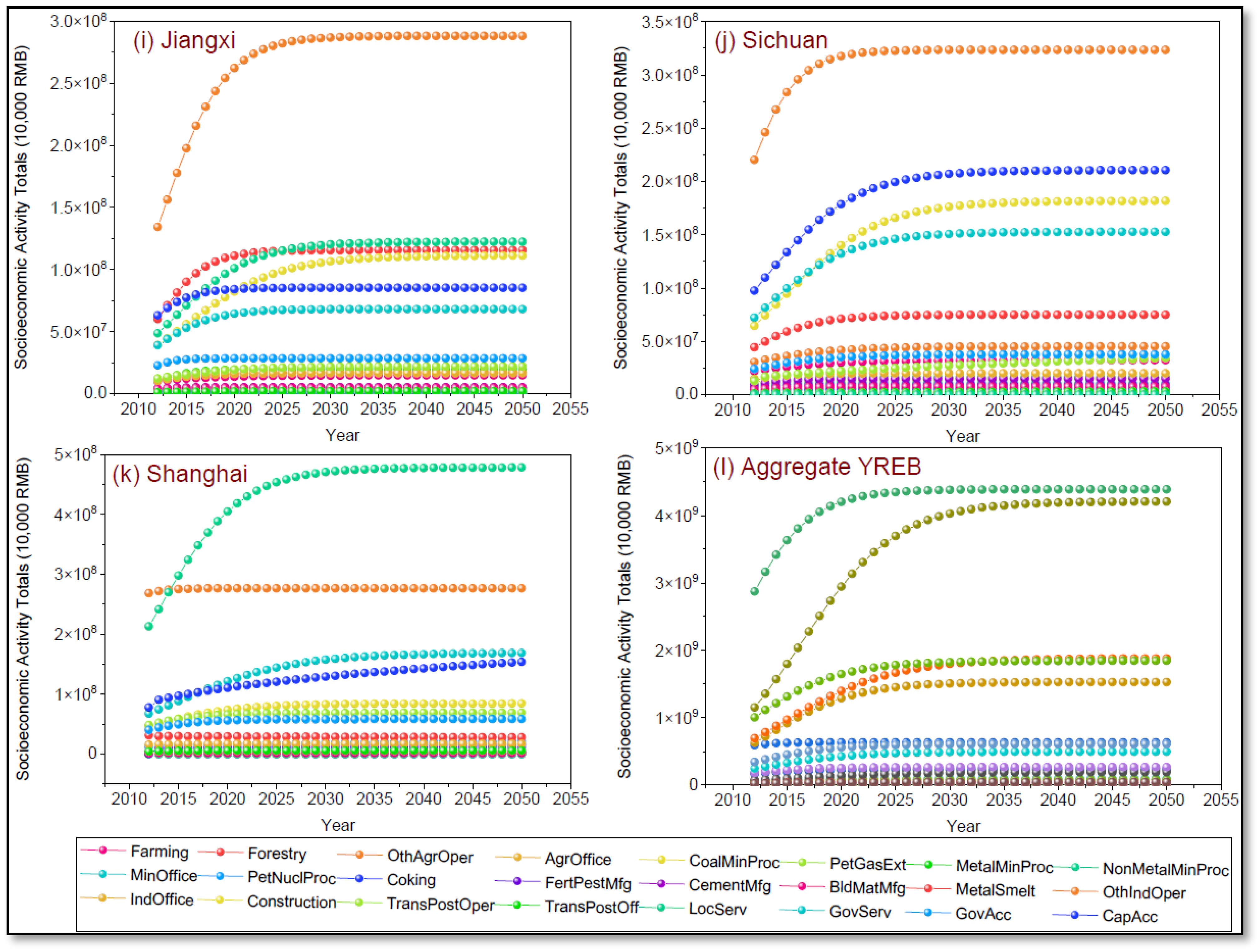
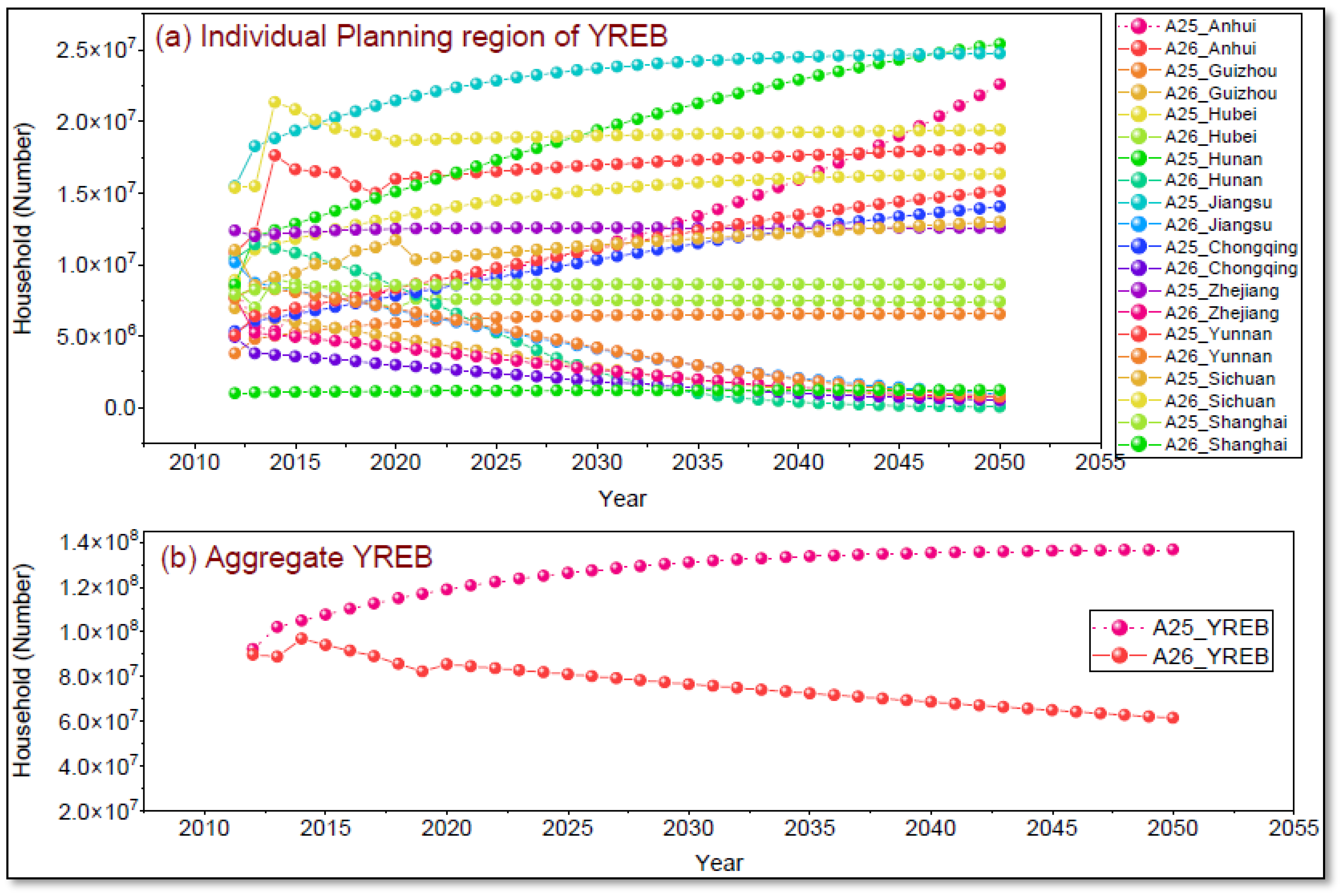
4.3. Results of Economic and Demographic Models
4.4. Results of Differential Spatial Activity Allocation
4.5. Forecast Results of Space Development Distribution
4.6. Forecast Results of Freight Distribution
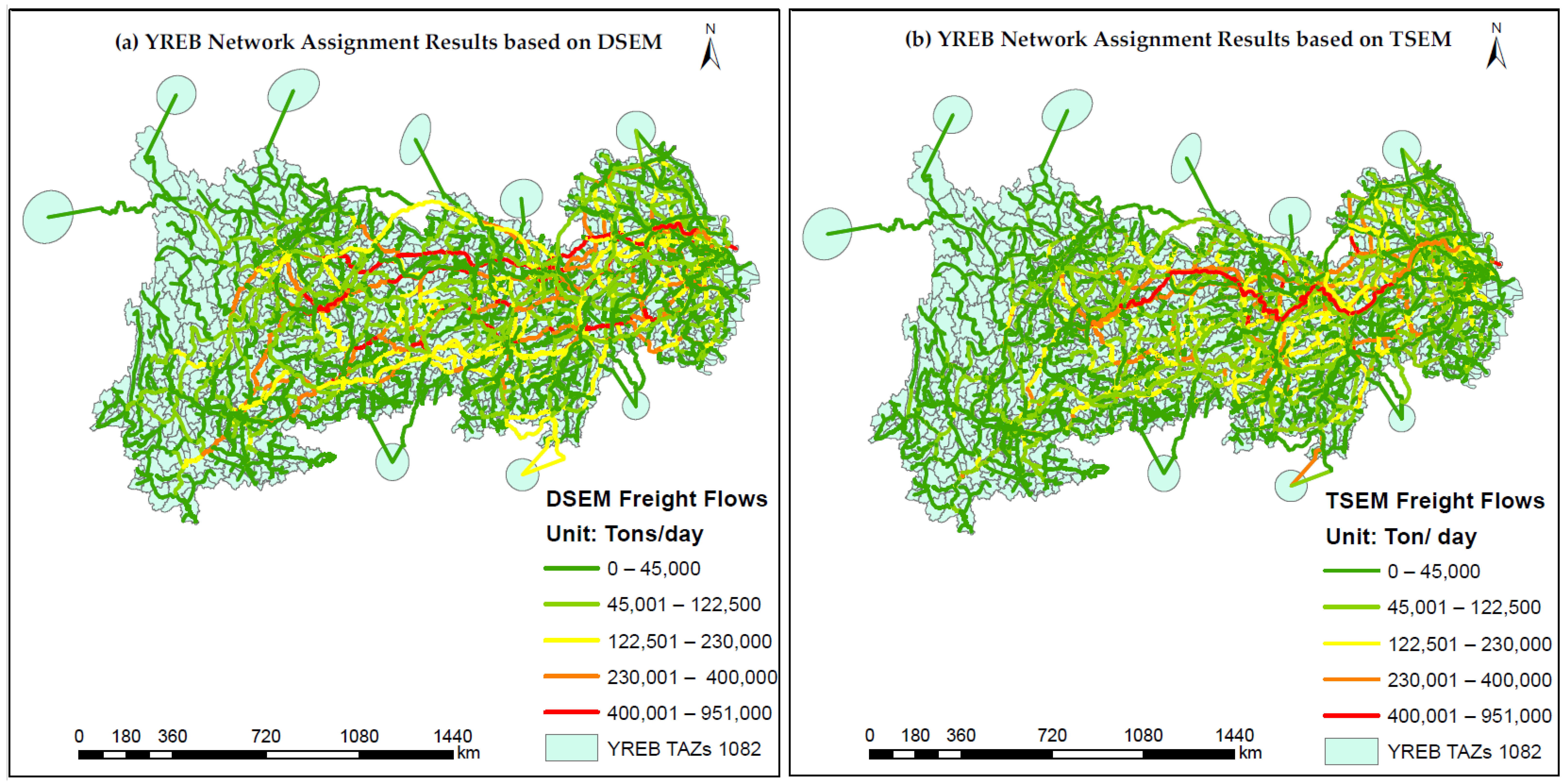
4.7. Results of Multimodal Freight Assignment Model
5. Conclusions and Discussion
- The calibration results for the proposed DSEM showed that the R2 values between the observed and estimated link flows were 0.951, 0.855, and 0.985 for the highways, railways, and waterways, respectively. Further comparisons were performed using the traditional aggregate SEM for freight assignment results. The R2 values between the observed and estimated link flows from TSEM were 0.879, 0.819, and 0.91 for the above modes. These results clearly demonstrate that the analytics of the proposed DSEM framework outperform its counterparts, indirectly confirming the model’s efficacy in predicting freight OD demand by mode and specific links.
- The Gini coefficient analysis highlights significant changes and sectoral variability in petroleum processing, coal mining, and non-metal mineral extraction, where high Gini values indicate ongoing transformations in TCs. Conversely, the agriculture, local services, and industrial operations sectors exhibit stable TCs, suggesting sectoral resilience despite broader economic shifts. These findings underscore the evolving technology patterns of the YREB, where certain industries undergo major restructuring, while others maintain structural continuity over time. This analysis underscores the inadequacy of TSEM’s averaged/aggregated TCs and validates DSEM’s capability to track both structural resilience and transformation.
- The EDF forecast analysis reveals substantial inter-regional differences in the distribution of economic activities within the YREB. While aggregated forecasts suggest cumulative growth in these activities, they mask the complete absence of some activities in individual provinces—such as coal mining in Shanghai or petroleum extraction in Jiangxi, Hunan, and others. These discrepancies highlight a critical limitation of relying on regional aggregates, which can result in misleading over- or underestimations of future growth. In contrast, a disaggregated, IPU analysis offers a more objective and accurate depiction of economic development growths. This corroborates the study’s main assumption: economic activity growth is shaped by localized regional characteristics—including demographic, cultural, geographical, and technological factors. Therefore, the findings strongly advocate for differentiated, region-specific planning and policy strategies to ensure realistic and effective industrial development across diverse economic zones.
- The DSAA analysis focuses on the redistribution of economic activities across regions due to differences in technological patterns. This analysis is crucial for understanding how regional specialization evolves over time and the impact of technological advancement on spatial distribution. TSEM, which assumes that all regions operate under homogeneous economic conditions, fails to capture the complexities of regional technological development and its spatial impacts. In contrast, the DSAA method allows for the simulation of spatial shifts in economic activities, offering policymakers a more realistic understanding of how technology can reshape regional economies. The results demonstrate that DSAA provides more accurate predictions, particularly in regions with marked technological and industrial differences. The use of region-specific technology coefficients in DSEM allows for a more precise representation of technological disparities, addressing the limitations of TSEM, such as PECAS and MEPLAN, which have been criticized for their reliance on averaged/aggregated TCs [27].
- Moreover, the DSEM results on land and space utilization indicate that accounting for regional disparities is critical for managing internal migration and preventing the over-concentration of population and economic activities in major urban centers such as Shanghai, Jiangsu, and Zhejiang. The findings suggest that spatially disaggregated economic planning can play a significant role in mitigating resource scarcity and infrastructure stress in rapidly urbanizing regions, while simultaneously supporting the development of underperforming or less-industrialized areas.
- From a transportation and infrastructure perspective, policymakers should prioritize the development of multimodal transport networks that align with projected shifts in industrial activity, taking into account the spatial configuration of production, consumption, and interregional trade. Such coordination between economic forecasts and infrastructure development can significantly enhance the efficiency and equity of transport investments. The model further demonstrates that dynamic land use and economic forecasting tools like DSEM can support adaptive planning under conditions of technological change and economic transition. As regions adopt new technologies and shift their industrial base, land and resource demands evolve accordingly. Ultimately, the results demonstrate that DSEM-based forecasts provide policymakers with a more rational foundation for implementing spatially targeted economic policies, infrastructure investments, and sustainable regional development strategies.
- The findings of this study offer several practical implications for regional economic planning, industrial policies, and sustainable development. Policymakers are encouraged to account for the unique technological structure and industrial composition of each province when designing policy interventions, thereby avoiding one-size-fits-all approaches that may exacerbate regional inequalities. These findings support the assumption that economic activities in the YREB are region-specific, driven by factors like geography, infrastructure, and industrial policies. A balanced regional development strategy, focusing on investment in underdeveloped provinces such as Yunnan and Guizhou, could enhance the overall economic stability and connectivity within the YREB. Furthermore, the findings highlight that relocating labor-intensive and high-emission industries from Shanghai and Zhejiang to Yunnan, Guizhou, and Sichuan could help achieve a spatially balanced industrial development.
Limitations and Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1
| Activities | Short Name and Code | Commodity/Services | Labor | Land/Space |
|---|---|---|---|---|
| Farming | A01Farming | Cereal | Management, technical labor | Urban residential space |
| Forestry | A02Forestry | Wood | Retail service labor | Rural residential space |
| Other Agriculture Operation | A03OthAgrOper | Other farming | Outdoor labor | Mining space |
| Agriculture-Office | A04AgrOffice | Agriculture support | Operator labor | Industrial space |
| Coal Mining and Processing | A05CoalMinProc | Coal | Other labor | Construction space |
| Petroleum and Natural Gas Extraction | A06PetGasExt | Oil, Gas and its product | Transportation space | |
| Metals Mining and Processing | A07MetalMinProc | Metallic mineral | Commercial space/land | |
| Nonmetal Minerals Mining and Processing | A08NonMetalMinProc | Nonmetal mineral | Office space | |
| Mining Office | A09MinOffice | Mining support | Agricultural space | |
| Petroleum and nuclear fuel processing | A10PetNuclProc | Oil, gas, and its product | Forest space | |
| Coking | A11Coking | Coal | Other agricultural space | |
| Fertilizer and pesticide manufacturing | A12FertPestMfg | Chemical fertilizers and pesticides | ||
| Cement, lime and gypsum manufacturing | A13CementMfg | Cement | ||
| Brick, stone and other building materials manufacturing | A14BldMatMfg | Mineral building materials | ||
| Smelting and Processing of Metals (Metal Products) | A15MetalSmelt | Steel and nonferrous metals | ||
| Other Industry Operation | A16OthIndOper | Other industrial products | ||
| Industry-Office | A17IndOffice | Manufacturing support | ||
| Construction | A18Construction | Construction | ||
| Transport and Post Operations | A19TransPostOper | Transportation product | ||
| Transport and Post Office | A20TransPostOff | Transportation support | ||
| Local Services | A21LocServ | Local services product | ||
| Government Services | A22GovServ | Government services | ||
| Government Accounts | A23GovAcc | Government accounts | ||
| Capital Accounts | A24CapAcc | Capital | ||
| Household-Urban | A25UrbanHH | |||
| Household-Rural | A26RuralHH |
Appendix A.2
| Activities | Cluster 1 | Cluster 2 | Cluster 3 | Cluster 4 | Cluster 5 | Cluster 6 |
|---|---|---|---|---|---|---|
| Farming | Hubei, Hunan, Chongqing, Sichuan, Yunnan, Guizhou, Anhui, Shanghai | Jiangxi, Jiangsu, Zhejiang | ||||
| Forestry | Hubei, Hunan, Chongqing, Sichuan, Yunnan, Guizhou, Anhui, Shanghai | Jiangxi, Jiangsu, Zhejiang | ||||
| OthAgrOper | Hubei, Hunan, Chongqing, Sichuan, Yunnan, Guizhou, Anhui, Shanghai | Jiangxi, Jiangsu, Zhejiang | ||||
| AgrOffice | Hubei, Hunan, Chongqing, Sichuan, Yunnan, Guizhou, Anhui, Shanghai | Jiangxi, Jiangsu, Zhejiang | ||||
| CoalMinProc | Yunnan | Hubei, Sichuan, Shanghai, Anhui | Jiangxi, Zhejiang, Hunan, Chongqing, Jiangsu | Guizhou | ||
| PetGasExt | Jiangxi, Hubei, Jiangsu, Sichuan, Anhui, Zhejiang, Shanghai | Hunan, Chongqing, Yunnan, Guizhou | ||||
| MetalMinProc | Jiangxi, Hubei, Hunan, Chongqing, Zhejiang | Sichuan, Yunnan, Guizhou, Anhui, Shanghai | Jiangsu | |||
| NonMetalMinProc | Jiangxi, Hubei, Hunan, Yunnan, Guizhou, Shanghai | Chongqing, Jiangsu, Anhui, Zhejiang | Sichuan | |||
| MinOffice | Jiangxi, Hubei, Hunan, Chongqing, Yunnan, Guizhou | Jiangsu, Sichuan, Anhui, Zhejiang, Shanghai | ||||
| PetNuclProc | Jiangxi, Hubei, Chongqing, Jiangsu, Sichuan, Yunnan, Guizhou, Anhui, Zhejiang, Shanghai | Hunan | ||||
| Coking | Jiangxi, Hubei, Chongqing, Jiangsu, Sichuan, Yunnan, Guizhou, Anhui, Zhejiang, Shanghai | Hunan | ||||
| FertPestMfg | Jiangxi, Guizhou, Anhui, Zhejiang, Shanghai | Hunan, Chongqing, Jiangsu, Sichuan | Hubei, Yunnan | |||
| CementMfg | Jiangxi, Hubei, Hunan, Guizhou, Anhui, Shanghai | Chongqing, Jiangsu, Sichuan, Yunnan | Zhejiang | |||
| BldMatMfg | Jiangxi, Hubei, Hunan, Jiangsu, Guizhou, Anhui, Zhejiang | Chongqing, Sichuan, Yunnan, Shanghai | ||||
| MetalSmelt | Hubei, Hunan, Yunnan, Guizhou | Jiangxi, Jiangsu, Anhui, Zhejiang | Chongqing, Sichuan, Shanghai | |||
| OthIndOper | Yunnan | Hubei, Hunan, Guizhou, Anhui | Jiangsu, Zhejiang, Shanghai | Chongqing | Jiangxi, Sichuan | |
| IndOffice | Chongqing, Jiangsu, Jiangxi, Anhui, Zhejiang, Shanghai | Hubei, Sichuan, Yunnan, Guizhou | Hunan | |||
| Construction | Jiangxi, Hunan, Chongqing, Jiangsu, Sichuan, Guizhou, Anhui, Zhejiang | Yunnan, Shanghai | Hubei | |||
| TransPostOper | Jiangxi, Hubei, Hunan, Chongqing, Sichuan, Yunnan, Guizhou, Anhui | Jiangsu, Zhejiang, Shanghai | ||||
| TransPostOff | Jiangxi, Hubei, Hunan, Chongqing, Sichuan, Yunnan, Guizhou, Anhui | Jiangsu, Zhejiang, Shanghai | ||||
| LocServ | Jiangxi, Hubei, Hunan, Chongqing, Jiangsu, Sichuan, Yunnan, Guizhou, Anhui, Zhejiang | Shanghai | ||||
| GovServ | Hunan, Jiangsu, Sichuan, Anhui | Hubei, Guizhou | Chongqing | Zhejiang | Jiangxi, Yunnan | Shanghai |
References
- Cao, X.; Ding, C.; Yang, J. Urban Transport and Land Use Planning: A Synthesis of Global Knowledge; Elsevier B.V.: Amsterdam, The Netherlands, 2022. [Google Scholar]
- Bardal, K.G.; Reinar, M.B.; Lundberg, A.K.; Bjørkan, M. Factors facilitating the implementation of the sustainable development goals in regional and local planning—Experiences from Norway. Sustainability 2021, 13, 4282. [Google Scholar] [CrossRef]
- Zhang, H.; Zhu, C.; Jiao, T.; Luo, K.; Ma, X.; Wang, M. Analysis of the Trends and Driving Factors of Cultivated Land Utilization Efficiency in Henan Province from 2000 to 2020. Land 2024, 13, 2109. [Google Scholar] [CrossRef]
- Luo, Q.; Zhao, C.; Luo, G.; Li, C.; Ran, C.; Zhang, S.; Xiong, L.; Liao, J.; Du, C.; Li, Z.; et al. Rural depopulation has reshaped the plant diversity distribution pattern in China. Resour. Conserv. Recycl. 2025, 215, 108054. [Google Scholar] [CrossRef]
- Zondag, B.; De Jong, G. The development of the TIGRIS XL model: A bottom-up approach to transport, land-use, and the economy. Res. Transp. Econ. 2011, 31, 55–62. [Google Scholar] [CrossRef]
- Donnelly, R.; Moeckel, R. Statewide and Megaregional Travel Forecasting Models: Freight and Passenger; National Academies of Sciences, Engineering, and Medicine, Transportation Research Board; NCHRP Synthesis Report; The National Academies Press: Washington, DC, USA, 2017; Available online: https://nap.nationalacademies.org/catalog/24927/statewide-and-megaregional-travel-forecasting-models-freight-and-passenger (accessed on 10 July 2024).
- Hensher, D.; Figliozzi, M.A. Behavioural insights into the modelling of freight transportation and distribution systems. Transp. Res.–Part B Methodol. 2007, 41, 921–923. [Google Scholar] [CrossRef]
- Moeckel, R. Integrated Transportation and Land Use Models. National Academies of Sciences, Engineering, and Medicine. 2018. Available online: https://nap.nationalacademies.org/catalog/25194/integrated-transportation-and-land-use-models (accessed on 11 July 2024).
- Zhong, M.; Hunt, J.D.; Abraham, J.E.; Wang, W.; Zhang, Y.; Wang, R. Advances in integrated land use transport modeling. Adv. Transp. Policy Plan. 2022, 9, 201–230. [Google Scholar]
- Wegener, M. Land-use transport interaction models. Handb. Reg. Sci. 2021, 229, 229–246. [Google Scholar]
- Gachanja, J.N. Towards Integrated Land Use and Transport Modelling: Evaluating Accuracy of the Four Step Transport Model—The Case of Istanbul, Turkey. Master’s Thesis, International Institute for Geo-Information Science and Earth Observation, Enschede, The Netherlands, 2010. Available online: https://essay.utwente.nl/90760/ (accessed on 31 March 2025).
- Deng, G.; Zhong, M.; Raza, A.; Hunt, J.D.; Wang, Z. Design and development of a regional, multi-commodity, multimodal freight transport model based on an integrated modeling framework: Case study of the Yangtze River Economic Belt. In Proceedings of the Transportation Research Board 101st Annual Meeting, Washington, DC, USA, 9–13 January 2022; Available online: https://trid.trb.org/View/1900892 (accessed on 3 March 2024).
- Thomas, I.; Jones, J.; Caruso, G.; Gerber, P. City delineation in European applications of LUTI models: Review and tests. Transp. Rev. 2018, 38, 6–32. [Google Scholar] [CrossRef]
- Hunt, J.D.; Kriger, D.S.; Miller, E.J. Current operational urban land-use–transport modelling frameworks: A review. Transp. Rev. 2005, 25, 329–376. [Google Scholar] [CrossRef]
- Acheampong, R.A.; Silva, E.A. Land use–transport interaction modeling: A review of the literature and future research directions. J. Transp. Land Use 2015, 8, 11–38. [Google Scholar] [CrossRef]
- Waddell, P. Urbansim: Modeling urban development for land use, transportation, and environmental planning. J. Am. Plan. Assoc. 2002, 68, 297–314. [Google Scholar] [CrossRef]
- Lee, J. Reflecting on an Integrated Approach for Transport and Spatial Planning as a Pathway to Sustainable Urbanization. Sustainability 2020, 12, 10218. [Google Scholar] [CrossRef]
- Moeckel, R.; Garcia, C.L.; Chou, A.T.M.; Okrah, M.B. Trends in integrated land-use/transport modeling. J. Transp. Land Use 2018, 11, 463–476. [Google Scholar] [CrossRef]
- Southworth, F. A Technical Review of Urban Land Use—Transportation Models as Tools for Evaluating Vehicle Travel Reduction Strategies; Oak Ridge National Laboratory, The United States Department Energy: Washington, DC, USA, 1995. [Google Scholar] [CrossRef]
- Wegener, M. Overview of Land Use Transport Models; Emerald Group Publishing Limited: Bingley, UK, 2004; Volume 5, pp. 127–146. [Google Scholar]
- Iacono, M.; Levinson, D.; El-Geneidy, A. Models of transportation and land use change: A guide to the territory. J. Plan. Lit. 2008, 22, 323–340. [Google Scholar] [CrossRef]
- Batty, M. Progress, success, and failure in urban modelling. Environ. Plan. 1979, 11, 863–878. [Google Scholar] [CrossRef]
- McFadden, D. Modelling the choice of residential location. In Cowles Foundation Discussion Papers No. 477; Yale University: New Haven, CT, USA, 1997; Available online: https://elischolar.library.yale.edu/cowles-discussion-paper-series/710/ (accessed on 13 March 2025).
- Alonso, W. Location and Land Use: Toward a General Theory of Land Rent; Harvard University Press: Cambridge, MA, USA, 1964. [Google Scholar]
- Leontief, W.W. Quantitative input and output relations in the economic systems of the United States. Rev. Econ. Stat. 1936, 18, 105–125. [Google Scholar] [CrossRef]
- Fuenmayor Molero, G.J. Building a Spatial Economic Model for Caracas Using PECAS. Ph.D. Dissertation, Department of Civil Engineering, University of Calgary, Calgary, AB, Canada, 2016. [Google Scholar]
- Deng, G.; Zhong, M.; Raza, A.; Hunt, J.D. A methodological study of multimodal freight transportation models for large regions based on an integrated modelling framework. J. Transp. Syst. Eng. Inf. Technol. 2022, 22, 30–42. [Google Scholar]
- Wang, Z.; Zhong, M.; Pan, X. Optimizing multi-period freight networks through industrial relocation: A land-use transport interaction modeling approach. Transp. Policy 2024, 158, 112–124. [Google Scholar] [CrossRef]
- Donnelly, R.; Upton, W.J.; Knudson, B. Oregon’s transportation and land use model integration program. J. Transp. Land Use 2018, 11, 19–30. [Google Scholar] [CrossRef]
- Safdar, M.; Zhong, M.; Ren, Z.; Hunt, J.D. An Integrated Framework for Estimating Origins and Destinations of Multimodal Multi-Commodity Import and Export Flows Using Multisource Data. Systems 2024, 12, 406. [Google Scholar] [CrossRef]
- Golias, M.; Mishra, S.; Psarros, I. A Guidebook for Best Practices on Integrated Land Use and Travel Demand Modeling; University of Memphis: Memphis, TN, USA, 2014. [Google Scholar]
- Miller, R.E.; Blair, P.D. Input-Output Analysis: Foundations and Extensions; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Hunt, J.D.; Abraham, J.E. PECAS—For Spatial Economic Modelling Theoretical Formulation System Documentation. Available online: https://www.hbaspecto.com/resources/PECAS-Software-User-Guide.pdf (accessed on 30 March 2024).
- Liu, X.; Zhou, X. Determinants of carbon emissions from road transportation in China: An extended input-output framework with production-theoretical approach. Energy 2025, 316, 134493. [Google Scholar] [CrossRef]
- Mascaretti, A.; Dell’Agostino, L.; Arena, M.; Flori, A.; Menafoglio, A.; Vantini, S. Heterogeneity of technological structures between EU countries: An application of complex systems methods to input–output tables. Expert Syst. Appl. 2022, 206, 117875. [Google Scholar] [CrossRef]
- Antille, G.; Fontela, E.; Guillet, S. Changes in technical coefficients: The experience with Swiss I/O tables. In Proceedings of the 13th International Conference on Input-Output Techniques, Macerat, Italy, 21–25 August 2000. [Google Scholar]
- Ikotun, A.M.; Ezugwu, A.E.; Abualigah, L.; Abuhaija, B.; Heming, J. K-means clustering algorithms: A comprehensive review, variants analysis, and advances in the era of big data. Inf. Sci. 2023, 622, 178–210. [Google Scholar] [CrossRef]
- Yang, X.; Zhao, W.; Xu, Y.; Wang, C.-D.; Li, B.; Nie, F. Sparse K-means clustering algorithm with anchor graph regularization. Inf. Sci. 2024, 667, 120504. [Google Scholar] [CrossRef]
- Hennig, C.; Liao, T.F. How to find an appropriate clustering for mixed-type variables with application to socio-economic stratification. J. R. Stat. Soc. Ser. C Appl. Stat. 2013, 62, 309–369. [Google Scholar] [CrossRef]
- Na, S.; Xumin, L.; Yong, G. Research on k-means clustering algorithm: An improved k-means clustering algorithm. In Proceedings of the 2010 Third International Symposium on Intelligent Information Technology and Security Informatics, Jinggangshan, China, 2–4 April 2010; IEEE: New York, NY, USA, 2010; pp. 63–67. [Google Scholar]
- Doni, A.F.; Negera, Y.D.P.; Maria, O.A.H. K-means clustering algorithm for determination of clustering of Bangkalan regional development potential. In Proceedings of the IOP Conference Series, Earth and Environmental Science, Malang, Indonesia, 21–22 October 2020; IOP Publishing: Bristol, UK, 2020; Volume 485, p. 022078. [Google Scholar]
- Çağlar, M.; Gürler, C. Sustainable Development Goals: A cluster analysis of worldwide countries. Environ. Dev. Sustain. 2022, 24, 8593–8624. [Google Scholar] [CrossRef]
- Kumari, R.; Raman, R. Regional disparities in healthcare services in Uttar Pradesh, India: A principal component analysis. GeoJournal 2022, 87, 5027–5050. [Google Scholar] [CrossRef]
- Azarafza, M.; Azarafza, M.; Akgün, H. Clustering method for spread pattern analysis of coronavirus (COVID-19) infection in Iran. medRxiv 2020. [Google Scholar] [CrossRef]
- Kallingal, F.R.; Firoz, M.C. Regional disparities in social development: A case of selected districts in Kerala India. GeoJournal 2023, 88, 161–188. [Google Scholar] [CrossRef]
- Liu, D.; Liang, J.; Xu, S.; Ye, M. Analysis of Carbon Emissions Embodied in the Provincial Trade of China Based on an Input–Output Model and k-Means Algorithm. Sustainability 2023, 15, 9196. [Google Scholar] [CrossRef]
- Yuan, C.; Yang, H. Research on K-Value Selection Method of K-Means Clustering Algorithm. J 2019, 2, 226–235. [Google Scholar] [CrossRef]
- Thorndike, R.L. Who belongs in the family? Psychometrika 1953, 18, 267–276. [Google Scholar] [CrossRef]
- Wang, J.; Biljecki, F. Unsupervised machine learning in urban studies: A systematic review of applications. Cities 2022, 129, 103925. [Google Scholar] [CrossRef]
- Den Teuling, N.G.P.; Pauws, S.C.; van den Heuvel, E.R. A comparison of methods for clustering longitudinal data with slowly changing trends. Commun. Stat.-Simul. Comput. 2023, 52, 621–648. [Google Scholar] [CrossRef]
- Liu, Y. Modelling Urban Development with Geographical Information Systems and Cellular Automata; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Petropoulos, F.; Apiletti, D.; Assimakopoulos, V.; Babai, M.Z.; Barrow, D.K.; Taieb, S.B.; Bergmeir, C.; Bessa, R.J.; Bijak, J.; Boylan, J.E. Forecasting: Theory and practice. Int. J. Forecast. 2022, 38, 705–871. [Google Scholar]
- HBA Specto Incorporated Production, Exchange, and Consumption Allocation System (PECAS). Available online: https://www.hbaspecto.com/ (accessed on 23 March 2024).
- Mir, M.S.; Rao, K.V.K.; Hunt, J.D. Space development modeling of urban regions in developing countries. J. Urban Plan. Dev. 2010, 136, 75–85. [Google Scholar] [CrossRef]
- Wang, W.; Zhong, M.; Zhang, Y.; Li, Y.; Ma, X.; Hunt, J.D.; Abraham, J.E. Testing microsimulation uncertainty of the parcel-based space development module of the Baltimore PECAS Demo Model. J. Transp. Land Use 2020, 13, 93–112. [Google Scholar] [CrossRef]
- Yamada, T.; Imai, K.; Nakamura, T.; Taniguchi, E. A supply chain-transport supernetwork equilibrium model with the behaviour of freight carriers. Transp. Res. Part E Logist. Transp. Rev. 2011, 47, 887–907. [Google Scholar] [CrossRef]
- Dios Ortúzar, J.d.; Willumsen, L.G. Modelling Transport; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Sebastian, I.; Li, J. Outline for Building China’s Strength in Transport; Deutsche Gesellschaft für Internationale Zusammenarbeit (GIZ) GmbH: Bonn and Eschborn, Germany, 2019; Available online: https://changing-transport.org/wp-content/uploads/2019_Outline_for_Building_Chinas_Strength_in_Transport.pdf (accessed on 12 March 2025).
- National Bureau of Statistics of China. In Obtenido de National Bureau of Statistics of China. 2016. Available online: https://www.stats.gov.cn/english/ (accessed on 13 March 2024).
- OpenStreetMap. OpenStreetMap Foundation. 2024. Available online: https://www.openstreetmap.org (accessed on 30 March 2024).
- Esri. ArcGIS Online. Esri 2024. Available online: https://www.arcgis.com (accessed on 30 March 2024).
- Department of National Economic Accounting, State Statistical Bureau of P.R. China. China Regional Input-Output Table 2007; China Statistical Publishing House: Beijing, China, 2007. [Google Scholar]
- Department of National Economic Accounting, State Statistical Bureau of P.R. China. China Regional Input-Output Table 2012; China Statistical Publishing House: Beijing, China, 2016. [Google Scholar]
- Department of National Economic Accounting, State Statistical Bureau of P.R. China. China Regional Input-Output Table 2017; China Statistical Publishing House: Beijing, China, 2020. [Google Scholar]
- Ren, Z.; Zhong, M.; Cui, G.; Li, L.; Zhao, H. An Iterative Method for Calibrating Freight Value-per-Ton Conversion Factors of Integrated Land Use Transport Models Based on Multi-Source Data. In Proceedings of the Transportation Research Board 103rd Annual Meeting, Washington, DC, USA, 7–11 January 2024; Available online: https://trid.trb.org/View/2317332 (accessed on 13 March 2025).
- Research and Markets, China Construction Market, Trends and Forecast Analysis to 2028-Construction Industry Set to Record an Average Annual Growth Rate of 3.9% Between 2025 and 2028. 2024. Available online: https://www.businesswire.com/news/home/20241111813514/en/China-Construction-Market-Trends-and-Forecast-Analysis-to-2028---Construction-Industry-Set-to-Record-an-Average-Annual-Growth-Rate-of-3.9-between-2025-and-2028---ResearchAndMarkets.com (accessed on 29 March 2025).
- GlobalData. China Construction Market Size, Trend Analysis by Sector, Competitive Landscape and Forecast to 2028-Q4 Update. 2025. Available online: https://www.globaldata.com/store/report/china-construction-market-analysis/ (accessed on 31 March 2025).
- Xu, H.; Hu, S.; Li, X. Urban Distribution and Evolution of the Yangtze River Economic Belt from the Perspectives of Urban Area and Night-Time Light. Land 2023, 12, 321. [Google Scholar] [CrossRef]
- Zheng, H.; Bai, Y.; Wei, W.; Meng, J.; Zhang, Z.; Song, M.; Guan, D. Chinese provincial multi-regional input-output database for 2012, 2015, and 2017. Sci. Data 2021, 8, 244. [Google Scholar] [CrossRef]
- Brakman, S.; Garretsen, H.; Van Marrewijk, C. An Introduction to Geographical Economics: Trade, Location and Growth; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Fujita, M.; Krugman, P.R.; Venables, A. The Spatial Economy: Cities, Regions, and International Trade; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Zondag, B. Joint Modeling of Land-Use, Transport and Economy. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2007. [Google Scholar]


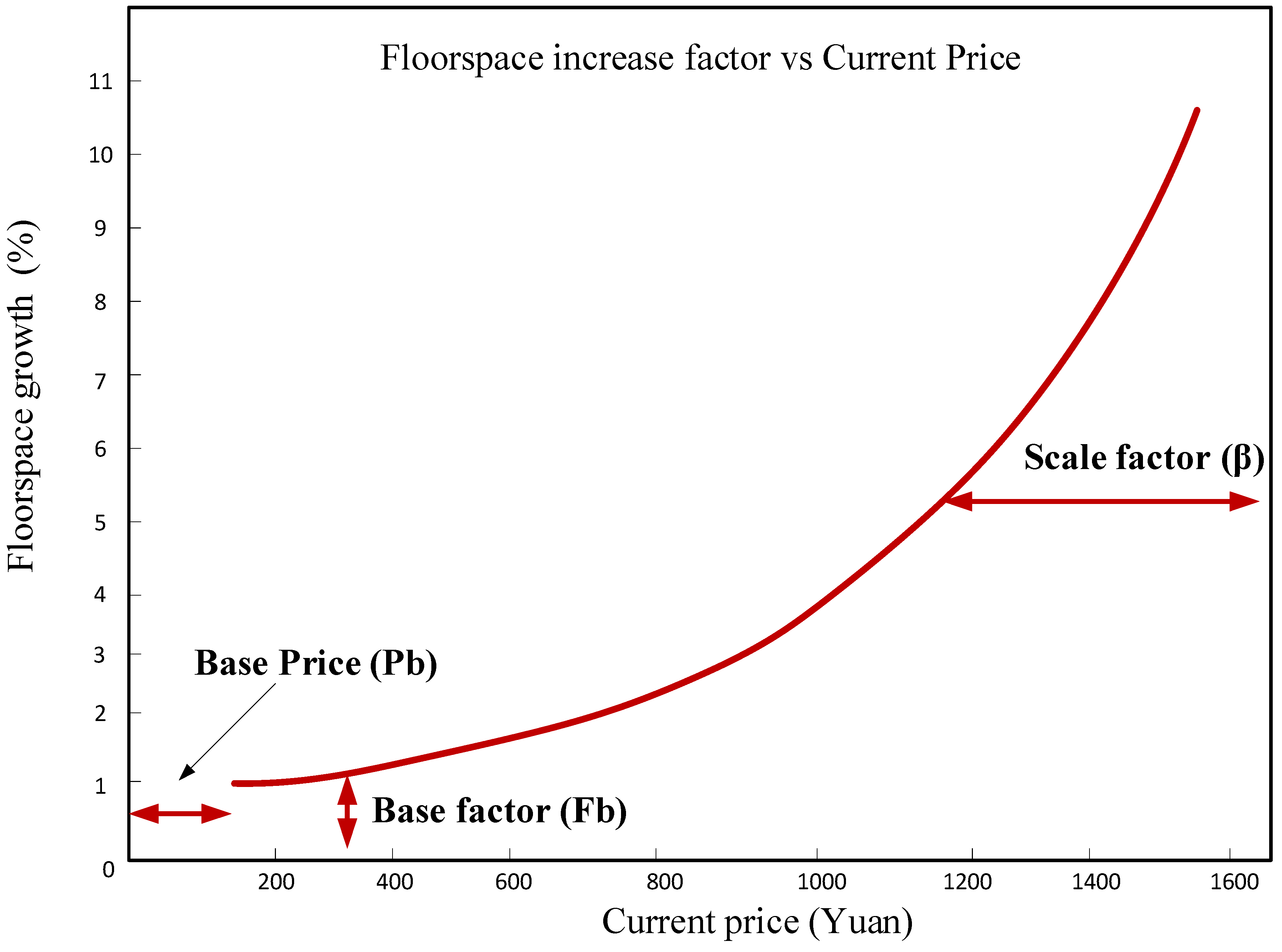











| Space Code | Space Name | Current Price | Base Factor | Scale Factor |
|---|---|---|---|---|
| S011 | UrbanResSpace | 220 | 0.2 | 0.7 |
| S012 | RuralResSpace | 220 | 0.2 | 0.7 |
| S03 | MiningSpace | 300 | 0.2 | 0.5 |
| S04 | IndustrialSpace | 300 | 0.2 | 0.5 |
| S051 | ConstSpace | 300 | 0.2 | 0.5 |
| S055 | TranspSpace | 300 | 0.2 | 0.5 |
| S052 | CommSpace | 600 | 0.3 | 0.7 |
| S054 | OfficeSpace | 400 | 0.3 | 0.6 |
| S021 | AgriSpace | 23 | 0.1 | 0.4 |
| S022 | ForestSpace | 23 | 0.1 | 0.4 |
| S023 | OthAgriSpace | 23 | 0.1 | 0.4 |
| Data Description | Data Source and Level | Timeframe |
|---|---|---|
| Economic Data | ||
| Provincial Statistical Yearbook (Population statistics, socio-economic data, product proportions). | All YREB regions (including 9 provinces and 2 municipalities). Source: Provincial Statistical Bureaus | 2010–2020 |
| Input–Output (IO) tables (139 and 42 activities formats) | All YREB regions (including 9 provinces and 2 municipalities) Source: Department of National Accounts, National Bureau of Statistics, China [59,62,63,64]. | 1997–2017 |
| Technical coefficients | Calculated using a specific method, as detailed in Section 3.3. All YREB regions (including 9 provinces and 2 municipalities) | 2007–2017 |
| Population census data | Urban and rural household and employment data. Source: National Data Website (https://data.stats.gov.cn/, accessed on 4 September 2024). | 2010, 2012, 2020 |
| China Labor Statistical Yearbook | Data by labor type (5 types). Source: National Data Website (https://data.stats.gov.cn/, accessed on 4 September 2024). | 2012 |
| Interregional IO tables | National Data Website (https://data.stats.gov.cn/, accessed on 4 September 2024). | 2012 |
| Socioeconomic and Demographic Activity totals | All YREB regions (including 9 provinces and 2 municipalities) | 2012–2050 |
| Wages by Labor Type | Source: industry recruitment information and public reports | 2012 |
| Observed Household Labor Force Ratio | Selected from partial counties due to data limitations. | 2012 |
| Land Use Data | ||
| Land Use TAZ .shp Layer | Source: Chinese Academy of Sciences, Resource and Environmental Science Data Center by county and districts (http://www.resdc.cn, accessed on 4 September 2024) | 2012 |
| Land Planning Standards | Divided by land type, obtained from national land resources departments by county and districts | 2012–2050 |
| Land Use/Cover Data .shp Layer | Divided by land type, land area data, remote sensing data, and by county and districts. Source: Chinese Academy of Sciences, Resource and Environmental Science Data Center (http://www.resdc.cn, accessed on 4 September 2024) | 2012–2050 |
| Total Developable Land Area | Total developable land area by land use type, by county and districts. Source: local government | 2012 |
| Floor Area Ratio | Divided by space type (10 types of construction land). Source: reference data from Wuhan by county and districts | 2012 |
| Space/land Consumption Coefficients | Divided by space type (urban and rural residential space, employment divided into 11 categories) by county and districts (see Appendix A.1). | 2012 |
| Employment Data | Obtained by applying to Provincial Statistical Bureau, used to estimate available land area by county and districts. Source: Provincial Statistical Bureau. | 2012 |
| Building Area | Sourced from a recent study [12]. | 2012 |
| Space Price | Divided by space type, referencing Wuhan’s data by county and district level | 2012 |
| Land Use Standards | Includes per capita land usage range, floor area ratio, etc. Source: local government | 2012 |
| Remote sensing data by space type | Chinese Academy of Sciences, http://english.igsnrr.cas.cn/, accessed on 4 September 2024). | 2012, 2015, 2020 |
| Multimodal Transportation Data | ||
| Multimodal Network .shp Layer | Three types: highways, railways, waterways. Source: Chinese Academy of Sciences, Resource and Environmental Science Data Center (http://www.resdc.cn, accessed on 10 April 2025); Openstreet maps (https://planet.openstreetmap.org, accessed on 4 September 2024), ArcGIS online | 2012 |
| Hub .shp Layer | Includes train stations, ports, logistics centers, etc. Source: Chinese Academy of Sciences, Resource and Environmental Science Data Center (http://www.resdc.cn, accessed on 4 September 2024) | 2012 |
| Freight Shipping Rates | Divided by goods and mode. Road, railway, and waterway industry websites. Sourced from a recent study, calculated by [12]. | 2012 |
| Freight Value | Divided by the ex-factory price of goods. Source: commodity trading websites, China | 2012 |
| Typical Transport Vehicle Load Weight | Divided by truck type, train type, and ship type (different tonnages). Source: domestic survey data, China | 2012 |
| Driver Wages | Divided by freight mode. Source: Industry recruitment information, China | 2012 |
| Time and Distance Impedance Coefficients | by road link | 2012 |
| Observed Average Travel Distance | Selected from partial counties by road link due to data limitations. | 2012 |
| Short-Distance Freight Transport Time | Calculated by dividing the shortest distance by free-flow speed, used as input data for AA module | 2012 |
| Short-Distance Freight Transport Distance | Based on GIS road network data, used as input for AA module. | 2012 |
| Loading/Unloading Rates | Unit cost for loading/unloading by goods and mode. Source: “Road Freight Classification Table” and “Loading/Unloading Fee Table” | 2012 |
| Transshipment Rates | Unit cost for transshipment by goods and mode. Source: literature “Research on Multi-modal Transport Path Optimization Based on Transportation Scenario” and “Coal Multi-modal Transport Optimization Considering Externality Costs”. | 2012 |
| Hub Waiting Time | Hub waiting time by mode. Source: survey [12] | 2012 |
| Transport Mode Capacity | Capacity of road segments by mode and grade. (1) Road: “Road Network Planning, Construction, and Management Methods” (2) Rail: “Discussion on Maximum Load of Single and Double Track Railways” | 2012 |
| Annual Average Daily Freight Volume by Mode | Used for model calibration, freight volume by mode. Sourced from a recent study [12]. (1) Road: “China Transportation Statistics Yearbook 2013” (2) Rail: Obtained from railway stations via project support. (3) Water: Ship signature data | 2012 |
| Annual Freight Volume by Mode | Source: National Data Network (https://data.stats.gov.cn/, accessed on 15 September 2024) | 2012–2018 |
| Annual Freight Turnover by Mode | Source: National Data Network (https://data.stats.gov.cn/, accessed on 15 September 2024) | 2012–2021 |
| Mode Share | Used for model calibration and validation. Source: calculated from annual freight volume statistics. | 2011–2021 |
| Transport cost (RMB/Km-ton) | Sourced from a recent study [12,65]. | 2012 |
| Methods | Highway | Railway | Waterway |
|---|---|---|---|
| DSEM | 0.951 | 0.855 | 0.985 |
| TSEM | 0.879 | 0.819 | 0.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Safdar, M.; Zhong, M.; Li, L.; Raza, A.; Hunt, J.D. Development of a Differential Spatial Economic Modeling Method for Improved Land Use and Multimodal Transportation Planning. Land 2025, 14, 886. https://doi.org/10.3390/land14040886
Safdar M, Zhong M, Li L, Raza A, Hunt JD. Development of a Differential Spatial Economic Modeling Method for Improved Land Use and Multimodal Transportation Planning. Land. 2025; 14(4):886. https://doi.org/10.3390/land14040886
Chicago/Turabian StyleSafdar, Muhammad, Ming Zhong, Linfeng Li, Asif Raza, and John Douglas Hunt. 2025. "Development of a Differential Spatial Economic Modeling Method for Improved Land Use and Multimodal Transportation Planning" Land 14, no. 4: 886. https://doi.org/10.3390/land14040886
APA StyleSafdar, M., Zhong, M., Li, L., Raza, A., & Hunt, J. D. (2025). Development of a Differential Spatial Economic Modeling Method for Improved Land Use and Multimodal Transportation Planning. Land, 14(4), 886. https://doi.org/10.3390/land14040886








