Spatial Heterogeneity of Driving Factors in Multi-Vegetation Indices RSEI Based on the XGBoost-SHAP Model: A Case Study of the Jinsha River Basin, Yunnan
Abstract
1. Introduction
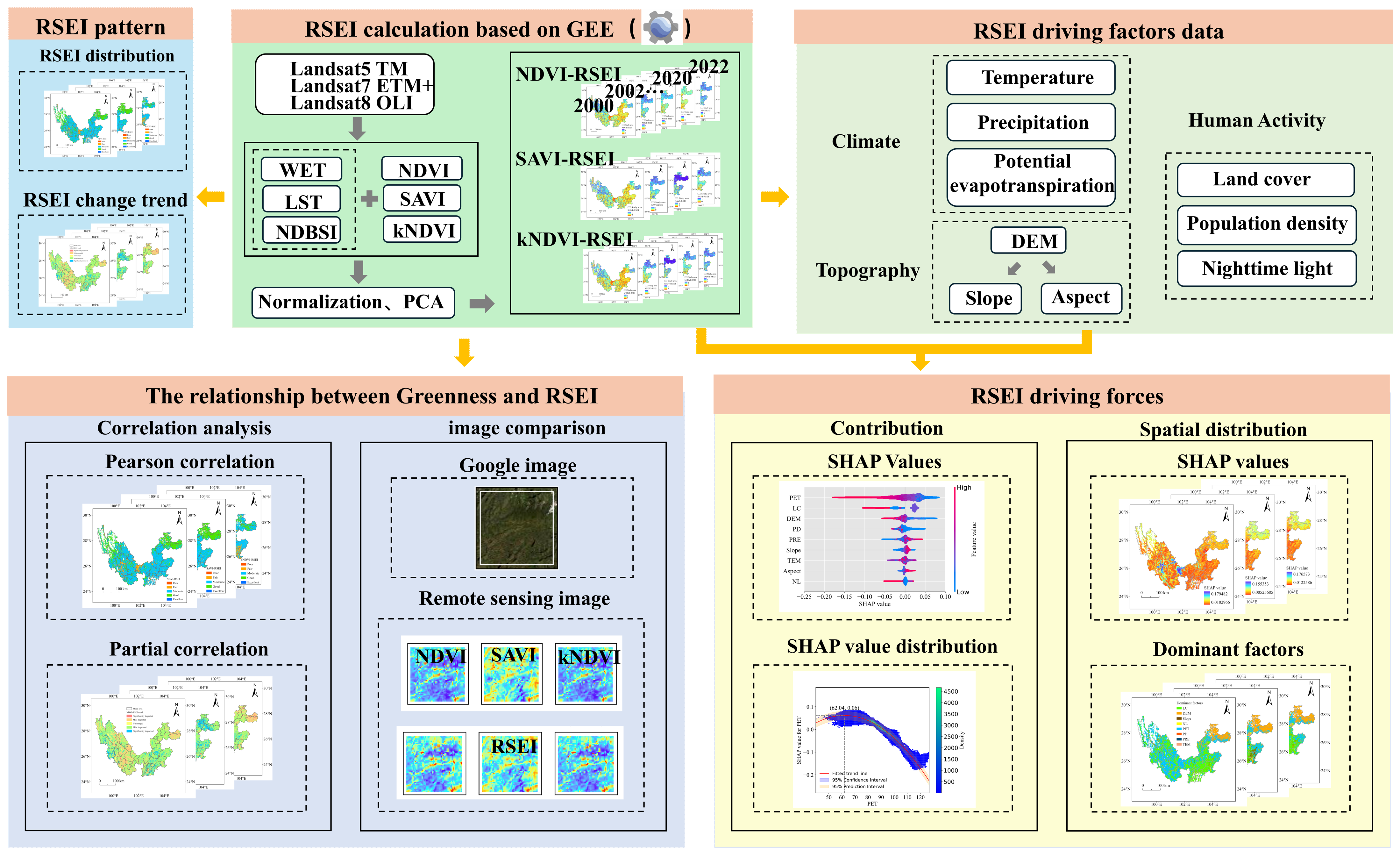
2. Materials and Methods
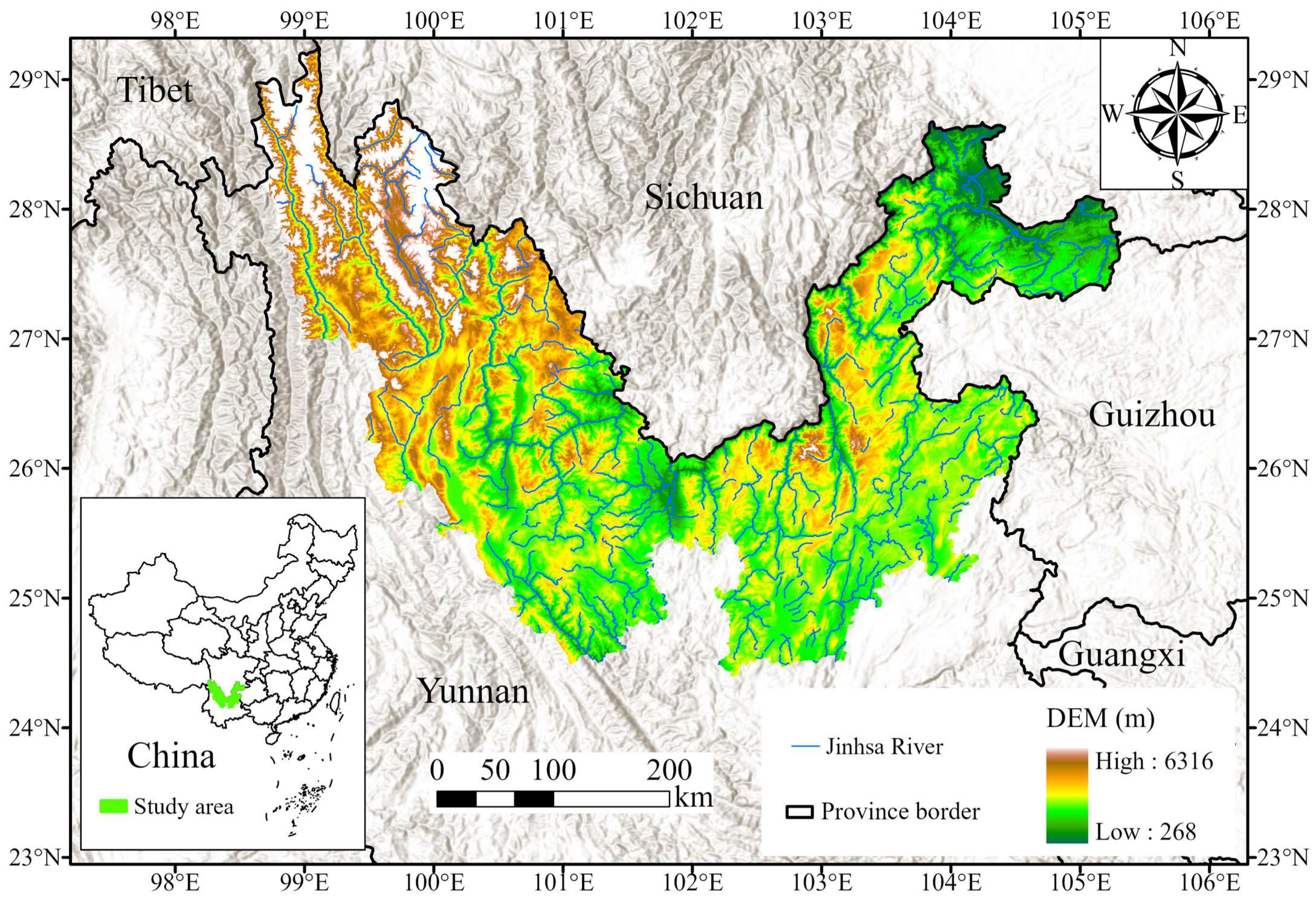
2.1. Research Area
2.2. Data Collection and Processing
2.3. Methods
2.3.1. Construction of RSEI
2.3.2. Trend Analysis
2.3.3. Correlation Analysis
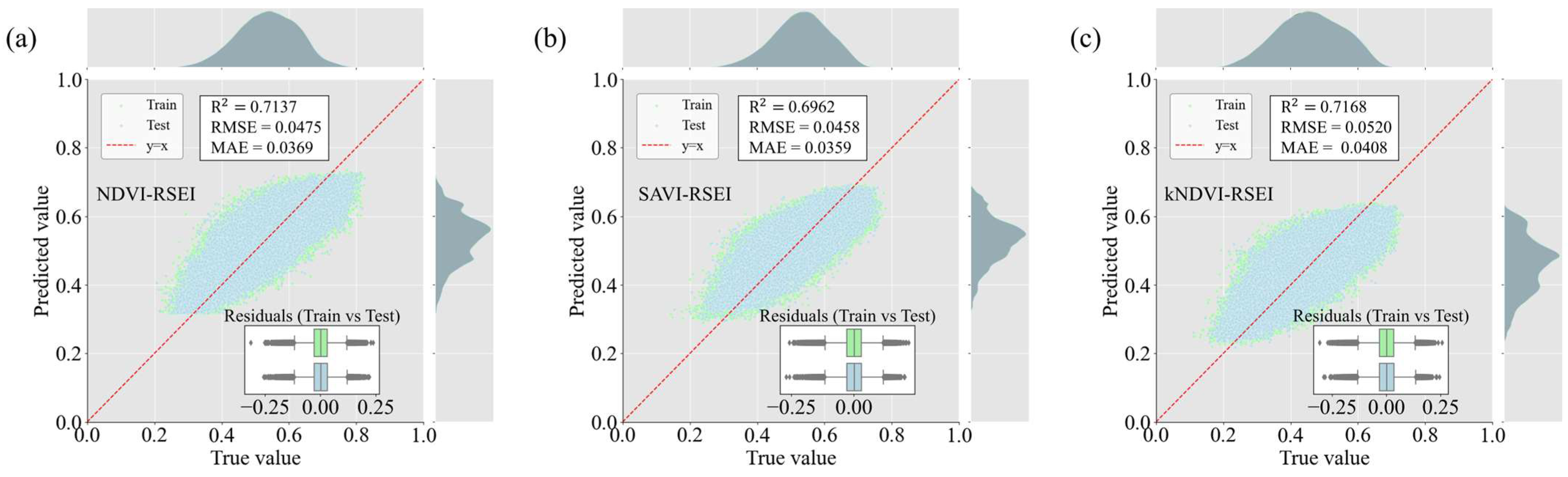
2.3.4. Explainable Machine Learning
3. Results
3.1. The Spatiotemporal Pattern of RSEI
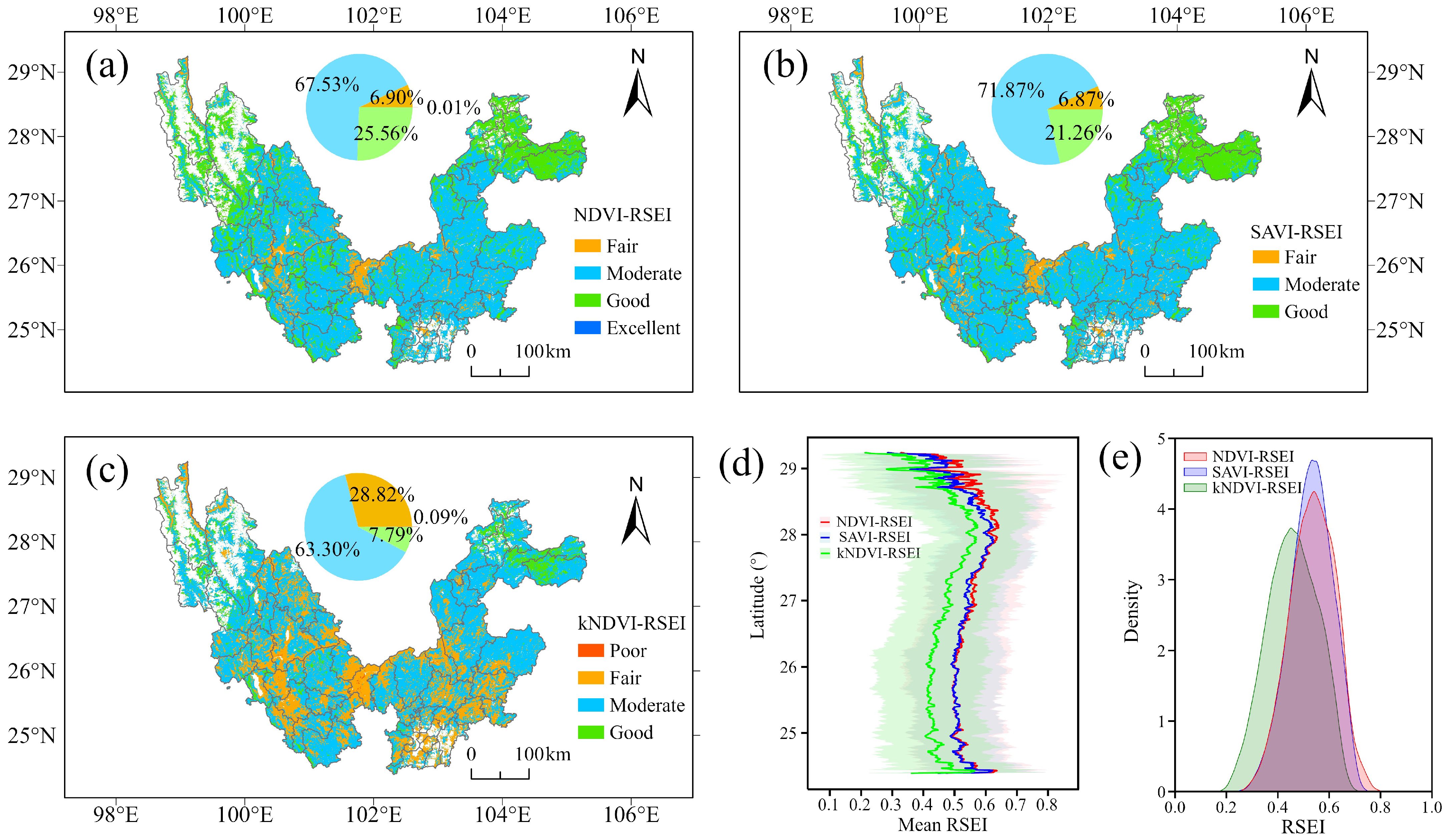
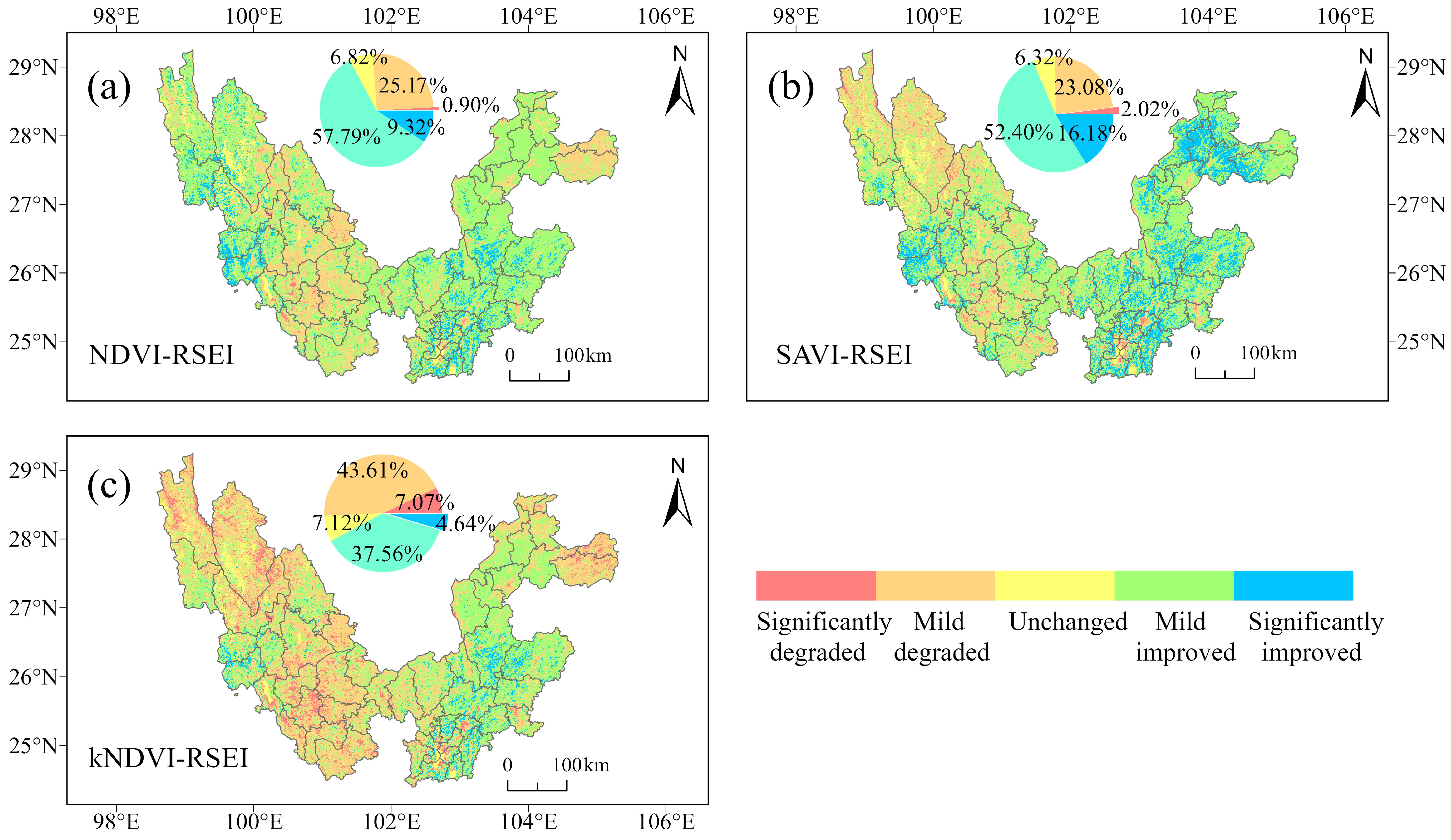
3.1.1. The Distribution of RSEI
3.1.2. The Trend of RSEI
3.2. The Relationship Between Greenness and RSEI
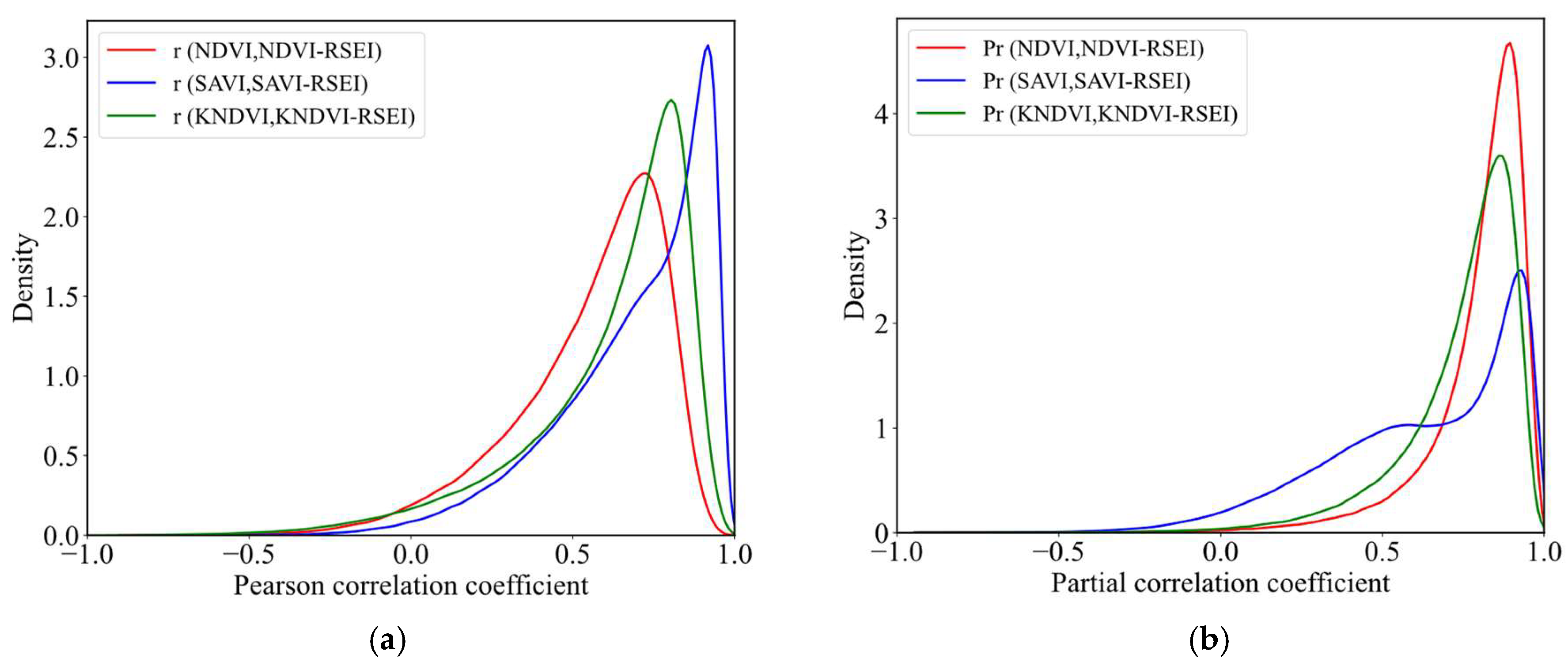
3.2.1. Correlation Analysis Between Greenness and RSEI
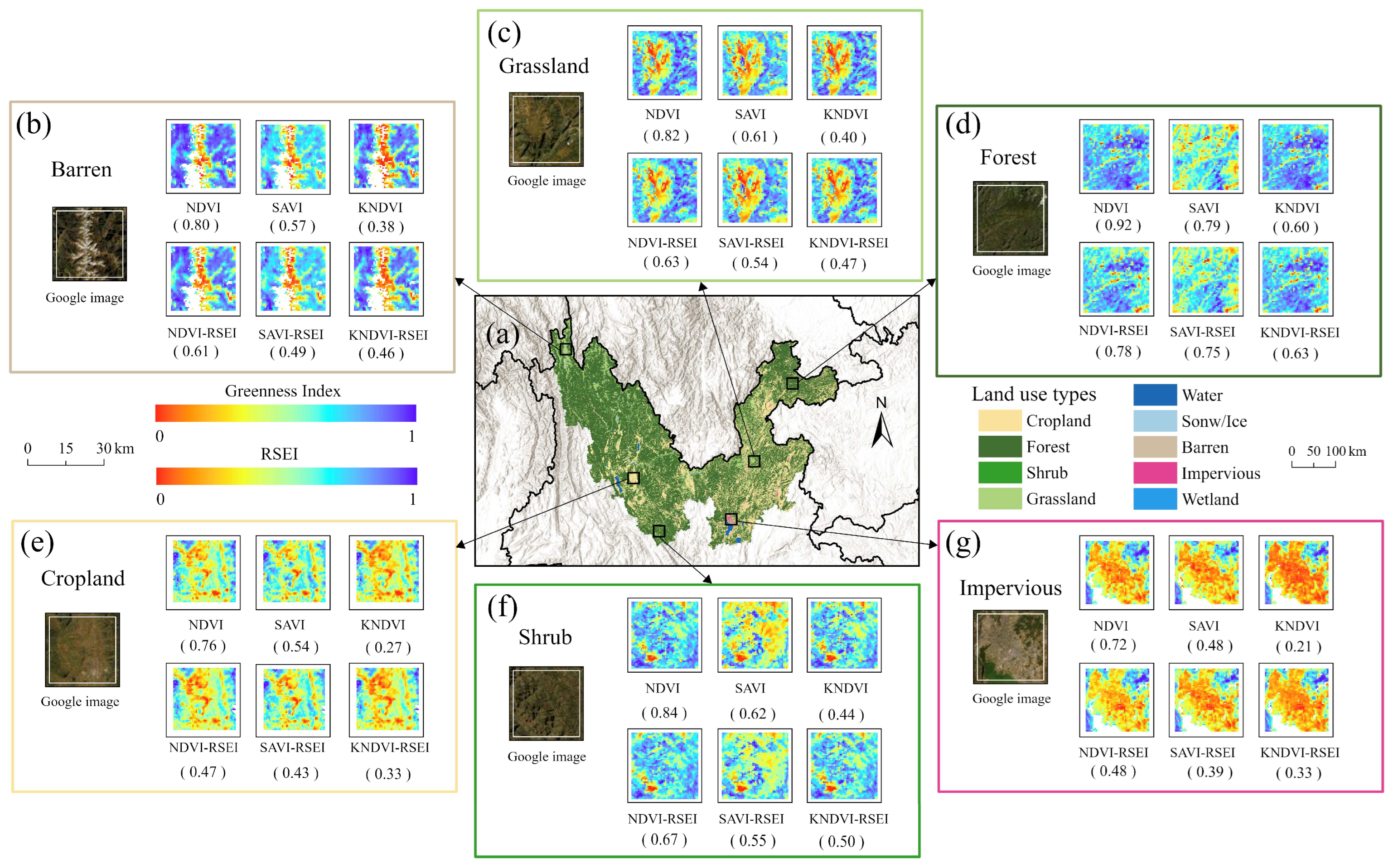
3.2.2. Comparison of Image Details Under Different Land Use Types
3.3. Driving Forces of RSEI
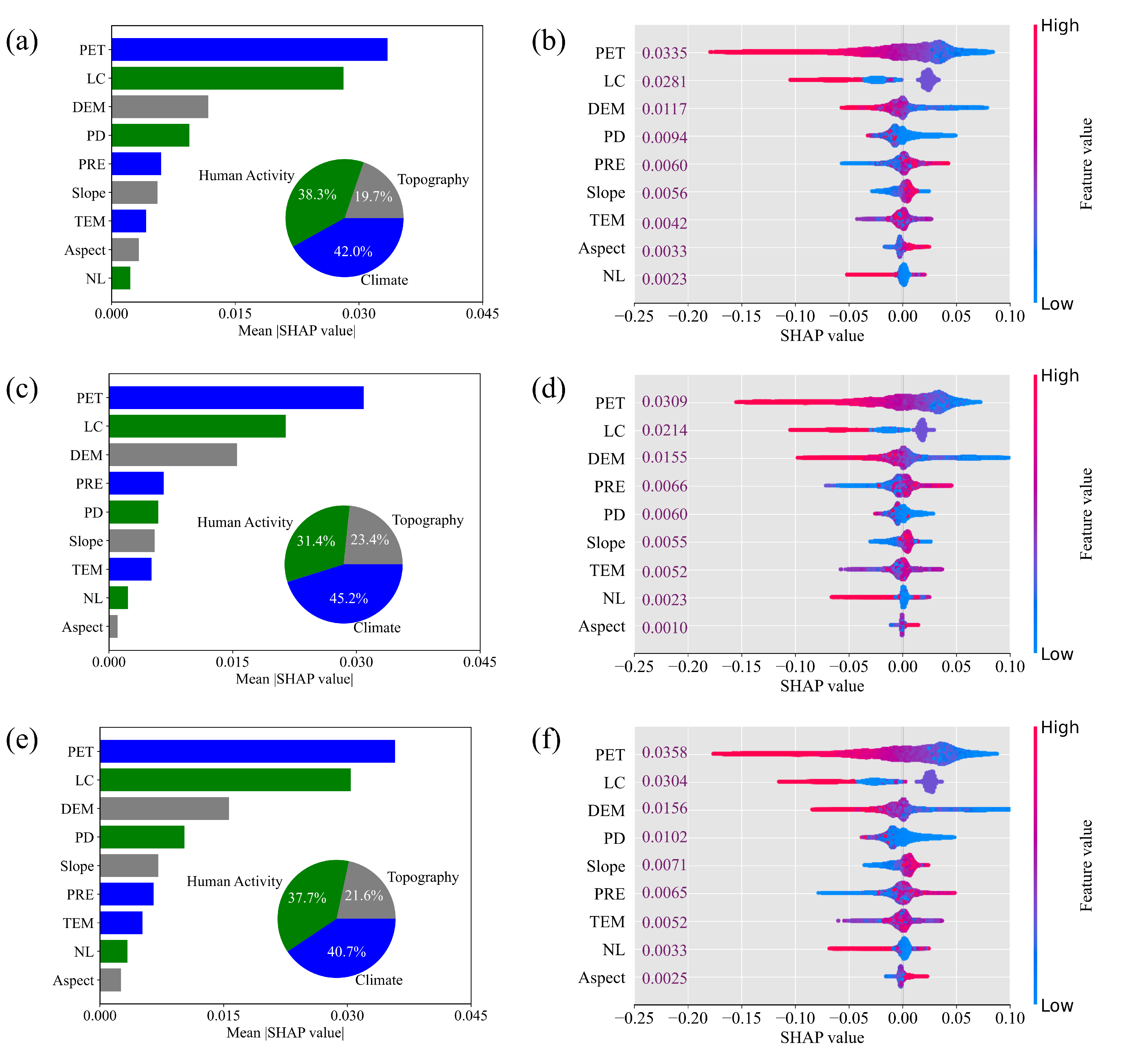
3.3.1. Contribution of Driving Forces
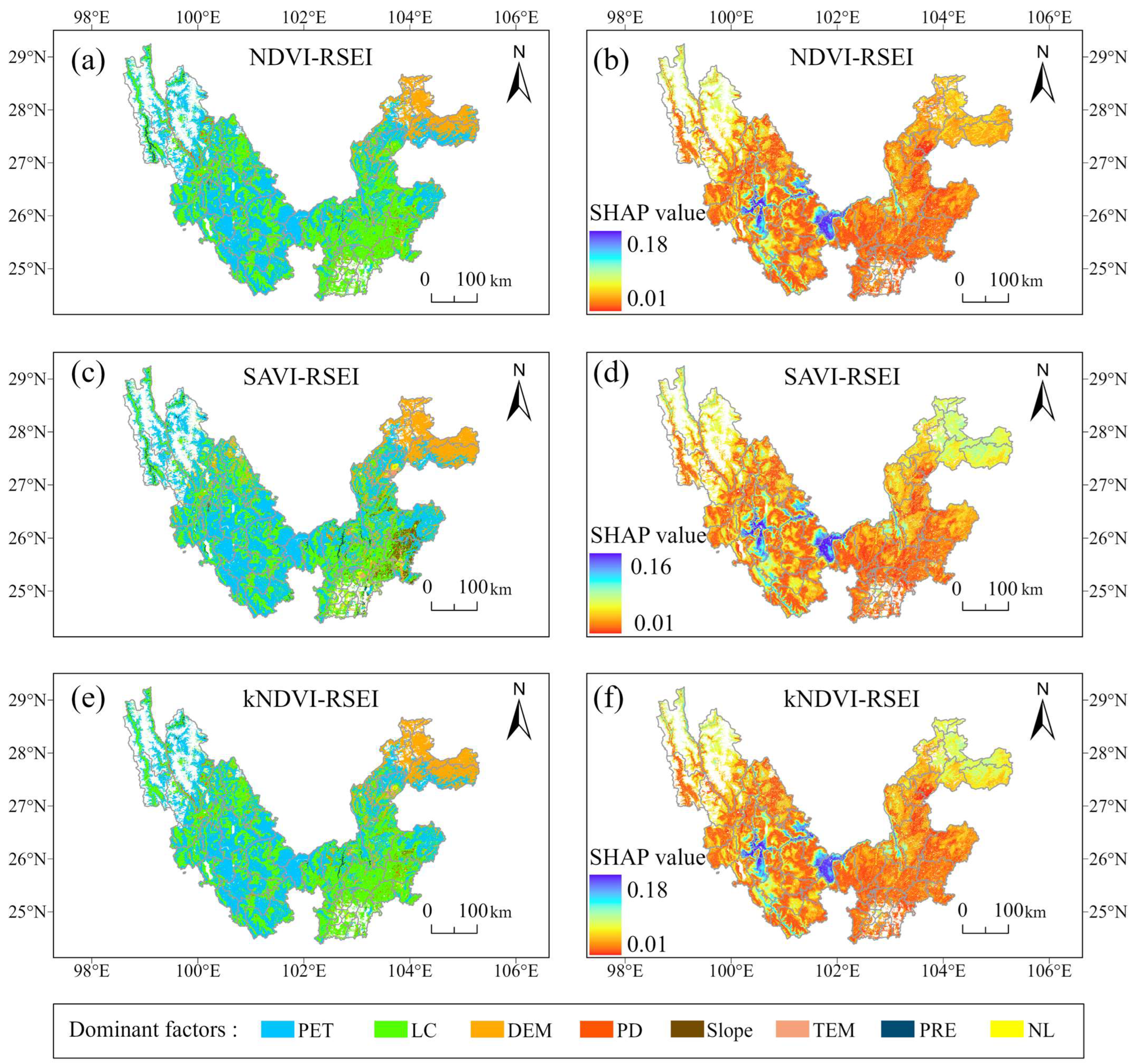
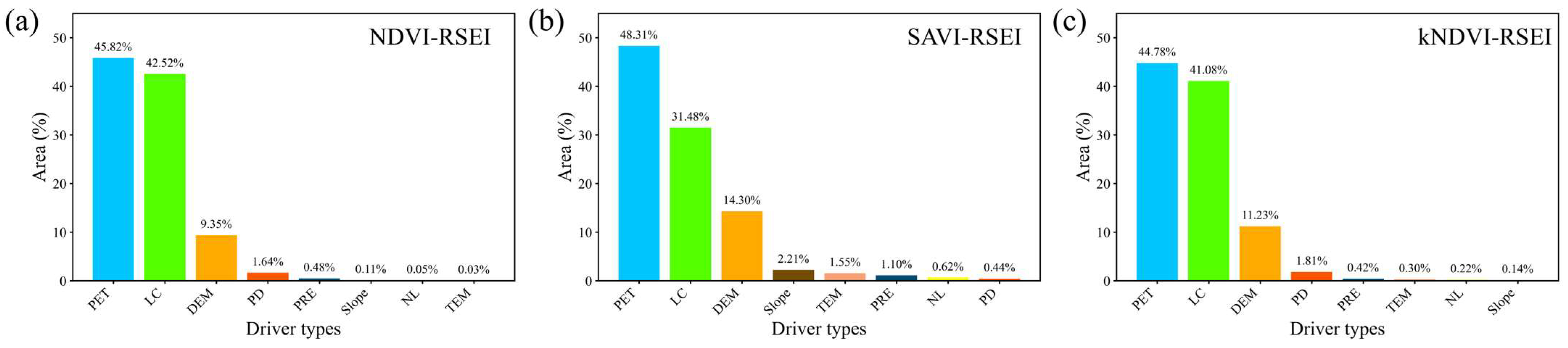
3.3.2. The Spatial Distribution of Dominant Driving Factors
4. Discussion
4.1. Spatial Distribution and Driving Factors of RSEI
4.2. The Coupling Relationship Between RSEI and Greenness
4.3. Advantages of IML in Identifying Driving Factors
- (1)
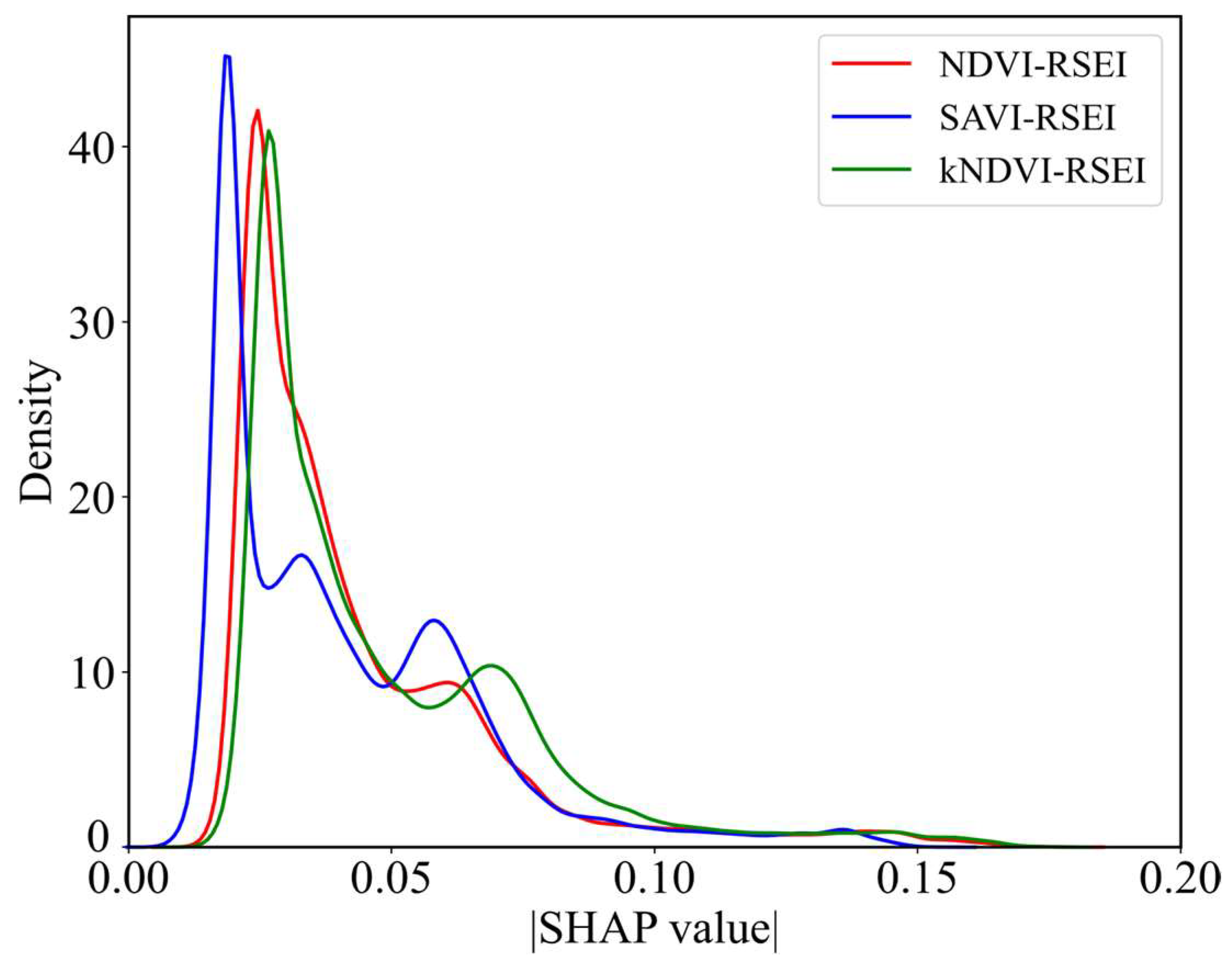
- XGBoost-SHAP quantifies the contribution of the nine driving factors to RSEI through feature importance ranking, while intuitively displaying the distribution characteristics of each factor’s contribution (Figure 10).
- (2)
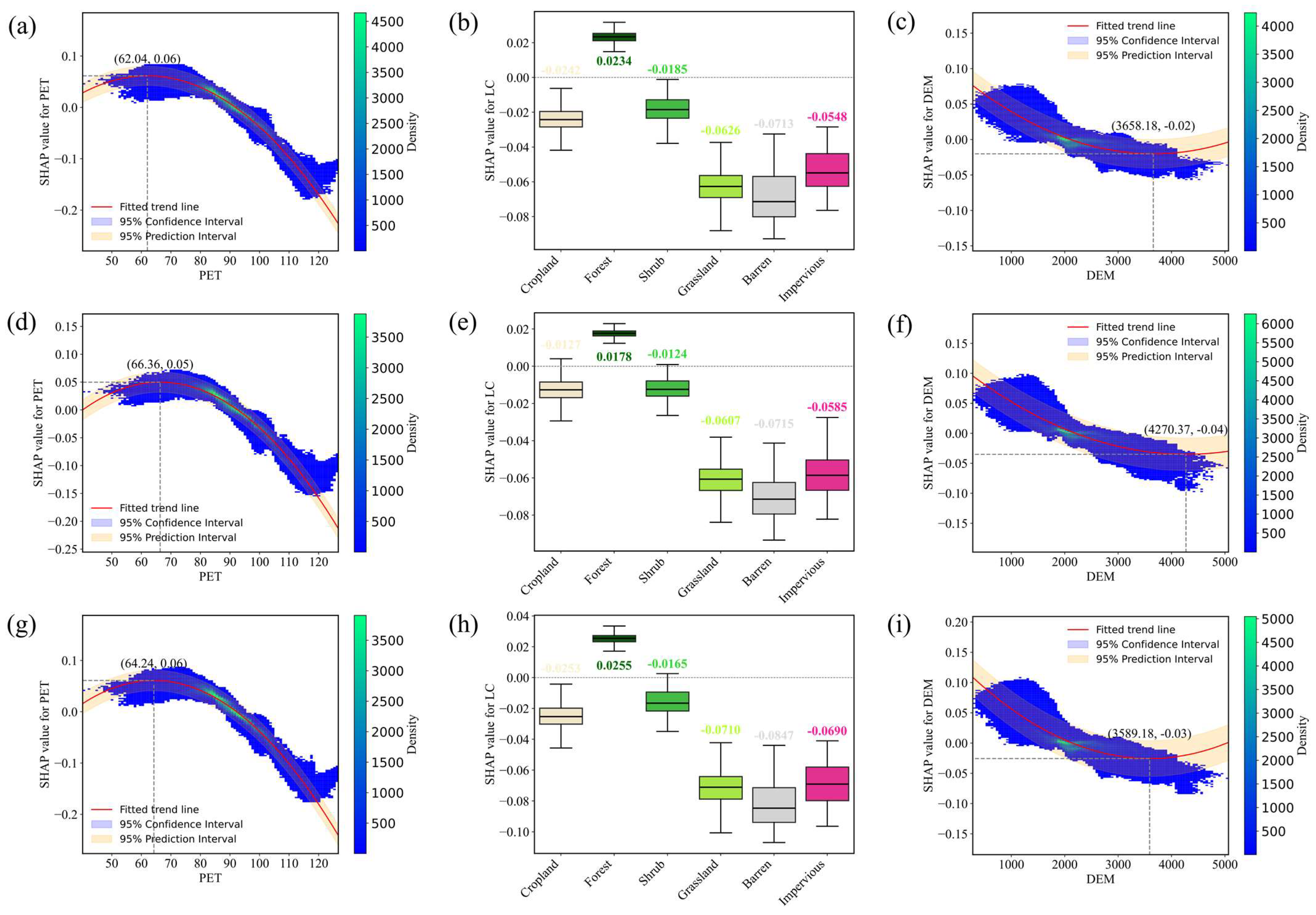
- XGBoost-SHAP provides both global and local explanations for individual driving factors. In our study (Figure 11), we plotted dependence plots for the three driving factors with the strongest contributions to RSEI (PET, LC, DEM), quantitatively explaining how changes in each factor affect RSEI. These local explanations are highly effective in developing targeted conservation measures to address specific ecological issues.
- (3)
- XGBoost-SHAP enables intuitive spatial visualization of model outputs. In our study (Figure 12), we visualized the dominant driving factors for each grid cell of RSEI, facilitating the understanding of complex driving mechanisms from a spatial perspective and translating the results into actionable insights.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, J.; Liu, W. Monitoring and Evaluation of Eco-Environment Quality Based on Remote Sensing-Based Ecological Index (RSEI) in Taihu Lake Basin, China. Sustainability 2022, 14, 5642. [Google Scholar] [CrossRef]
- Fan, Y.; Fang, C.; Zhang, Q. Coupling coordinated development between social economy and ecological environment in Chinese provincial capital cities-assessment and policy implications. J. Clean. Prod. 2019, 229, 289–298. [Google Scholar] [CrossRef]
- Hulme, P.E. Adapting to climate change: Is there scope for ecological management in the face of a global threat? J. Appl. Ecol. 2005, 42, 784–794. [Google Scholar] [CrossRef]
- Wei, Y.; An, M.; Huang, J.; Fang, X.; Song, M.; Wang, B.; Fan, M.; Wang, X. How human activities affect and reduce ecological sensitivity under climate change: Case study of the Yangtze River Economic Belt, China. J. Clean. Prod. 2024, 472, 143438. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, S.; Zhou, Y.; Ma, G.; Huang, W.; Zhu, Y. Method for quantitatively assessing the impact of an inter-basin water transfer project on ecological environment-power generation in a water supply region. J. Hydrol. 2023, 618, 129250. [Google Scholar] [CrossRef]
- Pandey, S.; Kumar, P.; Zlatic, M.; Nautiyal, R.; Panwar, V. Recent advances in assessment of soil erosion vulnerability in a watershed. Int. Soil Water Conserv. Res. 2021, 9, 305–318. [Google Scholar] [CrossRef]
- Liang, Y.; Liu, L. Simulating land-use change and its effect on biodiversity conservation in a watershed in northwest China. Ecosyst. Health Sustain. 2017, 3, 1335933. [Google Scholar] [CrossRef]
- Wang, D.; Alimohammadi, N. Responses of annual runoff, evaporation, and storage change to climate variability at the watershed scale. Water Resour. Res. 2012, 48, 2011WR011444. [Google Scholar] [CrossRef]
- Luck, G.W.; Chan, K.M.A.; Fay, J.P. Protecting ecosystem services and biodiversity in the world’s watersheds. Conserv. Lett. 2009, 2, 179–188. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhang, W.; Tian, C.; Mao, Y.; Zhou, R.; Wang, H.; Fu, K.; Sun, X. MCRN: A Multi-source Cross-modal Retrieval Network for remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2022, 115, 103071. [Google Scholar] [CrossRef]
- Sawut, R.; Li, Y.; Kasimu, A.; Ablat, X. Examining the spatially varying effects of climatic and environmental pollution factors on the NDVI based on their spatially heterogeneous relationships in Bohai Rim, China. J. Hydrol. 2023, 617, 128815. [Google Scholar] [CrossRef]
- Feng, R.; Wang, F.; Wang, K.; Wang, H.; Li, L. Urban ecological land and natural-anthropogenic environment interactively drive surface urban heat island: An urban agglomeration-level study in China. Environ. Int. 2021, 157, 106857. [Google Scholar] [CrossRef]
- Zhang, Q.; Huang, T.; Xu, S. Assessment of Urban Ecological Resilience Based on PSR Framework in the Pearl River Delta Urban Agglomeration, China. Land 2023, 12, 1089. [Google Scholar] [CrossRef]
- Nefeslioglu, H.A.; Sezer, E.A.; Gokceoglu, C.; Ayas, Z. A modified analytical hierarchy process (M-AHP) approach for decision support systems in natural hazard assessments. Comput. Geosci. 2013, 59, 1–8. [Google Scholar] [CrossRef]
- Hu, X.; Xu, H. A new remote sensing index for assessing the spatial heterogeneity in urban ecological quality: A case from Fuzhou City, China. Ecol. Indic. 2018, 89, 11–21. [Google Scholar] [CrossRef]
- Tang, Q.; Hua, L.; Tang, J.; Jiang, L.; Wang, Q.; Cao, Y.; Wang, T.; Cai, C. Advancing ecological quality assessment in China: Introducing the ARSEI and identifying key regional drivers. Ecol. Indic. 2024, 163, 112109. [Google Scholar] [CrossRef]
- Cai, C.; Li, J.; Wang, Z. Long-Term Ecological and Environmental Quality Assessment Using an Improved Remote-Sensing Ecological Index (IRSEI): A Case Study of Hangzhou City, China. Land 2024, 13, 1152. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, X.; Li, W.; Wu, X.; Cheng, X.; Zhou, Z.; Ling, Q.; Liu, Y.; Liu, X.; Hao, J.; et al. Dynamic Monitoring and Analysis of Ecological Environment Quality in Arid and Semi-Arid Areas Based on a Modified Remote Sensing Ecological Index (MRSEI): A Case Study of the Qilian Mountain National Nature Reserve. Remote Sens. 2024, 16, 3530. [Google Scholar] [CrossRef]
- Yi, S.; Zhou, Y.; Zhang, J.; Li, Q.; Liu, Y.; Guo, Y.; Chen, Y. Spatial-temporal evolution and motivation of ecological vulnerability based on RSEI and GEE in the Jianghan Plain from 2000 to 2020. Front. Environ. Sci. 2023, 11, 1191532. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.R.; Chen, J.; Chen, Y.; Li, J.; Yan, G.; Zhang, X. Analysis of NDVI and scaled difference vegetation index retrievals of vegetation fraction. Remote Sens. Environ. 2006, 101, 366–378. [Google Scholar] [CrossRef]
- Huete, A.R.; Liu, H.; Van Leeuwen, W.J.D. The use of vegetation indices in forested regions: Issues of linearity and saturation. In Proceedings of the IGARSS’97, 1997 IEEE International Geoscience and Remote Sensing Symposium Proceedings, Remote Sensing—A Scientific Vision for Sustainable Development, Singapore, 3–8 August 1997; Volume 4. [Google Scholar]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Campos-Taberner, M.; Moreno-Martínez, Á.; Walther, X.; Duveiller, G.; Cescatti, A.; Mahecha, M.; Muñoz-Marí, J.; García-Haro, F.; Guanter, L.; et al. A unified vegetation index for quantifying the terrestrial biosphere. Sci. Adv. 2021, 7, eabc7447. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Yang, B.; Feng, Y.; Ju, L. Evaluation of provincial forest ecological security and analysis of the driving factors in China via the GWR model. Sci. Rep. 2024, 14, 14299. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, P.; Wei, Y.; Li, Y.; Zhao, H. Measuring the efficiency and driving factors of urban land use based on the DEA method and the PLS-SEM model—A case study of 35 large and medium-sized cities in China. Sustain. Cities Soc. 2019, 50, 101646. [Google Scholar] [CrossRef]
- Cai, Z.; Zhang, Z.; Zhao, F.; Guo, X.; Zhao, J.; Xu, Y.; Liu, X. Assessment of eco-environmental quality changes and spatial heterogeneity in the Yellow River Delta based on the remote sensing ecological index and geo-detector model. Ecol. Inform. 2023, 77, 102203. [Google Scholar] [CrossRef]
- Jiang, S.; Sweet, L.; Blougouras, G.; Brenning, A.; Li, W.; Reichstein, M.; Denzler, J.; Shangguan, W.; Yu, G.; Huang, F.; et al. How Interpretable Machine Learning Can Benefit Process Understanding in the Geosciences. Earth’s Future 2024, 12, e2024EF004540. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30, pp. 4768–4777. [Google Scholar]
- Xie, J.; Liu, X.; Jasechko, S.; Berghuijs, W.; Wang, K.; Liu, C.; Reichstein, M.; Jung, M.; Koirala, S. Majority of global river flow sustained by groundwater. Nat. Geosci. 2024, 17, 770–777. [Google Scholar] [CrossRef]
- Yan, Y.; Piao, S.; Hammond, W.M.; Chen, A.; Hong, S.; Xu, H.; Munson, S.M.; Myneni, R.B.; Allen, C.D. Climate-induced tree-mortality pulses are obscured by broad-scale and long-term greening. Nat. Ecol. Evol. 2024, 8, 912–923. [Google Scholar] [CrossRef]
- Peng, S. 1-km Monthly Precipitation Dataset for China (1901–2023); [DS/OL]; National Tibetan Plateau Data Center: Beijing, China, 2024. [Google Scholar] [CrossRef]
- Peng, S. 1-km Monthly Mean Temperature Dataset for China (1901–2023); [DS/OL]; National Tibetan Plateau Data Center: Beijing, China, 2024. [Google Scholar] [CrossRef]
- Peng, S. 1-km Monthly Potential Evapotranspiration Dataset for China (1901–2023); [DS/OL]; National Tibetan Plateau Data Center: Beijing, China, 2024. [Google Scholar] [CrossRef]
- Wu, Y.; Shi, K.; Chen, Z.; Liu, S.; Chang, Z. An Improved Time-Series DMSP-OLS-Like Data (1992–2023) in China by Integrating DMSP-OLS and SNPP-VIIRS; [DS/OL]; Harvard Dataverse: Cambridge, MA, USA, 2021. [Google Scholar] [CrossRef]
- Li, J.; Gong, J.; Guldmann, J.M.; Yang, J. Assessment of Urban Ecological Quality and Spatial Heterogeneity Based on Remote Sensing: A Case Study of the Rapid Urbanization of Wuhan City. Remote Sens. 2021, 13, 4440. [Google Scholar] [CrossRef]
- Maity, S.; Das, S.; Pattanayak, J.M.; Bera, B.; Shit, P.K. Assessment of ecological environment quality in Kolkata urban agglomeration, India. Urban Ecosyst. 2022, 25, 1137–1154. [Google Scholar] [CrossRef]
- Schultz, M.; Clevers, J.G.P.W.; Carter, S.; Verbesselt, J.; Avitabile, V.; Quang, H.V.; Herold, M. Performance of vegetation indices from Landsat time series in deforestation monitoring. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 318–327. [Google Scholar] [CrossRef]
- Ermida, S.L.; Soares, P.; Mantas, V.; Göttsche, F.M.; Trigo, I.F. Google Earth Engine Open-Source Code for Land Surface Temperature Estimation from the Landsat Series. Remote Sens. 2020, 12, 1471. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Fernandes, R.; Leblanc, S.G. Parametric (modified least squares) and non-parametric (Theil–Sen) linear regressions for predicting biophysical parameters in the presence of measurement errors. Remote Sens. Environ. 2005, 95, 303–316. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson Correlation Coefficient. In Noise Reduction in Speech Processing; Springer Topics in Signal Processing; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2, pp. 1–4. [Google Scholar]
- Wang, C.; Shen, Y.; Fang, X.; Xiao, S.; Liu, G.; Wang, L.; Gu, B.; Zhou, F.; Chen, D.; Tian, H.; et al. Reducing soil nitrogen losses from fertilizer use in global maize and wheat production. Nat. Geosci. 2024, 17, 1008–1015. [Google Scholar] [CrossRef]
- Li, J.; Bevacqua, E.; Chen, C.; Wang, Z.; Chen, X.; Myneni, R.B.; Wu, X.; Xu, C.Y.; Zhang, Z.; Zscheischler, J. Regional asymmetry in the response of global vegetation growth to springtime compound climate events. Commun. Earth Environ. 2022, 3, 123. [Google Scholar] [CrossRef]
- Li, Z. Extracting spatial effects from machine learning model using local interpretation method: An example of SHAP and XGBoost. Comput. Environ. Urban Syst. 2022, 96, 101845. [Google Scholar] [CrossRef]
- Zhang, X.; Fan, H.; Zhou, C.; Sun, L.; Xu, C.; Lv, T.; Ranagalage, M. Spatiotemporal change in ecological quality and its influencing factors in the Dongjiangyuan region, China. Environ. Sci. Pollut. Res. 2023, 30, 69533–69549. [Google Scholar] [CrossRef]
- Fisher, J.B.; Whittaker, R.J.; Malhi, Y. ET come home: Potential evapotranspiration in geographical ecology. Glob. Ecol. Biogeogr. 2011, 20, 1–18. [Google Scholar] [CrossRef]
- Carpenter, C. The environmental control of plant species density on a Himalayan elevation gradient. J. Biogeogr. 2005, 32, 999–1018. [Google Scholar] [CrossRef]
- Luo, Z.; Sun, Y.; Tang, G.; He, Z.; Peng, L.; Qi, D.; Ou, Z. The Relationship between Reference Crop Evapotranspiration Change Characteristics and Meteorological Factors in Typical Areas of the Middle of the Dry-Hot Valley of Jinsha River. Water 2024, 16, 1512. [Google Scholar] [CrossRef]
- Deng, R.; Ding, X.; Wang, J. Landscape Ecological Risk Assessmentand Evaluation of Influencing Factors ofJinsha River Basin in Yunnan ProvinceBased on Land Use/Cover Change. Pol. J. Environ. Stud. 2024. [Google Scholar] [CrossRef]
- Xu, J.; Zheng, L.; Ma, R.; Tian, H. Correlation between Distribution of Rural Settlements and Topography in Plateau-Mountain Area: A Study of Yunnan Province, China. Sustainability 2023, 15, 3458. [Google Scholar] [CrossRef]
- Deng, Q.; Qin, F.; Zhang, B.; Wang, H.; Luo, M.; Shu, C.; Liu, H.; Liu, G. Characterizing the morphology of gully cross-sections based on PCA: A case of Yuanmou Dry-Hot Valley. Geomorphology 2015, 228, 703–713. [Google Scholar] [CrossRef]
- Dong, Y.; Xiong, D.; Su, Z.; Li, J.; Yang, D.; Shi, L.; Liu, G. The distribution of and factors influencing the vegetation in a gully in the Dry-hot Valley of southwest China. CATENA 2014, 116, 60–67. [Google Scholar] [CrossRef]
- Wang, X.; Biederman, J.A.; Knowles, J.F.; Scott, R.L.; Turner, A.J.; Dannenberg, M.P.; Köhler, P.; Frankenberg, G.; Litvak, M.E.; Flerchinger, G.N.; et al. Satellite solar-induced chlorophyll fluorescence and near-infrared reflectance capture complementary aspects of dryland vegetation productivity dynamics. Remote Sens. Environ. 2022, 270, 112858. [Google Scholar] [CrossRef]
- McDonald, A.J.; Gemmell, F.M.; Lewis, P.E. Investigation of the Utility of Spectral Vegetation Indices for Determining Information on Coniferous Forests. Remote Sens. Environ. 1998, 66, 250–272. [Google Scholar] [CrossRef]
- Zhang, P.; Liu, H.; Li, H.; Yao, J.; Chen, X.; Feng, J. Using enhanced vegetation index and land surface temperature to reconstruct the solar-induced chlorophyll fluorescence of forests and grasslands across latitude and phenology. Front. For. Glob. Change 2023, 6, 1257287. [Google Scholar] [CrossRef]
- Barati, S.; Rayegani, B.; Saati, M.; Sharifi, A.; Nasri, M. Comparison the accuracies of different spectral indices for estimation of vegetation cover fraction in sparse vegetated areas. Egypt. J. Remote Sens. Space Sci. 2011, 14, 49–56. [Google Scholar] [CrossRef]
- Wang, Q.; Moreno-Martínez, Á.; Muñoz-Marí, J.; Campos-Taberner, M.; Camps-Valls, G. Estimation of vegetation traits with kernel NDVI. ISPRS J. Photogramm. Remote Sens. 2023, 195, 408–417. [Google Scholar] [CrossRef]
- Qin, L.; Zhu, L.; Liu, B.; Li, Z.; Tian, Y.; Mitchell, G.; Shen, S.; Xu, W.; Chen, J. Global expansion of tropical cyclone precipitation footprint. Nat. Commun. 2024, 15, 4824. [Google Scholar] [CrossRef] [PubMed]

| Category | Metrics | Abbreviation | Spatial Resolution | Time Resolution | Year | Source | VIF |
|---|---|---|---|---|---|---|---|
| Climate | precipitation | PRE | 1 km | 1 month | 2000–2022 | https://data.tpdc.ac.cn/ (accessed on 3 September 2024) [32] | 2.38 |
| temperature | TEM | 1 km | 1 month | 2000–2022 | https://data.tpdc.ac.cn/ (accessed on 3 September 2024) [33] | 5.41 | |
| potential evapotranspiration | PET | 1 km | 1 month | 2000–2022 | https://data.tpdc.ac.cn/ (accessed on 3 September 2024) [34] | 2.44 | |
| Topography | DEM | DEM | 30 m | - | - | https://portal.opentopography.org/ (accessed on 3 September 2024) | 6.42 |
| slope | Slope | 30 m | - | - | 1.18 | ||
| aspect | Aspect | 30 m | - | - | 1.01 | ||
| Human Activity | land cover | LC | 30 m | 1 year | 2000–2022 | https://zenodo.org/records/12779975 (accessed on 3 September 2024) | 1.07 |
| population density | PD | 1 km | 1 year | 2000–2022 | https://landscan.ornl.gov/ (accessed on 3 September 2024) | 1.19 | |
| nighttime light | NL | 1 km | 1 year | 2000–2022 | https://dataverse.harvard.edu/ (accessed on 3 September 2024) [35] | 1.27 |
| Ecological Factors | RSEI Indices | Equations | Explanation |
|---|---|---|---|
| Greenness | NDVI | represents the reflectance in the near-infrared band; represents the reflectance in the red band [36]. | |
| SAVI | is the soil adjustment factor, typically set to 0.5 [38]. | ||
| kNDVI | represents the length scale parameter, indicating the sensitivity of the index to areas with sparse or dense vegetation. It is commonly assigned an average value of , allowing the formula to be simplified as [23]. | ||
| Humidity | WET | , , , , and represent the bands of remote sensing imagery [36]. | |
| Heat | LST | This calculation approach follows the methodology outlined in [39]. | |
| Dryness | NDBSI | , , , , and represent the bands of remote sensing imagery. is the soil index; is the index-based built-up index [36]. |
| Year | Loading Value | Eigenvalue | Contribution Rate/% | ||||||
|---|---|---|---|---|---|---|---|---|---|
| NDVI | SAVI | kNDVI | NDVI-RSEI | SAVI-RSEI | kNDVI-RSEI | NDVI-RSEI | SAVI-RSEI | kNDVI-RSEI | |
| 2000 | 0.55 | 0.42 | 0.69 | 0.03 | 0.03 | 0.04 | 66.94 | 61.26 | 69.80 |
| 2002 | 0.62 | 0.55 | 0.85 | 0.01 | 0.01 | 0.02 | 65.75 | 61.62 | 75.49 |
| 2004 | 0.65 | 0.50 | 0.76 | 0.03 | 0.02 | 0.04 | 83.42 | 79.20 | 85.71 |
| 2006 | 0.72 | 0.46 | 0.79 | 0.03 | 0.02 | 0.03 | 81.53 | 74.64 | 84.53 |
| 2008 | 0.62 | 0.34 | 0.71 | 0.02 | 0.02 | 0.03 | 74.50 | 71.26 | 75.96 |
| 2010 | 0.67 | 0.56 | 0.76 | 0.03 | 0.02 | 0.04 | 81.07 | 75.41 | 82.74 |
| 2012 | 0.56 | 0.35 | 0.70 | 0.04 | 0.03 | 0.05 | 72.25 | 68.00 | 74.48 |
| 2014 | 0.42 | 0.87 | 0.84 | 0.02 | 0.02 | 0.03 | 66.51 | 53.63 | 69.85 |
| 2016 | 0.48 | 0.89 | 0.86 | 0.01 | 0.02 | 0.03 | 63.88 | 59.19 | 70.58 |
| 2018 | 0.34 | 0.93 | 0.86 | 0.01 | 0.02 | 0.03 | 62.29 | 55.35 | 65.44 |
| 2020 | 0.36 | 0.68 | 0.81 | 0.02 | 0.02 | 0.03 | 67.97 | 56.27 | 68.81 |
| 2022 | 0.79 | 0.90 | 0.88 | 0.02 | 0.02 | 0.02 | 66.70 | 66.53 | 74.28 |
| Z | RSEI Trend | |
|---|---|---|
| Significantly improved | ||
| 1.96 | Mildly improved | |
| −0.0005 0.0005 | 1.96 | Unchanged |
| Mildly degraded | ||
| Significantly degraded |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, J.; Zhang, G.; Ma, S.; Pan, Y. Spatial Heterogeneity of Driving Factors in Multi-Vegetation Indices RSEI Based on the XGBoost-SHAP Model: A Case Study of the Jinsha River Basin, Yunnan. Land 2025, 14, 925. https://doi.org/10.3390/land14050925
Xia J, Zhang G, Ma S, Pan Y. Spatial Heterogeneity of Driving Factors in Multi-Vegetation Indices RSEI Based on the XGBoost-SHAP Model: A Case Study of the Jinsha River Basin, Yunnan. Land. 2025; 14(5):925. https://doi.org/10.3390/land14050925
Chicago/Turabian StyleXia, Jisheng, Guoyou Zhang, Sunjie Ma, and Yingying Pan. 2025. "Spatial Heterogeneity of Driving Factors in Multi-Vegetation Indices RSEI Based on the XGBoost-SHAP Model: A Case Study of the Jinsha River Basin, Yunnan" Land 14, no. 5: 925. https://doi.org/10.3390/land14050925
APA StyleXia, J., Zhang, G., Ma, S., & Pan, Y. (2025). Spatial Heterogeneity of Driving Factors in Multi-Vegetation Indices RSEI Based on the XGBoost-SHAP Model: A Case Study of the Jinsha River Basin, Yunnan. Land, 14(5), 925. https://doi.org/10.3390/land14050925







