Impacts of Spatial Expansion of Urban and Rural Construction on Typhoon-Directed Economic Losses: Should Land Use Data Be Included in the Assessment?
Abstract
1. Introduction
2. Research Methodology and Data Sources
2.1. Reserch Framework
2.2. Research Methodology
2.2.1. Prototype-Based Learning
2.2.2. Uncertainty Assessment
2.3. Data Sources
3. Results Analysis
3.1. Impact Factors Analysis
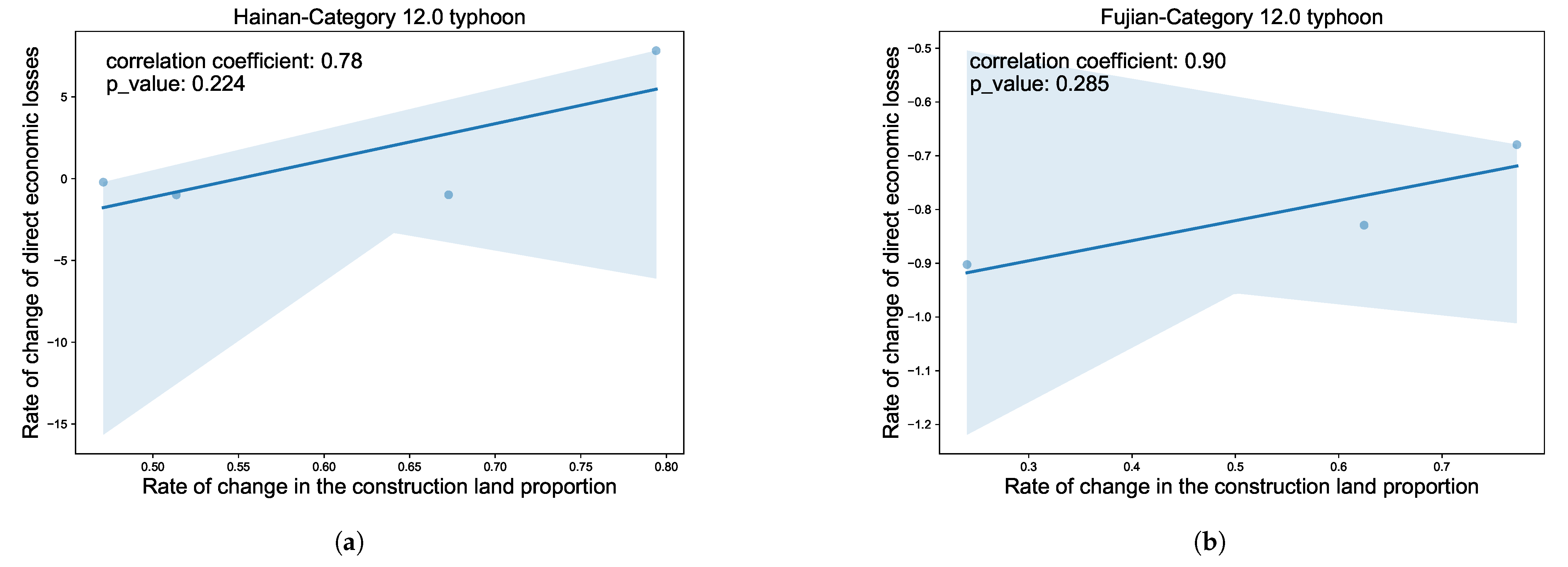
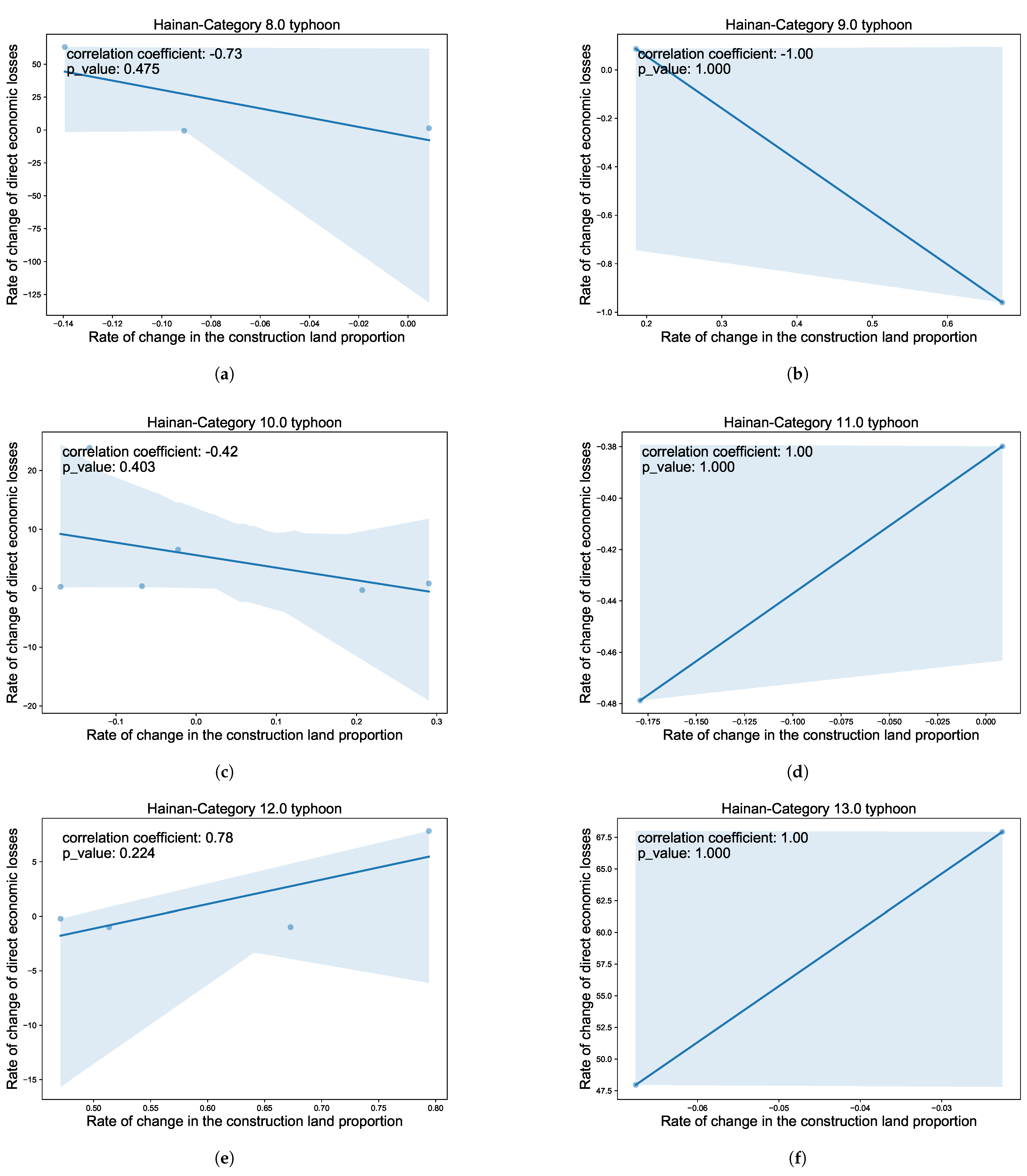
3.2. Analysis of the Impact of SEURC on Meteorological Disasters
4. Results Validation
4.1. Controlled Variable Experiment
4.2. Comparison Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qin, D.; Zhang, J.; Shan, C.; Song, L. China National Assessment Report on Risk Management and Adaptation of Climate Extremes and Disasters; Science Press: Beijing, China, 2015. (In Chinese) [Google Scholar]
- Emanuel, K.; Sundararajan, R.; Williams, J. Hurricanes and global warming: Results from downscaling IPCC AR4 simulations. Bull. Am. Meteorol. Soc. 2008, 89, 347–368. [Google Scholar] [CrossRef]
- Wang, G.; Chen, R.; Chen, J. Direct and indirect economic loss assessment of typhoon disasters based on EC and IO joint model. Nat. Hazards 2017, 87, 1751–1764. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhang, X.; Song, W. Ecological Risk Assessment of Land Use Change in the Tarim River Basin, Xinjiang, China. Land 2024, 13, 561. [Google Scholar] [CrossRef]
- Liu, F.; Yu, S.; Li, J.; Cao, X. The International Practice of Gentrification, and Its Research Process, Characteristics and Prospects. Mod. Urban Res. 2024, 38, 124–132. (In Chinese) [Google Scholar] [CrossRef]
- Keenan, J.M.; Hill, T.; Gumber, A. Climate gentrification: From theory to empiricism in Miami-Dade County, Florida. Environ. Res. Lett. 2018, 13, 054001. [Google Scholar] [CrossRef]
- Omar, H.; Cabral, P. Ecological risk assessment based on land cover changes: A case of Zanzibar (Tanzania). Remote Sens. 2020, 12, 3114. [Google Scholar] [CrossRef]
- Vickery, P.J.; Lin, J.; Skerlj, P.F.; Twisdale, L.A., Jr.; Huang, K. HAZUS-MH hurricane model methodology. I: Hurricane hazard, terrain, and wind load modeling. Nat. Hazards Rev. 2006, 7, 82–93. [Google Scholar] [CrossRef]
- Tao, Y.; Wang, T.; Sun, A.; Hamid, S.S.; Chen, S.C.; Shyu, M.L. Florida public hurricane loss model: Software system for insurance loss projection. Softw. Pract. Exp. 2022, 52, 1736–1755. [Google Scholar] [CrossRef]
- Huang, W.K.; Wang, J.J. Typhoon damage assessment model and analysis in Taiwan. Nat. Hazards 2015, 79, 497–510. [Google Scholar] [CrossRef]
- Gao, Z.; Geddes, R.R.; Ma, T. Direct and indirect economic losses using typhoon-flood disaster analysis: An application to Guangdong province, China. Sustainability 2020, 12, 8980. [Google Scholar] [CrossRef]
- Li, H.; Xu, E.; Zhang, H.; Zhong, S. A dynamic disastrous CGE model to optimize resource allocation in post-disaster economic recovery: Post-typhoon in an urban agglomeration area, China. Environ. Res. Lett. 2022, 17, 074027. [Google Scholar] [CrossRef]
- Sun, H.; Wang, J.; Ye, W. A data augmentation-based evaluation system for regional direct economic losses of storm surge disasters. Int. J. Environ. Res. Public Health 2021, 18, 2918. [Google Scholar] [CrossRef] [PubMed]
- Lou, W.-P.; Chen, H.-Y.; Qiu, X.-F.; Tang, Q.-Y.; Zheng, F. Assessment of economic losses from tropical cyclone disasters based on PCA-BP. Nat. Hazards 2012, 60, 819–829. [Google Scholar] [CrossRef]
- Yang, J.; Chen, S.; Tang, Y.; Lu, P.; Lin, S.; Duan, Z.; Ou, J. A tropical cyclone risk prediction framework using flood susceptibility and tree-based machine learning models: County-level direct economic loss prediction in Guangdong Province. Int. J. Disaster Risk Reduct. 2024, 114, 104955. [Google Scholar] [CrossRef]
- Kim, J.; Bae, J.; Adhikari, M.; Yum, S. Building loss assessment using deep learning algorithm from typhoon Rusa. Int. J. Heliyon 2024, 10, 1. [Google Scholar] [CrossRef]
- Yu, L.; Qin, H.; Huang, S.; Wei, W.; Jiang, H.; Mu, L. Quantitative study of storm surge risk assessment in an undeveloped coastal area of China based on deep learning and geographic information system techniques: A case study of Double Moon Bay. Nat. Hazards Earth Syst. Sci. 2024, 24, 2003–2024. [Google Scholar] [CrossRef]
- Liu, F.; Xu, E.; Zhang, H. Assessing typhoon disaster mitigation capacity and its uncertainty analysis in Hainan, China. Nat. Hazards 2024, 120, 9401–9420. [Google Scholar] [CrossRef]
- Tian, Z.; Zhang, Y.; Udo, K.; Lu, X. Regional economic losses of China’s coastline due to typhoon-induced port disruptions. Ocean Coast. Manag. 2023, 237, 106533. [Google Scholar] [CrossRef]
- Du, X.; Li, X.; Zhang, S.; Zhao, T.; Hou, Q.; Jin, X.; Zhang, J. High-accuracy estimation method of typhoon storm surge disaster loss under small sample conditions by information diffusion model coupled with machine learning models. Int. J. Disaster Risk Reduct. 2022, 82, 103307. [Google Scholar] [CrossRef]
- Wang, J.; Tan, J. Understanding the climate change and disaster risks in coastal areas of China to develop coping strategies. Prog. Geogr. 2021, 40, 870–882. (In Chinese) [Google Scholar] [CrossRef]
- Pan, Y.; Lin, Y.; Yang, R. Agricultural production space suitability in China: Spatial pattern, influencing factors and optimization strategies. Int. J. Environ. Res. Public Health 2022, 19, 13812. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Yuan, Y.; Tian, B. Analysis of the Driving Mechanism of Land Comprehensive Carrying Capacity from the Perspective of Urban Renewal. Land 2023, 12, 1377. [Google Scholar] [CrossRef]
- Yang, X.; Li, Y.; Jiang, W.; Ji, P.; Yang, Y. Study on Remote Sensing Dynamic Change of Ecological Environment Quality in Fugong County. J. Southwest For. Univ. 2023, 43, 99–108. (In Chinese) [Google Scholar] [CrossRef]
- Yang, Y.; Guo, F.; Han, G. Dynamic evolution and driving factors of tourism ecological security in the region of major function restricted development: A case study of Zhangjiajie. Acta Ecol. Sin. 2023, 43, 8404–8416. (In Chinese) [Google Scholar] [CrossRef]
- Ding, Y.; Dong, D. Study on comprehensive risk assessment of storm surges for Fujian Province from the perspective of resilience. J. Trop. Oceanogr. 2024, 43, 126–136. (In Chinese) [Google Scholar] [CrossRef]
- Yan, Y.; Gao, L.; Chen, R.; Zhang, C.; Ren, L.; Zhang, X.; Chen, C. Analysis of Disaster and Damage Process Caused by No. 2305 “Doksuri” Typhoon Disaster Chain in Fuzhou City. J. Catastrophol. 2024, 39, 228–234. (In Chinese) [Google Scholar] [CrossRef]
- Wang, J.; Liu, W.; Zhao, M.; Gou, A. Characteristics and Interaction of Spatial Expansion and Natural Disasters in the Guangdong-Hong Kong-Macao Greater Bay Area. Sci. Technol. Eng. 2023, 23, 11027–11040. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, Y.; Lin, T.; Zhang, J.; Lin, M.; Chen, Y.; Zheng, Y.; Wang, X.; Liu, Y.; Ye, H.; Zhang, G. Potential and Influencing Factors of Urban Spatial Development under Natural Constraints: A Case Study of the Guangdong-Hong Kong-Macao Greater Bay Area. Land 2024, 13, 783. [Google Scholar] [CrossRef]
- Xue, L.; Sun, X.; Zhao, W. The Impact of Climate Change and Economic Agglomeration on Agricultural Sustainability: A Case Study of Yunnan Province. Urban Environ. Stud. 2023, 3, 98–118. (In Chinese) [Google Scholar]
- Li, G.; Jampani, V.; Sevilla-Lara, L.; Sun, D.; Kim, J.; Kim, J. Adaptive prototype learning and allocation for few-shot segmentation. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 8334–8343. [Google Scholar] [CrossRef]
- Kim, H.S.; Kim, J.H.; Ho, C.H.; Chu, P.S. Pattern classification of typhoon tracks using the fuzzy c-means clustering method. J. Clim. 2011, 24, 488–508. [Google Scholar] [CrossRef]
- Bholowalia, P.; Kumar, A. EBK-means: A clustering technique based on elbow method and k-means in WSN. Int. J. Comput. Appl. 2014, 105, 17–24. [Google Scholar]
- Likas, A.; Vlassis, N.; Verbeek, J.J. The global k-means clustering algorithm. Pattern Recognit. 2003, 36, 451–461. [Google Scholar] [CrossRef]
- Teh, D.; Khan, T. Types, Definitions, Classifications, and Threat Levels of Natural Disasters. In Handbook for Reducing Disaster Risk and Enhancing Resilience: A New Framework for Building Disaster Resilience; Springer: Cham, Switzerland, 2021; pp. 27–56. [Google Scholar] [CrossRef]
- Seoh, R. Qualitative analysis of monte carlo dropout. arXiv 2020, arXiv:2007.01720. [Google Scholar] [CrossRef]
- Padarian, J.; Minasny, B.; McBratney, A. Assessing the uncertainty of deep learning soil spectral models using Monte Carlo dropout. Geoderma 2022, 425, 116063. [Google Scholar] [CrossRef]
- Bin, L.; Xu, K.; Pan, H.; Zhuang, Y.; Shen, R. Urban flood risk assessment characterizing the relationship among hazard, exposure, and vulnerability. Environ. Sci. Pollut. Res. 2023, 30, 86463–86477. [Google Scholar] [CrossRef]
- Pagliacci, F.; Russo, M. Be (and have) good neighbours! Factors of vulnerability in the case of multiple hazards. Ecol. Indic. 2020, 111, 105969. [Google Scholar] [CrossRef]
- Cohen, I.; Huang, Y.; Chen, J.; Benesty, J.; Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar] [CrossRef]
- Duncan, T.E. On the calculation of mutual information. SIAM J. Appl. Math. 1970, 19, 215–220. [Google Scholar] [CrossRef]
- Song, W.C.; Xie, J. Group feature screening via the F statistic. Commun. Stat.-Simul. Comput. 2022, 51, 1921–1931. [Google Scholar] [CrossRef]
- GB/T 19201-2006; National Standard for Tropical Cyclone Grades. Standardization Administration of China: Beijing, China, 2006.
- Zhang, B.; Liu, Y.; Liu, Y.; Lyu, S. Spatiotemporal Evolution and Influencing Factors for Urban Resilience in China: A Provincial Analysis. Buildings 2024, 14, 502. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, Y.; Wang, Y.; Ding, Y.; Yin, Y.; Dong, Z.; Wu, X. Analysis of temporal-spatial patterns and impact factors of typhoon disaster losses in China from 1978 to 2020. Trop. Geogr. 2024, 44, 1047–1063. (In Chinese) [Google Scholar] [CrossRef]
- Xu, M.; Lin, X.; Wen, C.; Xi, L. Research on Land Use Suitability Evaluation and Layout Optimization in Coastal Zones: Vulnerability Assessment Based on the Nature-social Economy. South Archit. 2024, 106–115. (In Chinese) [Google Scholar] [CrossRef]
- Yuan, H.; Hao, T.; Xu, Z.; Zhang, D. Path and Practice of Territorial Space Ecological Restoration in Coastal Areas from the Perspective of Land-Sea Integration. Planners 2024, 40, 89–97. (In Chinese) [Google Scholar]
- Li, J. Disaster emergency management in United States and its inspiration to China’s relevant management. J. Nat. Disasters 2006, 15, 6. (In Chinese) [Google Scholar]
- Miu, H.; Wang, N. An urban resilience measurement system based on decomposing post-disaster recovery process. J. Nat. Disasters 2021, 30, 10–27. (In Chinese) [Google Scholar] [CrossRef]
- Zhao, R.; Fang, C.; Liu, H. Progress and prospect of urban resilience research. Prog. Geogr. 2020, 39, 1717–1731. [Google Scholar] [CrossRef]
- Kingma, D.P. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]
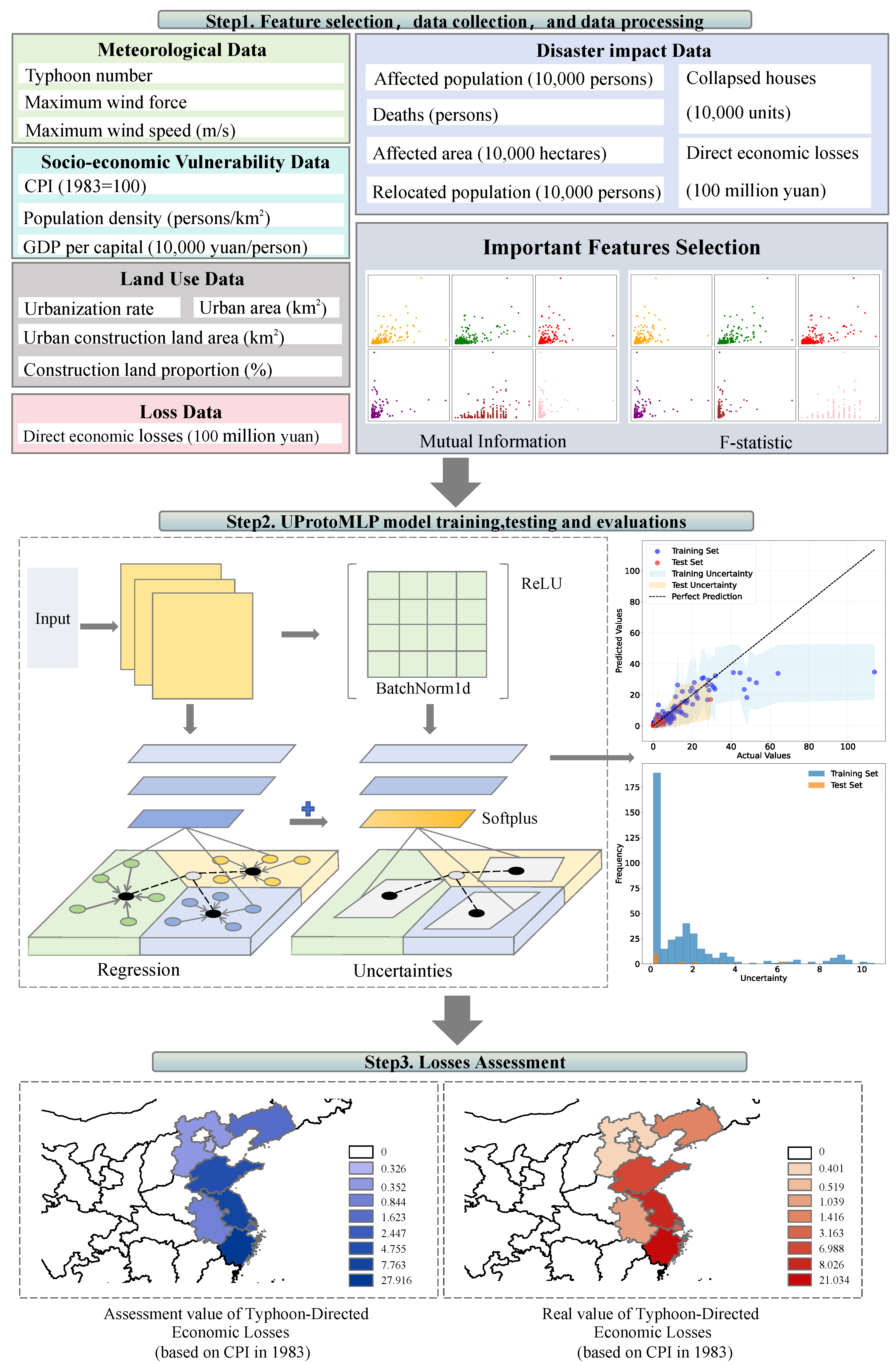
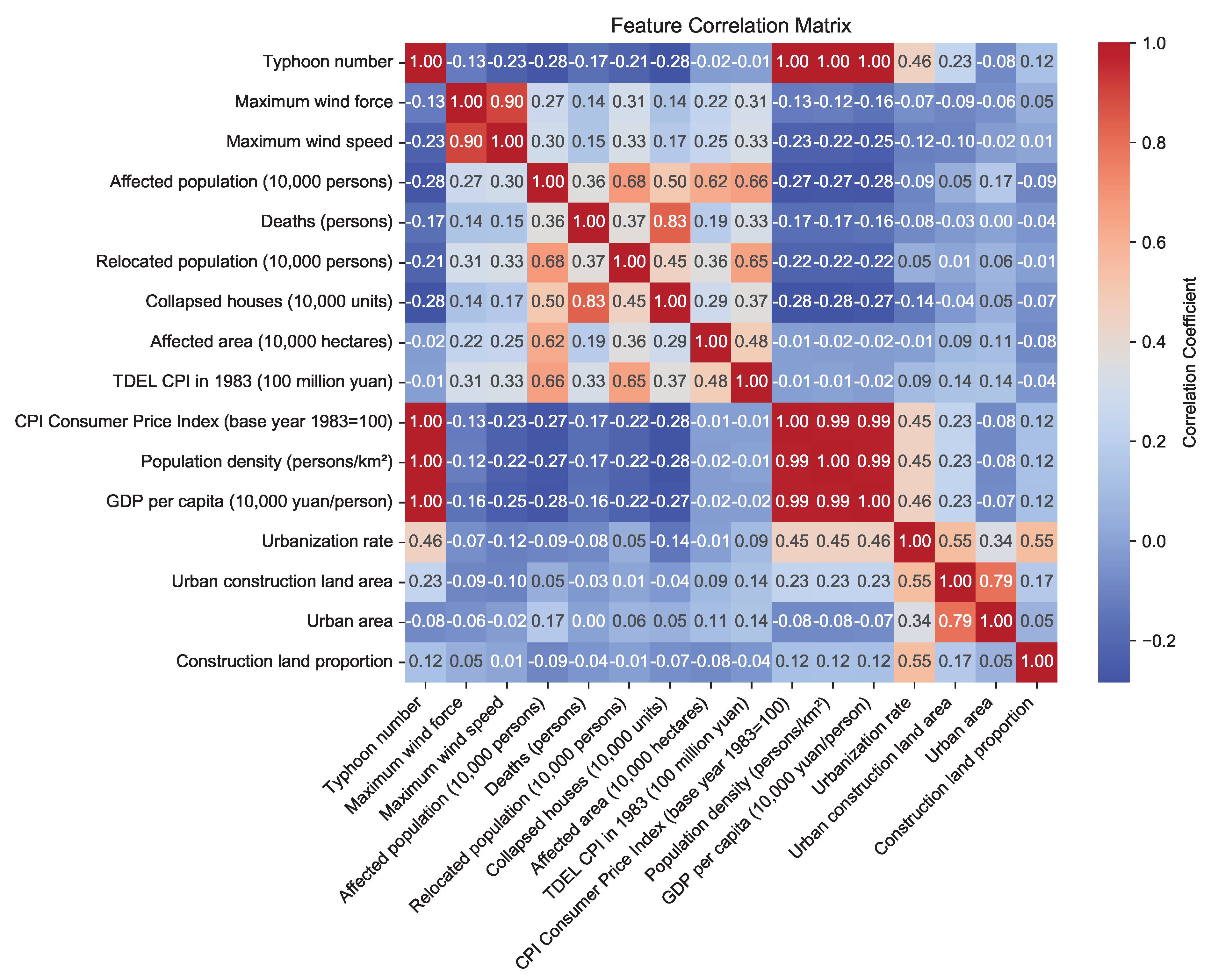


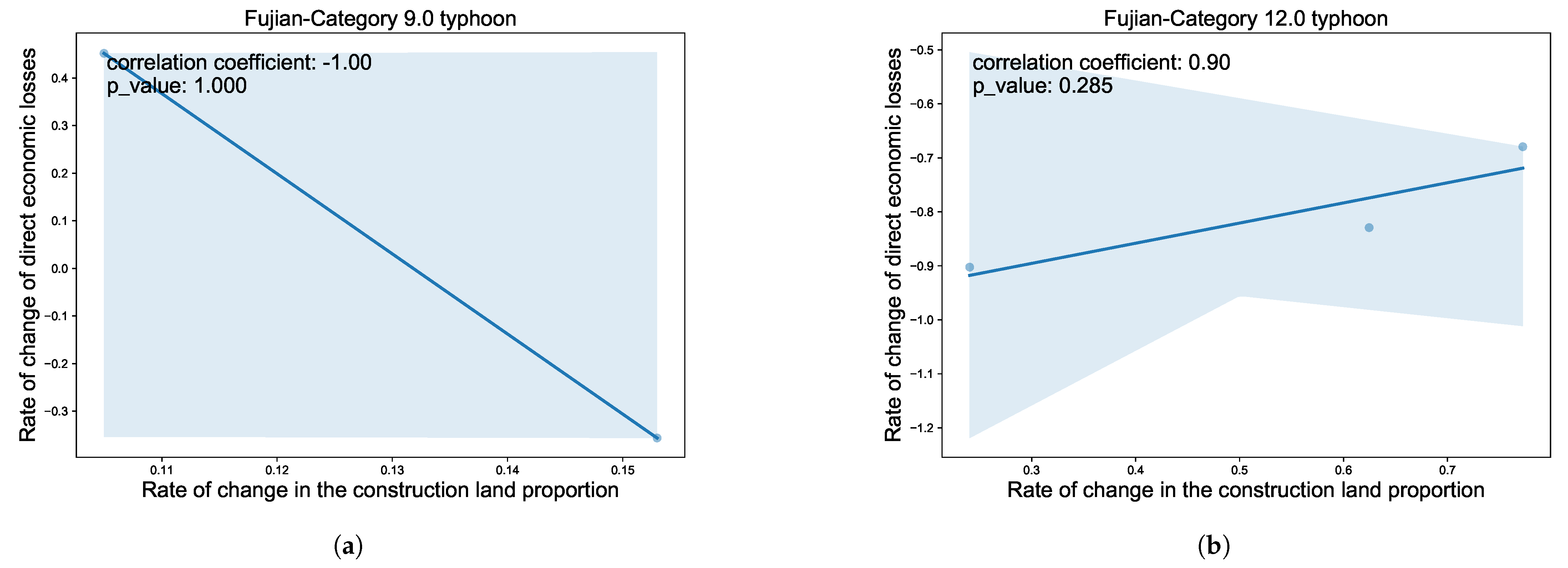
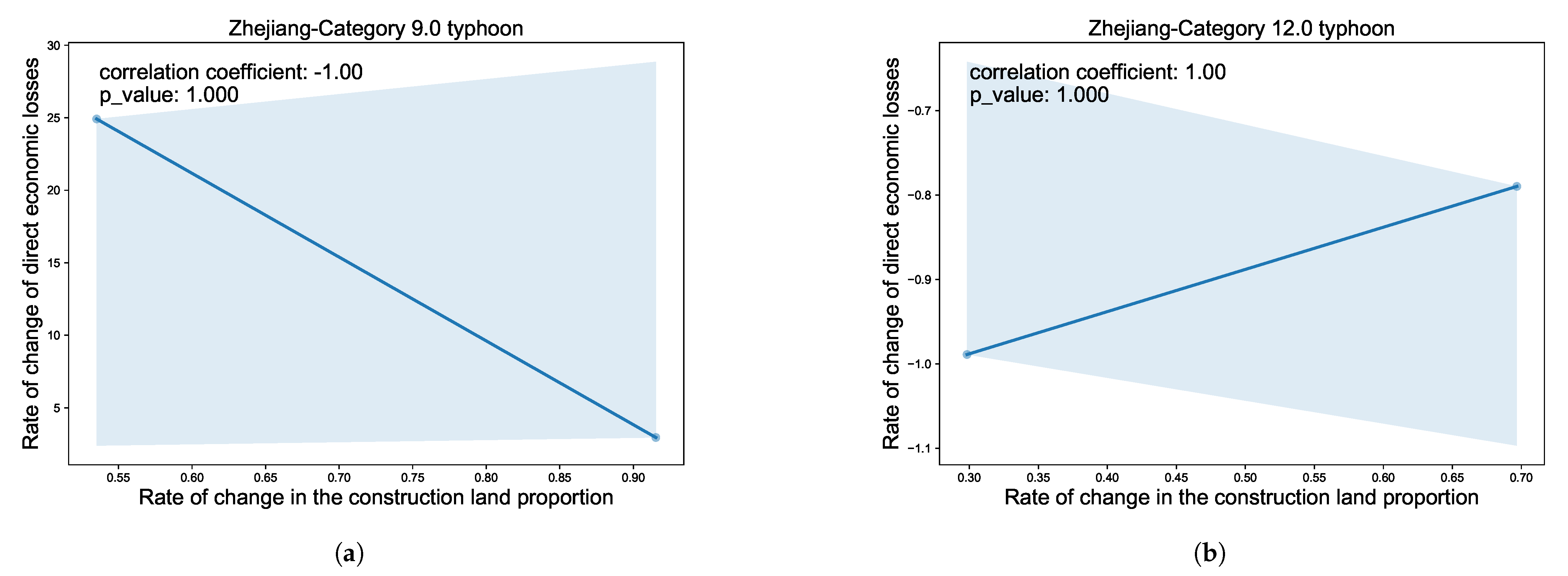
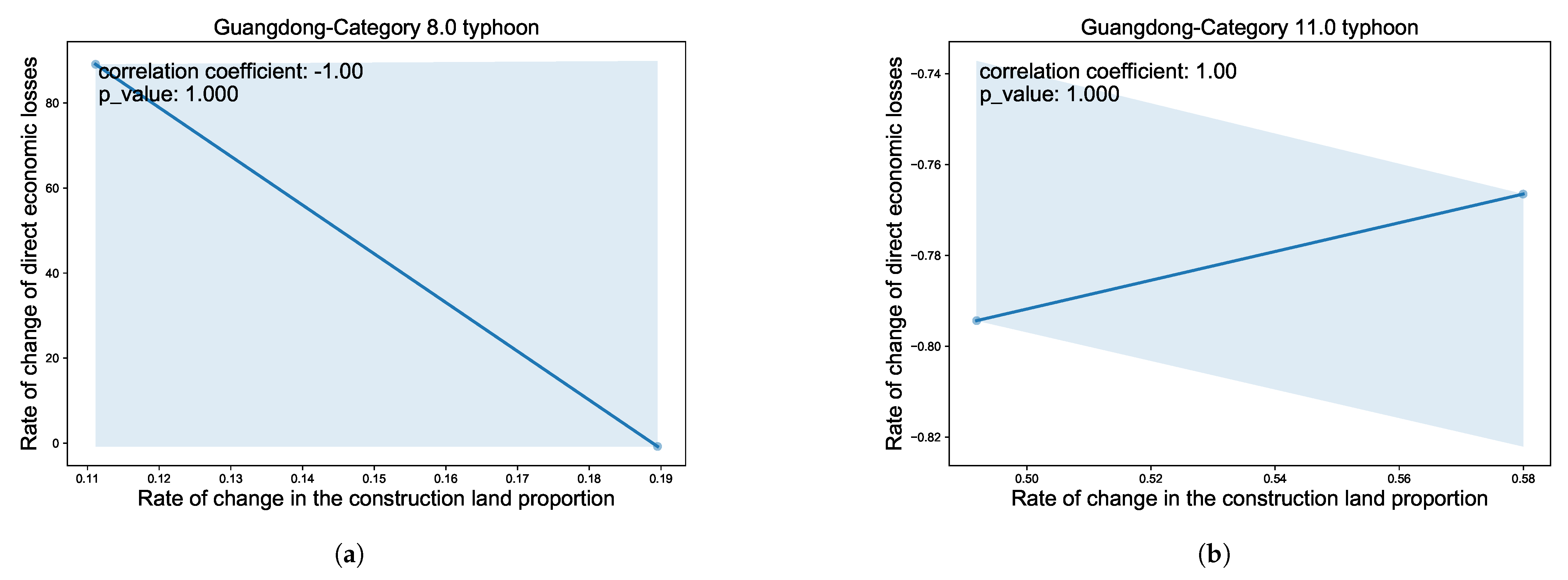

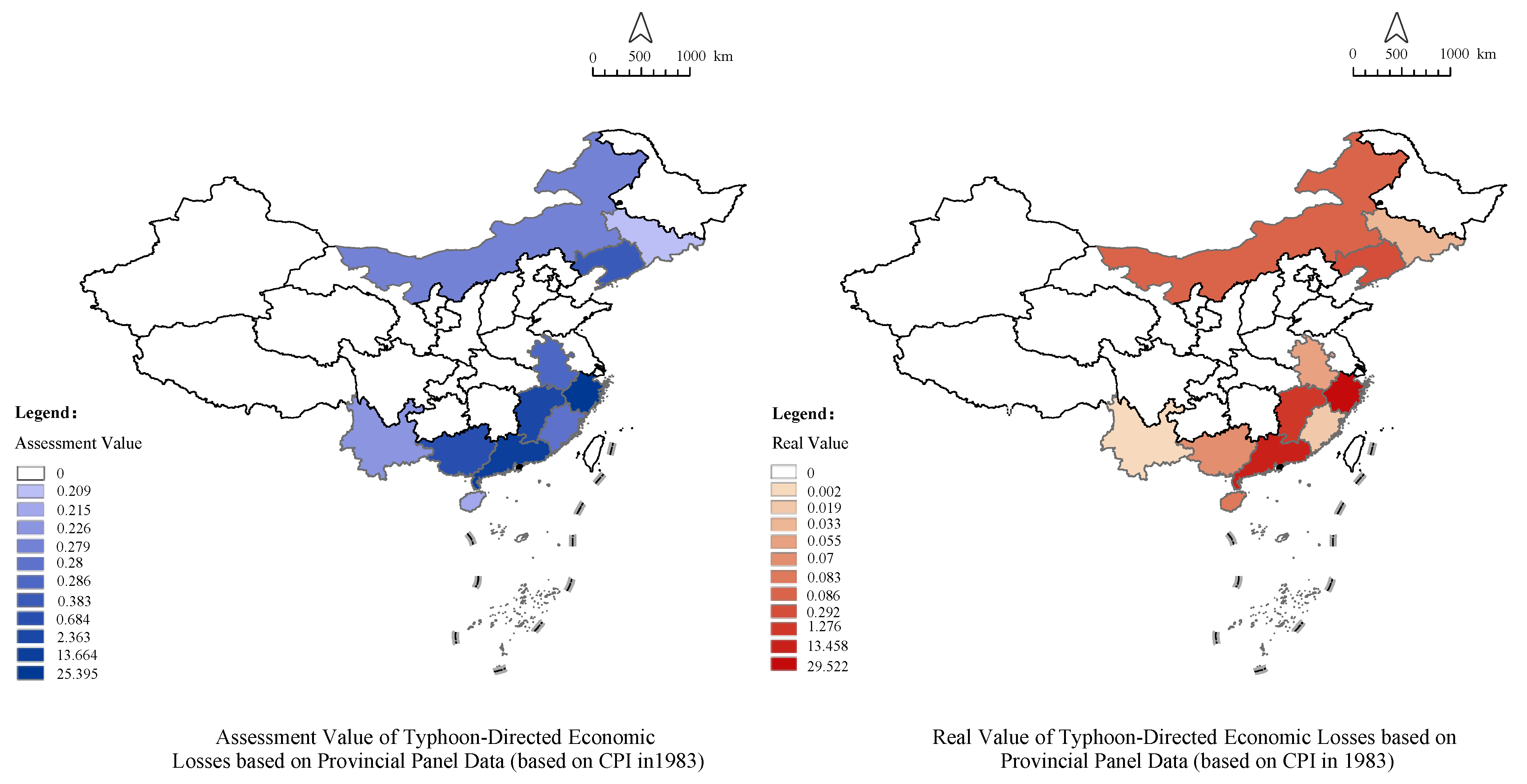
| Category | Variable | Description | Unit |
|---|---|---|---|
| Meteorological data | Typhoon number | Identifier number of the typhoon | - |
| Maximum wind force | Maximum wind force of the typhoon | - | |
| Maximum wind speed | Maximum wind speed of the typhoon | m/s | |
| Disaster impact data | Affected population | Number of affected people | 10,000 persons |
| Deaths | Number of deaths | persons | |
| Relocated population | Number of relocated people | 10,000 persons | |
| Collapsed houses | Number of collapsed houses | 10,000 units | |
| Affected area | Total affected area | 10,000 hectares | |
| Direct economic losses | Direct economic losses (CPI in 1983) | 100 million yuan | |
| Socio–economic vulnerability | CPI | Consumer price Index | (1983 = 100) |
| Population density | Population density | persons/km2 | |
| GDP per capita | GDP per capita | 10,000 yuan/person | |
| Land use data | Urbanization rate | Rate of urbanization | - |
| Urban construction land area | Area of urban construction land | km2 | |
| Urban area | Total urban area | km2 | |
| Construction land proportion | Proportion of construction land | % |
| Feature | VIF |
|---|---|
| Typhoon number | 523.9495 |
| Maximum wind force | 5.9174 |
| Maximum wind speed | 5.9636 |
| Affected population (10,000 persons) | 3.6049 |
| Deaths (persons) | 3.4113 |
| Relocated population (10,000 persons) | 2.5887 |
| Collapsed houses (10,000 units) | 4.0190 |
| Affected area (10,000 hectares) | 1.8646 |
| Typhoon Directed-economic losses (CPI in 1983) (100 million yuan) | 2.3933 |
| CPI Consumer Price Index (base year 1983 = 100) | 134.1705 |
| Population density (persons/km2) | 196.2581 |
| GDP per capita (10,000 yuan/person) | 170.6575 |
| Urbanization rate | 2.7689 |
| Urban construction land area | 4.1197 |
| Urban area | 3.6804 |
| Construction land proportion | 1.6218 |
| Actual Value | Assess Value | Confidence | Assess Interval | Affected Area |
|---|---|---|---|---|
| 0.085999 | 0.238724 | Above 99% | [−0.95, 1.42] | Neimenggu |
| 1.275510 | 2.872671 | Below 68% | [−7.71, 13.45] | Jiangxi |
| 0.054755 | 0.215413 | Above 99% | [−0.94, 1.37] | Anhui |
| 2.683178 | 1.130554 | Above 95% | [−1.15, 3.41] | Jilin |
| 0.001621 | 0.231469 | Above 99% | [−0.96, 1.43] | Yunnan |
| 3.230516 | 7.081117 | Below 68% | [−0.98, 15.15] | Zhejiang |
| 2.008717 | 3.412394 | Above 95% | [−0.13, 6.95] | Guangdong |
| 5.118515 | 3.766929 | Above 95% | [−0.10, 7.63] | Guangdong |
| 0.048630 | 0.217954 | Above 99% | [−0.95, 1.38] | Guangxi |
| 0.033267 | 0.243804 | Above 99% | [−1.00, 1.49] | Jilin |
| 2.135426 | 0.238536 | Above 99% | [−0.93, 1.41] | Hainan |
| 0.069573 | 0.437523 | Above 99% | [−1.27, 2.15] | Guangxi |
| 3.752132 | 1.117743 | Above 95% | [−1.36, 3.60] | Fujian |
| 0.083167 | 0.233785 | Above 99% | [−0.95, 1.41] | Hainan |
| 5.187513 | 4.994113 | Above 68% | [0.36, 9.63] | Guangdong |
| 29.522263 | 20.399832 | Below 68% | [7.19, 33.61] | Zhejiang |
| 0.291781 | 0.427232 | Above 99% | [−1.15, 2.00] | Liaoning |
| 0.019425 | 0.221588 | Above 99% | [−0.93, 1.37] | Fujian |
| 13.457792 | 13.363873 | Below 68% | [2.17, 24.55] | Guangdong |
| 0.041188 | 0.220396 | Above 99% | [−0.94, 1.38] | Guangdong |
| 2.985075 | 3.290345 | Above 95% | [−0.10, 6.68] | Guangxi |
| 0.099840 | 0.256749 | Above 99% | [−0.93, 1.45] | Zhejiang |
| Actual Value | Assess Value | Confidence | Assess Interval | Affected Area |
|---|---|---|---|---|
| 0.085999 | 0.279334 | Above 99% | [−0.41, 0.96] | Neimenggu |
| 1.275510 | 2.363345 | Above 68% | [−2.30, 7.03] | Jiangxi |
| 0.054755 | 0.286070 | Above 99% | [−0.61, 1.18] | Anhui |
| 2.683178 | 1.257801 | Above 95% | [−0.88, 3.39] | Jilin |
| 0.001621 | 0.225547 | Above 99% | [−0.34, 0.79] | Yunnan |
| 3.230516 | 7.365206 | Below 68% | [−1.45, 16.18] | Zhejiang |
| 2.008717 | 3.489299 | Above 95% | [−0.41, 7.39] | Guangdong |
| 5.118515 | 2.759948 | Above 95% | [−1.10, 6.62] | Guangdong |
| 0.048630 | 0.229537 | Above 99% | [−0.33, 0.79] | Guangxi |
| 0.033267 | 0.208982 | Above 99% | [−0.30, 0.72] | Jilin |
| 2.135426 | 1.514349 | Above 95% | [−1.15, 4.18] | Hainan |
| 0.069573 | 0.683942 | Above 99% | [−0.92, 2.29] | Guangxi |
| 3.752132 | 0.758362 | Above 99% | [−1.17, 2.69] | Fujian |
| 0.083167 | 0.214693 | Above 99% | [−0.31, 0.74] | Hainan |
| 5.187513 | 4.237987 | Above 68% | [−0.37, 8.84] | Guangdong |
| 29.522263 | 25.395420 | Below 68% | [10.55, 40.24] | Zhejiang |
| 0.291781 | 0.383230 | Above 99% | [−0.64, 1.40] | Liaoning |
| 0.019425 | 0.279708 | Above 99% | [−0.60, 1.16] | Fujian |
| 13.457792 | 13.664005 | Below 68% | [−0.16, 27.49] | Guangdong |
| 0.041188 | 0.217184 | Above 99% | [−0.30, 0.73] | Guangdong |
| 2.985075 | 3.599780 | Above 95% | [−0.23, 7.43] | Guangxi |
| 0.099840 | 0.209457 | Above 99% | [−0.31, 0.73] | Zhejiang |
| Model | MAE | MSE | R2 Score |
|---|---|---|---|
| XGBoost | 2.4501 | 19.0642 | 0.5441 |
| GBDT | 4.2499 | 156.6307 | 0.2442 |
| RF | 2.4678 | 22.2279 | 0.4684 |
| LightGBM | 3.1205 | 25.5531 | 0.3889 |
| AdaBoost | 2.1768 | 8.8089 | 0.7893 |
| MLP | 1.3194 | 5.0396 | 0.8795 |
| LSTM | 1.6484 | 5.8341 | 0.8126 |
| GRU | 1.3331 | 5.8768 | 0.8818 |
| MetaNet+ | 1.9628 | 15.0608 | 0.6398 |
| TADAM | 1.8886 | 11.7489 | 0.7191 |
| DN4++ | 1.4660 | 2.2565 | 0.8782 |
| UProtoMLP | 1.0176 | 3.4206 | 0.9182 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Zhao, Z.; Hu, J.; Liu, F.; Zheng, K. Impacts of Spatial Expansion of Urban and Rural Construction on Typhoon-Directed Economic Losses: Should Land Use Data Be Included in the Assessment? Land 2025, 14, 924. https://doi.org/10.3390/land14050924
Zhou S, Zhao Z, Hu J, Liu F, Zheng K. Impacts of Spatial Expansion of Urban and Rural Construction on Typhoon-Directed Economic Losses: Should Land Use Data Be Included in the Assessment? Land. 2025; 14(5):924. https://doi.org/10.3390/land14050924
Chicago/Turabian StyleZhou, Siyi, Zikai Zhao, Jiayue Hu, Fengbao Liu, and Kunyuan Zheng. 2025. "Impacts of Spatial Expansion of Urban and Rural Construction on Typhoon-Directed Economic Losses: Should Land Use Data Be Included in the Assessment?" Land 14, no. 5: 924. https://doi.org/10.3390/land14050924
APA StyleZhou, S., Zhao, Z., Hu, J., Liu, F., & Zheng, K. (2025). Impacts of Spatial Expansion of Urban and Rural Construction on Typhoon-Directed Economic Losses: Should Land Use Data Be Included in the Assessment? Land, 14(5), 924. https://doi.org/10.3390/land14050924







