Measuring Performances of a White-Box Approach in the IoT Context

Abstract

The internet of things (IoT) refers to all the smart objects that are connected to other objects, devices or servers and that are able to collect and share data, in order to “learn” and improve their functionalities. Smart objects suffer from lack of memory and computational power, since they are usually lightweight. Moreover, their security is weakened by the fact that smart objects can be placed in unprotected environments, where adversaries are able to play with the symmetric-key algorithm used and the device on which the cryptographic operations are executed. In this paper, we focus on a family of white-box symmetric ciphers substitution–permutation network (SPN)box, extending and improving our previous paper on the topic presented at WIDECOM2019. We highlight the importance of white-box cryptography in the IoT context, but also the need to have a fast black-box implementation (server-side) of the cipher. We show that, modifying an internal layer of SPNbox, we are able to increase the key length and to improve the performance of the implementation. We measure these improvements (a) on 32/64-bit architectures and (b) in the IoT context by encrypting/decrypting 10,000 payloads of lightweight messaging protocol Message Queuing Telemetry Transport (MQTT).

1. Introduction

The name internet of things (IoT), coined by the MIT researcher Kevin Ashton [1], usually refers to smart objects, connected through the internet to other sensors, devices and servers with which collect and/or share data for improving their functionalities. IoT can also be combined with other technologies, for example with cloud computing [2]. It is possible to create a sustainable smart home aiming to reduce resources’ consumption or develop specific applications in the medical field [3] such as wearable devices which monitor our physical conditions, specific devices used to check patients with chronic illnesses, and so on. Data collected by IoT devices need to be (a) processed to form informations by applying, for example, data mining techniques [4]; (b) evaluated in order to make decision by adopting agent based models [5,6], bayesian decision models [7], fuzzy logic [8] and so on; (c) protected from attacks, failures and leaks during communication [2].

Several issues have to be faced in securing IoT applications. An important example is given by the intrinsic constraints of the devices [9], that usually have a small amount of memory and cannot perform heavy computations. It is very likely to have such devices in non-protected environment, where an adversary can access them and perform attacks. In particular, she/he can perform an analysis of the controlled binary [10] or perform differential fault analysis [11,12]. Moreover, since these devices are connected, compromising one of them can open the way to botnet attacks [2,3]. We can observe that we are exactly in a white-box framework, and white-box cryptography [13] has been first developed to cope with the scenario in which an attacker can physically interact both with the implementation of the used cryptographic algorithm and with the device on which the encryption/decryption operations are executed. The usually studied scenario, namely black-box, in which the execution cannot be observed nor modified by the attacker, is not always suitable for IoT applications [14]. The reader can think about what happens in the context of digital rights management where discovering the key means to have the possibility to spread digital contents to people that have not payed such contents.

The effort of researchers towards white-box cryptographic schemes materialized with [13,15] where white-box versions of AES and DES have been implemented. Nevertheless, it is important to remark that these implementations have been attacked via algebraic attacks [16] (improved by [17]), [18,19,20]. Moreover, also Jacob et al. in [21] can easily break Chow’s implementations.

The need to have white-box algorithms for practical applications leads to develop some specific algorithms. Examples of block ciphers developed to be employed in the framework of white-box cryptography are ASASA [22] and SPACE [23]. However, these ciphers are not free of drawbacks or weaknesses. In particular, decomposition attacks can affect ASASA’s security while SPACE is heavy from a computational point of view [24]. An important step forward for white-box cryptography, was the development of substitution–permutation network (SPN)box [24], another block cipher that relies on internal block ciphers with the aim to reduce the computation time. In [9], the problem of intrinsic constraints on computational power and memory of IoT devices in unprotected environment is addressed. The authors refer to smart objects with limited computational power and memory that may contain sensitive data and can be easily lost or stolen. Differently from AES/DES white-box implementations, the authors do not decline a well-known cipher into the new framework, but they develop a new one, relying on a modification of Lai-Massey structure. The crucial point is that only the encryption is thought to be done on the IoT constrained device, while the decryption phase is supposed to be done on a computer or server and in a black box scenario. In [25] the authors refer to embedded distributed devices which collect and securely send information to centralized servers. Subsequently, these servers decrypt and process all the information. As previously mentioned, the collected information may be sensitive and it is possible for an attacker to get control of the whole device. The scheme proposed in [25] is lightweight and suitable for constrained devices. In particular, such a new design has the following peculiarities:

• the employed operations are very simple; they essentially consist of lookup tables and bit operations;
• the lookup tables and the structure containing sensitive data are small in memory;
• the provided security is medium-level (∼$2^{63}$) and protection is ensured for reasonable amount of time;
• it is possible to update the key at small costs.

The scheme is based on a Fesitel structure, but it adds two bijections, as a defence against attacks. Moreover, to cope with structural cryptanalysis [25,26] different size components are used.

This paper improves of a previous work entiteled “White-box Cryptography: A Time-security Trade-off for the SPNbox Family” [27], presented by F.Cioschi, N.Fornari and A.Visconti at the 2nd International Conference on International Conference on Wireless, Intelligent and Distributed Environment for Communication (WIDECOM 2019). In this paper, we (a) introduce the white-box approach in the IoT context, explaining the importance of protecting data in an environment where attackers have full control over the whole system; (b) explain the importance of having a fast black-box implementation of a white-box cipher; (c) summarize our previous idea [27] explaining how to modify the internal block ciphers of the SPNbox family in order to increase the size of the key space; (d) measure the performance of a black-box implementation (server-side) on 32- and 64-bit architectures and by encrypting/decrypting 10,000 payloads of a lightweight messaging protocol—i.e., MQTT—which contains the data sent over the internet.

The remainder of the paper is organized as following. In Section 2, block ciphers are introduced. In Section 3, we present several white-box implementations and related attacks published in literature. In Section 4 and Section 5, we summarize two block ciphers’ families, namely, SPACE and SPNbox, which are white-box friendly by design. In Section 6, we explain the importance of increasing the number of bits of the key used in each round. In Section 7, the testing activities are presented. Finally, Section 8 is devoted to discussion and conclusions.

2. Block Ciphers

There exist two main families of block ciphers: SPN and Feistel network. The main difference between them is that Feistel networks play only with one half of the cipher state in each round.

2.1. Substitution-Permutation Networks

A SPN is a design for block ciphers proposed by Shannon in [28], where he suggested to use multiple mixing layers interleaving substitutions and permutations. Although weak on its own, applying substitutions and then permutations presents good “mixing” properties. Substitutions contribute to local confusion and permutations spread such a local confusion to the more distant subblocks, thus providing diffusion [28]. If a single input bit is flipped, it affects the m output bits of a specific S-box which, subsequently, are sent to different S-boxes by a permutation. Considering the output of such a network, about fifty percent of the bits are affected by this change. Therefore an outcome of a single bit change at the input is difficult to predict, especially if the bit of the secret key are XORed into the block between the encryption layers. In order to get better diffusion properties, several block ciphers adopt linear (as in the case of AES) or affine mappings instead of permutations.

Definition 1.

Let $\varphi :{\left({\mathbb{F}}_2\right)}^r\times {\left({\mathbb{F}}_2\right)}^l\to {\left({\mathbb{F}}_2\right)}^r,$ with $r=bt$ be a block cipher with N rounds. Let $k\in {\left({\mathbb{F}}_2\right)}^l$ be the cipher key and $(k^{\left(0\right)},\cdots ,k^{\left(N\right)})$ be the $N+1$ round keys generated by k through the key schedule.

Then ϕ is an SPN block cipher if

$${\varphi }_k\left(x\right)={\tau }_N\circ {\tau }_{N-1}\circ \dots \circ {\tau }_0\left(x\right)x\in {\left({\mathbb{F}}_2\right)}^r$$

where ${\tau }_i={\sigma }_{k^{\left(i\right)}}\circ {\lambda }^{\left(i\right)}\circ {\gamma }^{\left(i\right)}$ and

• ${\gamma }^{\left(i\right)}:{\left({\mathbb{F}}_{2^t}\right)}^b\to {\left({\mathbb{F}}_{2^t}\right)}^b$ is a non linear substitution
• ${\lambda }^{\left(i\right)}\in AGL\left({\left({\mathbb{F}}_2\right)}^r\right)$ where $AGL\left({\left({\mathbb{F}}_2\right)}^r\right)$ is the subgroup of the affine transformations of ${\left({\mathbb{F}}_2\right)}^r$
• ${\sigma }_{k^{\left(i\right)}}$ is the addition with the round key

$$\begin{array}{llll}{\sigma }_{k^{\left(i\right)}}:& {\left({\mathbb{F}}_2\right)}^r& \to & {\left({\mathbb{F}}_2\right)}^r\hfill \\ & x& \mapsto & x\oplus k^{\left(i\right)}\hfill \end{array}$$

where by ⊕ we denote the bitwise addition (XOR).

2.2. Feistel Networks

A Feistel network is a block cipher introduced by H. Feistel and D. Coppersmith in 1973 [29] which has the advantage of having the encryption and decryption functions almost identical, making the implementation easier and cheaper compared to translation based ciphers.

Let us define the following functions before describing the encryption process.

Definition 2.

Let ${\pi }_t$ be a projection, with $t\in \{1,\dots ,2n\}$, defined as:

$$\begin{array}{cccc}{\pi }_t:& {\mathbb{F}}^{2n}& \to & {\mathbb{F}}^t\\ & (x_1,\dots ,x_{2n})& \mapsto & (x_1,\dots ,x_t)\end{array}$$

Considering $x\in {\mathbb{F}}^{2n}$ as a vector of bits, we can use projection ${\pi }_t$ to choose the t most significant bits of x.

Definition 3.

Let ${\varrho }_t$ be a projection, with $t\in \{1,\dots ,2n\}$, defined as:

$$\begin{array}{cccc}{\varrho }_t:& {\mathbb{F}}^{2n}& \to & {\mathbb{F}}^t\\ & (x_1,\dots ,x_{2n})& \mapsto & (x_{2n-t+1},\dots ,x_{2n})\end{array}$$

In the same way, using projection ${\varrho }_t$ we can choose the t least significant bits of x.

Given $m\in {\mathbb{F}}^{2n}$ (a message) and $k\in {\mathbb{F}}^l$ (a secret key), for some positive integer l, the encryption process works as follows:

• $N+1$ round keys $k_0,..k_N$ are generated from k by means of the key schedule
• message m is split into a left block and right block, initialized as

  $$L_0={\pi }_n\left(m\right)R_0={\varrho }_n\left(m\right)$$
• for $i\in \{1,\dots ,N+1\}$ the round function is applied in the following way:

  $$L_i=R_{i-1}{R}_i=L_{i-1}\oplus F(R_{i-1},k_{i-1})$$

  (1)
• final ciphertext c is $(R_{N+1},L_{N+1})$.

Encryption and decryption only differ in the reverse order of the round keys, as a matter of fact the decryption of ciphertext $(R_{N+1},L_{N+1})$ is accomplished computing for $i\in \{N,N-1,\dots ,0\}$

$$R_i=L_{i+1}{L}_i=R_{i+1}\oplus F(L_{i+1},k_i)$$

(2)

An advantage of Feistel networks is that Feistel function F is non-necessarily invertible.This can be clearly seen by analyzing how encryption and decryption work (see Equations (1) and (2)).

3. The White-Box Approach

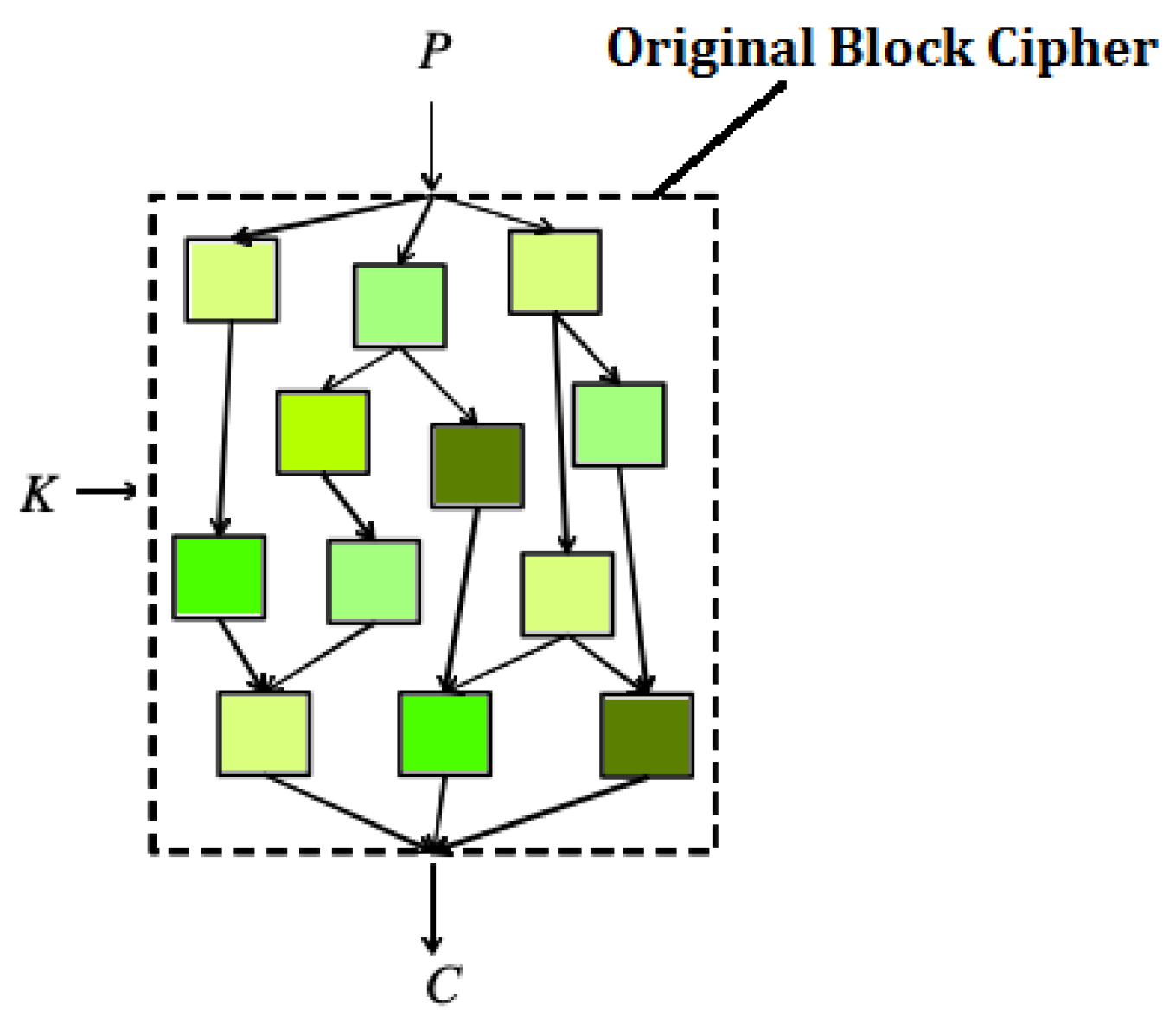
The White-Box approach aims to avoid key recovery attacks by embedding the cryptographic key into a robust representation of the cipher. Consider a block cipher $\varphi$. We compute a map $\psi :{\mathbb{F}}^n\to {\mathbb{F}}^n$ such that, given a key $\overline{k}\in {\mathbb{F}}^l$, it holds $\varphi (x,\overline{k})=\psi \left(x\right)\forall x\in {\mathbb{F}}^n$. If an attacker knows even both $\varphi$ and $\psi$, it should be very hard for him to find out the key.

Example 1.

Let ϕ and ψ be defined as follows:

$$\begin{array}{cc}\varphi \left(x\right):=k+xmod4\hfill & x\in \{0,\dots ,3\}\hfill \\ \psi \left(x\right):=S\left[x\right]\hfill & S=[3,0,1,2]\hfill \end{array}$$

If $k=3$, we can consider ψ as a white-box implementation of ϕ, by representing ψ as a lookup table.

The first white-box AES implementation has been proposed by Chow et al. in [13]. The authors suggest that key extraction can be avoided by a careful use of lookup tables. In particular, given a secret key and a block cipher, it is possible to create a lookup table which maps the plaintext in a corresponding ciphertext. In some cases, this lookup table may be huge and unusable due to its dimension. Therefore, a block cipher $\varphi$ can be represented as a network of smaller lookup tables (see Figure 1) that have to be read in a particular order [13]. Unfortunately, in the white-box framework an adversary has full access to these tables, exposing the cipher to possible attacks. Since there is no reason to make an attacker’s life easier, tables can be protected by means of internal encodings [13]. This means that a map is composed after table i and its inverse before table $(i+1)$, leaving the ciphertext unchanged. However, internal encoding does not protect against code-lifting attacks. Indeed, an attacker may recover the tables of the cipher and understand their concatenation order. Doing so, she/he is able to decrypt messages even though he had not recovered the secret key. Therefore, another protection is required: external encoding. Internal and external encodings are also discussed in [30], while a different approach, based on polynomial algebra techniques [31], gave rise to a perturbated white-box implementation of AES [32], broken by [33] in 2010.

Chow’s work is a milestone for white-box cryptography and its framework has also been used by some subsequent works such as [34,35]. However, researchers found attacks also for these new approaches:

• White-Box AES Implementation: Chow [13]; Attack: [16]; Work Factor: $2^{30}$;
• White-Box AES Implementation: Karroumi [34]; Attack: [18,20]; Work Factor: $2^{22}$;
• White-Box AES Implementation: Xiao Lai [35]; Attack: [18]; Work Factor: $2^{32}$;
• White-Box AES Implementation: Xiao Lai [35] generic linear version; Attack: [18]; Work Factor: $2^{38}$;
• White-Box AES Implementation: Xiao Lai [35] affine/non-affine version; Attack: [19]; Work Factor: at least $2^{49}$.

The attacks listed above may require to know the internal data representation and sometimes this means to produce a significant reverse engineering effort. An improved AES implementation is given in [36]. This implementation is immune to attacks described in [16,18] but it is not to the one presented in [37].

The first paper aiming to break all white-box implementations belonging to the framework introduced in [13] is [19], but it has the weak point to require some additional hypotheses. Differently, Derbez et al. [38] breaks all the papers in Chow’s framework by solving the affine equivalence problem (see [39,40]). Chow’s framework has also been used by [41] and subsequently attacked by [42].

A significant advance from the attacker’s point of view became feasible by shifting the focus from the attacks previously described to side channel attacks [43]. In particular, new approaches to verify the security of a white-box implementation have been proposed in [44] where Bos et al. present differential fault analysis (DFA) and differential computational analysis (DCA) attacks (further information on fault-injection and differential power analysis attacks can be found in [45,46] respectively). In addition, in [47,48] the authors explained more formally why DCA is effective against linear and nibble encoding, Rivain and Wang [43] provide an extensive analysis on the effectiveness of DCA, finally Biryukov and Udovenko [49] give a general protection method for white-box implementations against DCA.

Obfuscation techniques or the randomization of the location of the lookup tables can be used to enhance security of white-box algorithms [50], while [51] examines how these techniques are successful against both DCA and differential power attacks (DPA). The paper [52] exploits noncommutative groups to obfuscate operation that should be made on commutative ones and it is employed in the IoT framework. Finally, an evaluation on software protections to white-box implementations is provided by [51].

Some improvements to DCA have been developed by [43,53]. The first one extends DCA to successfully address implementations using masking and shuffling techniques [53]. The second one provide a DCA-like collision attack with a good complexity [43].

Some paper such as [54,55,56] address the problem of incompressibility or code hardness. The idea is that an attacker in the white-box framework should not be able to rewrite the code of some implementation in order to decrease the code-hardness. In [54] two incompressible white-box schemes called “WhiteKey” and “WhiteBlock” are introduced and one instance for each scheme is provided (called PuppyCipher and CoureurDesBois respectively), [55] describes the concept of code-hardness, time-hardness and memory-hardness, while [56] provides a new incompressible white-box implementation based on the assumption of one-way permutations.

We conclude our extensive analisys of implementations and attacks, citing a white-box signature scheme [57] and the methods [58] used to attack the most resistant implementation submitted to the white-box competition called “CHES 2017 CTF Challenge”.

In the sequel, we will analyze in detail two family of white-box cipher called SPACE (Section 4) and SPNbox (Section 5).

4. SPACE: A Block Cipher

SPACE is a block cipher developed by Bogdanov and Isobe in [23], that is based on a Feistel network. This cipher is designed so that security against key extraction in the white-box context reduces to the well studied problem of key recovery for block ciphers in the standard black-box setting.

SPACE is a generalized Feistel network [29]. Given a message $m\in {\mathbb{F}}^n$ and a secret key $k\in \mathcal{K}$, it encrypts m to a ciphertext $c\in {\mathbb{F}}^n$. In describing SPACE, three quantities are often employed: $n,n_a,n_b\in \mathbb{N}$. In particular, in [23] $n=128$, $n_a\in \{8,16,24,32\}$ and $n_b=n-n_a$.

We summarize here the encryption procedure:

• The state $X^r$ at round r can be seen as given by $l=n/n_a$ vectors $x_i^r\in {\mathbb{F}}^{n_a}$ so

  $$X^r=\{x_0^r,x_1^r,\dots ,x_{l-1}^r\}.$$
• $X^0=m$, so it is initialized with the plaintext.
• For $r\in \{1,\dots ,R+1\}$ the state is updated this way:

  $$X^{r+1}=\left(F_{n_a}^r\left(x_0^r\right)\oplus (x_1^r\Vert x_2^r\Vert \dots \Vert x_{l-1}^r)\right)\Vert x_0^r$$

  where $F_{n_a}^r:{\mathbb{F}}^{n_a}\to {\mathbb{F}}^{n_b}$ is the Feistel function and $\Vert$ is the concatenation.
• $X^{R+1}=c$ so we have found the ciphertext.

At each encryption round, the Feistel function takes $x_0^r$ as input. Then $F_{n_a}^r\left(x_0^r\right)$ is added to the rest of the state $(x_1^r\Vert \dots \Vert x_{l-1}^r)$. The first $n_b$ bits of the new state are given by the result of this operation. The last $n_a$ are filled with $x_0^r$.

Now, consider ${\pi }_t$ be the projection of Definition 2 and the Feistel function $F_{n_a}^r$ used by SPACE, specified in Definition 4.

Definition 4.

Let ${\varphi }_k$ be a block cipher and r the round number represented in binary with $n_b$ digits (so we see it as an element of ${\mathbb{F}}^{n_b}$). The Feistel function $F_{n_a}^r$is defined as

$$\begin{array}{llll}{F}_{n_a}^r\left(x\right):& {\mathbb{F}}^{n_a}& \to & {\mathbb{F}}^{n_b}\hfill \\ & x& \mapsto & ({\pi }_{n_b}({\varphi }_k(\stackrel{n_b}{\overbrace{0,\dots ,0}}\Vert x\left)\right))\oplus r.\hfill \end{array}$$

We give a specific notation for the round independent part of $F_{n_a}$.

Definition 5.

The round independent part of the Feistel function $F_{n_a}$ is

$$\begin{array}{llll}{F}_{n_a}^{{}^{\prime }}:& {\mathbb{F}}^{n_a}& \to & {\mathbb{F}}^{n_b}\hfill \\ & x& \mapsto & {\pi }_{n_b}({\varphi }_k(\stackrel{n_b}{\overbrace{0,\dots ,0}}\Vert x\left)\right)\hfill \end{array}$$

Notice that, differently from traditional Feistel networks, SPACE does not use round keys. There is one secret key k used by ${\varphi }_k$. This secret key cannot be hardcoded, hence ${\mathbb{F}}_{n_a}^{{}^{\prime }}$ is implemented as a look-up table. The reader might ask himself the reason for designing SPACE over another block cipher ${\varphi }_k$ when ${\varphi }_k$ could be directly implemented as a look-up table. It turns out that this second possibility cannot be developed. If we were to implement ${\varphi }_k$ as a look-up table we would need $2^n·n$ bits of space:

$$\begin{array}{ccc}\stackrel{n}{\overbrace{(0,\dots 0,0)}}& \mapsto & \stackrel{n}{\overbrace{{\varphi }_k(0,\dots 0,0)}}\\ (0,\dots 0,1)& \mapsto & {\varphi }_k(0,\dots 0,1)\\ & ⋮& \\ (1,\dots 1,1)& \mapsto & {\varphi }_k(1,\dots 1,1)\end{array}$$

For $n=128$ the construction of such a look-up table is practically impossible. Therefore Bogdanov and Isobe propose to truncate the output of ${\varphi }_k$, computed over a smaller domain (see Figure 2):

Since the first $n_b$ zeros are used as padding in order to form an n-bit input to provide to ${\varphi }_k$, it is completely useless to store them, hence the look-up table implementation needs $2^{n_a}·n_b$ bits. Thus, the size of the tables for different values of $n_a\in \{8,16,24,32\}$—SPACE($n_a$, R), where R is the suggested number of rounds—is the following:

• SPACE-(8,300); Table: 3.84 KB
• SPACE-(16,128); Table: 918 KB
• SPACE-(24,128); Table: 218 MB
• SPACE-(32,128); Table: 51.5 GB

Notice that (1) AES white-box implementations of Chow et al. [13] and Xiao Lai [35] has a table of 752 KB and 20.5 MB respectively; (2) not all $n_a$ values are suitable, indeed, for $n_a=32$ and $n_a=24$ the size of the table is not good enough to be used in practice. On the contrary, for $n_a=16$ the table has the same size of that described in [13].

5. The SPNbox Family

The SPACE family of space-hard block ciphers [23] benefits of the Feistel structure from a security point of view and prevents the use of parallel execution (see Section 4). However, as suggested in [24], using an SPN-type design it is possible to satisfy the requirement of parallelism maintaining a suitably high level of space hardness. Thus, Bogdanov et al. described the SPNbox family of space-hard block ciphers [24]. Let us briefly explain their idea.

SPNbox-$n_{in}$ is a substitution-permutation network (SPN) with a block length of n bits, a k-bit secret key, and based on $n_{in}$-bit substitution boxes.

State:

The state of SPNbox-$n_{in}$ is representable as a vector of $t=n/n_{in}$ elements of $n_{in}$ bits each:

$$X=\{X_0,\dots ,X_{t-1}\}$$

Key Schedule:

The k-bit master key is expanded, $k_0,\dots ,k_{R_{n_{in}}}$ round keys of $n_{in}$ bits, by means of a Key Derivation Function (KDF)—e.g., PBKDF2 [59,60,61,62], ARGON2 [63], Scrypt [64], and so on:

$$(k_0,\dots ,k_{R_{n_{in}}})=KDF(k,n_{in}·(R_{n_{in}}+1))$$

Round Transformation:

We encrypt a plaintext $X^0$ and we get a ciphertext $X^R$, by using the following R transformations—e.g., $R=10$:

$$X^R=\left({◯}_{r=1}^R({\sigma }^r\circ \theta \circ \gamma )\right)\left(X^0\right)$$

The nonlinear layer $\gamma$ is a substitution layer where t identical bijective $n_{in}$-bit S-boxes depending on the key are applied to the state:

$$\begin{array}{c}\gamma :\mathbb{F}{\left(2^{n_{in}}\right)}^t\to \mathbb{F}{\left(2^{n_{in}}\right)}^t\hfill \\ (X_0,\dots ,X_{t-1})\mapsto (S_{n_{in}}\left(X_0\right),\dots ,S_{n_{in}}\left(X_{t-1}\right))\hfill \end{array}$$

(3)

These identical S-boxes are constituted by an internal small block cipher of block length $n_{in}$ bit.

The linear layer $\theta$, a diffusion layer, applies a $t\times t$ MDS matrix to the state:

$$\theta :\mathbb{F}{\left(2^{n_{in}}\right)}^t\to \mathbb{F}{\left(2^{n_{in}}\right)}^t$$

$$(X_0,\dots ,X_{t-1})\mapsto (X_0,\dots ,X_{t-1})·M_{n_{in}}$$

The affine layer ${\sigma }^r$ takes the state and adds round-dependent constants to it:

$${\sigma }^r:\mathbb{F}{\left(2^{n_{in}}\right)}^t\to \mathbb{F}{\left(2^{n_{in}}\right)}^t$$

$$(X_0,\dots ,X_{t-1})\mapsto (X_0\oplus C_0^r,\dots ,X_{t-1}\oplus C_{t-1}^r),$$

with $C_i^r=(r-1)·t+i+1$ for $0\le i\le t-1$.

The Underlying Small Block Ciphers:

The identical $n_{in}$-bit S-boxes in the $\gamma$ layer (which depend on the key) are block ciphers. They are based on the round transformation of AES and they are formed by $R_{n_{in}}$ rounds operating on a state $x=\{x_0,\dots ,x_{l-1}\}$ of l bytes, where $l=n_{in}/8$:

$$S_{n_{in}}:\mathbb{F}{\left(2^8\right)}^l\to \mathbb{F}{\left(2^8\right)}^l$$

$$x\mapsto \left({◯}_{i=1}^{R_{n_{in}}}(A{K}^i\circ M{C}_{n_{in}}\circ SB)\right)\left(A{K}^0\left(x\right)\right)$$

where SB, MC and AK indicate the AES transformations SubBytes, MixColumns and AddRoundKey, respectively. Notice that (a) the number of rounds $R_{n_{in}}$ that [24] suggests are $R_{32}$ = 16, $R_{24}$ = 20, $R_{16}$ = 32 and $R_8$ = 64; (b) different matrices are employed in the $M{C}_{n_{in}}$ round transformation. More precisely, for $n_{in}$ = 32 we use the $MC$ matrix of AES, while in the other cases a sub-matrix of $MC$ is used. If $n_{in}$ = 8, $M{C}_{n_{in}}$ is the identity map’s matrix. Note that, as for the Feistel function in SPACE, in the white-box setting the small block ciphers $S_{n_{in}}$ are implemented as lookup tables.

6. Issues and Possible Solutions

Although the white-box implementation of the cipher is very important, it may have some limitations due to the key embedded into the device. If several devices have to communicate with a server and such devices do not support Transport Layer Security (TLS) protocol due to insufficient resources, the server needs to manage a number of keys (pre-shared or not) in order to decrypt the messages. In a white-box context this means having a number of different implementations that run on our server and this is not a good idea. Therefore, the server will be provided with a fast black-box implementation of the cipher.

Figure 3 helps us to visualize this idea, where a white-box implementation runs on a number of devices and a fast black-box implementation runs on our server.

In order to design a fast black-box implementation of a white-box cipher, we modify the inner round described in Section 5, increasing the number of bits of the key used in each round. In particular, we replace the AES’ ShiftRow transformation, omitted by [24], with a key-dependent circular bit shift transformation (see Figure 4 and Figure 5).

If we are shifting eight bits of the state, i.e., $n_{in}$ = 8, three bits are required to execute the circular shift. Thus, we use 11 bits of the key in each round i: eight of them for the AK${}^i$ transformation and three for the BitShift transformation. If the state doubled, tripled, or quadrupled, i.e., $n_{in}$ = 16, 24, 32, the bits of the key used are $11\times 2=22$, $11\times 3=33$ and $11\times 4=44$ respectively.

Notice that the implementation of [24] employs the AES-NI instructions, while the idea described in this paper does not. In the encryption phase ($n_{in}$ = 32, 24, 16), the matrices involved in the computation of the MixColumns transformation ($A_{24}$, and $A_{16}$ for short) are sub-matrices of that used in AES ($A_{32}$). On the contrary, in the decryption phase, we need to invert $A_{24}$ and $A_{16}$. Since their inverse matrices are not sub-matrices of $A_{32}^{-1}$ and the decryption instruction of AES-NI is based only on $A_{32}^{-1}$, for $n_{in}$ = 24, 16 we cannot use the AES-NI instructions. Anyway, in IoT context, the impossibility of using AES-NI instructions is not a problem in itself because not all IoT devices support this instruction set.

7. Testing Activities

The testing activity reported is twofold. In the first part, we measure the performance of internal layer $\gamma$ (see Algorithm 1)—the external part (layer $\theta$ and $\sigma$) is exactly the same as in [24], so it would be pointless to evaluate it.

Algorithm 1: Layer $\gamma$ with BitShift transformation.

We run our code on laptops with different hardware configurations. More precisely, our laptops are equipped with

• Intel^® Core^TM i3-330M, 2.13 GHz processor with 3 MB SmartCache, 8 GB RAM and Ubuntu 18.04.1 LTS 64-bit. The source code has been compiled with GCC 7.3.0 with -O3 optimization enabled (see

  Table 1. Results of tests on i3-330M with Ubuntu 18.04.1 LTS 64-bit.

  	$\mathit{\gamma }$	$\mathit{\gamma }$ with BitShift
  $n_{in}$ = 32, encryption	1.178316 s	0.955048 s
  $n_{in}$ = 32, decryption	1.447580 s	1.168507 s
  $n_{in}$ = 16, encryption	3.946748 s	3.222751 s
  $n_{in}$ = 16, decryption	4.193261 s	3.308678 s
  $n_{in}$ = 8, encryption	2.547156 s	2.192452 s
  $n_{in}$ = 8, decryption	2.564750 s	2.250102 s

  );
• Intel^® Core^TM i3-350M, 2.26 GHz processor with 3 MB SmartCache, 8 GB RAM and Ubuntu 18.04.2 LTS 64-bit. The source code has been compiled with GCC 7.4.0 with -O3 optimization enabled (see

  Table 2. Results of tests on i3-350M with Ubuntu 18.04.2 LTS 64-bit.

  	$\mathit{\gamma }$	$\mathit{\gamma }$ with BitShift
  $n_{in}$ = 32, encryption	1.116117 s	0.902140 s
  $n_{in}$ = 32, decryption	1.367435 s	1.150235 s
  $n_{in}$ = 16, encryption	3.717744 s	3.035942 s
  $n_{in}$ = 16, decryption	3.954781 s	3.116000 s
  $n_{in}$ = 8, encryption	2.395998 s	2.061877 s
  $n_{in}$ = 8, decryption	2.405397 s	2.114405 s

  );
• Intel^® Core^TM i7-2860QM, 2.50/3.60 GHz processor with 8 MB SmartCache, 16 GB RAM and Kubuntu 18.10 64-bit. The source code has been compiled with GCC 7.3.0 with -O3 optimization enabled (see

  Table 3. Results of tests on i7-2860QM with Kubuntu 18.10 64-bit.

  	$\mathit{\gamma }$	$\mathit{\gamma }$ with BitShift
  $n_{in}$ = 32, encryption	0.837671 s	0.668838 s
  $n_{in}$ = 32, decryption	0.925293 s	0.816856 s
  $n_{in}$ = 16, encryption	2.667934 s	2.147471 s
  $n_{in}$ = 16, decryption	2.811657 s	2.394600 s
  $n_{in}$ = 8, encryption	1.886357 s	1.565764 s
  $n_{in}$ = 8, decryption	2.030491 s	1.777118 s

  );
• Intel^® Core^TM i7-5500U, 2.40/3.00 GHz processor with 4 MB Cache, 8 GB RAM and Ubuntu 18.04.2 LTS 64-bit. The source code has been compiled with GCC 7.4.0 with -O3 optimization enabled (see

  Table 4. Results of tests on i7-5500U with Ubuntu 18.04.2 LTS 64-bit.

  	$\mathit{\gamma }$	$\mathit{\gamma }$ with BitShift
  $n_{in}$ = 32, encryption	0.861415 s	0.701899 s
  $n_{in}$ = 32, decryption	0.954985 s	0.782088 s
  $n_{in}$ = 16, encryption	2.980274 s	2.461575 s
  $n_{in}$ = 16, decryption	3.155612 s	2.543056 s
  $n_{in}$ = 8, encryption	1.860916 s	1.774127 s
  $n_{in}$ = 8, decryption	1.879749 s	1.785562 s

  );
• Intel^® Core^TM i7-8550U CPU, 1.80/4.00 GHz processor with 8 MB SmartCache, 32 GB RAM and Ubuntu 18.04.2 LTS 64-bit. The source code has been compiled with GCC 7.4.0 with -O3 optimization enabled (see

  Table 5. Results of tests on i7-8550U with Ubuntu 18.04.2 LTS 64-bit.

  	$\mathit{\gamma }$	$\mathit{\gamma }$ with BitShift
  $n_{in}$ = 32, encryption	0.681576 s	0.526522 s
  $n_{in}$ = 32, decryption	0.723118 s	0.587942 s
  $n_{in}$ = 16, encryption	2.396308 s	1.898987 s
  $n_{in}$ = 16, decryption	2.462049 s	1.933232 s
  $n_{in}$ = 8, encryption	1.160104 s	1.258072 s
  $n_{in}$ = 8, decryption	1.179036 s	1.248327 s

  );
• Intel^® Core^TM i3-350M, 2.26 GHz processor with 3 MB SmartCache, 4 GB RAM and Debian GNU/Linux 9 32-bit. The source code has been compiled with GCC 6.3.0 with -O3 optimization enabled (see

  Table 6. Results of tests on i3-350M with Debian GNU/Linux 9 32-bit.

  	$\mathit{\gamma }$	$\mathit{\gamma }$ with BitShift
  $n_{in}$ = 32, encryption	1.247818 s	1.041543 s
  $n_{in}$ = 32, decryption	1.967226 s	1.558086 s
  $n_{in}$ = 16, encryption	3.721377 s	3.381363 s
  $n_{in}$ = 16, decryption	4.164744 s	3.262065 s
  $n_{in}$ = 8, encryption	2.399780 s	2.065451 s
  $n_{in}$ = 8, decryption	2.412146 s	2.127425 s

  );

In the second part, as explained in Section 6, we examine the cipher in the IoT context, where black-box and white-box implementations are involved.

7.1. 32/64-Bit Architectures

We compared the performance of internal layer $\gamma$ (yellow rectangles of Figure 5) with and without BitShift transformation (green rectangles of Figure 5) for different $n_{in}$ sizes. We avoid the operations involved in $\theta$ and $\sigma$ layers.

Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6 show the time required to encrypt/decrypt one million of different plaintexts (fixed size of 128 bits) using the same key (randomly chosen). Notice that in addition to the key bits needed for the initial AddRoundKey $A{K}^0$, SPNbox layer $\gamma$ uses 512 key bits—i.e., 512 bit = 16 round × 32 bit ($n_{in}$ = 32), or 512 bit = 32 round × 16 bit ($n_{in}$ = 16), or 512 bit = 64 round × 8 bit ($n_{in}$ = 8). Therefore, we set to 512 the minimum amount of key bits to be used in our solution. In particular, we will execute: 12 rounds ($R_{n_{in}}$ = 12), using 528 key bits ($n_{in}$ = 32); 24 rounds ($R_{n_{in}}$ = 24), using 528 key bits ($n_{in}$ = 16); and finally 47 rounds ($R_{n_{in}}$ = 47), using 517 key bits ($n_{in}$ = 8).

Our testing activities show that implementations with BitShift are generally faster than those without it. In particular, several cases show that the improvement in the execution time exceeds 20%. Only in Table 5, $n_{in}$ = 8, encryption and decryption, we find a different result.

7.2. IoT Environment

The testing activity has been performed using MQTT [65], a lightweight communication protocol designed for small sensors and mobile devices in low bandwidth environments. By default data are sent in clear text over the internet, thus we encrypt data contained in the payload. We measure the performance of layer $\gamma$ as described in Algorithm 2. More precisely, we compare the performances with and without BitShift transformation for different $n_{in}$—size of 32, 16, and 8 bits—encrypting one million of different plaintexts—size of 16, 64, 256, and 1024 bytes—using the same key. Then, we send one hundred MQTT messages, each of which contains 10,000 encrypted payloads. Finally, adopting the same approach, the server collects and decrypts the same number of MQTT messages with encrypted payloads.

Algorithm 2: MQTT: testing activity executed for each payload (16, 64, 128, and 1024 bytes).

Our testing activity has been executed on a machine equipped with an Intel® Core™ i7-6500U CPU @ 2.50 GHz × 4 processor, with 12 GB SDRAM DDR4-2133, Intel® HD Graphics 520 (Skylake GT2) GPU and operating system Ubuntu™ 18.04.2 TLS. We used Eclipse Mosquitto™ [66] version 1.4.15, which implements the MQTT protocol versions 3.1.1. The source code has been compiled with GCC 7.4.0, “-O3” optimization enabled.

Table 7. Encryption/decryption operations with a black-box implementation (server-side).

Payload	${\mathit{n}}_{\mathit{in}}$	Encryption			Decryption
(Bytes)	(Bits)	w/o BitShift	with BitShift	Gain	w/o BitShift	with BitShift	Gain
	32	3.668 s	3.319 s	9.507%	0.893s	0.741s	16.999%
16	16	6.335 s	5.763 s	9.037%	3.096s	2.412s	22.091%
	8	4.510 s	4.882 s	−8.254%	1.479s	1.551s	−4.929%
	32	6.679 s	5.601 s	16.139%	3.636s	2.950 s	18.865%
64	16	14.869 s	12.362 s	16.860%	12.488 s	10.023 s	19.739%
	8	8.817 s	9.616 s	−9.060%	6.183s	6.446 s	−4.253%
	32	16.021 s	13.847 s	13.569%	14.166 s	11.827 s	16.512%
128	16	51.098 s	38.998 s	23.680%	50.632 s	39.596 s	21.798%
	8	24.280 s	25.709 s	−5.884%	24.454 s	25.825 s	−5.607%
	32	54.047 s	41.716 s	22.816%	56.494 s	47.065 s	16.690%
1024	16	191.262 s	151.101 s	20.998%	195.424 s	154.029 s	21.182%
	8	92.651 s	98.998 s	−6.850%	93.744 s	98.362 s	−4.926%

summarizes the results obtained.

In particular, for the encryption phase, we got a highest gain (23.680%) in the case of 128-byte payload and $n_{in}=16$, while the highest loss ($-9.060\%$) in the case of a 64-byte payload and $n_{in}=8$. For the decrypt phase, the highest gain ($22.091\%$) is obtained with a 16-byte payload and $n_{in}=16$, and the highest loss ($-5.607\%$) with a 128-byte payload and $n_{in}=8$. Notice that the case $n_{in}=8$ turned out to be the worst one.

8. Conclusions

In the era of the internet of things, the involved devices are usually lightweight, so they cannot perform heavy computations nor store a huge amount of data. In addition, these data might be sensitive—energy consumptions, medical records, and so on—and could be sent in an unprotected environment. In a white-box scenario, an attacker could easily read these data because she/he has full access to the whole execution platform and white-box cryptography can be used to secure data in this specific context.

Considering the effectiveness of side-channel attacks, new ciphers has been designed with white-box attack model in mind. In this paper, we focused on the SPNbox family [24], suggesting how to increase the number of key bits used in each round and showing that this improvement affects the performance of the cipher. The introduction of a key-dependent circular bit shift transformation helped us to increase the keyspace and to reduce the number of rounds of the cipher, reducing the execution time too.

We described and analyzed the performance of the modified cipher in the IoT context, where both white-box and black-box implementations may be required. In particular, we measured its performance (a) on 32/64-bit architectures and (b) encrypting the payload of an IoT messaging protocol. Our testing activities have been executed on consumer laptops. The results obtained encrypting and decrypting one million of different 128-bit plaintexts on 32/64-bit architectures showed that the execution time for layer $\gamma$ is reduced up to 22% while the highest loss is about 8%.

Moreover, the testing activities performed with lightweight protocol MQTT had a gain of about 23% and 22% (encryption and decryption phase, respectively) while a loss of about 9% and 5%. In all our testing activities the case $n_{in}=8$ turns out to be the worst one.

Possible future works are try to (a) understand in details why current implementation fails for $n_{in}=8$ and (b) implement a communication protocol based on Transport Layer Security pre-shared key ciphersuites (TLS-PSK) in order to compare the performance of white-box implementations with those of lightweight ciphers.