Tight-Binding Modeling of Nucleic Acid Sequences: Interplay between Various Types of Order or Disorder and Charge Transport
Abstract
:1. Introduction
2. Tight-Binding and Its Application in Nucleic Acids
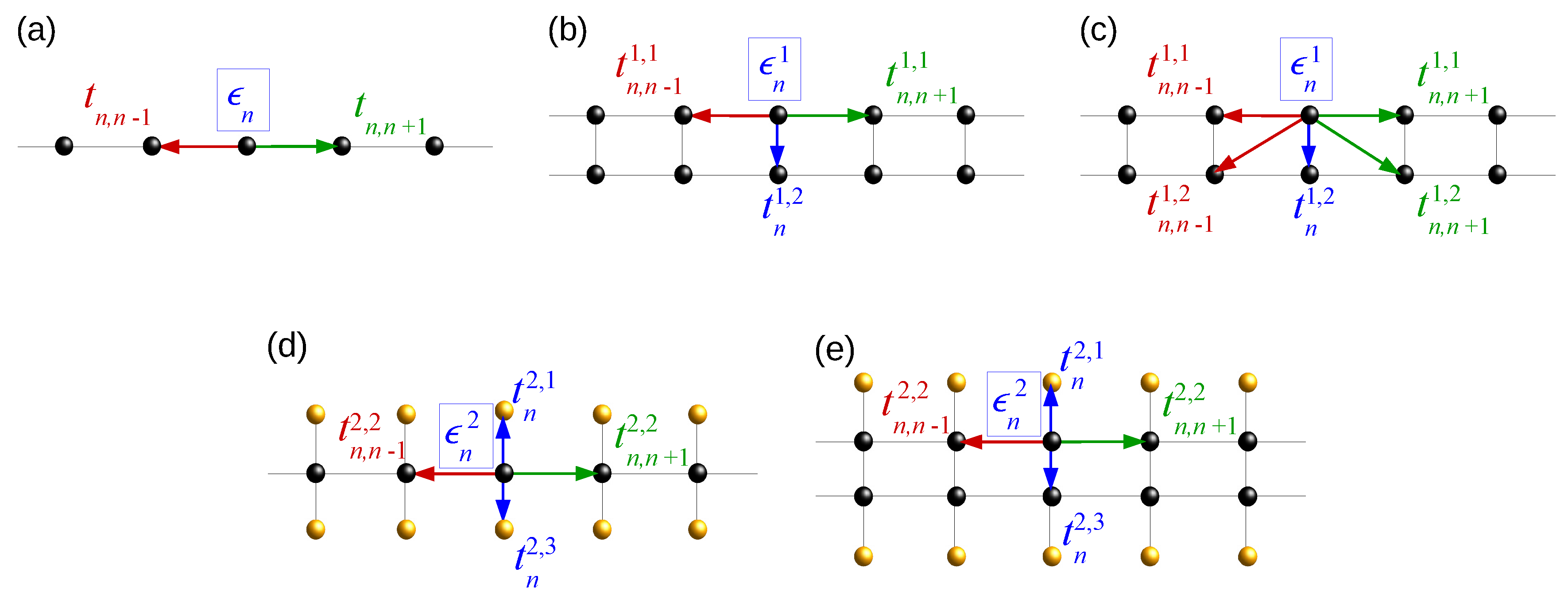
2.1. Wire Model
2.2. Ladder Model
2.3. Extended Ladder Model
2.4. Fishbone Model
2.5. Fishbone Ladder Model
2.6. Additional Remarks
3. Aperiodic One-Dimensional Wires
3.1. Aperiodic Substitutional Sequences
3.2. Primitive Substitutions and the Perron–Frobenius Eigenvalue
3.3. Induced Substitutions
3.4. The Pisot Property
- (1)
- strictly quasiperiodic sequences, in which the rank of the reciprocal lattice is finite and larger than the dimension of the physical space of the sequence m, and
- (2)
- limit-quasiperiodic sequences, in which the rank of reciprocal lattice is countably infinite (in a 1–1 correspondence with the natural numbers or integers).
- (3)
- limit-periodic, i.e., a superposition of countably infinite periodic structures. Some examples are the period doubling sequence and metallic means sequences with [96],
- (4)
- (5)
4. Energy Structure of Nucleic Acid Wires
Theorem 5.13 of Ref [108].Let be a Hamiltionian corresponding to the WM, where the coefficients (i.e., parameters) are determined by a primitive substitution on a finite alphabet. Then, the values of the IDOS of on the spectral gaps in belong to the module generated by the components of the eigenvectors and of the substitution matrices and , respectively.
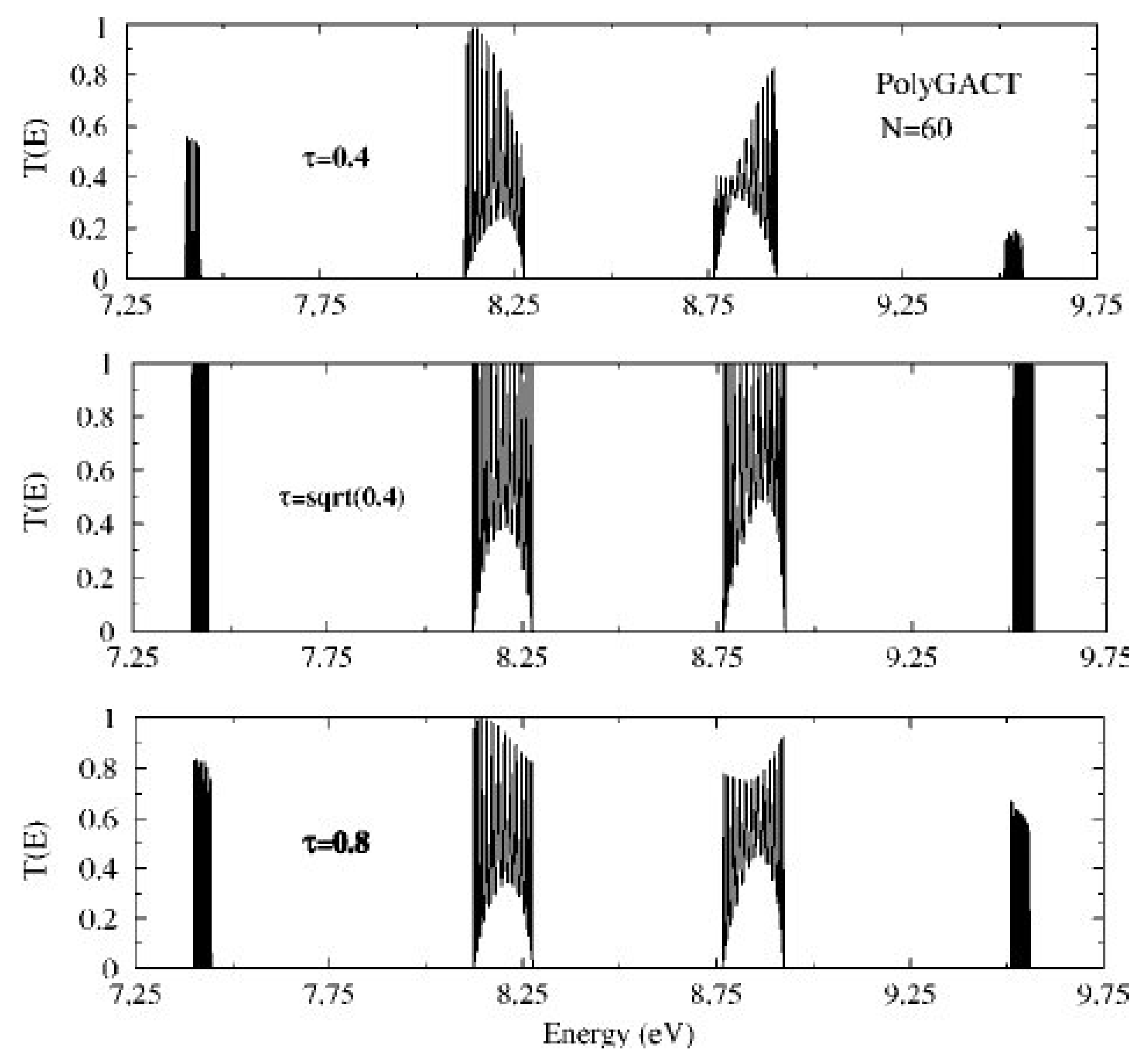
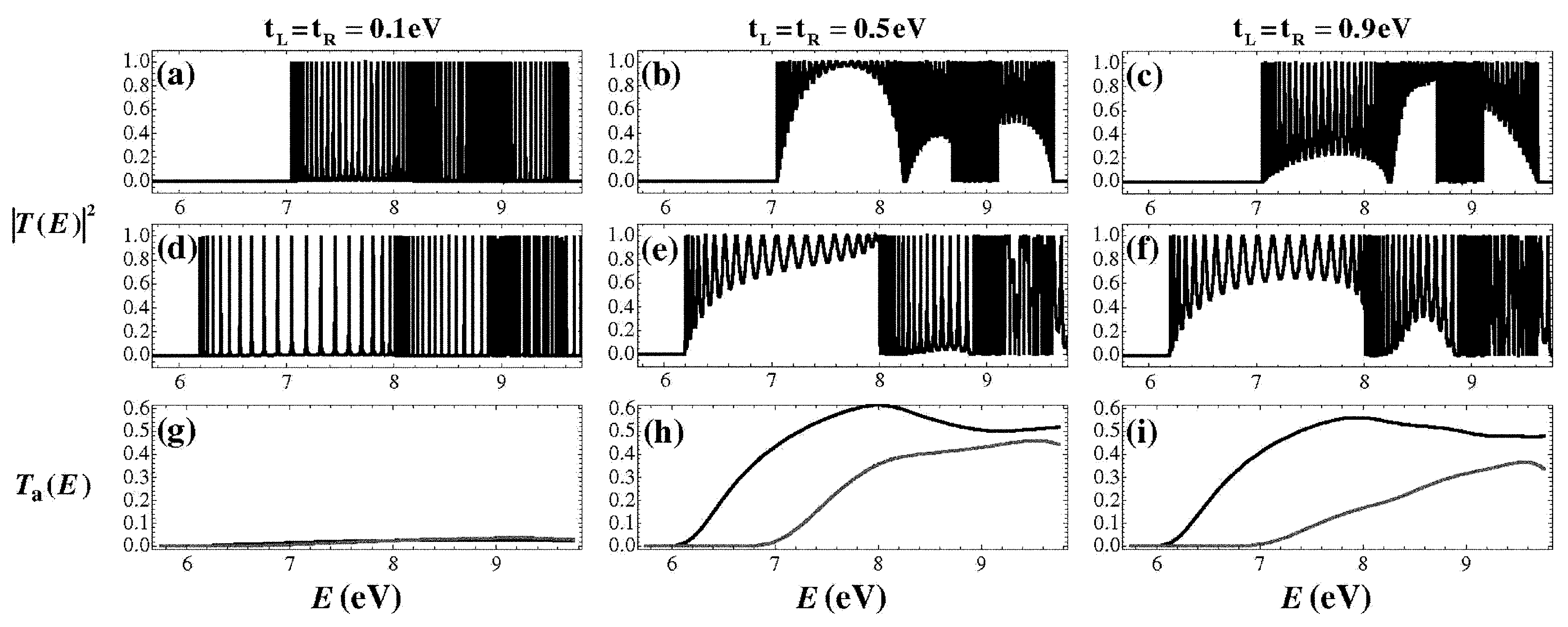
5. Coupling Nucleic Acids with Leads: Transmission Coefficients
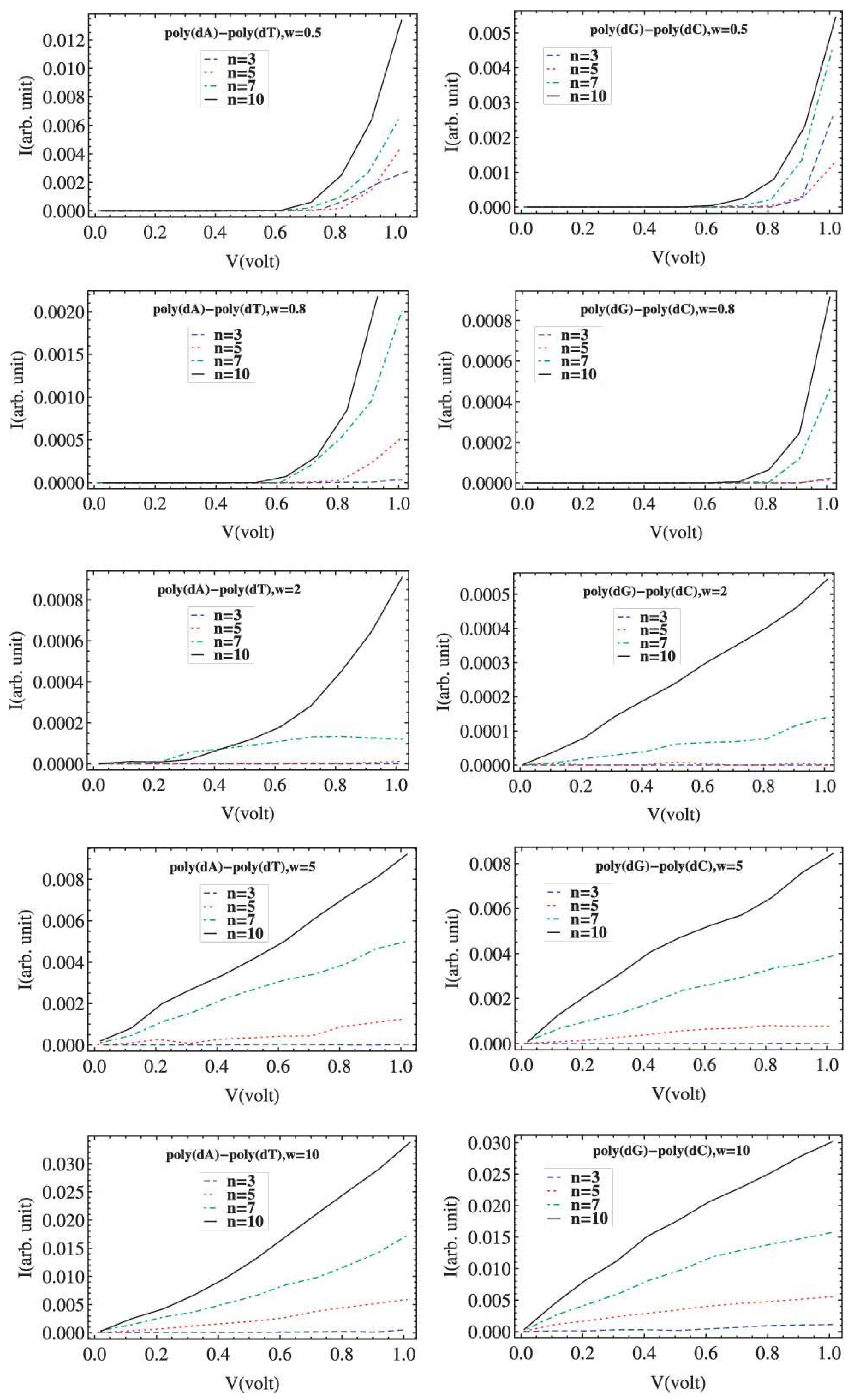
6. Current–Voltage Curves
- (a)
- The choice of the Fermi level of the leads , which coincides with if one electron per site is assumed. If is not aligned with an allowed energy region of the segment, then no currents occur in the vicinity of , while a metallic behavior is expected otherwise.
- (b)
- The way the external bias is applied. For example, only one of the leads’ energy bands can be shifted, so that , and , or, alternatively, both leads’ bands can be symmetrically shifted so that . This choice affects both the way the voltage drop is induced in the nucleic acid sequence and the energy limits of the conductance channel. At zero temperature, the Fermi–Dirac distributions become Heaviside step functions and determine the limits of integration. Hence, Equation (11) can be simplified towhile, at finite temperatures, it can be written in the formi.e., the curve occurs from the modulation of the hyperbolic function by the integral factor expression [119].
- (c)
- Whether or not the transmission coefficient is considered as bias-dependent. Although assuming bias-independent transmission coefficient could be a justified choice in the small bias regime, and it is indeed less computationally costly, this assumption cannot lead, under any circumstances, to the occurrence of negative differential resistance, since an increasingly larger part (as V increases) of a nonnegative function is integrated.
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DNA | Deoxyribonucleic Acid |
| RNA | Ribonucleic acid |
| G | Guanine |
| A | Adenine |
| C | Cytosine |
| T | Thymine |
| U | Uracil |
| TB | Tight-Binding |
| WM | Wire Model |
| LM | Ladder Model |
| ELM | Extended Ladder Model |
| FM | Fishbone Model |
| FLM | Fishbone Ladder Model |
| DOS | Density of States |
| IDOS | Integrated Density of States |
References
- Watson, J.D.; Crick, F.H.C. Molecular Structure of Nucleic Acids: A Structure for Deoxyribose Nucleic Acid. Nature 1953, 171, 737–738. [Google Scholar] [CrossRef] [PubMed]
- Page, C.C.; Moser, C.C.; Dutton, P.L. Mechanism for electron transfer within and between proteins. Curr. Opin. Chem. Biol. 2003, 7, 551–556. [Google Scholar] [CrossRef] [PubMed]
- Gray, H.B.; Winkler, J.R. Electron flow through metalloproteins. Biochim. Biophys. Acta 2010, 1797, 1563–1572. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moser, C.C.; Ross Anderson, J.L.; Dutton, P.L. Guidelines for tunneling in enzymes. Biochim. Biophys. Acta 2010, 1797, 1573–1586. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Artés, J.M.; López-Martínez, M.; Díez-Pérez, I.; Sanz, F.; Gorostiza, P. Nanoscale charge transfer in redox proteins and DNA: Towards biomolecular electronics. Electrochim. Acta 2014, 140, 83–95. [Google Scholar] [CrossRef]
- Kannan, A.M.; Renugopalakrishnan, V.; Filipek, S.; Li, P.; Audette, G.F.; Munukutla, L. Bio-Batteries and Bio-Fuel Cells: Leveraging on Electronic Charge Transfer Proteins. J. Nanosci. Nanotechnol. 2009, 9, 1665–1678. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dandliker, P.J.; Holmlin, R.E.; Barton, J.K. Oxidative Thymine Dimer Repair in the DNA Helix. Science 1997, 275, 1465–1468. [Google Scholar] [CrossRef]
- Rajski, S.R.; Jackson, B.A.; Barton, J.K. DNA repair: models for damage and mismatch recognition. Mutat. Res. 2000, 447, 49–72. [Google Scholar] [CrossRef]
- Giese, B. Electron transfer through DNA and peptides. Bioorg. Med. Chem. 2006, 14, 6139–6143. [Google Scholar] [CrossRef]
- Shih, C.T.; Cheng, Y.Y.; Wells, S.A.; Hsu, C.L.; Römer, R.A. Charge transport in cancer-related genes and early carcinogenesis. Comput. Phys. Commun. 2011, 182, 36–38. [Google Scholar] [CrossRef] [Green Version]
- Endres, R.G.; Cox, D.L.; Singh, R.R.P. Colloquium: The quest for high-conductance DNA. Rev. Mod. Phys. 2004, 76, 195–214. [Google Scholar] [CrossRef]
- Wohlgamuth, C.H.; McWilliams, M.A.; Slinker, J.D. DNA as a Molecular Wire: Distance and Sequence Dependence. Anal. Chem. 2013, 85, 8634–8640. [Google Scholar] [CrossRef] [PubMed]
- Abouzar, M.H.; Poghossian, A.; Cherstvy, A.G.; Pedraza, A.M.; Ingebrandt, S.; Schöning, M.J. Label-free electrical detection of DNA by means of field-effect nanoplate capacitors: Experiments and modeling. Phys. Status Solidi A 2012, 209, 925–934. [Google Scholar] [CrossRef]
- Ye, Y.J.; Shen, L.L. DFT approach to calculate electronic transfer through a segment of DNA double helix. J. Comput. Chem. 2000, 21, 1109–1117. [Google Scholar] [CrossRef]
- Ye, Y.J.; Jiang, Y. Electronic structures and long-range electron transfer through DNA molecules. Int. J. Quantum Chem. 2000, 78, 112–130. [Google Scholar] [CrossRef]
- Voityuk, A.A. Electronic couplings and on-site energies for hole transfer in DNA: Systematic quantum mechanical/molecular dynamic study. J. Chem. Phys. 2008, 128, 115101. [Google Scholar] [CrossRef] [Green Version]
- Kubař, T.; Woiczikowski, P.B.; Cuniberti, G.; Elstner, M. Efficient Calculation of Charge-Transfer Matrix Elements for Hole Transfer in DNA. J. Phys. Chem. B 2008, 112, 7937–7947. [Google Scholar] [CrossRef]
- Tassi, M.; Morphis, A.; Lambropoulos, K.; Simserides, C. RT-TDDFT study of hole oscillations in B-DNA monomers and dimers. Cogent Phys. 2017, 4, 1361077. [Google Scholar] [CrossRef]
- Artacho, E.; Machado, M.; Sánchez-Portal, D.; Ordejón, P.; Soler, J.M. Electrons in dry DNA from density functional calculations. Mol. Phys. 2003, 101, 1587–1594. [Google Scholar] [CrossRef] [Green Version]
- Mehrez, H.; Anantram, M.P. Interbase electronic coupling for transport through DNA. Phys. Rev. B 2005, 71, 115405. [Google Scholar] [CrossRef] [Green Version]
- Adessi, C.; Walch, S.; Anantram, M.P. Environment and structure influence on DNA conduction. Phys. Rev. B 2003, 67, 081405. [Google Scholar] [CrossRef]
- Barnett, R.N.; Cleveland, C.L.; Landman, U.; Boone, E.; Kanvah, S.; Schuster, G.B. Effect of Base Sequence and Hydration on the Electronic and Hole Transport Properties of Duplex DNA: Theory and Experiment. J. Phys. Chem. A 2003, 107, 3525–3537. [Google Scholar] [CrossRef]
- Cuniberti, G.; Craco, L.; Porath, D.; Dekker, C. Backbone-induced semiconducting behavior in short DNA wires. Phys. Rev. B 2002, 65, 241314. [Google Scholar] [CrossRef]
- Roche, S.; Bicout, D.; Maciá, E.; Kats, E. Long Range Correlations in DNA: Scaling Properties and Charge Transfer Efficiency. Phys. Rev. Lett. 2003, 91, 228101. [Google Scholar] [CrossRef] [Green Version]
- Roche, S. Sequence Dependent DNA-Mediated Conduction. Phys. Rev. Lett. 2003, 91, 108101. [Google Scholar] [CrossRef]
- Palmero, F.; Archilla, J.F.R.; Hennig, D.; Romero, F.R. Effect of base-pair inhomogeneities on charge transport along the DNA molecule, mediated by twist and radial polarons. New J. Phys. 2004, 6, 13. [Google Scholar] [CrossRef]
- Yamada, H. Localization of electronic states in chain models based on real DNA sequence. Phys. Lett. A 2004, 332, 65–73. [Google Scholar] [CrossRef] [Green Version]
- Apalkov, V.M.; Chakraborty, T. Electron dynamics in a DNA molecule. Phys. Rev. B 2005, 71, 033102. [Google Scholar] [CrossRef] [Green Version]
- Klotsa, D.; Römer, R.A.; Turner, M.S. Electronic Transport in DNA. Biophys. J. 2005, 89, 2187–2198. [Google Scholar] [CrossRef] [Green Version]
- Shih, C.T.; Roche, S.; Römer, R.A. Point-Mutation Effects on Charge-Transport Properties of the Tumor-Suppressor Gene p53. Phys. Rev. Lett. 2008, 100, 018105. [Google Scholar] [CrossRef]
- Joe, Y.S.; Lee, S.H.; Hedin, E.R. Electron transport through asymmetric DNA molecules. Phys. Lett. A 2010, 374, 2367–2373. [Google Scholar] [CrossRef]
- Yi, J. Conduction of DNA molecules: A charge-ladder model. Phys. Rev. B 2003, 68, 193103. [Google Scholar] [CrossRef]
- Caetano, R.A.; Schulz, P.A. Sequencing-Independent Delocalization in a DNA-Like Double Chain with Base Pairing. Phys. Rev. Lett. 2005, 95, 126601. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.F.; Chakraborty, T. Charge Transfer via a Two-Strand Superexchange Bridge in DNA. Phys. Rev. Lett. 2006, 97, 106602. [Google Scholar] [CrossRef] [Green Version]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Saunders College: Philadelphia, PA, USA, 1976. [Google Scholar]
- Slater, J.C.; Koster, G.F. Simplified LCAO Method for the Periodic Potential Problem. Phys. Rev. 1954, 94, 1498–1524. [Google Scholar] [CrossRef]
- Harrison, W.A. Electronic Structure and the Properties of Solids: The Physics of the Chemical Bond (Dover Books on Physics), 2nd ed.; Dover Publications: Ney York, NY, USA, 1989. [Google Scholar]
- Papaconstantopoulos, D.A.; Mehl, M.J. The Slater-Koster tight-binding method: A computationally efficient and accurate approach. J. Phys. Condens. Matter 2003, 15, 413–440. [Google Scholar] [CrossRef]
- Foulkes, W.M.C. Tight-Binding Models and Coulomb Interactions for s, p, and d Electrons. In Quantum Materials: Experiments and Theory; Pavarini, E., Koch, E., van den Brink, J., Sawatzky, G., Eds.; Modeling and Simulation, Forschungszentrum Jülich: Jülich, Germany, 2016; Volume 6. [Google Scholar]
- Molinari, L. Transfer matrices and tridiagonal-block Hamiltonians with periodic and scattering boundary conditions. J. Phys. A Math. Gen. 1997, 30, 983–997. [Google Scholar] [CrossRef]
- Molinari, L. Spectral duality and distribution of exponents for transfer matrices of block-tridiagonal Hamiltonians. J. Phys. A Math. Gen. 2003, 36, 4081–4090. [Google Scholar] [CrossRef] [Green Version]
- Cuniberti, G.; Maciá, E.; Rodríguez, A.; Römer, R.A. Tight-Binding Modeling of Charge Migration in DNA Devices. In Charge Migration in DNA: Perspectives from Physics, Chemistry, and Biology; Chakraborty, T., Ed.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 1–20. [Google Scholar] [Green Version]
- Albuquerque, E.L.; Fulco, U.L.; Freire, V.N.; Caetano, E.W.S.; Lyra, M.L.; de Moura, F.A.B.F. DNA-based nanobiostructured devices: The role of quasiperiodicity and correlation effects. Phys. Rep. 2014, 535, 139–209. [Google Scholar] [CrossRef]
- Zarea, M.; Berlin, Y.; Ratner, M.A. Effect of the reflectional symmetry on the coherent hole transport across DNA hairpins. J. Chem. Phys. 2017, 146, 114105. [Google Scholar] [CrossRef]
- Simserides, C. A systematic study of electron or hole transfer along DNA dimers, trimers and polymers. Chem. Phys. 2014, 440, 31–41. [Google Scholar] [CrossRef] [Green Version]
- Albuquerque, E.L.; Vasconcelos, M.S.; Lyra, M.L.; de Moura, F.A.B.F. Nucleotide correlations and electronic transport of DNA sequences. Phys. Rev. E 2005, 71, 021910. [Google Scholar] [CrossRef]
- Lambropoulos, K.; Chatzieleftheriou, M.; Morphis, A.; Kaklamanis, K.; Lopp, R.; Theodorakou, M.; Tassi, M.; Simserides, C. Electronic structure and carrier transfer in B-DNA monomer polymers and dimer polymers: Stationary and time-dependent aspects of a wire model versus an extended ladder model. Phys. Rev. E 2016, 94, 062403. [Google Scholar] [CrossRef] [Green Version]
- Xu, M.; Endres, R.; Tsukamoto, S.; Kitamura, M.; Ishida, S.; Arakawa, Y. Conformation and Local Environment Dependent Conductance of DNA Molecules. Small 2005, 1, 1168–1172. [Google Scholar] [CrossRef]
- Iguchi, K. π-electrons in a single strand DNA: A phenomenological approach. Int. J. Mod. Phys. B 2004, 18, 1845–1910. [Google Scholar] [CrossRef]
- Kundu, S.; Karmakar, S.N. Localization phenomena in a DNA double-helix structure: A twisted ladder model. Phys. Rev. E 2014, 89, 032719. [Google Scholar] [CrossRef] [Green Version]
- Malakooti, S.; Hedin, E.; Joe, Y. Tight-binding approach to strain-dependent DNA electronics. J. Appl. Phys. 2013, 114, 014701. [Google Scholar] [CrossRef]
- Varela, S.; Mujica, V.; Medina, E. Effective spin–orbit couplings in an analytical tight-binding model of DNA: Spin filtering and chiral spin transport. Phys. Rev. B 2016, 93, 155436. [Google Scholar] [CrossRef]
- Díaz, E. Analysis of the interband optical transitions: Characterization of synthetic DNA band structure. J. Chem. Phys. 2008, 128, 175101. [Google Scholar] [CrossRef] [Green Version]
- Maciá, E. Electronic structure and transport properties of double-stranded Fibonacci DNA. Phys. Rev. B 2006, 74, 245105. [Google Scholar] [CrossRef] [Green Version]
- Maciá, E.; Roche, S. Backbone-induced effects in the charge transport efficiency of synthetic DNA molecules. Nanotechnology 2006, 17, 3002–3007. [Google Scholar] [CrossRef]
- Lambropoulos, K.; Chatzieleftheriou, M.; Morphis, A.; Kaklamanis, K.; Theodorakou, M.; Simserides, C. Unbiased charge oscillations in B-DNA: Monomer polymers and dimer polymers. Phys. Rev. E 2015, 92, 032725. [Google Scholar] [CrossRef]
- Lambropoulos, K.; Vantaraki, C.; Bilia, P.; Mantela, M.; Simserides, C. Periodic polymers with increasing repetition unit: Energy structure and carrier transfer. Phys. Rev. E 2018, 98, 032412. [Google Scholar] [CrossRef] [Green Version]
- MacKinnon, A.; Kramer, B. The scaling theory of electrons in disordered solids: Additional numerical results. Z. Phys. B 1983, 53, 1–13. [Google Scholar] [CrossRef]
- Dwivedi, V.; Chua, V. Of bulk and boundaries: Generalized transfer matrices for tight-binding models. Phys. Rev. B 2016, 93, 134304. [Google Scholar] [CrossRef] [Green Version]
- Lambropoulos, K.; Simserides, C. Spectral and transmission properties of periodic 1D tight-binding lattices with a generic unit cell: An analysis within the transfer matrix approach. J. Phys. Commun. 2018, 2, 035013. [Google Scholar] [CrossRef]
- Datta, S. Electronic Transport in Mesoscopic Systems; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar] [CrossRef]
- Hawke, L.G.D.; Kalosakas, G.; Simserides, C. Electronic parameters for charge transfer along DNA. Eur. Phys. J. E 2010, 32, 291–305. [Google Scholar] [CrossRef]
- Capobianco, A.; Landi, A.; Peluso, A. Modeling DNA oxidation in water. Phys. Chem. Chem. Phys. 2017, 19, 13571–13578. [Google Scholar] [CrossRef]
- Sugiyama, H.; Saito, I. Theoretical Studies of GG-Specific Photocleavage of DNA via Electron Transfer: Significant Lowering of Ionization Potential and 5’-Localization of HOMO of Stacked GG Bases in B-Form DNA. J. Am. Chem. Soc. 1996, 118, 7063–7068. [Google Scholar] [CrossRef]
- Hutter, M.; Clark, T. On the Enhanced Stability of the Guanine-Cytosine Base-Pair Radical Cation. J. Am. Chem. Soc. 1996, 118, 7574–7577. [Google Scholar] [CrossRef]
- Zhang, H.; Li, X.Q.; Han, P.; Yu, X.Y.; Yan, Y. A partially incoherent rate theory of long-range charge transfer in deoxyribose nucleic acid. J. Chem. Phys. 2002, 117, 4578–4584. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Cai, Z.; Sevilla, M.D. Investigation of Proton Transfer within DNA Base Pair Anion and Cation Radicals by Density Functional Theory (DFT). J. Phys. Chem. B 2001, 105, 10115–10123. [Google Scholar] [CrossRef]
- Li, X.; Cai, Z.; Sevilla, M.D. Energetics of the Radical Ions of the AT and AU Base Pairs: A Density Functional Theory (DFT) Study. J. Phys. Chem. A 2002, 106, 9345–9351. [Google Scholar] [CrossRef]
- Shukla, M.K.; Leszczynski, J. A Theoretical Study of Excited State Properties of Adenine-Thymine and Guanine-Cytosine Base Pairs. J. Phys. Chem. A 2002, 106, 4709–4717. [Google Scholar] [CrossRef]
- Mantela, M.; Morphis, A.; Tassi, M.; Simserides, C. Lowest ionisation and excitation energies of biologically important heterocyclic planar molecules. Mol. Phys. 2016, 114, 709–718. [Google Scholar] [CrossRef]
- Voityuk, A.A.; Jortner, J.; Bixon, M.; Rösch, N. Electronic coupling between Watson–Crick pairs for hole transfer and transport in desoxyribonucleic acid. J. Chem. Phys. 2001, 114, 5614–5620. [Google Scholar] [CrossRef]
- Ivanova, A.; Shushkov, P.; Rösch, N. Systematic Study of the Influence of Base-Step Parameters on the Electronic Coupling between Base-Pair Dimers: Comparison of A-DNA and B-DNA Forms. J. Phys. Chem. A 2008, 112, 7106–7114. [Google Scholar] [CrossRef]
- Migliore, A.; Corni, S.; Varsano, D.; Klein, M.L.; Di Felice, R. First, Principles Effective Electronic Couplings for Hole Transfer in Natural and Size-Expanded DNA. J. Phys. Chem. B 2009, 113, 9402–9415. [Google Scholar] [CrossRef]
- Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J.W. Metallic Phase with Long-Range Orientational Order and No Translational Symmetry. Phys. Rev. Lett. 1984, 53, 1951–1953. [Google Scholar] [CrossRef] [Green Version]
- International Union of Crystallography. Report of the Executive Committee for 1991. Acta Crystallogr. A 1992, 48, 922–946. [Google Scholar] [CrossRef] [Green Version]
- Maciá, E. On the Nature of Electronic Wave Functions in One-Dimensional Self-Similar and Quasiperiodic Systems. ISRN Condens. Matter Phys. 2014, 2014, 165943. [Google Scholar] [CrossRef]
- Kosuri, S.; Church, G.M. Large-scale de novo DNA synthesis: technologies and applications. Nat. Methods 2014, 11, 499–507. [Google Scholar] [CrossRef]
- Beaucage, S.; Caruthers, M. Deoxynucleoside phosphoramidites—A new class of key intermediates for deoxypolynucleotide synthesis. Tetrahedron Lett. 1981, 22, 1859–1862. [Google Scholar] [CrossRef]
- Palluk, S.; Arlow, D.H.; de Rond, T.; Barthel, S.; Kang, J.S.; Bector, R.; Baghdassarian, H.M.; Truong, A.N.; Kim, P.W.; Singh, A.K.; et al. De novo DNA synthesis using polymerase-nucleotide conjugates. Nat. Biotechnol. 2018, 36, 645–650. [Google Scholar] [CrossRef]
- Perron, O. Zur Theorie der Matrices. Math. Ann. 1907, 64, 248–263. [Google Scholar] [CrossRef]
- Frobenius, G. Über Matrizen aus nicht Negativen Elementen; Sitzungsberichte Königlich Preussischen Akademie Wissenschaften Berlin: Berlin, Germany, 1912; pp. 456–477. (In German) [Google Scholar]
- Baake, M.; Grimm, U. Aperiodic Order: Volume 1, A Mathematical Invitation; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Lambropoulos, K.; Simserides, C. Periodic, quasiperiodic, fractal, Kolakoski, and random binary polymers: Energy structure and carrier transport. Phys. Rev. E 2019, 99, 032415. [Google Scholar] [CrossRef] [Green Version]
- Berthé, V.; Siegel, A. Basic notions on substitutions. In Substitutions in Dynamics, Arithmetics and Combinatorics; Fogg, N.P., Berthé, V., Ferenczi, S., Mauduit, C., Siegel, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 1–32. [Google Scholar]
- Canterini, V.; Siegel, A. Geometric Representation of Substitutions of Pisot Type. Trans. Am. Math. Soc. 2001, 353, 5121–5144. [Google Scholar] [CrossRef]
- Bombieri, E.; Taylor, J.E. Which distributions of matter diffract? An initial investigation. J. Phys. Colloq. 1986, 47, 19–28. [Google Scholar] [CrossRef]
- Bombieri, E.; Taylor, J.E. Quasicrystals, Tilings, and Algebraic Number Theory: Some Preliminary Connections. In The Legacy of Sonya Kovalevskaya; Keen, L., Ed.; Contemporary Mathematics, American Mathematical Society: Providence, RI, USA, 1987; Volume 64, pp. 241–264. [Google Scholar]
- Solomyak, B. Dynamics of Self-Similar Tilings. Ergod. Theory Dyn. Syst. 1997, 17, 695–738. [Google Scholar] [CrossRef]
- Luck, J.M.; Godrèche, C.; Janner, A.; Janssen, T. The nature of the atomic surfaces of quasiperiodic self-similar structures. J. Phys. A Math. Gen. 1993, 26, 1951–1999. [Google Scholar] [CrossRef]
- Kolář, M. New class of one-dimensional quasicrystals. Phys. Rev. B 1993, 47, 5489–5492. [Google Scholar] [CrossRef]
- Kolář, M.; Iochum, B.; Raymond, L. Structure factor of 1D systems (superlattices) based on two-letter substitution rules. I. delta (Bragg) peaks. J. Phys. A Math. Gen. 1993, 26, 7343–7366. [Google Scholar] [CrossRef]
- Sigler, L. Fibonacci’s Liber Abaci: A Translation into Modern English of Leonardo Pisano’s Book of Calculation; Springer: New York, NY, USA, 2003. [Google Scholar]
- Birch, J.; Severin, M.; Wahlström, U.; Yamamoto, Y.; Radnoczi, G.; Riklund, R.; Sundgren, J.E.; Wallenberg, L.R. Structural characterization of precious-mean quasiperiodic Mo/V single-crystal superlattices grown by dual-target magnetron sputtering. Phys. Rev. B 1990, 41, 10398–10407. [Google Scholar] [CrossRef]
- Fu, X.; Liu, Y.; Zhou, P.; Sritrakool, W. Perfect self-similarity of energy spectra and gap-labeling properties in one-dimensional Fibonacci-class quasilattices. Phys. Rev. B 1997, 55, 2882–2889. [Google Scholar] [CrossRef] [Green Version]
- Maciá, E. Spectral Classification of One-Dimensional Binary Aperiodic Crystals: An Algebraic Approach. Ann. Phys. 2017, 529, 1700079. [Google Scholar] [CrossRef]
- Baake, M.; Grimm, W.; Mañibo, N. Spectral analysis of a family of binary inflation rules. Lett. Math. Phys. 2018, 108, 1783–1805. [Google Scholar] [CrossRef] [Green Version]
- Prouhet, E. Mémoire sur quelques relations entre les puissances des nombres. CR Acad. Sci. Paris 1851, 33, 225. (In French) [Google Scholar]
- Nagell, T.; Selberg, A.; Selberg, S.; Thalberg, K. (Eds.) Selected Mathematical Papers of Axel Thue; Universitetsforlaget: Oslo, Norway, 1977. [Google Scholar]
- Morse, H.M. Recurrent Geodesics on a Surface of Negative Curvature. Trans. Am. Math. Soc. 1906, 22, 84–100. [Google Scholar] [CrossRef]
- Rudin, W. Some theorems on Fourier coefficients. Proc. Am. Math. Soc. 1959, 10, 855–895. [Google Scholar] [CrossRef]
- Shapiro, H.S. Extremal Problems for Polynomials and Power Series. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1951. [Google Scholar]
- Cantor, G. Über unendliche, lineare Punktmannigfaltigkeiten. Math. Ann. 1883, 21, 545–586. (In German) [Google Scholar] [CrossRef]
- Vaidya, A.M.; Simon, H.; Garrett, P.; Shapiro, H.S.; Kolakoski, W.; Dapkus, F.; Gross, F.; Cohen, M.J.; Comtet, L.; Feller, E.H. Advanced Problems: 5300–5309. Am. Math. Mon. 1965, 72, 673–675. [Google Scholar] [CrossRef]
- Oldenburger, R. Exponent trajectories in symbolic dynamics. Trans. Am. Math. Soc. 1939, 46, 453–466. [Google Scholar] [CrossRef] [Green Version]
- Sing, B. Kolakoski sequences—An example of aperiodic order. J. Non-Cryst. Solids 2004, 334, 100–104. [Google Scholar] [CrossRef]
- Sing, B. Kolakoski-(2m,2n) are limit-periodic model sets. J. Math. Phys. 2003, 44, 899–912. [Google Scholar] [CrossRef] [Green Version]
- Bovier, A.; Ghez, J.M. Remarks on the spectral properties of tight-binding and Kronig-Penney models with substitution sequences. J. Phys. A Math. Gen. 1995, 28, 2313–2324. [Google Scholar] [CrossRef] [Green Version]
- Bellisard, J.; Bovier, A.; Ghez, J.M. Gap Labelling Theorems for One Dimensional Discrete Schrödinger operators. Rev. Math. Phys. 1992, 4, 1–37. [Google Scholar] [CrossRef]
- Bellisard, J.; Bovier, A.; Ghez, J.M. Discrete Schrödinger Operators with Potentials Generated by Substitutions. In Differential Equations with Applications to Mathematical Physics; Ames, W.F., Harrell, E.M., Herod, J.V., Eds.; Elsevier: Amsterdam, The Netherlands, 1993; Volume 192, pp. 13–23. [Google Scholar] [CrossRef]
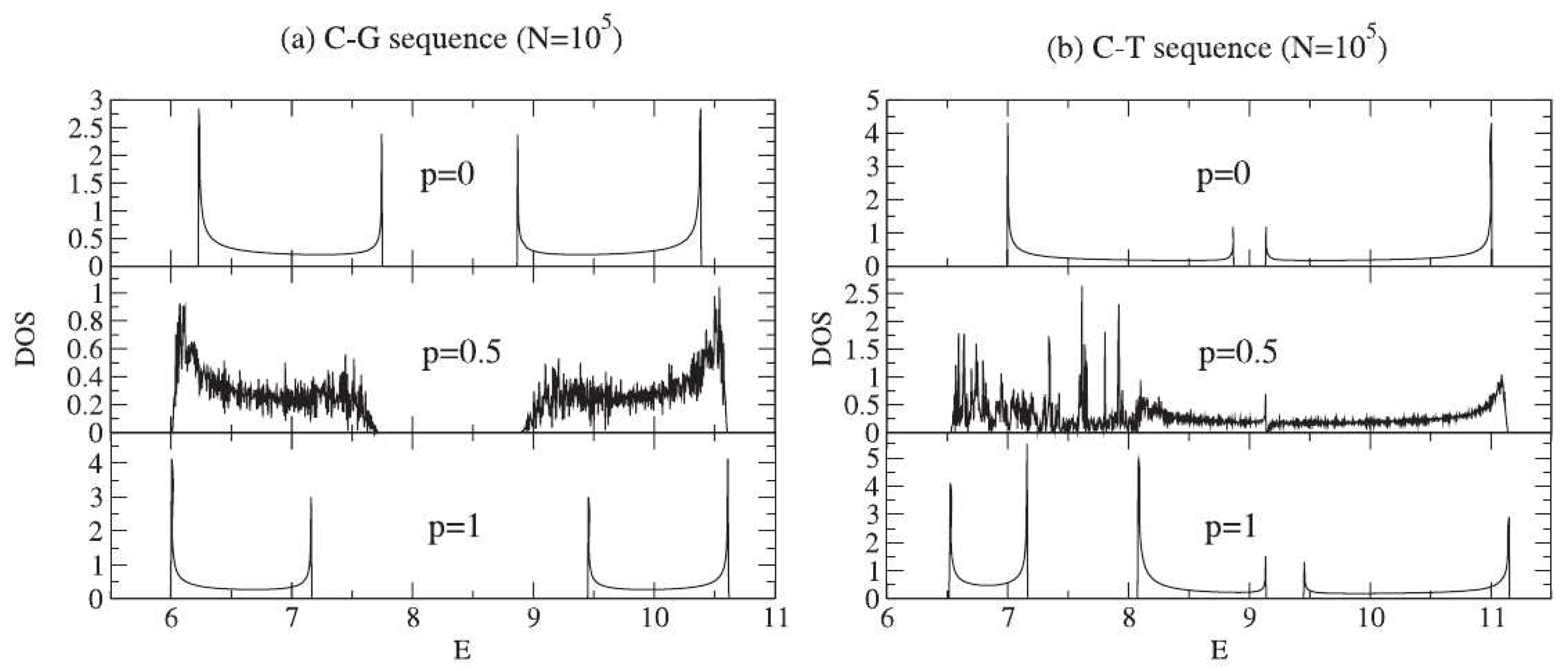
- De Oliveira, B.P.W.; Albuquerque, E.L.; Vasconcelos, M.S. Electronic density of states in sequence dependent DNA molecules. Surf. Sci. 2006, 600, 3770–3774. [Google Scholar] [CrossRef]
- De Moura, F.A.B.F.; Lyra, M.L.; Albuquerque, E.L. Electronic transport in poly(CG) and poly(CT) DNA segments with diluted base pairing. J. Phys. Condens. Matter 2008, 20, 075109. [Google Scholar] [CrossRef]
- De Moura, F.A.B.F.; Lyra, M.L.; de Almeida, M.L.; Ourique, G.S.; Fulco, U.L.; Albuquerque, E.L. Methylation effect on the ohmic resistance of a poly-GC DNA-like chain. Phys. Lett. A 2016, 380, 3559–3563. [Google Scholar] [CrossRef]
- MaciáBarber, E. Aperiodic Structures in Condensed Matter: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar] [CrossRef]
- Maciá, E.; Triozon, F.; Roche, S. Contact-dependent effects and tunneling currents in DNA molecules. Phys. Rev. B 2005, 71, 113106. [Google Scholar] [CrossRef] [Green Version]
- Mason, J.; Handscomb, D.C. Chebyshev Polynomials; Chapman and Hall/CRC: London, UK, 2002. [Google Scholar]
- Malakooti, S.; Hedin, E.R.; Kim, Y.D.; Joe, Y.S. Enhancement of charge transport in DNA molecules induced by the next nearest-neighbor effects. J. Appl. Phys. 2012, 112, 094703. [Google Scholar] [CrossRef]
- Landauer, R. Spatial Variation of Currents and Fields Due to Localized Scatterers in Metallic Conduction. IBM J. Res. Dev. 1957, 1, 223–231. [Google Scholar] [CrossRef]
- Buttiker, M. Symmetry of electrical conduction. IBM J. Res. Dev. 1988, 32, 317–334. [Google Scholar] [CrossRef]
- Roche, S.; Maciá, E. Electronic Transport and Thermopower in Aperiodic DNA Sequences. Mod. Phys. Lett. B 2004, 18, 847–871. [Google Scholar] [CrossRef]
- Plazas, C.A.; Fonseca-Romero, K.M.; Rey-González, R.R. Insulator-to-Semiconductor-to-Conductor Phase-Like Transition of DNA Chains. J. Nanosci. Nanotechnol. 2018, 18, 5042–5048. [Google Scholar] [CrossRef]
- Kundu, S.; Karmakar, S.N. Conformation dependent electronic transport in a DNA double-helix. AIP Adv. 2015, 5, 107122. [Google Scholar] [CrossRef] [Green Version]
- Joe, Y.S.; Lee, S.H.; Hedin, E.R.; Kim, Y.D. Temperature and Magnetic Field Effects on Electron Transport Through DNA Molecules in a Two-Dimensional Four-Channel System. J. Nanosci. Nanotechnol. 2013, 13, 3889–3896. [Google Scholar] [CrossRef]
- De Almeida, M.L.; Oliveira, J.I.N.; Lima Neto, J.X.; Gomes, C.E.M.; Fulco, U.L.; Albuquerque, E.L.; Freire, V.N.; Caetano, E.W.S.; de Moura, F.A.B.F.; Lyra, M.L. Electronic transport in methylated fragments of DNA. Appl. Phys. Lett. 2015, 107, 203701. [Google Scholar] [CrossRef]
- Oliveira, J.I.N.; Albuquerque, E.L.; Fulco, U.L.; Mauriz, P.W.; Sarmento, R.G.; Caetano, E.W.S.; Freire, V.N. Conductance of single microRNAs chains related to the autism spectrum disorder. EPL 2014, 107, 68006. [Google Scholar] [CrossRef]
- Sarmento, R.G.; Silva, R.N.O.; Madeira, M.P.; Frazão, N.F.; Sousa, J.O.; Macedo-Filho, A. Electronic Transport in Single-Stranded DNA Molecule Related to Huntington’s Disease. Braz. J. Phys. 2018, 48, 155–159. [Google Scholar] [CrossRef]
- Walker, F.O. Huntington’s disease. Lancet 2007, 369, 218–228. [Google Scholar] [CrossRef]



| Model | L | |||
|---|---|---|---|---|
| WM | 1 | |||
| LM | 2 | |||
| ELM | 2 | |||
| FM | 3 | |||
| FLM | 4 |
| Sequence | Substitution Rule | S | |
|---|---|---|---|
| Fibonacci | s(A) = AB s(B) = A | ||
| Precious means | s(A) = AB s(B) = A | ||
| Fibonacci-class | s(A) = BAB s(B) = BA | ||
| Mixed means | s(A) = ABs(B) = A | ||
| Metallic means | s(A) = ABs(B) = A | ||
| Period doubling | s(A) = AB s(B) = AA | ||
| Thue–Morse | s(A) = AB s(B) = BA | ||
| Rudin–Shapiro | |||
| s(A) = AB s(B) = AC | |||
| s(C) = DB s(D) = DC | |||
| Triadic Cantor set | s(A) = ABA s(B) = BBB | ||
| Asymmetric Cantor set | s(A) = ABAA s(B) = BBBB | ||
| Generalized Cantor set | s(A) = ABAs(B) = B | ||
| Kolakoski | s(A) = ABs(B) = AB | ||
| Kolakoski | |||
| , | s(A) = ABCs(B) = ABC | ||
| C | s(C) = ABC | ||
| Kolakoski () or | undefinable | ||
| () |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lambropoulos, K.; Simserides, C. Tight-Binding Modeling of Nucleic Acid Sequences: Interplay between Various Types of Order or Disorder and Charge Transport. Symmetry 2019, 11, 968. https://doi.org/10.3390/sym11080968
Lambropoulos K, Simserides C. Tight-Binding Modeling of Nucleic Acid Sequences: Interplay between Various Types of Order or Disorder and Charge Transport. Symmetry. 2019; 11(8):968. https://doi.org/10.3390/sym11080968
Chicago/Turabian StyleLambropoulos, Konstantinos, and Constantinos Simserides. 2019. "Tight-Binding Modeling of Nucleic Acid Sequences: Interplay between Various Types of Order or Disorder and Charge Transport" Symmetry 11, no. 8: 968. https://doi.org/10.3390/sym11080968
APA StyleLambropoulos, K., & Simserides, C. (2019). Tight-Binding Modeling of Nucleic Acid Sequences: Interplay between Various Types of Order or Disorder and Charge Transport. Symmetry, 11(8), 968. https://doi.org/10.3390/sym11080968






