1. Introduction
It is well known that several problems in control and system theory are closely related to a generalized Sylvester matrix equation of the form
where
and
F are given matrices of conforming dimensions. Equation (
1) includes the following special cases:
known respectively as the Sylvester equation, the Lyapunov equation, and the Kalman–Yakubovich equation. Equations (
1)–(
4) have important applications in stability analysis, optimal control, observe design, output regulation problem, and so on; see e.g., [
1,
2,
3]. Equation (
1) can be solved directly using the vector operator and the Kronecker product. Here, recall that the vector operator
turns each matrix into a column vector by stacking its columns consecutively. The Kronecker product of two matrices
and
B is defined to be the block matrix
. In fact, Equation (
1) can be reduced to the linear system
Thus, (
1) has a unique solution if and only if
P is non-singular. In particular for the Sylvester Equation (
2), the uniqueness of the solution is equivalent to the condition that
A and
have no common eigenvalues. For Equation (
4), the uniqueness condition is that all possible products of the eigenvalues of
A and
B are not equal to
. The exact solution
is, in fact, computationally difficult due to the large size of the Kronecker multiplication. This inspires us to investigate certain iterative schemes to generate a sequence of approximate solutions, which are arbitrarily close to the exact solution. Efficient iterative methods produce a satisfactory approximated solution in a small iteration number.
Many researchers have developed such iterative methods for solving a class of matrix Equations (
1)–(
4); see e.g., [
4,
5,
6,
7,
8,
9,
10]. One of an interesting iterative method, called the Hermitian and skew Hermitian splitting iterative method (HSS), was investigated by many authors, e.g., [
11,
12,
13,
14]. Gradient-based iterative methods were firstly introduced by Ding and Chen for solving (
1), (
2) and (
4). After that, there are many iterative methods for solving (
1)–(
4) based on gradients and hierarchical identification principle, e.g., [
15,
16,
17]. Convergence analyses of such methods are often relied on the Frobenius norm
and the spectral norm
, defined for each matrix
A by
Method 1 ([
15])
. Assume that the matrix Equation (1) has a unique solution X. ConstructIf we choose , then the sequence converges to the exact solution X for any given initial matrices .
A least-squares based iterative method for solving (
1) was introduced as follows:
Method 2 ([
15])
. Assume that the matrix Equation (1) has a unique solution X. For each construct,If we choose , then the sequence converges to the exact solution X for any given initial matrices .
In this paper, we propose a gradient-based iterative method with an optimal convergent factor (GIO) for solving the generalized Sylvester matrix Equation (
1). This method is derived from least-squares optimization and hierarchical identification principle (see
Section 2). Convergence analysis (see
Section 3) reveals that the sequence of approximated solutions converges to the exact solution for any initial value if and only if the convergent factor is chosen properly. Then we discuss the convergent rate and error estimates for the method. Moreover, the convergent factor will be determined so that the convergent rate is fastest, or equivalently, the spectral radius of associated iteration matrix is minimized. In particular, the GIO method can solve the Sylvester Equation (
2) (see
Section 4). To illustrate the efficiency of the proposed method, we provide numerical experiments in
Section 5. We compare the efficiency of our method for solving (
2) with other iterative methods such as gradient based iterative method (GI) [
15], least-squares iterative method (LS) [
17], relaxed gradient based iterative method (RGI) [
18], modified gradient based iterative method (MGI) [
19], Jacobi-gradient based iterative method (JGI) [
20,
21] and accelerated Jacobi-gradient based iterative method AJGI [
22]. In
Section 6, we apply the GIO method to the convection–diffusion and the diffusion equation. Finally, we conclude the overall work in
Section 7.
2. Introducing a Gradient Iterative Method
Let us denote by
the set of
real matrices. Let
be such that
Consider the matrix Equation (
1) where
,
,
are given constant matrices and
is an unknown matrix to be found. Suppose that (
1) has a unique solution, i.e., the matrix
P is invertible. Now, we discuss how to solve (
1) indirectly using an effective iterative method. According to the hierarchical identification principle, the system (
1) is decomposed into
p subsystems. For each
, set
Our aim is to approximate the solution of
p subsystems:
so that the following least-squares error is minimized:
The gradient of each
can be computed as follows:
Let
be the estimate or iterative solution at iteration
k, associated with the subsystem (
6). From the gradient formula (
8), the iterative scheme for
is given by the following equation:
where
is a convergent factor. According to the hierarchical identification principle, the unknown parameter
X in (
9) is replaced by its estimate
. After taking the arithmetic mean of
, we obtain the following process:
Method 3. Gradient-based iterative method with optimal convergent factor
Initializing step: For , set and Choose . Set . Choose initial matrix
Updating step: For to end, do: Note that the terms were introduced in order to eliminate duplicated computations. To stop the process, one may impose a stopping rule such as the relative error is less than a tolerance error . The convergence property of this method depends on the convergent factor . A discussion of possible/optimal values of will be presented in the next section.
3. Convergence Analysis
In this section, we show that the approximated solutions derived from Method 3 converge to the exact solution. First, we transform a recursive equation of the error of approximated solutions into a first-order linear iterative system where is a vector and T is an iteration matrix. Then, we investigate the iteration matrix T to obtain the convergence rate and error estimations. Finally we discuss the fastest convergent factor and find the number of iterations corresponding to a given satisfactory error.
Theorem 1. Assume that the matrix Equation (1) has a unique solution X. Let . Then the approximate solutions derived from (9) converge to the exact solution for any initial value if and only if In this case, the spectral radius of the associated iteration matrix is given by Proof. At each
k-th iteration, consider the error matrix
. We have
We shall show that
by showing that
or
By taking the vector operator to the above equation, we get
We see that (
12) is a first-order linear iterative system in the form
. Thus,
for any initial values
if and only if the iteration matrix
T has spectral radius less than 1. Since
T is symmetric, all its eigenvalues are real. Note that any eigenvalue of
T is of the form
where
is an eigenvalue of
. Thus, its spectral radius is given by (
11). It follows that
if and only if
Since
P is invertible, the matrix
is positive definite. Thus,
. The condition (
13) now becomes
Hence, we arrive at (
10). □
Theorem 2. Assume the hypothesis of Theorem 1, so that the sequence converges to the exact solution X for any initial value .
- (1).
We have the following error estimates Moreover, the asymptotic convergence rate of Method 3 is governed by in (11). - (2).
Let be a satisfactory error. We have after the k-th iteration for any that satisfies
Proof. According to (
12), we have
Since
T is symmetric, we have
. Thus for each
, the approximation (
14) holds. By induction, we obtain the estimation (
15). The estimate (
15) implies that the asymptotic convergence rate of the method depends on
. To prove the assertion, we have by taking logarithms that the condition (
16) is equivalent to
Thus if (
16) holds, then
□
The convergence rate exhibits how fast of the approximated solutions converge to the exact solution. Theorem 2 reveals that the smaller the spectral radius
, the faster the approximated solutions go to the exact solution. Moreover, by taking
in (
16), we have that
has an accuracy of
n decimal digits if
k satisfies
Recall that the condition number of a matrix
A (relative to the spectral norm) is defined by
Theorem 3. Assume the hypothesis of Theorem 1. Then the optimal value of for which Method 3 has the fastest asymptotic convergence rate is determined by In this case, the spectral radius of the iteration matrix is given by Proof. The convergence of Method 3 implies that (
10) holds. Then, Method 3 has the convergence rate as the same to the linear iteration (
12), and thus, it is governed by the spectral radius
in (
11). The fastest convergence rate is equivalent to the smallest of
. Thus, we make the following minimization:
Thus, the optimal value is reached at (
17) so that the minimum is given by (
18). □
We see that if the condition number of P is closer to 1 then the approximate solutions converge faster to the exact solution. Note that the condition number of P is close to 1 if and only if the maximum eigenvalue of is close to the minimum eigenvalue of .
4. The GIO Method for the Sylvester Equation
In this section, we discuss the gradient-based iterative method with optimal convergent factor for solving Sylvester matrix equation. Moreover we discover convergence criteria, convergence rate, error estimate and optimal factor.
Let
be such that
and
. Consider the Sylvester matrix Equation (
2) where
,
,
are given constant matrices and
is an unknown matrix to be found. Suppose that (
2) has a unique solution, i.e.,
is invertible, or equivalently,
A and
have no common eigenvalues.
Method 4. Initializing step: Set Choose . Set . Choose initial matrix .
Updating step: For to end, do: Corollary 1. Assume that the Sylvester matrix Equation (2) has a unique solution X. Let . Then the following hold: - (i)
The approximate solutions generated by Method 4 converge to the exact solution for any initial value if and only if In this case, the spectral radius of the associated iteration matrix is given by - (ii)
The asymptotic convergence rate of Method 4 is governed by in (20). - (iii)
The optimal value of for which Method 4 has the fastest asymptotic convergence rate is determined by
Remark 1. Note that Q is the Kronecker sum of A and . Thus, if A and B are positive semidefinite, then 5. Numerical Examples for Generalized Sylvester Matrix Equation
In this section, we show the capability and efficiency of the proposed method by illustrating some numerical examples. To compare the performance of any algorithms, we must use the same PC environment, and consider informed errors together with iteration numbers (IT) and computational times (CT: in seconds). Our iterations have been carried out by MATLAB R2013a, Intel(R) Core(TM) i5-760 CPU @ 2.80 GHz, RAM 8.00 GB PC environment. We measure the computational time taken for an iterative process by the MATLAB functions tic and toc. In Example 1, we show that our method is also efficient although matrices are non-square and we discuss the effect of changing the convergent factor . In Example 2, we consider a larger square matrix system and show that our method is still efficient. In Example 3, we compare the efficiency of our method to another recent iterative methods. The matrix equation considered in this example is the Sylvester equation with square coefficient matrices since it fits with all of the recent methods. In all illustrated examples, we compare the efficiency of iterative methods to the direct method mentioned in Introduction. Let us denote by the tridiagonal matrix with main diagonal and w.
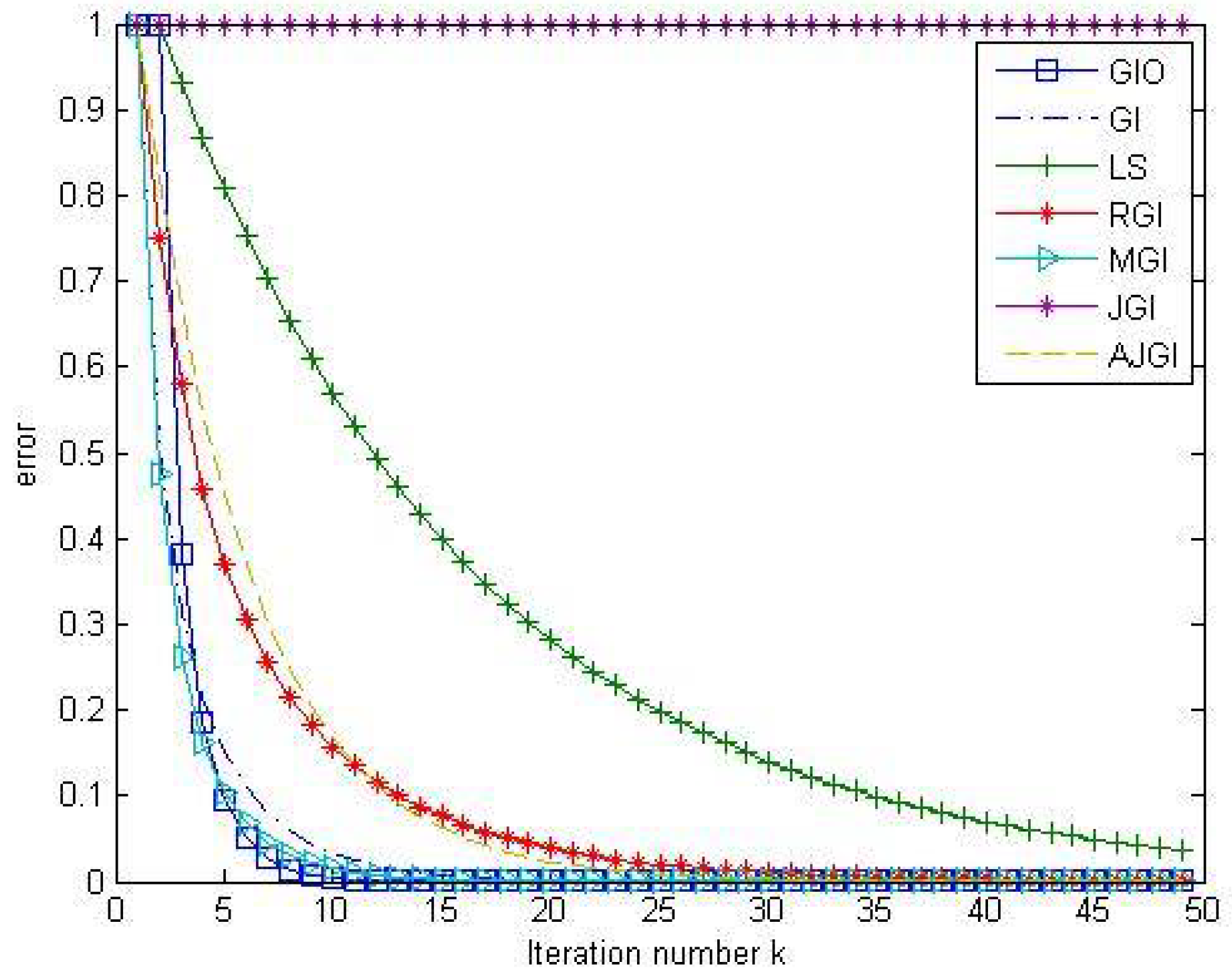
Example 1. Consider the matrix equation when , and are tridiagonal matrices given by Here, the exact solution is given by . We apply Method 3 to compute the sequence of approximated solutions. Take initial point The optimal convergent factor can be computed as follows: The effect of changing convergent factors τ is illustrated in Figure 1. We see that as k large enough, the relative error for goes faster to 0 than for other convergent factors. If τ does not satisfy the condition (10), then the approximated solutions diverge for the given initial matrices. Moreover, Table 1 shows that the computational time of our algorithm (GIO) is significantly less than the time of the direct method. Table 1 also demonstrates that, when we fix the error to be less than , the GIO algorithm outperforms another GI algorithms with different convergent factors in both iteration numbers and computational times. Example 2. Consider the matrix equation where all matrices are tridiagonal matrices given by Here, the exact solution is . To apply Method 3, we take initial matrix We can compute Figure 2 shows that the relative error for goes faster to 0 than for other convergent factors. If τ does not satisfy (10), then the approximate solutions diverge for the given initial matrices. From Table 2, we see that the computational time of our algorithm is significantly less than the time of the direct method. Furthermore, when the satisfactory error is less than , the GIO algorithm has more efficiency than another GI algorithms in both iteration numbers and computational times. Example 3. Consider the Sylvester equation , where are given by We compare the efficiency of our method (GIO) with another iterative methods such as GI, LS, RGI, MGI, JGI and AJGI. We choose the same convergent factor and the same initial matrix . To compare the efficiency of these methods, we fix the iteration number to be 50 and consider the relative errors . The results are displayed in Figure 3. The iteration numbers and the computational times when we fix the error to be less than are illustrated in Table 3. We see that our method is outperform to the direct method and another iterative methods with less iteration number and lower computational time. In particular, the approximated solutions generated from JGI method diverge. 6. An Application to Discretization of the Convection-Diffusion Equation
In this section, we apply the GIO method to a discretization of convection–diffusion equation in the form
where
and
are the convection and diffusion coefficients, respectively. Equation (
22) is accompanied by the initial condition
and boundary conditions
where
are given functions. To make a discretization of Equation (
22), we divide
into
M subintervals, each of equal length
In the same manner, we define a grid for the N subintervals
Then we make discretization at the grid point
where
for
and
By applying the forward time central space method, we have
Rearranging the above equation leads to
where
and
are the convection and diffusion numbers, respectively. We can transform (
22) into a linear system of
unknowns
in the form
where
has
blocks of the form
on its diagonal and
under its diagonal. The vector
b is partitioned in
M blocks as
where
and
here
We can see that Equation (
24) is the generalized Sylvester equation where
,
,
,
and
. From Method 3, we obtain the following:
Method 5. Input as number of partition. Set .
Initializing step: Choose . For each and , compute , as in Equation (23) and Updating step: For to end, do: To stop the method, one may impose a stopping rule such as where ϵ is a tolerance error.
Now, we provide a numerical experiment for a convection-diffusion equation.
Example 4. Consider the convection–diffusion equationwith the initial and boundary conditions given as: Let , so that is of dimension . In this case, we have and We choose
After compiling Method 5 for 100 iterations, we see from Figure 4 that the relative error goes faster to 0 than for other methods such as GI, LS, RGI, MGI, JGI and AJGI. Moreover, Table 4 displays comparison of numerical and direct solutions for the convection–diffusion equation. A particular case
of Equation (
22) is called the diffusion equation. In this case, the formulas of
and
are reduced as
Example 5. Consider the diffusion equation with the initial and boundary conditions given as: Let In this case, we have and We choose initial matrix
After compiling Method 5 for 200 iterations (Figure 5), we see that our method is outperform to another iterative methods with less iteration number and lower computational time. The 3D-plot in Figure 6 shows that the iterative solution is well approximated to the exact solution.