Homomorphic Encryption-Based Robust Reversible Watermarking for 3D Model

Abstract

Robust reversible watermarking in an encrypted domain is a technique that preserves privacy and protects copyright for multimedia transmission in the cloud. In general, most models of buildings and medical organs are constructed by three-dimensional (3D) models. A 3D model shared through the internet can be easily modified by an unauthorized user, and in order to protect the security of 3D models, a robust reversible 3D models watermarking method based on homomorphic encryption is necessary. In the proposed method, a 3D model is divided into non-overlapping patches, and the vertex in each patch is encrypted by using the Paillier cryptosystem. On the cloud side, in order to utilize addition and multiplication homomorphism of the Paillier cryptosystem, three direction values of each patch are computed for constructing the corresponding histogram, which is shifted to embed watermark. For obtaining watermarking robustness, the robust interval is designed in the process of histogram shifting. The watermark can be extracted from the symmetrical direction histogram, and the original encrypted model can be restored by histogram shifting. Moreover, the process of watermark embedding and extraction are symmetric. Experimental results show that compared with the existing watermarking methods in encrypted 3D models, the quality of the decrypted model is improved. Moreover, the proposed method is robust to common attacks, such as translation, scaling, and Gaussian noise.

1. Introduction

Due to the development of outsourced storage in the cloud, reversible watermarking in an encrypted domain has been developed for security in the cloud [1,2,3,4]. However, the cloud cannot introduce distortion of original content during watermark embedding. Therefore, the reversible watermarking method is required [5,6]. In addition, the watermark carrier is vulnerable during transmission, and the embedded watermark is expected to resist common attacks [7,8]. Therefore, robust reversible watermarking in an encrypted domain has greatly attracted researchers for potential applications.

In general, watermarking can be divided into robust and fragile watermarking methods in terms of their robustness. Robust watermarking [9] is used to protect security and resist attacks, while fragile watermarking [10,11] is used to provide integrity authentication. For the occasions with high data security requirements, such as judicial authentication, medical images, etc., more researchers focus on fragile watermarking in the encrypted domain.

Reversible watermarking in the encrypted domain can be divided into reserving room before encryption (RRBE) and vacating room after encryption (VRAE). The RRBE method reserves embedding room before encrypting the original image [12,13,14,15]. For example, the vacated bits, which are reserved by self-embedding before encryption, can be substituted by the watermark in the encrypted domain [4]. With the development of reversible watermarking [16,17], the original image can be restored absolutely after extracting the watermark. The second type directly implements watermark embedding by modified the encrypted image [18,19] after encryption. For instance, Xiang divided the original image into patches to be encrypted, and then the histogram of statistical values was calculated in the encrypted domain for shifting to embed watermark [20].

However, these methods are only applied to images, and cannot be used in 3D models directly due to different structures between images and 3D models. Ke et al. proposed a robust watermarking method on the basis of self-similarity [21]. In that method, a 3D model is divided into patches, and watermark bits were embedded by changing the local vector length of a point in each patch. Feng et al. divided a 3D model into patches, then embedded a watermark into each patch by modulating angle quantization [22]. However, those methods are not reversible. Jiang et al. proposed a 3D model watermarking method on the basis of stream cipher encryption [1]. The watermark was embedded by flipping the least significant bits (LSBs) of the vertex coordinates. Since the original 3D models have high spatial correlation, the watermark can be extracted successfully. Shah proposed a watermarking method based on the homomorphic Paillier cryptosystem, which used VRAE framework to vacate space before encryption [2]. However, those methods are fragile to attacks and cannot protect their copyrights.

To our best of knowledge, although the aforementioned watermarking methods on encrypted 3D models have been developed, the research on robustness for encrypted 3D models is rarely reported. In this paper, in order to protect the security of a 3D model in the cloud, we proposed a homomorphic encryption-based robust reversible watermarking method. In this method, the original model is first divided into patches to facilitate patch encryption using the Paillier cryptosystem. Then, the watermark is embedded by constructing the symmetrical direction histogram and shifting histogram in the encrypted domain, and the robust interval is reserved during the histogram shifting. Last, the receiver extracts the watermark in the encrypted model or the decrypted model by constructing a direction histogram of patches, and restores the original model through the method of histogram shifting which is the opposite to the embedding process. The contributions of the paper are organized as follows.

(1) The proposed method can directly construct direction histogram in the encrypted model so that the watermark can be extracted and the original encrypted model can be restored in the encrypted domain.

(2) The proposed method is robust to several common attacks by reserving the robust interval during the histogram shifting for watermark embedding.

(3) The proposed method not only has higher security and capacity, but also has less distortion compared with the original model.

The rest of this paper is organized as follows. In the second part, the Paillier cryptosystem is briefly introduced. In the third part, the related robust reversible watermarking method flow is proposed. The experimental results are shown in Section 4. The conclusions of the thesis are discussed in Section 5.

2. Paillier Cryptosystem

The Paillier cryptosystem [23], which was proposed by Paillier Pascal in 1999, has homomorphism and probability. Homomorphism means that one arithmetic operation of two ciphertexts are equal to another arithmetic operation of two corresponding plaintext. Moreover, homomorphism includes addition and multiplication homomorphism. Probability means that different ciphertexts, which are obtained by encrypting the same plaintext with different parameters, can be decrypted to the same plaintext. The following describes the processes of key generation, encryption, and decryption, two properties, and the application of modular multiplication inverse (MMI) [24] in the Paillier cryptosystem.

• Key Generation

Randomly pick up two large primes numbers $p$ and $q$. Calculate $N=pq$ and $\lambda =lcm(p-1,q-1)$, where $lcm(\cdot )$ stand for the lowest common multiple. Afterwards, select $g\in Z_{N^2}^{\ast }$ randomly, which satisfies

$$\gcd (L(g^{\lambda }\mathrm{mod}{N}^2),N)=1$$

(1)

where $L(u)=(u-1)/N$, and $\gcd (\cdot )$ means the greatest common divisor of two inputs. $Z_{N^2}=\{0,1,2,\dots ,N^2-1\}$ and $Z_{N^2}^{\ast }$ are the numbers in $Z_{N^2}$ which prime with $N^2$. Finally, we get the public key $(N,g)$ and corresponding private key $\lambda$.

• Encryption

Select a parameter $r\in Z_{N^2}^{\ast }$ randomly. The plaintext $m\in Z_N$ can be encrypted to the corresponding ciphertext $c$ by

$$c=E[m,r]=g^m\cdot r^N\mathrm{mod}{N}^2$$

(2)

where $E[\cdot ]$ denotes the encryption function. Due to the nature of the Paillier cryptosystem, for the same plaintext $m$, different ciphertexts $c$ can be obtained by choosing different $r$. After decryption, different ciphertexts can be restored to the same plaintext $m$, which ensures the security of the ciphertext.

• Decryption

The original plaintext $m$ can be obtained by

$$m=D[c]=\frac{L(c^{\lambda }\mathrm{mod}{N}^2)}{L(g^{\lambda }\mathrm{mod}{N}^2)}\mathrm{mod}N$$

(3)

Moreover, two important characteristics are described as follows (which has been applied in the proposed method).

• Lemma One

For two plaintexts $m_1,m_2\in Z_N$, compute corresponding ciphertexts $c_1,c_2$ with $r_1,r_2$ according to Equation (1), respectively. The Equation $c_1=c_2$ holds if and only if $m_1=m_2$ and $r_1=r_2$.

• Homomorphic Multiplication

For $\forall r_1,r_2\in Z_N^{\ast }$, two plaintexts $m_1,m_2\in Z_N$ and corresponding ciphertexts $E[m_1,r_1],E[m_2,r_2]\in Z_{N^2}^{\ast }$ satisfy

$$c_1\cdot c_2=E[m_1,r_1]\cdot E[m_2,r_2]=g^{m_1+m_2}\cdot {(r_1\cdot r_2)}^N\mathrm{mod}{N}^2$$

(4)

$$D[c_1\cdot c_2]=D[E[m_1,r_1]\cdot E[m_2,r_2]\mathrm{mod}{N}^2]=m_1+m_2\mathrm{mod}N$$

(5)

The original Paillier cryptosystem only has addition homomorphism and multiplication homomorphism. The subtraction homomorphism can be achieved through modular multiplication inverse (MMI).

• Modular Multiplication Inverse (MMI)

For two coprime integers $y$ and $z$, the existence of an integer $\theta$ satisfies

$$\theta \cdot y=1\mathrm{mod}z$$

(6)

where $\theta$ is called the modular multiplicative inverse of $y$, and $\theta$ can be obtained according to the extended Euclidean method [25].

3. The Proposed Method

In order to protect the security of 3D model in the cloud, a homomorphic encryption-based robust reversible watermarking method is proposed. Figure 1 shows the flowchart of the proposed method. Firstly, the original model is divided into patches, and vertices in each patch are encrypted using the Paillier cryptosystem. In the cloud, three direction values of each patch are computed, and the direction histogram is constructed for shifting to embed the watermark. At last, the watermark can be extracted from direction histogram, and the original 3D model can be restored by histogram shifting.

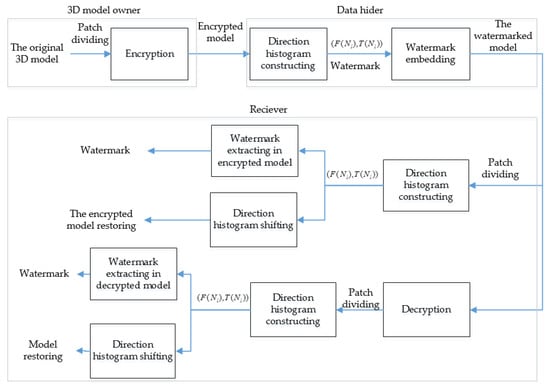
Figure 1. Flowchart of the proposed method.

3.1. Preprocessing

Because the input of the Paillier cryptosystem should be a positive integer, the vertex coordinates firstly are converted from decimal to positive integer.

3D models are consisted of vertex data and connectivity data. The vertex data includes the coordinates of each vertex in the spatial domain. The connectivity data reflects the connection relationship between vertices. A 3D model devil and its local region are illustrated in Figure 2. Each vertex and each face of the 3D model have a corresponding index number, respectively. For a 3D model $M$, let ${\left\{v_i\right\}}_{i=0}^{N_V}$ represents the sequence of vertices, where $v_i=(v_{i,x},v_{i,y},v_{i,z})$ and $N_V$ is the number of vertices. Note that each coordinate $\left|v_{i,j}\right|<1,j\in \{x,y,z\}$, and the significant digit of each coordinate is 6.

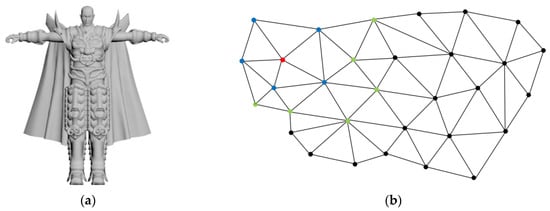
Figure 2. A 3D model devil; (a) original model, (b) local region.

Normally, uncompressed vertices are 32-bit floating point numbers with a precision of 6 digits. The first four significant digits of vertex coordinates can accurately display the 3D model. Therefore, the vertex coordinates are converted into an integer with four significant digits by using Equation (7).

$${v^{\prime }}_{i,j}=\lfloor v_{i,j}\cdot {10}^4\rfloor ,j\in \{x,y,z\}$$

(7)

Moreover, all vertex coordinates should be converted to positive integers for encryption by using Equation (8).

$${v^{\prime }}_{i,j}={v^{\prime }}_{i,j}+10000,j\in \{x,y,z\}$$

(8)

After preprocessing, the pre-processed 3D model is computed, and denoted as $M^{\prime }$.

3.2. Patch Dividing and Patch Encryption

The section describes how to divide the model into several non-overlapping patches and perform encryption by using the Paillier cryptosystem.

3.2.1. Patch Dividing

For the vertex of the 3D model, if two vertices $v_i$ and $v_k$ are connected by a edge, $v_k$ is a neighbor of $v_i$. All neighbors of $v_i$ constitute the 1-ring neighborhood of $v_i$, and all 1-ring neighborhood of the neighbors of the vertex $v_i$ constitute its 2-ring neighborhood. $N(v_i)$ is the 2-ring neighborhood of the vertex $v_i$, and $N(v_i)$ is computed by

$$N(v_i)=\left\{v_k\right|0\le \left|v_i{v}_k\right|\le 2,k=0,1,\dots ,N_V\}$$

(9)

where $N_V$ are the number of the vertices of the 3D model, and $\left|v_i{v}_k\right|$ represents the number of vertices between $v_i$ and $v_k$. As illustrated in Figure 2, the blue vertices are the 1-ring neighborhood of the red vertex, and the green vertices are the 2-ring neighborhood of the red vertex.

When the 3D model is divided into patches, it is necessary to ensure patches do not overlap each other. Suppose that the unclassified and classified sets are $S_Y$ and $S_N$, respectively. $S_Y={\left\{v_i\right\}}_{i=0}^{N_V}$ and $S_N$ are initially empty. Suppose that the $l^{th}$ patch is denoted as $P^{(l)}$. A 3D model is divided into patches by the following rules, and initially $l=1$.

Step 1: The first vertex $v_i$ is selected according to the order of vertex index, and $v_i$ and its 1-ring neighborhood are used as the $P^{(l)}$. Vertices in $P^{(l)}$ are sorted by

$$P^{(l)}(p)=\{\begin{array}{ll}{v}_i,& p=1\\ v_k,& p=2,3,\dots N_l\end{array}$$

(10)

where $N_l$ is the number of vertices in $P^{(l)}$.

Step 2: Update the unclassified set and the classified set by using Equation (11).

$$S_N=S_N\cup N(v_i),S_Y=S_Y-N(v_i)$$

(11)

where $S_N\cup N(v_i)$ is the union of two sets, and $S_Y-N(v_i)$ is the vertex set that exist in $S_Y$ but not in $N(v_i)$. $N(v_i)$ is put into the classified set for ensuring patches do not overlap each other.

Step 3: Determine whether the unclassified set $S_Y$ is empty. If $S_Y$ is empty, then the division of patches ends. If $S_Y$ is not empty, then continue to select the $(l+1{)}^{th}$ patch from Step 1, until $S_Y$ is empty.

As illustrated in Figure 3, the local region of 3D model devil can be divided into five patches, and each color in Figure 3 represents a patch.

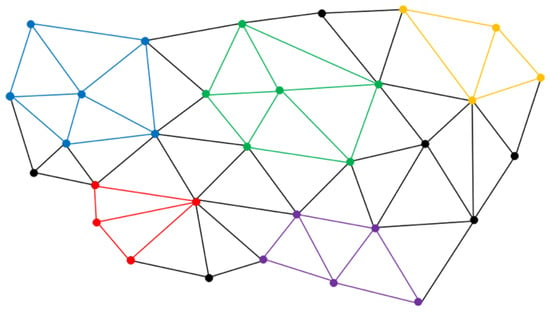
Figure 3. Patch dividing of 3D model devil.

3.2.2. Patch Encryption

Let $P^{(l)}(p,j),j\in \{x,y,z\}$ be the $j$-axis coordinates of the $p^{th}$ vertex in $P^{(l)}$. Referring to Equation (2), an integer $r_1(l)\in Z_N^{\ast }$ can be randomly selected to encrypt $P^{(l)}(p,j)$ with the public key $(N,g)$.

$$C^{(l)}(p,j)=E[P^{(l)}(p,j),r_1(l)]=g^{P^{(l)}(p,j)}\cdot r_1{(l)}^N\mathrm{mod}{N}^2$$

(12)

where $p\in [1,N_l],j\in \{x,y,z\}$, $C^{(l)}$ denotes the encrypted vertex coordinates, and $E[M^{\prime }]$ represents the encrypted model.

3.3. Watermark Embedding

Firstly, three direction values of each patch in ciphertext are computed. Then, according to the possible values of the direction in ciphertext, the mapping table is constructed to map the direction values in ciphertext to the direction values in plaintext. The direction histogram is constructed by counting the direction values of all patches. Lastly, the watermark is embedded by histogram shifting.

3.3.1. Three Direction Values Calculation of Each Patch

In order to calculate three direction values of each patch, a vector $M(p)$ is defined by using Equation (13).

$$M(p)=\{\begin{array}{ll}1& ifp=2,3,\dots N_l\\ -1& ifp=1\end{array}$$

(13)

Suppose that $d^{(l)}(j),j\in \{x,y,z\}$ denotes the $j$-axis direction value of the $l^{th}$ patch $P^{(l)}$, which is calculated by Equation (14).

$$d^{(l)}(j)={\displaystyle \sum _{p=2}^{N_l}[P^{(l)}(p,j)\cdot M(p)}+P^{(l)}(1,j)\cdot M(1)]$$

(14)

In the encrypted domain, without the private key $\lambda$, the encrypted vertex coordinates cannot by decrypted to obtain the vertex coordinate in plaintext, so the direction value $d^{(l)}(j)$ cannot be directly calculated. In the proposed method, the direction value in ciphertext can be calculated using the MMI method. $C^{(l)}$ represents the encrypted patch corresponding to the original patch $P^{(l)}$. In order to calculate the direction value in ciphertext, the modular multiplicative inverse ${\theta }_{C^{(l)}(p,j)}$ of $C^{(l)}(p,j)$ should be calculated through the extended Euclidean method. ${\theta }_{C^{(l)}(p,j)}$ satisfies

$${\theta }_{C^{(l)}(p,j)}\cdot C^{(l)}(p,j)=1\mathrm{mod}{N}^2$$

(15)

For the $l^{th}$ patch, the vectors $M_1^{(l)}$ and $M_2^{(l)}$ are defined by using Equations (16) and (17), respectively.

$$M_1^{(l)}(p,j)=\{\begin{array}{ll}{C}^{(l)}(p,j)& ifp=2,3,\dots N_l\\ {\theta }_{C^{(l)}(p,j)}& ifp=1\end{array}$$

(16)

$$M_2^{(l)}(p,j)=\{\begin{array}{ll}{\theta }_{C^{(l)}(p,j)}& ifp=2,3,\dots N_l\\ C^{(l)}(p,j)& ifp=1\end{array}$$

(17)

Since the direction value $d^{(l)}(j)$ may be negative, two direction values $c_{d1}^{(l)}(j)$ and $c_{d2}^{(l)}(j)$ are re-defined. If $d^{(l)}(j)$ is positive, $c_{d1}^{(l)}(j)$ is the ciphertext corresponding to $d^{(l)}(j)$. If $d^{(l)}(j)$ is negative, $c_{d2}^{(l)}(j)$ is the ciphertext corresponding to $d^{(l)}(j)$. $c_{d1}^{(l)}(j)$ and $c_{d2}^{(l)}(j)$ can be calculated by Equation (18).

$$\{\begin{array}{l}{c}_{d1}^{(l)}(j)=M_1^{(l)}{(1,j)}^3{\displaystyle \prod _{p=2}^{N_l}{M}_1^{(l)}(p,j)\mathrm{mod}{N}^2}\\ c_{d2}^{(l)}(j)=M_2^{(l)}{(1,j)}^3{\displaystyle \prod _{p=2}^{N_l}{M}_2^{(l)}(p,j)\mathrm{mod}{N}^2}\end{array}$$

(18)

After $c_{d1}^{(l)}(j)$ and $c_{d2}^{(l)}(j)$ are calculated, $d^{\left(l\right)}(j)$ is obtained by querying the mapping table. The following is the corresponding equation derivation and proof. To facilitate understanding, a patch consisting of four vertices is used as an example. Suppose that $P_1^{},P_2^{},P_3^{},P_4^{}$ denote the $j$-axis coordinate of the $p^{th}$ vertex as illustrated in Figure 4, and ${\widehat{c}}_1,{\widehat{c}}_2,{\widehat{c}}_3,{\widehat{c}}_4$ is the ciphertext corresponding to $P_1,P_2,P_3,P_4$. ${\theta }_1^{},{\theta }_2^{},{\theta }_3^{},{\theta }_4^{}$ is the modular multiplicative inverses corresponding to ${\widehat{c}}_1,{\widehat{c}}_2,{\widehat{c}}_3,{\widehat{c}}_4$, which satisfies

$$\{\begin{array}{l}{\theta }_1\cdot c_1={\theta }_1\cdot g^{P_1}\cdot r_1{}^N=1\mathrm{mod}{N}^2\\ {\theta }_2\cdot c_2={\theta }_2\cdot g^{P_2}\cdot r_1{}^N=1\mathrm{mod}{N}^2\\ {\theta }_3\cdot c_3={\theta }_3\cdot g^{P_3}\cdot r_1{}^N=1\mathrm{mod}{N}^2\\ {\theta }_4\cdot c_4={\theta }_4\cdot g^{P_4}\cdot r_1{}^N=1\mathrm{mod}{N}^2\end{array}$$

(19)

Figure 4. The patch with four vertices. (a) $M(p)$ correspond to the vertex. (b) The encrypted coordinate.

Then the direction value in ciphertext can be calculated by using Equation (20).

$$\{\begin{array}{l}{c}_{d1}^{}(j)=M_1^{}{(1,j)}^3{\displaystyle \prod _{p=2}^{N_l}{M}_1^{}(p,j)\mathrm{mod}{N}^2={\theta }_1{}^3\cdot {\widehat{c}}_2\cdot {\widehat{c}}_3\cdot {\widehat{c}}_4}\\ c_{d2}^{}(j)=M_2^{}{(1,j)}^3{\displaystyle \prod _{p=2}^{N_l}{M}_2^{}(p,j)\mathrm{mod}{N}^2={\widehat{c}}_1{}^3\cdot {\theta }_2\cdot {\theta }_3\cdot {\theta }_4}\end{array}$$

(20)

It can be derived to the following equation.

$$\{\begin{array}{l}{c}_{d1}^{(l)}(j)=g^{P_2+P_3+P_4}\cdot r_1{}^{3N}\cdot {\theta }_1\mathrm{mod}{N}^2\\ c_{d2}^{(l)}(j)=g^{3P_1}\cdot r_1{}^{3N}\cdot {\theta }_1\cdot {\theta }_2\cdot {\theta }_3\mathrm{mod}{N}^2\end{array}$$

(21)

According to Carmichael theory, the following equation holds.

$$\{\begin{array}{l}{g}^{N\lambda }=1\mathrm{mod}{N}^2\\ r_1{}^{N\lambda }=1\mathrm{mod}{N}^2\end{array}$$

(22)

Hence, the following equation holds.

$$g^{N\lambda }\cdot r_1{}^{N\lambda }=1\mathrm{mod}{N}^2$$

(23)

According to Equations (19) and (23), Equation (24) can be derived.

$$\{\begin{array}{l}{\theta }_1=g^{N\lambda -P_1}·r_1{}^{N(\lambda -1)}\mathrm{mod}{N}^2\\ {\theta }_2=g^{N\lambda -P_2}·r_1{}^{N(\lambda -1)}\mathrm{mod}{N}^2\\ {\theta }_3=g^{N\lambda -P_3}·r_1{}^{N(\lambda -1)}\mathrm{mod}{N}^2\\ {\theta }_4=g^{N\lambda -P_4}·r_1{}^{N(\lambda -1)}\mathrm{mod}{N}^2\end{array}$$

(24)

According to Equations (22) and (24), Equation (20) can be simplified as

$$\{\begin{array}{l}{c}_{d1}^{(l)}(j)=g^{3N\lambda +P_2+P_3+P_4-3P_1}\mathrm{mod}{N}^2\\ c_{d2}^{(l)}(j)=g^{3N\lambda +3P_1-P_2-P_3-P_4}\mathrm{mod}{N}^2\end{array}$$

(25)

3.3.2. Constructing the Mapping Table

Due to the spatial correlation of the 3D model, the vertex coordinates are relatively close in space. According to the experiments on multiple 3D model, the direction values are usually in a certain range, and the maximum direction value is usually related to the number of vertices in the patch. As illustrated in Figure 5, the blue line shows the change in the maximum direction value when the number of vertices in the patch changes. The red line is the fitted curve of the blue line, and its fitting function $F(N_l)$ satisfies

$$F(N_l)=1.925\cdot {(N_l-1)}^3-60.6\cdot {(N_l-1)}^2+528\cdot (N_l-1)-609$$

(26)

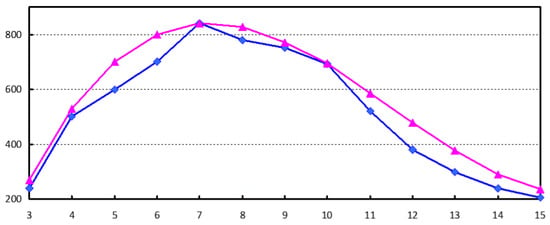
Figure 5. The blue line represents relationship between the maximum direction value and the number of vertices of the patch, and the red line is the fitted curve of the blue line.

Therefore, the direction values are all within a certain range. When the number of vertices of the patch changes, the direction values does not exceed $F(N_l)$. Moreover, in order to obtain robustness, the robust interval $T(N_l)$ is designed in the process of histogram shifting. The robust interval $T(N_l)$ is related to the number of the patch, which is defined by

$$T(N_l)=t\cdot (N_l-1)$$

(27)

where $t$ represents the strength of robustness. Hence, the change of direction values is $F(N_l)+T(N_l)$ at most.

Suppose that $d_p$ denotes the absolute of direction values, then $d_p\in [0,2F(N_l)+T(N_l)]$. With the public key, and the ciphertext $c_{d_p}$ corresponding to $d_p$ can be calculated by

$$c_{d_p}=g^{d_p}\mathrm{mod}{N}^2,d_p=0,1,2,\dots ,2F(N_l)+T(N_l)$$

(28)

Hence, the mapping table can be constructed as illustrated in Figure 6, and the direction values in ciphertext can be mapped to the direction values in plaintext through the mapping table $c_{d_p}$. The mapping method is described as follows: $c_{d_p}$ is a ciphertext set obtained by encrypting all possible values $d_p$. When $c_{{}_{d1}}^{(l)}(j)$ matches the value $c_{d_p}[m]$ in $c_{d_p}$, it indicates $d^{(l)}(j)\ge 0$, and $d^{(l)}(j)=d_p[m]$. When $c_{{}_{d2}}^{(l)}(j)$ matches the value $c_{d_p}[m]$ in $c_{d_p}$, it indicates $d^{(l)}(j)<0$, and $d^{(l)}(j)=-d_p[m]$, where $m\in [0,2F(N_l)+T(N_l))$, and $d_p[m]$ represents the $m^{th}$ value in the mapping table. Therefore, without the private key, the direction values in plaintext can be obtained by querying the mapping table.

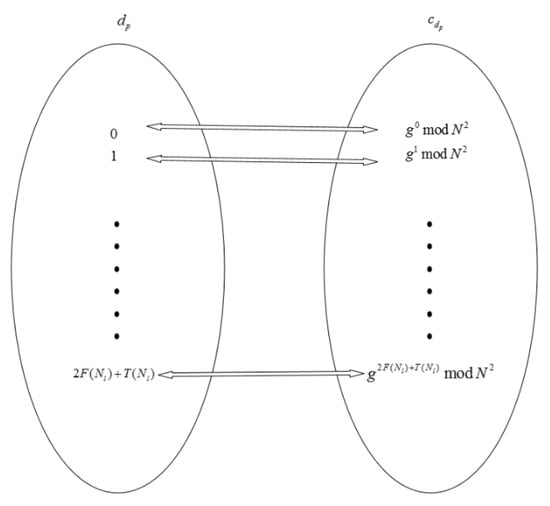
Figure 6. The mapping table.

3.3.3. Constructing the Symmetrical Direction Histogram

In the proposed method, the direction values in ciphertext are first calculated using the MMI method. Then, according to all possible direction values, the mapping table can be constructed, so the direction values in ciphertext can be mapped to direction values in plaintext. Last, the direction histogram can be constructed by counting all direction values. The direction histogram of all patches with six vertices is shown as Figure 7. It is found that most direction values are concentrated in the central area, and only a small part of the direction values are beyond the central area. Moreover, the direction histogram is symmetrical visually.

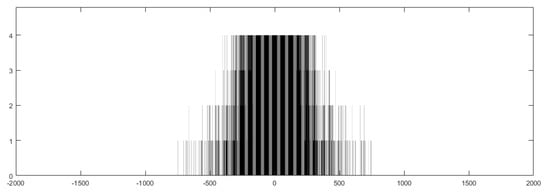
Figure 7. The direction histogram of patches with seven vertices.

3.3.4. Embedding Watermark by Histogram Shifting

In the proposed method, the watermark is embedded by shifting the direction histogram. In order to embed the watermark, the changed direction values should exceed the range of original histogram. Using $F(N_l)$ and $T(N_l)$ as embedding keys, the embedded function $B(N_l)$ is defined by Equation (29) to change the direction values.

$$B(N_l)=\lceil \frac{F(N_l)+T(N_l)}{N_l-1}\rceil =t+528+\phi (N_l-1)$$

(29)

where $\phi (N_l-1)$ is the function about $N_l-1$, $\phi (N_l-1)$ will not change, and $\lceil \cdot \rceil$ means to round up. Suppose that $\beta =t+528$, and $B(N_l)$ can be changed by modifying $\beta$. Moreover, three bits can be embedded by changing three direction values of a patch. Suppose that $C_w^{(l)}$ denotes the encrypted patch with watermark. If the watermark bit ‘0′ needs to be embedded, the vertex coordinate is not changed, which means $C_w^{(l)}=C^{(l)}$. If the bit ‘1′ needs to be embedded, the ciphertext $C^{(l)}(p,j)$ in the patch $C_w^{(l)}$ is changed by Equation (30) to obtain $C_w^{{}^{(l)}}(p,j)$.

$$C_w^{(l)}(p,j)=\{\begin{array}{l}{C}^{(l)}(p,j)\cdot g^{B(N_l)}=g^{P^{(l)}(p,j)+B(N_l)}\cdot r_1{(k)}^N\mathrm{mod}N,if{d}^{(l)}(j)\in [0,f(N_l))andp=2,3,\dots ,N\\ C^{(l)}(p,j)\cdot g^{B(N_l)}=g^{P^{(l)}(p,j)+B(N_l)}\cdot r_1{(k)}^N\mathrm{mod}N,if{d}^{(l)}(j)\in (-f(N_l),0)andp=1\end{array}$$

(30)

where $C_w^{{}^{(l)}}(p,j)$ is the encrypted patch with watermark. Suppose that $P_w^{(l)}(p,j)$ denotes the decrypted patch with watermark. The operation in ciphertext is equivalent to change the coordinates $P^{(l)}(p,j)$ to $P_w^{(l)}(p,j)$ in plaintext.

$$P_w^{(l)}(p,j)=\{\begin{array}{l}{P}^{(l)}(p,j)+B(N_l),if{d}^{(l)}(j)\in [0,F(N_l))andp=2,3,\dots ,N\\ P^{(l)}(p,j)+B(N_l),if{d}^{(l)}(j)\in (-F(N_l),0)andp=1\end{array}$$

(31)

Suppose that $d_w^{(l)}(j)$ denotes the direction value with watermark. After embedding the bit ‘0′, $d_w^{(l)}(j)$ is still in the range $(-F(N_l),F(N_l))$, so $(-F(N_l),F(N_l))$ is called the 0-bit area. After embedding the bit ‘1′, $d^{(l)}(j)$ will be changed by the size of $F(N_l)+T(N_l)$ for making $d_w^{(l)}(j)$ within the range $(-2F(N_l)-T(N_l),-F(N_l)-T(N_l)]$ or $[F(N_l)+T(N_l),2F(N_l)+T(N_l))$. $(-2F(N_l)-T(N_l),-F(N_l)-T(N_l)]$ and $[F(N_l)+T(N_l),2F(N_l)+T(N_l))$ are called the 1-bit area. Finally, the encrypted model with watermark can be obtained. For example, after embedding 1000 bits, the direction histogram is shown in Figure 8. When embedding the bit ‘0′, the direction values are still in the 0-bit area. When embedding the bit ‘1′, the direction values will be shifted into the 1-bit area. Moreover, the 0-bit area and the 1-area are separated by the robust interval of size $T(N_l)$. Hence, the watermark is embedded successfully.

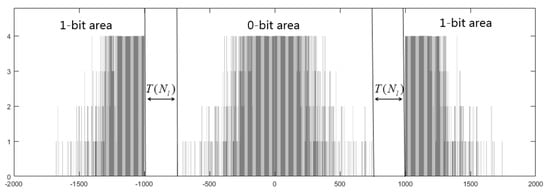
Figure 8. The watermarked histogram. After embedding the watermark, the original direction histogram can be divided into 0-bit area and 1-bit area. The 0-bit area and 1-bit area are separated by the robust interval of size $T(N_l)$.

3.4. Watermark Extraction

Watermark extraction includes extracting the watermark in the encrypted model and extracting the watermark in the decrypted model.

3.4.1. Extracting Watermark in an Encrypted Domain and Restore the Original Encrypted Model

The watermarked model is firstly divided into patches, and the direction values in ciphertext is calculated and mapped to the direction values in plaintext using the MMI method and the mapping table. Then, the direction histogram is constructed, and the watermark is extracted from direction histogram. Finally, with the embedding key $(F(N_l),T(N_l))$, the embedding function $B(N_l)$ can be obtained to restore the original encrypted model. Let $w^{(l)}(j)$ be the watermark embedded in the $j$-axis of the $l^{th}$ patch, and $w^{(l)}(j)$ is extracted by Equation (32).

$$w^{(l)}(j)=\{\begin{array}{l}0,if{d}^{(l)}(j)\in (-F(N_l),F(N_l))\\ 1,else\end{array}$$

(32)

The original encrypted model can be restored by histogram shifting, which is reverse to the embedding process. In order to restore the original encrypted model, the modular multiplicative inverse ${\theta }_{g^{B(N_l)}}$ of $g^{B(N_l)}$ need to be calculated through the extended Euclidean method.

$${\theta }_{g^{B(N_l)}}\cdot g^{B(N_l)}=1\mathrm{mod}{N}^2$$

(33)

Therefore, the original encrypted vertex coordinate $C^{(l)}(p,j)$ can be obtained by Equation (34).

$$C^{(l)}(p,j)=\{\begin{array}{ll}{C}_w^{(l)}(p,j)\cdot & {\theta }_{g^{B(N_l)}}=C^{(l)}(p,j)\cdot g^{B(N_l)}\cdot {\theta }_{g^{B(N_l)}}\mathrm{mod}{N}^2\\ & if{d}^{(l)}(j)\in [F(N_l)+T(N_l),2F(N_l)+T(N_l))andp=2,..,N\\ C_w^{(l)}(p,j)\cdot & {\theta }_{g^{B(N_l)}}=C^{(l)}(p,j)\cdot g^{B(N_l)}\cdot {\theta }_{g^{B(N_l)}}\mathrm{mod}{N}^2\\ & if{d}^{(l)}(j)\in (-2F(N_l)-T(N_l),-F(N_l)-T(N_l)]andp=1\\ C_w^{(l)}(p,j)& \\ & if{d}^{(l)}(j)\in (-F(N_l),F(N_l))\end{array}$$

(34)

where $C_w^{(l)}(p,j)$ is the vertex coordinate with watermark in the patch $C_w^{(l)}$, and the processing in ciphertext is equivalent to the change in plaintext by using Equation (35).

$$P^{(l)}(p,j)=\{\begin{array}{ll}{P}_w^{(l)}(p,j)-B(N_l),& if{d}^{(l)}(j)\in [F(N_l)+T(N_l),2F(N_l)+T(N_l))andp=2,..,N\\ P_w^{(l)}(p,j)-B(N_l),& if{d}^{(l)}(j)\in (-2F(N_l)-T(N_l),-F(N_l)-T(N_l)]andp=1\\ P_w^{(l)}(p,j),& if{d}^{(l)}(j)\in (-F(N_l),F(N_l))\end{array}$$

(35)

After the above process, $d_w^{(l)}$ is restored to $d^{(l)}$, and the original encrypted model can be obtained.

3.4.2. Extracting Watermark in Decrypted Model

With the private key, the watermarked model can be decrypted. With the embedding key, the watermark can be extracted and the original 3D model can be restored. Firstly, the watermarked model is divided into patches and the direction values of each patch are calculated by using Equation (14). Then, the direction histogram is constructed and the watermark is extracted from direction histogram by using Equation (32). Finally, with the embedding key, the original model can be restored by using Equation (35).

The decrypted model with watermark may be vulnerable to some common attacks such as noise interference during transmission. Since the robust interval during histogram shifting is reserved, the proposed method is robust to common attacks, such as Gaussian noise, translation, scaling, etc. As illustrated in Figure 8, the 0-bit area and the 1-bit area are separated by the robust interval of size $T(N_l)$. After the decrypted watermarked model is attacked slightly, it will cause a small range fluctuation of the direction values. However, if the direction values do not enter the error area, the receiver can still correctly extract the watermark. In order to improve the accuracy of watermark extraction after being disturbed, the watermark is extracted by using

$$w^{(l)}(j)=\{\begin{array}{l}0,if{d}^{(l)}(j)\in (-F(N_l)-T(N_l)/3,F(N_l)+T(N_l)/3)\\ 1,else\end{array}$$

(36)

4. Experimental Results and Discussion

The proposed method processed 3D model and implemented the watermark method in MATLAB R2016b under Window 7. We implemented the following experiment on 40 3D models and calculated the average of 40 3D models. Figure 9 shows six models used in the experiment.

Figure 9. Six tested 3D models. (a) Fairy. (b) Boss. (c) Solider. (d) Devil. (e) Thing. (f) Lord.

The quality of the decrypted watermarked model is evaluated by the signal-to-noise ratio ($SNR$). The higher the value $SNR$, the better the imperceptibility after embedding watermark. $SNR$ is computed as

$$SNR=10\lg \frac{{\displaystyle \sum _{i=1}^{N_V}[{(v_{i,x}-{\overline{v}}_x)}^2+{(v_{i,y}-{\overline{v}}_y)}^2+{(v_{i,z}-{\overline{v}}_z)}^2]}}{{\displaystyle \sum _{i=1}^{N_V}[{(g_{i,x}-v_{i,x})}^2+{(g_{i,y}-v_{i,y})}^2+{(g_{i,z}-v_{i,z})}^2]}}$$

(37)

where ${\overline{v}}_x,{\overline{v}}_y,{\overline{v}}_z$ are the mean of vertex coordinates, $v_i(v_{i,x},v_{i,y},v_{i,z})$ are the original coordinates, and $g_i(g_{i,x},g_{i,y},g_{i,z})$ are the coordinates of the watermarked model $M_w$.

In addition, the bit error rate (BER) is used to measure the error rate of the extracted watermark. The lower the value, the higher the accuracy of the extracted watermark.

4.1. The Value of $\beta$

According to Equation (29), $B(N_l)=\beta +\phi (N_l-1)$, and the embedding function $B(N_l)$ is changed by changing the value of $\beta$. According to Equation (31), if the value of $\beta$ is large, the distortion of the decrypted model is high and the accuracy of watermark extracting is high, and vice versa. In order to observe the effect of $\beta$ on the quality of decrypted model and the bit error rate of the extracted watermark, we changed the value of $\beta$ to perform on 40 tested models and calculated their average. The relationship between the value of $\beta$ and the distortion $SNR$ is illustrated in Figure 10a. As $\beta$ increases, $SNR$ gradually decreases. When $\beta$ = 588, $SNR$ of the decrypted model is slightly greater than 30 dB. Based on imperceptible considerations, in order to obtain better model quality, the value of $\beta$ cannot exceed 588. The relationship between the value of $\beta$ and BER is shown in Figure 10b. When $\beta \ge 528$, the watermark was correctly extracted without being attacked. Therefore, the value of b cannot be less than 528.

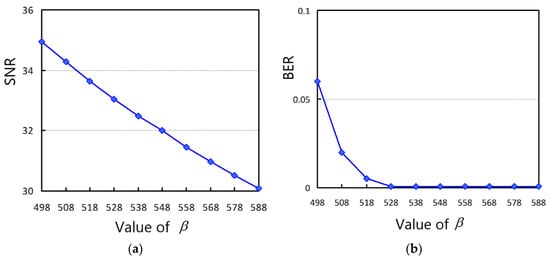
Figure 10. The effect of $\beta$ on the distortion of decrypted model and the bit error rate of the extracted watermark. (a) $\beta$ is related to signal-to-noise ratio ($SNR$ ). (b) $\beta$ is related to bit error rate (BER).

4.2. The Value of $t$

As shown in Figure 7, the 0-bit area and 1-bit area are separated by the robust interval of size $t\cdot (N_l-1)$. If the robust interval is large, the robustness is high. However, as $t$ increases, the quality of the decrypted model is reduced. Therefore, $t$ needs to be adjusted according to the actual application scenario. If higher robustness is required, a greater value of $t$ can be assigned. If better quality of decrypted model is required, a smaller value of $t$ is set. In order to choose a suitable value, experiments were conducted on 40 models to test the robustness with different values of $t$.

As illustrated in Figure 11, the BER of watermark extraction is low under Gaussian noise (0.01). By increasing $t$, the BER could be reduced. When $t=50$, the watermark could be extracted correctly. Therefore, when higher robustness is required, the value of $t$ can be assigned to be 50.

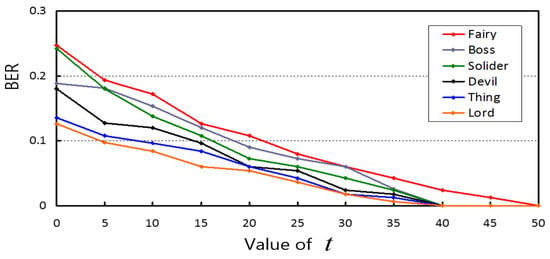
Figure 11. The BER under Gaussian attacks (the strength is 0.01).

4.3. Feasibility of the Watermarking

In order to show the feasibility of the proposed watermarking method, the 3D model devil with 30,000 vertices was tested, and other models had similar results. The watermark was a 1024-bit pseudo-random sequence. Firstly, the original model was divided into patches and the encrypted model was obtained by encrypting the 3D model with the public key as illustrated in Figure 12. Secondly, with the embedding key, the watermark was embedded to obtain the watermarked model as illustrated in Figure 12c. Then, the directly decrypted model (as shown in Figure 12d) is obtained by decrypting the encrypted model; $SNR$ of the decrypted model was 30.93. Lastly, the watermark was extracted and the model was restored (as shown in Figure 12e), and the $SNR$ of the restored model approaches infinity, which shows that the restored model was exactly the same as the original model. Figure 12f shows that all watermark bits were correctly extracted. The experimental results showed that the proposed method achieved reversibility of embedding and extraction, and the restoration of the original model. Figure 13 shows five decrypted 3D models had less distortion compared to the original 3D model, and Figure 13f shows the SNR of the decrypted models were close to 30, which denotes the proposed method can obtain good quality.

Figure 12. Experiment with 3D model ‘devil’ (a) The original model; (b) the encrypted model; (c) the watermarked model; (d) the decrypted model. After decryption, the $SNR$ was 30.93. (e) The restored model. After restoration, the $SNR$ approached infinity. (f) The bit error rate after watermark extraction.

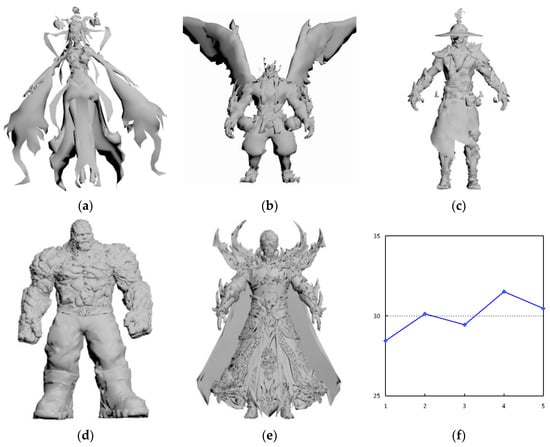
Figure 13. Five watermarked 3D models. (a) The watermarked “Fairy”; (b) the watermarked “Boss”; (c) the watermarked “Solider”; (d) the watermarked “Thing”; (e) the watermarked “Lord”; (f) $SNR$ of the five watermarked models.

4.4. Robustness Analysis

In order to compare the robustness under attacks, several attacks were performed on the decrypted 3D model. Table 1 shows the bit error rate of watermark extraction under different attacks.

Table 1. The BER under several common attacks.

Model	t	SNR	Gaussian			Translation	Scaling
			(0.005)	(0.01)	(0.02)		0.8	1.2	1.5
Fairy	40	30.96	1.75%	2.63%	6.15%	1	0.21	0.073	0.18
Boss	40	30.96	1.24%	1.52%	6.26%	1	0.17	0.064	0.19
Solider	35	31.44	1.98%	2.67%	5.98%	1	0.13	0.053	0.15
Devil	30	31.44	2.06%	2.41%	6.74%	1	0.16	0.069	0.19
Thing	30	31.44	1.68%	2.47%	6.45%	1	0.18	0.057	0.21
Lord	25	32.1	2.28%	3.24%	8.64%	1	0.23	0.071	0.24

4.4.1. Robustness Against Translation Attacks

The robustness against the translation attacks was tested. As shown in Table 1, the method perfectly resisted translation attacks. When the model was subjected to a translation attack, the vertex coordinates of the patch increased by a certain value at the same time. According to Equation (14), when the vertex coordinates in a patch are changed by the same size, it can be known that its direction values will not change. Therefore, the watermark can be extracted correctly.

4.4.2. Robustness Against Scaling Attacks

The robustness against scaling attacks was tested by different levels (0.8, 1.2, 1.5) on the decrypted 3D model. As shown in Table 1, the proposed method was robust to scaling attacks. When the model was attacked, the vertex coordinates of the patch were multiplied by a certain coefficient at the same time. According to Equation (14), its direction values also increased or decreased accordingly. As illustrated in Figure 7, the direction values of most patches were concentrated in the central area. Therefore, when the scaling size was increased, most of the vertices were still in the original area, and only a small number of vertices were offset. On this condition, the robustness was high. When the scaling size was decreased, the 1-bit area was easily shifted to the 0-bit area, which affected the accuracy of extracting the watermark. Therefore, the robustness was much higher when the 3D model was amplified compared with other levels of attacks.

4.4.3. Robustness to Gaussian Noise Attacks

The robustness against Gaussian noise attacks was tested by performing different degrees (0.005, 0.01, 0.02) on the decrypted 3D model. As shown in Table 1, the robustness against Gaussian noise attacks was high. When the model was attacked by Gaussian noise, the vertex coordinates were slightly disturbed. According to Equation (14), its direction values were also slightly modified. As illustrated in Figure 7, the direction values of most patches were concentrated in the central area, and only a few vertices were in the non-central area. Therefore, when the model was slightly disturbed, the direction values of the central area were slightly disturbed, and only a few direction values of non-central area were shifted.

However, the proposed method cannot resist the attacks of cropping and simplification, it is because those attacks will influence the order of the vertices. Moreover, the proposed method cannot resist salt and pepper noise, mainly because the attack obviously changes the relative position between vertices.

4.5. Compared with the Existing Watermark Method in an Encrypted Domain

To our knowledge, few effective robust reversible watermarking methods for 3D model in the encryption domain has been reported in the literature. In order to show the effectiveness of the proposed method, Jiang [1] is extended to the encrypted 3D model. From Table 2, the proposed method has a slightly higher embedding capacity compared with the Jiang [1], and it is mainly because a patch has three coordinate axes and three bits can be embedded. To sum up, the proposed method has good security and robustness, and the decrypted 3D model has low distortion.

Table 2. Compared to the method of Jiang [1].

	Capability	Robustness	Security	SNR of Decrypted Model	SNR of Restored Model	BER
The proposed method	0.396	yes	high	30.08	+∞	0
Method of Jiang [1]	0.365	no	low	5.35	31.97	4.22%

5. Conclusions

In this paper, a robust reversible three-dimensional (3D) model watermarking method based on homomorphic encryption is presented for protecting the copyright of 3D models. The 3D model is divided into non-overlapping patches, and the vertex in each patch is encrypted by using the Paillier cryptosystem. On the cloud side, three direction values of each patch are computed, and the symmetrical direction histogram is constructed for shifting to embed watermark. In order to obtain robustness, the robust interval is designed in the process of histogram shifting. The watermark can be extracted from the direction histogram, and the original encrypted model can be restored by histogram shifting. Experimental results show that the decrypted 3D models have less distortion compared with the existing methods, which denotes the proposed method can embed more secret data without increasing the 3D models distortion. Moreover, the proposed method can resist a series of attacks compared to the existing watermarking methods on encrypted 3D model. Thus, the proposed method is efficient to protect copyright of 3D models in the cloud when the cloud administrator does not know the content of the 3D models, but the existing methods have no ability.

In the future, we will investigate the following two possible research directions. (1) Reduce the distortion of the directly decrypted 3D model. (2) Further improve the robustness against more kinds of attacks, such as cropping and salt and pepper noise.