Despeckling Algorithm for Removing Speckle Noise from Ultrasound Images
Abstract
:1. Introduction
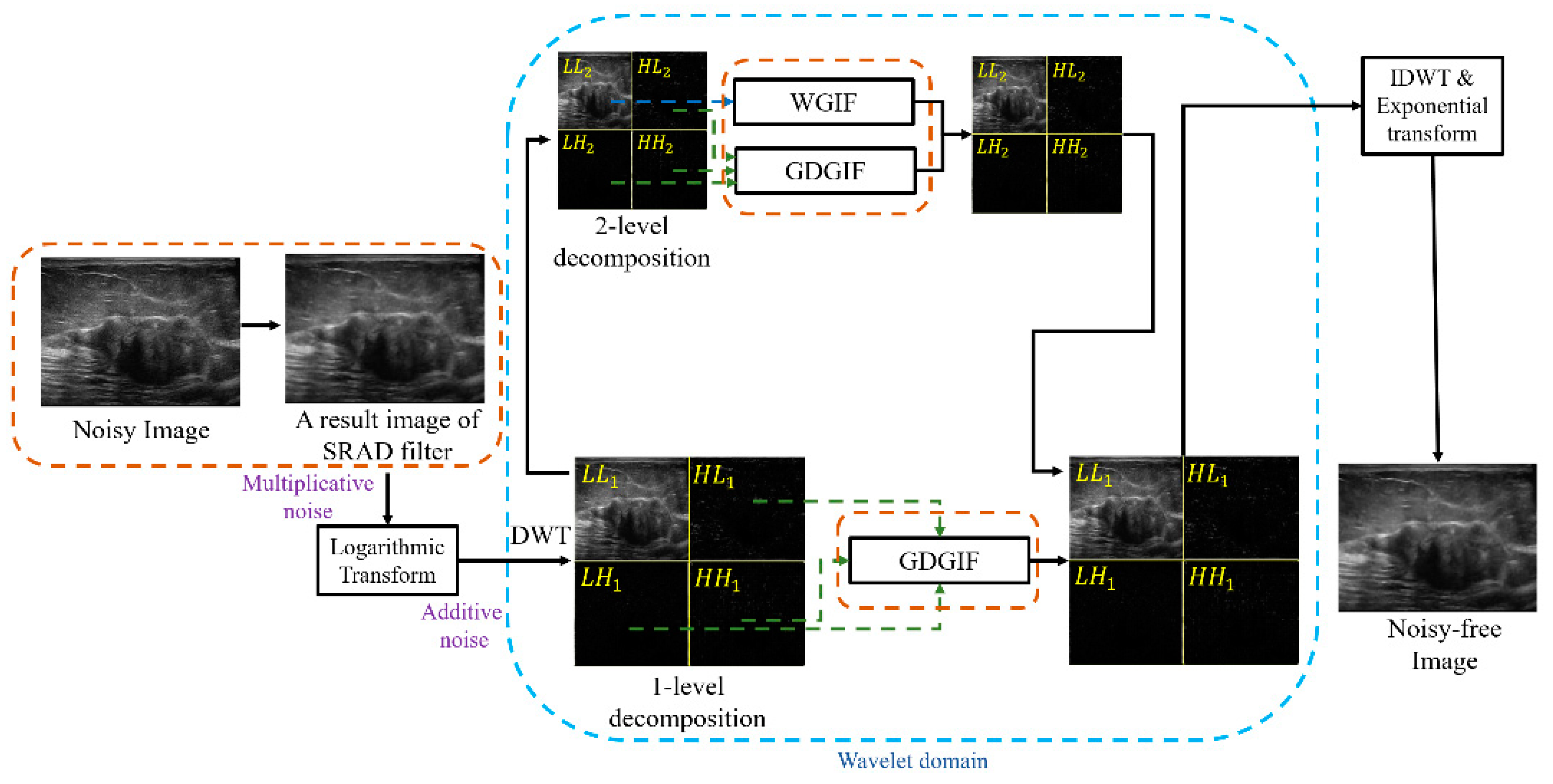
2. Proposed Algorithm
2.1. Speckle Reducing Anisotropic Diffusion Filter
2.2. A Model of Speckle Noise
2.3. Discrete Wavelet Transform
2.4. Gradient Domain Guided Image Filtering in the High-Frequency Sub-Band Images
2.5. Weighted Guided Image Filtering in the Low-Frequency Sub-Band Image
2.6. Evaluation Metrics
3. Experimental Results
3.1. Experimental Environments of Standard Images and US Images
3.1.1. Experiments on Standard Images
3.1.2. Experiments on Real US Images
3.2. Computational Cost of Standard Images and US Images
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, S.; Huang, T.-Z.; Zhao, X.-L.; Mei, J.-J.; Huang, J. Speckle noise removal in ultrasound images by first- and second-order total variation. Numer. Algorithm 2018, 78, 513–533. [Google Scholar] [CrossRef]
- Alex, D.M.; Christinal, A.H.; Chandy, D.A.; Singh, A.; Pushkaran, M. Speckle noise suppression in 2D ultrasound kidney images using local pattern based topological derivative. Pattern Recognit. Lett. 2020, 131, 49–55. [Google Scholar] [CrossRef]
- Elyasi, I.; Pourmina, M.A. Reduction of speckle noise ultrasound images based on TV regularization and modified bayes shrink techniques. Optik 2016, 127, 11732–11744. [Google Scholar] [CrossRef]
- Duff, V.; Greenleaf, J.F. Adaptive speckle reduction filter for log compressed B-scan images. IEEE Trans. Med. Imaging 1996, 15, 802–813. [Google Scholar]
- Sanches, J.; Laine, A.; Suri, J. Ultrasound Imaging: Advances and Applications; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Lee, J.S. Refined filtering of image noise using local statistics. Comput. Graph. Image Process. 1981, 15, 380–389. [Google Scholar] [CrossRef]
- Kuan, D.; Sawchuk, A.; Strand, T.; Chavel, P. Adaptive noise smoothing filter for images with signal-dependent noise. IEEE Trans. Pattern Anal. Mach. Intell. 1985, PAMI-7, 165–177. [Google Scholar] [CrossRef]
- Frost, V.S.; Stiles, J.A.; Shanmugan, K.S.; Holtzman, J.C. A model for radar images and its application to adaptive digital filtering of multiplicative noise. IEEE Trans. Pattern Anal. Mach. Intell. 1982, PAMI-4, 157–166. [Google Scholar] [CrossRef]
- Lopes, A.; Touzi, R.; Nezry, E. Adaptive speckle filters and scene heterogeneity. IEEE Trans. Geosci. Remote Sens. 1990, 28, 992–1000. [Google Scholar] [CrossRef]
- Abd, E.K.; Youssef, A.; Kadah, Y. Real-Time speckle reduction and coherence enhancement in ultrasound imaging via nonlinear anisotropic diffusion. IEEE Trans. Biomed. Eng. 2002, 49, 997–1014. [Google Scholar]
- Tang, C.; Wang, L.; Yan, H. Overview of anisotropic filtering methods based on partial differential equations for electronic speckle pattern interferometry. Appl. Opt. 2012, 51, 4916–4926. [Google Scholar] [CrossRef]
- Coupe, P.; Hellier, P.; Kervrann, C.; Barillot, C. Nonlocal means-based speckle filtering for ultrasound images. IEEE Trans. Image Process. 2009, 18, 2221–2229. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, J.; Fan, J.; Ai, D.; Wang, X.; Tang, S.; Wang, Y. Local statistics and non-local mean filter for speckle noise reduction in medical ultrasound image. Neurocomputing 2016, 195, 88–95. [Google Scholar] [CrossRef] [Green Version]
- Radlak, K.; Smolka, B. Adaptive non-local means filtering for speckle noise reduction. In International Conference on Computer Vision and Graphics; Springer: Cham, Switzerland, 2014; pp. 518–525. [Google Scholar]
- Sudeep, P.V.; Palanisamy, P.; Rajan, J.; Baradaran, H.; Saba, L.; Gupta, A.; Suri, J.S. Speckle reduction in medical ultrasound images using an unbiased non-local means method. Biomed. Signal Process. Control 2016, 28, 1–8. [Google Scholar] [CrossRef]
- Tounsi, Y.; Kumar, M.; Nassim, A.; Mendoza-Santoyo, F.; Matoba, O. Speckle denoising by variant nonlocal means methods. Appl. Opt. 2019, 58, 7110–7120. [Google Scholar] [CrossRef]
- Tounsi, Y.; Kumar, M.; Nassim, A.; Mendoza-Santoyo, F. Speckle noise reduction in digital speckle pattern interferometric fringes by nonlocal means and its related adaptive kernel-based methods. Appl. Opt. 2018, 57, 7681–7690. [Google Scholar] [CrossRef]
- Santos, C.A.N.; Martins, D.L.N.; Mascarenhas, N.D.A. Ultrasound Image Despeckling Using Stochastic Distance-Based BM3D. IEEE Trans. Image Process. 2017, 26, 2632–2643. [Google Scholar] [CrossRef]
- Portilla, J.; Strela, V.; Wainwright, M.J.; Simoncelli, E.P. Image denoising using scale mixtures of Gaussians in the wavelet domain. IEEE Trans. Image Process. 2003, 12, 1338–1351. [Google Scholar] [CrossRef] [Green Version]
- Rabbani, H.; Vafadust, N.; Abolmaesumi, P.; Gazor, S. Speckle noise reduction of medical ultrasound images in complex wavelet domain using mixture priors. IEEE Trans. Biomed. Eng. 2008, 55, 2152–2160. [Google Scholar] [CrossRef]
- Rami, H.; Belmerhnia, L.; Maliani, A.E.; Hassouni, M.E. Texture retrieval using mixtures of generalized Gaussian distribution and Cauchy–Schwarz divergence in wavelet domain. Signal Process. Image Commun. 2016, 42, 45–58. [Google Scholar] [CrossRef]
- Hassan, A.R.; Bhuiyan, M.I. An automated method for sleep staging from EEG signals using normal Gaussian parameters and adaptive boosting. Neurocomputing 2017, 219, 76–87. [Google Scholar] [CrossRef]
- Rabbani, H. Image denoising in steerable pyramid domain based on a local Laplace prior. Pattern Recognit. 2009, 42, 2181–2193. [Google Scholar] [CrossRef]
- Hill, P.R.; Achim, A.M.; Bull, D.R.; Mualla, M.E. Dual-tree complex wavelet coefficient magnitude modeling using the bivariate Cauchy–Rayleigh distribution. Signal Process. 2014, 105, 464–472. [Google Scholar] [CrossRef]
- Zada, S.; Yassine, T.; Kumar, M.; Mendoza-Santoyo, F.; Nassim, A. Contribution study of monogenic wavelets transform to reduce speckle noise in digital speckle pattern interferometry. Opt. Eng. 2019, 58, 034109. [Google Scholar] [CrossRef]
- Trusiak, M.; Patorski, K.; Wielgus, M. Adaptive enhancement of optical fringe patterns by selective reconstruction using FABEMD algorithm and Hilbert spiral transform. Opt. Express 2012, 20, 23463–23479. [Google Scholar] [CrossRef]
- Luisier, F.; Blu, T.; Unser, M. A new SURE approach to image denoising intrascale orthonormal wavelet thresholding. IEEE Trans. Image Process. 2007, 16, 593–606. [Google Scholar] [CrossRef] [Green Version]
- Fathi, A.; Naghsh, A.R. Efficient image denoising method based on a new adaptive wavelet packet thresholding function. IEEE Trans. Image Process. 2012, 21, 3981–3990. [Google Scholar] [CrossRef]
- Sun, D.; Gao, Q.; Lu, Y.; Huang, Z.; Li, T. A novel image denoising algorithm using linear Bayesian MMSE estimation based on sparse representation. Signal Process. 2014, 100, 132–145. [Google Scholar] [CrossRef]
- Baselice, F.; Ferraioli, G.; Ambrosanio, M.; Pascazio, V.; Schirinzi, G. Enhanced Wiener filter for ultrasound image restoration. Comput. Methods Programs Biomed. 2018, 153, 71–81. [Google Scholar] [CrossRef]
- Yu, Y.; Acton, S.T. Speckle reducing anisotropic diffusion. IEEE Trans. Image Process. 2002, 11, 1260–1270. [Google Scholar]
- Kou, F.; Chen, W.; Wen, C.; Li, S. Gradient domain guided image filtering. IEEE Trans. Image Process. 2015, 24, 4528–4539. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, J.; Zhu, Z.; Yao, W.; Wu, S. Weighted guided image filtering. IEEE Trans. Image Process. 2015, 24, 120–129. [Google Scholar] [PubMed]
- Xie, H.; Pierce, L.E.; Ulaby, F.T. Statistical properties of logarithmically transformed speckle. IEEE Trans. Geosci. Remote Sens. 2002, 40, 721–727. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, G.; Wu, L.; Cheng, Y. Speckle filtering of medical ultrasonic images using wavelet and guided filter. Ultrasonics 2016, 65, 177–193. [Google Scholar] [CrossRef]
- Wagner, R.; Smith, S.; Sandrik, J.; Lopez, H. Statistics of speckle in ultrasound B-scans. IEEE Trans. Sonics Ultrason. 1983, 30, 156–163. [Google Scholar] [CrossRef]
- Donoho, D.L.; Johnstone, I.M. Ideal spatial adaptation via wavelet shrinkage. Biometrika 1994, 81, 425–455. [Google Scholar] [CrossRef]
- Donoho, D.L. De-noising by soft-thesholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef] [Green Version]
- Chang, S.G.; Yu, B.; Vetterli, M. Adaptive wavelet thresholding for image denoising and compression. IEEE Trans. Image Process. 2000, 9, 1532–1546. [Google Scholar] [CrossRef] [Green Version]
- Nasri, M.; Nezamabadi-pour, H. Image denoising in the wavelet domain using a new adaptive thresholding function. Neurocomputing 2009, 72, 1012–1025. [Google Scholar] [CrossRef]
- Thakur, A.; Anand, R.S. Image quality based comparative evaluation of wavelet filters in ultrasound speckle reduction. Digit. Signal Process. 2005, 15, 455–465. [Google Scholar] [CrossRef]
- Zhang, M.; Gunturk, B.K. Multiresolution bilateral filtering for image denoising. IEEE Trans. Image Process. 2008, 17, 2324–2333. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Sun, J.; Tang, X. Guided image filtering. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1397–1409. [Google Scholar] [CrossRef]
- Choi, H.; Jeong, J. Speckle noise reduction for ultrasound images by using speckle reducing anisotropic diffusion and Bayes threshold. J. X-ray Sci. Technol. 2019, 27, 885–898. [Google Scholar] [CrossRef]
- Rawat, N.; Singh, M.; Singh, B. Wavelet and Total Variation Based Method Using Adaptive Regularization for Speckle Noise Reduction in Ultrasound Images. Wirel. Pers. Commun. 2019, 106, 1547–1572. [Google Scholar] [CrossRef]
- Ultrasouind cases.info. Available online: http://ultrasoundcases.info/Category.aspx?cat=117 (accessed on 16 April 2019).
- Ramos-Llordén, G.; Vegas-Sánchez-Ferrero, G.; Martin-Fernández, M.; Alberola-López, C.; Aja-Fernández, S. Anisotropic diffusion filter with memory based on speckle statistics for ultrasound images. IEEE Trans. Image Process. 2015, 24, 345–358. [Google Scholar] [CrossRef] [Green Version]
- Farbman, Z.; Fattal, R.; Lischinshi, D.; Szeliski, R. Edge-preserving decompositions for multi-scale tone and detail manipulation. ACM Trans. Graph. 2008, 27, 1–10. [Google Scholar] [CrossRef]
- Treece, G. The Bitonic Filter: Linear Filtering in an Edge-Preserving Morphological Framework. IEEE Trans. Image Process. 2016, 25, 5199–5211. [Google Scholar] [CrossRef]
- Parrilli, S.; Poderico, M.; Angelino, C.V.; Verdoliva, L. A nonlocal SAR image denoising algorithm based on LLMMSE wavelet shrinkage. IEEE Trans. Geosci. Remote Sens. 2012, 50, 606–616. [Google Scholar] [CrossRef]
- Xu, B.; Cui, Y.; Li, Z.; Zuo, B.; Yang, J.; Song, J. Patch Ordering-Based SAR Image Despeckling Via Transform-Domain Filtering. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1682–1695. [Google Scholar] [CrossRef]
- Nair, J.J.; Govindan, V. Speckle noise reduction using fourth order complex diffusion based homomorphic filter. In Advances in Computing and Information Technology; Springer: Berlin/Heidelberg, Germany, 2013; pp. 895–903. [Google Scholar]
- Prabusankarlal, K.M.; Manavalanm, R.; Sivaranjani, R. An optimized non-local means filter using automated clustering based preclassification through gap statistics for speckle reduction in breast ultrasound images. Appl. Comput. Inform. 2018, 14, 48–54. [Google Scholar] [CrossRef]














| SRAD | GDGIF | WGIF | |
|---|---|---|---|
| Airplane | Time step = 0.01 Exponential rate = 1 Number of iterations = 130 | Mask size = 9 9 Regularization parameter = 0.01 | Mask size = 9 9 Regularization parameter = 1 × 10−6 |
| Boat | Time step = 0.01 Exponential rate = 1 Number of iterations = 100 | Mask size = 9 9 Regularization parameter = 0.01 | Mask size = 9 9 Regularization parameter = 1 × 10−6 |
| Cameraman | Time step = 0.01 Exponential rate = 1 Number of iterations = 180 | Mask size = 9 9 Regularization parameter = 0.01 | Mask size = 9 9 Regularization parameter = 1 × 10−6 |
| Man | Time step = 0.01 Exponential rate = 1 Number of iterations = 120 | Mask size = 9 9 Regularization parameter = 0.01 | Mask size = 9 9 Regularization parameter = 1 × 10−6 |
| Lena | Time step = 0.01 Exponential rate = 1 Number of iterations = 150 | Mask size = 9 9 Regularization parameter = 0.01 | Mask size = 9 9 Regularization parameter = 1 × 10−6 |
| Peppers | Time step = 0.01 Exponential rate = 1 Number of iterations = 150 | Mask size = 9 9 Regularization parameter = 0.01 | Mask size = 9 9 Regularization parameter = 1 × 10−6 |
| SRAD | GDGIF | WGIF | |
|---|---|---|---|
| US image 1 | Time step = 0.01 Exponential rate = 1 Number of iterations = 130 | Mask size = 9 9 Regularization parameter = 0.01 | Mask size = 9 9 Regularization parameter = 1 × 10−6 |
| US image 2 | Time step = 0.01 Exponential rate = 1 Number of iterations = 80 | Mask size = 9 9 Regularization parameter = 0.01 | Mask size = 9 9 Regularization parameter = 1 × 10−6 |
| US image 3 | Time step = 0.01 Exponential rate = 1 Number of iterations = 140 | Mask size = 9 9 Regularization parameter = 0.01 | Mask size = 9 9 Regularization parameter = 1 × 10−6 |
| US image 4 | Time step = 0.01 Exponential rate = 1 Number of iterations = 90 | Mask size = 9 9 Regularization parameter = 0.01 | Mask size = 9 9 Regularization parameter = 1 × 10−6 |
| US image 5 | Time step = 0.01 Exponential rate = 1 Number of iterations = 60 | Mask size = 9 9 Regularization parameter = 0.01 | Mask size = 9 9 Regularization parameter = 1 × 10−6 |
| US image 6 | Time step = 0.01 Exponential rate = 1 Number of iterations = 100 | Mask size = 9 9 Regularization parameter = 0.01 | Mask size = 9 9 Regularization parameter = 1 × 10−6 |
| Six Standard Images | Six US Images | |
|---|---|---|
| Guided | Mask size = 3 3 Regularization parameter = 0.001 | Mask size = 3 3 Regularization parameter = 0.001 |
| Lee | Mask size = 3 3 | Mask size = 3 3 |
| Frost | Mask size = 3 3 | Mask size = 3 3 |
| Gaussian | Mask size = 5 5 | Mask size = 5 5 |
| Bitonic | Mask size = 3 3 | Mask size = 3 3 |
| WLS | = 0.5 | = 0.5 |
| ADMSS | = 0.5, = 0.1, = 15 | = 0.5, = 0.1, = 15 |
| SAR-BM3D | Number of rows/cols of block = 9, Maximum size of the 3rd dimension of a stack = 16, Diameter of search area = 39, Dimension of step = 3, Parameter of the 2D Kaiser window = 2, Transform: undecimated wavelet transform (UDWT) = daub4 | Number of rows/cols of block = 9, Maximum size of the 3rd dimension of a stack = 16, Diameter of search area = 39, Dimension of step = 3, Parameter of the 2D Kaiser window = 2, Transform: UDWT = daub4 |
| Airplane | Boat | Cameraman | Man | Lena | Peppers | |
|---|---|---|---|---|---|---|
| Noisy | 16.5259 | 18.4571 | 18.6368 | 20.6950 | 18.8416 | 18.5572 |
| GIF | 19.1425 | 18.4571 | 24.3955 | 24.1908 | 22.3112 | 20.7189 |
| Lee | 23.7811 | 24.9209 | 23.0668 | 27.4333 | 25.8835 | 25.5090 |
| Frost | 22.0637 | 23.3875 | 22.3281 | 25.5420 | 24.2903 | 23.3401 |
| Gaussian | 25.1845 | 25.3322 | 22.5199 | 27.5073 | 27.4245 | 27.6756 |
| Bitonic | 26.1829 | 26.4246 | 24.3955 | 26.7991 | 28.5419 | 28.2365 |
| WLS | 25.6469 | 26.3535 | 25.9689 | 28.4255 | 28.0356 | 28.7923 |
| ADMSS | 23.4343 | 20.1359 | 17.5853 | 23.6321 | 21.8759 | 18.2932 |
| SRAD | 26.5703 | 27.4141 | 26.3295 | 29.2499 | 29.6899 | 30.4284 |
| SRAD-Bayes | 27.0275 | 27.4154 | 26.4097 | 29.5813 | 29.6899 | 30.4284 |
| SAR-BM3D | 32.9288 | 27.2015 | 26.3454 | 28.8885 | 29.9061 | 29.7615 |
| Proposed | 27.4755 | 27.7553 | 26.4681 | 29.6691 | 29.9126 | 30.5983 |
| Airplane | Boat | Cameraman | Man | Lena | Peppers | |
|---|---|---|---|---|---|---|
| Noisy | 0.2141 | 0.3358 | 0.4173 | 0.4978 | 0.2870 | 0.2886 |
| GIF | 0.2835 | 0.3358 | 0.6702 | 0.5986 | 0.4309 | 0.4220 |
| Lee | 0.4961 | 0.5972 | 0.5638 | 0.7132 | 0.5995 | 0.6351 |
| Frost | 0.3653 | 0.4738 | 0.4710 | 0.6085 | 0.4549 | 0.4464 |
| Gaussian | 0.6560 | 0.6532 | 0.6160 | 0.7330 | 0.7141 | 0.7598 |
| Bitonic | 0.6557 | 0.6783 | 0.6702 | 0.7041 | 0.7261 | 0.8164 |
| WLS | 0.6159 | 0.6657 | 0.6851 | 0.7553 | 0.6963 | 0.7526 |
| ADMSS | 0.7254 | 0.3865 | 0.3579 | 0.5492 | 0.4726 | 0.2911 |
| SRAD | 0.8043 | 0.7103 | 0.7840 | 0.7872 | 0.8093 | 0.7723 |
| SRAD-Bayes | 0.7587 | 0.7104 | 0.7824 | 0.7986 | 0.8093 | 0.8445 |
| SAR-BM3D | 0.9193 | 0.7236 | 0.8027 | 0.7864 | 0.8393 | 0.8559 |
| Proposed | 0.8271 | 0.7377 | 0.7910 | 0.8019 | 0.8260 | 0.8593 |
| US Image 1 | US Image 2 | US Image 3 | ||||
|---|---|---|---|---|---|---|
| ROI-1 | ROI-2 | ROI-1 | ROI-2 | ROI-1 | ROI-2 | |
| GIF | 21.4976 | 9.2061 | 10.8467 | 13.0614 | 35.9332 | 5.9912 |
| Lee | 29.2625 | 10.4813 | 14.4238 | 15.9266 | 64.1074 | 12.0654 |
| Frost | 27.8564 | 10.2496 | 13.8844 | 15.5675 | 57.7815 | 10.8900 |
| Gaussian | 29.1324 | 10.4348 | 14.2828 | 15.7657 | 100.7314 | 18.0757 |
| Bitonic | 33.0059 | 10.9510 | 15.8999 | 16.9290 | 93.1637 | 17.1567 |
| WLS | 43.3577 | 13.4256 | 18.7544 | 19.8149 | 223.7867 | 16.4700 |
| ADMSS | 21.5470 | 9.0889 | 15.2790 | 11.9555 | 34.6900 | 34.5554 |
| SRAD | 34.6307 | 11.2436 | 14.9490 | 16.5835 | 142.7407 | 14.8044 |
| SRAD-Bayes | 34.5921 | 11.5086 | 14.9769 | 16.5751 | 142.7472 | 14.8048 |
| SAR-BM3D | 29.5615 | 10.4383 | 14.8830 | 16.6464 | 77.9813 | 14.2999 |
| Proposed | 36.7761 | 11.8523 | 15.2899 | 16.8020 | 199.1937 | 14.9264 |
| US Image 4 | US Image 5 | US Image 6 | ||||
|---|---|---|---|---|---|---|
| ROI-1 | ROI-2 | ROI-1 | ROI-2 | ROI-1 | ROI-2 | |
| GIF | 10.2034 | 14.9478 | 50.4453 | 37.1283 | 18.7762 | 28.4937 |
| Lee | 12.1528 | 18.4038 | 40.1959 | 31.6776 | 15.0236 | 22.5928 |
| Frost | 11.8881 | 17.6928 | 38.4305 | 30.5600 | 14.5445 | 21.8719 |
| Gaussian | 13.7501 | 20.9189 | 39.5283 | 31.3656 | 16.9306 | 25.8945 |
| Bitonic | 12.4643 | 20.1317 | 45.3041 | 33.4917 | 15.5404 | 25.1755 |
| WLS | 17.7059 | 29.5167 | 67.1322 | 51.5178 | 26.3737 | 38.0826 |
| ADMSS | 10.8299 | 15.8205 | 47.8042 | 34.3954 | 15.2125 | 23.7334 |
| SRAD | 12.8285 | 19.8875 | 40.4638 | 31.8749 | 16.8350 | 25.5281 |
| SRAD-Bayes | 12.9219 | 19.8853 | 40.5353 | 31.9014 | 16.8584 | 25.4082 |
| SAR-BM3D | 11.7274 | 18.5588 | 42.4447 | 32.6953 | 14.7869 | 23.8162 |
| Proposed | 13.6607 | 22.2331 | 48.3190 | 35.7300 | 18.2626 | 29.0689 |
| US Image 1 | US Image 2 | US Image 3 | US Image 4 | US Image 5 | US Image 6 | |
|---|---|---|---|---|---|---|
| GIF | 0.0039 | 0.0021 | 0.0045 | 0.0034 | 0.0546 | 0.0345 |
| Lee | 1.0557 | 1.0321 | 0.3894 | 0.8698 | 1.0687 | 1.0694 |
| Frost | 0.7264 | 0.9332 | 0.1239 | 0.9067 | 0.7383 | 0.8171 |
| Gaussian | 1.0205 | 0.9743 | 0.8490 | 0.9846 | 1.0789 | 1.2483 |
| Bitonic | 0.0136 | 0.1484 | 0.1609 | 0.0774 | 0.0668 | 0.0431 |
| WLS | 0.0121 | 0.0012 | 9.4080 × 10−4 | 0.0125 | 6.4136 × 10−4 | 0.0030 |
| ADMSS | 0.4380 | 3.1276 | 0.9641 | 1.5678 | 0.4402 | 2.0410 |
| SRAD | 0.0332 | 0.0065 | 0.0028 | 0.0132 | 0.0080 | 0.0027 |
| SRAD-Bayes | 0.0301 | 0.0107 | 0.0024 | 5.5133 × 10−4 | 0.0014 | 0.0016 |
| SAR-BM3D | 0.2348 | 0.4185 | 0.9725 | 0.4167 | 0.1717 | 0.2409 |
| Proposed | 0.0293 | 0.0097 | 0.0019 | 0.0115 | 0.0010 | 0.0015 |
| Airplane | Boat | Camera-Man | Man | Lena | Peppers | Avg. | |
|---|---|---|---|---|---|---|---|
| GIF | 0.1920 | 0.5129 | 0.1908 | 0.1401 | 0.5927 | 0.0882 | 0.2861 |
| Lee | 7.4367 | 7.2911 | 3.9978 | 7.9348 | 7.8594 | 1.9135 | 6.0722 |
| Frost | 2.8992 | 2.8982 | 1.9820 | 7.9381 | 2.8543 | 1.9149 | 3.4145 |
| Gaussian | 0.1451 | 0.0084 | 0.0068 | 0.0180 | 0.0041 | 0.0036 | 0.0310 |
| Bitonic | 0.3478 | 0.2759 | 0.2985 | 0.3058 | 0.2746 | 0.1210 | 0.2706 |
| WLS | 4.6115 | 1.5751 | 0.8674 | 3.3873 | 1.9842 | 0.7238 | 2.1915 |
| ADMSS | 196.8743 | 174.2224 | 21.6495 | 776.3370 | 171.9674 | 180.7599 | 253.6351 |
| SRAD | 7.5007 | 5.0790 | 1.2836 | 26.1363 | 8.0667 | 7.9028 | 9.3282 |
| SRAD-Bayes | 7.6464 | 5.1421 | 1.5484 | 27.3693 | 8.1877 | 8.1928 | 9.6811 |
| SAR-BM3D | 61.4958 | 61.0734 | 14.4467 | 247.0835 | 60.1611 | 180.2394 | 104.0833 |
| Proposed | 7.6866 | 5.5351 | 2.0058 | 27.9753 | 8.1832 | 8.5619 | 9.9913 |
| US Image1 | US Image2 | US Image3 | US Image4 | US Image5 | US Image6 | Avg. | |
|---|---|---|---|---|---|---|---|
| Guided | 0.0517 | 0.4765 | 0.0577 | 0.0966 | 0.0766 | 0.0994 | 01431 |
| Lee | 1.9322 | 1.8176 | 1.8549 | 2.5629 | 2.5800 | 2.6019 | 2.2249 |
| Frost | 0.5220 | 0.4761 | 0.4718 | 0.7371 | 0.7583 | 0.7560 | 0.6202 |
| Gaussian | 0.0605 | 0.0589 | 0.0350 | 0.0431 | 0.0492 | 0.0434 | 0.0484 |
| Bitonic | 1.1764 | 0.0925 | 0.0697 | 0.0760 | 0.1336 | 0.1409 | 0.2815 |
| WLS | 0.2254 | 0.2138 | 0.1892 | 0.1810 | 0.1712 | 0.1924 | 0.1955 |
| ADMSS | 30.5155 | 28.3062 | 31.9945 | 28.9282 | 28.6991 | 30.0238 | 29.7446 |
| SRAD | 0.5224 | 0.8178 | 1.4117 | 0.9247 | 0.8791 | 1.1196 | 0.9459 |
| SRAD-Bayes | 1.4276 | 0.8238 | 1.4502 | 0.8411 | 0.9827 | 1.0840 | 1.1016 |
| SAR-BM3D | 44.3160 | 44.4698 | 42.8047 | 44.1249 | 45.0229 | 45.4545 | 44.3655 |
| Proposed | 1.4505 | 0.9163 | 1.4982 | 1.1999 | 1.0002 | 1.1718 | 1.2061 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, H.; Jeong, J. Despeckling Algorithm for Removing Speckle Noise from Ultrasound Images. Symmetry 2020, 12, 938. https://doi.org/10.3390/sym12060938
Choi H, Jeong J. Despeckling Algorithm for Removing Speckle Noise from Ultrasound Images. Symmetry. 2020; 12(6):938. https://doi.org/10.3390/sym12060938
Chicago/Turabian StyleChoi, Hyunho, and Jechang Jeong. 2020. "Despeckling Algorithm for Removing Speckle Noise from Ultrasound Images" Symmetry 12, no. 6: 938. https://doi.org/10.3390/sym12060938
APA StyleChoi, H., & Jeong, J. (2020). Despeckling Algorithm for Removing Speckle Noise from Ultrasound Images. Symmetry, 12(6), 938. https://doi.org/10.3390/sym12060938






