1. Introduction
Robots have been rapidly developed and widely used in the past decades, especially in typical transportation application scenarios such as airports, ports, warehousing, and logistics. In addition to traditional fixed industrial robots, mobile and humanoid robots have developed the fastest. Autonomous navigation is a basic ability of mobile and humanoid robots. Achieving reliable, safe, and efficient autonomous navigation is a popular research topic in the field of robotics, and it is also a challenge. The four general problems of navigation are perception, localization, motion control, and path planning [
1,
2,
3]. Among these areas, it may be argued that path planning is the most important for navigation processes. Symmetry is widely used in the research of path planning. A* is a path planning algorithm based on graph search, with the search process based on the current node as the center to search for surrounding nodes; this search process is symmetrical. In this manuscript, bidirectional search is one of the optimization strategies of the A* algorithm. Bidirectional search is also a symmetrical path search method. This symmetrical search method can double the efficiency of the algorithm.
Path planning is the determination of a collision-free path in a given environment, which may often be cluttered in the real world [
4]. The planned path determines whether a mobile robot can achieve reliable and efficient autonomous navigation. Therefore, path planning plays an essential role in mobile robot navigation. With the widespread application of mobile robots, research on path planning is becoming increasingly popular.
Path planning algorithms can be divided into multiple classifications according to different ways. Graph search-based planners include the Dijkstra algorithm [
5], the A-star algorithm (A*) [
6], the state lattice algorithm [
7] etc. Sampling-based planners include rapidly-exploring random trees (RRT) [
8], interpolating curve planners, including lines and circles, clothoid curves, polynomial burves, Bezier curves, spline curves; function optimization planners, including the genetic algorithm [
9], swarm particle optimization, etc. Other path planning methods include vision-based path planning, artificial intelligence path planning, etc.
For application scenarios such as warehousing and logistics, path planning in a static environment assumes that the robot perceives the environment and uses local path planning algorithms when the environmental information is not fully grasped. A* is used for shortest path evaluation based on the information regarding the obstacles present in the static environment [
10], The shortest path evaluation for the known static environment is a two-level problem which comprises a selection of feasible node pairs and a shortest path evaluation based on the obtained feasible node pairs [
11]. Both of the above-mentioned criteria are not available in a dynamic environment, which makes the algorithm inefficient and impractical in dynamic environments. The A* algorithm was chosen because it is among the foundational algorithms used in contemporary real-time path planning solutions in a static environment. Novel research builds on the algorithm to find additional performance and efficiency.
Robustness and efficiency are the two essential factors of the path planning algorithms. Robustness reflects the reliability of the algorithm and is a prerequisite for the safe, stable and fast travel of mobile robots. The path closely fitting obstacles and right-angle turns is among the essential factors that affect the reliability of a mobile robot’s path. Efficiency reflects the speed of the algorithm for path planning and searching, and is one of the basic necessities for high work efficiency in mobile robots. Because robustness and efficiency are also the focus of algorithm improvement, we are also carrying out research along with this thought. This study investigates how to improve the efficiency of the algorithm and enhance the robustness of the algorithm. The research problems are how to reduce the runtime of the algorithm and the number of search nodes, and how to avoid collision and reduce the number of right-angle turns.
To address these two issues, an improvement method named the EBHSA* algorithm is proposed in this paper. It incorporates a series of improvements to the traditional A* algorithm, including the expansion distance, bidirectional search, heuristic function optimization and smoothing. The expansion distance extends a certain distance from obstacles to improve path robustness by avoiding collisions. A bidirectional search is a strategy that searches for a path from the start node and the goal node at the same time. Heuristic function optimization designs a new heuristic function to replace the traditional heuristic function. Smoothing improves path robustness by reducing the number of right-angle turns.
The main contributions of this paper as follows: the EBHSA* algorithm is proposed in this paper, and it includes four optimization strategies in the traditional A* algorithm: expansion distance, bidirectional search, heuristic function optimization and smoothing. Of them, the expansion distance and smoothing are employed to enhance the robustness of the path. The bidirectional search, heuristic function optimization and expansion distance are employed to improve the efficiency of the algorithm. In addition, the EBHSA* algorithm was tested through simulation and compared with other algorithms. The results show that EBHSA* algorithm performs better in terms of robustness and efficiency. In addition to test the effectiveness of the EBHSA* algorithm in actual application scenarios, the EBHSA* algorithm is transplanted to an FS-AIROBOTB mobile robot produced by China HuaQing YuanJian, and tested in the real world.
The rest of this manuscript is organized as follows. A review of the literature on the A* algorithm from the past few years is introduced in
Section 2. In
Section 3, the basic theory of the A* algorithm and the four optimization methods of the EBHSA* algorithm are introduced. In
Section 4, the coarse-grained time complexity analysis of the EBHSA* algorithm is given. The EBHSA* algorithm is tested and compared in
Section 5. In
Section 6, the EBHSA* algorithm is transplanted to a mobile robot to verify the effectiveness of the algorithm in actual scenarios. Finally, conclusions are given in
Section 7.
2. Related Work
The emphasis of path planning is algorithm design. The algorithm processes a geometric model with a certain complexity to generate an appropriate path, and the algorithm verification is completed by means of a robot traveling in the real world. The Dijkstra algorithm [
8] and its variants are commonly used in applications such as Google Maps and other traffic routing systems. To overcome Dijkstra’s computational-intensity doing blind searches, A* [
12] and its variants are presented as state-of-the-art algorithms for use within static environments [
10].
The A* algorithm can plan the shortest path in a map, but it needs to traverse around the path nodes and select the minimum path cost. Therefore, the algorithm performs a large amount of calculation and long calculation time, and the efficiency of the algorithm will decrease with the expansion of the map scale [
13]. Due to the characteristics of the graph search algorithm itself, the A* algorithm uses rasterized maps as its map representation method, which makes its path smoothness poor and reliant on too many right-angle turns, resulting in reduced reliability.
Extensive research has been performed on the A* algorithm, mainly focusing on obstacle avoidance, different application scenarios, and algorithm performance optimization in the progress of the A* algorithm. The A* algorithm is a popular graph traversal path planning algorithm. The A* algorithm similar to Dijkstra’s because it is a Dijkstra algorithm modification, in a sense. A* aims to find a shortest path and guides its search towards the shortest path states by a heuristic function. Therefore, the efficiency of the A* algorithm is better than Dijkstra’s. Many works of literature show that the A* algorithm has been widely used in many fields, such as transportation industry [
14,
15], and with the development of artificial intelligence, the A* algorithm has since been improved, including automated guided vehicle (AGV) [
16,
17] or unmanned surface vehicle (USV) path planning [
18,
19] and robot path planning [
20,
21]. The A* algorithm is simpler and uses less search node, which means less computation than some other path planning algorithms, so it lends itself to more constrained scenarios [
22,
23].
The A* algorithm needs to search for the shortest path in a map and through a heuristic function for guidance. The heuristic function mainly includes Euclidean distance [
24], Manhattan distance [
21], diagonal distance [
25], and Chebyshev distance. An algorithm is performed and governed by a heuristic function for computation time or run time for the performance of the task.
An A* optimization method with two improvements is proposed to solve the problem of slow search speed and low efficiency of the algorithm [
26]. Firstly, the evaluation function is weighted to ensure the reliability of the heuristic function. Secondly, in the rasterized maps, a set of nodes centered on a certain point is constructed. When the set of nodes contains obstacle nodes, this node is defined as an untrusted point and will not be searched. These improvements are used to improve the efficiency of the A* algorithm. However, the optimization method is only one strategy and it increases the calculation amount of the algorithm; moreover, its optimization is not thorough. To improve the efficiency of the A* algorithm, some researchers focused on the storage of traversed nodes and proposed an improved A* storage array method [
27]. The storage method is to access the array element by looking up the sequence number when accessing the specified element. This can be completed in one operation, while the traditional A* algorithm needs to traverse multiple nodes to find the specified element. This method only optimizes the storage and access of nodes, and only reduces the calculation amount of the algorithm without improving its path planning. To shorten the calculation time of the A* algorithm, an improved algorithm, called time efficiency A*, is proposed [
28]. The proposed algorithm determines the value of the heuristic function before the collision phase, instead of during the initialization phase. Therefore, the algorithm has higher efficiency in calculation time. This optimization method only optimizes the opportunity of determining the value of the heuristic function and does not optimize the heuristic function or decrease the number of search nodes. Therefore, the improvement of efficiency is limited.
Variants of the A* algorithm seem to be invented endlessly. Several A* optimization algorithms are used for a comparison, evaluation, and application scenario selection in [
6], including several modifications (Basic Theta*, Phi*) and improvements (RSR, JPS). A hybrid A* algorithm is proposed, improving the traditional A* algorithm when employed in autonomous vehicles. This method can plan the shortest possible path in a hybrid environment for a vehicle.
The A* optimization methods introduced above all only incompletely optimize the efficiency of the algorithm, which means that the efficiency of the algorithm can still be more thoroughly optimized. None of the above algorithms consider optimizing the robustness of the algorithm. Therefore, the improvements and variants of the A* algorithm are still flawed.
A constrained A* approach is proposed for USV in a maritime environment [
21], determining the approach path with a USV enclosed by a circular boundary as a safety distance constraint on the generation of optimal waypoints to avoid collision. This means the USV is surrounded by a circuit and reflects the performance of a collision-free approach. The concept of safety distance is also proposed, but the approach with an unmanned surface vehicle enclosed by a circular boundary as a safety distance places a constraint on the generation of optimal waypoints to avoid collision. This means the USV is surrounded by a circuit and not considering the obstacles on the maps.
The path being not smooth enough to dynamically avoid collision is another obvious shortcoming of the traditional A* algorithm. To solve this problem, a global path planning method that perceives the characteristics of the local environment is proposed [
29]. This method first uses the A* algorithm to generate the global optimal planning path in a known static map and deletes redundant nodes, and then generates local sequence nodes on the deleted global path to optimize the global path. This method guarantees the performance of the A* algorithm when it is used in a dynamic environment.
Smoothing is one of the most well-known methods to overcome the collision issue. The traditional A* algorithm plans some sharp turns which causes some problems for mobile robots. A smoothing of the A* algorithm is introduced in [
20]. The smoothed A* algorithm [
19] generates a path and redundant waypoints by using cubic spline interpolation and three path smoothers. Smoothing is one of the most effective methods to reduce right-angle turns and reduce the risk of collision. The A* algorithm is computationally simple relative to other path planning algorithms. With adjustments for vehicle kinematics, steering angle, and other factors, A* and its variants are suitable for AGV [
30]. An improved A* path planning algorithm considering economic performance is proposed in [
12] to solve the problem of global path planning for autonomous vehicles. New cost functions can be created with respect to equal step sampling, as in the case of Equation (1). The shown cost function includes distance and costs. The above considerations avoid sudden turns and, in this manner, improve the path smoothness [
10].
where
,
,
are weights with a positive value,
and
are the same as the base A* function, and
is the penalty factor based on the turning cost.
A visibility diagram was one of the very first graph-based search algorithms used in path planning in robotics [
10,
31]. A hybrid A* algorithm with the visibility diagram planning algorithm is proposed in [
14] to overcome the issue of high run costs to convergence.
3. The Proposed Methods
In this section, the basic principles of the traditional A* algorithm are introduced, and the deficiencies of the A* algorithm and the reasons for these deficiencies are analyzed. Four optimization methods for the A* algorithm are proposed.
The basic development process of the new algorithm is: the Robot Operating System (ROS) is used as the development platform and we modified the source code. The Dijkstra algorithm contained in ROS is modified and incorporated into the breadth-first search (BFS) method to construct a traditional A* algorithm. On the basis of the A* algorithm, the expansion distance, bidirectional search, new heuristic function, and smoothing are sequentially added, and the EA*, EBA*, EBHA*, and EBHSA* algorithms are developed in sequence. In the following section, we introduce these four optimization strategies and algorithms respectively, and carry out a series of tests on the algorithms.
3.1. Basic Theory of the Traditional A* Algorithm
The A* algorithm is a graph search algorithm for path planning, and its search method is based on breadth-first search. In the algorithm, visit to nodes is similar to tree traversal. Only by completing the search of all nodes in this layer can the nodes of the next layer be searched. This may cause blind search and lead to low search efficiency. However, as long as there is a feasible path, it must be able to find and is the optimal path. The process of BFS is shown as
Figure 1.
The A* algorithm is one of the best-known path planning algorithms and is a classic heuristic search algorithm. The A* algorithm aims to find a path from a start node to a goal node with the smallest cost by searching all possible paths. The heuristic information related to the characteristics of the problem is utilized to guide its performance, so it is superior to blind search algorithms [
31]. The A* algorithm consists of an OPEN list, a CLOSED list, and a heuristic function, and it employs the heuristic function to evaluate the distance from an arbitrary node to the goal node on a 2D plane. The A* algorithm is defined as a best-first algorithm because each cell in the configuration space is evaluated by the value:
where
is the cost of the path from the start node to the current node n,
is the cost of the path from node n to the goal node through the selected sequence of nodes, and
is the heuristic function of the A* algorithm.
is denoted as the evaluation function of node n. This sequence ends in the actually evaluated node. Each adjacent node of the actually reached node is evaluated by
. The node with the minimum
is chosen as the next node in the sequence. The advantage of the A* algorithm is that other distances can be used, modified, or added as standard distances.
3.2. Expansion Distance
The paths obtained by the A* algorithm come close to obstacles. This is unreliable during the movement of a robot. Therefore, a concept is proposed in this paper based on the experience of Euclidean geometry: the expansion distance.
The expansion distance is a certain distance expanding outward along the edge of obstacles before path planning. This is the shortest distance to which the path can approach obstacles. The expansion distance sets a safe buffer area between the path and the obstacles. The nodes of the expansion distance are regarded as obstacle boundaries. In the path planning process, the critical nodes cannot be selected as candidate nodes. The expansion distance can be adjusted according to the size of the robot and the physical environment. A schematic diagram of the expansion distance is shown in
Figure 2. The critical node is the node that is in contact with the obstacle, and the expansion node is the node that the algorithm has traversed.
As the expansion distance is introduced, critical nodes are not traversed during path planning, which is equivalent to reducing the map scale and reducing the total number of nodes that need to be traversed, thereby improving the efficiency of the algorithm.
Because the algorithm does not traverse these critical nodes, the total number of nodes traversed by the algorithm decreases, and the path planning efficiency improves. The main function of the expansion distance is to maintain a certain safe distance between the path and obstacles to ensure the safety of the robot during the traveling process and to facilitate the smooth processing of the path afterward.
3.3. Bidirectional Search Optimization
The search process of the traditional A* algorithm is a unidirectional search, finding a path from the start node to the end node. The bidirectional search method is introduced in this paper. The search is conducted from the start node and the end node at the same time. The search process finishes when the forward and reverse search nodes are adjacent during the search process. The positive and negative incomplete paths are spliced together to form a complete collision-free path. A schematic diagram of the search optimization is shown in
Figure 3. The left figure is the single search, and the right figure is the bidirectional search.
The search method introduces this parallel idea and searches from the start node and the goal node at the same time. A function call completes the two searches from the start node and the end node. This reduces the number of function calls and improves the path planning efficiency of the algorithm. In addition, the bidirectional search traverses fewer nodes than the unidirectional search, which further improves the path planning efficiency.
3.4. The Heuristic Function
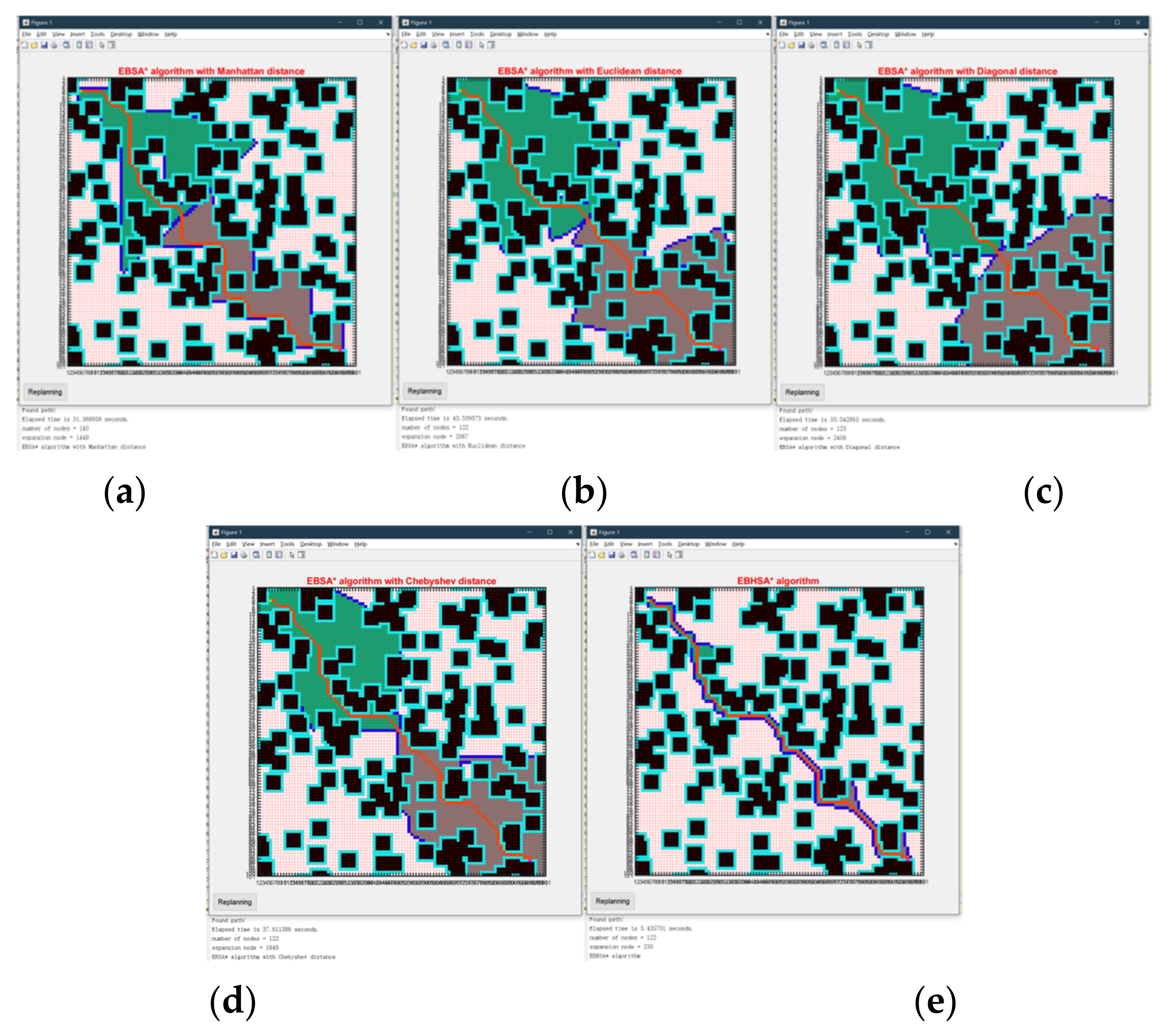
The heuristic function is the minimum cost evaluation value of the A* algorithm from any node to the goal node and helps to reduce the number of nodes traversed. Therefore, the choice of heuristic function has a direct impact on the efficiency of the algorithm. The heuristic function of the traditional A* algorithm uses the Manhattan distance, and subsequent improvements include the Euclidean distance, diagonal distance and Chebyshev distance. These four heuristic functions are the most widely used functions, and their theories are shown in Formulas (3)–(6).
- 2.
Euclidean distance heuristic function
- 3.
Diagonal distance heuristic function
- 4.
Chebyshev distance heuristic function
h(n) is the heuristic function, and are the coordinates of the goal node. are the coordinates of any node.
The Manhattan distance is mostly used for a 4-direction search. In the case of an 8-direction search, there are too many nodes to traverse. When the Euclidean distance is used, the estimated function value is very similar when the path is close to the goal node, and the node selection may be unclear. When the diagonal distance is used, if there are few obstacles, it is not easy to obtain the shortest path near the goal node. When the Chebyshev distance is used, only the maximum value of the abscissa difference or the ordinate difference is used, and the path always starts from a straight line and then a diagonal, If the search path encounters an obstacle, the shortest path is not obtained.
Based on the analysis of the heuristic function and the experience of repeated experiments, we propose a new heuristic function, as shown in Formula (6).
The optimized heuristic function is composed of the Euclidean distance and Chebyshev assignment, according to different weights. This heuristic function not only takes into account the advantages of the Euclidean distance and Chebyshev distance, but also weakens their disadvantages. The first part of the heuristic function ensures that the path is searched along the diagonal direction, and the latter part effectively reduces the number of nodes that are searched around after encountering obstacles in the search process. This advantage is clearly demonstrated in subsequent experiments.
3.5. Smoothing Optimization for Right-Angle Turns
There are three primary disadvantages in the traditional A* algorithm path [
19]. The A* algorithm sacrifices the turning cost to find the shortest path length. In addition, a mobile robot needs to decelerate sharply when turning at right-angles, which affects the efficiency and robustness of the algorithm. To overcome these disadvantages, the A* algorithm needs to be improved and smoothed.
In the moving process of the mobile robot, if the turning angle is a right-angle, the turning motion of the mobile robot is broken down into three steps: deceleration, turning on the spot, and movement. This greatly reduces the speed of the mobile robot.
This section mainly optimizes the right-angle turns that are prone to occur during the path planning process. The idea for smoothing right-angle turns is decomposing a 90° turn into multiple small-angle turns to improve the smoothness of the planned path. There are two cases: namely, a single turn, and a continuous turn.
When there are no obstacles on the inside of the corner, the inflection point is deleted, its adjacent two nodes are used as the turning point in the corner, and a right-angle turn is decomposed into two 45° angles, as shown in
Figure 4. When there are continuous right-angle turns, the inflection points are removed, and the adjacent nodes are directly connected to convert multiple right-angle turns into a small number of 45° acute-angle turns, as shown in
Figure 5. The smoothing optimization of the right-angle turns improves the smoothness of the path, which not only improves the robustness of the algorithm but also improves the overall travel efficiency of the robot.
4. EBHSA* Algorithm Time Complexity Analysis
In this section, combining the optimization strategies proposed in
Section 3, we conduct a coarse-grained time complexity analysis of the EBHSA* algorithm. This algorithm uses two loops: the inner loop traverses adjacent nodes with the current node as the center, and the node with lowest cost is marked and added to the open table. The outer loop traverses the nodes of the open table until the queue traversal ends. There are several factors that have obvious effects on the time complexity of various path planning algorithms, such as the map scale, starting node and target node location, etc. In general, the time complexity of various algorithms is given by Formula (8):
In Formula (8), where
and
are the length and width of the map, respectively. Since a bidirectional search is a strategy that searches in two directions, when the path is solvable, the path formed by each search direction is smaller than the whole path, which reduces the number of nodes added to the open table and reduces the loop frequency. Therefore, the time complexity of the EBHSA* algorithm is less than or equal to half that of the traditional A* algorithm. The pseudocode of the EBHSA* algorithm is shown as Algorithm 1.
| Algorithm 1: The pseudocode of the algorithm. |
| Function: Search(node_i, goal, CLOSE_LIST_i) |
| Input: Current search node node_i, goal node goal and positive close list CLOSE _LIST_i |
| Output: A path PATH from Start_i to End_i |
| Effect: Renew the open list and close list to find the target. |
| 1: Find the surrounding nodes “node(0)”, “node(1)”, “node(2)”, “node(3)” of the node_i |
| 2: for i = 0, i = 3, repeat |
| 3: if node(i) ∉ CLOSE_LIST_i |
| 4: heuristic(i) = sqrt((goal_x-node(i)_x)^2 + (goal_y-node(i)_y)^2) |
| + max(abs(goal_x-node(i)_x),abs(goal_y-node(i)_y)) × 2 |
| 5: OPEN_LIST_i <- node(i) |
| 6: else heuristic(i) = ∞ |
| 7: end if |
| 8: end for |
For the path planning algorithm, the theoretical time complexity of the algorithm is the size of the entire map, which is O(n2) in this article, but the actual time complexity of the algorithm will vary with the actual map. When there are no obstacles in the map and the algorithm traverses all nodes in the map, the actual time complexity of the algorithm is a theoretical value of O(n2), and the actual complexity must be less than or equal to this value.
6. Effectiveness Test
To verify the effectiveness of the EBHSA* algorithm on a real mobile robot platform, the EBHSA* algorithm was transplanted to the FS-AIROBOTB mobile robot hardware platform produced by China HuaQing YuanJian. The algorithm in the open source Robot Operating System (ROS) was rewritten to realize the transplantation of the algorithm. The components are shown in
Figure 9, and the parts of each component in
Figure 9 are shown in
Table 11.
In this experiment, we made several main assumptions to ensure the rationality of the test.
A real environment is set, and the start point and goal point are set in the scene.
Since the wheels of the robot are Mecanum wheels with 360-degree steering capability, the initial state of the robot does not require a small space.
In order to verify the obstacle-free ability of the robot, a certain number of obstacles are set in the real scene.
The effectiveness test is divided into 3 steps: (1) EBHSA* algorithm transplantation, (2) simultaneous localization and mapping (SLAM) test, and (3) a robot autonomous navigation test. The algorithm transplantation involved writing the EBHSA* algorithm into the robot system. The SLAM test built a test map to use the radar on the robot in the real world. The robot autonomous navigation test verified the effectiveness of the algorithm in the real world. To enable other researchers to reproduce our experimental process, we are sharing the source and instructions of this paper on GitHub.
This section mainly introduces the implementation of robot autonomous navigation tests through EBHSA* algorithm transplantation and SLAM map construction to verify the effectiveness of the EBHSA* algorithm in real applications. The corresponding digital map of the real environment constructed through SLAM is shown in
Figure 10.
As shown in
Figure 11, the left picture is the rviz interface of the ROS navigation and the right picture is the extracted path.
In this experiment, we provide a real-world application scenario for the algorithm and carried out basic autonomous navigation tests to verify the effectiveness of the EBHSA* algorithm. The developed algorithm was written into a real mobile robot. The robot could independently plan a reliable and smooth path according to the algorithm and complete the autonomous navigation test from the starting point to the target point. This experiment verifies that the EBHSA* algorithm can be applied to real robots and has the potential to be applied to industrial scenarios.