Abstract
The magnetic Hooke-Newton transmutation, which emerges from the transformation design of the quadratic conformal mapping for the system of charged particles moving in the uniform magnetic field, is investigated in the momentum space. It is shown that there are two ways to turn the linear interaction force of the system into the inverse square interaction. The first one, which involves simply applying the mapping to the system, has the spectrum with the Landau levels of even angular momentum quantum number. The second one considers the geometric structure of the mapping as an effective potential which leads us to the transmuted Coulomb system with the novel quantum spectrum. The wave functions of momentum for the bound and scattering states of the transmutation system are given. It is also shown that the effective potential due to the geometric structure can be generalized to a general 2D surface, and the Schrödinger equation of a particle moving on the surface while under the action of the potential can be solved by the form-invariant Schrödinger equation of the free particle. The solution of a particle moving on the hyperbolic surface under the potential is given with the conclusion. The presentation manifests the transformation design of the quantum state, depending mainly on the geometric structure of the representation space, not on the action of the specific potential field. This characteristic makes it possible for us to use the geometric structure of different representation spaces to explore some novel behaviors of quantum particles.
1. Introduction
The transformation design method (TDM) was introduced in optics [1,2], and has been extensively applied to the diverse wave phenomena (e.g., [3]). Through the reinterpretation of the geometric structure of the transformation as the material properties, the method enables novel devices such as invisibility cloaks (e.g., [4]). Recently, researchers have been interested in the applications of transformation design to the steering of matter waves (e.g., [5,6]). Due to the interaction nature of the quantum particle with external fields, the concept of the transformation design in quantum physics could exhibit more fertile content such as leading us to reveal new quantization systems (e.g., [7]) and more general monopole fields [8].
In quantum mechanics, one of the interesting contents is the representation theory that allows us to perceive quantum phenomena from different viewpoints, and may afford an easier way to comprehend a quantum system. It is acknowledged that the momentum representation has its own virtue in offering the visible image of the quantum wave functions (e.g., [9]) and the understanding of the quantum condensation phenomena. So far, few of the transformation designs have been discussed through the momentum space (p-space) [10]. Thus, it would be worth exploring the topic in the p-space that may enlarge the application of the representation theory. In this paper, we investigate the magnetic Hooke-Newton transmutation in the p-space through reinterpreting the geometric structure of the quadratic conformal mapping as an effective interacting potential. The exploration offers an alternative viewpoint to inspect the system while confirming the effectiveness of the TDM in the representation spaces other than the coordinate space.
Our discussion is arranged as follows: In Section 2, the quadratic conformal mapping is applied to the momentum representation of the Schrödinger equation for the charge particle coupling to a uniform magnetic field, and obtains the equation of a transmuted Coulomb system. It is shown that the transmutation system only has the Landau levels of even angular momentum quantum number. In Section 3, an additional interaction due to an effective potential defined by the geometric structure of the conformal mapping is considered in the equation of the Landau level system. It is then shown that the mapping turns the new equation into the transmuted Coulomb system with the novel quantum spectrum discovered in the recent investigation of the transformation design of quantum states [11]. The momentum wave functions of bounded and scattering states are obtained. Our conclusion is presented in Section 4. Finally, in the Appendix A, the definition of the effective potential is generalized to a general 2D surface, and we explain how to construct the form-invariant Schrödinger equation on the surface with the potential, and solve the quantum problem of a particle interacting with the potential.
2. The Quadratic Conformal Image of the Equation for a Charge in the Uniform Magnetic Field in Momentum Space
In the coordinate space, the Hamilton operator of a charged particle coupling to a magnetic field is known to be
For a uniform magnetic field with strength B and pointing along the z-axis, the vector potential can be chosen as
In the following content, we shall restrict our discussion to the 2D plane since along the z-axis the particle just performs free motion. The substitution of (2) in (1) gives the expression of the operator
where , and in the components. The quantum states corresponding to the operator are determined by the Schrödinger equation
The momentum representation of the states is associated with by the Fourier transformation
By replacing the wave function in (4) by the integral representation, the Schrödinger equation is shown as
Here stands for the first component of , i.e., . Multiply both sides of the equation by from the right, and note that
Then, taking the integration over the coordinate space , and employing the welcome formula of the Dirac’s function,
we get the momentum representation of Equation (4),
where , and the parameter . The kinetic energy operator in the p-space becomes the potential function on the right hand side. Because of the system with cylindrical symmetry, it is convenient to discuss the equation in the polar coordinates defined by and . The relationship between the Cartesian coordinates and the polar coordinates is given by , , and the derivatives between these two coordinate systems are associated with
and
Using these expressions, it is easy to show that Equation (9) has the polar representation
Although the solution of the equation is a well-known result, let us spend a little space to state it for comparison with the later works. By inserting the ansatz into the equation, the radial momentum wave is found to satisfy the equation
with the constant for short. The asymptotic behaviors at and of the equation require that the radial wave must be the product form
Substitution of the form in (13) gives the equation for the function u,
where the variable . This is the standard form of the confluent hypergeometric equation (see, e.g., p. 268, [12]). Its analytic solution around is the confluent hypergeometric function with the parameters
The condition of the bound states requires
Thus, the energy levels hidden in k read
The quantization values of m are determined by the single-valuedness condition of the wave function.
What we are interested in is the transmutation of (12) due to the quadratic conformal mapping
where is a constant with the units of momentum used to balance the units of both sides. It will be determined in the next section. We shall see that the mapping would associate the Landau-level system with the Coulomb system in the p-space. Change the variables with the mapping. The derivatives in (12) turn into
and
where and , which make (12) become
By the decomposition of the wave function, the equation is transformed into
where
It is noticed that Equation (23) is the radial equation of the Coulomb system in variable . However, on the right hand side of (23) is not an eigenenergy to be evaluated. It is just a constant composed of the proper constants of the system. One can regard as the eigenvalue, and we can solve the equation to find the genuine eigenenergy E hidden in the coupling constant now. With the asymptotic solutions of the equation at the near and far zones of p, the radial wave can be written in the form
The replacement of the product form in (23) gives the equation satisfied by
where was defined. We see the confluent hypergeometric equation again, and its solution is the confluent hypergeometric function with the parameters
The bound state condition requires
With the parameters in (24), the energy levels are found to have the expression
The value of the constant is determined by the single-valuedness condition of the wave function of the transmuted system which shows
It follows that the energy levels (29) with the single-valuedness wave function are
Therefore, the conformal mapping turns the Landau levels of odd angular momentum quantum number into even number. It does not alter the physical processes associated with the transition among even quantum numbers. However, the processes with the levels of odd angular momentum are cancelled. The transmutation between the linear force law and the inverse square force law was first pointed out by Issac Newton in his book (Cor. III, Prop. VII, [13], and, e.g., [14,15,16]). The magnetic version of the transmutation with a novel spectrum was discussed in the recent works [11,17,18].
Remark 1.
In References [11,17,18], the quantum number μ of the transmutation system was taken as which leads to the solution of the Schrödinger equation in the target space being two-value function, thus violating the single-valuedness condition of the wave function. The single-valuedness solution can be obtained by replacing the quantum number m by 2 m therein. A similar mistake also appeared in [8]. The author very much appreciates the referee for his comments on this point.
3. The Magnetic Hooke-Newton Transmutation Due to the Action of an Effective Potential
What is more interesting in the transmutation caused by the quadratic mapping is additionally considering the geometric structure of the mapping as an effective potential which could turn the Schrödinger equation with the potential in the p-space into the form-invariant equation of the free particle (see Appendix A for details). The potential due to the mapping under consideration is defined by
The first term on the right hand side simply gives , and the equation becomes
where
Equation (34) is the radial equation for a Coulomb system in variable . In contrast to (23), the right hand side of the transmuted system has the eigenvalue , not just a constant. The physical energy level E can be extracted from as soon as is known. One of the interesting features of the system is that the interaction, attractive or repulsive, is determined by both the signatures of the angular momentum and the charge shown in the current coupling:
Since , , and , it has the conditions
for bound states, and
for scattering states, i.e., for a bound state, the electron (anti-electron) can only move counterclockwise (clockwise) if the direction of the angular momentum is defined as counterclockwise. This observation is consistent with the discussion of the system in the coordinate space [11].
3.1. Bound State
Using the asymptotic forms of Equation (34) at and , one can put the radial wave in the form
where with . Substitution in (34) shows that satisfies
where . We have the confluent hypergeometric equation. Its solution is the confluent hypergeometric function . Bound states are determined by the quantization condition
It gives the finite polynomial solution of the bound state wave function. The energy levels are then found to be
It is the place to determine . The spectrum was recently obtained in the coordinate space and has the definite expression ([11], and Equation (37) in [17])
with and the characteristic length of the system . A comparison of these two equations shows that
This can be regarded as the characteristic length of the system in the p-space. The length depends on the quantum number m of the angular momentum. This is due to the fact that the Coulomb interaction in (34) depends on m. Thus, it is better to consider different m corresponding to the independent system in the transmutation. Without any indefinite coefficient, the energy levels have the explicit expression
Using (35) and the condition of the bound states, one can know that the condition for the charges that enable them to occupy the levels is . Given a value of , there are infinite states corresponding to the values of available. An alternative viewpoint for the condition can be given by the wave length. If we express the energy of the charge by , and express p in terms of the wave length of the matter wave, the condition of a charge occupying a bound state in Equation (35) becomes
where and is the characteristic length of the system of the simple harmonic oscillator. The radial wave function is now known as
This can also be expressed as
with C being constant since the generalized Laguerre polynomials (p. 240, [12]). Employing the normalization condition,
the recurrence relation , and the orthogonal relation (p. 241, [12])
the radial wave function is found to be
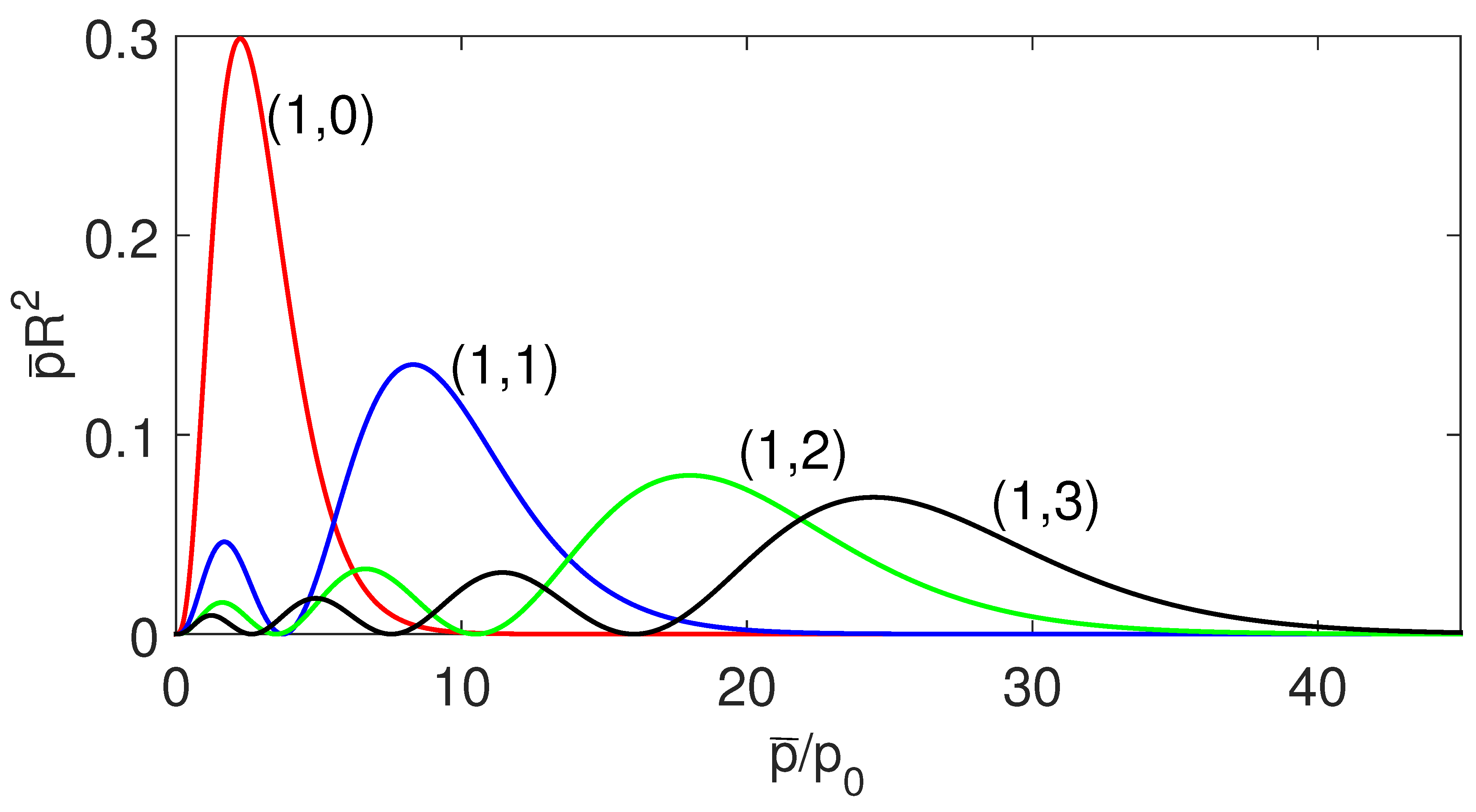
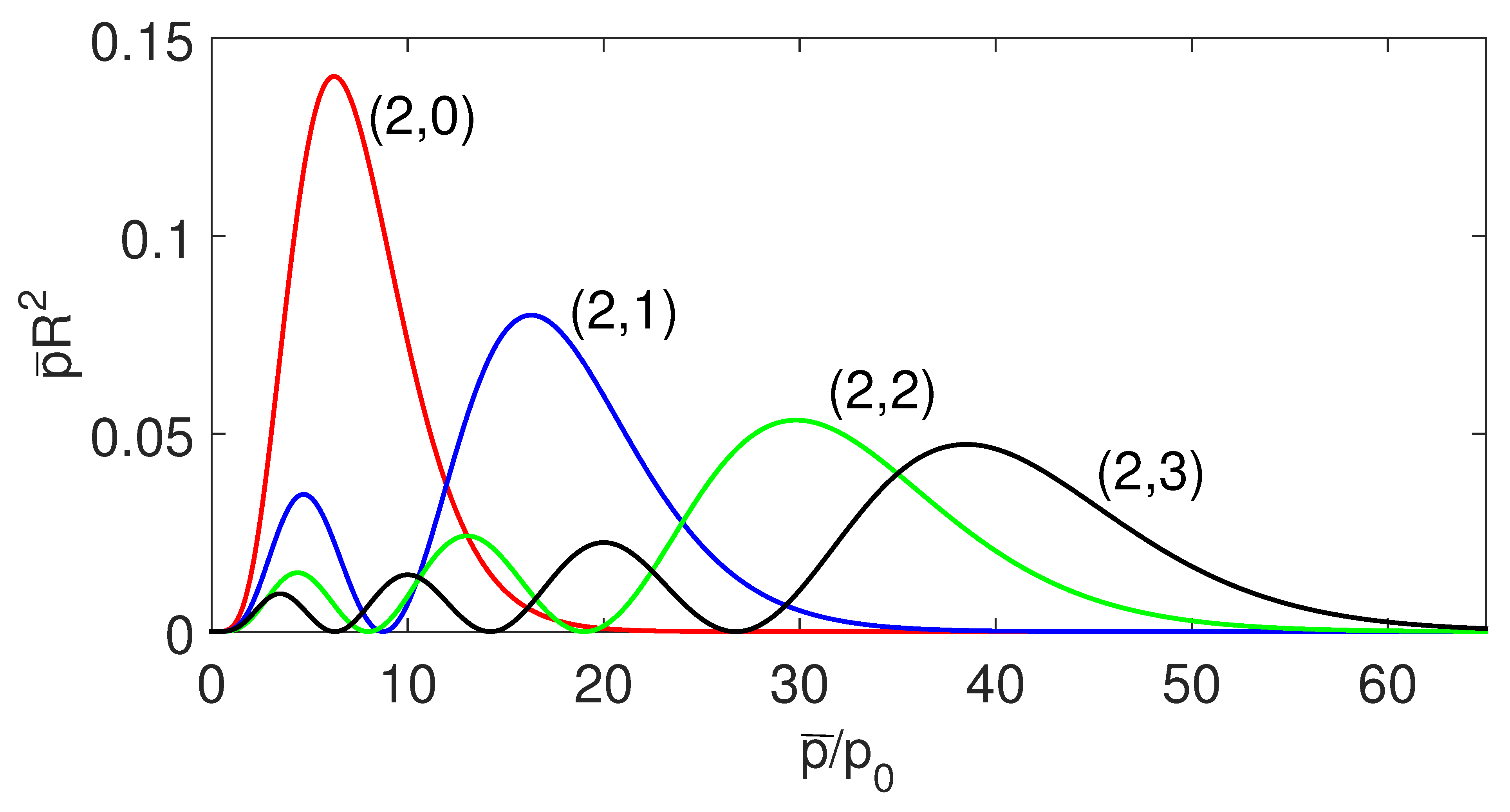
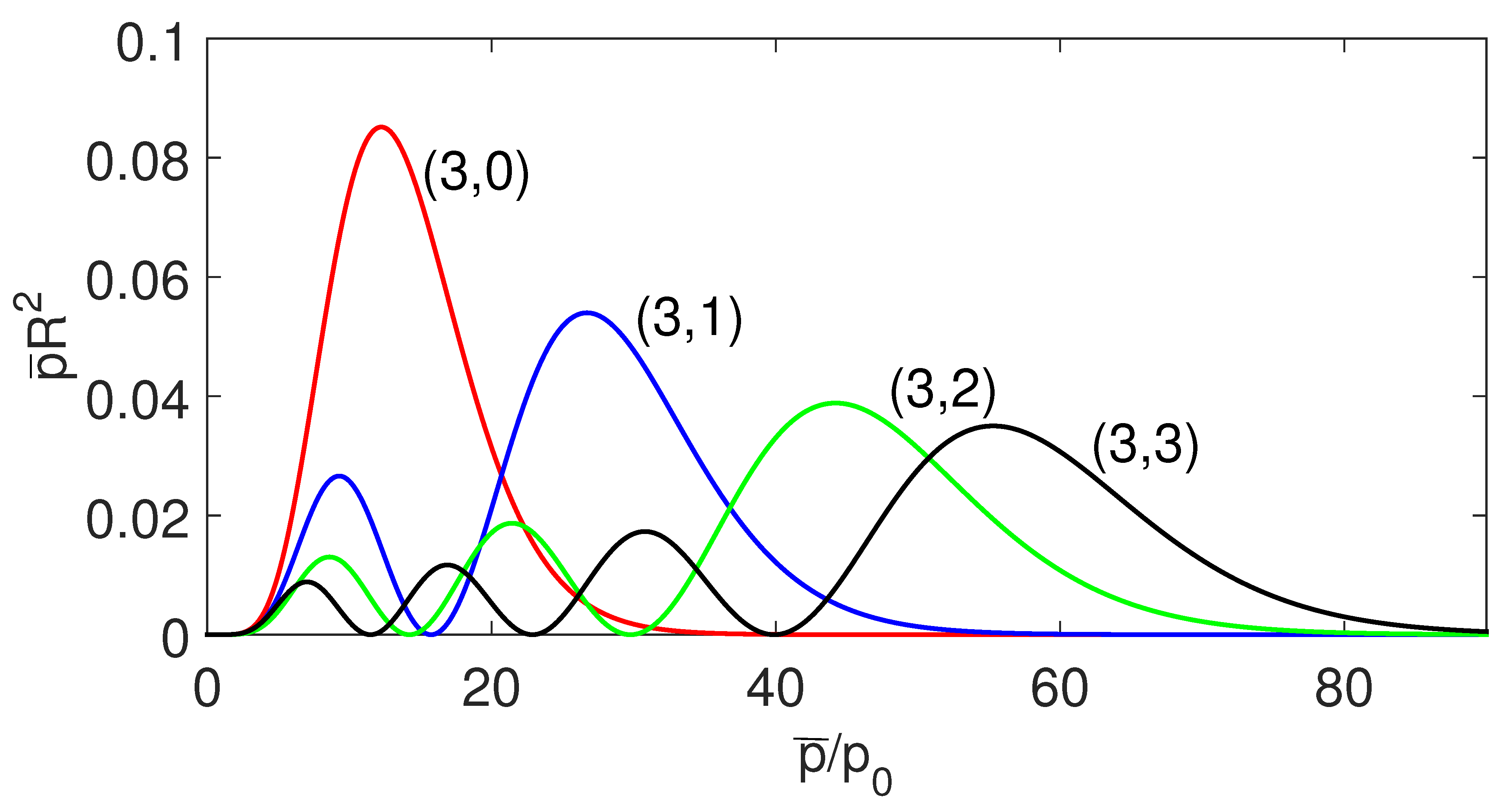
Here the constant factor has been replaced by the explicit form . Figure 1, Figure 2 and Figure 3, show the probability distributions of several bound states corresponding to the quantum number . There are no corresponding states for a charge with in the transmutation system. This point is clear from the coupling constant (36).
Figure 1.
(Color online) The radial probability distribution of the magnetic Hooke-Newton transmutation system in the momentum space. The distribution is classified by the quantum number , where . Given several m equivalent to giving the strength of the interaction, there is an infinite number of possible states corresponding to available. The number of labels the number of the nodes in a distribution.
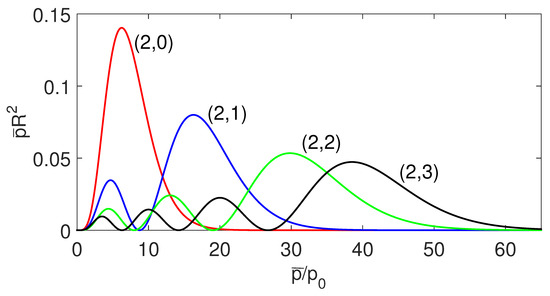
Figure 2.
(Color online) The radial probability distribution of the pair .
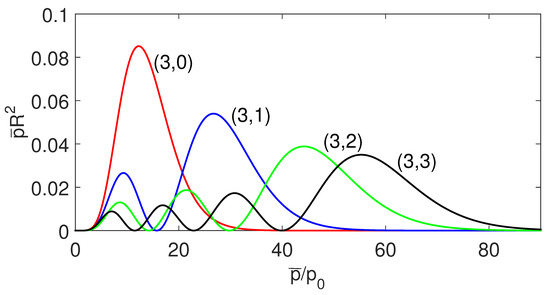
Figure 3.
(Color online) The radial probability distribution of the pair .
3.2. Scattering State
As shown in (38), a particle with a state of different signatures of the angular momentum and the charge in the transmutation system experiences the Coulomb-like repulsive force. It suffers scattering. The radial wave of the scattering state satisfies the same equation of (34), but with the constant and non-quantized spectrum . So the parameters , , and we have the wave function for the scattering state
where . It is of interest to know the asymptotic representation of a scattering state as . Using the asymptotic formula of the confluent hypergeometric function (p. 611, [19])
when and , and defining the phase shift of the scattering state by
such that
we have the representation at the far region
4. Conclusions
This paper investigates the magnetic Hooke-Newton transmutation in the momentum space. On the one hand, it shows the effectiveness of the transformation design method in a representation space other than the coordinate space that may enlarge the application of the representation theory. On the other hand, it clarifies the difference between the transmuted Coulomb systems by directly performing the quadratic conformal mapping with respect to the equation of the Landau level problem and that presented in the recent works due to the transformation design which exhibits a novel quantum spectrum. The latter includes the action of an effective potential defined through the conformal structure of the mapping, while the former does not. Three remarks are worth making as follows:
(a) The transmuted Coulomb system due to the transformation design in the momentum space intrinsically differs from the common Coulomb system since the dynamics of the usual Coulomb system in the momentum space exhibit its behavior as the free particle on the unit sphere (e.g., [20]). Our presentation shows that the transmuted Coulomb system is caused by the action of the effective potential which is determined by the geometric structure of considered representation spaces. It has the same form either in the momentum or in the coordinate space.
(b) The potential effect coming from the geometric structure fractionalizes and turns down the ground state energy of the charged particle in the uniform magnetic field. The quantum number m determines the coupling strength of interaction as shown in (36). A series of energy levels are physically allowed after being given m. The energy of the ground state of the given m reads
where the suffix labels the quantum number , which fractionalizes . The ground state energy never comes to zero in any value of finite m, and the energy levels of the particle grow with the increase of the radial quantum number . Experimentally, a better way for the observation of the effect of the levels in Equation (45) is through offering the potential field
to the Landau level system in the coordinate space, where , as given above (44), and the energy E should be chosen as the highest critical energy of the bound states to have enough attractive force in the region of to trap the charges with lower energy. The system under the quadratic conformal mapping has the same spectrum as (45). For , the spectrum has the lowest energy level , and the level of the first excited state. Therefore, the energy of an emitted photon generated by the transition from to the ground state is
For an electron with charge and the magnetic field Tesla, eV. With the definite value of , the constant in the potential U can be evaluated. We find μm such that the potential field can be set up in the laboratory. The energy difference is now given by eV which corresponds to the wave length Å. It is about the range of microwaves, and should not be difficult to observe using the technique of the spectroscopy.
(c) The phase transition and symmetry breaking are important topics (e.g., [21,22,23,24]). Two points for the ground state of a 2D system generated by the processes are stated as follows: (i) The behavior of the ground state would not be altered by the quadratic conformal mapping. The reason is as follows: If the interaction in the system can be described by a potential and has ground state, it stands for the potential of the system has minimum to support the ground state. Since the potential at its minimum can always be expanded and approximated by the harmonic trap potential, the question comes a similar appearance to the section II of the paper where the ground state of the potential of the harmonic trap under the quadratic conformal mapping does not alter by the mapping as shown in Equation (31). (ii) If the system with ground state is added by the effective potential presented in (61), the level of the ground state would be lowered under the quadratic conformal mapping as shown in Equation (45) in Section 3. The cause is due to the fact that the effective potential offers an additional attractive (repulsive) force when . The attractive region would lower the ground state in the target space of conformal mapping. On the other hand, the repulsive region helps to establish the possible scattering state in the spectrum of the transmutation system such as the result shown in Section 3. For a general conformal mapping, the influence on the ground state needs to be further investigated.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The author thanks C. R. Harrington for her critical reading of the manuscript. My work has been supported by the Ministry of Science and Technology of Taiwan under Contract No. MOST 108-2112-M-110-008-MY2.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A. The Conformal Structure of the Form-Invariant Line Element and the Effective Potential
Here we prove that the quadratic conformal mapping turns the Schrödinger equation of a particle interacting with the effective potential defined by the conformal structure of the 2D p-space into the form-invariant Schrödinger equation of the free particle on the 2D plane. Consider the form-invariant line element in the 2D p-space
It is assumed that and . The line element has the equivalent expression
The condition of the line element (A1) generated by a conformal mapping is
This is equivalent to the statement
with being a constant. So we have the mapping
where is a constant with the units of momentum used to balance the units. Accordingly, has the conformal representation
Through the conformal factor, define the effective potential
The Schrödinger equation in the polar coordinates with the action of the potential is given by
The relations between the derivatives of the variables , and read
With , and , the replacement of (A9) in (A8) results in the form-invariant Schrödinger equation of the free particle
The statement above is confirmed.
Using the geometric structure of the conformal mapping to define the effective potential can be generalized to a general 2D surface. The conformal mapping of the surface has the efficiency of turning the Schrödinger equation of a particle under the action of the potential into the form-invariant equation of the free particle on the surface. The solution of the particle with the interaction on the surface can thus be solved by the form-invariant solution of the free particle. The verification of the statement is as follows. Consider a 2D surface in the p-space described by the line element
Define a form-invariant element by
with only. It can also be expressed as
Here . The condition of the line element (A12) generated by conformal mapping is
So
where and . Equation (A14) is equivalent to
with C being an arbitrary constant which shows
and the determinants of two kinds of metric are associated with the equality
The state of a particle moving on an arbitrary 2D surface with orthogonal frame (A11) while experiencing the action of the potential U satisfies the equation
where
Inserting the identities and into the equation makes it become
The summation terms become
Equation (A21) reduces to
Using (A17) and (A18) again, it is easy to prove
and the equation becomes the form-invariant Schrödinger equation
It is obvious that the discussion and conclusion are true in any representation space. As an application, let us construct the form-invariant equation on the hyperbolic surface (H2) and discuss its quantum mechanics. The Riemannian metric on the surface can be expressed as
where , , and is a constant. The negative constant curvature of the surface is given by . Consider the form-invariant metric
with and . The equalities in (A16) imply
Here we just take in (A16). The explicit representation of the form-invariant coordinates (, ) are found by integrations. They are
where the dimensionless variables and were introduced for short. Obviously, the variable y has the same range as u. With the help of the half angle formula , the transformation relation between and y has the expression
or
Both functions are anti-symmetric with respect to the index , i.e.,
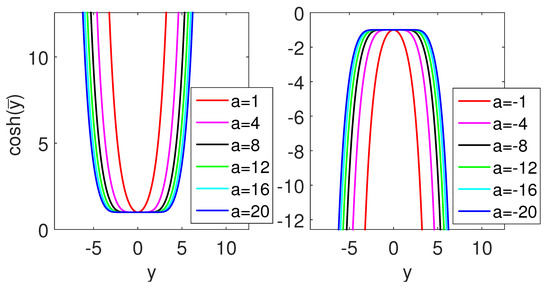
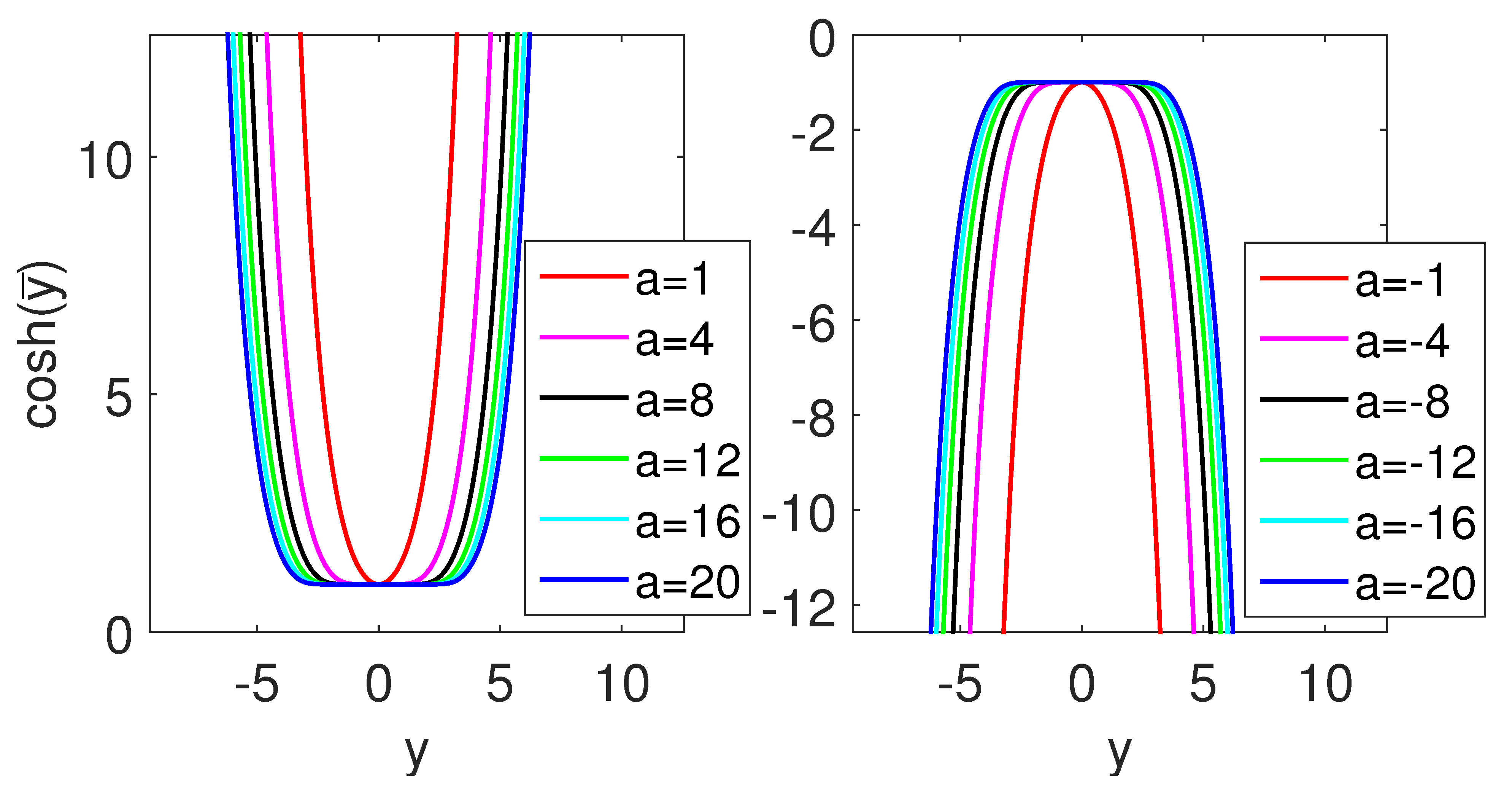
Figure A1 and Figure A2 show some graphs of the hyperbolic functions where the range of the transverse y-axis was extended to the negative value for exhibiting their symmetric properties. It is easy to verify that the familiar relationship of the hyperbolic functions holds. Moreover, the derivative relations
 and
are also true, where
and
are also true, where

Figure A1.
(Color online) The graphs of the hyperbolic function cosh for some values of the conformal index a in (A31). Here the range of the transverse y-axis is extended to the negative values for the exhibition of the symmetric property of the function.
Figure A1.
(Color online) The graphs of the hyperbolic function cosh for some values of the conformal index a in (A31). Here the range of the transverse y-axis is extended to the negative values for the exhibition of the symmetric property of the function.


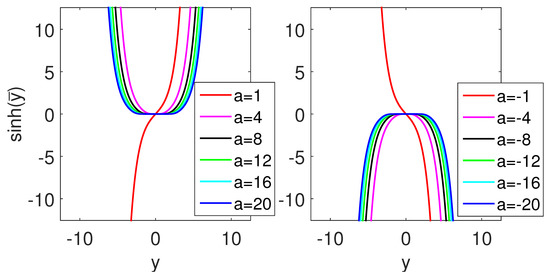
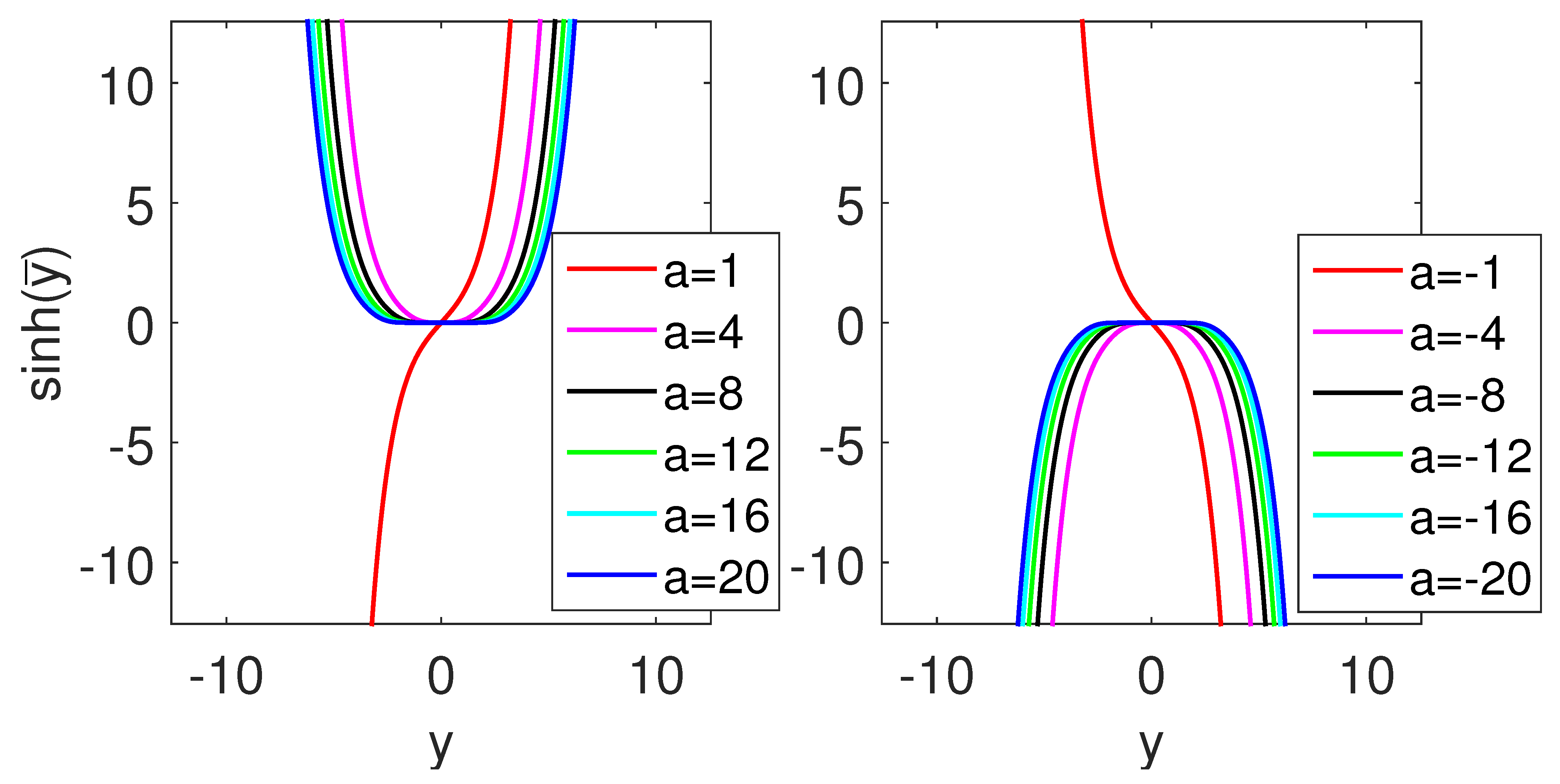
Figure A2.
(Color online) The graphs of the hyperbolic function sinh for some values of a in (A32). Both functions, cosh and sinh , are anti-symmetric to the negative values of a.
Figure A2.
(Color online) The graphs of the hyperbolic function sinh for some values of a in (A32). Both functions, cosh and sinh , are anti-symmetric to the negative values of a.

The transformations (A30) and (A32) are conformal mapping. This is confirmed by the conformal condition
The form-invariant metric (A28) is associated with by a conformal factor as
where . It can be proved that the conformal space has the same Gauss curvature as H2. Since the metric of H2 is diag , the form-invariant metrics of the conformal surface of H2 are
where and were used. Accordingly, we get the form-invariant Schrödinger equation on H2
from (A26). It describes the evolution of a quantum particle moving on H2 while it experiences the action of the potential field
The wave function permits the factorization such that the radial wave satisfies the equation
Here . If we perform a transformation of R by , the equation reduces to
where . The value of is determined by the single-valuedness condition of the wave function which means , implying that is an arbitrary integer
Notice the existence of the bound states only if . Then, the potential would offer an attractive force on the particle to form the bound states. For the H2 surface, it was supposed to only have the scattering states (e.g., [25]). To solve the equation, introduce the new variable turning (A44) into
where . If we perform the transformation , we find that satisfies the equation
Put
The equation becomes the form of the hypergeometric equation (e.g., p. 272, [26])
One solution of the equation is the hypergeometric function . Therefore, the solution of (A44) is
A convenient way to obtain the energy levels is through the positions of the pole of the scattering wave. For this, using the asymptotic formula of the hypergeometric function at (e.g., p. 273, [26])
and noting that , the wave F has the asymptotic representation
When , the eigenvalue with in (A44). The first term in (A52) cannot meet the finite boundary condition when unless it has the condition
which gives the quantization levels
The parameter with was inserted to obtain the expression. When , a normalizable solution requires , , which gives the same spectrum. The dynamic behavior of a particle on the H2 surface has been of interest to many of our colleagues over the decades (e.g., [27,28]). The conformal surface of H2 offers an additional degree of freedom, the conformal parameter to modulate the dynamic behavior of the particle, which can be achieved by the interaction with the external effective potential.
References
- Leonhardt, U. Optical conformal mapping. Science 2006, 312, 1777–1780. [Google Scholar] [CrossRef] [PubMed]
- Pendry, J.B.; Schurig, D.; Smith, D.R. Controlling electromagnetic fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Chan, C.T. Acoustic cloaking and transformation acoustics. J. Phys. D Appl. Phys. 2010, 43, 113001. [Google Scholar] [CrossRef]
- Ni, X.; Wong, Z.-J.; Mrejen, M.; Wang, Y.; Zhang, X. An ultrathin invisibility skin cloak for visible light. Science 2015, 349, 1310–1313. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Genov, D.A.; Sun, C.; Zhang, X. Cloaking of matter waves. Phys. Rev. Lett. 2008, 100, 123002–123004. [Google Scholar] [CrossRef] [PubMed]
- Lin, D.-H. A mass-independent conformal quantum cloak. New J. Phys. 2017, 19, 113003. [Google Scholar] [CrossRef]
- Lin, D.-H. Transformation design method for quantum states. Phys. Rev. A 2012, 85, 053605. [Google Scholar] [CrossRef]
- Lin, D.-H. Form-invariant solution to quantum state on the sphere. J. Phys. Commun. 2020, 4, 085012. [Google Scholar] [CrossRef]
- Weigold, E.; McCarthy, I.E. Electron Momentum Spectroscopy; Kluwer Academic: New York, NY, USA, 1999. [Google Scholar]
- Lin, D.-H. Controlling matter waves in momentum space. Phys. Rev. A 2014, 90, 012709. [Google Scholar] [CrossRef]
- Lin, D.-H. Quantum states emerging from charged transformation-wave in a uniform magnetic field. Eur. Phys. J. D 2016, 70, 141. [Google Scholar] [CrossRef]
- Magnus, W.; Oberhettinger, F.; Soni, R.P. Formulas and Theorems for the Special Functions of Mathematical Physics; Springer: New York, NY, USA, 1966. [Google Scholar]
- Newton, I. Philosophiae Naturalis Principia Mathematica; Cambridge University Press: Cambridge, UK, 1687. [Google Scholar]
- Arnol’d, V.I. Huygens & Barrow, Newton & Hooke; Birkhäuser Verlag: Basel, Switzerland, 1990. [Google Scholar]
- Needham, T. Newton and the transmutation of force. Am. Math. Mon. 1993, 100, 119–137. [Google Scholar] [CrossRef]
- Leonhardt, U.; Philbin, T. Geometry and Light: The Science of Invisibility; Dover: New York, NY, USA, 2010. [Google Scholar]
- Lin, D.-H. The Hooke-newton transmutation system of magnetic force. J. Phys. Commun. 2018, 2, 065017. [Google Scholar] [CrossRef]
- Lin, D.-H. On the magnetic Hooke-newton transmutation of electrons. J. Phys. Commun. 2019, 3, 085014. [Google Scholar] [CrossRef]
- Morse, P.M.; Feshbach, H. Methods of Theoretical Physics; McGraw Hill: New York, NY, USA, 1953. [Google Scholar]
- Lin, D.-H. On solutions of Coulomb system and its generalization to the Aharonov–Bohm effect. Ann. Phys. 2008, 323, 371–387. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical model of elementary particles based on an analogy with superconductivity. I. Phys. Rev. 1961, 122, 345. [Google Scholar] [CrossRef]
- Goldstone, J.; Salam, A.; Weinberg, S. Broken symmetries. Phys. Rev. 1962, 127, 965. [Google Scholar] [CrossRef]
- Gu, S.-J.; Yu, W.-C.; Lin, H.-Q. Construct order parameters from the reduced density matrix spectra. Ann. Phys. 2013, 336, 118–129. [Google Scholar] [CrossRef]
- Arraut, I. The Nambu-Goldstone theorem in nonrelativistic systems. Int. J. Mod. Phys. A 2017, 32, 1750127. [Google Scholar] [CrossRef]
- Dane, C.; Verdiyev, Y.A. Integrable systems of group SO(1,2) and Green’s functions. J. Math. Phys. 1996, 37, 39–60. [Google Scholar] [CrossRef]
- Flügge, S. Practical Quantum Mechanics; Springer: Berlin/Heidelberg, Germany, 1971; Volume 2. [Google Scholar]
- Gutzwiller, M.C. Chaos in Classical and Quantum Mechanics; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Grosche, C. Path Integrals, Hyperbolic Spaces and Selberg Trace Formulae; World Scientific: Singapore, 2013. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).