2.2. Registration of the Femur
For measuring the postoperative displacement of the Hansson pins, it is necessary to select a reference with rigid morphological properties. Depending on the setting in which the Hansson pin is used, the shape and X-ray absorptivity of the proximal femur does not change unless structural damage occurs, which satisfies the requirements for use as a reference. Femur image registration is the transfer of images containing femur and implants from the same patient at different times, different scanning devices, different scenes, and others to the same spatial coordinate system and strict alignment with femur as the reference. After this transformation, it is possible to measure the position information of Hansson pins at different times.
Typically for CT image alignment, at least two sets of images containing the same target information are required. The matching criterion is to achieve maximum similarity between the fixed and floating images, a combination of feature space matching algorithm, spatial search algorithm, optimization algorithm, and similarity measure. Commonly used rigid medical image registration algorithms include point set matching based, a genetic algorithm-based, and mutual information-based 3D image registration. The alignment of the femur image in this paper is rigid, i.e., no affine transformation of the graph is required, which requires high alignment accuracy.
We choose a multi-resolution framework, which uses negative mutual information as the similarity metric function. The framework contains four parts: spatial transformation module, similarity metric module, interpolator, and optimizer, as shown in
Figure 5.
This framework is widely used in medical image registration due to its high accuracy, robustness, and fast alignment speed. Its core idea is to input the images in the fixed image pyramid and floating image pyramid into the framework layer by layer. An optimizer is used to drive the alignment process, and an interpolator is used to map the floating images into the new coordinate system [
24,
25].
The method of negative mutual information in the similarity measurement module was proposed by Mattes et al. in 2003. Mutual information forms a continuous histogram estimate of the underlying grayscale image using the Parzen window virtually eliminates the effect on the similarity calculation due to interpolation quantization and binary data discretization during the image space transformation. Image registration can be seen essentially as the process of minimizing the negative similarity function. When we define the set of discrete grayscales for a fixed image as
and the set of discrete grayscales for a floating image as
, the negative similarity function model can be expressed as
where
is the joint distribution function, which can be calculated from the values of the Parzen window cubic spline and zero-order B-splines.
are the grayscale values in
and
, respectively.
is the floating image edge probability distribution and
is the fixed image edge probability distribution.
is the image transformation parameter.
Mattes mutual information function has continuously differentiable characteristics. The optimizer needs to meet the conditions of high speed, low resource consumption, and high robustness to obtain the optimal spatial transformation parameters. Therefore, we choose a multi-resolution algorithm as the optimization search strategy. In this section, we select the patient’s CT images before the one-year recovery period as fixed images and the CT data after the one-year recovery period as floating images to construct the Gaussian pyramid. Gaussian pyramids are constructed using Gaussian smoothing and downsampling to create a series of images of varying sizes. These images form a pyramid model from large to small and from bottom to top, as the fixed image and floating image modules present in
Figure 5.
We take the original fixed image and floating image as the bottom level 0 of the pyramid, and after the discrete low-pass filter calculation, an upper level 1 of the upper pyramid is obtained, and the iterative process is repeated. For getting the Gaussian pyramid layer
, it is necessary to perform Gaussian low-pass filtering on its previous level image and then downsample it by inter-row and inter-column, usually for removing pixels in even rows and even columns of the image. The mathematical expression is
where
is the number of Gaussian pyramid layers,
and
are the number of rows and columns of the image of the ith layer of the Gaussian pyramid, respectively;
is a two-dimensional 5 × 5 window function with the expression as
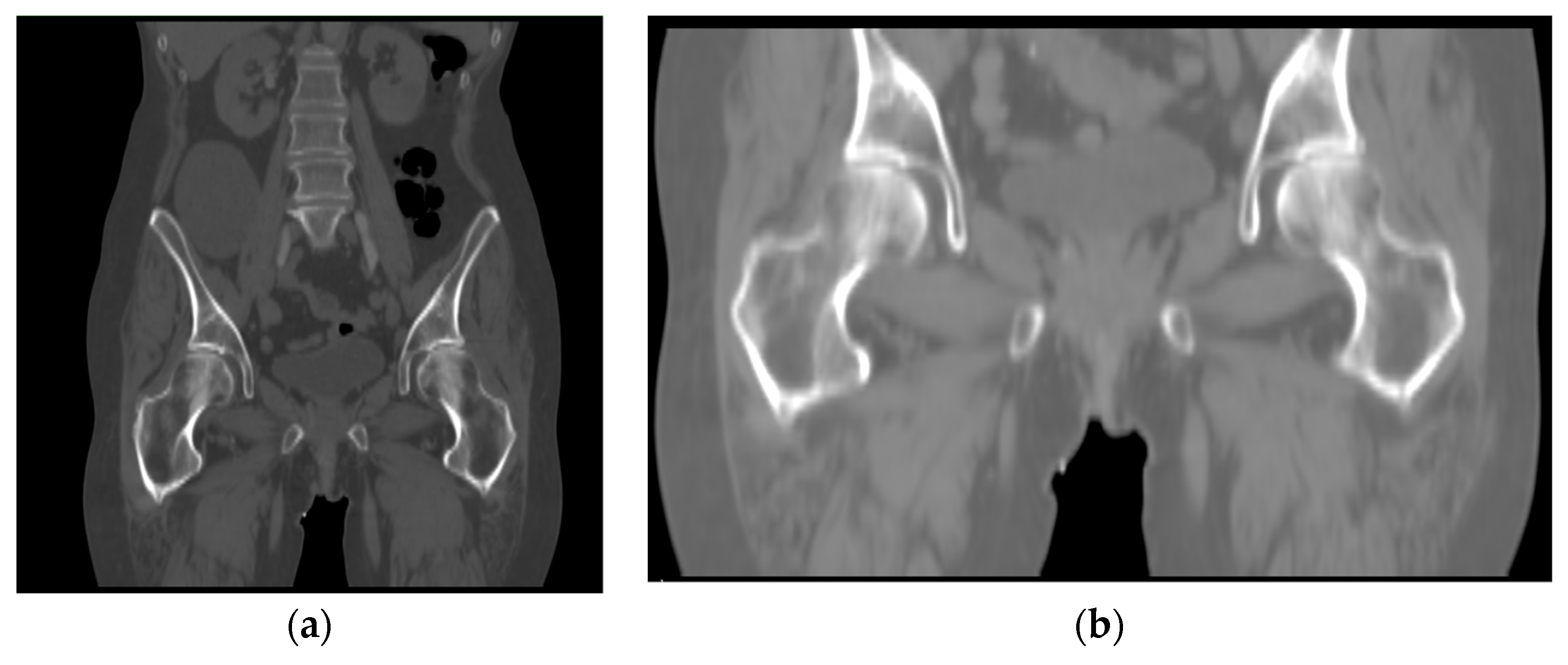
When two 3D images containing femur are input to the framework, the registration range defaults to the whole image, and the optimal spatial transformation parameters obtained after iteration corresponds to the global search space. In other words, although the spatially transformed floating image matches the fixed image, the purpose of our study is to align the femur. The tissues or organs around the pelvis, such as the pelvic bone, will significantly affect the similarity calculation. In this case, the spatial transformation mostly matches the pelvis’s position rather than the proximal femur. Therefore, we use the above framework to perform coarse alignment on the images containing the femur. After that, we use the femur’s mask and perform fine registration on the region containing the only femur.
2.3. D-UNet Framework
To extract the region of interest, we segmented the proximal femur without the femoral head in the patient’s CT images using a model trained by the 3D-UNet framework.
3D-UNet is an end-to-end training model proposed by Özgün Çiçek et al., which is mainly used for semantic segmentation of medical images [
26]. The model inherits the features of the 2D-UNet network by using encoder and decoder structures to extract features and recover the semantic feature maps into volumetric images with the same resolution as the original images. Compared with the 2D-UNet network, 3D-UNet uses the image interlayer information to ensure the continuity of mask changes in adjacent images. Moreover, different from the fully convolutional network, which only deconvolutes the feature map, 3D-UNet achieves the multi-scale feature recognition of image features by the symmetric structure of four downsampling and four upsampling, and the skip connection method, i.e., it fuses the shallow features of the same scale in the encoder and the in-depth features from the upsampling to avoid the loss of edge information. The downsampled low-resolution information provides contextual information to the target, and the upsampled high-resolution features improve the network’s ability to recognize edge information such as gradients.
Figure 6 illustrates the 3D UNet network framework used in this paper. In the encoder structure, we set the network structure to 5 layers, and the number of channels in each layer is 16, 32, 64, 128, and 256, respectively.
This study uses dice loss as the loss function, which is widely used in neural networks for medical image segmentation. Dice score coefficient (DSC) is used to evaluate the degree of overlap of two samples, and in binary semantic segmentation, the segmentation effect is evaluated based on ground truth [
27]. Hence, we can maximize the overlap of two samples using
. Dice loss was first proposed and used in the VNet framework by Milletari et al. and is defined as
where
and
represent the predicted label and ground truth of each voxel, respectively, during the training process.
is the number of voxels in the input image.
CT images vary depending on patient condition and scanner model. The output segmented femur is often accompanied by segmentation noise, as shown in
Figure 7. The noise appears as small, separated coherent voxels. The model outputs segmented images in which the femur has the largest number of coherent voxels. To correct this problem of non-femur parts being incorrectly identified, we retain only the largest coherent components in the post-processing of the model output. The mathematical model can be expressed as
where
is a function to calculate the maximum number of contiguous adjacent voxels.
2.4. Principal Component Analysis (PCA)
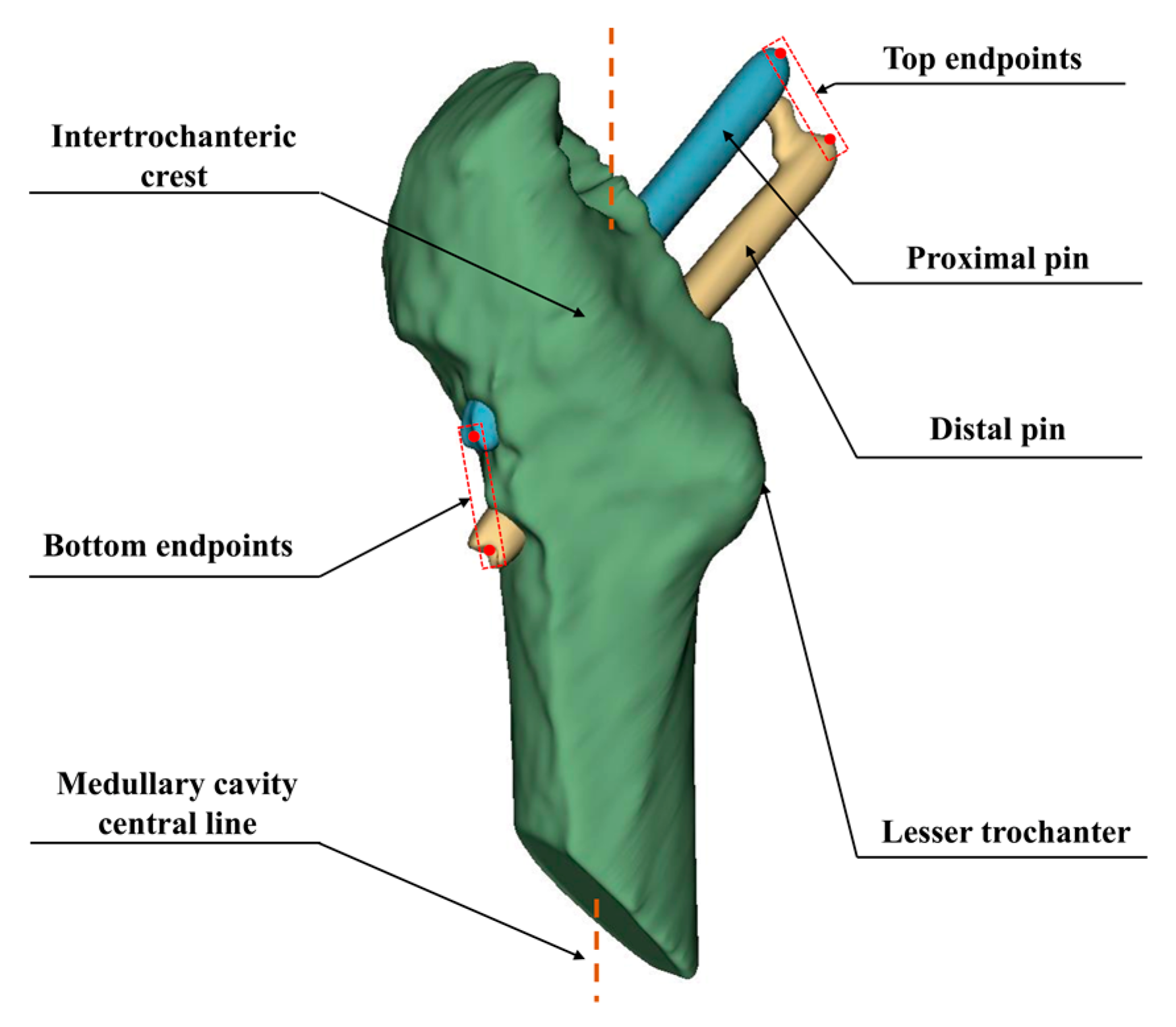
Based on the aligned CT images, the Hansson pins were reconstructed as a 3D model. We use the point cloud data to calculate the displacement distance after locating the endpoints of the pins. In this subsection, we apply the principal component analysis method to fit the pins’ axes, as shown in
Figure 8. The point cloud size and the obtained axes are used to draw the outer envelope of the pins, and the point intersecting the envelope in the direction of the axes is the endpoint of the pins.
The principal component analysis is a multivariate statistical method commonly used for dimensionality reduction of multidimensional data [
28]. The main principle is that the m-dimensional feature vector is mapped to the n-dimensional vector using the orthogonal transformation. This n-dimensional vector is an orthogonal vector constructed based on the original features, where the first vector is the direction with the most considerable variance in the original data.
The algorithm is:
We define a single point in the point cloud as
. The point cloud can be represented as a sample set
, by inputting
into the PCA algorithm above, we solve the feature vectors (
) and form the orthogonal matrix
after standard orthogonalization of each feature vector.
,
, and
are the main directions of the input point cloud, and the center of mass of the point cloud is taken as the origin of the new coordinate system. Using the point cloud’s center of mass as the origin of the coordinate system,
,
, and
as the axes to form the coordinate system shown in
Figure 8, where
is the blue axis,
, is the green axis, and
is the blue axis. The original point cloud data is converted to the new coordinate system using Equation (7). Subsequently, the red enclosing box is constructed according to the point cloud’s maximum and minimum values in the three directions of
X,
Y, and
Z.