Principal Component Wavelet Networks for Solving Linear Inverse Problems
Abstract
:1. Introduction
2. Literature Review
2.1. Deep Learning Based Techniques
2.2. Image Representations
- The filters are learnt from the data, rather than hard coded, usually by a back-propagation algorithm.
- The number of filters is generally much larger than in wavelet analysis.
- The high-pass subbands are themselves subjected to further rounds of filtering.
- Non-linear components are generally introduced, such as ReLU activation functions and max pooling operators.
- Inversion generally requires the training of a separate decoder network, although reversible networks do exist [22].
3. Aims and Contributions
- The introduction of Principal Component Wavelet Networks (PCWNs) and the demonstration that the resulting architecture is equivalent to a CNN.
- An inversion algorithm, which allows the trained networks to be used as an autoencoder.
- An example application to linear inverse problems, where the proposed networks show good potential, outperforming the original OnetNet [12] on 6 out of 9 tasks and showing state-of-the-art performance for a general purpose solution on three tasks (superresolution for face images, and pixelwise inpaint denoising and scattered inpainting on ImageNet).
4. Method: Decomposition, Training and Reconstruction
4.1. Decomposition Algorithm
4.2. Training Algorithm
4.3. Reconstruction Algorithm
| Algorithm 1: Overview of the training algorithm |
 |
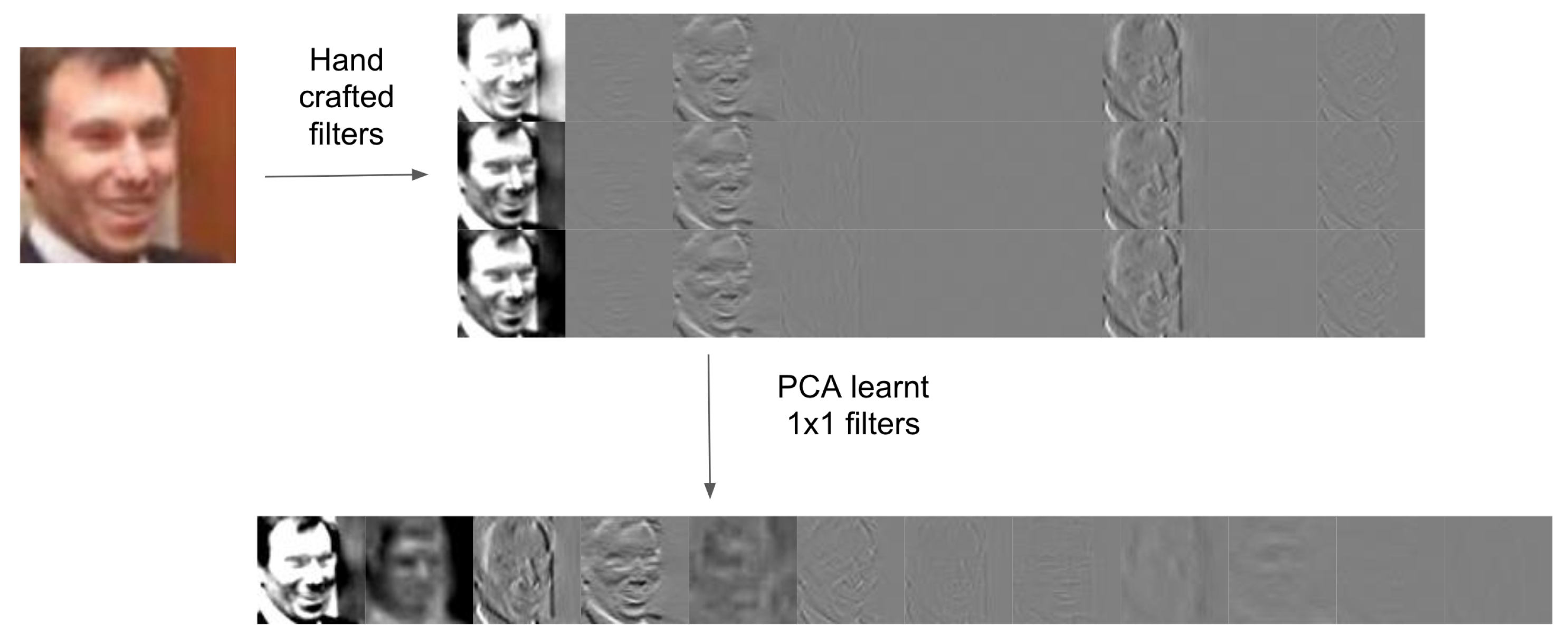
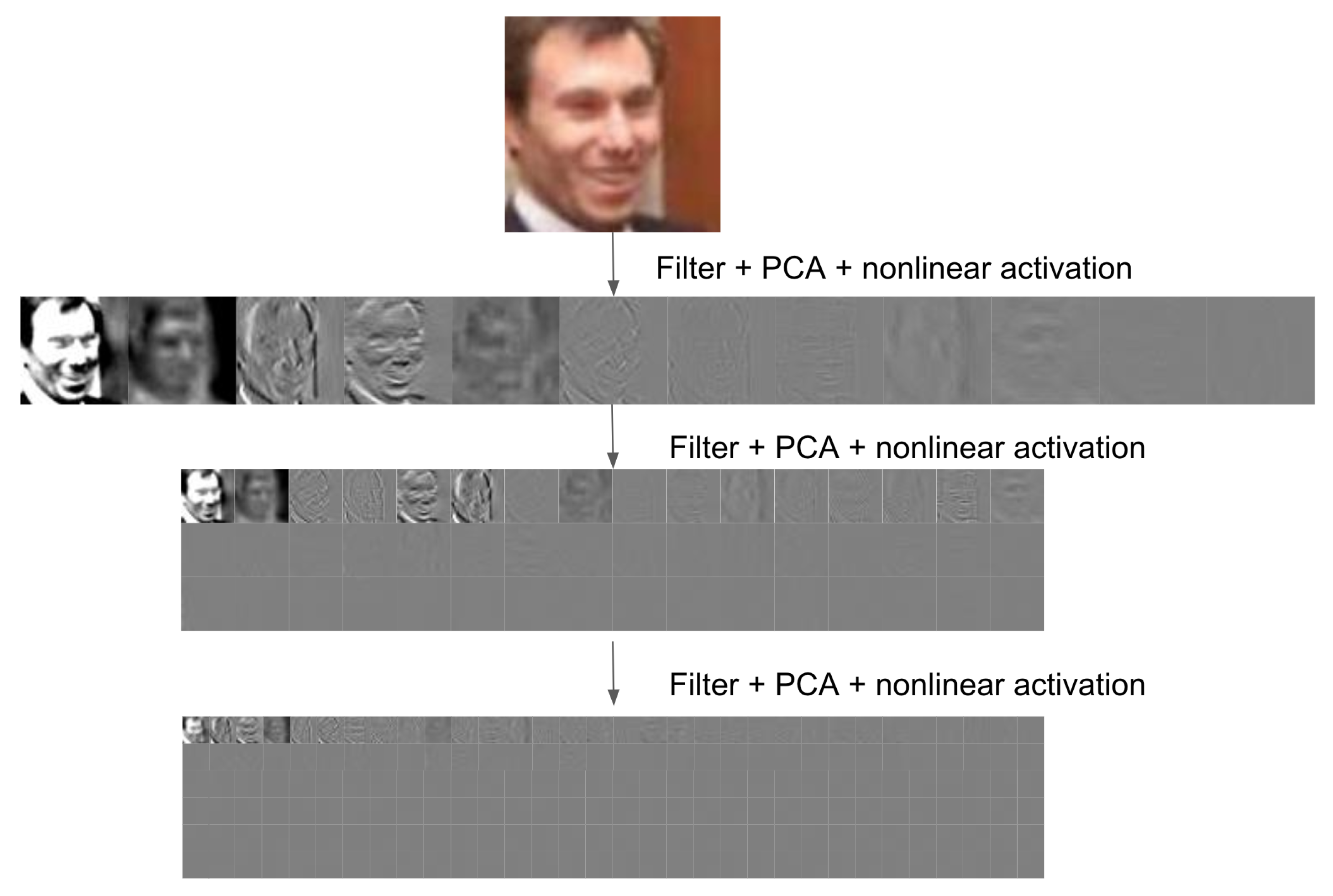
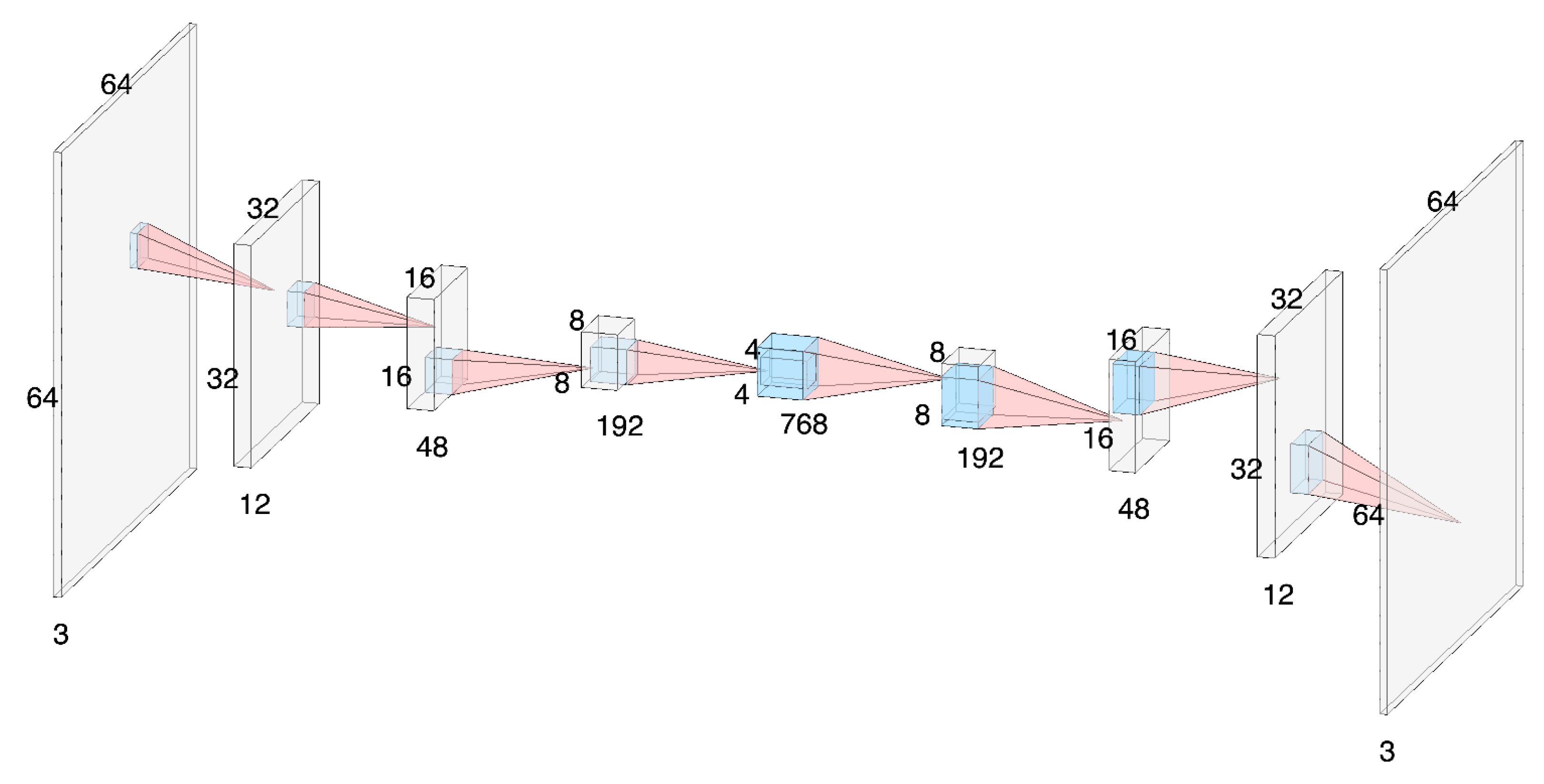
4.4. Discussion of Architecture
4.5. Computational Complexity
4.6. Implementation
5. Example Application: Linear Inverse Problems
Integration with ADMM
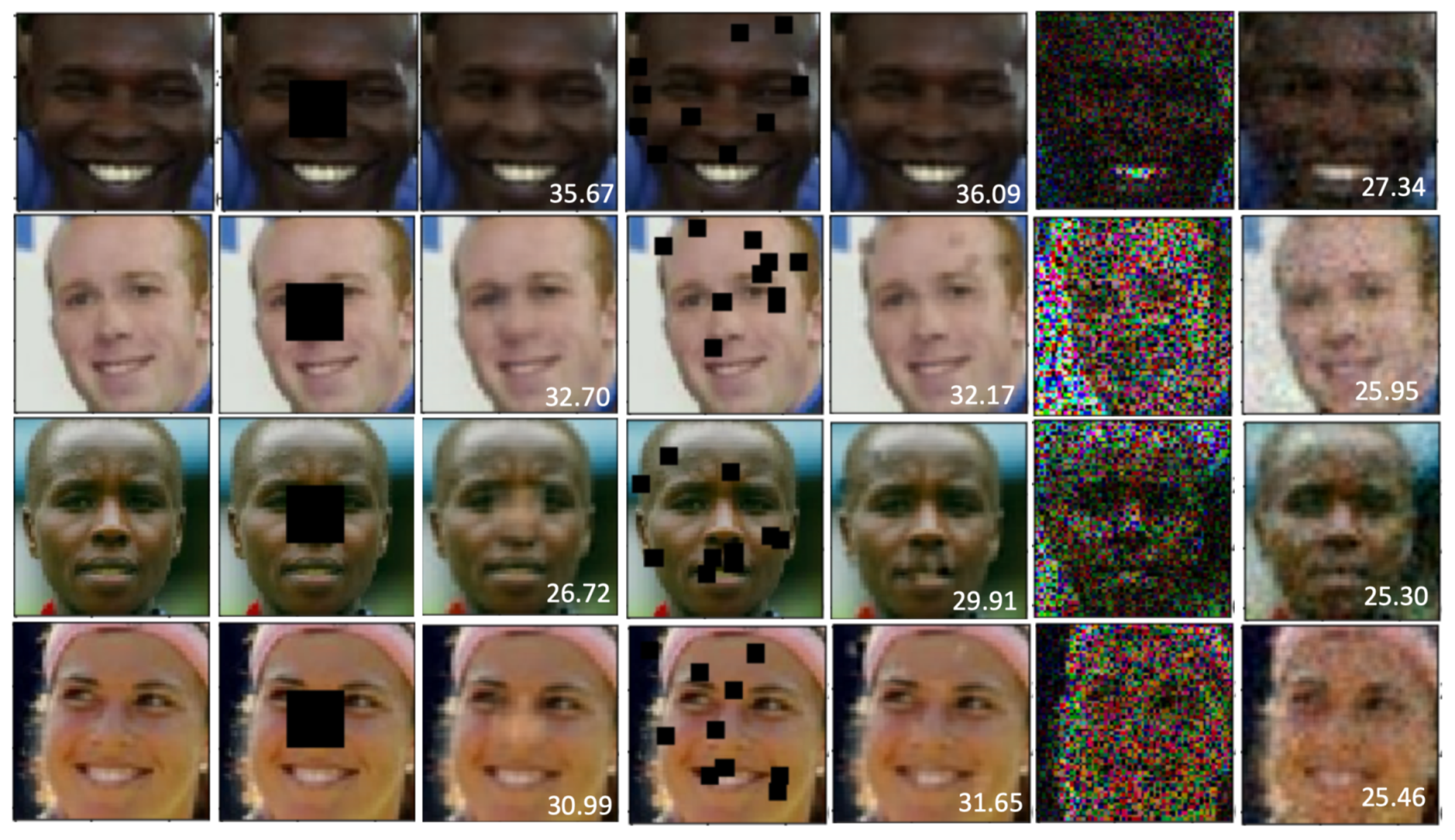
6. Experiments
- The face images used previously for testing and training were a random subset of the dataset, so even if we used the same dataset they wouldn’t necessarily be the same images.
- They are both celebrity face images, of the same resolution, scraped off the web, so should be comparable.
- Deep learning usually benefits from using more data (to avoid overfitting), so arguably we are setting ourselves a harder task or, alternatively, demonstrating that our method is more resistant to overfitting.
Results
7. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Donoho, D.L. De-noising by soft-thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef] [Green Version]
- Portilla, J.; Strela, V.; Wainwright, M.J.; Simoncelli, E.P. Image denoising using scale mixtures of Gaussians in the wavelet domain. IEEE Trans. Image Process. 2003, 12, 1338–1351. [Google Scholar] [CrossRef] [Green Version]
- Mairal, J.; Sapiro, G.; Elad, M. Learning multiscale sparse representations for image and video restoration. Multiscale Model. Simul. 2008, 7, 214–241. [Google Scholar] [CrossRef] [Green Version]
- Chan, T.F.; Shen, J.; Zhou, H.M. Total variation wavelet inpainting. J. Math. Imaging Vis. 2006, 25, 107–125. [Google Scholar] [CrossRef]
- Dong, W.; Zhang, L.; Shi, G.; Wu, X. Image deblurring and super-resolution by adaptive sparse domain selection and adaptive regularization. IEEE Trans. Image Process. 2011, 20, 1838–1857. [Google Scholar] [CrossRef] [Green Version]
- Pathak, D.; Krahenbuhl, P.; Donahue, J.; Darrell, T.; Efros, A.A. Context encoders: Feature learning by inpainting. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2536–2544. [Google Scholar]
- Mousavi, A.; Baraniuk, R.G. Learning to invert: Signal recovery via deep convolutional networks. In Proceedings of the 2017 IEEE international conference on acoustics, speech and signal processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 2272–2276. [Google Scholar]
- Kulkarni, K.; Lohit, S.; Turaga, P.; Kerviche, R.; Ashok, A. Reconnet: Non-iterative reconstruction of images from compressively sensed measurements. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 449–458. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 184–199. [Google Scholar]
- Xu, L.; Ren, J.S.; Liu, C.; Jia, J. Deep convolutional neural network for image deconvolution. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 1790–1798. [Google Scholar]
- Rick Chang, J.; Li, C.L.; Poczos, B.; Vijaya Kumar, B.; Sankaranarayanan, A.C. One Network to Solve Them All–Solving Linear Inverse Problems Using Deep Projection Models. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 5888–5897. [Google Scholar]
- Lucic, M.; Kurach, K.; Michalski, M.; Bousquet, O.; Gelly, S. Are GANs Created Equal? A Large-Scale Study. In Proceedings of the 32nd International Conference on Neural Information Processing Systems (NIPS’18), Montreal, QC, Canada, 3–8 December 2018; Curran Associates Inc.: Red Hook, NY, USA, 2018; pp. 698–707. [Google Scholar]
- Arjovsky, M.; Bottou, L. Towards Principled Methods for Training Generative Adversarial Networks. In Proceedings of the 5th International Conference on Learning Representations (ICLR 2017), Toulon, France, 24–26 April 2017. [Google Scholar]
- Milacski, Z.A.; Póczos, B.; Lorincz, A. Differentiable Unrolled Alternating Direction Method of Multipliers for OneNet. In Proceedings of the British Machine Vision Conference, Cardiff, UK, 9–12 September 2019. [Google Scholar]
- Raj, A.; Li, Y.; Bresler, Y. GAN-Based Projector for Faster Recovery With Convergence Guarantees in Linear Inverse Problems. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 5601–5610. [Google Scholar]
- Mallat, S. A Wavelet Tour of Signal Processing, 3rd ed.; Academic Press: Cambridge, MA, USA, 2008; pp. 1–832. [Google Scholar]
- Freeman, W.T.; Adelson, E.H. The design and use of steerable filters. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 891–906. [Google Scholar] [CrossRef]
- Kingsbury, N. Complex wavelets for shift invariant analysis and filtering of signals. J. Appl. Comput. Harmon. Anal. 2001, 10, 234–253. [Google Scholar] [CrossRef] [Green Version]
- Selesnick, I.W.; Baraniuk, R.G.; Kingsbury, N.C. The dual-tree complex wavelet transform. IEEE Signal Process. Mag. 2005, 22, 123–151. [Google Scholar] [CrossRef] [Green Version]
- Selesnick, I.W. The double-density dual-tree DWT. IEEE Trans. Signal Process. 2004, 52, 1304–1314. [Google Scholar] [CrossRef]
- Kingma, D.P.; Dhariwal, P. Glow: Generative flow with invertible 1x1 convolutions. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 10215–10224. [Google Scholar]
- Bruna, J.; Mallat, S. Invariant Scattering Convolution Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1872–1886. [Google Scholar] [CrossRef] [Green Version]
- Oyallon, E.; Zagoruyko, S.; Huang, G.; Komodakis, N.; Lacoste-Julien, S.; Blaschko, M.; Belilovsky, E. Scattering networks for hybrid representation learning. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 2208–2221. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Angles, T.; Mallat, S. Generative networks as inverse problems with scattering transforms. arXiv 2018, arXiv:1805.06621. [Google Scholar]
- Gupta, M.R.; Jacobson, N.P. Wavelet Principal Component Analysis and its Application to Hyperspectral Images. In Proceedings of the 2006 International Conference on Image Processing, Las Vegas, NV, USA, 26–29 June 2006; pp. 1585–1588. [Google Scholar] [CrossRef]
- Feng, G.C.; Yuen, P.C.; Dai, D.Q. Human face recognition using PCA on wavelet subband. J. Electron. Imaging 2000, 9, 226–233. [Google Scholar]
- Naik, G.R.; Pendharkar, G.; Nguyen, H.T. Wavelet PCA for automatic identification of walking with and without an exoskeleton on a treadmill using pressure and accelerometer sensors. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 1999–2002. [Google Scholar] [CrossRef] [Green Version]
- Chan, T.H.; Jia, K.; Gao, S.; Lu, J.; Zeng, Z.; Ma, Y. PCANet: A simple deep learning baseline for image classification? IEEE Trans. Image Process. 2015, 24, 5017–5032. [Google Scholar] [CrossRef] [Green Version]
- Kong, J.; Chen, M.; Jiang, M.; Sun, J.; Hou, J. Face recognition based on CSGF (2D) 2 PCANet. IEEE Access 2018, 6, 45153–45165. [Google Scholar] [CrossRef]
- Rick Chang, J.; Li, C.L.; Poczos, B.; Vijaya Kumar, B.; Sankaranarayanan, A.C. OneNet Tensorflow Implementation. Available online: https://github.com/rick-chang/OneNet/tree/master/admm (accessed on 17 February 2021).
- Wang, Y.; Yin, W.; Zeng, J. Global convergence of ADMM in nonconvex nonsmooth optimization. J. Sci. Comput. 2019, 78, 29–63. [Google Scholar] [CrossRef] [Green Version]
- Huang, G.B.; Ramesh, M.; Berg, T.; Learned-Miller, E. Labeled Faces in the Wild: A Database for Studying Face Recognition in Unconstrained Environments; Technical Report 07-49; University of Massachusetts: Amherst, MA, USA, 2007. [Google Scholar]
- Harvey, A.; LaPlace, J. MegaPixels: Origins, Ethics, and Privacy Implications of Publicly Available Face Recognition Image Datasets. 2019. Available online: https://megapixels.cc (accessed on 17 February 2021).
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef] [Green Version]
- Joshi, M.R.; Nkenyereye, L.; Joshi, G.P.; Islam, S.M.R.; Abdullah-Al-Wadud, M.; Shrestha, S. Auto-Colorization of Historical Images Using Deep Convolutional Neural Networks. Mathematics 2020, 8, 2258. [Google Scholar] [CrossRef]
- Rajendran, G.B.; Kumarasamy, U.M.; Zarro, C.; Divakarachari, P.B.; Ullo, S.L. Land-Use and Land-Cover Classification Using a Human Group-Based Particle Swarm Optimization Algorithm with an LSTM Classifier on Hybrid Pre-Processing Remote-Sensing Images. Remote Sens. 2020, 12, 4135. [Google Scholar] [CrossRef]
- Jäntschi, L. A Test Detecting the Outliers for Continuous Distributions Based on the Cumulative Distribution Function of the Data Being Tested. Symmetry 2019, 11, 835. [Google Scholar] [CrossRef] [Green Version]
- Jäntschi, L. Detecting Extreme Values with Order Statistics in Samples from Continuous Distributions. Mathematics 2020, 8, 216. [Google Scholar] [CrossRef] [Green Version]






| Filter | Filter Coefficients | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 4 | 6 | 4 | 1 | |||||
| 0 | −1 | 2 | −1 | 0 | |||||
| 0 | 1 | 0 | −1 | 0 | |||||
| 0 | 0 | 1 | 8 | 14 | 8 | 1 | 0 | 0 | |
| −1 | −8 | −20 | −56 | 170 | −56 | −20 | −8 | −1 | |
| 1 | 8 | 30 | 136 | 0 | −136 | −30 | −8 | −1 | |
| Input Size | Type/Stride | Filter Shape |
|---|---|---|
| Subtract mean | ||
| Conv2D/s2 | ||
| Conv2D/s2 | ||
| Conv2D/s2 | ||
| Conv2D/s2 | ||
| Decomposition | - | |
| Activation | - | |
| Conv2DTranspose/s2 | ||
| Conv2DTranspose/s2 | ||
| Conv2DTranspose/s2 | ||
| Conv2DTranspose/s2 | ||
| Add mean | ||
| Reconstruction | - |
| Method | BI | SR | PID | CS | SI |
|---|---|---|---|---|---|
| DU-ADMM | - | ||||
| OneNet | - | ||||
| Wavelet | - | ||||
| Ours |
| Method | BI | SR | PID | CS | SI |
|---|---|---|---|---|---|
| DU-ADMM | - | ||||
| OneNet | |||||
| Wavelet | |||||
| Ours |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tiddeman, B.; Ghahremani, M. Principal Component Wavelet Networks for Solving Linear Inverse Problems. Symmetry 2021, 13, 1083. https://doi.org/10.3390/sym13061083
Tiddeman B, Ghahremani M. Principal Component Wavelet Networks for Solving Linear Inverse Problems. Symmetry. 2021; 13(6):1083. https://doi.org/10.3390/sym13061083
Chicago/Turabian StyleTiddeman, Bernard, and Morteza Ghahremani. 2021. "Principal Component Wavelet Networks for Solving Linear Inverse Problems" Symmetry 13, no. 6: 1083. https://doi.org/10.3390/sym13061083
APA StyleTiddeman, B., & Ghahremani, M. (2021). Principal Component Wavelet Networks for Solving Linear Inverse Problems. Symmetry, 13(6), 1083. https://doi.org/10.3390/sym13061083






