Universal Approach for DEM Parameters Calibration of Bulk Materials
Abstract
1. Introduction
- Code dependence (depending on DEM software and contact model).
- A possibility for several sets of DEM parameters to provide similar bulk responses in the simulation.
- The need to significantly simplify the model (including the shape and size of particles) to speed up the calculation. Thus, the use of calibrated values of DEM parameters is limited, as well as their dependence on a specific application (technological process).
- Imperfection and inaccuracy of modern measuring tools (including visual estimation of the bulk material responses using machine vision).
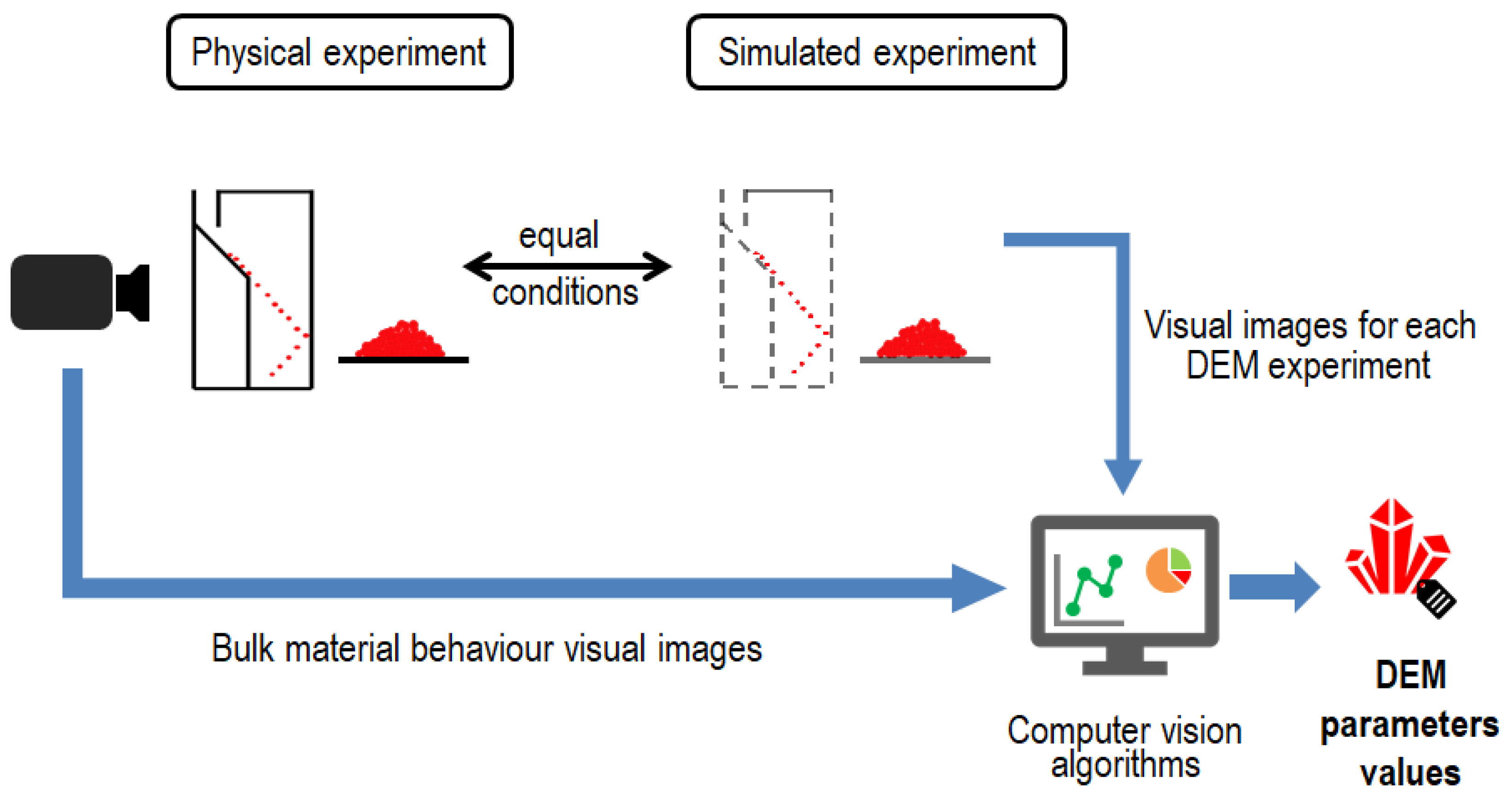
2. Materials and Methods
- For static friction (SF), this is the slope (tangent of the repose angle) at which the particle begins to slide over the surface (Figure 1a):
- For dynamic friction, the value is determined by the sliding time on a surface with a certain angle of repose (Figure 1a):
- For the coefficient of restitution, the value is determined by the angles and velocities of rupture and reflection (Figure 1b):
3. Results
3.1. Experiment Setup
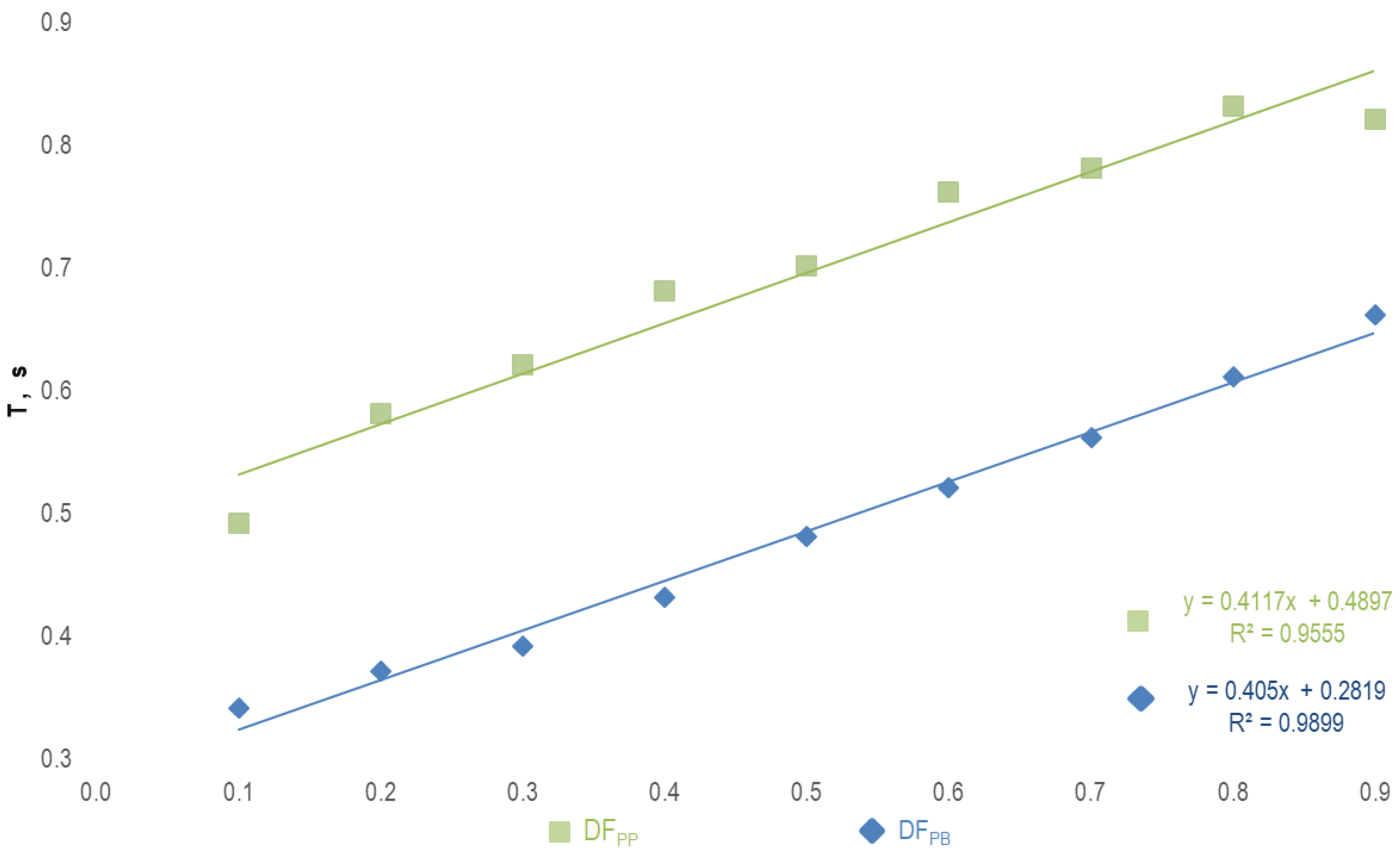
3.2. Determining DFPB and DFPP
3.3. Determining CoRPB and CoRPP
3.4. Determining SFPB and SFPP. Refinement of Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Sizyakov, V.M.; Vlasov, A.A.; Bazhin, V.Y. Strategic tasks of Russian metallurgical complex. Tsvetnye Met. 2016, 32–38. [Google Scholar] [CrossRef]
- Gospodarikov, A.P.; Vykhodtsev, Y.N.; Zatsepin, M.A. Mathematical modeling of seismic explosion waves impact on rock mass with a working. J. Min. Inst. 2017, 226, 405–411. [Google Scholar]
- Koteleva, N.; Frenkel, I. Digital Processing of Seismic Data from Open-Pit Mining Blasts. Appl. Sci. 2021, 11, 383. [Google Scholar] [CrossRef]
- Iakovleva, E.; Belova, M.; Soares, A. Allocation of potentially environmentally hazardous sections on pipelines. Geosciences 2021, 11, 1–11. [Google Scholar]
- Klyuev, R.; Bosikov, I.; Gavrina, O.; Madaeva, M.; Sokolov, A. Improving the energy efficiency of technological equipment at mining enterprises. Adv. Intell. Syst. Comput. 2021, 1258, 262–271. [Google Scholar]
- Kalala, J.T.; Breetzke, M.; Moys, M.H. Study of the influence of liner wear on the load behaviour of an industrial dry tumbling mill using the Discrete Element Method (DEM). Int. J. Miner. Process. 2008, 86, 33–39. [Google Scholar] [CrossRef]
- Wu, C.Y. DEM simulations of die filling during pharmaceutical tabletting. Particuology 2008, 6, 412–418. [Google Scholar] [CrossRef]
- Ye, F.; Wheeler, C.; Chen, B.; Hu, J.; Chen, K.; Chen, W. Calibration and verification of DEM parameters for dynamic particle flow conditions using a backpropagation neural network. Adv. Powder Technol. 2019, 30, 292–301. [Google Scholar] [CrossRef]
- Zhukovskiy, Y.L.; Suslikov, P.K.; Arapova, E.G.; Alieva, L.Z. Digital platform as a means of process optimization of integrating electric vehicles into electric power networks. J. Phys. Conf. Ser. 2020, 1661, 012162. [Google Scholar] [CrossRef]
- Yan, Z.; Wilkinson, S.K.; Stitt, E.H.; Marigo, M. Discrete element modelling (DEM) input parameters: Understanding their impact on model predictions using statistical analysis. Comput. Part. Mech. 2015, 2, 283–299. [Google Scholar] [CrossRef]
- Coetzee, C.J. Calibration of the discrete element method and the effect of particle shape. Powder Technol. 2016, 297, 50–70. [Google Scholar] [CrossRef]
- Westbrink, F.; Elbel, A.; Schwung, A.; Ding, S. Optimization of DEM Parameters using Multi-Objective Reinforcement Learning. Powder Technol. 2021, 309, 602–616. [Google Scholar] [CrossRef]
- Gröger, T.; André, K. On the numerical calibration of discrete element models for the simulation of bulk solids. Comput. Aided Chem. Eng. 2006, 21, 533–538. [Google Scholar]
- Do, H.Q.; Aragón, A.M.; Schott, D.L. A calibration framework for discrete element model parameters using genetic algorithms. Adv. Powder Technol. 2018, 29, 1393–1403. [Google Scholar] [CrossRef]
- Asaf, Z.; Rubinstein, D.; Shmulevich, I. Determination of discrete element model parameters required for soil tillage. Soil Tillage Res. 2007, 92, 227–242. [Google Scholar] [CrossRef]
- Zhao, S.; Zhou, X.; Liu, W. Discrete element simulations of direct shear tests with particle angularity effect. Granul. Matter 2015, 17, 793–806. [Google Scholar] [CrossRef]
- Turkia, S.; Wilke, D.; Pizette, P.; Govender, N.; Abriak, N. Benefits of virtual calibration for discrete element parameter estimation from bulk experiments. Granul. Matter 2019, 21, 110. [Google Scholar] [CrossRef]
- Frankowski, P.; Morgeneyer, M. Calibration and validation of DEM rolling and sliding friction coefficients in angle of repose and shear measurements. AIP Conf. Proc. 2013, 1542, 851–854. [Google Scholar]
- Zhou, H.; Hu, Z.; Chen, J.; Lv, X.; Xie, N. Calibration of DEM models for irregular particles based on experimental design method and bulk experiments. Powder Technol. 2018, 332, 210–223. [Google Scholar] [CrossRef]
- Ghodki, B.M.; Patel, M.; Namdeo, R.; Carpenter, G. Calibration of discrete element model parameters: Soybeans. Comput. Part. Mech. 2019, 6, 3–10. [Google Scholar] [CrossRef]
- Rackl, M.; Hanley, K.J. A methodical calibration procedure for discrete element models. Powder Technol. 2017, 307, 73–83. [Google Scholar] [CrossRef]
- Al-Hashemi, H.M.B.; Al-Amoudi, O.S.B. A review on the angle of repose of granular materials. Powder Technol. 2018, 330, 397–417. [Google Scholar] [CrossRef]
- Malone, K.F.; Xu, B.H. Determination of contact parameters for discrete element method simulations of granular systems. Particuology 2008, 6, 521–528. [Google Scholar] [CrossRef]
- El-Kassem, B.; Salloum, N.; Brinz, T.; Heider, Y.; Markert, B. A multivariate regression parametric study on DEM input parameters of free-flowing and cohesive powders with experimental data-based validation. Comput. Part. Mech. 2020, 8, 87–111. [Google Scholar] [CrossRef]
- Roessler, T.; Richter, C.; Katterfeld, A.; Will, F. Development of a standard calibration procedure for the DEM parameters of cohesionless bulk materials—Part I: Solving the problem of ambiguous parameter combinations. Powder Technol. 2019, 343, 803–812. [Google Scholar] [CrossRef]
- Boikov, A.V.; Savelev, R.V.; Payor, V.A. DEM Calibration Approach: Design of experiment. J. Phys. Conf. Ser. 2018, 1015, 032017. [Google Scholar] [CrossRef]
- Wang, L. Experimental determination of parameter effects on the coefficient of restitution of differently shaped maize in three-dimensions. Powder Technol. 2015, 284, 187–194. [Google Scholar] [CrossRef]
- Hlosta, J.; Žurovec, D.; Rozbroj, J.; Ramírez-Gómez, Á.; Nečas, J.; Zegzulka, J. Experimental determination of particle–particle restitution coefficient via double pendulum method. Chem. Eng. Res. Des. 2018, 135, 222–233. [Google Scholar] [CrossRef]
- Imre, B.; Räbsamen, S.; Springman, S.M. A coefficient of restitution of rock materials. Comput. Geosci. 2008, 34, 339–350. [Google Scholar] [CrossRef]
- Google Patents. Available online: https://patents.google.com/patent/RU168916U1/ru (accessed on 15 April 2021).
- Beloglazov, I.I.; Petrov, P.A.; Bazhin, V.Y. The concept of digital twins for tech operator training simulator design for mining and processing industry. Eurasian Min. 2020, 2020, 50–54. [Google Scholar] [CrossRef]
- Grigorev, M.B.; Tananykhin, D.S.; Poroshin, M.A. Sand management approach for a field with high viscosity oil. J. Appl. Eng. Sci. 2020, 18, 64–69. [Google Scholar] [CrossRef][Green Version]
- Morenov, V.; Leusheva, E. Influence of the solid phase’s fractional composition on the filtration characteristics of the drilling mud. Int. J. Eng. Trans. B Appl. 2019, 32, 794–798. [Google Scholar]
- Beloglazov, I.I.; Stepanyan, A.S.; Feoktistov, A.Y.; Yusupov, G.A. Disintegration process modeling for a jaw crusher with complex jaws swing. Obogashchenie Rud 2018, 2, 3–8. [Google Scholar] [CrossRef]
- Koteleva, N.; Buslaev, G.; Valnev, V.; Kunshin, A. Augmented reality system and maintenance of oil pumps. Int. J. Eng. Trans. B Appl. 2020, 33, 1620–1628. [Google Scholar]
- Vasilyeva, N.V.; Erokhina, O.O. Post-impact recovery coefficient calibration in DEM modeling of granular materials. Obogashchenie Rud 2020, 2020, 42–48. [Google Scholar] [CrossRef]










| Particle–Particle, PP | Particle–Boundary, PB | |
|---|---|---|
| Dynamic Friction (DF) | DFPP | DFPB |
| Static Friction (SF) | SFPP | SFPB |
| Coefficient of Restitution (CoR) | CoRPP | CoRPB |
| Parameter | Ore | Waste Rock | Boundary (Steel) |
|---|---|---|---|
| Poisson’s ratio | 0.3 | 0.3 | |
| Young modulus, kPa | 106 | 2.95 × 106 | |
| Density, kg/m3 | 3120 | 2700 | 7700 |
| Shape | 10-sided polyhedron | - | |
| Particle size, mm distribution | 100% 9.5—12.5 | - | |
| Contact model | Nonlinear Hertz–Mindlin | ||
| Gravity acceleration, m/s2 | 9.81 | ||
| Ore | Flow Time, s | |||
|---|---|---|---|---|
| Material/Experiment | I | II | III | Average |
| Steel 1 | 0.45 | 0.47 | 0.49 | 0.47 |
| Steel 2 | 0.47 | 0.45 | 0.46 | 0.46 |
| Steel 3 | 0.56 | 0.47 | 0.43 | 0.49 |
| Particle–particle | 0.54 | 0.6 | 0.57 | 0.57 |
| Waste Rock | Flow Time, s | |||
| Material/Experiment | I | II | III | Average |
| Steel 1 | 0.45 | 0.43 | 0.42 | 0.43 |
| Steel 2 | 0.46 | 0.48 | 0.47 | 0.47 |
| Steel 3 | 0.47 | 0.47 | 0.50 | 0.48 |
| Particle–particle | 0.59 | 0.56 | 0.52 | 0.56 |
| Ore | Steel 1 | Steel 2 | Steel 3 | |
|---|---|---|---|---|
| DFPB | - | 0.46 | 0.44 | 0.51 |
| DFPP | 0.20 | - | - | - |
| CoRPB | - | 0.29 | 0.31 | 0.35 |
| CoRPP | 0.35 | - | - | - |
| Waste Rock | Steel 1 | Steel 2 | Steel 3 | |
| DFPB | - | 0.37 | 0.46 | 0.49 |
| DFPP | 0.16 | - | - | - |
| CoRPB | - | 0.27 | 0.28 | 0.31 |
| CoRPP | 0.19 | - | - | - |
| Angle of Repose | Angle of Rupture | |||
|---|---|---|---|---|
| Simulation | Experiment | Simulation | Experiment | |
| Ore | 30 | 28 | 44 | 41 |
| Waste Rock | 34 | 35 | 42 | 38 |
| Ore | Steel 1 | Steel 2 | Steel 3 | |
|---|---|---|---|---|
| SFPB | - | 0.33 | 0.32 | 0.35 |
| SFPP | 0.26 | - | - | - |
| DFPB | - | 0.46 | 0.44 | 0.51 |
| DFPP | 0.20 | - | - | - |
| CoRPB | - | 0.29 | 0.31 | 0.35 |
| CoRPP | 0.35 | - | - | - |
| Waste Rock | Steel 1 | Steel 2 | Steel 3 | |
| SFPB | - | 0.31 | 0.32 | 0.33 |
| SFPP | 0.32 | - | - | - |
| DFPB | - | 0.37 | 0.46 | 0.49 |
| DFPP | 0.16 | - | - | - |
| CoRPB | - | 0.27 | 0.28 | 0.31 |
| CoRPP | 0.19 | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boikov, A.; Savelev, R.; Payor, V.; Potapov, A. Universal Approach for DEM Parameters Calibration of Bulk Materials. Symmetry 2021, 13, 1088. https://doi.org/10.3390/sym13061088
Boikov A, Savelev R, Payor V, Potapov A. Universal Approach for DEM Parameters Calibration of Bulk Materials. Symmetry. 2021; 13(6):1088. https://doi.org/10.3390/sym13061088
Chicago/Turabian StyleBoikov, Aleksei, Roman Savelev, Vladimir Payor, and Alexander Potapov. 2021. "Universal Approach for DEM Parameters Calibration of Bulk Materials" Symmetry 13, no. 6: 1088. https://doi.org/10.3390/sym13061088
APA StyleBoikov, A., Savelev, R., Payor, V., & Potapov, A. (2021). Universal Approach for DEM Parameters Calibration of Bulk Materials. Symmetry, 13(6), 1088. https://doi.org/10.3390/sym13061088






