Quark Self-Energy and Condensates in NJL Model with External Magnetic Field
Abstract
:1. Introduction
2. The Gap Equations
2.1. NJL Model and Mean-Field Approximation
2.2. The Gap Equations
2.3. The Coupling Constant and Cut-Off Parameter
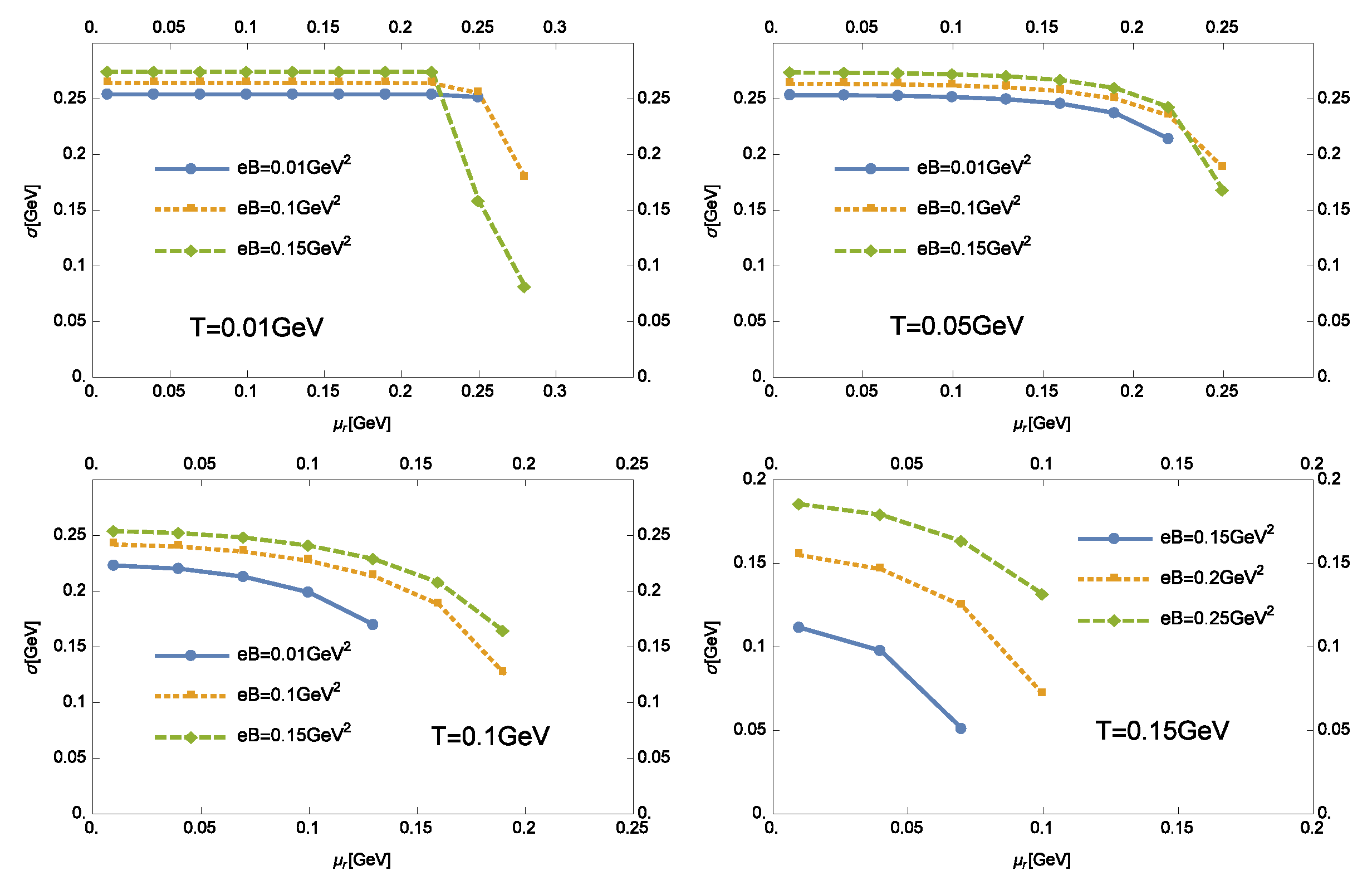
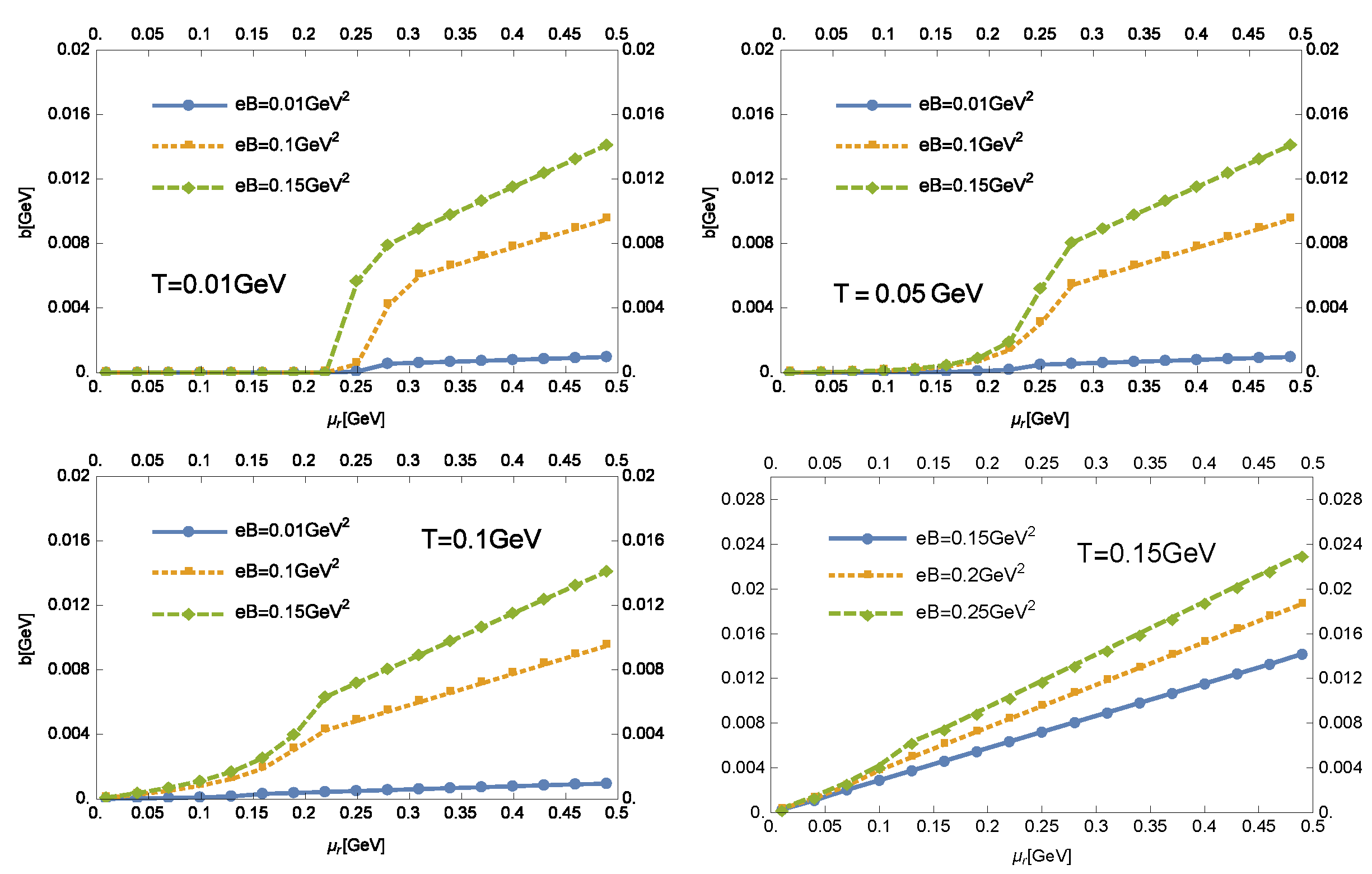
3. The Solutions of the Gap Equations
3.1. The Approximate Solutions in Chiral Symmetry Broken Phase
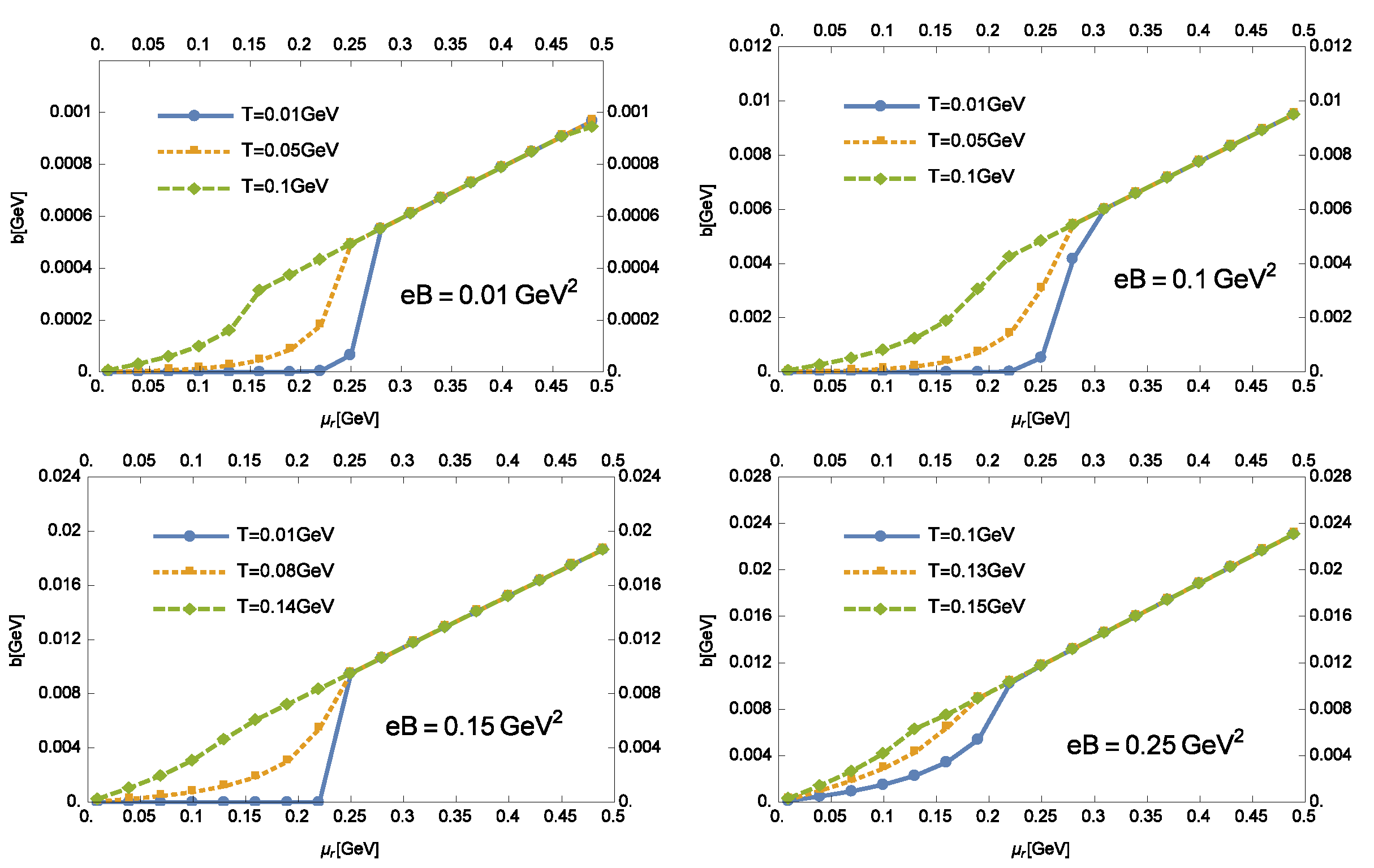
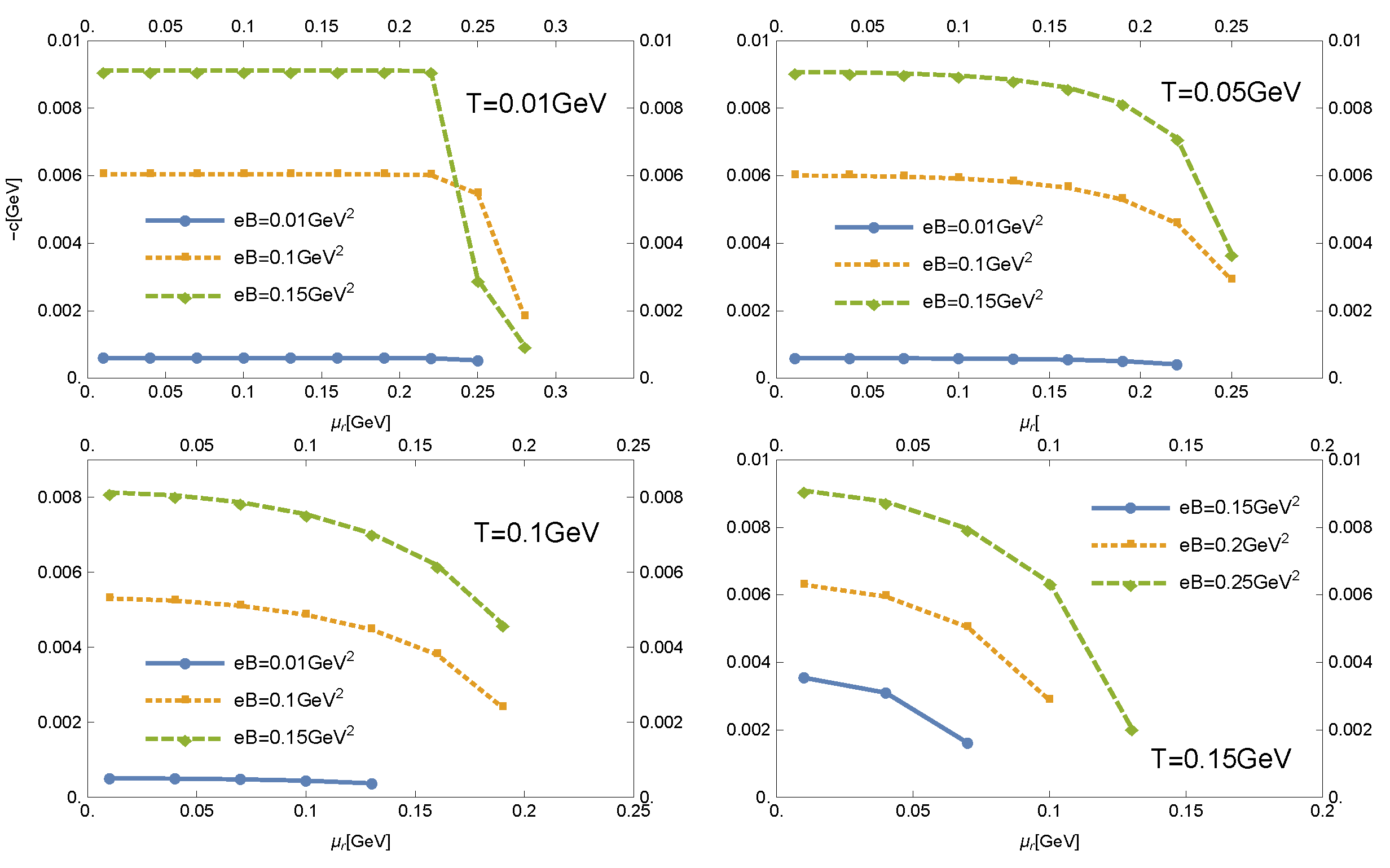
3.2. The Solutions in Chiral Symmetry Restored Phase
4. Conclusions and Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. The Properties of |m, p3; n, α〉
Appendix B. The Expressions of f1, f2, f3, f4
References
- Fukushima, K. Phase diagrams in the three-flavor Nambu–Jona-Lasinio model with the Polyakov loop. Phys. Rev. D 2008, 77, 114028. [Google Scholar] [CrossRef] [Green Version]
- Costa, P.; de Sousa, C.A.; Ruivo, M.C.; Kalinovsky, Y.L. The QCD critical end point in the SU(3) Nambu–Jona-Lasinio model. Phys. Lett. B 2007, 647, 431. [Google Scholar] [CrossRef] [Green Version]
- Shi, C.; Wang, Y.-L.; Jiang, Y.; Cui, Z.-F.; Zong, H.-S. Locate QCD critical end point in a continuum model study. J. High Energy Phys. 2014, 7, 014. [Google Scholar] [CrossRef] [Green Version]
- Zhao, A.-M.; Cui, Z.-F.; Jiang, Y.; Zong, H.-S. Nonlinear susceptibilities under the framework of Dyson-Schwinger equations. Phys. Rev. D 2014, 90, 114031. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.; Luo, L.-J.; Zong, H.-S. A model study of quark number susceptibility at finite temperature beyond rainbow-ladder approximation. J. High Energy Phys. 2011, 2, 66. [Google Scholar] [CrossRef] [Green Version]
- Xu, S.-S.; Cui, Z.-F.; Wang, B.; Shi, Y.-M.; Yang, Y.-C.; Zong, H.-S. Chiral phase transition with a chiral chemical potential in the framework of Dyson-Schwinger equations. Phys. Rev. D 2015, 91, 056003. [Google Scholar] [CrossRef] [Green Version]
- Fu, W.-J.; Zhang, Z.; Liu, Y.-X. 2+1 flavor Polyakov–Nambu–Jona-Lasinio model at finite temperature and nonzero chemical potential. Phys. Rev. D 2008, 77, 014006. [Google Scholar] [CrossRef] [Green Version]
- Kharzeev, D.E.; McLerran, L.D.; Warringa, H.J. The effects of topological charge change in heavy ion collisions: “Event by event P and CP violation”. Nucl. Phys. A 2008, 803, 227. [Google Scholar] [CrossRef] [Green Version]
- Gusynin, V.P.; Miransky, V.A.; Shovkovy, I.A. Dimensional reduction and dynamical chiral symmetry breaking by a magnetic field in 3+1 dimensions. Phys. Lett. B 1995, 349, 477. [Google Scholar] [CrossRef] [Green Version]
- Gusynin, V.P.; Miransky, V.A.; Shovkovy, I.A. Dynamical chiral symmetry breaking by a magnetic field in QED. Phys. Rev. D 1995, 52, 4747. [Google Scholar] [CrossRef] [Green Version]
- Ebert, D.; Klimenko, K.G.; Vdovichenko, M.A.; Vshivtsev, A.S. Magnetic oscillations in dense cold quark matter with four-fermion interactions. Phys. Rev. D 1999, 61, 025005. [Google Scholar] [CrossRef] [Green Version]
- Kharzeev, D.; Landsteiner, K.; Schmitt, A.; Yee, H.-U. Strongly Interacting Matter in Magnetic Fields. Lect. Notes Phys. 2013, 871, 13. [Google Scholar]
- Chodos, A.; Everding, K.; Owen, D.A. QED with a chemical potential: The case of a constant magnetic field. Phys. Rev. D 1990, 42, 2881. [Google Scholar] [CrossRef] [PubMed]
- Andersen, J.O.; Naylor, W.R.; Tranberg, A. Phase diagram of QCD in a magnetic field. Rev. Mod. Phys. 2016, 88, 025001. [Google Scholar] [CrossRef]
- Endrödi, G. Critical point in the QCD phase diagram for extremely strong background magnetic fields. J. High Energy Phys. 2015, 7, 173. [Google Scholar] [CrossRef]
- Bali, G.S.; Bruckmann, F.; Endrödi, G.; Fodor, Z.; Katz, S.D.; Schäfer, A. QCD quark condensate in external magnetic fields. Phys. Rev. D 2012, 86, 071502. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, S.; Mandal, S.; Chakrabarty, S. Chiral properties of the QCD vacuum in ultrastrong magnetic fields: A Nambu-Jona-Lasinio model with a semiclassical approximation. Phys. Rev. C 2007, 75, 015805. [Google Scholar] [CrossRef] [Green Version]
- Menezes, D.P.; Pinto, M.B.; Avancini, S.S.; Martínez, A.P. Quark matter under strong magnetic fields in the Nambu–Jona-Lasinio model. Phys. Rev. C 2009, 79, 035807. [Google Scholar] [CrossRef] [Green Version]
- Menezes, D.P.; Pinto, M.B.; Avancini, S.S.; Providência, C. Quark matter under strong magnetic fields in the su(3) Nambu–Jona-Lasinio model. Phys. Rev. C 2009, 80, 065805. [Google Scholar] [CrossRef] [Green Version]
- Shi, S.; Yang, Y.-C.; Xia, Y.-H.; Cui, Z.-F.; Liu, X.-J.; Zong, H.-S. Dynamical chiral symmetry breaking in the NJL model with a constant external magnetic field. Phys. Rev. D 2015, 91, 036006. [Google Scholar] [CrossRef] [Green Version]
- Du, Y.-L.; Cui, Z.-F.; Xia, Y.-H.; Zong, H.-S. Discussions on the crossover property within the Nambu–Jona-Lasinio model. Phys. Rev. D 2013, 88, 114019. [Google Scholar] [CrossRef] [Green Version]
- Cui, Z.-F.; Hou, F.-Y.; Shi, Y.-M.; Wang, Y.-L.; Zong, H.-S. Progress in vacuum susceptibilities and their applications to the chiral phase transition of QCD. Ann. Phys. 2015, 358, 172. [Google Scholar] [CrossRef] [Green Version]
- Du, Y.-L.; Lu, Y.; Xue, S.-S.; Cui, Z.-F.; Shi, C.; Zong, H.-S. Susceptibilities and critical exponents within the Nambu–Jona-Lasinio model. Int. J. Mod. Phys. A. 2015, 30, 1550199. [Google Scholar] [CrossRef]
- Lu, Y.; Du, Y.-L.; Cui, Z.-F.; Zong, H.-S. Critical behaviors near the (tri-)critical end point of QCD within the NJL model. Eur. Phys. J. C 2015, 75, 495. [Google Scholar] [CrossRef] [Green Version]
- Volkov, M.K.; Radzhabov, A.E. Forty-fifth anniversary of the Nambu-Jona-Lasinio model. arXiv 2005, arXiv:0508263v2. [Google Scholar]
- Asakawa, M.; Yazaki, K. Chiral restoration at finite density and temperature. Nucl. Phys. A 1989, 504, 668. [Google Scholar]
- Klevansky, S.P. The Nambu—Jona-Lasinio model of quantum chromodynamics. Rev. Mod. Phys. 1992, 64, 649. [Google Scholar] [CrossRef]
- Ferrer, E.J.; Incera, V.; Portillo, I.; Quiroz, M. New look at the QCD ground state in a magnetic field. Phys. Rev. D 2014, 89, 085034. [Google Scholar] [CrossRef] [Green Version]
- Creutz, M. One flavor QCD. Ann. Phys. 2007, 322, 1518. [Google Scholar] [CrossRef] [Green Version]
- Cahill, R.T.; Gunner, S.M. Global Colour Model of QCD and its Relationship to the NJL Model, Chiral Perturbation Theory and Other Models. Aust. J. Phys. 1997, 50, 103. [Google Scholar] [CrossRef] [Green Version]
- Buballa, M. NJL-model analysis of dense quark matter. Phys. Rep. 2005, 407, 205. [Google Scholar] [CrossRef] [Green Version]
- Kapusta, J.I.; Gale, C. Finite-Temperature Field Theory: Principles and Applications; Cambridge University Press: Cambridge, NY, USA, 1989; p. 50. [Google Scholar]
- Inagaki, T.; Kimura, D.; Murata, T. Four-Fermion Interaction Model in a Constant Magnetic Field at Finite Temperature and Chemical Potential. Prog. Theor. Phys. 2004, 111, 371. [Google Scholar] [CrossRef] [Green Version]
- Metlitski, M.A.; Zhitnitsky, A.R. Anomalous axion interactions and topological currents in dense matter. Phys. Rev. D 2005, 72, 045011. [Google Scholar] [CrossRef] [Green Version]
- Fukushima, K.; Kharzeev, D.E.; Warringa, H.J. Chiral magnetic effect. Phys. Rev. D 2008, 78, 074033. [Google Scholar] [CrossRef]
- Vilenkin, A. Equilibrium parity-violating current in a magnetic field. Phys. Rev. D 1980, 22, 3080. [Google Scholar] [CrossRef]
- Giovannini, M.; Shaposhnikov, M.E. Primordial hypermagnetic fields and the triangle anomaly. Phys. Rev. D 1998, 57, 2186. [Google Scholar] [CrossRef] [Green Version]
- Fukushima, K.; Morales, P.A. Spatial Modulation and Topological Current in Holographic QCD Matter. Phys. Rev. Lett. 2013, 111, 051601. [Google Scholar] [CrossRef] [Green Version]
- Maruyama, T.; Tatsumi, T. Ferromagnetism of nuclear matter in the relativistic approach. Nucl. Phys. A 2001, 693, 710. [Google Scholar] [CrossRef] [Green Version]
- Nakano, E.; Maruyama, T.; Tatsumi, T. Spin polarization and color superconductivity in quark matter. Phys. Rev. D 2003, 68, 105001. [Google Scholar] [CrossRef] [Green Version]
- Tatsumia, T.; Maruyama, T.; Nakano, E.; Nawa, K. Ferromagnetism in quark matter and origin of the magnetic field in compact stars. Nucl. Phys. A 2006, 774, 827. [Google Scholar] [CrossRef] [Green Version]
- Sakurai, J.J. Advanced Quantum Mechanics; Addison-Wesley: Reading, MA, USA, 1967; pp. 108–110. [Google Scholar]
- Ferreira, M.; Costa, P.; Lourenço, O.; Frederico, T.; Providência, C. Inverse magnetic catalysis in the (2+1)-flavor Nambu–Jona-Lasinio and Polyakov–Nambu–Jona-Lasinio models. Phys. Rev. D 2014, 89, 116011. [Google Scholar] [CrossRef] [Green Version]
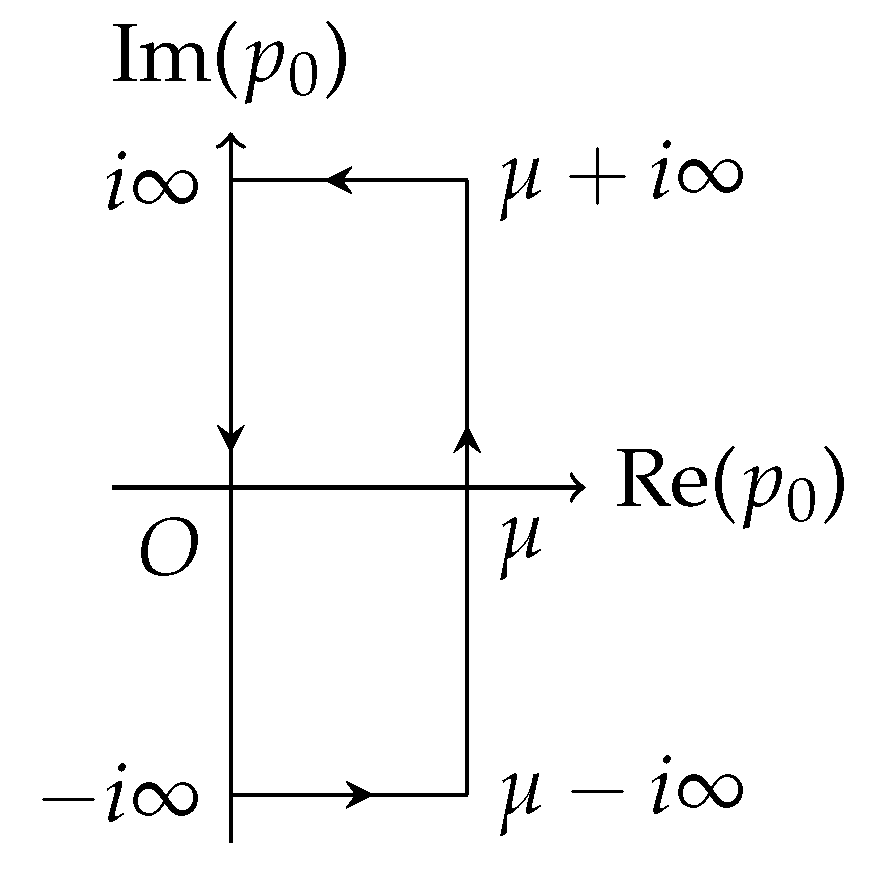
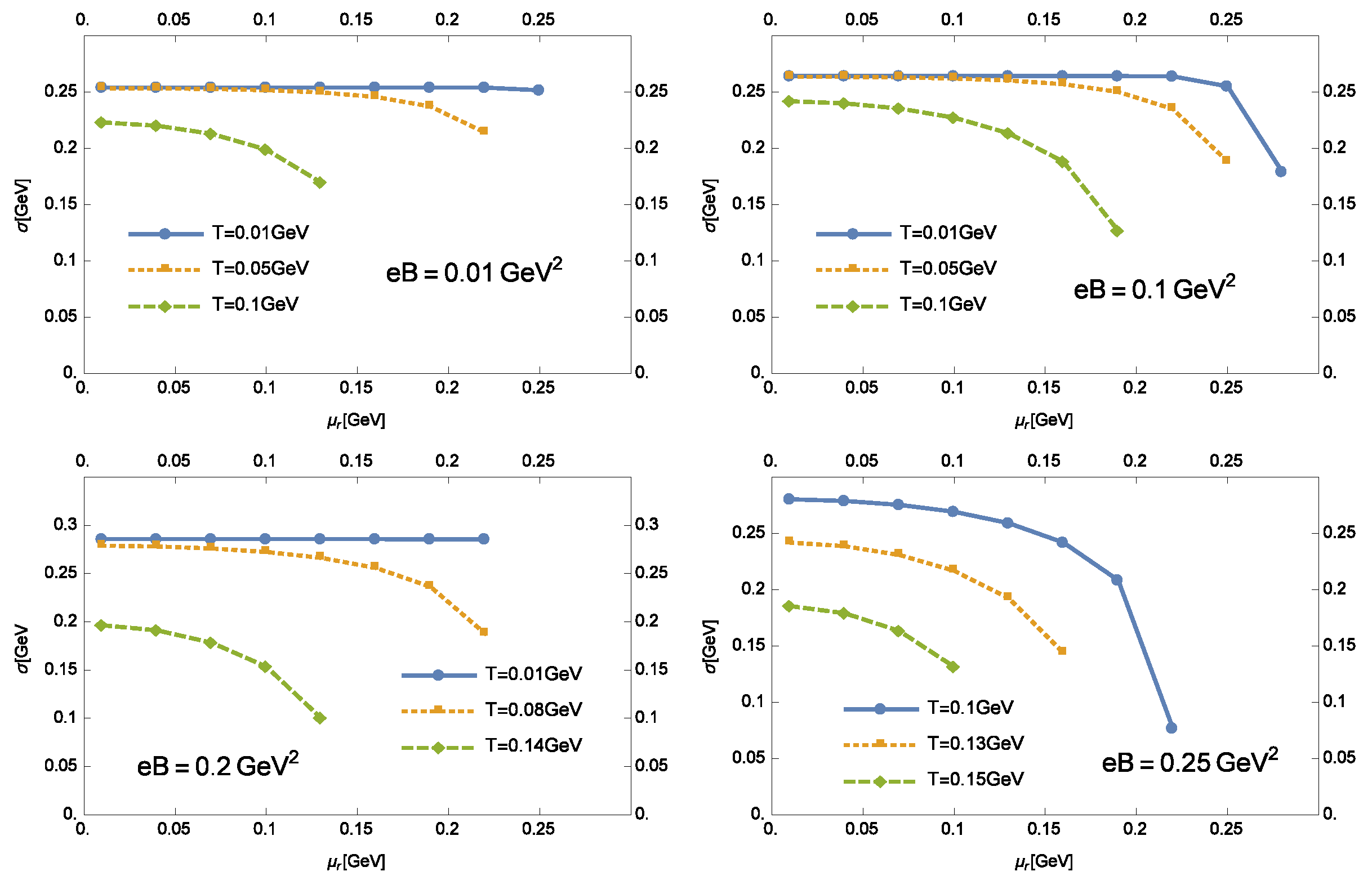
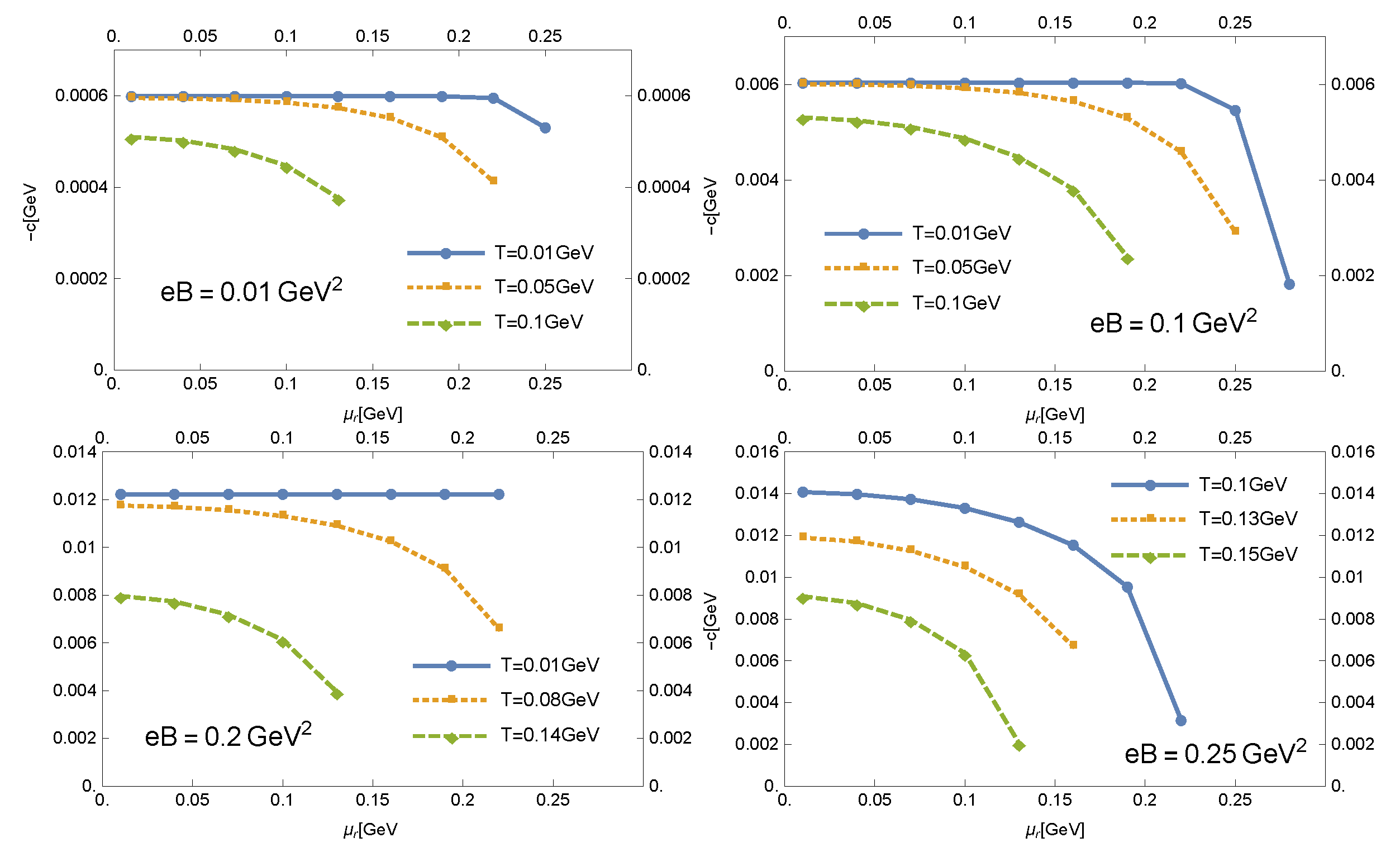
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Du, Y.; Shi, S. Quark Self-Energy and Condensates in NJL Model with External Magnetic Field. Symmetry 2021, 13, 1410. https://doi.org/10.3390/sym13081410
Liu J, Du Y, Shi S. Quark Self-Energy and Condensates in NJL Model with External Magnetic Field. Symmetry. 2021; 13(8):1410. https://doi.org/10.3390/sym13081410
Chicago/Turabian StyleLiu, Juan, Yilun Du, and Song Shi. 2021. "Quark Self-Energy and Condensates in NJL Model with External Magnetic Field" Symmetry 13, no. 8: 1410. https://doi.org/10.3390/sym13081410
APA StyleLiu, J., Du, Y., & Shi, S. (2021). Quark Self-Energy and Condensates in NJL Model with External Magnetic Field. Symmetry, 13(8), 1410. https://doi.org/10.3390/sym13081410





